Synergy of the catalytic activation on Ni and the CeO₂–TiO₂/Ce₂Ti₂O₇ stoichiometric redox cycle for dramatically enhanced solar fuel production

Abstract

Solar thermochemical approaches to CO₂ and H₂O splitting have emerged as an attractive pathway to solar fuel production. However, efficiently producing solar fuel with high redox kinetics and yields at lower temperature remains a major challenge. In this study, Ni promoted ceria–titanium oxide (CeO₂–TiO₂) redox catalysts were developed for highly effective thermochemical CO₂ and H₂O splitting as well as partial oxidation of CH₄ at 900 °C. Unprecedented CO and H₂ production rates and productivities of about 10–140 and 5–50 times higher than the current state-of-the-art solar thermochemical carbon dioxide splitting and water splitting processes were achieved with simultaneous close to complete CH₄ conversions and high selectivities towards syngas. The underlying mechanism for the exceptional reaction performance was investigated by combined experimental characterization and density functional theory (DFT) calculations. It is revealed that the metallic Ni and the Ni/oxide interface manifest catalytic activity for both CH₄ activation and CO₂ or H₂O dissociation, whereas CeO₂–TiO₂ enhances the lattice oxygen transport via the CeO₂–TiO₂/Ce₂Ti₂O₇ stoichiometric redox cycle for CH₄ partial oxidation and the subsequent CO₂ or H₂O splitting promoted by catalytically active Ni. Such findings substantiate the significance of the synergy between the reactant activation by catalytic sites and the stoichiometric redox chemistry governing oxygen ion transport, paving the way for designing prospective materials for sustainable solar fuel production.

---

Broader context

Solar energy, with tremendous potential as an environmentally sound and sustainable energy source, dwarfs all the derivative sources by a wide margin. The challenge, however, is to take full advantage of the abundant and infinite solar energy and to convert it into readily utilisable and storable forms. Solar thermochemical CO₂ and H₂O splitting, tapping sunlight directly and storing solar energy in renewable fuel, are emerging technologies towards meeting this goal. Successful adoption of solar-to-fuel technologies is predicated upon identifying advanced materials with higher efficiency. The present work demonstrates the application of novel Ni promoted ceria–titanium oxide redox catalysts for solar thermochemical CO₂ and H₂O splitting coupled with CH₄ partial oxidation, which exhibit considerably higher CO and H₂ production rates and productivities than the conventional solar thermochemical CO₂ and H₂O splitting processes with ∼100% CH₄ utilization. Supported by detailed experimental characterization and DFT calculations, a synergism between the catalytic activation on Ni and the CeO₂–TiO₂/Ce₂Ti₂O₇ stoichiometric redox cycle is shown to be responsible for the high efficiency of CO₂ and H₂O splitting as well as CH₄ conversion. These findings provide fundamental insights into the mechanisms underlying the remarkable reactivity and constitute a basis for engineering efficient materials for enhanced solar energy conversion.

1. Introduction

Access to carbon-neutral, affordable and sustainable energy sources is widely recognized as the cornerstone of sustained economic growth and increasing prosperity of modern society.^1,2 Solar-based routes hold great promise given sunlight's infinite abundance and accessibility, since the annual sunlight striking the earth (∼120 000 TW) is far exceeding the world energy consumption rate (estimated at ∼43 TW by 2100).^2–5 Solar fuel production via two-step solar thermochemical carbon dioxide splitting (STCDS) and water splitting (STWS) is an attractive alternative to artificial photosynthesis, biomass production and conversion, and photovoltaic-driven electrolysis in particular as it can be potentially more energy efficient and require less land and water to implement.^6,7 In the two-step redox cycle, the metal oxide is first reduced at low oxygen partial pressures and elevated temperatures (above 1400 °C) utilizing concentrated solar energy. Following thermal reduction, the oxygen deficient metal oxide is re-oxidized at lower temperatures (below 1100 °C) with CO₂ and/or H₂O, yielding CO and/or H₂. Although extensive research efforts have been devoted to two-step STCDS and STWS processes,^8–12 challenges associated with rather high operating temperatures,^8,9 limited fuel yields restricted by the thermodynamics,¹⁰ and thermal shocks induced by temperature swing⁸ greatly hamper their practical implementation.

Alternatively, introducing reducing agents such as methane,^13,14 syngas¹⁵ or hydrogen^16–19 notably lowers the external oxygen partial pressure, thereby facilitating lattice oxygen extraction from metal oxides. Among them, methane (the main constituent of natural gas) is particularly attractive as an economically accessible primary energy source, albeit it has shown poor reactivity with metal oxides compared to syngas or hydrogen. Integrating partial oxidation of methane into the reduction step allows for operating the redox cycle isothermally at significantly lower temperatures (800–1100 °C)^13,14,20,21 with higher fuel yields and a theoretically predicted solar-to-fuel efficiency greater than 45%,^22–24 hence increasing the practicality of these processes. A schematic diagram of two-step STCDS and STWS processes coupled with methane driven reduction (MDR) is illustrated in Fig. 1. In the endothermic MDR step, the lattice oxygen of the redox metal oxide is well exploited in partial oxidation of CH₄, generating syngas with a suitable H₂ : CO ratio for downstream methanol or Fischer–Tropsch synthesis. In the subsequent exothermic oxidation step, the lattice oxygen abstracted by CH₄ is replenished by CO₂ and/or H₂O splitting, producing concentrated CO and/or H₂. The overall reaction is highly endothermic, thus permitting efficient storage of solar energy in chemical form (CO, H₂).²²

Fig. 1 Schematic of two-step solar thermochemical carbon dioxide splitting and water splitting processes coupled with methane driven reduction (MDR-STCDS, MDR-STWS).

The metal oxides function as the redox intermediates to store and deliver oxygen ions in between the MDR and the following CO₂ (H₂O) splitting step. Therefore, the thermodynamic and kinetic properties of the metal oxides dictate the techno-economic feasibility of two-step MDR-STCDS and MDR-STWS technologies. Among the various redox metal oxides developed, iron- and ceria-based oxides have attracted significant attention.^{13,14,21,23–26} Iron oxide represents a very promising candidate by virtue of its earth abundance, low cost and minimal environmental impact.²⁶ Nevertheless, the poor reactivity with CH₄, low selectivity toward syngas, slow re-oxidation kinetics with CO₂ and H₂O and the susceptibility to sintering with successive redox cycles constitute significant drawbacks.^25,26 Recent studies indicated that the activity, selectivity and stability of iron-based oxides can be significantly enhanced promoted by tailored supports, such as lanthanum strontium ferrite (LSF)^13,14 and calcium manganese oxide (Ca_0.5Mn_0.5O).²¹ Unfortunately, the CO₂ or H₂O splitting kinetics was still far from satisfactory, which may render these processes less efficient.

In comparison to iron oxide, ceria is particularly attractive owing to its (i) rapid redox kinetics, (ii) excellent syngas selectivity, and (iii) robust structural and crystallographic stability.^{23,24,27–29} Nonetheless, the solar fuel yield is limited by the low ceria reduction extent (Ce⁴⁺ → Ce³⁺: 0.2–1.6 mol%) via the nonstoichiometric redox cycle (CeO₂ ↔ CeO_2−δ without phase transitions) and the inferior CH₄ reactivity (CH₄ conversion: 2–20%).²³ This is primarily due to the high activation energy required for lattice oxygen removal and the low surface activity for CH₄ activation. To address the aforementioned challenges, two potential strategies have been proposed. The first one is through doping or lattice site substitution (Ce_xZr_1−xO₂, Ce_xFe_1−xO₂, Ce_xHf_1−xO₂, etc.), in an attempt to introduce crystallographic defects that facilitate oxygen ion diffusion.^30–32 However, such metal doping approaches have achieved limited success in enhancing the ceria reduction extent and CH₄ reactivity based on nonstoichiometric chemistries. For example, Ce_0.8Zr_0.2O₂ solid solutions were evaluated for CH₄ partial oxidation and H₂O splitting at 800 °C, which exhibited restricted CH₄ conversions of 36–55% with Ce⁴⁺ reduction degrees ranging between 50% and 70%.³³ The second strategy is to promote CeO₂ with noble metal catalysts such as Pt and Pd.³⁴ While this remarkably decreased the activation energy for CH₄ partial oxidation at the gas–solid interface and enhanced the lattice oxygen consumption from the bulk, the cost-effectiveness and cycling stability of incorporating noble metals are debatable.

In the current work, we explore and demonstrate a new approach operating by stoichiometric redox chemistry. This novel chemistry enables a complete reduction of Ce⁴⁺ to Ce³⁺ with a reversible phase change (CeO₂–TiO₂ ↔ Ce₂Ti₂O₇), dramatically different from current metal oxide cycles utilizing oxygen non-stoichiometry in ceria. Note that stoichiometric redox chemistry has recently drawn significant attention in enhancing solar fuel production for two-step STCDS and STWS processes,^10,12,35 and in enhancing the robustness of catalysts via the unique phase transition for sorption enhanced steam reforming of bio-glycerol,³⁶ yet it is still rarely exploited in two-step MDR-STCDS and MDR-STWS processes. Furthermore, non-noble metal Ni was introduced to accelerated CH₄ partial oxidation, as it has been proposed in heterogeneous catalysis that metallic nickel has sufficient catalytic activity for CH₄ activation by lowering the dissociation barrier of C–H bond cleavage.^37,38 Encouragingly, the Ni promoted ceria–titanium oxide nanocomposite (CeO₂–TiO₂) developed here exhibited exceptional efficacy for CO₂ and H₂O splitting as well as partial oxidation of CH₄. One to two orders of magnitude higher CO/H₂ production rates and productivities were achieved as compared to the state-of-the-art STCDS/STWS and MDR-STCDS/MDR-STWS processes regarding CO₂ and H₂O splitting, and nearly complete CH₄ conversions with excellent syngas selectivities were achieved in the MDR step. By combining detailed experimental characterization of the physicochemical properties during the redox cycles with density functional theory (DFT) calculations, a synergistic effect between reduced Ni species and ceria–titanium oxide is suggested to be responsible for the superior CH₄ reactivity and CO₂ and H₂O splitting performance. Specifically, the metallic Ni and Ni/oxide interface act as active sites to lower the reaction barrier for CH₄ activation during reduction and accelerate CO₂ and H₂O dissociation kinetics during oxidation. On the other hand, the CeO₂–TiO₂ oxide solid compound serves as the reactive intermediates to transport active lattice oxygen for CH₄ partial oxidation and the subsequent CO₂ and H₂O splitting via the CeO₂–TiO₂/Ce₂Ti₂O₇ stoichiometric chemistry with a complete Ce⁴⁺ ↔ Ce³⁺ redox cycle readily accessible. The lower formation energies of oxygen vacancies on Ti-doped CeO₂ indicate that the incorporation of TiO₂ into CeO₂ weakens the Ce–O bonds and thus enhances the lattice oxygen transport. The combination of experimental investigation and theoretical calculations allows for a step forward in the understanding of the structure–activity relationship in designing highly promising candidates for solar fuel production applications.

2. Experimental section

2.1 Catalyst synthesis

The nickel-promoted ceria–titanium oxide catalysts were fabricated by a two-step synthesis approach. First, the ceria–titanium oxide solid compound (CeO₂–TiO₂) was synthesized, followed by deposition of nickel via a simple incipient wetness technique. The CeO₂–TiO₂ solid compound was prepared via a co-precipitation method. Briefly, stoichiometric amounts of Ce(NO₃)₃·6H₂O and (C₄H₉O)₄Ti were dissolved in 200 mL deionized water and 200 mL ethanol, respectively. The molar ratio of Ce⁴⁺ to Ti⁴⁺ was 1 : 1. Subsequently, the transparent solution was mixed under continuous stirring. Afterwards, a precipitating agent (NH₃·H₂O, 25%) was added dropwise to the mixed solution to adjust the pH to 9, keeping it at 80 °C for 3 h with stirring. The resulting precipitate was aged for another 1 h, filtered and washed thoroughly with deionized water. The washed precipitate was dried in an oven at 110 °C overnight, and subsequently calcined under stagnant air at 900 °C for 4 h (a heating rate of 5 °C min⁻¹). Finally, the calcined sample was ground into a fine powder using a mortar and pestle.

The supported nickel catalysts were synthesized by wet impregnation of the as-synthesized CeO₂–TiO₂ solid compound with an appropriate amount of Ni(NO₃)₂·6H₂O dissolved in deionized water. The obtained slurry was then dried in a vacuum at room temperature to evaporate excess moisture. Finally, the impregnated catalysts were dried at 110 °C overnight and annealed at 900 °C in air for 8 hours (a heating rate of 5 °C min⁻¹) to stabilize the structure properties. Catalysts with nominal Ni loadings of 5, 2, 1, and 0.5 wt% were prepared and are referred to as 5Ni/CeO₂–TiO₂, 2Ni/CeO₂–TiO₂, 1Ni/CeO₂–TiO₂, and 0.5Ni/CeO₂–TiO₂, respectively.

2.2 Reactivity investigation

Catalytic activity tests were carried out at atmospheric pressure in a differential quartz tube microreactor (10 mm i.d.) positioned in an infrared image furnace (VTH-E44, ULVAC-RIKO). Typically, 200 mg of the catalyst sample was sandwiched between two layers of quartz wool, and the temperature was measured with an alumina-shielded R-type thermocouple (±3.8 °C) in direct contact with the catalyst bed. The cyclic redox reactions were performed isothermally at 900 °C. Inlet gas flow rates were regulated by electronic mass flow controllers. In the MDR step, the catalysts were reduced using methane (1.5 mL min⁻¹) diluted in argon (148.5 mL min⁻¹) for 6 min. The following CO₂ or H₂O splitting reaction was initiated by introducing CO₂ (99.999%) or water vapor balanced with Ar (H₂O/Ar at yH₂O = 4.2 mol%) into the reactor at a total flow rate of 700 mL min⁻¹ for 10 min. The line for the steam to the reactor was heated to 150 °C to prevent H₂O condensation. In between each half cycle, the reactor was purged with Ar (500 mL min⁻¹) for 5–10 min to avoid poorly defined mixtures, thereby allowing clear determination of products from each segment. To initiate each experiment, several reduction–oxidation cycles were conducted until syngas production stabilized. Besides, preliminary experiments were also conducted to identify reduction durations to avoid coke formation. The outlet gas concentrations were constantly analyzed and recorded after condensation of H₂O via a calibrated quadrupole mass spectrometer (MS, GAM200 InProcess Instruments), and the effective volumetric flow rates (V_i) of observed species were determined. The MS signals were calibrated before each experiment using standard calibration gases. CH₄ was monitored at m/z 16, CO₂ at m/z 44 and 28, CO again at m/z 28, H₂ at m/z 2 and Ar at m/z 40. The fraction originating from CO₂ was subtracted from the signal at m/z 28 before the CO quantification. The CH₄ conversion (X_CH4), CO selectivity (S_CO) and H₂/CO molar ratio (R_H2/CO) during the reduction half-cycle were calculated using:


A carbon balance was performed to check the accuracy of the measurement and a maximum deviation of 5% was obtained for the reported experiments.

The transient CO or H₂ evolution rate during the oxidation half-cycle was calculated as:

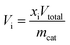where V_i denotes the volumetric rates of CO or H₂ produced per unit of mass of the catalyst; x_i denotes the mole fraction of CO or H₂ monitored by the mass spectrometer; V_total is the total volumetric flow rate regulated by the digital mass flow controller; and m_cat is the mass of the catalyst. The corresponding CO or H₂ yield was calculated by integrating the transient CO or H₂ evolution rate with respect to time.

2.3 Catalyst characterization

The catalysts were characterized at various stages (after synthesis, after CH₄ reduction, and after multicycle reactive tests) via thorough physical and chemical techniques. Powder X-ray diffraction (XRD) was performed to investigate the crystallographic phase evolution of the catalysts using a PANalytical diffractometer (40 kV, 40 mA), with Cu Kα radiation (λ = 1.5418 Å). The diffraction patterns were collected at ambient conditions between 2θ values of 20 and 70° with a step size of 0.02° and 30 s counting time per angle. The crystal phases were identified using the JCPDS database and the lattice spacing derived from the peak position was determined based on Bragg's diffraction law.

X-ray photoelectron spectroscopy (XPS) measurements were conducted on an ESCALAB 250 photoelectron spectrometer (Thermo Fisher Scientific, Al Kα, hν = 1486.6 eV) with a chamber pressure of 3 × 10⁻⁸ Pa to probe the near-surface element states. All binding energies were calibrated with respect to the C 1s peak centered at 284.8 eV. Deconvolution of the peaks was processed with the XPSPEAK program using Shirley background subtraction and a mix of Gaussian–Lorentzian functions.

The redox behavior of the catalysts was assessed via temperature-programmed reduction using H₂ (H₂-TPR) instead of CH₄ to avoid complications from possible carbon deposition. H₂-TPR measurements were carried out using Micromeritics Auto Chem II 2920 apparatus equipped with a thermal conductivity detector (TCD). In a typical experiment, approximately 0.1 g of the catalyst sample was loaded in a U-shape quartz tube. Pretreatment was carried out in flowing Ar (30 mL min⁻¹) at 350 °C for 30 min to eliminate water and gas adsorbed on the surface of the sample, followed by cooling down to 50 °C. Thereafter, TPR analysis was performed under 10% H₂/Ar (30 mL min⁻¹) up to 900 °C at a ramp rate of 10 °C min⁻¹.

High-resolution scanning electron microscopy (HRSEM; JSM-7800F, 1 kV accelerating voltage) was applied to observe the microstructure and morphology of the catalyst samples before and after redox cycles. High-resolution transmission electron microscopy (HRTEM) and scanning transmission electron microscopy combined with energy-dispersive X-ray spectroscopy (STEM-EDX) were employed to identify the morphology, crystallinity, and elemental distribution and composition of samples after various process steps. These techniques were implemented on a JEOL JEM-2200F microscope operated at 200 kV and with a linear resolution of 0.10 nm. Prior to the measurement, the samples were crushed into fine powders and dispersed ultrasonically in ethanol. After dispersion, a few droplets of each sample were deposited on a carbon coated Cu grid and allowed to dry.

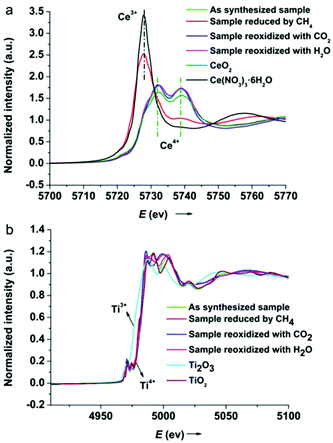
X-ray absorption near edge structure (XANES) experiments were carried out at the BL14W1 beamline of the Shanghai Synchrotron Radiation Facility (SSRF) with a ring current of 140–210 mA at 3.5 GeV. Samples (∼10 mg) diluted with BN (∼90 mg) were ground finely and pressed into self-supporting wafers for XANES measurements. Spectra were collected at the Ce L_III and Ti K edges in transmission mode with a Si(111) double-crystal monochromator. Reagent grade CeO₂ and Ce(NO₃)₃·6H₂O were used as Ce⁴⁺ and Ce³⁺ standards respectively, whereas TiO₂ (Degussa-P25) and Ti₂O₃ were used as Ti⁴⁺ and Ti³⁺ standards respectively. Data processing and analysis were performed with the Athena software program in a standard curve-fitting procedure.

Inductively coupled plasma atomic emission spectroscopy (ICP-AES) measurements were performed on an IRIS Intrepid II XSP instrument (Thermo Electron Corporation) to quantify the actual Ni loadings in the as-prepared catalysts.

2.4 Computational details

Electronic structure methods. All the spin-polarized DFT calculations were carried out using the Vienna Ab-initio Simulation Package (VASP).^39–41 The projected-augmented wave (PAW) pseudopotentials were utilized to describe the core electrons, and plane-wave basis sets with a kinetic energy cutoff of 400 eV were adopted to treat the valence electrons.⁴² The Perdew–Burke–Ernzerhof (PBE) exchange–correlation functional of the generalized gradient approximation (GGA) was used.⁴³ The k-point sampling was performed using the Monkhorst–Pack scheme,⁴⁴ and the meshes used for the bulk and surfaces are given in Table S1 (ESI†). The DFT + U method was used to treat the on-site Coulomb and exchange interactions of highly localized states in the d or f orbitals of the metal oxides.^45,46 An effective U = 4.5 eV was used for both the 4f orbital of Ce and 3d orbital of Ti in metal oxides, consistent with previous values in the studies of ceria⁴⁷ and titania.⁴⁸ All the structures were relaxed until the forces on each ion were less than 0.02 eV Å⁻¹, and the convergence criterion for the energy was set as 10⁻⁵ eV. The nudged elastic band combined with minimum-mode following dimer method was used to locate the transition state structure of the reaction.^49,50 All the transition state structures were identified by vibrational analysis.

Surface models. To study the catalytic activity of the 5Ni/CeO₂–TiO₂ catalyst, a series of surface models were used, including Ni(111), CeO₂(111), TiO₂(110), Ce₂Ti₂O₇(211), Ni/CeO₂(111), Ni/TiO₂(110) and Ni/Ce₂Ti₂O₇(211). The explicit surface structures are shown in Fig. S1 and S2 (ESI†). The optimized lattice constants of the corresponding metal and metal oxides are listed in Table S2 (ESI†). The Ni(111) surface was modelled as a four atomic layer slab of FCC Ni to mimic the active sites of Ni nanoparticles. The CeO₂(111) and TiO₂(110) surfaces were also represented using slab models to study the activity of CeO₂–TiO₂ metal oxide. The crystal structure of Ce₂Ti₂O₇ with a space group P21 was used⁵¹ and the metal oxide active sites were modelled using the Ce₂Ti₂O₇(211) surface. As the interface between Ni nanoparticles and the metal oxide support may also exhibit high activity for reactions,⁵² we built interface models for Ni/CeO₂(111), Ni/TiO₂(110) and Ni/Ce₂Ti₂O₇(211) as shown in Fig. S2 (ESI†). For all the metal–oxide interface sites, the close-packed Ni(111) surface was in contact with the metal oxide facets. The two-layer thick Ni nanorods with two-atom width were anchored on the top of the metal oxide surfaces. The appropriate designs of the Ni nanorod/oxide models bear only small lattice mismatches: 4.01% for Ni/CeO₂(111), 2.78% for Ni/TiO₂(110) and 0.83% for Ni/Ce₂Ti₂O₇(211), which avoids the large strain in the metal overlayers. Detailed structural parameters concerning the size of supercells, the number of atomic layers and the vacuum space of surface slabs etc. are provided in Table S3 (ESI†).

3. Results and discussion

3.1 Redox performance and stability

Since the feasibility of two-step MDR-STCDS and MDR-STWS processes is contingent upon satisfactory performance for CO₂ and H₂O splitting as well as CH₄ conversion, consecutive redox cycles were carried out to investigate the activity and stability of Ni/CeO₂–TiO₂ catalysts. Fig. 2a and b show the transient CO and H₂ formation rates during the CO₂ and H₂O splitting steps (indicated by the red curves) for 5Ni/CeO₂–TiO₂ after the isothermal MDR step, respectively. As can be seen, both reactions proceeded rapidly with extraordinary peak CO and H₂ evolution rates followed by a quick decay, indicating very fast CO₂ and H₂O splitting kinetics. The peak CO/H₂ production rates and CO/H₂ productivities reported here exceed virtually all of those reported in the STCDS/STWS, HDR-STCDS (H₂ driven reduction solar thermochemical CO₂ splitting)/HDR-STWS (H₂ driven reduction solar thermochemical H₂O splitting) and MDR-STCDS/MDR-STWS processes, as summarized in Tables S4 and S5 (ESI†). Specifically, 5Ni/CeO₂–TiO₂ showed unprecedented CO/H₂ production rates and total CO/H₂ yields of about 10–140 and 5–50 times higher than the state-of-the-art ceria-based materials and perovskites in conventional STCDS and STWS processes performed at significantly higher temperatures (above 1250 °C). Moreover, 5Ni/CeO₂–TiO₂ also far outperformed most redox materials in the MDR-STCDS/MDR-STWS processes and even in HDR-STCDS/HDR-STWS redox schemes. Note that no detectable amount of CO₂ or CO was observed during the H₂O splitting half-cycle (Fig. 2b), indicating that almost no carbon deposition occurred after the MDR step. To further disclose the impact of Ni species on the CO₂ and H₂O splitting performance, CeO₂–TiO₂ in the absence of Ni was chemically reduced with 1% H₂/Ar at 900 °C to ensure complete reduction. Subsequently, the completely reduced CeO₂–TiO₂ was subjected to CO₂ and H₂O splitting reactions at identical operating conditions as in the oxidation half cycle of two-step MDR-STCDS and MDR-STWS processes. As shown in Fig. 2a and b, it is evident that the reduced CeO₂–TiO₂ (indicated by the black curves) behaved significantly differently. The peak CO and H₂ production rates were less than 19% and 21% of the reduced 5Ni/CeO₂–TiO₂, with CO and H₂ evolution profiles being lower and broader, and it can be attributed to the considerably slower CO₂ and H₂O splitting kinetics over the reduced CeO₂–TiO₂. These results strongly suggest that the reduced Ni species substantially accelerated the catalytic splitting of CO₂ and H₂O, which will be discussed in detail in Section 3.3. In heterogeneous catalysis,^53–55 Heine et al.⁵⁵ also showed that CO₂ molecules could be activated on Ni(111) and dissociated into CO and atomic oxygen in the methanation reaction. Carrasco et al.⁵⁴ demonstrated that the strong electronic perturbations induced by nickel/ceria interactions could lead to an unexpectedly low H₂O dissociation activation barrier and thus faster dissociation of H₂O in the water-gas shift reaction as compared to bare CeO₂. Consecutive CO₂/H₂O splitting cycles verified the stability of the 5Ni/CeO₂–TiO₂ redox catalyst (see Fig. 2c and d), which showed reproducible kinetic curves of CO and H₂ evolution rates in the second and subsequent oxidation. The CO (Fig. 2c) or H₂ (Fig. 2d) productivity, estimated by integrating the corresponding transient CO or H₂ evolution rate with respect to time, stayed relatively constant over the course of 10 repetitive cycles. Interestingly, the CO or H₂ productivity was comparable to the theoretically expected value (44.5 mL CO/H₂ g⁻¹ assuming a full reduction to Ce³⁺) stoichiometrically available for complete oxidation of Ce³⁺ to Ce⁴⁺. These results might imply that the 5Ni/CeO₂–TiO₂ redox catalyst was completely reoxidized after the CO₂ or H₂O splitting step. The slightly excess amount of CO or H₂ above the theoretical maximum might result from the partial reoxidation of the reduced Ni species on the surface of 5Ni/CeO₂–TiO₂ with CO₂ or H₂O as no carbon was deposited.

Fig. 2 (a) Transient CO evolution rate during the CO₂ splitting half cycle for 5Ni/CeO₂–TiO₂ of the isothermal MDR-STCDS process at 900 °C, the CO evolution rate for CeO₂–TiO₂ reduced by H₂ is also shown. (b) Transient H₂ evolution rate during the H₂O splitting half cycle for 5Ni/CeO₂–TiO₂ of the isothermal MDR-STWS process at 900 °C, the H₂ evolution rate for CeO₂–TiO₂ reduced by H₂ is also shown. Transient CO and H₂ evolution rates for 5Ni/CeO₂–TiO₂ during the CO₂ and H₂O splitting half cycles of the isothermal (c) MDR-STCDS and (d) MDR-STWS processes over 10 redox cycles. The dashed horizontal lines give the theoretically expected quantities of CO and H₂, i.e., 44.5 mL CO/H₂ g⁻¹ for 5Ni/CeO₂–TiO₂ assuming a full reduction to Ce³⁺.

In regard to the MDR step, representative CH₄ isothermal reduction results are illustrated in Fig. 3a and b. For both processes, the as-prepared 5Ni/CeO₂–TiO₂ catalyst exhibited promising CH₄ conversions (>99%) with negligible CH₄ detected. As can be seen, the reaction between CH₄ and 5Ni/CeO₂–TiO₂ followed a similar pattern characterized by two distinct regions. The initial stage (region I) was dominated by complete oxidation of CH₄ to CO₂, which was typically attributed to oxygen derived from NiO and/or loosely bonded surface oxygen^56,57 on CeO₂–TiO₂. The second stage (region II) was dominated by partial oxidation of CH₄ to CO and H₂ by the strongly bonded bulk oxygen of CeO₂–TiO₂ that was sufficiently favored over the metallic nickel.⁵⁸ The amount of oxygen converted to CO for 5Ni/CeO₂–TiO₂ reached 36.3 mL g⁻¹ and 40.5 mL g⁻¹ in MDR-STCDS and MDR-STWS processes, respectively, which was close to the theoretical removable oxygen (44.5 mL g⁻¹) assuming a complete reduction from Ce⁴⁺ to Ce³⁺. Notably, the reaction of CeO₂–TiO₂ with CH₄ in the absence of Ni shows drastically different results. As evidenced in Fig. S3a (ESI†), the CH₄ concentration rapidly reached the nominal value during the reduction step in the MDR-STWS process with inferior CH₄ conversion (5.9%), and the amount of oxygen converted to CO was only 1.0 mL g⁻¹, indicating the bulk oxygen of CeO₂–TiO₂ remained largely unconsumed without Ni promotion. Additionally, the conversion of CH₄ using CeO₂–TiO₂ samples with different Ni loadings (0, 0.5, 1, 2 and 5 wt%) is illustrated in Fig. S3b (ESI†). It is evident that CH₄ conversion increased concurrently with increasing Ni content. The above observations reveal that the presence of Ni species is vital for catalyzing CH₄ activation, thereby enhancing the bulk oxygen consumption originating from CeO₂–TiO₂ and hence the partial oxidation of CH₄. The instantaneous gaseous product concentrations during the reduction of 5Ni/CeO₂–TiO₂ varied slightly among 10 isothermal MDR-STCDS and MDR-STWS cycles (Fig. S4a and b, ESI†), confirming that 5Ni/CeO₂–TiO₂ could be reduced with CH₄ repeatedly with high reproducibility. The corresponding catalytic performance of 5Ni/CeO₂–TiO₂ during CH₄ reduction is summarized in Fig. 3c and d, in terms of the CH₄ conversion (CH₄ Con), H₂/CO ratio, and CO selectivity (CO Sele). Remarkably, essentially complete conversions of CH₄ were achieved for both processes over the entire 10 redox cycles, with H₂ : CO ratios stabilized at ∼1.8 (Fig. 3c) and ∼1.9 (Fig. 3d), i.e., close to the typically desired ratio for downstream Fischer–Tropsch or methanol synthesis. The CO selectivity for 5Ni/CeO₂–TiO₂ in the isothermal MDR-STCDS and MDR-STWS processes amounted to ∼76 and ∼85%, respectively, which is most likely due to the different surface oxygen species as will be discussed later. To summarize, the extraordinary CO₂ and H₂O splitting performance and the superior CH₄ partial oxidation activity render 5Ni/CeO₂–TiO₂ a highly promising redox catalyst in the MDR-STCDS and MDR-STWS processes.

Fig. 3 Temporal gaseous product concentrations for 5Ni/CeO₂–TiO₂ during the CH₄ reduction half cycle of the isothermal (a) MDR-STCDS and (b) MDR-STWS processes at 900 °C. Average CH₄ conversion, CO selectivity and H₂/CO ratio for 5Ni/CeO₂–TiO₂ during the CH₄ reduction half cycle of the isothermal (c) MDR-STCDS and (d) MDR-STWS processes over 10 redox cycles.

3.2 Redox catalyst characterization

In order to elucidate the underlying reasons for the exceptional efficacy of the 5Ni/CeO₂–TiO₂ redox catalyst, various physicochemical characterization techniques complemented by detailed theoretical studies were applied to probe the redox chemistry and reaction pathways. Fig. 4 illustrates the XRD patterns of the 5Ni/CeO₂–TiO₂ redox catalyst at various stages (after synthesis, after the MDR step, and after multicycle reactive tests). As observed in Fig. 4a, the as synthesized sample exhibited distinct reflections characteristic of NiO, CeO₂, and TiO₂ (rutile, JCPDS 01-083-2242; brookite, JCPDS 01-076-1934), evidencing the solid state reactions between individual compounds remained negligible after the initial calcination process. Intriguingly, reflection peaks attributable to CeO₂ and TiO₂ completely disappeared for the reduced sample after the MDR step, accompanied by the emergence of new reflection peaks indexable to Ce₂Ti₂O₇ pyrochlore (JCPDS 00-047-0667) with decreased crystallinity (Fig. 4b). Additional peaks attributed to metallic Ni (JCPDS 00-001-1272) were also observed at about 2θ = 46.5° and 67.9° (Fig. 4b) with a crystallite size of 17.4 ± 0.8 nm determined by the Scherrer equation, which contributed essentially to CH₄ activation. On the contrary, no apparent structure change was identified for the CeO₂–TiO₂ sample in the absence of NiO, illustrating the negligible phase transformation of CeO₂–TiO₂ after the MDR step (Fig. S7, ESI†). Hence, it can be concluded that a stoichiometric reaction between CeO₂ and TiO₂ occurred for the 5Ni/CeO₂–TiO₂ catalyst after reducing with CH₄, forming Ce₂Ti₂O₇ pyrochlore promoted by the presence of Ni species. Meanwhile, catalytically active metallic Ni dispersed on Ce₂Ti₂O₇ pyrochlore was obtained after the reduction treatment. Furthermore, regeneration of CeO₂ and TiO₂ was clearly indicated by the XRD spectra of 5Ni/CeO₂–TiO₂ catalysts after isothermal MDR-STCDS and MDR-STWS redox cycling, where the peaks corresponding to Ce₂Ti₂O₇ pyrochlore totally vanished (Fig. 4c). Thus, it is evidenced that the transformation between Ce₂Ti₂O₇ pyrochlore and CeO₂ and TiO₂ mixed oxides was entirely reversible during the redox cycles, substantiating the excellent recyclability of the 5Ni/CeO₂–TiO₂ redox catalyst. Additionally, weak NiO peaks as well as the reduced metallic Ni were identified after the final CO₂ and H₂O reoxidation half cycle (Fig. 4c), confirming the surface oxidation of the reduced Ni species despite the bulk oxidation not being thermodynamically favorable.⁵⁹

Fig. 4 X-ray powder diffraction patterns of (a) as synthesized 5Ni/CeO₂–TiO₂, (b) 5Ni/CeO₂–TiO₂ after the CH₄ reduction half cycle and (c) 5Ni/CeO₂–TiO₂ after isothermal MDR-STCDS (up) and MDR-STWS (below) redox cycling at 900 °C. The following compounds were identified: (●) CeO₂, (*) TiO₂ (rutile), (✦) TiO₂ (brookite), (♥) NiO, (♠) Ni, () Ce₂Ti₂O₇ (JCPDS 00-047-0667) and () Ni (JCPDS 00-001-1272).

H₂-TPR experiments were performed to investigate the redox properties of the as synthesized 5Ni/CeO₂–TiO₂ and CeO₂–TiO₂ samples, together with those of TiO₂ and CeO₂ as references, and the results are presented in Fig. 5. TiO₂ exhibited no appreciable reduction in the temperature range of 100–900 °C. For CeO₂ two weak reduction peaks were observed. The first peak located at about 480 °C was generally ascribed to the reduction of surface capping oxygen,^60,61 and the second peak centered at about 800 °C was related to the removal of bulk lattice oxygen,^60,61 which still proceeded significantly at above 900 °C, revealing that bulk lattice oxygen of CeO₂ was extremely stable. Notably, in the case of CeO₂–TiO₂ mixed oxides, the H₂-TPR profile featured a single broad peak ranging from 400 to 700 °C with intensity much greater than pure CeO₂, indicative of relatively high lattice oxygen mobility. The enhanced reducibility can potentially be explained by the reduction of the energy barrier for oxygen anion migration via the stoichiometric reaction between CeO₂ and TiO₂ during reduction, resulting in Ce₂Ti₂O₇ pyrochlore as indicated by the XRD pattern of CeO₂–TiO₂ after the H₂-TPR measurement (see Fig. S8, ESI† for further details). The anion-deficient Ce₂Ti₂O₇ pyrochlore may enable efficient oxygen anion transport and facilitate the accessibility of bulk lattice oxygen. These results correspond well with the earlier work of Luo et al.,⁶² whereby the reduction degree of CeO₂–TiO₂ mixed oxides was greatly enhanced owing to incorporation of TiO₂ into the CeO₂ lattice. It is noteworthy that the presence of NiO can further improve the oxygen anion diffusivity within CeO₂–TiO₂. This is validated by the fact that the reduction peak of 5Ni/CeO₂–TiO₂ shifted down to ∼350 °C, overlapping with the reduction band of NiO,^63,64 while the H₂-TPR profile was characterized by a narrower intense reduction peak at 300–400 °C, compared to CeO₂–TiO₂ without NiO. Such superior lattice oxygen mobility is highly beneficial for CH₄ partial oxidation and the subsequent CO₂ and H₂O splitting reactions.

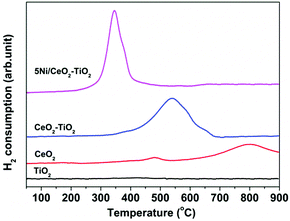Fig. 5 H₂-TPR profiles of as synthesized 5Ni/CeO₂–TiO₂ and CeO₂–TiO₂. For comparison, the data for TiO₂ and CeO₂ are also shown.

X-ray photoelectron spectroscopy (XPS) was employed to shed light on the evolution of the surface Ni and O species of the 5Ni/CeO₂–TiO₂ catalyst. The Ni 2p_3/2 spectra of the catalyst at different stages are compared in Fig. 6a. The as synthesized catalyst showed a strong peak at 855.4 eV (red) along with a broad satellite peak at 861.5 eV (blue). These features could be assigned to the Ni²⁺ in NiO,^65,66 evidencing that the surface Ni species were present as NiO. After the MDR step, a peak at 852.2 eV (yellow) associated with zero-valent metallic Ni⁰ was clearly identified,^66,67 indicating that metallic nickel was evolved after CH₄ isothermal reduction. In addition, a NiO contribution resulting from air exposure was observed due to the ex situ and surface sensitivity of XPS measurements as described elsewhere.^66,67 Apparently, for 5Ni/CeO₂–TiO₂ catalysts after isothermal MDR-STCDS and MDR-STWS redox cycling, the contributions of metallic Ni⁰ decreased remarkably, pointing toward the reoxidation of the surface reduced Ni species by CO₂ and H₂O combined with the post-reaction air exposure. Furthermore, the O 1s spectra of the catalysts after isothermal MDR-STCDS and MDR-STWS redox cycling are displayed in Fig. 6b. Deconvolution of the O 1s band showed two distinct components. The predominant component at about 529.5 eV (pink) agrees well with the signature of lattice oxygen,^55,65 while the minor components centered at 531.5 eV (26.3%) and 532.0 eV (20.4%) may originate from low coordination surface oxygen in hydroxyl and carbonate species of the catalysts after the MDR-STCDS and MDR-STWS cyclic experiments, respectively.^55,68 The electrophilic surface oxygen species have been associated with deep oxidation of CH₄ to CO₂,^68,69 and this is consistent with the fact that a higher CO selectivity was obtained on the 5Ni/CeO₂–TiO₂ catalyst in MDR-STWS redox cycling as the surface oxygen species were relatively fewer.

Fig. 6 (a) Ni 2p_3/2 XPS spectra of the 5Ni/CeO₂–TiO₂ sample: (i) as synthesized, (ii) after the CH₄ reduction half cycle, (iii) after isothermal MDR-STCDS redox cycling at 900 °C and (iv) after isothermal MDR-STWS redox cycling at 900 °C. (b) O 1s XPS spectra of the 5Ni/CeO₂–TiO₂ sample: (i) after isothermal MDR-STCDS redox cycling at 900 °C, and (ii) after isothermal MDR-STWS redox cycling at 900 °C.

To gain further insight into the redox chemistry during solar fuel production, the oxidation states of cerium and titanium were probed using XANES spectroscopy. Fig. 7 shows the normalized Ce L_III and Ti K edge XANES spectra of the 5Ni/CeO₂–TiO₂ redox catalyst after three different stages in isothermal MDR-STCDS and MDR-STWS redox cycling. For comparison, standard reference spectra of Ce⁴⁺ (CeO₂), Ce³⁺ (Ce(NO₃)₃·6H₂O), Ti⁴⁺ (TiO₂), and Ti³⁺ (Ti₂O₃) are also included. The spectrum of Ce⁴⁺ is characterized by two absorption peaks at around 5732.2 eV and 5739.0 eV, whereas the spectrum of Ce³⁺ is dominant with one intense absorption peak at around 5727.9 eV.^70,71 As observed in Fig. 7a, the Ce L_III-edge XANES spectrum of the as synthesized catalyst resembled that of Ce⁴⁺ in CeO₂. Remarkably, the spectrum of the catalyst after the MDR step exhibited exclusively features characteristic of cerium in the completely reduced state (Ce³⁺), indicating the complete reduction of Ce⁴⁺ after reacting with CH₄. Contrary to 5Ni/CeO₂–TiO₂, only minute changes are observed in the Ce L_III-edge spectra of CeO₂–TiO₂ after the MDR step (Fig. S9, ESI†), suggesting no significant change in the oxidation state of cerium in CeO₂–TiO₂ without Ni promotion. The reduced 5Ni/CeO₂–TiO₂ after the final CO₂ or H₂O splitting step recovered the initial doublet feature indicative of Ce⁴⁺. Therefore, the valence state of cerium in 5Ni/CeO₂–TiO₂ changed reversibly during the redox reactions. On the other hand, Ti K-edge XANES spectra of 5Ni/CeO₂–TiO₂ were in close resemblance to TiO₂ irrespective of the different processing steps, i.e., after initial synthesis, after reduction with CH₄ or after CO₂ or H₂O splitting redox cycling (Fig. 7b). The absence of shifts in the Ti K-edge position reveals that unlike cerium, all titanium remained in the formal +4 oxidation state upon reduction and oxidation. In conclusion, XANES analysis establishes that a complete Ce⁴⁺ ↔ Ce³⁺ redox cycle was attainable for the 5Ni/CeO₂–TiO₂ catalyst promoted by Ni species, while negligible change in the cerium oxidation state was observed for CeO₂–TiO₂ without Ni promotion, and this can account for the superior CH₄ partial oxidation activity and outstanding CO and H₂ productivities of 5Ni/CeO₂–TiO₂ in MDR-STCDS and MDR-STWS processes.

Fig. 7 Normalized XANES spectra for the 5Ni/CeO₂–TiO₂ catalyst after various steps in isothermal MDR-STCDS and MDR-STWS redox cycling at (a) the Ce L_III-edge and (b) the Ti K-edge, together with the spectra of standard reference compounds for different oxidation states.

The morphological and the structural changes of the catalyst were confirmed via HRSEM analysis. Representative HRSEM images of the as synthesized 5Ni/CeO₂–TiO₂ along with the ones after two-step MDR-STCDS and MDR-STWS redox cycling are presented in Fig. 8a–c. Fig. 8a shows that the fresh catalyst was composed of small nanosized grains with relatively uniform diameters (50–100 nm). No significant grain size growth was observed over multiple redox cycles (Fig. 8b and c), confirming the stability and robustness of the 5Ni/CeO₂–TiO₂ nanocomposite and its potential application in MDR-STCDS and MDR-STWS processes for solar fuel production.

Fig. 8 Representative SEM images of the 5Ni/CeO₂–TiO₂ catalyst: (a) as synthesized, (b) after isothermal MDR-STCDS redox cycling at 900 °C and (c) after isothermal MDR-STWS redox cycling at 900 °C.

The elemental distribution and structure of the 5Ni/CeO₂–TiO₂ catalyst were further characterized by STEM-EDX and HRTEM techniques and the results are indicated in Fig. 9. For the initial catalyst, STEM-based EDX mapping (Fig. 9b₁–b₄) showed an inhomogeneous distribution of the elements with distinct Ce, Ti, and Ni rich regions (see Fig. S10, ESI† for more details). The corresponding HRTEM images exhibited well-resolved lattice fringes of 0.31, 0.35, and 0.24 nm, which can be ascribed to CeO₂(111), TiO₂(210), and NiO(111) facets, respectively (Fig. 9c). The above results further confirm the intimately mixed oxides of CeO₂, TiO₂, and NiO in the as-prepared catalyst. In contrast, elemental mapping for 5Ni/CeO₂–TiO₂ after reduction with CH₄ (Fig. 9e₁–e₄) demonstrates clearly that the distributions of Ce, Ti, and O overlap with each other, whereas Ni was at oxidation state Ni⁰ as no clear O element was identified within the same region. Besides, clear lattice fringes of 0.29 and 0.20 nm corresponding to (112) Ce₂Ti₂O₇ (JCPDS 00-047-0667) and (111) Ni (JCPDS 00-001-1272) structural domains, respectively, were revealed (Fig. 9f). These results thus provide unambiguous evidence that TiO₂ was incorporated into the CeO₂ lattice, resulting in Ce₂Ti₂O₇ pyrochlore, while NiO was reduced to metallic nickel after CH₄ reduction, in accordance with the XRD analysis. However, the distribution of Ce and Ti remained inhomogeneous for CeO₂–TiO₂ before and after the MRD step (Fig. S11, ESI†), indicating the incorporation of TiO₂ into CeO₂ appeared to be negligible. Additionally, STEM-EDX mapping of 5Ni/CeO₂–TiO₂ catalysts after MDR-STCDS and MDR-STWS redox cycling verified a homogeneous distribution of Ce, Ti, and O elements (Fig. S12, ESI†), implying that CeO₂ and TiO₂ were regenerated with a homogeneous dispersion, with Ni species dispersed on the CeO₂–TiO₂ matrix. In essence, the STEM-EDX mapping and HRTEM analysis visualized the crystalline phase evolution of the 5Ni/CeO₂–TiO₂ catalyst, i.e., the as-prepared catalyst existed in the form of mixed oxides, which transformed into Ce₂Ti₂O₇ pyrochlore and metallic Ni after the MDR step and regenerated with uniformly distributed CeO₂ and TiO₂ upon CO₂ or H₂O splitting.

Fig. 9 (a) STEM image, (b₁–b₄) the corresponding element-mapping images and (c) HRTEM images of as synthesized 5Ni/CeO₂–TiO₂; (d) STEM image, (e₁–e₄) the corresponding element-mapping images and (f) HRTEM images of 5Ni/CeO₂–TiO₂ after the CH₄ reduction half cycle.

3.3 DFT studies

To provide a more fundamental understanding of the observed catalytic performance, DFT calculations were undertaken to probe the reaction landscape associated with CH₄ dissociation and CO₂/H₂O splitting, as well as the performance of oxygen anion migration within the CeO₂–TiO₂ support. For the methane driven reduction step, the breaking of the first C–H bond in CH₄ was studied on the metal, oxide and metal–oxide interface, respectively, as shown in Fig. 10a. The CH₄ dissociation on metal oxide surfaces, CeO₂(111) and TiO₂(110), is endothermic with a reaction energy larger than 1.00 eV and possesses high reaction barriers. In contrast, on the Ni(111) surface the reaction is slightly endothermic (0.17 eV) and the reaction barrier decreases to 0.73 eV, much lower than that on metal oxide surfaces with 1.44 eV for CeO₂(111) and 1.27 eV for TiO₂(110). Furthermore, at the interface of Ni/CeO₂(111) and Ni/TiO₂(110), despite the reaction barriers being slightly higher than that on Ni(111), the reaction energies change to significantly exothermic, indicating that the Ni/CeO₂–TiO₂ interfaces are more preferential for CH₄ dissociation. Therefore, our calculation results suggest that both Ni and the Ni/CeO₂–TiO₂ interface are more active than the pure metal oxide, which echoes the constructive role of Ni in metal oxides for methane driven reduction.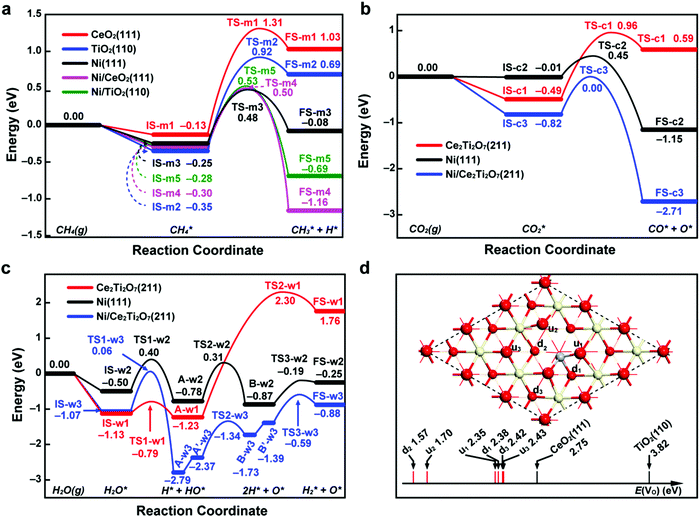

Fig. 10 DFT calculation results. Potential energy diagrams for (a) methane dissociation (CH₄(g) → CH₃* + H*), (b) carbon dioxide splitting (CO₂(g) → CO* + O*) and (c) water splitting (H₂O(g) → H₂* + O*) on the metal, oxide and metal–oxide interface. (d) The formation energies of oxygen vacancies (E(V_O)) at different sites of Ti-doped CeO₂(111), and E(V_O) for CeO₂(111) and TiO₂(110) are also shown as references. The zero energy reference corresponds to the sum of energies of gas-phase molecules and a clean surface. The reaction energies and activation energies for the elementary steps involved in the three reactions are displayed in Tables S6–S8 (ESI†). The geometric structures of states labelled in (a–c) are displayed in Fig. S13–S15 (ESI†). On the Ti-doped CeO₂(111) in (d), the oxygen atoms in the first atomic layer are labelled with “u” and the oxygen atoms in the third atomic layer are labelled with “d”. The surface structures with oxygen vacancies are displayed in Fig. S16 (ESI†). The red, yellow and gray spheres represent O, Ce and Ti atoms, respectively.

In the process of CO₂ or H₂O splitting, the reduced Ce₂Ti₂O₇(211), Ni(111) and Ni/Ce₂Ti₂O₇(211) interfaces were considered as active sites. As shown in Fig. 10b, the CO₂ dissociation on Ce₂Ti₂O₇(211) is an endothermic reaction with a reaction energy of 1.08 eV and a large reaction barrier of 1.45 eV. On Ni(111) the reaction energy becomes exothermic with a value of −1.14 eV and the reaction barrier is as low as 0.46 eV. However, the adsorption energy of CO₂ on Ni(111) is insignificant (only −0.01 eV), which can lead to a low coverage of adsorbed CO₂ and thus is detrimental to the total rate of CO₂ dissociation. At the interface between Ni and Ce₂Ti₂O₇(211), though the reaction barrier is increased by 0.36 eV compared to that on Ni(111), the reaction is more exothermic and the adsorption of CO₂ is dramatically enhanced with an adsorption energy of −0.82 eV, suggesting the Ni/Ce₂Ti₂O₇(211) interface is more favorable for CO₂ splitting. For the water dissociation reaction on the Ce₂Ti₂O₇(211) surface (Fig. 10c), the breakage of the first O–H bond only needs to overcome a small reaction barrier of 0.34 eV, resulting in the OH group binding with metal atoms and the H atom binding with surface oxygen atoms (state A-w1). However, the subsequent hydrogen formation on the Ce₂Ti₂O₇(211) surface is extremely difficult as the reaction barrier and the reaction energy are up to 3.53 eV and 2.99 eV, respectively. On the Ni(111) surface, water first experiences two steps of O–H bond breaking, then followed by one step of hydrogen generation. The breaking of the second O–H bond (from state A-w2 to B-w2) is the rate-determining step with a reaction barrier of 1.09 eV. At the interface of Ni/Ce₂Ti₂O₇(211), water needs to go through three steps similar to that on Ce₂Ti₂O₇(211) and two steps of hydrogen atom diffusion (state A-w3 to A′-w3 and state B-w3 to B′-w3). The reaction barrier of the rate-determining step (the breaking of the first O–H bond) is 1.13 eV, which is only 0.04 eV higher than that on the Ni(111) surface. However, the adsorption of water at interface sites (−1.07 eV) is stronger than that on Ni(111) (−0.50 eV). Therefore, Ni and the Ni/Ce₂Ti₂O₇ interface show comparable activity in water splitting, but are much more active than the pure Ce₂Ti₂O₇ surface.

Additionally, to explore the effect of TiO₂ on the oxygen anion diffusivity within CeO₂, the formation energies of oxygen vacancies E(V_O) of Ti-doped CeO₂ were calculated with CeO₂ and TiO₂ as references (Fig. 10d). The calculated results indicate that the E(V_O) of Ti-doped CeO₂(111) are lower than those of CeO₂(111) and TiO₂(110). Moreover, the oxygen atoms (u₂, d₂ in Fig. 10d) with lower coordination numbers after replacing one Ce atom with a Ti atom are more likely to be removed from the surface with the lowest E(V_O) of 1.57 eV and 1.70 eV. Overall, the lower formation energies of oxygen vacancies approaching the Ti atom on Ti-doped CeO₂(111) reflect the weakening of the Ce–O bond induced by the Ti atom, which indicates the promotional effect of TiO₂ on oxygen anion diffusion within CeO₂.

3.4 Reaction mechanism

On the basis of the experimental evidence and DFT calculations presented above, the potential reaction mechanism for the 5Ni/CeO₂–TiO₂ redox catalyst in MDR-STCDS and MDR-STWS processes is depicted in Fig. 11. We propose that in the MDR step, oxygen originating from NiO and loosely bonded surface oxygen were responsible for the total oxidation of CH₄ to CO₂ and H₂O with simultaneous reduction of NiO to metallic Ni. Furthermore, a stoichiometric reaction between CeO₂ and TiO₂ was promoted by the presence of Ni, providing lattice oxygen necessary for partial oxidation of CH₄ and resulting in Ce₂Ti₂O₇ pyrochlore. In the subsequent CO₂ or H₂O splitting step, the anion-deficient Ce₂Ti₂O₇ pyrochlore was reoxidized back to CeO₂ and TiO₂ after incorporation of O anions, producing CO or H₂. Meanwhile, the surface metallic Ni was partially reoxidized by CO₂ or H₂O. The reduced Ni species in 5Ni/CeO₂–TiO₂ are identified as the active sites for CH₄ activation and accelerate CO₂ and H₂O dissociation in the reduction and oxidation steps, as strongly indicated by the drastically enhanced CH₄ reactivity (Fig. 3 and Fig. S3, ESI†) and CO₂ and H₂O splitting kinetics (Fig. 2a and b) over those of CeO₂–TiO₂. The phase transformations between CeO₂–TiO₂ and Ce₂Ti₂O₇ pyrochlore proceeded reversibly with the promotion of Ni species for enhanced lattice oxygen transport, accompanied by the complete Ce⁴⁺ ↔ Ce³⁺ redox cycle through reduction with CH₄ and oxidation with CO₂ or H₂O, and it was backed up by XRD, XANES and electron microscopy (STEM-EDX, HRTEM) observations. DFT calculations also indicate that the metallic Ni and Ni/CeO₂–TiO₂ interface sites enhance the CH₄ activation and the dissociation of CO₂ and H₂O. The calculated formation energies of oxygen vacancies suggest that the incorporation of TiO₂ into CeO₂ can weaken the Ce–O bond and thus promote the oxygen anion diffusion within CeO₂. Overall, the synergistic effect between the catalytic activation on Ni and the CeO₂–TiO₂/Ce₂Ti₂O₇ stoichiometric redox cycle enabled the highly effective solar fuel production in MDR-STCDS and MDR-STWS processes.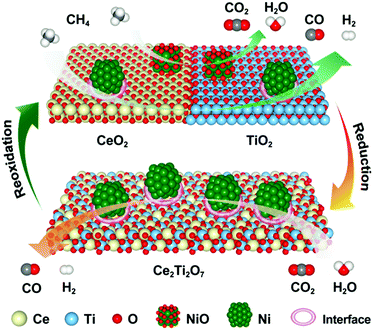

Fig. 11 Schematic of the proposed reaction mechanism for MDR-STCDS and MDR-STWS processes over the 5Ni/CeO₂–TiO₂ redox catalyst.

4. Conclusions

In summary, 5Ni/CeO₂–TiO₂ has emerged as an exceptional catalytic system for robust operation in MDR-STCDS and MDR-STWS processes. The redox catalyst featured ∼100% CH₄ conversions and syngas selectivities up to ∼76 and ∼85% in the MDR step. In regard to the CO₂ and H₂O splitting steps, one to two orders of magnitude higher CO/H₂ production rates and productivities were achieved compared to the state-of-the-art STCDS/STWS and MDR-STCDS/MDR-STWS studies. In addition, the catalyst developed here possesses excellent stability over multiple redox cycles. As revealed by the experimental investigations and DFT calculations, the superior performance of 5Ni/CeO₂–TiO₂ is driven by the synergy between the catalytic activation on Ni and the CeO₂–TiO₂/Ce₂Ti₂O₇ stoichiometric redox cycle as they provide active sites and reactive intermediates to transport lattice oxygen for CH₄ partial oxidation and CO₂ or H₂O splitting in a complementary fashion. We anticipate the fundamental understanding on the crucial roles of the catalytic sites for reactant activation and the stoichiometric redox chemistry for enhanced lattice oxygen availability can provide important guidance for the rational design of advanced materials toward solar fuel production.

Conflicts of interest

The authors declare no competing financial interest.

Acknowledgements

This work was supported by National Natural Science Foundation of China (21476232, 21590792, 21776271, 21676269, 21603170, 91645203), National Key Projects for Fundamental Research and Development of China (2016YFA0202801), the “Strategic Priority Research Program” of the Chinese Academy of Sciences (XDB17020100) and Department of Science and Technology of Liaoning province under contract 2015020086-101. C. R. C. gratefully acknowledges the China Postdoctoral Science Foundation (2018T111034), the Fundamental Research Funds for the Central Universities (xtr0218016 and cxtd2017004) and the support of K. C. Wong Education Foundation. The calculations were performed by using the HPC Platform at Xi’an Jiaotong University and National Supercomputing Center in Shenzhen. This paper is dedicated to the 70th anniversary of the Dalian Institute of Chemical Physics, Chinese Academy of Sciences.

References

1. S. Chu and A. Majumdar, Nature, 2012, 488, 294–303.
2. N. S. Lewis and D. G. Nocera, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 15729–15735.
3. N. S. Lewis, Science, 2016, 351, 1920–1929.
4. J. Liu, Y. Liu, N. Liu, Y. Han, X. Zhang, H. Huang, Y. Lifshitz, S.-T. Lee, J. Zhong and Z. Kang, Science, 2015, 347, 970–974.
5. E. M. Nichols, J. J. Gallagher, C. Liu, Y. Su, J. Resasco, Y. Yu, Y. Sun, P. Yang, M. C. Chang and C. J. Chang, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 11461–11466.
6. D. S. Mallapragada, N. R. Singh, V. Curteanu and R. Agrawal, Ind. Eng. Chem. Res., 2013, 52, 5136–5144.
7. J. A. Herron, J. Kim, A. A. Upadhye, G. W. Huber and C. T. Maravelias, Energy Environ. Sci., 2015, 8, 126–157.
8. W. C. Chueh, C. Falter, M. Abbott, D. Scipio, P. Furler, S. M. Haile and A. Steinfeld, Science, 2010, 330, 1797–1801.
9. M. Tou, R. Michalsky and A. Steinfeld, Joule, 2017, 146–154,  DOI:10.1016/j.joule.2017.07.015.
10. C. L. Muhich, B. W. Evanko, K. C. Weston, P. Lichty, X. Liang, J. Martinek, C. B. Musgrave and A. W. Weimer, Science, 2013, 341, 540–542.
11. A. H. Bork, M. Kubicek, M. Struzik and J. L. M. Rupp, J. Mater. Chem. A, 2015, 3, 15546–15557.
12. C. Ruan, Y. Tan, L. Li, J. Wang, X. Liu and X. Wang, AIChE J., 2017, 63, 3450–3462.
13. F. He, J. Trainham, G. Parsons, J. S. Newman and F. Li, Energy Environ. Sci., 2014, 7, 2033–2042.
14. F. He and F. Li, Energy Environ. Sci., 2015, 8, 535–539.
15. J. R. Scheffe, M. D. Allendorf, E. N. Coker, B. W. Jacobs, A. H. McDaniel and A. W. Weimer, Chem. Mater., 2011, 23, 2030–2038.
16. Z. Zhao, M. Uddi, N. Tsvetkov, B. Yildiz and A. F. Ghoniem, J. Phys. Chem. C, 2017, 121, 11055–11068.
17. Z. Zhao, M. Uddi, N. Tsvetkov, B. Yildiz and A. F. Ghoniem, Phys. Chem. Chem. Phys., 2017, 19, 25774–25785.
18. D. Maiti, B. J. Hare, Y. A. Daza, A. E. Ramos, J. N. Kuhn and V. R. Bhethanabotla, Energy Environ. Sci., 2018, 11, 648–659.
19. B. J. Hare, D. Maiti, Y. A. Daza, V. R. Bhethanabotla and J. N. Kuhn, ACS Catal., 2018, 8, 3021–3029.
20. R. Michalsky, D. Neuhaus and A. Steinfeld, Energy Technol., 2015, 3, 784–789.
21. J. Zhang, V. Haribal and F. Li, Sci. Adv., 2017, 3, e1701184.
22. P. T. Krenzke and J. H. Davidson, Energy Fuels, 2014, 28, 4088–4095.
23. P. T. Krenzke, J. R. Fosheim, J. Zheng and J. H. Davidson, Int. J. Hydrogen Energy, 2016, 41, 12799–12811.
24. K. J. Warren, J. Reim, K. Randhir, B. Greek, R. Carrillo, D. W. Hahn and J. Scheffe, Energy Technol., 2017, 5, 2138–2149.
25. A. Steinfeld, P. Kuhn and J. Karni, Energy, 1993, 18, 239–249.
26. Q. Imtiaz, N. S. Yüzbasi, P. M. Abdala, A. M. Kierzkowska, W. van Beek, M. Broda and C. R. Müller, J. Mater. Chem. A, 2016, 4, 113–123.
27. M. M. Nair and S. Abanades, Energy Fuels, 2016, 30, 6050–6058.
28. X. Gao, A. Vidal, A. Bayon, R. Bader, J. Hinkley, W. Lipiński and A. Tricoli, J. Mater. Chem. A, 2016, 4, 9614–9624.
29. M. Welte, K. Warren, J. R. Scheffe and A. Steinfeld, Ind. Eng. Chem. Res., 2017, 56, 10300–10308.
30. Y. Zheng, Y. Wei, K. Li, X. Zhu, H. Wang and Y. Wang, Int. J. Hydrogen Energy, 2014, 39, 13361–13368.
31. X. Zhu, Y. Wei, H. Wang and K. Li, Int. J. Hydrogen Energy, 2013, 38, 4492–4501.
32. J. R. Scheffe, R. Jacot, G. R. Patzke and A. Steinfeld, J. Phys. Chem. C, 2013, 117, 24104–24114.
33. Y. Zheng, K. Li, H. Wang, X. Zhu, Y. Wei, M. Zheng and Y. Wang, Energy Fuels, 2016, 30, 638–647.
34. K. Otsuka, Y. Wang, E. Sunada and I. Yamanaka, J. Catal., 1998, 175, 152–160.
35. D. Arifin, V. J. Aston, X. Liang, A. H. McDaniel and A. W. Weimer, Energy Environ. Sci., 2012, 5, 9438.
36. C. Dang, Y. Li, S. M. Yusuf, Y. Cao, H. Wang, H. Yu, F. Peng and F. Li, Energy Environ. Sci., 2018, 11, 660–668.
37. D. R. Killelea, V. L. Campbell, N. S. Shuman and A. L. Utz, Science, 2008, 319, 790–793.
38. Z. Liu, D. C. Grinter, P. G. Lustemberg, T. D. Nguyen-Phan, Y. Zhou, S. Luo, I. Waluyo, E. J. Crumlin, D. J. Stacchiola, J. Zhou, J. Carrasco, H. F. Busnengo, M. V. Ganduglia-Pirovano, S. D. Senanayake and J. A. Rodriguez, Angew. Chem., Int. Ed., 2016, 55, 7455–7459.
39. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50.
40. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
41. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251–14269.
42. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
43. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
44. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192.
45. V. I. Anisimov, J. Zaanen and O. K. Andersen, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 44, 943–954.
46. S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505–1509.
47. S. Fabris, G. Vicario, G. Balducci, S. de Gironcoli and S. Baroni, J. Phys. Chem. B, 2005, 109, 22860–22867.
48. J. B. Park, J. Graciani, J. Evans, D. Stacchiola, S. D. Senanayake, L. Barrio, P. Liu, J. F. Sanz, J. Hrbek and J. A. Rodriguez, J. Am. Chem. Soc., 2010, 132, 356–363.
49. G. Henkelman and H. Jonsson, J. Chem. Phys., 1999, 111, 7010–7022.
50. H. Jónsson, G. Mills and K. W. Jacobsen, in Classical and Quantum Dynamics inCondensed Phase Simulations, ed. B. J. Berne, G. Ciccotti and D. F. Coker, World Scientific, Singapore, 1998, pp. 385–404.
51. A. Preuss and R. Gruehn, J. Solid State Chem., 1994, 110, 363–369.
52. L. Foppa, T. Margossian, S. M. Kim, C. Müller, C. Copéret, K. Larmier and A. Comas-Vives, J. Am. Chem. Soc., 2017, 139, 17128–17139.
53. S. Takenaka, N. Hanaizumi, V. T. D. Son and K. Otsuka, J. Catal., 2004, 228, 405–416.
54. J. Carrasco, D. Lopez-Duran, Z. Liu, T. Duchon, J. Evans, S. D. Senanayake, E. J. Crumlin, V. Matolin, J. A. Rodriguez and M. V. Ganduglia-Pirovano, Angew. Chem., Int. Ed., 2015, 54, 3917–3921.
55. C. Heine, B. A. Lechner, H. Bluhm and M. Salmeron, J. Am. Chem. Soc., 2016, 138, 13246–13252.
56. Q. G. Yan, W. Z. Weng, H. L. Wan, H. Toghiani, R. K. Toghiani and C. U. Pittman, Appl. Catal., A, 2003, 239, 43–58.
57. S. Chen, L. Zeng, H. Tian, X. Li and J. Gong, ACS Catal., 2017, 7, 3548–3559.
58. M. Rydén, M. Johansson, A. Lyngfelt and T. Mattisson, Energy Environ. Sci., 2009, 2, 970.
59. A. Löfberg, J. Guerrero-Caballero, T. Kane, A. Rubbens and L. Jalowiecki-Duhamel, Appl. Catal., B, 2017, 212, 159–174.
60. I. Atribak, A. Buenolopez and A. Garciagarcia, J. Catal., 2008, 259, 123–132.
61. X. Wang, D. Liu, J. Li, J. Zhen and H. Zhang, NPG Asia Mater., 2015, 7, e158.
62. M. F. Luo, J. Chen, L. S. Chen, J. Q. Lu, Z. Feng and C. Li, Chem. Mater., 2001, 13, 197–202.
63. T. J. Lin, H. Xie, X. Meng and L. Shi, Catal. Commun., 2015, 68, 88–92.
64. H. Zhu, D. C. Rosenfeld, D. H. Anjum, S. S. Sangaru, Y. Saih, S. Ould-Chikh and J.-M. Basset, J. Catal., 2015, 329, 291–306.
65. M. A. Peck and M. A. Langell, Chem. Mater., 2012, 24, 4483–4490.
66. A. Antzara, E. Heracleous, L. Silvester, D. B. Bukur and A. A. Lemonidou, Catal. Today, 2016, 272, 32–41.
67. V. V. Galvita, H. Poelman and G. B. Marin, J. Power Sources, 2015, 286, 362–370.
68. Y. Gao, L. M. Neal and F. Li, ACS Catal., 2016, 6, 7293–7302.
69. O. Mihai, D. Chen and A. Holmen, J. Catal., 2012, 293, 175–185.
70. T. Yamamoto, A. Suzuki, Y. Nagai, T. Tanabe, F. Dong, Y. Inada, M. Nomura, M. Tada and Y. Iwasawa, Angew. Chem., Int. Ed., 2007, 119, 9413–9416.
71. S. Zhang, S. Muratsugu, N. Ishiguro, S.-I. Ohkoshi and M. Tada, ChemCatChem, 2012, 4, 1783–1790.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c8ee03069c

‡ Co-first authors.

---