Synthesis of a germanosilicate zeolite HPM-12 using a short imidazolium-based dication: structure-direction by charge-to-charge distance matching

Abstract

A short imidazolium based dication, with only three methylene units in the spacer linker, selectively directs the crystallization of zeolite HPM-12 (*UOE) as long as there is enough germanium present in the synthesis gel. The integrity of the dication is proved by dissolution of the zeolite and ¹H and ¹³C NMR spectroscopy, where significant effects of organic dication concentration and the presence and concentration of HF need to be taken into account. For the as-made HPM-12 zeolite, a large shift of 9 ppm of one resonance in the ¹³C MAS NMR spectrum is due to the particular conformation of the dication imposed by confinement in the zeolite framework, as found by DFT calculations. The structure-directing ability of this kind of dication with varying length of the linker suggests that matching of the distance between positive charges (imidazolium moieties) and negative charges (double four rings in which fluoride resides) plays a crucial role during crystallization.

---

Introduction

In the synthesis of zeolites, the concept of structure-direction by organic cations may be considered to rely on the organic cation transferring, to some extent, its shape and size to the inorganic pores. The extent to which this effect occurs is largely variable and, depending on the specificity of the interaction and on the degree of geometric correspondence between the inorganic and organic components of the as-made hybrid zeolite, the structure-direction effect can range from loose (with the organic cation acting as a mere pore filler) to highly specific (true templating) with most cases falling in between both categories.¹ Frequently, an interplay of many factors, and not only the organic cation (structure-directing agent, SDA), is decisive in the crystallization of a given zeolite. Generally, the size, shape and rigidity of the organics, rather than the location of the positive charges, are considered, together with hydrophobicity, as the main features determining structure direction.² Thus, van der Waals contacts, rather than coulombic interactions, are generally considered with regard to structure-direction. A notable exception is a very recent comparative study conducted by Jo and Hong on the structure direction of imidazolium and pyrazolium isomers, showing that pairs with the same size and shape but markedly different charge distribution produce different zeolites.³

The successful use of organic dications in the discovery of new zeolites was pioneered by Casci and coworkers who reported in the patent literature the synthesis of EU-1 (Zeolite Framework Type EUO),⁴ EU-2 (an intergrowth of NSI and CAS frameworks),⁵ both using hexamethonium (hexamethylhexamethylenediammonium), and Nu-87 (NES) using decamethonium (hexamethyldecamethylenediammonium).⁶ Zeolite type codes are assigned by the International Zeolite Association to unique zeolite frameworks.⁷ Later on, a series of diquaternary cations (“diquats”) of varying length, determined by the number n of methylene units in the bridge between the quaternary ammonium atoms (with n = 5–14), were investigated as SDAs, and an ‘oscillatory’ pattern was found: for specific values of n, zeolites with 12MR pores (open through a 12 membered ring, i.e., windows composed of 12 tetrahedra) or pockets were formed, while for any other value zeolite MTT, with 10MR pores and considered a “default” structure, appeared.⁸ In this context, the term default structure is understood as a material that does not need a strong structure-direction effect to crystallize. Thus, the obtained zeolites were EUO (with 10MR pockets) for n = 5 and 6, MTW (with 12MR pores) for n = 9 and 14 and NES (with 10MR and 12MR pores) for n = 10, while MTT crystallized for any other n tested. Modelling studies suggested that for EUO and NES the ammonium groups are located in the 12MR portions of the structure, with the bridge residing in the 10MR sections. A preference of the ammonium heads towards 12MR sections could then explain the observed oscillatory pattern, since those sections are separated by fixed distances in these zeolites (except in the 12MR pore MTW). Here again, the size and shape, rather than coulombic interactions, appear to be of importance in our understanding of structure-direction.

Since the last two decades we have been exploring the structure-direction ability of non-quaternary imidazolium cations in fluoride media.⁹ In the case of imidazolium-based dications we have found consistent evidence of length-dependent structure-direction effects. For instance, dications based on 1-methylimidazolium tend to give zeolite TON (10MR) as the default phase, and only for n = 4, 8 and 9, MFI appears under highly concentrated conditions.^10,11 For the slightly larger 1,2-dimethylimidazolium analogues, the default phase under pure silica conditions is invariably MTW, with a remarkable exception: for n = 4 the chiral STW zeolite is obtained, and we even observed that under dilute conditions MTW crystallizes first and then transforms into STW.¹² This structure-directing ability decreased with a slight increase in n, so that the synthesis of STW required highly concentrated conditions for n = 5 and the addition of Ge for n = 6. A further increment in the length to n = 8 and 10 totally suppressed the ability to produce STW while *BEA and MWW were obtained under highly concentrated conditions (dilution yielded the default MTW) in the pure silica system.¹³ However, addition of Ge to the synthesis with n = 8 and 10 led to the crystallization of HPM-8 (an intergrowth of polymorphs E and D of the beta family with a large predominance of polymorph D) and HPM-7 (POS structure).¹⁴ Pervasive along these studies was the finding of a commensurate effect between the length of the dication and the separation between consecutive fluoride-containing units in the zeolite (with the exception of STW where these units are everywhere). In the study of bisdimethylimidazolium-based dications, the dication with n = 3 was tested to a limited extent because it gave no crystalline product under pure silica conditions and showed barely any crystallinity after adding a small amount of Ge (Ge_f = Ge/(Ge + Si) = 0.1), which was initially interpreted as a consequence of a lack of stability of this cation upon hydrothermal treatment. Dications with n = 3 have been reported to be unstable to hydrothermal treatments.^8,10,15 Here we show that this dication is stable enough and that, with a higher amount of Ge added (Ge_f ≥ 0.2), it displays a selective structure-direction effect towards zeolite HPM-12 (structure code *UOE).¹⁶ Here again, a commensurate effect between the length of the dication and the fluoride-containing units is found, supporting the notion of the contribution of specific coulombic interactions, in addition to van der Waals contacts, during structure-direction.

Experimental

Synthesis of the structure-directing agent (SDA)

A short imidazolium-based dication, consisting of two 1,2-dimethylimidazolium moieties linked by a trimethylene chain, denoted as 3BDMI, was synthesized and used as the organic SDA in this work. The synthesis procedure of 3BDMI is as follows. 0.14 mol of 1,2-dimethylimidazole (Sigma-Aldrich, 98%) was dissolved in 100 mL of methanol followed by addition of 0.07 mol of 1,3-dibromopropane (Sigma-Aldrich, 99%) in a one-neck round flask equipped with a condenser. The resulting mixture was refluxed under magnetic stirring for 7 days and then subjected to rotoevaporation to remove the solvent. Finally, a transparent oily product was obtained. This oil was dissolved in hot MeOH and addition of ethyl acetate resulted in the precipitation of a thick white solid. The solid was filtered and washed with THF. The purity of the product was confirmed by ¹H and ¹³C NMR spectra by dissolving the bromide salts in D₂O. The spectra demonstrate that high purity 3BDMI was successfully synthesized (see the NMR section below).

The above bromide salt was converted to its corresponding hydroxide form by anion exchange using 550A (OH) resin (Sigma-Aldrich, 1.1 meq per 1 mL) following a reported procedure.¹⁴ The hydroxide solution was concentrated by rotoevaporation and its final concentration was determined by titration using phenolphthalein as the indicator.

Synthesis of zeolites

The synthesis gel was prepared by adding first, if needed, germanium oxide (GeO₂, Aldrich, 99.998%) and then TEOS to the hydroxide solution. The mixture was stirred to remove the ethanol generated by hydrolysis together with some water. The desired composition was achieved by monitoring the mixture weight. Then, HF (Sigma-Aldrich, 48% aqueous solution) was added and the resulting viscous gel was homogenized with a spatula by hand for 15 min. The final gel composition was (1 − x) SiO₂:xGeO₂:0.25R(OH)₂:0.5HF:yH₂O, where x = Ge/(Ge + Si) is the molar ratio of germanium oxide and will be denoted as Ge_f in the following text, y = 5, 10 and 15, and R is the 3BDMI dication. The final gel was transferred to Teflon vessels inside stainless steel autoclaves, which were heated in an oven at 150 °C while tumbling at 60 rpm. The autoclaves were taken out at preselected times and quenched with tap water. The product was washed with deionized water, filtered and dried at 100 °C.

Characterization

The products were identified using powder X-ray diffraction (PXRD). The diffraction patterns were obtained on a Bruker D8 Advance diffractometer using Cu Kα radiation (λ = 1.5418 Å). Field emission scanning electron micrographs were collected using an FEI Nova NanoSEM 230. Multinuclear magic angle spinning (MAS) NMR spectroscopy of as-synthesized samples was performed at room temperature on Bruker AV-400-WB equipment and the details have been given elsewhere.¹⁷ The amount of organic moieties occluded in the as-made zeolites was determined by CHN elemental analysis using a LECO CHNS-932 analyzer. Thermogravimetric analysis was carried out on an SDT Q600 TA instrument under air flow (100 mL min⁻¹) heating from 25 °C to 1000 °C at a heating rate of 10 °C min⁻¹.

Computational details

Molecular mechanics simulations were initially performed in order to find the most stable location of 3BDMI within the *UOE framework; simulations were carried out using the Forcite module implemented in Materials Studio,¹⁸ using the Dreiding forcefield;¹⁹ the most stable conformations of 3BDMI were obtained with the Conformers Search module of Materials Studio.²⁰ Due to the size of the SDA cations, 2 × 2 × 2 *UOE supercells have been used as zeolite models. The 3BDMI cations were manually docked in the framework in different positions/orientations and conformations, and the most stable location was then obtained by simulated annealing.

The stability of the different locations of the host–guest systems and the theoretical ¹³C NMR chemical shifts (both in vacuo and within the zeolite) were studied by full geometry-optimisation of pure-silica zeolite models with DFT + D methods, which were performed with the CASTEP code,²¹ using plane waves (with an energy cut off of 571.4 eV), and the PBE functional (including the Grimme dispersion term);²² F anions were placed within the D4R units, as indicated by ¹⁹F MAS NMR (see below). Calculation of the ¹³C NMR chemical shieldings of 3BDMI dications was carried out by the gauge-including projector augmented-wave (GIPAW) method developed by Pickard and Mauri,²³ as implemented in the CASTEP code. The chemical shift for a nucleus in a given position (δ(r)) is defined as: δ(r) = σ_ref – σ(r), where σ(r) is the isotropic shielding obtained in the calculations. In order to compare with experimental ¹³C chemical shifts, a σ_ref value of 174 ppm (the same as in our previous work)¹³ was used, so that the experimental and theoretical values roughly coincide.

Results and discussion

Zeolite synthesis

The zeolite syntheses were carried out at 150 °C while varying three parameters: Ge_f, water amount and heating duration. With regard to the pure silica synthesis trials, amorphous phases were mainly obtained with a H₂O/T ratio in the starting gel from 5 to 15. The only hint of a crystalline phase was MTW at an H₂O/T ratio of 15 and a heating time of 5 days (Table 1, entry 6). When Ge was introduced, a germanosilicate zeolite lab-coded HPM-12 appeared (HPM stands for the Nanostructured Hybrid, Biohybrid and Porous Materials Group in the Institute of Materials Science of Madrid). We found that the synthesis of HPM-12 was robust and strongly depended on the addition of Ge to the starting gel. We studied the effect of Ge_f while keeping the H₂O/T ratio at 10. An amorphous phase with traces of HPM-12 was obtained with a Ge_f of 0.1 (Table 1, entries 7–10), and the corresponding XRD pattern remained essentially invariant even after prolonging the heating time up to 7 days (Fig. S1†). This suggests that Ge may be a limiting reagent in this synthesis system, suggesting in turn that Ge is necessary in at least a minimum amount (Ge_f > 0.1) in the HPM-12 structure. Thus, this synthesis appears to require the cooperative structure-direction effects of the organic SDA, Ge and fluoride. Better crystallized HPM-12 was obtained by further increasing Ge_f to 0.2 with a crystallization time of 3 and 5 days (Table 1, entries 11 and 12). Above that Ge_f level only minor differences in crystallinity were observed (Fig. S2†; Table 1, entries 16–18, 23 and 24).

Table 1 Summary of synthesis results using 3BDMI as the SDA at 150 °C

Entry	Gef	H2O/T	Time (day)	Phase^a
a AM: amorphous phase. b Poorly crystallized.
1	0	5	3	AM
2		5	5	AM
3		10	3	AM
4		10	7	AM
5		15	3	AM
6		15	5	AM(MTW)
7	0.1	10	1	AM + HPM-12
8		10	3	AM + HPM-12
9		10	5	AM + HPM-12
10		10	7	AM + HPM-12
11	0.2	10	3	HPM-12
12		10	5	HPM-12
13	0.3	5	3	BEC-like^b
14		5	5	BEC-like^b
15		10	1	AM
16		10	3	HPM-12
17		10	5	HPM-12
18		10	7	HPM-12
19		15	3	HPM-12
20		15	5	HPM-12
21	0.5	5	2	AM + HPM-12
22		5	4	HPM-12
23		10	3	HPM-12
24		10	5	HPM-12

---

The water content in the synthesis gel was also found to be a key factor for obtaining highly crystalline HPM-12. A poorly crystallized BEC-like (beta zeolite polymorph C) product was obtained under more concentrated conditions (H₂O/T = 5) (Table 1, entries 13 and 14). BEC has been considered as a default phase in syntheses carried out in the germanosilicate gel system, especially under highly concentrated conditions, since it is a frequently obtained product through a wide range of synthesis parameters, e.g. ingredients, temperatures and SDA types, among others.²⁴ When the starting gel was diluted, the crystallization of HPM-12 became easier (Table 1, entries 16–20), and a trend of increasing crystallinity was observed as illustrated by the XRD patterns (Fig. S3†). On the basis of the Villaescusa's rule,²⁵ the substitution of BEC by HPM-12 when increasing the dilution of the synthesis mixture suggested that HPM-12 had a higher framework density than BEC. Finally, for Ge_f = 0.5, HPM-12 was obtained even under concentrated conditions (H₂O/T = 5, Table 1, entries 21 and 22).

Characterization

The XRD pattern of HPM-12 shows broad and sharp reflections suggesting its intergrown nature and making difficult its indexing (Fig. 1). Looking for clues and given the preferential structure-directing ability of 3BDMI toward zeolite HPM-12, we considered previously reported zeolites synthesized using related imidazolium-based SDAs. The structure of 3BDMI is comprised of two 1,2-dimethylimidazolium moieties connected by a linker of three methylene units. This is formally just one methylene longer than a dimer of trimethylimidazolium (TMIm), a cation that has been shown to be a strong SDA for the synthesis of the ITW zeolite. In fact, we found that the XRD patterns of HPM-12 and ITW have clear similarities, especially beyond 15° 2θ, although there are also significant differences, particularly at low angles (Fig. 1). After a very recent report on zeolite IM-18,¹⁶ a zeolite presenting a complex structure with multidimensional disorder (structure type *UOE) and that is in fact structurally related to zeolite ITW, we realized that HPM-12 possesses the same zeolite structure, although the much broader reflections in HPM-12 suggest either more disorder or smaller coherent domains. IM-18 is a germanosilicate zeolite synthesized through the fluoride route using 4-dimethylaminopyridine as the OSDA. It possesses a 3D system of small and medium channels (8 × 8 × 10 T-rings). Both *UOE and ITW are monoclinic and have very similar a, b, c and β unit cell parameters in their as-made forms, explaining the similarity of their XRD patterns (Fig. 1). As opposed to HPM-12, which can be obtained pure under a considerably wide range of synthesis conditions, the synthesis of pure IM-18 requires a narrow range of Ge_f (around 0.2), with ZSM-48, NON, and the dense phases quartz, cristobalite or argutite as competing phases under different conditions. As expected, the framework density of the *UOE zeolite type (FD_Si = 17.6 T/1000 ų) is larger than that of BEC (15.1 T/1000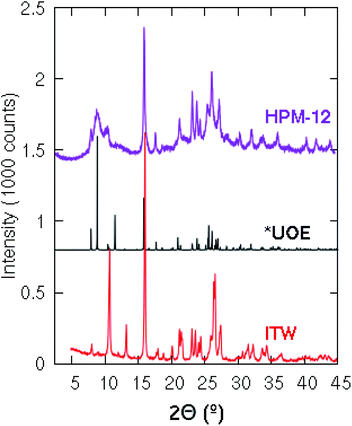 ų).

Fig. 1 XRD patterns of the ITW zeolite synthesized using 123TMI (bottom) and the simulated patterns of *UOE (middle) and HPM-12 zeolites (top) synthesized using 3BDMI.

As discussed above, the water content of the synthesis mixture exerts a significant influence on the crystallinity of the as-made HPM-12 in this work. Some peaks that are indiscernible become well-resolved after the gel was diluted, especially the peaks in the low angle region. In comparison with the *UOE simulated pattern, the as-made HPM-12 samples show similar reflections though the relative intensities are different especially in the low angle region between 7° and 11°. The XRD pattern was also collected for the calcined HPM-12 zeolite, as shown in Fig. S4,† compared with the as-made HPM-12. It can be seen that the overall intensity more than halved upon calcination, while the major peaks are roughly retained though severely broadened (e.g. the peaks in the angle range between 7° and 11°, and 14.7° and 29.4°). Thus, it can be concluded that the framework of HPM-12 is unstable after SDA removal, which might be due to hydrolysis of framework germanium under ambient humidity and which thus is expected to be worse the higher the Ge content of the zeolite. This is at odds with IM-18, which is described as stable under atmospheric humidity. Since IM-18 has a similar Ge_f (0.2) to the HPM-12 samples examined, the lack of stability of HMP-12 might be due to its much smaller crystal size, to its different morphology (needles versus plates) or to a different final content and/or location of Ge in both zeolites. As observed in Fig. 2, HPM-12 is made of aggregates of very small needle-like crystals, less than 0.05 μm thick and less than 1 μm long, much smaller than the 1.5 × 1.5 × 0.05 μm³ platelets reported for IM-18.

Fig. 2 SEM image of the as-made HPM-12 zeolite synthesized with a Ge_f of 0.5 and a H₂O/TO₂ ratio of 5. The scale bar is 2 μm.

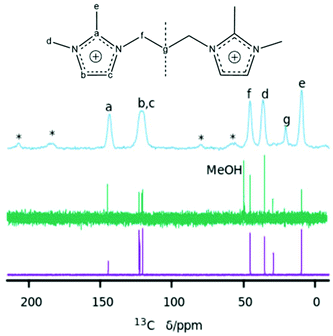
The chemical compositions of several as-made HPM-12 zeolites are shown in Table 2.²⁶ The C/N molar ratios of the organics entrapped in the zeolites are a little higher than the theoretical values for the pristine 3BDMI, suggesting that the SDAs, while roughly intact in the as-made zeolites, may have suffered significant decomposition. This would not be very surprising, given previous reports of low hydrothermal stability of short dications based on propylene linkers.^8,11,15 To check the integrity of the SDAs, the ¹³C MAS NMR spectrum of an as-made sample was collected and is shown in Fig. 3 (top trace). The spectrum shows six broadened resonances consistent with the number of lines in the ¹³C NMR spectrum of the pristine 3BDMI collected in D₂O. Five of these resonances are in the expected chemical shift range ascribed to the aromatic (a, b and c) and alkyl (e, f and d) carbons. However, one resonance, which would be assigned to the carbon in the middle of the propylene chain (carbon g), shows an up-field shift from 29 ppm in the pristine 3BDMI in D₂O to 20.1 ppm in the zeolite, suggesting that either there has been decomposition of the dication or there has been a significant shielding of this particular atom in the zeolite. Due to the uncertainty in the integrity of the SDA, we liberated the organics occluded by dissolving the as-made zeolite following our previously reported procedure.²⁷ The ¹³C and ¹H NMR spectra of the resulting solution are shown in Fig. 3 (middle) and Fig. 4 (bottom), respectively.

Fig. 3 ¹³C NMR spectra in D₂O solution of the pristine 3BDMI bromides (bottom) and of the dissolved as-made 3BDMI-HPM-12 zeolite (middle; methanol added as a chemical shift reference, the methyl group at 49.50 ppm) and solid-state ¹³C MAS NMR spectrum of the as-made zeolite (top). Spinning side bands are marked with “*”.

Fig. 4 ¹H NMR spectra in D₂O solution of the pristine 3BDMI bromides (bottom) and of the dissolved as-made 3BDMI-HPM-12 zeolite (top, methanol added as a chemical shift reference, the methyl group at 3.34 ppm).

Table 2 Chemical analysis results of as-made HPM-12 zeolites in this work

Gef (entry)^a	C(%)	H(%)	N(%)	C/N^b	H/N^b	TG^c	Empirical composition^d
a Entry in Table 1. b Molar ratios, the theoretical values are given in parentheses. c Solid residues after thermal analysis at 1000 °C (the amount in parentheses stands for the TO2 content in a unit cell given in the last column). d SDA calculated from the N percent assuming the organics are intact and are charge-balanced by the F^− ion, TO2 (T represents Si or Ge or both) from the residue after TG and H2O from the excess H. Here, we assume no loss of Ge during TG, although there is ample evidence of redox processes affecting Ge, potentially leading to sublimation of GeO, during calcination.^26
0.3 (17)	9.65	1.44	3.14	3.58 (3.25)	6.39 (5.5)	81.6 (82.7)	|C13H22N4F2|2.42[Si0.7Ge0.3O2]48(H2O)4.3
0.5 (23)	8.66	1.33	2.68	3.77 (3.25)	6.88 (5.5)	83.4 (84.4)	|C13H22N4F2|2.27[Si0.5Ge0.5O2]48(H2O)6.3
0.3 (20)	8.09	1.17	2.56	3.69 (3.25)	6.33 (5.5)	85.3 (86.0)	|C13H22N4F2|1.90[Si0.7Ge0.3O2]48(H2O)3.1

---

These two spectra confirm the integrity of the occluded imidazolium dications. The ¹³C NMR spectrum of the dissolved zeolite (Fig. 3, middle) shows distinct and well-resolved resonances within the range of the expected chemical shifts of each carbon atom, and the low field resonances of carbon atoms of the imidazolium ring (carbons b and c), which are overlapped into a single band in the zeolite, are clearly resolved in the spectrum of the dissolved zeolite. More importantly, the resonance of the carbon atom in the middle of the methylene chain (carbon g) is at the right chemical shift at ∼29 ppm in the dissolved zeolite instead of the ∼20 ppm observed in the as-made zeolite. Thus, the up-field shift in the as-made zeolite must be due to the occlusion of the dication in the pores (see Computational results below).

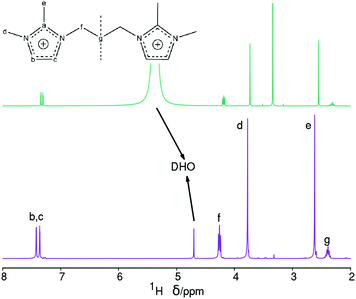
On the other hand, the ¹H NMR spectrum of the dissolved zeolite (Fig. 4, top) exhibits all the expected resonances with the correct multiplicities and relative intensities. However, we note a large ¹H chemical shift displacement when this spectrum is compared to the spectrum of the pristine bromide. An overall chemical shift of 0.16–0.20 ppm to a higher field is featured for the liberated dication compared to the bromide. By contrast, the DHO signal shifted to a lower field and by a much larger amount (around 0.54 ppm). Similar shift trends, although by smaller amounts, were found in our previous work.²⁷ The shift in DHO could be attributed to the effect of HF enhancing hydrogen bonds, because the shift is too large to be caused by a different measurement temperature.²⁸ On the other hand, the effect on the cation could be due to its different concentration in each studied solution. Thus, as the changes in chemical shifts may cause some uncertainty in our results and conclusions, and for the benefit of clarifying the methodology of analyzing dissolved zeolites, we recorded the ¹H NMR spectra of four blank solutions containing the same concentration of dication as in the dissolved zeolite. Two of these blank solutions contain also SiO₂ in the same amount as in the dissolved zeolite, one of them contains also the same concentration of HF (blank 1, mimicking the dissolved zeolite solution), and the other blank a quarter of that concentration (blank 2). The third blank contains only the dication and the fourth contains also HCl in the required amount to provide the same pH as in the first blank. All the blanks had a small amount of methanol added as a chemical shift reference (H at the methyl group at 3.34 ppm) as recommended for experiments in D₂O.²⁸ Finally, we recorded the ¹H NMR spectrum of concentrated solution of the SDA in D₂O (blank 5, 20 times as concentrated in 3BDMI as the other blanks). These experiments are obviously aimed at discerning the effect of cation concentration, HF concentration and pH on the ¹H chemical shifts.

The ¹H NMR blank experiments corroborate our guesses (Fig. 5²⁹ and Table 3). First, the blank mimicking the dissolved zeolite (blank 1) has a DHO resonance at 5.5 ppm, while the blank having a quarter HF (blank 2) has a DHO resonance at 5.0, and the blank containing only the SDA has a DHO resonance at a more typical 4.8 ppm, demonstrating a downfield shift of the DHO signal as the fluoride concentration increases, which we attribute to an enhanced hydrogen bonding.³⁰ Second, there is also a small but noticeable dependency of the chemical shift of the SDA protons on the concentration of the SDA, with a 0.2–0.3 ppm downfield shift of all the protons as the concentration increases 20 times (Fig. 5 and Table 3, blank 5); note that in this case the DHO signal at around 4.7 ppm remains unaltered. The last three rows in Table 3 show variability in “routine” analysis of pristine 3BDMI. On the other hand, the influence of HF and the SDA concentration on the ¹³C chemical shifts is much less noticeable, as they are small (≤1 ppm) compared to the whole span of the spectra (over 110 ppm, Table S1†).

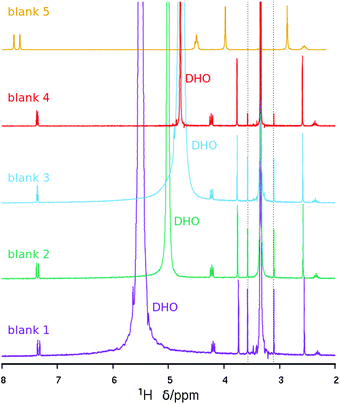Fig. 5 ¹H NMR spectra of the blank solutions listed in Table 3. The intensity of the concentrated blank has been decreased to give approximately the same intensity as the rest. The spectra have been referenced to the methyl protons in methanol at 3.34 ppm (the dashed lines mark satellite lines due to ¹H–¹³C coupling).²⁹

Table 3 ¹H NMR chemical shifts in ppm of the dissolved zeolite and of blank solutions designed to show the dependencies of chemical shifts on the concentration and presence of other species

Experiment	3BDMIBr^a	HF^a	SiO2 ^a	DHO	b,c^b	f	d	e	g
a Relative to the concentration in the dissolved zeolite NMR experiment. b Measured at the center of the multiplet. c Hard to detect due to the high SDA concentration and overlap with the tail of the SDA's “f” resonance. d HCl to achieve the same pH as in the zeolite NMR experiment. e The spectrum in Fig. 4, bottom. f Routine NMR experiments to check the purity of the SDA (concentration not determined and variable in different experiments) showing significant variability.
Dissolved zeolite	1	1	1	5.4	7.33	4.19	3.73	2.55	2.31
Blank 1	1	1	1	5.5	7.34	4.20	3.74	2.55	2.31
Blank 2	1	1/4	1	5.0	7.36	4.22	3.76	2.58	2.34
Blank 3	1	0	0	4.8	7.36	4.22	3.76	2.58	2.35
Blank 4	1	1 (HCl)^d	0	4.8	7.36	4.23	3.77	2.59	2.36
Blank 5	20	0	0	—^c	7.73	4.50	3.98	2.86	2.55
Pristine SDA^e	—^f	0	0	4.7	7.40	4.26	3.78	2.62	2.39
Pristine SDA	—^f	0	0	4.7	7.31	4.18	3.71	2.53	2.31
Pristine SDA	—^f	0	0	4.7	7.34	4.21	3.73	2.56	2.34

---

Finally, we note also that there is an interesting influence of both the presence of HF and the concentration of SDA on the signals of ¹H attached to the imidazolium ring (Fig. S5†). For the diluted SDA without HF the signal is a typical AB spin system. Addition of HF increases a bit the separation of the multiplet, while a 20 time increase in concentration not only causes a downfield shift but also converts the AB multiplet into an AZ spin system consisting of two doublets. This is not due to the effect of pH, since a solution with the same pH attained by addition of HCl does not show such a big effect. We reckon these effects must be due to interaction of the imidazolium ring with F in the first case and to imidazolium-imidazolium interactions in the latter. These observations suggest that imidazolium-fluoride and imidazolium-imidazolium interactions may be of interest during the crystallization of zeolites under fluoride and imidazolium structure-direction because of the similar conditions: in these systems there is typically a 1 : 1 SDA : F ratio (as in blank 1) and the H₂O/TO₂ ratios (typically 3–10) are in a similar range as in our concentrated blank (D₂O/SDA = 9.26, equivalent to H₂O/TO₂ = 4.63 for a typical SDA/TO₂ ratio of 0.5).

The ¹H and ¹³C NMR spectra of the dissolved zeolite, with the understanding of the effects of SDA concentration and the presence of HF, unambiguously demonstrate that 3BDMI, and not decomposed products, is the actual organic SDA in the crystallization of HPM-12. In addition, the ¹H and ¹³C NMR spectra of the dissolved zeolite suggest that 3BDMI is a rather stable organic SDA under the hydrothermal conditions used, as opposed to some other dications containing a three methylene bridge. This in part may be due to our close to neutral synthesis conditions, but in part may be also due to the fact that the positive charges are not strongly located at the N atoms attached to the bridge but they are widely distributed over the imidazolium ring according to our calculation of Mülliken charges by DFT (not included). Nonetheless, this stability is remarkable and contrasts with our prior observation of reduced stability of another imidazolium-based three methylene bridged dication under similar conditions.¹⁰

The up-field shift of carbon g resonance by around 9 ppm in the ¹³C MAS NMR spectrum (Fig. 3) must be thus due to the occlusion of 3BDMI in the zeolite pores and is, in our opinion, notable because of its magnitude. It is much larger, for instance, than the up-field shift experienced by tetramethylammonium cations upon encapsulation in large supercages (1 ppm) or small gmelinite (2 ppm) or sodalite cages (3 ppm) in different zeolites,³¹ and is similar to the 10 ppm up-field shift experienced by the central two carbons of the small and neutral tetramethyl-1,2-ethylenediamine in ZSM-39 (10 ppm). The large shift in ZSM-39 is caused by the double amine spanning two cages by crossing through a small 6MR, a very peculiar situation that causes a strong electronic shielding of the –C₂H₄– group by the very close oxygen atoms in the window.³²

The thermal gravimetric analysis (TG) of as-made HPM-12 samples is shown in Fig. S6.† It can be seen that fewer organics were entrapped for samples synthesized with higher Ge_f and the same water content (see curves a and c). However, as-made HPM-12 zeolites obtained with the same Ge_f but different water contents show that fewer organics were occluded upon dilution (see curves a and b). We, anyway, warn that TG measurements of Ge-containing zeolites may be affected by redox reactions of framework Ge, with possible loss of Ge in the form of volatile GeO, which is more likely for zeolites with no large pores.²⁶

The ¹⁹F MAS NMR spectrum of HPM-12 shows the presence of fluoride anions occluded in D4R units with varying Ge content as a function of the Ge_f of the samples. The assignment of sites may be done based on our previous analysis of the STW zeolite Si, Ge substitutional series.³³ It is necessary to take also into account that, probably due to structural reasons, the ¹⁹F resonances of F in D4R in STW are about 2–5 ppm downfield shifted compared to other zeolites: for instance the chemical shift of F in pure silica D4R in STW is at −35.7 ppm,²⁷ whereas it is in the −38/−41 ppm range in other zeolites.^16,34 With this in mind, the main resonance in both ¹⁹F spectra in Fig. 6 must be assigned to F in D4R with Ge–Ge pairs (but not larger clusters, i.e. resonance type III). The material with lower Ge content has also a clear resonance at −21.7 ppm, assigned to F in D4R with Ge but without Ge–Ge pairs (resonance type II). This resonance is also present with a very low intensity in the material with a higher Ge fraction. Finally, a small resonance at −39.8 ppm assigned to fluoride occluded in pure silica D4R (resonance type I) is only present in the more siliceous zeolite.

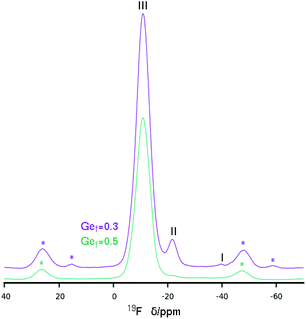Fig. 6 ¹⁹F MAS NMR of two HPM-12 samples obtained at different Ge_f. Spinning side bands are marked with *. Main resonances are ascribed to types I–III following ref. 33.

Computational results

An initial conformational search of 3BDMI gave two most stable conformers with a very similar stability (Table 4, relative energies, REs, in entries 1 and 4). In these conformations, 3BDMI displays a molecular elongated shape, with the two imidazolium rings in a torsional (C_a–N–C_f–C_g) angle of around (±) 100° (hereafter referred to as the ‘vac’ configuration). The two conformers differ in the relative orientation of the two imidazolium rings, with the methyl C_e groups pointing to the same (labelled as ‘ss’) or opposite (‘op’) sides (see the relevant conformations in Fig. S7†).

Table 4 Stability (relative energy, RE, with respect to the most stable case in vacuo, entries 1, 2, 4, 5, or confined within *UOE, entries 3, 6, calculated by DFT + D methods and given in kcal mol⁻¹), and theoretical ¹³C NMR chemical shifts (C labels as in Fig. 3) of 3BDMI dications in different environments (in vacuo and confined in *UOE)

Conformer	System	Imid.	Orient./*UOE	Entry	Stability	^13C NMR calculated chemical shift
					R.E.	e	g	d	f	c	b	a
ss	vacuo	vac	—	1	0.0	4.6	33.1	36.1	46.7	121.8	128.2	144.4
		conf	—	2	1.7	5.3	22.9	34.9	47.2	118.1	126.4	145.4
	*UOE	conf	[010]	3	0.0	11.1	22.0	39.7	48.7	124.1	126.0	144.6
op	vacuo	vac	—	4	0.0	4.7	32.9	35.3	47.2	122.7	127.7	144.2
		conf	—	5	3.9	5.0	27.6	35.9	50.8	119.8	127.9	145.4
	*UOE	conf	[010]	6	6.9	10.4	26.7	39.4	52.8	124.6	126.7	144.6

---

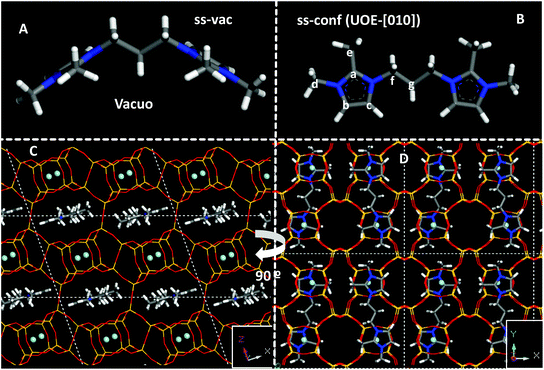
We next studied the docking of both conformers within the *UOE framework. After analyzing the void volume of this zeolite (Fig. S8†), we realized that there are two potential orientations for the 3BDMI cations: along the 10MR elliptical channels in the ‘b’ axis (labelled as [010]), or along the ‘a’ axis, spanning two 10MR channels, and with the alkyl spacer passing through distorted 8MR windows (labelled as [100]) (Fig. S8,† white arrow). Both orientations were studied by DFT + D, with the two possible orientations of the conformers (‘ss’ and ‘op’) (Fig. S9†). A much higher stability was found for the orientation along the 10MR channels ([010]), with energy differences higher than 24 kcal mol⁻¹ for 3BDMI. This is explained due to the small size of the distorted 8MR windows where the alkyl spacer passes through the [100] orientation (Fig. S9,† bottom). Hence, we discarded the latter SDA orientation and focused on the [010] orientation. In this case, for each of the two conformers (‘ss’ and ‘op’), we also studied two possible packing arrangements: with SDA cations in adjacent 10MR channels in the same orientation or turning 180° around the channel axis. Energy results showed that the most stable situation was found for 3BDMI dications in ‘ss’ orientation and turning 180° between adjacent SDAs (Fig. 7, bottom). It is very interesting to note that the 3BDMI dications confined within the *UOE framework (along the [010] axis) display a different conformation than the most stable conformation in vacuo: upon confinement, the elliptical shape of the 10MR channels causes that the imidazolium rings are arranged perpendicularly to the most stable orientation in vacuo, giving a C_a–N–C_f–C_g torsional angle of ∼180° (compare orientations in Fig. 7A, in vacuo, and Fig. 7B, confined in *UOE). We refer to the latter conformation as ‘conf’ (for confined, with a torsional angle of ∼180°) and ‘vac’ for the stable conformation in vacuo (torsional angle ∼100°).

Fig. 7 Most stable conformers of 3BDMI in vacuo (A, top-left) and when confined within the *UOE framework (B, top-right). Bottom: two views (C and D) of the most stable location of the 3BDMI cation within the *UOE framework, aligned with the [010] axis in “ss” conformation. F anions are displayed as balls.

We then calculated the theoretical ¹³C NMR chemical shifts of the 3BDMI dication as a function of its conformation (‘ss’/'op’ or ‘vac’/‘conf’) in vacuo and within the *UOE framework (Table 4). No large differences are observed for 3BDMI dications (in vacuo) in the ‘vac’ configuration as a function of the orientation of the rings (‘ss’/‘op’: compare entries 1 and 4, both showing a similar stability in vacuo). These ¹³C NMR theoretical shifts are in reasonable agreement with the experimental values in aqueous solution of the pristine cation. If we now compare with the conformation that 3BDMI cations display when confined within the *UOE framework (‘conf’, calculated in vacuo, entry 2), we observe that all the ¹³C δ are similar to those of the ‘vac’ conformation (entry 1), except for C_g, which shows a very large upfield shift of ∼10 ppm. This might be caused by the closeness of C_g to the C_c imidazolium C atom in the ‘conf’ configuration (Fig. 7B). In the ‘op’ conformation (entries 5 and 6), such δ shift is less marked because the conformation of the alkyl chain is different; however, this location is notably less stable in the ‘conf’ configuration in *UOE (by 7 kcal mol⁻¹), and hence we discarded this case. We then compared the ¹³C δ of the ‘ss’ conformation confined within the *UOE framework (in [010] orientation), which is the most stable host–guest system, and we again observed a similar upfield shift of the C_g NMR signal (to 22 ppm, Table 4, entry 3). This clearly indicates that the experimental observation of the shift of the NMR signal of C_g is caused by the change in the conformation of 3BDMI in aqueous solution (assumed to be the same as in vacuo) and when confined within the *UOE framework. If we compare the effect of confinement with 3BDMI in the same ‘conf’ conformation (entries 2 and 3), we observe also a smaller shift of the methyl C atoms (C_e and C_d), which is not reproduced in the experimental NMR. This might be caused by the freezing of the –CH₃ group in the theoretical calculations, or by solvent effects of H₂O not taken into account in the calculations. It is interesting to note that our calculations, which are validated by the accurate calculation of a large experimental shift in a ¹³C NMR resonance, clearly show that the confinement of 3BDMI in the *UOE zeolite induces a change in the organic dications to a less stable conformation, which must be compensated by strong host–guest interactions.

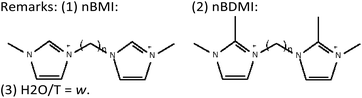
Finally, worth noting is the spatial relationship between the imidazolium rings and the location of F anions in the *UOE framework (see Fig. 7D): it can be appreciated that both oppositely-charged units, imidazolium (+) and F (−), are located close to each other. Therefore, the separation between the positive charges imposed by the length of the alkyl spacer in the SDA dication imposes the distance between adjacent F ions and, as a consequence, between adjacent D4R units that host those F anions, similar to our observations in more-open frameworks.¹⁴Table 5 summarizes the observed effects with two series of dications, where the existence of “default phases” can be clearly discerned: these phases (TON or MTW, for methylimidazolium, nBMI, and dimethylimidazolium-based, nBDMI, dications, respectively) appear when the degree of dilution increases, a condition typically leading to a loss of specificity in structure-direction, in our experience.³⁵ Thus, under those dilute conditions only 4BDMI shows a robust structure-direction action, leading to STW even when MTW crystallizes first. under concentrated conditions, the nBMI series yields MFI for n = 4, 8 and 10 and the default TON at any other n tried, while the nBDMI series yields STW for n = 4 and 5, *BEA for n = 8, MWW for n = 10, and MTW or amorphous for the rest. In the presence of Ge, only phases containing D4R are obtained, with a strong dependency on n: *UOE (n = 3), STW (n = 4, 5, 6) and HPM-7 (POS) and HPM-8 (intergrowth of polymorphs D and E of the beta family, with a predominance of polymorph D) for n = 8 and 10.

Table 5 Summary of structure-directing effects observed in the synthesis of zeolites using two series of dications of varying length and fluoride

SDA	n	Si Low w	Si High w	Si, Ge
nBMI	3	TON ^10	TON ^10
	4	MFI ^10	TON ^10
	5	TON ^10	TON ^10
	6	TON ^10	TON ^10
	8	MFI ^11	TON ^11
	10	MFI ^11	TON ^11
nBDMI	3	Amorphous	Amorphous	*UOE
	4	STW ^12	STW ^12	STW ^12
	5	STW ^12	MTW ^12	STW ^12
	6	MTW ^12	MTW ^12	STW ^12
	8	*BEA ^13	MTW ^13	POS, BetaDE ^14
	10	MWW ^13	MTW ^13	POS, BetaDE ^14

---

Although these results are similar to those observed years ago for linear diquats, in that case the effect was interpreted only in a purely topological way, while here we think both the topology and coulombic effects are in place. We think that the fact that the fluoride location is very specific in zeolites, compared to the Al or silanolate location, makes the difference. Hence, the length of the alkyl spacer seems to be of importance in the structure-direction toward particular frameworks with specific distances between D4R units in synthesis mediated by fluoride.

Conclusions

The 3BDMI dication studied in this work shows a remarkable structure-direction specificity toward the *UOE zeolite, as long as germanium is present in the synthesis mixture in sufficient amounts (Ge_f equal to or above 0.2). The hydrothermal stability of this dication, in which the charged moieties are separated by a short link of only three methylene units, is also remarkable. The integrity of the dication inside the zeolite is demonstrated by ¹³C and ¹H NMR in D₂O after dissolution of the zeolite. Large shifts of the ¹H NMR resonances of DHO and the dication are due to the presence of HF and dilution effects, respectively. The observation of a large ¹³C shift in the central carbon of the bridge after occlusion in the zeolite is explained by a change in conformation that brings two C atoms close together, as demonstrated by DFT calculations. This explanation validates our theoretical approach. The conformation taken by the dication in the zeolite incurs an energetic penalty that must be compensated by the host–guest interactions. This work shows once again that the separation of positively charged moieties of dications matches the separation of F-containing D4R units in zeolites prepared by the fluoride route, further supporting the notion of a structure-direction based on the distances between charges in the SDA and the zeolite.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors acknowledge financial support from the Spanish Ministerio de Economía y Competitividad, the Spanish Agencia Estatal de Investigación and the EU's Fondo Europeo de Desarrollo Regional under projects MAT2016-77496-R (AEI/FEDER, UE) and MAT2015-71117-R (MINECO/FEDER, UE). We acknowledge the support of the publication fee by the CSIC Open Access Publication Support Initiative through its Unit of Information Resources for Research (URICI). P.L. is grateful to the China Scholarship Council (CSC) for a fellowship and to the Dalian Institute of Chemical Physics for permission to leave. Centro Técnico Informático-CSIC is acknowledged for running the calculations and Biovia for providing the computational software. We also thank L. A. Villaescusa for helpful comments.

Notes and references

1. M. E. Davis and R. F. Lobo, Chem. Mater., 1992, 4, 156–768.
2. Y. Kubota, M. M. Helmkamp, S. I. Zones and M. E. Davis, Microporous Mater., 1996, 6, 213–229.
3. D. Jo and S. B. Hong, Chem. Commun., 2018, 54, 487–490.
4. J. L. Casci, B. M. Lowe and T. V. Whittam, Zeolite EU-1, Eur. Pat, 42226A1, 1981.
5. J. L. Casci, B. M. Lowe and T. V. Lowe, Method of Making Zeolite EU-2, US Pat, 1989, 4836996.
6. J. L. Casci and A. Stewart, Zeolite, Eur. Pat, 1990, 377291.
7. Ch. Baerlocher and L. B. McCusker, Database of Zeolite Structures: http://www.iza-structure.org/databases/, accessed on August 29th 2019.
8. A. Moini, K. D. Schmitt, E. W. Valyosick and R. F. Polomsky, Zeolites, 1994, 14, 504–511.
9. L. Gómez-Hortigüela and M. A. Camblor, Struct. Bonding, 2018, 175, 1–41.
10. A. Rojas, L. Gómez-Hortigüela and M. A. Camblor, J. Am. Chem. Soc., 2012, 134, 3845–3856.
11. P. Lu, L. Gómez-Hortigüela and M. A. Camblor, Dalton Trans., 2018, 47, 7498–7504.
12. P. Lu, L. Gómez-Hortigüela, L. Xu and M. A. Camblor, J. Mater. Chem. A, 2018, 6, 1485–1495.
13. P. Lu, L. Gómez-Hortigüela and M. A. Camblor, Chem. – Eur. J., 2019, 25, 1561–1572.
14. P. Lu, A. Mayoral, L. Gómez-Hortigüela, Y. Zhang and M. A. Camblor, Chem. Mater., 2019, 31, 5484–5493.
15. S.-H. Lee, C.-H. Shin, D.-K. Yang, S.-D. Ahn, I.-S. Nam and S. B. Hong, Microporous Mesoporous Mater., 2004, 68, 97–104.
16. M. O. Cichocka, Y. Lorgouilloux, S. Smeets, J. Su, W. Wan, P. Caullet, N. Bats, L. B. McCusker, J. L. Paillaud and X. Zou, Cryst. Growth Des., 2018, 18, 2441–2451.
17. A. Rojas, E. Martínez-Morales, C. M. Zicovich-Wilson and M. A. Camblor, J. Am. Chem. Soc., 2012, 134, 2255–2263.
18. Forcite Module, Material Studio 2017 R2, BIOVIA.
19. S. L. Mayo, B. D. Olafson and W. A. Goddard, J. Phys. Chem., 1990, 94(26), 8897–8909.
20. Conformer Calculation Module, Material Studio 2017 R2, BIOVIA.
21. S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. J. Probert, K. Refson and M. C. Payne, Z. Kristallogr., 2005, 220, 567–570.
22. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
23. C. J. Pickard and F. Mauri, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 245101.
24. P. Lu, L. A. Villaescusa and M. A. Camblor, Chem. Rec., 2018, 18, 713–723.
25. M. A. Camblor, L. A. Villaescusa and M. J. Díaz-Cabañas, Top. Catal., 1999, 9, 59–76; M. A. Camblor and S. B. Hong, Synthetic Silicate Zeolites: Diverse Materials Accessible Through Geoinspiration, in Porous Materials, John Wiley & Sons, Chichester, 2011, pp. 265–325.
26. L. A. Villaescusa and M. A. Camblor, Chem. Mater., 2016, 28, 7544–7550.
27. A. Rojas, O. Arteaga, B. Kahr and M. A. Camblor, J. Am. Chem. Soc., 2013, 135, 11975–11984.
28. H. E. Gottlieb, V. Kotlyar and A. Nudelman, J. Org. Chem., 1997, 62, 7512–7515.
29. M. Pecul and T. Helgaker, Int. J. Mol. Sci., 2003, 4(3), 143–157.
30. H. Eckert, J. P. Yesinowski, L. A. Silver and E. M. Stolper, J. Phys. Chem., 1988, 92, 2055–2064.
31. S. Hayashi, K. Suzuki, S. Shin, K. Hayamizu and O. Yamamoto, Chem. Phys. Lett., 1985, 113, 368–371.
32. X. Tang, Y. Sun, T. Wu, L. Wang and L. Fei, J. Chem. Soc., Faraday Trans., 1993, 89, 1839–1841.
33. R. T. Rigo, S. R. G. Balestra, S. Hamad, R. Bueno-Pérez, A. R. Ruiz-Salvador, S. Calero and M. A. Camblor, J. Mater. Chem. A, 2018, 6, 15110–15122.
34. P. Caullet, J. L. Guth, J. Hazm, J. M. Lamblin and H. Gies, Eur. J. Solid State Inorg. Chem., 1991, 28, 345–361; L. A. Villaescusa, P. A. Barrett and M. A. Camblor, Chem. Mater., 1998, 10, 3966–3973; L. A. Villaescusa, P. A. Barrett and M. A. Camblor, Angew. Chem., Int. Ed., 1999, 38, 1997–2000; A. Rojas, M. L. San-Roman, C. M. Zicovich-Wilson and M. A. Camblor, Chem. Mater., 2013, 25, 729–738; A. Rojas and M. A. Camblor, Dalton Trans., 2014, 43, 10760–10766.
35. L. A. Villaescusa, PhD thesis, Universitat Politècnica de València, 1999.

---

Footnotes

† Electronic supplementary information (ESI) available: Additional PXRD patterns, details of ¹H NMR blank spectra, thermogravimetric analyses, the void volume of zeolite *UOE and the location of the organic SDA, and a table showing ¹³C NMR chemical shifts of the dissolved zeolite and of the blank experiments. See DOI: 10.1039/C9DT04089G

‡ Present Address: Johns Hopkins University, 3400 Charles ST, Institute for Nanobiotechnology/WSE, Baltimore, MD, USA.

---