Mechanism and origins of ligand-controlled Pd(ii)-catalyzed regiodivergent carbonylation of alkynes†
Abstract
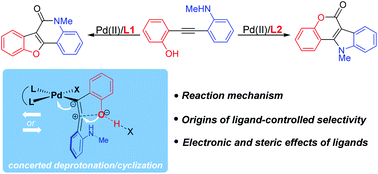
Transition-metal-catalyzed carbonylation provides a useful approach to synthesize carbonyl-containing compounds and their derivatives. Controlling the regio-, chemo-, and stereoselectivity remains a significant challenge and is the key to the success of transformation. In the present study, we explored the mechanism and origins of the ligand-controlled regiodivergent carbonylation of alkynes with competitive nucleophilic amino and hydroxy groups by density functional theory (DFT) calculations. The proposed mechanism involves O(N)-cyclization, CO insertion, N–H(O–H) cleavage, C–N(C–O) reductive elimination and regeneration of the catalyst. The chemoselectivity is determined by cyclization. Instead of the originally proposed switch of competitive coordination sites, a new type of concerted deprotonation/cyclization model was proposed to rationalize the ligand-tuned chemoselectivity. The electron-deficient nitrogen-containing ligand promotes the flow of electrons during cyclization, and so it favors the O-cyclization/N-carbonylation pathway. However, sterically bulky and electron-rich phosphine controls the selectivity by a combination of electronic and steric effects. The improved mechanistic understanding will enable further design of selective transition-metal-catalyzed carbonylation.


 Please wait while we load your content...
Please wait while we load your content...