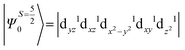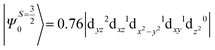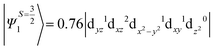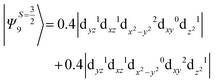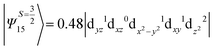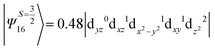Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Investigation of the magnetic anisotropy in a series of trigonal bipyramidal Mn(II) complexes†
Moya A.
Hay
 a,
Arup
Sarkar
a,
Arup
Sarkar
 b,
Katie E. R.
Marriott
a,
Claire
Wilson
b,
Katie E. R.
Marriott
a,
Claire
Wilson
 a,
Gopalan
Rajaraman
a,
Gopalan
Rajaraman
 *b and
Mark
Murrie
*b and
Mark
Murrie
 *a
*a
aWestCHEM, School of Chemistry, University of Glasgow, Glasgow, G12 8QQ, UK. E-mail: mark.murrie@glasgow.ac.uk
bDepartment of Chemistry, Institute of Technology Bombay, Powai, Mumbai, Maharashtra 400 076, India. E-mail: rajaraman@chem.iitb.ac.in
First published on 28th June 2019
Abstract
Understanding how the magnetic anisotropy in simple coordination complexes can be manipulated is instrumental to the development of single-molecule magnets (SMMs). Clear strategies can then be designed to control both the axial and transverse contributions to the magnetic anisotropy in such compounds, and allow them to reach their full potential. Here we show a strategy for boosting the magnetic anisotropy in a series of trigonal bipyramidal Mn(II) complexes – [MnCl3(HDABCO)(DABCO)] (1), [MnCl3(MDABCO)2]·[ClO4] (2), and [MnCl3(H2O)(MDABCO)] (3). These have been successfully synthesised using the monodentate [DABCO] and [MDABCO]+ ligands. Through static (DC) magnetic measurements and detailed theoretical investigation using ab initio methods, the magnetic anisotropy of each system has been studied. The calculations reveal that the rhombic zero-field splitting (ZFS) term (E) can be tuned as the symmetry around the Mn(II) ion is changed. Furthermore, an in silico investigation reveals a strategy to increase the axial ZFS parameter (D) of trigonal bipyramidal Mn(II) by an order of magnitude.
Introduction
Magnetic anisotropy gives rise to a preference for the magnetisation to be pinned in one of two orientations for an easy-axis type system.1 In the context of molecular magnetism the associated axial anisotropy (D), along with spin ground state (S), dictate the resulting magnetic properties of single-molecule magnets (SMMs)2,3–6 due to their potential applications in areas such as data storage, quantum computing, and molecular spintronics.7,8 Magnetic anisotropy in particular transpires due to zero-field splitting (ZFS) which removes the degeneracy of Ms states in zero-field for axially symmetric molecules where S > 1/2 through the effects of spin–orbit coupling (SOC).1 This gives rise to two distinct ZFS terms – the axial and rhombic ZFS parameters, denoted by D and E respectively. Candidates of particular interest for studying the ZFS parameters are monometallic single-molecule magnets, otherwise known as single-ion magnets (SIMs), which by their simplest definition consist of a single paramagnetic centre in a given ligand environment.9 In particular, the use of 3d based systems to investigate the role of magnetic anisotropy has surged in recent years with changes in both structural and electronic environment altering the ZFS parameters in a noticeable and detectable manner.10 Although not expected to exhibit slow relaxation of the magnetisation, due to their essentially isotropic spin ground state, high spin MnII monometallic complexes present an additional opportunity to probe the nature of magnetic anisotropy in certain coordination environments,11,12 and magneto-structural correlations can be developed.13–17 Here we report an experimental and computational investigation into a series of trigonal bipyramidal MnII monometallic complexes. Furthermore, we propose a strategy for increasing the axial zero-field splitting parameter using magneto-structural correlations developed via ab initio methods. These suggest the potential for an increase in D by an order of magnitude for complexes of this type, which would surpass the current record for MnII mononuclear complexes.18Experimental section
Materials and physical methods
All reagents and solvents were obtained from commercial suppliers and used without further purification. The ligand [MDABCO][I] was prepared as previously reported, with minor modifications.13,19 [MnCl3(DABCO)(HDABCO)] (1) was synthesised following the same method as previously reported.20 CAUTION! [ClO4]− salts are potentially explosive, and so should be handled with care and in small quantities. Elemental analysis (EA) was performed in-house by the microanalysis service at the School of Chemistry, University of Glasgow. Additionally, air-sensitive EA was carried out on 2via the Elemental Analysis Service, University of Strathclyde. IR spectra were collected using a Shimadzu FTIR spectrometer in the range 4000–600 cm−1. Crystallographic data were collected for 1–3 at 100 K with Mo-Kα radiation (λ = 0.71073 Å) using a Bruker APEXII CCD diffractometer with an Oxford Cryosystems n-Helix low-temperature device mounted on a sealed tube generator. Structures were solved using SHELXT and refined using full-matrix least-squares refinement using Olex2 software.21,22 The powder X-ray patterns were collected on a PANalytical XPert MPD, with Cu Kα1 radiation at ambient temperature over a range of 5° < 2θ < 50° using a step size of 0.0167°. In each case, the calculated pattern was generated from Mercury using the .cif file of the structure at 100 K.23 All magnetic measurements were carried out on powdered crystalline samples restrained in eicosane using a Quantum Design MPMS-XL SQUID magnetometer. The diamagnetic contribution of the sample holder and eicosane were both corrected for by measurements, and the magnetic susceptibility of each sample using Pascal's constants.Synthetic methods
Results and discussion
Crystal structure descriptions
Complex 1 crystallises in the trigonal R32 space group with the corresponding crystallographic data given in Table S1.† The complex has two DABCO moieties coordinated in the axial positions of a central MnII, each through a single N donor (see Fig. 1, left) and with 3 symmetry related Cl sites occupying the equatorial positions completing the trigonal bipyramidal (TBP) coordination geometry. The Cl–Mn–Cl, Cl–Mn–N and N–Mn–N angles are 120°, 90° and 180°, respectively. Considering the first coordination sphere, the Mn centre possesses D3h symmetry. The asymmetric unit contains 1/6 of a molecule, a Mn site, a third of a DABCO and one Cl site with a 3-fold rotation axis through the Mn and the N atoms of the DABCO moieties and 2-fold axes along each of the Mn–Cl relating the two DABCO moieties. The shortest intermolecular Mn⋯Mn distance is 7.42 Å. There is a strong intermolecular hydrogen bonding interaction (N⋯H–N) with a N⋯N distance of 2.644(7) Å pseudo-forming a chain (see Fig. S2†). Note, the position of this proton is clear in the difference Fourier map and the symmetry necessitates it being disordered over two symmetry related half-occupied sites suggesting the hydrogen bonded chains run in both directions along the c-axis. SHAPE studies were carried out on complex 1 to quantify the extent of distortion away from the ideal TBP coordination environment. This involved the calculation of continuous shape measures (CShMs) which provides a value corresponding to the agreement of the experimentally obtained atomic positions, and those expected from an ideal polyhedron with the same number of vertices.24 This then affords the geometry which most closely fits the experimental data obtained, with a value of 0 assigned to an ideal geometry. The results are summarised in Table S4† and confirm a very small distortion away from the ideal trigonal bipyramidal geometry with a CShM value of 0.007.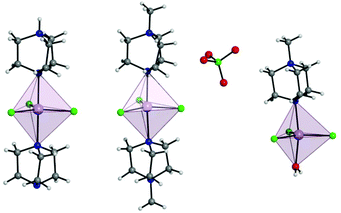 | ||
| Fig. 1 Depiction of a full molecule of 1 (left), 2 (middle), and 3 (right) with trigonal bipyramidal coordination polyhedra depicted. C, grey; Cl, green; H, white; Mn, lavender; N, blue. | ||
The use of [MDABCO]+ as a ligand was proposed to change the separation and orientation of the individual molecules in the crystal lattice to establish what impact this change in environment might have on the associated magnetic properties. This resulted in two different structures depending on the Mn(II) starting material employed: anhydrous MnCl2 leads to [MnCl3(MDABCO)2]·[ClO4] (2) whereas hydrated MnCl2 leads to [MnCl3(MDABCO)(H2O)] (3) as shown in Fig. 1 (see Table S1† for crystallographic data). Complex 2 crystallises in the orthorhombic Pca21 space group and is structurally analogous to the previously reported [NiCl3(MDABCO)2]·[ClO4] complex.13 Complex 3 however crystallises in the lower symmetry monoclinic P21/m space group. Similarly to complex 1, complex 2 contains a central MnII ion with TBP geometry (confirmed via CShMs) whereby three Cl− ligands are coordinated in the equatorial positions with a [MDABCO]+ moiety now occupying each of the axial positions. A perchlorate counter-ion is also present within the asymmetric unit along with a full molecule of 2, with four symmetry related, but differently oriented, molecules present in the unit cell (see Fig. S3†). In the case of complex 3 however, one of the axial positions is instead occupied by a coordinated H2O. Half a molecule is present within the asymmetric unit and two molecules are aligned antiparallel within the unit cell with respect to their C2 mirror planes (see Fig. S4†). A greater degree of distortion away from the ideal TBP geometry is present in 3 compared to 2 (see Fig. 1 and 2). This increase in distortion is additionally reflected in the bond lengths and angles surrounding the central MnII in 2 and 3 which are summarised in Tables S2 and S3.† Due to the perchlorate counter-ion in 2, the individual [MnCl3(MDABCO)2]+ cations are further separated within the crystal lattice compared to 1, with a minimum intermolecular Mn⋯Mn distance of 8.50 Å. This is longer when compared to 1 whereas in 3, the molecules are able to pack much more closely together with a minimum intermolecular Mn⋯Mn distance of 6.56 Å.
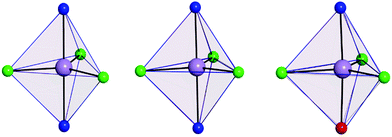 | ||
| Fig. 2 Coordination polyhedron of the central Mn(II) of 1 (left), 2 (middle) and 3 (right) shown in pale purple with the closest reference polyhedron for TBP geometry outlined in blue, as calculated using SHAPE.24–26 | ||
Magnetic properties
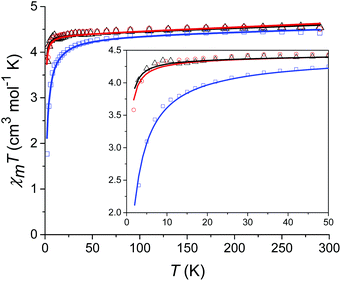
Prior to magnetic measurements, powder X-ray diffraction (PXRD) was used to confirmed phase purity by comparison to the pattern calculated from the single-crystal data using the software Mercury23 (see Fig. S5–S7†). PXRD reveals that upon grinding in air complex 2 decomposes to form complex 3, so for 2 air-sensitive CHN analysis and PXRD techniques were employed and SQUID samples prepared in an Argon-filled glovebox. The variable-temperature magnetic susceptibility data for 1–3 were collected between 290 K and 2 K under an applied DC field of 1000 Oe (see Fig. 3). In each case, the measurement was performed on a powdered crystalline sample restrained in eicosane to prevent torqueing or reorientation. At 290 K, all χmT values were in each case slightly higher than that based on the spin only formula value of 4.38 cm3 mol−1 K (where S = 5/2, g = 2). In all cases, this value slowly decreases until approximately 50 K after which varying low temperature behaviour is observed. This could be attributed to differences in short-range correlations between molecules within the three different structures. In the case of 1, two distinct maxima in χmT are observed – at 32 K and 10 K reaching values of 4.41 cm3 mol−1 K and 4.36 cm3 mol−1 K, respectively – with a final minimum value of 3.80 cm3 mol−1 K observed at 2 K. No clear maxima are observed for 2 and 3 and after 50 K, χmT drops off more rapidly due to a small zero-field splitting reaching a minimum value of 3.88 and 1.76 cm3 mol−1 K at 2 K respectively. The magnetisation measurements (M vs. H) were carried out between 0 and 5 T at 2, 4 and 6 K on all complexes (see Fig. S8†) and in each case the magnetisation was within range of the expected saturation value of 5.0Nβ at 2 K with values of 4.9, 5.0 and 4.8Nβ respectively. Attempts to fit the χmT vs. T and M vs. H data were carried out using the program Phi27 with the Hamiltonian given in eqn (1).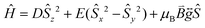 | (1) |
For complexes 1 and 2 the χmT vs. T data were fitted simultaneously with the M vs. H data (see Fig. 3). For complex 3 fits attempted that included the M vs. H data, either in conjunction with the χmT vs. T data or independently, failed to converge. Thus, an optimum fit using only the magnetic susceptibility data for 3 is shown in Fig. 3. In order to improve the fit, the g-factor and ZFS parameters were fixed, with values taken from the calculations (see Table 1). Parameters which were then fitted included a temperature independent paramagnetic (TIP) contribution to the susceptibility, which was required to replicate the high temperature data. Note, for high-spin Mn(II) a TIP contribution towards the susceptibility can be present if there are low-lying excited states to which the ground state can mix,28 consistent with the results of the ab initio calculations (vide infra). The second parameter determined from the fit was a contribution to the susceptibility from intermolecular interactions (zJ) which was required in order to replicate the low temperature data and was necessary for the fit to converge. The magnitude of zJ parameters extracted from the fits are similar for both complexes 1 and 2, however for complex 3 which has the smallest intermolecular distance between adjacent Mn(II) centres, this value is larger. Both the fixed and fitted parameters are summarised for complexes 1–3 in Table 1.
| D (cm−1) | E (cm−1) | TIP (cm3 mol−1) | zJ (cm−1) | R (%) | |
|---|---|---|---|---|---|
| 1 | −0.133 | 0 | 0.0008 | −0.013 | 99.9 |
| 2 | −0.137 | 0.004 | 0.0009 | −0.017 | 99.7 |
| 3 | −0.129 | 0.009 | 0.0005 | −0.126 | 99.7 |
Theoretical calculations
Before starting our discussion on the theoretical studies on these three Mn(II) complexes, we would like to give a brief outline regarding the computational methodology applied here to probe the zero-field splitting. Although these complexes possess a d5 isotropic electronic configuration, small but significant magnetic anisotropy arises from the excited quartet state due to the spin–orbit interaction. Also spin–spin coupling here cannot be ignored. Therefore we computed both the spin–orbit and spin–spin interactions towards the zero-field splitting on these three complexes.To probe the origin of the magnetic anisotropy of complexes 1–3 arising from spin–orbit interactions we performed CASSCF/NEVPT2 ab initio calculations, which are known to yield accurate estimation of Spin Hamiltonian parameters for such molecules.29–31 The high spin MnII ion has a totally symmetric 6A1 ground state and thus is expected to exhibit only a very small zero-field splitting. Calculations yield DSOC values of −0.112 cm−1, −0.113 cm−1 and −0.108 cm−1 for complexes 1–3, respectively (see Table 2). The computed g anisotropy is found to be isotropic and the estimated value of 2.00 also matches with the experimental magnetic data. Although DFT methods (CP-KS) have successfully predicted the zero-field splitting values for some reported Mn(II) complexes,12,32,33 these methods are proven to be inferior for the estimation of ZFS parameters. DFT-estimated spin–orbit values for complexes 1–3 are given in Table S8 (see ESI†) and these values are significantly overestimated when compared to the values obtained from ab initio methods.
| D SOC | D SS | D net | |E/D|SOC | g iso | |
|---|---|---|---|---|---|
| 1 | −0.112 | −0.021 | −0.133 | 0 | 2.0 |
| 2 | −0.113 | −0.024 | −0.137 | 0.036 | 2.0 |
| 3 | −0.108 | −0.021 | −0.129 | 0.079 | 2.0 |
The ground sextet state does not contribute to the ZFS and here the ZFS essentially arises due to the spin–flip excited quartet states which are greater than 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 higher in energy compared to the ground state, leading to a small contribution to the DSOC value (Tables S5–S7†). In the present case, all three complexes are in a trigonal bipyramidal geometry possessing ∼D3h point group symmetry. The computed ground state electronic configuration in all cases is dxz1dyz1dx2−y21dxy1dz21 and reflects a TBP shape (Fig. 4). The DZZ axis points towards the axial Mn–N bond, which is also colinear with the C3-axis of the molecule(s).
000 cm−1 higher in energy compared to the ground state, leading to a small contribution to the DSOC value (Tables S5–S7†). In the present case, all three complexes are in a trigonal bipyramidal geometry possessing ∼D3h point group symmetry. The computed ground state electronic configuration in all cases is dxz1dyz1dx2−y21dxy1dz21 and reflects a TBP shape (Fig. 4). The DZZ axis points towards the axial Mn–N bond, which is also colinear with the C3-axis of the molecule(s).
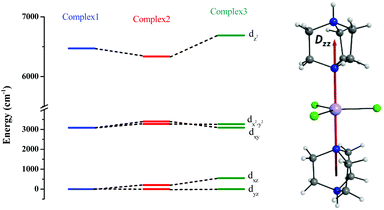 | ||
| Fig. 4 CASSCF-LFT d-orbital splitting of the ground state in complexes 1, 2 and 3, respectively (left). The DZZ anisotropy axis of complex 1 (right). | ||
The DSOC values of complexes 1–3 are small (around −0.1 cm−1) and here the ZFS arises from several spin–flip excitations. The corresponding equation, which is the sole term contributing to D is given below,29,34
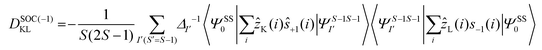 | (2) |
The above equation corresponds to the expression of the D parameter which arises due to the spin value less than one from the ground state spin. Here, DSOCKL is the axial ZFS parameter arising from the spin–orbit coupling (SOC) contribution, S is the total spin ground state of Mn(II), ẑK(i)ŝ+1(i) is the one-electron SOC operator and Ψ is the corresponding wavefunction of the system. From Tables S5–S7,† it can be seen that the first two quartet states at ∼22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 contribute significantly to the D value and their combined contribution is close to −0.6 cm−1 in all three complexes. The corresponding wavefunctions for these states are given below,
000 cm−1 contribute significantly to the D value and their combined contribution is close to −0.6 cm−1 in all three complexes. The corresponding wavefunctions for these states are given below,
The above two wavefunctions in the quartet states Ψ0 and Ψ1 contribute 76% each to the overall wavefunctions. The next significant contribution arises from the quartet excited state Ψ9 (10th excited state) and it is the same for the three complexes contributing around 1.5 cm−1 to the overall D value and it constitutes
i.e., a hole created in a dxy or dx2−y2 orbital respectively. Though this state is ∼30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 higher in energy compared to the ground state, its contribution is very large compared to the other contributions. Such large positive contributions compensate the negative contributions shown earlier, leading to small net D value for complexes 1–3. Another two significant negative contributions arise from the quartet excited states Ψ15 and Ψ16 (16th and 17th excited states),
000 cm−1 higher in energy compared to the ground state, its contribution is very large compared to the other contributions. Such large positive contributions compensate the negative contributions shown earlier, leading to small net D value for complexes 1–3. Another two significant negative contributions arise from the quartet excited states Ψ15 and Ψ16 (16th and 17th excited states),
These two states contribute −0.5 cm−1 each to the overall D value. Other than these major contributions, there are also other minor contributions which are very small in magnitude. The g values of these three complexes are totally isotropic in nature, 2.00, as the g value depends only on the ground electronic state. The sign of DSOC here cannot be rationalized using the ML value of the d-orbitals and their excitation, as has been routinely done in other cases,35 as here the contributions arise solely due to spin–flip transitions.36
Despite the significant structural variations observed, the magnitude of the computed D values is nearly the same in all three complexes. This observation can be rationalized by analyzing the electronic states and their contribution towards the overall D values (Tables S5–S7 in ESI†). Let us start with complex 1, which possesses the highest symmetry (D3h) among the three complexes (Fig. 4 and Table S4†) and therefore the first two quartet states are degenerate (Table S5 in ESI†). These degenerate quartet states contribute equally to the D value. As we move to complexes 2 and 3, the symmetry is lowered, leading to a lifting of the degeneracy between the dxz and dyz and dx2−y2 and dxy pairs of orbitals. Furthermore, the separation increases as we go from complex 1 to complex 3 (see Fig. 4). This symmetry consideration is also in agreement with the CShM analysis (Table S4†). As the separation of these orbitals increases, the states which are lower in energy contribute more to the D value while the states which are higher in energy contribute less to the overall D value. Since these two factors compensate each other, the net magnitude of D remains approximately constant across complexes 1–3. The rhombic ZFS (E) values of the three complexes increases from 0 in complex 1 to 0.0041 in complex 2, and 0.0085 in complex 3 (see Table 1). A detailed analysis of the state-wise contribution to the E values (Tables S6 and S7 in ESI†) suggests a similar pattern of contributions for both complexes 2 and 3, with the main contributions arising from the first two quartet excited states (corresponding wavefunctions are 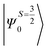 and
and 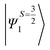 see above) from spin-forbidden dz2 → dxz and dz2 → dyz transitions which give contributions to E of opposite sign. As the symmetry is lower than D3h for complexes 2 and 3, the dxz and dyz orbitals do not remain degenerate (Fig. 4), yielding an overall non-zero E parameter. Complexes 1–3 show that the trigonal symmetry around the MnII ion can be fine-tuned to obtain smaller/larger rhombic ZFS. Importantly, this has potential applications in qubits where a larger rhombic ZFS is desired, as this leads to strong mixing of the states and a greater tunneling probability.37,38
see above) from spin-forbidden dz2 → dxz and dz2 → dyz transitions which give contributions to E of opposite sign. As the symmetry is lower than D3h for complexes 2 and 3, the dxz and dyz orbitals do not remain degenerate (Fig. 4), yielding an overall non-zero E parameter. Complexes 1–3 show that the trigonal symmetry around the MnII ion can be fine-tuned to obtain smaller/larger rhombic ZFS. Importantly, this has potential applications in qubits where a larger rhombic ZFS is desired, as this leads to strong mixing of the states and a greater tunneling probability.37,38
While ab initio calculations are known to accurately yield the DSOC contributions to D, the DSS contributions are underestimated.29 To estimate the DSS contributions, we have employed density functional methods as this has been shown to yield a good numerical estimate of the DSS contributions in other examples studied.39 The DSS values computed using the BP86/TZVP level of theory are −0.021 cm−1, −0.024 cm−1, and −0.021 cm−1 for complexes 1–3, respectively. The DSS values are found to be similar for all three complexes and are an order of magnitude smaller than the DSOC contribution obtained from ab initio calculations. The net sum D values showing DSS contributions from DFT and DSOC from ab initio calculations are given in Table S8 (see ESI†).
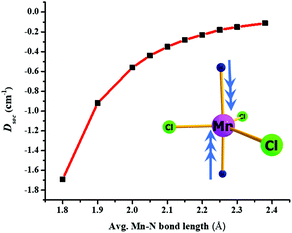
We have developed magneto-structural correlations in order to increase the axial ZFS (or D value) of the complexes. After analysing the ligand field states, their electronic configurations and their individual contributions to the overall D value, we present an efficient way to fine tune the magnetic anisotropy. The correlation is developed using complex 2, where we have shortened the Mn–N distances symmetrically from 2.38 Å (experimental) to 1.8 Å artificially in silico. We were encouraged to explore this correlation based on our recent studies on [Ni(MDABCO)2Cl3]ClO4 under high pressure.40 Shortening of the Mn–N bond distance along the direction where the dz2 orbital lies, leads to destabilization of this orbital, and assuming a dominant σ interaction of the ligand, the energies of the dxz and dyz orbitals are unaltered. The destabilization of the dz2 orbital effectively favours this electron to be paired up with the lowest dxz/dyz orbitals: this decreases the energy of the corresponding first and second excited quartet states, with the shortest Mn–N distances leading to a smaller sextet-quartet gap. This energy lowering of the first two quartet states results in an increase of the DSOC value in the computed data (see Fig. 5 and Fig. S14†). The DSOC value is found to increase by an order of magnitude in complex 2 to −1.69 cm−1 in the model complex for a Mn–N distance of 1.8 Å (see Table S9, ESI†). This suggests that the magnitude of the D value could be further enhanced in trigonal bipyramidal high-spin d5 systems by using stronger N-donor ligands in the axial positions to reduce the metal–N distances.
Conclusions
Three mononuclear trigonal bipyramidal MnII complexes have been successfully synthesised, [MnCl3(HDABCO)(DABCO)] (1), [MnCl3(MDABCO)2]·[ClO4] (2), and [MnCl3(H2O)(MDABCO)] (3). Ab initio and density functional calculations performed on complexes 1–3 provided the ZFS parameters that were then used to successfully fit the dc magnetic data. In addition, the ab initio calculations were used to rationalise the increase in rhombic ZFS across the series. Inspired by our previous work on the NiII analogue of 2 we have shown a potential route to increase the axial magnetic anisotropy in mononuclear d5 systems of this type. This is based on magneto-structural correlations, and achieved through shortening of the axial bond lengths (N–Mn–N′) in silico, which predict a >10-fold increase in D from the values reported for 1–3. Synthetic efforts towards related trigonal bipyramidal complexes where stronger σ-donors reside in both axial positions and/or heavier ligands such as Br that reside in the equatorial positions, which could increase spin–orbit effects and increase D, would be interesting. This should result in a shortening of the axial bonds and thus to an increase in the axial ZFS parameter.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We would like to thank the University of Glasgow and the UK Engineering and Physical Sciences Research Council for financial support (grant ref. EP/J018147/1, EP/K033662/1 and EP/M508056/1). GR would like to thank SERB for funding (CRG/2018/000430). Arup would like to thank CSIR for SRF fellowship and NPSF CDAC for HPC facility at Pune. The relevant data corresponding to this work is available at http://dx.doi.org/10.5525/gla.researchdata.840.Notes and references
- D. Gatteschi, R. Sessoli and J. Villain, Molecular Nanomagnets, OUP Oxford, Oxford, 2006 Search PubMed.
- G. Christou, D. Gatteschi, D. N. Hendrickson and R. Sessoli, MRS Bull., 2000, 25, 66–71 CrossRef CAS.
- R. Sessoli, H. L. Tsai, A. R. Schake, S. Wang, J. B. Vincent, K. Folting, D. Gatteschi, G. Christou and D. N. Hendrickson, J. Am. Chem. Soc., 1993, 115, 1804–1816 CrossRef CAS.
- R. Sessoli, D. Gatteschi, A. Caneschi and M. A. Novak, Nature, 1993, 365, 141–143 CrossRef CAS.
- C. J. Milios, A. Vinslava, W. Wernsdorfer, S. Moggach, S. Parsons, S. P. Perlepes, G. Christou and E. K. Brechin, J. Am. Chem. Soc., 2007, 129, 2754–2755 CrossRef CAS PubMed.
- Y. C. Chen, J. L. Liu, L. Ungur, J. Liu, Q. W. Li, L. F. Wang, Z. P. Ni, L. F. Chibotaru, X. M. Chen and M. L. Tong, J. Am. Chem. Soc., 2016, 138, 2829–2837 CrossRef CAS PubMed.
- M. Affronte, F. Troiani, A. Ghirri, A. Candini, M. Evangelisti, V. Corradini, S. Carretta, P. Santini, G. Amoretti, F. Tuna, G. Timco and R. E. P. Winpenny, J. Phys. D: Appl. Phys., 2007, 40, 2999 CrossRef CAS.
- L. Bogani and W. Wernsdorfer, Nat. Mater., 2008, 7, 179–186 CrossRef CAS PubMed.
- G. A. Craig and M. Murrie, Chem. Soc. Rev., 2015, 44, 2135–2147 RSC.
- S. Gómez-Coca, D. Aravena, R. Morales and E. Ruiz, Coord. Chem. Rev., 2015, 289–290, 379–392 CrossRef.
- C. Duboc, Chem. Soc. Rev., 2016, 45, 5834–5847 RSC.
- S. Zein, C. Duboc, W. Lubitz and F. Neese, Inorg. Chem., 2008, 47, 134–142 CrossRef CAS PubMed.
- K. E. R. Marriott, L. Bhaskaran, C. Wilson, M. Medarde, S. T. Ochsenbein, S. Hill and M. Murrie, Chem. Sci., 2015, 6, 6823–6828 RSC.
- W. H. Harman, T. D. Harris, D. E. Freedman, H. Fong, A. Chang, J. D. Rinehart, A. Ozarowski, M. T. Sougrati, F. Grandjean, G. J. Long, J. R. Long and C. J. Chang, J. Am. Chem. Soc., 2010, 132, 18115–18126 CrossRef CAS PubMed.
- Y. Rechkemmer, F. D. Breitgoff, M. van der Meer, M. Atanasov, M. Hakl, M. Orlita, P. Neugebauer, F. Neese, B. Sarkar and J. van Slageren, Nat. Commun., 2016, 7, 10467 CrossRef CAS PubMed.
- J. Krzystek and J. Telser, Dalton Trans., 2016, 45, 16751–16763 RSC.
- P. Comar, T. Rajeshkumar, G. S. Nichol, M. B. Pitak, S. J. Coles, G. Rajaraman and E. K. Brechin, Dalton Trans., 2015, 44, 19805–19811 RSC.
- C. Pichon, P. Mialane, E. Rivière, G. Blain, A. Dolbecq, J. Marrot, F. Sécheresse and C. Duboc, Inorg. Chem., 2007, 46, 7710–7712 CrossRef CAS PubMed.
- J. V. Quagliano, A. K. Banerjee, V. L. Goedken and L. M. Vallarino, J. Am. Chem. Soc., 1970, 92, 482–488 CrossRef CAS.
- R. G. Pritchard, M. Ali, A. Munim and A. Uddin, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 2006, 62, m507–m509 CrossRef PubMed.
- O. V. Dolomanov, L. J. Bourhis, R. J. Gildea, J. A. K. Howard and H. Puschmann, J. Appl. Crystallogr., 2009, 42, 339–341 CrossRef CAS.
- G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Adv., 2015, 71, 3–8 CrossRef PubMed.
- C. F. Macrae, P. R. Edgington, P. McCabe, E. Pidcock, G. P. Shields, R. Taylor, M. Towler and J. Van De Streek, J. Appl. Crystallogr., 2006, 39, 453–457 CrossRef CAS.
- M. Pinsky and D. Avnir, Inorg. Chem., 1998, 37, 5575–5582 CrossRef CAS PubMed.
- D. Casanova, J. Cirera, M. Llunell, P. Alemany, D. Avnir and S. Alvarez, J. Am. Chem. Soc., 2004, 126, 1755–1763 CrossRef CAS PubMed.
- S. Alvarez, Chem. Rev., 2015, 115, 13447–13483 CrossRef CAS PubMed.
- N. F. Chilton, R. P. Anderson, L. D. Turner, A. Soncini and K. S. Murray, J. Comput. Chem., 2013, 34, 1164–1175 CrossRef CAS PubMed.
- R. Boča, Theoretical Foundations of Molecular Magnetism, Elsevier Science, 1999 Search PubMed.
- M. Atanasov, D. Aravena, E. Suturina, E. Bill, D. Maganas and F. Neese, Coord. Chem. Rev., 2015, 289–290, 177–214 CrossRef CAS.
- S. S. Kumar, G. Tulika, B. Prashi and R. Gopalan, Chem. – Eur. J., 2014, 20, 10305–10313 CrossRef PubMed.
- A. Sarkar, G. Velmurugan, T. Rajeshkumar and G. Rajaraman, Dalton Trans., 2018, 47, 9980–9984 RSC.
- C. Duboc, T. Phoeung, S. Zein, J. Pécaut, M.-N. Collomb and F. Neese, Inorg. Chem., 2007, 46, 4905–4916 CrossRef CAS PubMed.
- S. Zein and F. Neese, J. Phys. Chem. A, 2008, 112, 7976–7983 CrossRef CAS PubMed.
- F. Neese and E. I. Solomon, Inorg. Chem., 1998, 37, 6568–6582 CrossRef CAS PubMed.
- T. Gupta and G. Rajaraman, Chem. Commun., 2016, 52, 8972–9008 RSC.
- S. K. Singh and G. Rajaraman, Nat. Commun., 2016, 7, 10669–10676 CrossRef CAS PubMed.
- M. S. Fataftah, J. M. Zadrozny, S. C. Coste, M. J. Graham, D. M. Rogers and D. E. Freedman, J. Am. Chem. Soc., 2016, 138, 1344–1348 CrossRef CAS PubMed.
- M. S. Fataftah, S. C. Coste, B. Vlaisavljevich, J. M. Zadrozny and D. E. Freedman, Chem. Sci., 2016, 7, 6160–6166 RSC.
- F. Neese, J. Am. Chem. Soc., 2006, 128, 10213–10222 CrossRef CAS PubMed.
- G. A. Craig, A. Sarkar, C. H. Woodall, M. A. Hay, K. E. R. Marriott, K. V. Kamenev, S. A. Moggach, E. K. Brechin, S. Parsons, G. Rajaraman and M. Murrie, Chem. Sci., 2018, 9, 1551–1559 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: Crystallographic data, selected bond lengths and angles, crystal packing diagrams, information on SHAPE studies conducted, powder X-ray diffraction for complexes 1–3, and further magnetic data. CCDC 1881218–1881220. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c9dt02187f |
| This journal is © The Royal Society of Chemistry 2019 |