Open Access Article
Open Access ArticleMagnetic anisotropy in trigonal planar Fe(II) bis(trimethylsilyl)amido complexes of the type [Fe{N(SiMe3)2}2L]—experiment and theory†
Tilmann
Bodenstein‡
* and
Andreas
Eichhöfer
 *
*
Institut für Nanotechnologie, Karlsruher Institut für Technologie (KIT), Campus Nord, Hermann-von-Helmholtz-Platz 1, 76344 Eggenstein-Leopoldshafen, Germany. E-mail: tilmann.bodenstein@kit.edu; andreas.eichhoefer@kit.edu; Fax: +49-(0)721-608-26368; Tel: +49-(0)721-608-26371
First published on 20th September 2019
Abstract
Systematic ac (alternating current) magnetic investigations on four new trigonal planar high-spin Fe2+ complexes [Fe{N(SiMe3)2}2L] reveal that complexes which comprise a phosphine or arsine type ligand (L = PPh3, PMe3 and AsPh3) display slow magnetic relaxation at temperatures below 8 K under applied dc (direct current) fields, whereas a complex with a phosphine oxide ligand (L = OPPh3) does not. Accordingly, the parameters characteristic for magnetic anisotropy, derived both from dc magnetic measurements and quantum chemical calculations, reveal distinct differences for these two types of complexes. Extensive ab initio calculations of multi-reference wave function type were performed on the four new complexes listed above and the related reported ones with L = py, thf and PCy3 in order to get a reasonable description of the local electronic states involved in the magnetic relaxation. These calculations confirm that strong spin–orbit effects generate the magnetic anisotropy of complexes with L = PPh3, PMe3, AsPh3 and PCy3. On the other hand, the complexes with L = OPPh3, py and THF exhibit only small spin–orbit splittings, consistent with the fast relaxation found experimentally.
Introduction
Single-ion molecule magnet behavior, which was first observed in lanthanide-containing complexes,1,2 and meanwhile also in several transition metal complexes,3–6 may once enable the utilization of such molecules as the smallest possible units in spin-based computational or data storage devices.7 However, the task to control slow relaxation of the magnetization as a desired property in these molecules is still a challenge.Maximization of the anisotropy of the magnetic moment for a respective molecule will in principle increase its energy barrier which determines the Orbach relaxation process.8 Successful strategies based upon magneto-structural correlations have been developed to achieve these goals.3–6 In this respect, the most promising properties of 3d transition metal complexes have been found recently for coordinatively unsaturated compounds. For example, the linearily coordinated cobalt complex [Co(C(SiMe2ONaph)3)2] displays a record spin reversal barrier of 450 cm−1 in a zero applied direct current field due to the realiziation of an unusual maximum of the orbital momentum of L = 3 arising from a non-Aufbau ground state.9 A similarly high barrier has also been described for a NHC complex of cobalt(II), [(sIPr)Co(II)NDmp] (sIPr = 1,3-bis(2′,6′-diisoproplphenyl)-4,5-dihydro-imidazol-2-ylidene; Dmp = 2,6-dimesitylphenyl) with a value of 413 cm−1, although the orbital momentum is thought to amount to a value of L = 2 only.10 In comparison, the two-coordinate complexes of iron(I) and iron(II), [Fe(C(SiMe3)3)2]– and [Fe(C(SiMe3)3)2]7,11,12 display slow magnetic relaxation without application of an external dc field with smaller effective spin reversal barriers of Ueff = 226 cm−1 and 146 cm−1, respectively. In view of the same L = 2 ground state like the aforementioned cobalt NHC complex, this difference most probably originates from smaller spin–orbit coupling constants in the iron compounds.
Related investigations have been performed on trigonal planar iron(II) complexes [Fe{N(SiMe3)2}2(L)] (L = PCy3,13 thf, N(SiMe3)2−,14 PCyp3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 15). For this type of complexes one usually expects spatially non-degenerate ground states with L = 0. However, small ligand field splittings could in principle allow for a coupling to low lying excited states, and the recent findings suggest an influence of the type of ligand L on the dc and ac magnetic properties of such complexes. Concerning the understanding of the magnetic properties of such compounds, quantum chemical studies based on wave function based methods have been shown to be able to predict and describe electronic properties of open-shell ion complexes quite accurately (for reviews, see for example ref. 16 and 17) and may be used as a guideline for experimentalists for designing novel complexes with desired magnetic anisotropy.
15). For this type of complexes one usually expects spatially non-degenerate ground states with L = 0. However, small ligand field splittings could in principle allow for a coupling to low lying excited states, and the recent findings suggest an influence of the type of ligand L on the dc and ac magnetic properties of such complexes. Concerning the understanding of the magnetic properties of such compounds, quantum chemical studies based on wave function based methods have been shown to be able to predict and describe electronic properties of open-shell ion complexes quite accurately (for reviews, see for example ref. 16 and 17) and may be used as a guideline for experimentalists for designing novel complexes with desired magnetic anisotropy.
Herein, we report on the experimental and theoretical characterization of seven trigonal planar Fe2+ bis(trimethylsilyl)amido complexes of the type [Fe{N(SiMe3)2}2(L)] with a focus on the influence of the ligand L on their electronic and magnetic properties.
Results and discussion
Table 1 introduces the molecular formulas and the numbering scheme of the complexes 1–7 which are considered in this work. The synthesis and structural as well as magnetic data have already been published for 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 14,18,19 and 7
14,18,19 and 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 13,14 in preceding papers whereas for 5 only an experimental procedure has been published so far.20
13,14 in preceding papers whereas for 5 only an experimental procedure has been published so far.20
| No. | Ligand L |
|---|---|
| 1 | PPh3 |
| 2 | PMe3 |
| 3 | AsPh3 |
| 4 | OPPh3 |
| 5 | py |
| 6 | thf |
| 7 | PCy3 |
Synthesis and structure
The new complexes 1–4 were synthesized in good yields by the reaction of [Fe{N(SiMe3)2}2]2 with the respective ligand either in heptane (1, 3 and 4) or in a solvent free reaction (2) upon heating in accordance to earlier papers on related complexes.18,195 was synthesized prior by sublimation of [Fe{N(SiMe3)2}2(py)2] but no single crystal XRD has been performed.20 We obtained single crystals of 5 from reactions of [Fe{N(SiMe3)2}2]2 and 1 equiv. of pyridine in pentane according to Scheme 1. However, powder XRD and elemental analysis indicate that the material isolated in this way is not pure. Therefore, apart from a single crystal structure determination, 5 is only considered in the theoretical investigations.
The complexes 1 and 3 crystallize both in the triclinic space group P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) (Table S1†) with similar lattice constants. Complex 2 crystallizes as a racemic twin in the orthorhombic space group Pna21 whereas 4 crystallizes in the monoclinic space group P21/n. Complex 5 crystallizes in the orthorhombic space group P21212 with two independent molecules (denoted 5a and 5b) in the asymmetric unit and was refined as a racemic twin. The coordination of the three coordinating atoms around the iron is in all complexes 1–7 almost trigonal planar with a maximum deviation of the position of the iron atom by 3.5 pm in 3 out of the trigonal plane (Table 2, Fig. 1 and S1–S5†). Notably in complexes 1–4 the ligands, PPh3, PMe3, AsPh3 and OPPh3 are not symmetrically situated between the two bis(trimethylsilyl)amido nitrogen ligands meaning that the trigonal planar FeN2L coordination arrangement comprises no symmetry. Deviations from the theoretical mean position amount to 3.07° (1), 1.39° (2), 3.3° (3) and 1.64° in 4. The N–Fe–N angles differ in 1 (135.71(8)°), 2 (139.03(8)°), 3 (141.0(1)°), 4 (136.48(9)°) and 5a/5b (144.14(16)/141.7(2)°) most probably due to steric reasons. The Fe–O–P bond angle in 4 differs with 154.41(12)° distinctly from 180° indicating that π-type orbitals are involved in the P–O bonding. Apart from that, geometrical parameters of 1–5 are similar to the related and known complexes 6,18,197
(Table S1†) with similar lattice constants. Complex 2 crystallizes as a racemic twin in the orthorhombic space group Pna21 whereas 4 crystallizes in the monoclinic space group P21/n. Complex 5 crystallizes in the orthorhombic space group P21212 with two independent molecules (denoted 5a and 5b) in the asymmetric unit and was refined as a racemic twin. The coordination of the three coordinating atoms around the iron is in all complexes 1–7 almost trigonal planar with a maximum deviation of the position of the iron atom by 3.5 pm in 3 out of the trigonal plane (Table 2, Fig. 1 and S1–S5†). Notably in complexes 1–4 the ligands, PPh3, PMe3, AsPh3 and OPPh3 are not symmetrically situated between the two bis(trimethylsilyl)amido nitrogen ligands meaning that the trigonal planar FeN2L coordination arrangement comprises no symmetry. Deviations from the theoretical mean position amount to 3.07° (1), 1.39° (2), 3.3° (3) and 1.64° in 4. The N–Fe–N angles differ in 1 (135.71(8)°), 2 (139.03(8)°), 3 (141.0(1)°), 4 (136.48(9)°) and 5a/5b (144.14(16)/141.7(2)°) most probably due to steric reasons. The Fe–O–P bond angle in 4 differs with 154.41(12)° distinctly from 180° indicating that π-type orbitals are involved in the P–O bonding. Apart from that, geometrical parameters of 1–5 are similar to the related and known complexes 6,18,197![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 13 and [Fe{N(SiMe3)2}2(PCyp3)].15 Shortest interatomic distances between the metal atoms in the crystal lattices are in the range between 891 and 1018 pm (1: 978, 2: 891, 3: 961, 4: 951, 5: 1018 pm).
13 and [Fe{N(SiMe3)2}2(PCyp3)].15 Shortest interatomic distances between the metal atoms in the crystal lattices are in the range between 891 and 1018 pm (1: 978, 2: 891, 3: 961, 4: 951, 5: 1018 pm).
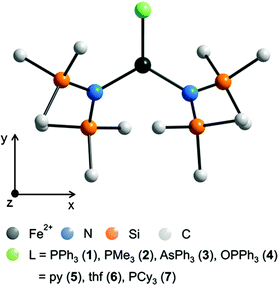 | ||
| Fig. 1 Schematic molecular structure of 1–7 (H atoms omitted) and scheme of the coordinate system employed in the quantum chemical calculations. For respective molecular structures see Fig. S1 to S5.† For selected bond lengths [pm] and angles [°] see Table 2. | ||
| Fe–N | Fe–P/As/O/N | N–Fe–N | N–Fe–P/As/O/N | Shortest Fe⋯Fe | Δ plane | |
|---|---|---|---|---|---|---|
| a This work. b From ref. 19. c From ref. 13. | ||||||
| 1 | 192.6, 192.5(2) | 253.1(1) | 135.71(8) | 109.08(6), 115.15(6) | 978 | 2.9(1) |
| 2 | 192.3, 194.6(2) | 247.5(1) | 139.03(8) | 109.11(8), 111.85(8) | 891 | 2.9(1) |
| 3 | 191.7, 192.0(2) | 263.0(1) | 141.0(1) | 106.2(1), 111.7(1) | 961 | 3.5(1) |
| 4 | 192.9, 193.3(2) | 197.6(2) | 136.48(9) | 110.12(9), 113.38(9) | 951 | 1.2(1) |
| 5a | 192.4, 193.1(4) | 210.1(4) | 141.7(2) | 109.14(11), 109.14(11) | 1018 | 3.1(1) |
| 5b | 191.8, 191.8(4) | 211.5(4) | 144.14(16) | 108.75(16), 107.03(15) | 0 | |
| 6 | 191.6(5) | 207.1(6) | 144.0(3) | 108.0(1) | 874 | 0 |
| 7 | 192.7, 192.9(2) | 261.9(12) | 128.11(2) | 115.72(2), 116.15(2) | 924 | 1.8(1) |
The measured powder patterns of 1–4 show a good agreement with the calculated ones based on the single crystal data (Fig. S6–S8†), which proves the crystalline purity of the compounds.
Experimental electronic spectra
Electronic spectra of 1–4 have been measured in a region from 45![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 450–4000 cm−1 (220 to 2500 nm) in solution (Fig. S9 and S10†). Due to the occurrence of sharp bands which can be assigned to vibration overtones, the spectra were not recorded further into the IR-region. In view of the extinction coefficients of the bands (ε > 2000 and ε < 150 l mol−1 cm−1), all spectra can be roughly divided into a region above and below 20
450–4000 cm−1 (220 to 2500 nm) in solution (Fig. S9 and S10†). Due to the occurrence of sharp bands which can be assigned to vibration overtones, the spectra were not recorded further into the IR-region. In view of the extinction coefficients of the bands (ε > 2000 and ε < 150 l mol−1 cm−1), all spectra can be roughly divided into a region above and below 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 (500 nm), the former ones belonging to charge transfer bands and the latter ones to d–d transitions. In the region 20
000 cm−1 (500 nm), the former ones belonging to charge transfer bands and the latter ones to d–d transitions. In the region 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000–4000 cm−1 (500–2500 nm), one observes for the iron complexes 1–3 two bands at 10
000–4000 cm−1 (500–2500 nm), one observes for the iron complexes 1–3 two bands at 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 672/8065 cm−1 in 1, 11
672/8065 cm−1 in 1, 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 561/8217 cm−1 in 2 and 9921/7981 cm−1 in 3, whereas the broad band of 4 can be modelled as a superposition of two close lying bands with maxima at 10
561/8217 cm−1 in 2 and 9921/7981 cm−1 in 3, whereas the broad band of 4 can be modelled as a superposition of two close lying bands with maxima at 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 631 and 9916 cm−1. In agreement with findings for 6 and 7, we assign these two d–d bands as the higher energy ones of the theoretically possible four transitions in a distorted trigonal planar, high spin Fe2+ (d6) complex.14 For a comparison of the experimental values with the calculated d–d transitions see Table 5 and S3.†
631 and 9916 cm−1. In agreement with findings for 6 and 7, we assign these two d–d bands as the higher energy ones of the theoretically possible four transitions in a distorted trigonal planar, high spin Fe2+ (d6) complex.14 For a comparison of the experimental values with the calculated d–d transitions see Table 5 and S3.†
Magnetic behavior
For all complexes 1–4 dc and ac magnetic properties have been studied on crystalline powders.The static magnetic properties of complexes 1–4 were measured between 1.8 and 300 K in a field of 0.1 T and by magnetization measurements from 0 to 7 T at 2, 3, 4, 6, 10 and 25 K.
The values of χT for 1–3 display distinct downturns below 100 K (Fig. 2 and 3). This deviation from the ideal Curie behavior is in the absence of close Fe⋯Fe contacts attributable to magnetic anisotropy which is indicative of a significant zero-field splitting and g-tensor anisotropy resulting from the pseudo-trigonal crystal field. Magnetic anisotropy for these three complexes is also indicated by the room temperature values of χT (1: 4.14, 2: 4.27, 3: 4.35 cm3 mol−1 K) which are much larger than the theoretical spin-only value of 3 cm−3 mol−1 K for one Fe2+ ion (high-spin, S = 2). Comparably large values for χT at room temperature have been reported for 7 (χT = 4.10, 5.12 cm3 mol−1 K).13,14
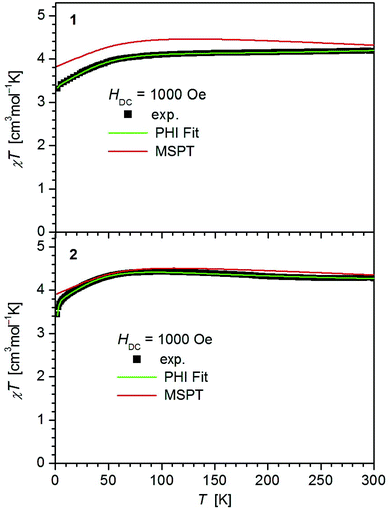 | ||
| Fig. 2 Temperature dependence of χT for 1 and 2. Solid green lines represent the results of the simultaneous fittings with the temperature dependent magnetization (Table 3, Fig. S11†) according to a spin Hamiltonian (eqn (S1)†) by the PHI program.21 Red lines represent the results of the quantum chemical calculations (MS-CAS(12,13)PT2) (see also Fig. S23†). | ||
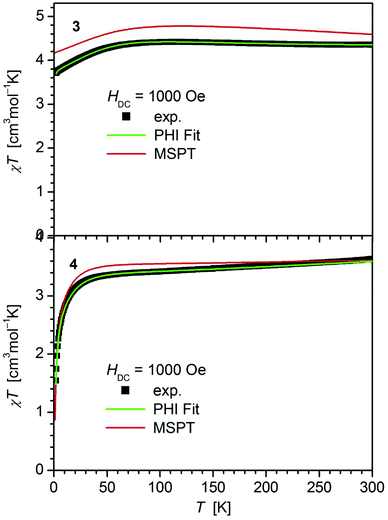 | ||
| Fig. 3 Temperature dependence of χT for 3 and 4. Solid green lines represent the results of the simultaneous fittings with the temperature dependent magnetization (Table 3, Fig. S12†) according to a spin Hamiltonian (eqn (S1)†) by the PHI program.21 Red lines represent the results of the quantum chemical calculations (MS-CAS(12,13)PT2) (see also Fig. S24†). | ||
In contrast, 4 does not display such an early deviation from the ideal Curie behavior and a distinctly lower value for χT at room temperature (3.63 cm3 mol−1 K) comparable to those of 5 (3.51 cm3 mol−1 K)20 and 6 (3.70 cm3 mol−1 K).14 Also, the value of χT at 2 K for 4 (1.55 cm3 mol−1 K) differs distinctly from those observed for 1–3 (3.30, 3.44, 3.71 cm3 mol−1 K). In agreement, the curves of the field dependence of the magnetization (M) of 1–3 on the one, and 4 on the other hand are also different (Fig. S11 and S12†), suggesting either different ground state properties for these complexes or distinct different magnetic anisotropies or both.
In order to probe this magnetic anisotropy further, we modeled the μeffvs. T and M versus H curves at different temperatures simultaneously by least-squares fits using the program PHI.21 The model includes both axial (D) and rhombic (E) ZFS terms as well as Zeeman interactions with an anisotropic treatment of g (eqn (S1)† with gx = gy, gz). The best sets of parameters are listed in Table 3 and shown as solid green lines in Fig. 2, 3 and S11, S12.† Complexes 1–3 display anisotropic g parameters and large negative D values, whereas fits of the anisotropic g-factor of 4 resulted in less anisotropic g-values as well as a less negative D (D = −15.4 cm−1). The lower increase of the magnetization curves (MSvs. H) in 4 (most visible at low T and H < 2 T, Fig. S12†) is reflected in the large E/D ratio obtained in the fit. This lifts the ground state degeneracy present in 1–3, 7 as confirmed by the ab initio calculations (see Theory section). We note that the data of 4 can in principle also be fitted by a set of parameters comprising a positive value of D = +12.7 cm−1 (gx = gy = 2.17, gz = 2.10, E = ±4.35, TIP = 0.34 × 10−3 cm3 mol−1) but with a worse goodness-of-fit factor R = 0.214, compared to R = 0.006 for the first option. Related negative values of D have been observed in [(IPr)Fe{N(SiMe3)2}2] (IPr = 1,3-bis(diisopropylphenyl)imidiazol-2ylidene) (D = −18.2 cm−1) and [(IMes)Fe{N(SiMe3)2}2] (IMes = 1,3-bis(2,4,6-trimethylphenyl)imidiazol-2ylidene) (D = −23.3 cm−1),226 (D = −20 cm−1), 7 (D = −33 cm−1)14 and [Fe{N(SiMe3)2}2(PCyp3)] (D = −38 cm−1).15 A positive D value has been recently reported for the trigonal planar iron(II) complex [Fe{N(SiMe3)2}3]2− (D = +9.9 cm−1).14
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a
a
| g x = gy | g z | D [cm−1] | E [cm−1] | TIPc [cm3 mol−1] | R [10−3] | |
|---|---|---|---|---|---|---|
| a Parameters: g, uniaxial magnetic anisotropy D, transversal magnetic anisotropy E, temperature independent paramagnetism TIP, goodness-of-fit factor R (least square approach). b Data from ref. 14. c The TIP values are about an order of magnitude higher than expected which might be reasoned by an inappropriate diamagnetic correction and/or slight decomposition of the extremely air sensitive compounds. | ||||||
| 1 | 2.08 | 2.50 | −39.6 | ±0.22 | 0.96 × 10−3 | 18.9 |
| 2 | 2.12 | 2.71 | −37.9 | ±4.22 | 0.175 × 10−3 | 2.7 |
| 3 | 2.08 | 2.65 | −42.3 | ±0.52 | 0.47 × 10−3 | 9.6 |
| 4 | 1.98 | 2.25 | −15.4 | ±5.0 | 1.06 × 10−3 | 0.61 |
| 6 | 2.07 | 2.28 | −20 | ±4.0 | 0.7 × 10−3 | 0.25 |
| 7 | 2.14 | 2.61 | −33 | ±3.4 | 3.15 | |
In order to probe the dynamic magnetic behavior further, ac measurements were performed in the 1.8–10 K range using a 3.0 Oe ac field, oscillating at frequencies between 1 and 1500 Hz (Fig. 4–6 and S13–S22†). In the absence of an external dc field, the out-of-phase components of the ac susceptibility (χ′′) of 1–4 have much lower intensity than the in-phase component (χ′) and display no maximum, indicating that spin lattice relaxation is faster than the timescale of the experiment. With the application of a static dc field, the intensity of χ′′ is significantly enhanced for 1–3, but not for 4. This effect can in 1–3 be ascribed to a lifting of degeneracy of the electronic states by the dc field which impedes relaxation processes via Quantum Tunneling (QTM).23,24 In contrast, the absence of slow relaxation of magnetization for complex 4 is in line with a smaller magnitude of D and less axial anisotropy expressed by its g-factors (Table 3) being not sufficient to establish a significant intrinsic barrier for reversal of the magnetization. This is similar to the behavior of 6.14 In addition, the fitted value of the rhombic ZFS parameter E = ±5.0 is quite high. Quantum tunneling due to transversal fields expressed by E is among others thought to be one of the reasons for lowering the theoretical spin reversal barrier especially in non-Kramers ions through mixing of the MS ± 1,2 states.25,26
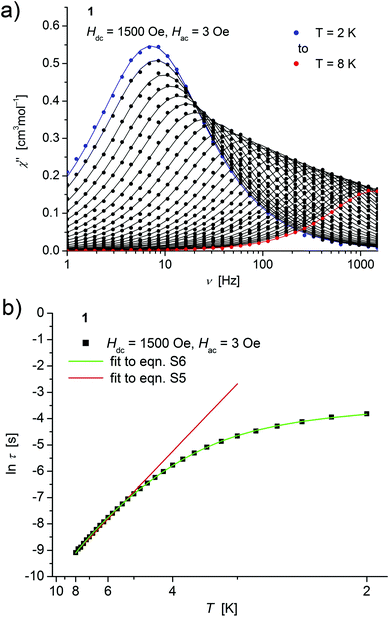 | ||
| Fig. 4 (a) Temperature dependence of the out-of-phase χ′′ component of the ac magnetic susceptibility at Hdc = 1500 Oe at different frequencies for 1 (solid lines correspond to the fits to a distribution of single relaxation processes (eqn (S2) and (S3)†); (b) relaxation time (τ) versus the inverse temperature (T−1) for 1. Red and green lines represent fits according to an Arrhenius law (eqn (S5)†) and to eqn (S6),† respectively. | ||
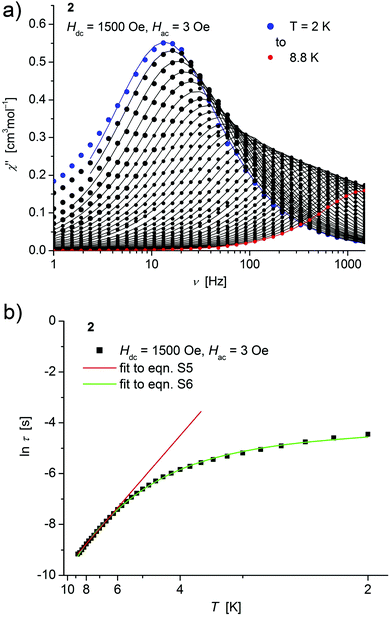 | ||
| Fig. 5 (a) Temperature dependence of the out-of-phase χ′′ component of the ac magnetic susceptibility at Hdc = 1500 Oe at different frequencies for 2 (solid lines correspond to the fits to a distribution of single relaxation processes (eqn (S2) and (S3)†); (b) relaxation time (τ) versus the inverse temperature (T−1) for 2. Red and green lines represent fits according to an Arrhenius law (eqn (S5)†) and to eqn (S6),† respectively. | ||
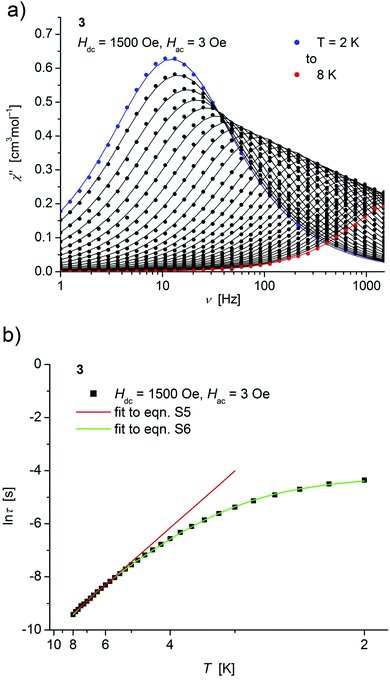 | ||
| Fig. 6 (a) Temperature dependence of the out-of-phase χ′′ component of the ac magnetic susceptibility at Hdc = 1500 Oe at different frequencies for 3 (solid lines correspond to the fits to a distribution of single relaxation processes (eqn (S2) and (S3)†); (b) relaxation time (τ) versus the inverse temperature (T−1) for 3. Red and green lines represent fits according to Arrhenius laws (eqn (S5)†) and eqn (S6),† respectively. | ||
Both, the temperature and field dependence of the relaxation time provide an experimental probe for the processes responsible for spin reversal in a magnetic system. The magnetic relaxation times for 1–3 where therefore assessed by measuring the frequency dependencies at different fields (Fig. S13–S18†) and temperatures (Fig. 4–6 and S19†), and were subsequently extracted (from these measurements) by fits to eqn (S2) and (S3).†
For 1–3, the field dependence of the inverse relaxation time at 2 K displays a curvature feature with a minimum around 1500 Oe and a negative slope for smaller and a positive for larger fields (Fig. S14, S16, S18†). Such a behaviour was for example also observed in the low field region (<3000 Oe) of dilute samples of Cu2+ in (NH4)2Zn(SO4)2·6H2O27 and in recent investigations on linear coordinated molecular Fe2+ complexes,11 and is commonly attributed to quantum tunneling effects. Approximate fits to these data of 1–3 can be obtained using eqn (S4),† where the first term represents the direct process, while the second corresponds to the zero-field tunneling process, accordingly to a procedure recently used for linear Fe(II) complexes.11 The resulting curves are shown as green lines in Fig. S14(a), S16(a) and S18(a)† and the respective parameters displayed in Table S2.†
Concerning temperature dependence, plots of the logarithmic relaxation times of 1–3vs. the reciprocal temperature show two different regions with an approximately linear behavior at higher temperatures (Fig. 4(b)–6(b)). In order to describe the energy transfer between the magnetic spin system and the lattice vibrations, different possible processes are considered:28,44 A direct process of a resonant phonon, a Raman and an Orbach process describing multiphonon processes via real and virtual intermediate states, respectively. In addition, quantum tunneling may play an important role at zero dc fields. Firstly, the thermal variation of τ at higher temperatures was fitted to an Arrhenius expression29 (eqn (S5)†) where τ0 is a preexponential factor and Ueff is the principal energy barrier for reversing the magnetization direction, leading to slightly differing values of Ueff for 1–3 (Table 4) and relaxation times in the order of 10−6 s, typical for an Orbach process in such compounds. However, the observed energy barriers are by far smaller than the calculated ones (U ∼ S2|D| for integer spin) which is a commonly observed phenomenon and could be assigned to the presence of quantum tunnelling effects.30 Secondly, the whole temperature dependence of τ, showing a strong curvature feature down to low temperature was fitted by eqn (S6)† including contributions from direct, Raman, quantum tunneling and Orbach relaxation mechanisms. Starting values for the Orbach process (Ueff and τ0) were taken from the ‘Arrhenius fits’ and the parameters B1 and B2 of the quantum tunneling term were taken as fixed parameters from fits of the field dependence of the relaxation time according to eqn (S4)† (Fig. 4(b)–6(b)).
| H dc [Oe] | U eff [cm−1] | τ 0 [s] | U eff [cm−1] | τ 0 [s] | A Dir [s−1 K−1] | C Ram [s−1 K−5] | |
|---|---|---|---|---|---|---|---|
| a Parameters: external magnetic field Hdc, effective energy barrier Ueff, relaxation time τ0, parameters for direct and Raman relaxation process ADir and BRam. b The parameters B1 and B2 of the quantum tunneling term in eqn (S6)† were taken as fixed values from fittings of the field dependence of τ according to eqn (S4),† (Fig. S14(a), S16(a) and S18(a)†). c The temperature dependence of ln(τ−1) for 2 was fitted only with data points in a region from 2.6 to 8.8 K due to the increasing broadening of the χ′′ peaks at T < 2.8 K. d Data from ref. 14. | |||||||
| 1 | 1500 | 21.4(4) | 2.4(1) × 10−6 | 20.5(2) | 9.7(7) × 10−6 | 12.2(3) | 0.192(6) |
| 2 | 1500 | 23.7(3) | 2.2(1) × 10−6 | 26.2(9) | 6(1) × 10−6 | 41.0(1) | 0.142(9) |
| 3 | 1500 | 17.9(2) | 3.4(2) × 10−6 | 14.2(2) | 2.0(1) × 10−5 | 15.6(6) | 0.223(6) |
| 7 | 600 | 16.0(3) | 1.6(2) × 10−6 | 17.1(16) | 7(3) × 10−7 | 53.2(11) | 1.079(77) |
These fits also result in similar parameter sets (Table 4) for 1–3. The values for Ueff and τ0 for the Orbach process change only moderatly compared to those of the ‘Arrhenius Fits’, and the parameters ADir and CRam for the direct and Raman relaxation process are of similar magnitude for all three compounds. We note that in the case of 2, a reasonable fit could not be obtained including the low temperature data. Therefore, only values of τ for temperatures above 2.6 K were considered. The broadening of the χ′′ vs. ν curve of 2 at low temperature (Fig. 5a) might be indicative for a second relaxation pathway or the occurrence of a phonon bottleneck effect.31
The Cole–Cole/Argand plots χ′′ vs. χ′ (see Fig. S20–S22†) show semicircular isotherms. Values of the distribution coefficient α were found to decrease upon heating which additionally supports the presence of other relaxation processes at lower temperatures.
Theory
In order to investigate the electronic and magnetic structures, multi reference ab initio calculations (see Experimental section for details) were performed for 1–7. All states corresponding to the 5D state of the free Fe2+ (d6, high-spin) ion are considered, differing mainly in the form of the doubly occupied d-orbital. The results of these calculations are summarized in Tables 5–7 and Fig. 7 as well as Tables S3–S9.†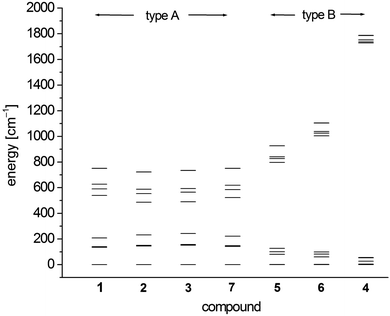 | ||
| Fig. 7 SO-RASSI energies of the first ten states of 1–7 based on CAS(12,13)SCF wave functions and MS-CAS(12,13)PT2 energies (Table 6 and S4†). | ||
| E with respect to the ground state | |||||
|---|---|---|---|---|---|
| a For more results from comparative calculations and concerning restrictions on the excitation manifold, see Table S3.† b Experimental values from ref. 14. | |||||
| 1 | 0 | 266 | 3816 | 8094 (8065) | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 740 (10 740 (10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 672) 672) |
| 2 | 0 | 344 | 4052 | 8995 (8217) | 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 547 (11 547 (11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 561) 561) |
| 3 | 0 | 253 | 4181 | 8061 (7981) | 9873 (9921) |
| 4 | 0 | 1673 | 3403 | 9670 (9916) | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 273 (10 273 (10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 631) 631) |
| 5a | 0 | 661 | 3574 | 8368 | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 377 377 |
| 6 | 0 | 897 | 3622 | 9224 (8631) | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 549 (10 549 (10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 083) 083) |
| 7 | 0 | 309 | 3386 | 8576 (8308) | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 735 (10 735 (10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 728) 728) |
| 1 | 2 | 3 | 4 | 5a | 6 | 7 | |
|---|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 0 | 0 | 0 | 4 | 1 | 2 | 0 |
| 3 | 136 | 146 | 152 | 27 | 81 | 61 | 142 |
| 4 | 140 | 151 | 157 | 53 | 101 | 83 | 148 |
| 5 | 208 | 232 | 243 | 56 | 127 | 99 | 222 |
| 6 | 539 | 486 | 490 | 1728 | 797 | 1004 | 523 |
| 7 | 591 | 554 | 565 | 1736 | 827 | 1025 | 585 |
| 8 | 627 | 588 | 593 | 1752 | 841 | 1038 | 619 |
| 9 | 750 | 722 | 734 | 1786 | 927 | 1104 | 750 |
| 10 | 751 | 723 | 735 | 1788 | 927 | 1105 | 751 |
| 11 | 4264 | 4053 | 4429 | 3482 | 3722 | 3742 | 3621 |
| g x | g y | g z | D [cm−1] | E [cm−1] | |
|---|---|---|---|---|---|
| a Note that these parameters may be less meaningful because of the quasi-degeneracy found in complexes 1–3 and 7. b For values calculated by CAS and SSPT2 see Table S6.† c Note that g is given with respect to the principal axis of the g-tensor, i.e. only in axial systems (D ≪ 0) the relation g3 = gz holds. d The sign of the calculated D becomes ambiguous in the limit of extreme rhombicity (E/D → 1/3). | |||||
| 1 | 1.89 | 1.92 | 2.88 | −54.27 | ±0.75 |
| 2 | 1.93 | 1.93 | 2.89 | −49.39 | ±0.62 |
| 3 | 1.87 | 1.92 | 3.04 | −56.77 | ±0.73 |
| 4 | 1.99 | 2.14 | 2.31 | +12.46d | ±3.82 |
| 5a | 1.96 | 2.09 | 2.63 | −30.81 | ±3.14 |
| 5b | 1.97 | 2.11 | 2.58 | −27.42 | ±3.48 |
| 6 | 1.98 | 2.11 | 2.51 | −23.67 | ±3.61 |
| 7 | 1.90 | 1.95 | 2.77 | −52.41 | ±1.17 |
The scalar-relativistic CAS(12,13)SCF and CAS(12,13)PT calculations reveal quasi-degenerate ground manifolds for the phosphine and arsine complexes 1–3 and 7, in the following denoted type A (Table 5 and S3†). On the other hand, the scalar-relativistic ground state of the other complexes 4–6 with an OPPh3, pyridine and thf ligand respectively (denoted type B) is, especially in 4, well isolated from the first excited state. As the mixing of the two first states anticorrelates with the energy gap, one has to expect large spin–orbit coupling between the ground state and first excited state in 1–3 and 7 whereas in 4, this effect should be very small. Indeed, this different influence of spin–orbit coupling can also be seen from the SO-RASSI energies (Fig. 7, Table 6 and S4†) where type B complexes show a clear energy gap after the first five spin–orbit coupled states whereas the first ten states in type A complexes are mixed heavily.32 From the evaluation of the contributions of the spin–orbit-free states to each spin–orbit state, the amount of mixing with excited states becomes clear (Table S5†). For example, for the first five spin–orbit states (MSCASPT2), contributions from the second spin-free state amount to 33% in 1–3, 7 but only up to 15% in 5, 6 and very low in 4 (<3.3%). In addition, SO-RASSI energies (Fig. 7, Table 6 and S4†) reveal degenerate ground states for 1–3, 7 with a clear separation from the 3rd state, whereas for 4, 5 and 6, the ground doublet is split by a few cm−1, and the gap to the 3rd state is, particularly in 4, less pronounced.
The computed magnetic susceptibilities and magnetization curves are in reasonable agreement with measured curves considering the approximations made in the quantum chemical calculations (Fig. 2, 3 and S23–S28†).36 This holds also for the extracted g, D and E parameters (Table 7 and S6†) which reproduce the trends found in experiment (Table 4). That is, distinct axial anisotropy for the g-factors of 1–3 and 7 (resulting from spin–orbit coupling with the low lying second S = 2 manifold) in combination with large negative D and small E values. In contrast, the g-factor anisotropy of 4 is smaller, transversal anisotropy due to E larger and the calculations indicate a positive sign for D with a 2–1–2 energy level scheme of the spin–orbit states (Table 6 and S4†). In this respect we note, that in general the sign of D becomes ambiguous in the limit of extreme rhombicity E/D → 1/3 and in addition, gz > gx,y does not correspond to the sign of D predicted by the consistency criterion derived from pertubation theory (D = 1/2λ(gz − gx)).33 However, a bigger transversal anisotropy due to E is thought to increase the probability of quantum tunneling through mixing of ground ±MS levels (for non-Kramers ions) which, together with a small D, might rationalize the fast relaxation of 4 observed in the ac magnetic measurements. Complexes 5 and 6 also comprise distinct values of the calculated E together with D values lying in between those of 4 and 1–3, 7. As reported previously, 6 does not show slow relaxation of the magnetization in related ac experiments.14 So far, we did not succeed to obtain pure samples of 5 what prevents us to perform related ac measurements. In view of the slightly larger D and slightly smaller E than in 6, it is difficult to predict the magnetic ac properties of 5.
In case of type A complexes, an analysis using an S = 2 spin Hamiltonian may be less meaningful considering the mixing of the lowest CAS states. However, even in this case, an analysis of the lowest two states can be done using an effective S = 1/2 spin Hamiltonian34H(S = 1/2) = g′zμBSzBz + ΔSx where Δ models the zero-field splitting between the two states in H(S = 1/2) and is related to the D and E values of H(S = 2) (eqn (4)) by 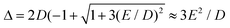 assuming D < 0. g′z is an effective g-factor with 8 < g′z ≤ 12.37 Though reproducing the low-lying spectrum, H(S = 1/2) cannot be used to interpret magnetic relaxation in terms of electronic states because of the symmetry properties of the zero-field term. Extracted g-factors for pseudo spins S = 2 and S = 1/2 models, together with main magnetic axes can be found in Table S7.† The main magnetic axes for the lowest pseudo spin multiplet (both S = 2 and S = 1/2) is oriented for 1–7 in the molecular plane defined by the two nitrogen atoms and the ligand L (along x in Fig. 1, Table S7†). Following ref. 37, the spin-only contribution to g′z amounts to 2Sge = 8.0092. Consequently, large orbital contributions are found in type A complexes with 3 > 2 > 1 > 7 and smaller contributions in type B complexes with 5a > 5b > 6 > 4, implying a higher degree of quenching of angular momentum in the latter. The same trend can be found for S = 2, where the orbital contributions to g are most pronounced in z-direction, with gz being collinear to g′z, with smaller deviation from ge in x- and y-direction. A very similar trend has been found in a related Fe2+ chloro-β-diketiminate complex.37
assuming D < 0. g′z is an effective g-factor with 8 < g′z ≤ 12.37 Though reproducing the low-lying spectrum, H(S = 1/2) cannot be used to interpret magnetic relaxation in terms of electronic states because of the symmetry properties of the zero-field term. Extracted g-factors for pseudo spins S = 2 and S = 1/2 models, together with main magnetic axes can be found in Table S7.† The main magnetic axes for the lowest pseudo spin multiplet (both S = 2 and S = 1/2) is oriented for 1–7 in the molecular plane defined by the two nitrogen atoms and the ligand L (along x in Fig. 1, Table S7†). Following ref. 37, the spin-only contribution to g′z amounts to 2Sge = 8.0092. Consequently, large orbital contributions are found in type A complexes with 3 > 2 > 1 > 7 and smaller contributions in type B complexes with 5a > 5b > 6 > 4, implying a higher degree of quenching of angular momentum in the latter. The same trend can be found for S = 2, where the orbital contributions to g are most pronounced in z-direction, with gz being collinear to g′z, with smaller deviation from ge in x- and y-direction. A very similar trend has been found in a related Fe2+ chloro-β-diketiminate complex.37
Following ref. 37, the splitting Δε between dyz and dz2 orbitals may be computed from the effective g-factor at S = 1/2 using a spin–orbit coupling constant λ = (436.2 cm−1)/4 (Landé-rule, value taken from NIST35) by eqn (1)
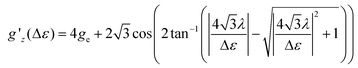 | (1) |
The relation between gz′ and the splitting is plotted in Fig. S29.† The values found using this simple method amount to 412, 339, 3020, 818, 954, 1160, and 607 cm−1 for 1, 2, 4–7, whereas the value for 3 is undetermined. These values are similar to the values computed with quantum chemical methods (Table S8†).
The complicated nature of electron correlation in multireference-type computations makes it difficult to deduct general rules that can be used for the prediction of electronic and magnetic properties, respectively. However, natural orbitals and energies may be used to construct effective one-particle models that can be useful to a certain extent.3,36 Therefore, effective d-orbital splittings have been computed from the CAS(12,13)SCF wave functions in order to investigate the energetic position of the dz2 orbital relative to the others (note that the complexes lie in the xy-plane with the ligand L pointing along the y-axis; Fig. 1). The computed splittings for type A (1–3 and 7) and type B (4–6) complexes are shown in Fig. 8. Due to many-body interactions, it is not unexpected that these values do not reproduce the classical trigonal-planar splitting derived for the d1 case.37,38,43 However, the findings from above are confirmed, i.e. upon ‘filling’ the levels with six electrons, type B complexes possess a doubly occupied dz2 orbital yielding a non-degenerate ground state, whereas in type A complexes, dz2 and dyz orbitals are close in energy with dyz being lower. Hence, the d-orbital splittings can be used to interpret the low-energy spectrum and thus the magnetic anisotropy in these types of complexes. In order to do that, we computed the d-orbital splittings at different levels of theory by three different methods (Table S8†),39 each of which accounts for electronic effects to a different extent: (1) CAS(5,5)SCF (ROHF) computations on d5 (Mn(II)) derivatives of the complexes include leading interactions between ligands and the d-shell, (2) CAS(6,5)CI computations include d–d correlation effects on top of the orbitals generated by method (1), (3) state average CAS(6,5)SCF computations in which the orbitals of method (2) are allowed to relax. The results are then compared to the CAS(12,13)SCF results shown above, as well as to well-established time-dependent density functional theory results which are known to yield good results in cases with non-degenerate states (complexes 4–6).14
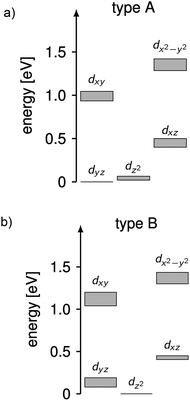 | ||
| Fig. 8 Splittings of the d-orbital of (a) 1–3 and 7 (type A) and (b) 4–6 (type B) computed from CAS(12,13)SCF wave functions and energies (Table S8†). The grey areas mark the distribution of energies found in the different complexes. | ||
Using these methods, the ‘bare’ splitting of d-orbitals is obtained from method (1) by eliminating multi-reference correlation effects in the d-shell going from the 5D ground manifold of Fe(II) to the spatially non-degenerate 6S ground state of Mn(II). These results already reflect the findings of the CAS(12,13)SCF reference calculations with respect to the orbital occupation in the ground state, but in the case of type A complexes do not show the quasi-degeneracy. This is improved by considering d–d correlation and orbital relaxation effects in methods (2) and (3), respectively. For complexes 4 and 6, the results from method 1 are slightly better than the ones obtained with method (3) although the latter is considered superior. However, the differences are generally small and all methods reproduce the findings of the reference calculations qualitatively. The wave functions from method 3 where used to further investigate the mechanistic origin of the differences in type A and type B complexes (see below).
Using the combination of the analysis of the spin–orbit states and the d occupation in the spin-free states, the difference of type A and type B complexes may be summarized as follows, keeping in mind the limitations of ligand-field theory. The spin-free ground states of type A and B complexes are significantly different. In type B complexes, the dz2 orbital is doubly occupied in the ground state, the next states are separated by more than 900 cm−1 and their spin–orbit coupling is weak. In consequence, the energy range of the first five spin–orbit states is small inhibiting single molecular magnet behavior in combination with a large E/D value and a rather isotropic g-factor. In contrast for type A complexes, the spin-free ground state is quasi-degenerate (with an energy difference <350 cm−1) due to the quasi-degeneracy of the dz2 and dyz orbitals. For these complexes spin–orbit coupling is large resulting in ten spin–orbit states at low energies which mainly consist of the first two spin-free quintet states. The first two spin–orbit states are degenerate and separated by ∼150 cm−1 from the next states enabling single molecular magnetism in combination with a large negative D value and strong g-factor anisotropy.
Chemically, a major difference is that the ligands in type A complexes comprise phosphine and arsine moieties while the coordinating atoms in type B complexes are oxygen and nitrogen. In ref. 11, the bonding mechanisms of σ-donor methanide, amide and alkoxide ligands in linearly coordinated Fe(II) complexes has been studied in detail, revealing complicated mechanisms, involving 3d–s mixing, π-bonding anisotropy and orbital mixing of ‘σ–π type’. Due to its π-acceptor capabilities via σ*-orbitals involving the second ligand shell,40,41 a proper ligand field consideration of type A complexes can be considered to be even more complicated in terms of the orbitals involved. However, since the compounds investigated are fairly symmetric (see Table 2), one may distinguish bonding interactions using symmetry arguments: in terms of the Stevens operator equivalents,42 an ideal trigonal planar crystal field splitting is induced by the axially symmetric terms O02 and O04.43 The other terms can thus in principle be assigned to distortions from the ideal D3h symmetry. The ligand field splitting of the atomic 5D ground manifold of Fe(II) may therefore be described by means of the effective Hamiltonian (eqn (2))
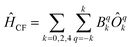 | (2) |
In order to investigate the relative strength of these interactions, effective model Hamiltonians describing the splitting of the atomic 5D state in complexes 1–7 where constructed using CAS(6,5)SCF energies and wave functions, and subsequently decomposed to give the coefficients Bqk in the unit cm−1. The results are summarized in Table S9.† In these computations, the only significant differences distinguishing type A from type B complexes are observed in the B22 coefficients. This term describes an interaction potential that has the shape of a dx2−y2 orbital in the xy-plane pointing towards the y-axis. Thus, it has in principle the correct symmetry to describe ‘σ-type’ interactions between the iron atom and the ligand L. On the other hand, the coefficients B44 and B34 which may be related to the respective ‘π-type’ bonding in the yz and xy planes, respectively, do not display such obvious differences and are by far overpowered by the ‘σ-type’ term B22. Note, however, that all interactions contributing to a symmetry splitting induced by a term (k,q) are collected in B(k,q), i.e. π-bondings may indirectly contribute to terms of σ-symmetry and vice versa.
In order to check the impact of the B22, B34, and B44 terms on the ground state symmetry, test simulations have been performed keeping the totally symmetric terms B02 and B04 fixed at their average values (779 cm−1 for B02 and 9 cm−1 for B04) while varying (a) B22 and B34 and (b) B22 and B44 independently in the range found in complexes 1–7 (−1000 cm−1 ≤ B22 ≤ 0 cm−1, −200 cm−1 ≤ B34, B44 ≤ +200 cm−1). The resulting surfaces are depicted in Fig. S30.† The transition between a doubly occupied dz2 and dyz ground state configuration is, given the average values of B02 and B04, found to be at around B22 = −555 cm−1 with less negative values corresponding to a doubly occupied dz2 orbital in the ground state of the Fe(II) complexes, which is consistent with the B22 values found for the complexes (type A: −597, −471, −537, −521 cm−1, type B: −278, −375, −350, −363 cm−1).
From this symmetry analysis, we conjecture that ‘σ-type’ interactions, i.e. integrals of B22-symmetry dominate the differences in the ligand field splitting of the atomic 5D ground manifold of Fe(II) in the complexes 1–7. Effectively, B22 is connected to a stabilization of the dyz orbital in comparison to dz2 and dxz. The stabilization is larger in type A than in type B complexes and induces a change in the ground state occupation to a quasi-degenerate ground state. Whether this change is really attributable to differences in the σ-bonds of the different ligands L or whether it is connected to π-back-bonding indirectly changing B22, cannot be distinguished finally. Furthermore, due to the fact that the operator coefficients computed depend on the choice of the quantization axis (see Experimental section) employed in the computational frame work, we cannot exclude that other mechanisms contribute significantly to the electronic structure in the complexes investigated.
Summarizing discussion and conclusion
In this paper, we present a combined experimental and computational analysis of the electronic structure and magnetic properties of a series of trigonal planar iron(II) complexes [Fe{N(SiMe3)2}2L] (L = PPh3, PMe3, AsPh3, OPPh3, thf, py,§ PCy3). In terms of their experimental dynamic magnetic properties, the complexes can be divided into two classes: type A with ligands L = PPh3, PMe3, AsPh3, PCy3 showing slow magnetic relaxation and those of type B i.e. L = OPPh3, thf which relax faster than the time scale of the experiment (ν = 1500 s−1).Extensive quantum chemical ab initio calculations allow for a more refined picture of the origin of the experimental findings. In all complexes, the first two spin–orbit states are degenerate or quasi-degenerate with an uniaxial g-tensor obtained with pseudospin S = ½. However, the spin-free electronic origins of these states are quite different: type A complexes reveal quasi-degenerate spin-free scalar-relativistic ground manifolds, whereas the ground state of the type B complexes (including L = py) is well isolated from the first excited state, indicating different importance of spin–orbit interaction in these types. This difference is mirrored by the SO-RASSI energy spectrum, where type B (second order) complexes show a substantial energy gap after the first five spin–orbit coupled states (the gap ΔEL increases for the complexes in the order L = py, thf, OPPh3). Their ground state wave functions are dominated by the first spin-free quintet state, whereas in the first ten states of type A (first order) complexes the first two spin-free quintet states are heavily mixed.
As already pointed out in an earlier paper,14 this different magnetic behavior seems to be related to the heuristic σ/π donor/acceptor strength of the ligands and its effects on the splitting of the d-orbitals. Accordingly, three cases can be distinguished: (1) trigonal planar [Fe{N(SiMe3)2}2L] complexes with pure σ donor ligands L like L = OPPh3 give rise to a low-lying, isolated, doubly occupied dz2 orbital. As evident from the experiments and quantum chemical calculations, this type of complexes comprises only second order spin–orbit coupling and thus a small magnetic anisotropy of the g tensors (obtained with S = 2) together with a small D value. Furthermore, a large calculated value of E rationalizes the fast relaxation observed in this complex. (2) In complexes with ligands L = thf, py, which, in addition to σ-donor properties, also possess weak π-acceptor capabilities, the dz2 orbital is still lowest in energy. However, the experimental and computational data indicate stronger spin–orbit interaction, leading to an increased g-factor anisotropy and larger D values compared to the complex with the pure σ-donor ligand L = OPPh3. Despite this, the relaxation of [Fe{N(SiMe3)2}2thf] is still fast (not observable in ac measurements up to ν = 1500 s−1 even under applied dc fields). (3) The third case is depicted by type A complexes where L possesses stronger π-acceptor capabilities. Here, the calculations reveal that the dyz orbital becomes lowest in energy (doubly occupied in the ground state), being almost degenerate with the slightly higher dz2 orbital (singly occupied). Thus, strong orbital contributions to the angular momentum arising from spin–orbit coupling of first order type are induced in these complexes which means that a S = 2 pseudo-spin description of the magnetic anisotropy tensors has to be taken with care. However, there is still an energy gap after the first five spin–orbit states whose energies are reasonably well reproduced with a second order spin Hamiltonian (Table S10†). While these considerations overall rationalize the magnetic properties, a quantitative assessment with respect to the σ/π acceptor/donor properties of the ligands L remains challenging as a symmetry analysis of the ligand field interaction shows.
Concluding, in type A complexes (L = PPh3, PMe3, AsPh3, PCy3), the quasi-degenerate spin-free relativistic ground state leads to an axial magnetic anisotropy via first order spin–orbit coupling, enabling the observation of single-ion magnet behavior, whereas the second order spin–orbit coupling in type B complexes (L = OPPh3, py, thf) induces transversal fields resulting in a faster relaxation.
Experimental section
Synthesis
Standard Schlenk techniques were employed throughout the syntheses using a double-manifold vacuum line with high-purity dry nitrogen (99.9994%) and an MBraun glovebox with high-purity dry argon (99.9990%). The solvent heptane was dried over LiAlH4, diethyl ether over sodium-benzophenone and both distilled under nitrogen. LiN(SiMe3)2, PCy3 (Cy = cyclohexyl, C6H11), PPh3, AsPh3, OPPh3 and anhydrous FeCl2 were purchased from Aldrich. LiN(SiMe3)2 was distilled prior to use. [Fe{N(SiMe3)2}2]2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 45 and PMe3
45 and PMe3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 46 were synthesized according to a literature procedure.
46 were synthesized according to a literature procedure.
[Fe{N(SiMe3)2}2(PCy3)] (7) was synthesized according to a procedure recently published by us.14
Compounds [Fe{N(SiMe3)2}2(L)] (L = PPh3 (1), AsPh3(3), OPPh3 (4)) can be synthesized by a procedure analogous to that of 7. [Fe{N(SiMe3)2}2]2 (0.2 g, 0.27 mmol) and two equivalents of the corresponding ligand (1: PPh3 (0.139 g, 0.53 mmol), 3: AsPh3 (0.162 g, 0.53 mmol) and 4: OPPh3 (0.148 g, 0.53 mmol) were dissolved with 2 ml of heptane in a Schlenk tube and heated by an oil bath for five minutes to give a clear pale green solution (1: 100 °C, 3: 85 °C, 4: 100 °C). After cooling down to rt the amount of solvent was reduced by half under a reduced pressure and the reaction solutions stored in a freezer (−42 °C). If the compounds did not crystallize after three days we ‘shock-freeze’ the solutions with liquid N2, slightly warmed them till everything is dissolved again and put them in the freezer again. In this way 1, 3 and 4 can be obtained as pale green crystals or crystalline precipitates. For their isolation the supernatant solutions were disposed and the crystalline residues in the case of 1 and 4 washed two times with 3 ml of −70 °C cold pentane to give total yields of 1: 0.24 g (72%) and 4: 0.28 g (81%). In the case of 3 washing was not possible due to its high solubility in pentane even at low temperatures (yield: 0.27 g (75%)).
(1) C30H51FeN3PSi6 (638.90): calcd C 56.4, H 8.1, N 4.4 found C 56.9, H 8.0, N 4.3%.
(3) C30H51FeN3AsSi6 (682.90): calcd C 52.8, H 7.5, N 4.1 found C 53.1, H 7.7, N 4.2%.
(4) C30H51FeN3OPSi6 (654.90): calcd C 55.0, H 7.9, N 4.3 found C 54.5, H 7.3, N 4.5%.
[Fe{N(SiMe3)2}2(PMe3)] (2) can be synthesized by a direct solvent-free reaction of [Fe{N(SiMe3)2}2]2 (0.3 g, 0.8 mmol) and a slight excess of PMe3 (0.130 g, 1.7 mmol). The reaction mixture was carefully heated to 70 °C forming a green clear melt. After cooling to rt excess PMe3 was removed under reduced pressure to give 2 as a solid, pale green crystalline residue.
(2) C15H45FeN3PSi6 (452.69): calcd C 39.8, H 10.0, N 6.2 found C 39.3, H 10.0, N 6.3%.
Crystallography
Due to the extreme air and moisture sensitivity of the compounds crystals suitable for single crystal X-ray diffraction were selected in perfluoroalkylether oil in a glove box and transferred rapidly under argon atmosphere to the diffractometer equipped with an Oxford Cryosystem. Single-crystal X-ray diffraction data of 1–5 were collected using graphite-monochromatised Mo-Kα radiation (λ = 0.71073 Å) on a STOE IPDS II (Imaging Plate Diffraction System). Raw intensity data were collected and treated with the STOE X-Area software Version 1.39. Data for all compounds were corrected for Lorentz and polarisation effects.Based on a crystal description a numerical absorption correction was applied for 1–5.47 The structures were solved with the direct methods program SHELXS of the SHELXTL PC suite programs,48 and were refined with the use of the full-matrix least-squares program SHELXL. Molecular diagrams were prepared using Diamond.49
In 1–5 all Fe, As, N, O, P, Si, and C atoms were refined with anisotropic displacement parameters whilst H atoms were computed and refined, using a riding model, with an isotropic temperature factor equal to 1.2 times the equivalent temperature factor of the atom which they are linked to. In 1–4 some of the C atoms of methyl groups were refined isotropic with a split model of site disorder.
CCDC 1902301 (1), 1902303 (2), 1902305 (3), 1902304 (4) and 1902302 (5) contain the supplementary crystallographic data for this paper.†
X-ray powder diffraction patterns (XRD) for 1–4 (powder of crystals), were measured at rt on a STOE STADI P diffractometer (Cu-Kα1 radiation, Germanium monochromator, Debye-Scherrer geometry, Mythen 1 K detector) in sealed glass capillaries. The theoretical powder diffraction patterns were calculated on the basis of the atom coordinates obtained from single crystal X-ray analysis (180 K) by using the program package STOE WinXPOW.50
Physical measurements
C, H, S elemental analyses were performed on an ‘Elementar vario Micro cube’ instrument.UV-Vis absorption spectra of 1–4 in C6D6 were measured on a PerkinElmer Lambda 900 spectrophotometer in quartz cuvettes.
Zero-Field-Cooled temperature dependent susceptibilities were recorded for 1–4 in dc mode using a MPMS-III (Quantum Design) SQUID magnetometer over a temperature range from 2 to 300 K in a homogeneous 0.1 T external magnetic field. The magnetization curves were measured on the same instrument up to a dc field of 7 T. The ac susceptibility measurements have been performed using a MPMS-XL (Quantum Design) SQUID magnetometer with an oscillating ac field of 3 Oe and ac frequencies ranging from 1 to 1500 Hz. The samples were contained in gelatine capsules filled in a glove box under argon atmosphere owing to the high degree of moisture and oxygen sensitivity of the compounds. The samples were transferred in sealed Schlenk tubes from the glove box to the magnetometer and then rapidly transferred to the helium-purged sample space of the magnetometer. The data were corrected for the sample holder including the gelatine capsule and for diamagnetism using Pascal's constants.51–53
Details about the simulations are given in the ESI.†
Quantum chemical calculations
Electronic and magnetic structures of the complexes 1–5 were studied by ab initio methods. For comparison, calculations were also performed on the published compounds [Fe{N(SiMe3)2}2L] (L = thf (6),14 PCy3 (7),13,14). All calculations were performed on the crystal structures in gas phase using the MOLCAS program package in version 8.0.15-06-18.54Multi reference wave function models were employed to account for the complicated nature of electron correlation in 1–7: orbitals were optimized using the complete active space self-consistent field (CASSCF) method, energy corrections were obtained using second order perturbation theory with a complete active space self-consistent field reference function (CASPT2), and spin–orbit coupling was accounted for by using the restricted active space state interaction (RASSI) method in conjunction with the atomic-mean field approximation (AMFI) for the spin–orbit operator (SO-RASSI). Scalar relativistic effects were accounted for in the orbital optimization by means of decoupling of one-electron operators (X2C)55 using the relativistic ANO-type basis sets (ANO-RCC) of triple zeta quality for iron56 and the atoms of the first coordination shell57 and of double zeta quality for the remaining atoms.58 Two active spaces have been investigated for orbital optimization (1) 3d-shell of the iron centers (CAS(6,5)) and (2) 3d-shell of iron plus a second 3d′ shell with ligand orbital admixtures, as well as the three lone pairs located on the atoms constituting the first coordination sphere pointing towards the iron center (CAS(12,13)). In all cases, the orbitals were optimized using an average density, constructed from the five lowest quintet states with equal weights. Additionally, a CAS(12,13)CI was performed using the CAS(6,5)SCF orbitals in order to distinguish between the effects stemming from orbital optimization and configuration interaction expansion, respectively. On top of the CASSCF wave functions, single- as well as multi-state CASPT2 calculations where performed using the “afreeze” option to freeze certain inactive orbitals as described in the MOLCAS documentation59 with thresholds 0.1 and 0.01 (see Table S3†). In all CAS(12,13) computations, the lowest spin-free states of the CAS(12,13) calculations are spanned by the 100 spin-states of the CAS(6,5)-manifold, i.e. 5 quintets, 45 triplets and 50 singlets. The states arising from different occupation patterns are much higher in energy, with an energy gap of around 200![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1. Spin–orbit interaction was thus accounted for in a perturbative manner in the subspace of the components of the lowest 100 CAS(12,13) spin-states spanning an energy range of about 100
000 cm−1. Spin–orbit interaction was thus accounted for in a perturbative manner in the subspace of the components of the lowest 100 CAS(12,13) spin-states spanning an energy range of about 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1. In order to account for dynamic correlation effects, the diagonal elements of the spin–orbit CI matrix which are associated to the components of the five quintet states were shifted by the SS- and MS-CASPT2 correlation energies Ecorr(i) (i = 1, …, 5) (eqn (S7)†).60 The energies of the remaining 95 states where shifted by an arithmetic average correlation energy, i.e.
000 cm−1. In order to account for dynamic correlation effects, the diagonal elements of the spin–orbit CI matrix which are associated to the components of the five quintet states were shifted by the SS- and MS-CASPT2 correlation energies Ecorr(i) (i = 1, …, 5) (eqn (S7)†).60 The energies of the remaining 95 states where shifted by an arithmetic average correlation energy, i.e.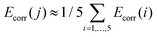 for all j > 5. Note that all results are based on CASSCF wave functions.
for all j > 5. Note that all results are based on CASSCF wave functions.
In order to interpret the ab initio spectrum and compare to experimentally derived values, the parameters of phenomenological spin Hamiltonians where computed from the ab initio data using the SINGLE_ANISO moduls documented in detail in ref. 61. These Hamiltonians are used to model the input spectrum in terms of fictitious spins and matrix-valued parameters, e.g. HZFS = SDS where S is a spin (vector) operator and D a symmetric 3 × 3 matrix which describes the second-order zero-field splitting of a multiplet with pseudo spin S. In the case of large spins S, i.e. 2S + 1 degrees of freedom, other (spin–orbit) coupling schemes, or generally in order to increase the accuracy, HZFS may be augmented with higher rank terms, e.g. D′Sz4.
While being in principle able to describe any system of 2S + 1 states, a spin Hamiltonian model is physically valid only if there is a clear correspondence between the pseudo-spin and the wave functions of the true Hamiltonian. In lanthanide systems, S usually corresponds to the atomic multiplet. In the case of the second-order interaction modeled by HZFS in transition metal complexes, this requires the ligand-field split multiplet to be sufficiently isolated from other states. Then, D describes the splitting induced by second-order spin–orbit and first order spin–spin coupling and may be computed using perturbation theory arguments.3,33,34,44 However, in some cases such a low-rank analysis can be performed anyways, and the spectrum of HZFS, may serve as a marker for assessing the validity of the model.
Magnetic experiments are often conducted at cryogenic temperatures. Therefore, only the lowest states contribute to the properties observed. It is therefore not necessary to reproduce the entire spectrum to high accuracy, but rather the lowest states. Furthermore, adding higher-rank terms promotes overparametrization of the problem, in particular if non-collinear tensors are used at different orders, but give little physical insight on the other hand.
If not mentioned otherwise, the spin Hamiltonian parameters were computed using an effective spin S = 2, justified by the energy gap observed after the first five SO-RASSI states. The spin Hamiltonians are given in their main axes by eqn (3) and (4), respectively.28,44
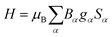 | (3) |
| H = D(Sz2 − 1/3S(S + 1)) + E(Sx2 − Sy2) | (4) |
Because of the quasi-degeneracy of the first two SO-RASSI states, g-factors were also obtained using a pseudo-spin of S = ½ in eqn (3).
In order to assess the accuracy of the S = 2 pseudo spin model, we computed the eigenvalues of eqn (4) with the parameters from Table 7. The results can be found in Table S10† and should be compared to Table 6. The agreement is very good in type B complexes. Discrepancies in the higher-lying states of type A complexes are not unexpected but have negligible effects on the low-temperature properties in terms of a Boltzmann distribution (150 cm−1∼216 K). In this case, a model featuring higher-rank spin operators might improve the accuracy of the values, but not the validity of the S = 2 pseudo spin description for type A complexes in the first place.34 For the computation of magnetic susceptibilities, all 210 microstates where considered in the Boltzmann-averaging.
Further CAS computations for analyzing the bonding situation have been carried-out using the Bochum suite of ab initio programs.62,63 In these calculations, the metal atom was equipped with a def2-TZVPP(–f) basis,64,65 while the remaining atoms where described by a def2-SVP basis.64,65
The Kohn–Sham time dependent density functional theory (TDDFT) calculations where performed with the TURBOMOLE program package.66 In these calculations, all atoms where equipped with def2-TZVPP bases.64,65 In these calculations, the B3-LYP functional67 was used together with a grid of size m3 and the RI-J approximation.
D-orbital splittings where derived from energies and occupations of state-specific natural orbitals as follows: using the state-average CAS orbitals, state-specific density matrices are constructed and diagonalized to give the natural orbitals. Due to the Full CI nature of the CAS method, the corresponding energies of the states are invariant under this transformation. In the case of ROHF (CAS(5,5)SCF) and TDDFT computations, orbital energies and Jacobian eigenvalues have been used, respectively. The assignments to metal 3d-orbitals have been made by inspecting the orbitals used in the above calculations.
The Hamiltonian decompositions into contributions from irreducible tensor operators have been computed from the CAS energies En and wave functions |n〉 using the program package recently developed in Karlsruhe and Kaiserslautern.68 In this method, the effective Hamiltonian describing the splitting of the atomic 5D state of the Fe(II) complexes is constructed from the eigenfunctions |ñ〉 of the microscopic Lz operator (with L = 2 and a quantization axis coinciding with the molecular z-axis, see Fig. 1) in the basis of the lowest five CAS states |n〉, i.e.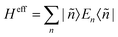 . The corresponding 5 × 5 Hamiltonian matrix
. The corresponding 5 × 5 Hamiltonian matrix 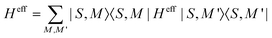 was then used to compute the coefficients Bqk (eqn (2)) by projecting the effective Hamiltonian onto the matrix representation Oqk of the Stevens operator equivalents Oqk
was then used to compute the coefficients Bqk (eqn (2)) by projecting the effective Hamiltonian onto the matrix representation Oqk of the Stevens operator equivalents Oqk![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40 (see eqn (S8)–(S11)†) and then tracing over all pseudo spin functions as described in ref. 61:
40 (see eqn (S8)–(S11)†) and then tracing over all pseudo spin functions as described in ref. 61:
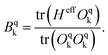 | (5) |
Author contributions
T. Bodenstein: quantum chemical calculations, A. Eichhöfer: synthesis and characterization.Conflicts of interest
The authors declare no financial interests.Acknowledgements
This work was supported by the Karlsruhe Institut für Technologie (KIT, Campus Nord) and the Karlsruhe Nano-Micro-Facility (KNMF). The authors thank K. Fink for substantial help in the preparation of the manuscript and S. Stahl for the performance of the elemental analysis. A. E. thanks A. K. Powell for generous support. T. B. thanks the Danish Research Council (DFF) for funding via FNU (Grant No. DFF-4191-00537) and the German Science Foundation DFG via SFB/TRR88, projects A1 and C1.References
- N. Ishikawa, M. Sugita, T. Ishikawa, S. Koshihara and Y. Kaizu, J. Am. Chem. Soc., 2003, 125, 8694–8695 CrossRef CAS.
- D. N. Woodruff, R. E. P. Winpenny and R. A. Layfield, Chem. Rev., 2013, 113, 5110–5148 CrossRef CAS PubMed.
- S. Gómez-Coca, D. Aravena, R. Morales and E. Ruiz, Coord. Chem. Rev., 2015, 289–290, 379–392 CrossRef.
- G. A. Craig and M. Murrie, Chem. Soc. Rev., 2015, 44(8), 2135–2147 RSC.
- A. K. Bar, C. Pichon and J.-P. Sutter, Coord. Chem. Rev., 2016, 308, 346–380 CrossRef CAS.
- J. M. Frost, K. L. M. Harriman and M. Murugesu, Chem. Sci., 2016, 7, 2470–2491 RSC.
- J. M. Zadrozny, D. J. Xiao, M. Atanasov, G. J. Long, F. Grandjean, F. Neese and J. R. Long, Nat. Chem., 2013, 577–581 CrossRef CAS PubMed.
- C. B. P. Finn, R. Orbach and W. P. Wolf, Proc. Phys. Soc., 1961, 77, 261–268 CrossRef CAS.
- P. C. Bunting, M. Atanasov, E. Damgaard-Møller, M. Perfetti, I. Crassee, M. Orlita, J. Overgaard, J. van Slageren, F. Neese and J. R. Long, Science, 2018, 362(6421), 1–9 CrossRef PubMed.
- X.-N. Yao, J.-Z. Du, Y.-Q. Zhang, X.-B. Leng, M.-W. Yang, S.-D. Jiang, Z.-X. Wang, Z.-W. Ouyang, L. Deng, B.-W. Wang and S. Gao, J. Am. Chem. Soc., 2017, 139, 373–380 CrossRef CAS PubMed.
- M. Zadrozny, M. Atanasov, A. Bryan, C.-Y. Lin, B. D. Rekken, P. P. Power, F. Neese and J. R. Long, Chem. Sci., 2013, 4, 125–138 RSC.
- M. Atanasov, M. Zadrozny, J. R. Long and F. Neese, Chem. Sci., 2013, 4, 139–156 RSC.
- P.-H. Lin, N. C. Smythe, S. I. Gorelsky, S. Maguire, N. J. Henson, I. Korobkov, B. L. Scott, J. C. Gordon, R. T. Baker and M. Murugesu, J. Am. Chem. Soc., 2011, 133, 15806–15809 CrossRef CAS.
- A. Eichhöfer, Y. Lan, V. Mereacre, T. Bodenstein and F. Weigend, Inorg. Chem., 2014, 53, 1962–1974 CrossRef PubMed.
- C. G. Werncke, L. Vendier, S. Sabo-Etienne, J.-P. Sutter, C. Pichon and S. Bontemps, Eur. J. Inorg. Chem., 2017, 1041–1046 CrossRef CAS.
- M. Atanasov, D. Aravena, E. Suturina, E. Bill, D. Maganas and F. Neese, Coord. Chem. Rev., 2015, 289–290, 177–214 CrossRef CAS.
- J. P. Malrieu, R. Caballol, C. J. Calzado, C. de Graaf and N. Guihéry, Chem. Rev., 2014, 114(1), 429–492 CrossRef CAS.
- R. A. Andersen, K. Faegri, J. C. Green, A. Haaland, M. F. Lappert, A.-P. Leung and K. Rypdal, Inorg. Chem., 1988, 27, 1782–1786 CrossRef CAS.
- M. M. Olmstead, P. P. Power and S. C. Shoner, Inorg. Chem., 1991, 30, 2547–2551 CrossRef CAS.
- A. Panda, M. Stender, M. M. Olmstead, P. Klavins and P. P. Power, Polyhedron, 2003, 22, 67–73 CrossRef CAS.
- N. F. Chilton, R. P. Anderson, L. D. Turner, A. Soncini and K. S. Murray, J. Comput. Chem., 2013, 34, 1164–1175 CrossRef CAS PubMed.
- R. A. Layfield, J. J. McDouall, M. Scheer, C. Schwarzmaier and F. Tuna, Chem. Commun., 2011, 47, 10623–10625 RSC.
- D. Gatteschi, R. Sessoli and J. Villain, Molecular Nanomagnets, Oxford University Press, Oxford, 2006 Search PubMed.
- S. Koizumi, M. Nihei, T. Shiga, M. Nakano, H. Nojiri, R. Bircher, O. Waldmann, S. T. Ochsenbein, H. U. Güdel, F. Fernandez-Alonso and H. Oshio, Chem. – Eur. J., 2007, 13, 8445–8453 CrossRef CAS PubMed.
- J. M. Zadrozny and J. R. Long, J. Am. Chem. Soc., 2011, 138, 20732–20734 CrossRef PubMed.
- H. A. Kramers, Proc. R. Acad. Sci. Amsterdam, 1930, 33, 959–972 CAS.
- A. C. De Vroomen, F. F. Lijphart and N. J. Poulis, Physica, 1970, 47, 458–484 CrossRef CAS.
- R. L. Carlin and A. J. Duyneveldt, Magnetic Properties of Transition Metal Compounds, Springer, Berlin, Heidelberg, New York, 1977 Search PubMed.
- R. J. Glauber, J. Math. Phys., 1963, 4, 294–307 CrossRef.
- D. E. Freedman, W. H. Harman, T. D. Harris, G. J. Long, C. J. Chang and J. R. Long, J. Am. Chem. Soc., 2010, 132, 1224–1225 CrossRef CAS PubMed.
- J. Soeteman, L. Bevaart and A. J. van Duyneveldt, Physica, 1974, 74, 126–134 CrossRef CAS.
- F. Neese, J. Am. Chem. Soc., 2006, 128(31), 10213–10222 CrossRef CAS PubMed.
- R. Boča, Coord. Chem. Rev., 2004, 248, 757 CrossRef.
- H. Bolvin and J. Autschbach, Relativistic Methods for Calculating Electron Paramagnetic Resonance (EPR) Parameters, in Handbook of Relativistic Quantum Chemistry, ed. W. Liu, Springer, Berlin Heidelberg, 2019 Search PubMed.
- NIST Atomic Spectra Database (ver. 5.6.1), https://www.nist.gov/pml/atomic-spectra-database.
- S. Gómez-Coca, E. Cremades, N. Aliaga-Alcalde and E. Ruiz, J. Am. Chem. Soc., 2013, 135, 7010–7018 CrossRef PubMed.
- H. Andres, E. L. Bominaar, J. M. Smith, N. A. Eckert, P. L. Holland and E. J. Münck, Am. Chem. Soc., 2002, 124, 3012 CrossRef CAS.
- A. L. Companion and M. A. Komorynskyl, J. Chem. Ed., 1964, 41, 257 CrossRef CAS.
- Regarding the quantum chemical methods employed, one has to distinguish between effects stemming from the self-consistent field (SCF) relaxation of the orbitals and from changing the flexibility of the configuration interaction (CI) wave function in terms of explicitly interacting states.
- D. G. Gilheany, Chem. Rev., 1994, 94, 1339–1374 CrossRef CAS.
- J. E. Huheey, E. A. Keiter and R. L. Keiter, Anorganische Chemie, Prinzipien von Struktur und Reaktivität, hrsg. v. R. Steudel, bearb. v. F. Breher, M. Finze, D. Johrendt, M. Kaupp, H.-J. Lunk, U. Radius, U. Schatzschneider, 5te Auflage, 2014, Kap. 15, S. 797, Walter de Gruyter GmbH & Co. KG Berlin/Boston.
- K. W. H. Stevens, Proc. Phys. Soc., London, Sect. A, 1952, 65(3), 209–215 CrossRef.
- J. S. Griffith, The theory of transition-metal ions, Cambridge University Press, Cambridge, 1971, ISBN 978–0521051507 Search PubMed.
- A. Abragam and B. Bleaney, Electron Paramagnetic Resonance of Transition Ions, Oxford University Press, 1970 Search PubMed.
- D. L-J. Broere, I. Coric, A. Brosnahan and P. L. Holland, Inorg. Chem., 2017, 56(6), 3140–3143 CrossRef CAS PubMed.
- W. Wolfsberger and H. Schmidbaur, Synth. React. Inorg. Met.-Org. Chem., 1974, 4(2), 149–156 CrossRef CAS.
- X-RED32 1.01, Data Reduction Program, Stoe & Cie GmbH, Darmstadt, Germany, 2001 Search PubMed.
- G. M. Sheldrick, SHELXTL PC version 5.1 An Integrated System for Solving, Refining, and Displaying Crystal Structures from Diffraction Data, Bruker Analytical X-ray Systems, Karlsruhe, 2000 Search PubMed.
- K. Brandenburg, Diamond Version 2.1d, Crystal Impact GbR, 1996–2000 Search PubMed.
- STOE, WinXPOW, STOE & Cie GmbH, Darmstadt, 2000 Search PubMed.
- O. Kahn, Molecular Magnetism, Wiley-VCH, Weinheim, 1993 Search PubMed.
- H. Lueken, in Magnetochemie, ed. B. G. Teubner, Stuttgart, Leibzig, 1999, p. 426 Search PubMed.
- W. Haberditzl, Angew. Chem., Int. Ed. Engl., 1966, 5, 288–323 CrossRef CAS.
- F. Aquilante, J. Autschbach, R. K. Carlson, L. F. Chibotaru, M. G. Delcey, L. De Vico, I. Fdez Galván, N. Ferré, L. M. Frutos, L. Gagliardi, M. Garavelli, A. Giussani, C. E. Hoyer, G. Li Manni, H. Lischka, D. Ma, P.-Å. Malmqvist, T. Müller, A. Nenov, M. Olivucci, T. B. Pedersen, D. Peng, F. Plasser, B. Pritchard, M. Reiher, I. Rivalta, I. Schapiro, J. Segarra-Martí, M. Stenrup, D. G. Truhlar, L. Ungur, A. Valentini, S. Vancoillie, V. Veryazov, V. P. Vysotskiy, O. Weingart, F. Zapata and R. Lindh, J. Comput. Chem., 2016, 37, 506–541 CrossRef CAS.
- D. Peng and M. Reiher, Theor. Chem. Acc., 2012, 131, 1081 Search PubMed.
- B. O. Roos, R. Lindh, P.-Å. Malmqvist, V. Veryazov and P.-O. Widmark, J. Phys. Chem. A, 2005, 109, 6575–6579 CrossRef CAS.
- B. O. Roos, R. Lindh, P.-Å. Malmqvist, V. Veryazov and P.-O. Widmark, J. Phys. Chem. A, 2004, 108, 2851–2858 CrossRef CAS.
- P.-O. Widmark, P.-Å. Malmqvist and B. O. Roos, Theor. Chim. Acta, 1990, 77, 291–306 CrossRef CAS.
- http://molcas.org/documentation/manual/node70.html .
- P. Schwerdtfeger, Relativistic electronic structure theory, part 2: Applications, Elsevier, Amsterdam, 2004 Search PubMed.
- L. F. Chibotaru and L. Ungur, J. Chem. Phys., 2012, 137, 064112 CrossRef CAS.
- U. Meier and V. Staemmler, Theor. Chim. Acta, 1989, 76(2), 95–111 CrossRef CAS.
- J. Wasilewski, Int. J. Quantum Chem., 1989, 36(4), 503–524 CrossRef CAS.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065 RSC.
- TURBOMOLE V6.6, TURBOMOLE GmbH Karlsruhe, 2012, http://www.turbomole.de. TURBOMOLE is a development of University of Karlsruhe and Forschungszentrum Karlsruhe 1989–2007, TURBOMOLE GmbH since 2007.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS PubMed.
- T. Bodenstein, Entwicklung und Anwendung von Multireferenzverfahren zur Beschreibung magnetischer Eigenschaften von Metallkomplexen, Ph.D. thesis, Karlsruhe Institute of Technology, 2015 Search PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Equations, crystallographic data, molecular structures, XRD powder patterns, magnetic data, comprehensive data of quantum chemical calculations. CCDC 1902301–1902305. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c9dt01702j |
| ‡ Present address: Hylleraas Center, Department of Chemistry, University of Oslo, P. O. Box 1033, 0315 Oslo, Norway; former address: Theoretical Chemistry, Department of Chemistry, Aarhus University, Langelandsgade 140, 8000 Aarhus C, Denmark. |
| § Magnetic data have not been measured for [Fe{(N(SiMe3)2}2py] as it could not be isolated purely. |
| This journal is © The Royal Society of Chemistry 2019 |