Open Access Article
Open Access ArticleDinuclear manganese(III) complexes with bioinspired coordination and variable linkers showing weak exchange effects: a synthetic, structural, spectroscopic and computation study†
Sergiu
Shova
a,
Angelica
Vlad
a,
Maria
Cazacu
 a,
J.
Krzystek
a,
J.
Krzystek
 b,
Andrew
Ozarowski
b,
Andrew
Ozarowski
 b,
Michal
Malček
c,
Lukas
Bucinsky
c,
Peter
Rapta
c,
Joan
Cano
b,
Michal
Malček
c,
Lukas
Bucinsky
c,
Peter
Rapta
c,
Joan
Cano
 d,
Joshua
Telser
d,
Joshua
Telser
 *e and
Vladimir B.
Arion
*e and
Vladimir B.
Arion
 *f
*f
aInorganic Polymers Department, “Petru Poni” Institute of Macromolecular Chemistry, Aleea Gr. Ghica Voda 41 A, Iasi 700487, Romania
bNational High Magnetic Field Laboratory, Florida State University, Tallahassee, Florida 32310, USA
cInstitute of Physical Chemistry and Chemical Physics, Slovak University of Technology in Bratislava, Radlinského 9, 81237 Bratislava, Slovak Republic
dInstitut de Ciència Molecular, Universitat de València, Catedrático José Beltrán Martínez 2, 46980 Paterna, Spain
eDepartment of Biological, Physical and Health Sciences, Roosevelt University, 430 S. Michigan Avenue, Chicago, Illinois 60605, USA. E-mail: jtelser@roosevelt.edu
fInstitute of Inorganic Chemistry of the University of Vienna, Währinger Strasse 42, A1090 Vienna, Austria. E-mail: vladimir.arion@univie.ac.at
First published on 7th January 2019
Abstract
Three dimanganese(III) complexes have been synthesised and fully characterised by standard spectroscopic methods and spectroelectrochemistry. Each MnIII ion is chelated by a salen type ligand (H2L), but there is variation in the bridging group: LMn(OOCCH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CHCOO)MnL, LMn(OOCC6H4COO)MnL, and LMn(OOCC6H4C6H4COO)MnL. X-ray diffraction revealed an axial compression of each six-coordinate high-spin d4 MnIII ion, which is a Jahn–Teller-active ion. Temperature dependent magnetic susceptibility and variable temperature-variable field (VTVH) magnetisation measurements, as well as high-frequency and -field EPR (HFEPR) spectroscopy were used to accurately describe the magnetic properties of the complexes, not only the single-ion spin Hamiltonian parameters: g-values and zero-field splitting (ZFS) parameters D and E, but also the exchange interaction constant J between the two ions, which has been seldom determined for a di-MnIII complex, particularly when there is more than a single bridging atom. Quantum chemical calculations reproduced well the electronic and geometric structure of these unusual complexes, and, in particular, their electronic absorption spectra along with the spin Hamiltonian and exchange parameters.
CHCOO)MnL, LMn(OOCC6H4COO)MnL, and LMn(OOCC6H4C6H4COO)MnL. X-ray diffraction revealed an axial compression of each six-coordinate high-spin d4 MnIII ion, which is a Jahn–Teller-active ion. Temperature dependent magnetic susceptibility and variable temperature-variable field (VTVH) magnetisation measurements, as well as high-frequency and -field EPR (HFEPR) spectroscopy were used to accurately describe the magnetic properties of the complexes, not only the single-ion spin Hamiltonian parameters: g-values and zero-field splitting (ZFS) parameters D and E, but also the exchange interaction constant J between the two ions, which has been seldom determined for a di-MnIII complex, particularly when there is more than a single bridging atom. Quantum chemical calculations reproduced well the electronic and geometric structure of these unusual complexes, and, in particular, their electronic absorption spectra along with the spin Hamiltonian and exchange parameters.
Introduction
Dimanganese units have been discovered in a number of metalloenzymes, such as non-heme catalases,1–3 class 1b ribonucleotide reductases,4,5 Mn arginase,6 and bacterial thiosulfate oxidases.7 Therefore, the coordination chemistry of manganese has been in part developed by the desire to mimic the structure and spectroscopic properties of the active sites of these enzymes, and their catalytic activity. A large number of dimanganese complexes in various oxidation states with single fluorido,8 oxido/hydroxido/alkoxido,9–11 bis-μ-oxido/hydroxido/alkoxido,12 μ1,3-carboxylato13 and mixed oxido/hydroxido/alkoxido-carboxylato14–16 bridges and terminal carboxylato ligands17 have been synthesised and characterised over the years revealing structural, spectroscopic, or catalytic resemblance to the native enzymes. The progress in design and synthesis of low-molecular weight antioxidant catalysts as catalase-mimics has been recently reviewed.18 The Mn⋯Mn separation in these model compounds is usually around 3.0–3.7 Å, mimicking well the Mn–Mn distance in native enzymes. This di-Mn structure has been achieved by judicious ligand design. Dinucleating proligands,19,20 tridentate capping proligands such as tris(imidazole-2-yl)phosphine (TMIP),21 1,4,7-triazacyclononane (tacn)22 and its derivatives, 1,4,7-trimethyl-1,4,7-triazacyclononane (Me3tacn),8,23,24 and proline-derived trispyrrolidine-1,4,7-triazacyclononane,10,11 as well as hydrotris(pyrazol-1-yl)borate (HB(pz)3)22,25 have often been employed to facilitate the assembly of desired dimanganese cores by preventing polymeric chain formation.Examples of dinuclear complexes with longer manganese-manganese distances are rare in the literature. Of note are the di-MnIII complexes with two salen-type ligands separated by one or two xanthene spacer(s), in which the Mn⋯Mn separation was ∼5.1 Å,26 and with two salicaldehyde/diketonate-derived ligands in which the Mn⋯Mn separation was ∼5.3 Å, and Mn–Mn exchange interactions were observed.27,28 Also notable are di-MnII expanded porphyrins with Mn–Mn distance of 5.4 Å,29 and di-MnII complexes of bis(pentadentate) ligands derived from bis-tacn species with longer Mn⋯Mn distances (≥6.8 Å)30 with no evidence of coupling between paramagnetic centres.
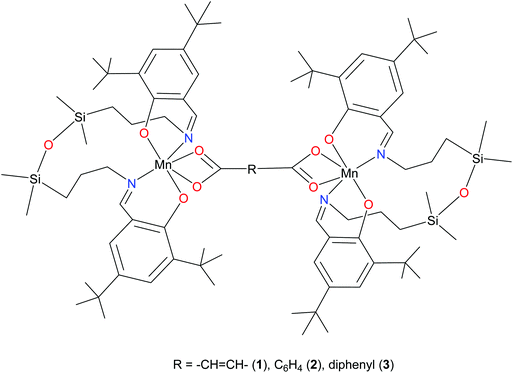
Recently, we reported on the synthesis of mononuclear 3d metal complexes with salen-type ligands bearing a disiloxane moiety (H2L), which were shown to form a central 12-membered chelate cycle when binding to first row transition metal ions, e.g., CuII, FeIII, and MnIII.31–34 In case of manganese, MnIIIL(OAc) and MnIIIL(NCS) were isolated and characterised by single crystal X-ray diffraction, routine spectroscopic methods (UV-vis, IR), spectroelectrochemistry, magnetochemistry, and high-frequency and -field EPR (HFEPR). We show herein that the 12-membered chelate cycle formed by coordination of this unusual salen-type ligand to manganese(III) precludes polymer formation and facilitates the assembly of di-MnIII complexes by using as bridging ligands dicarboxylic acids. Dimanganese(III) complexes with fumarato, terephthalato, and/or p-diphenylcarboxylato bridging ligands were prepared and fully characterised. These complexes are depicted in Fig. 1 and feature Mn⋯Mn distances ranging from 8.7 to 15.1 Å as controlled by the spacer group of the dicarboxylate. Previously reported dimanganese(III,IV) and dimanganese(II,III) systems have been investigated by HFEPR,35–37 and more importantly, so have dimanganese(III) complexes, such as a μ-oxido complex by Retegan et al.,10 a μ-fluorido complex by Pedersen et al.,8 and a system more relevant to those reported here, namely a dimanganese(III,III) complex without any bridging atoms, but with covalent connections between the two MnIII ions via two trans four-bond π-conjugated O–C–C–C–O pathways.28 A tetranuclear complex comprising a square grid of MnIII ions linked by Schiff base ligands has also been studied by HFEPR,38 but this complicated spin system is beyond the present study.
Interestingly, the HFEPR spectra observed here for the dinuclear complexes proved to be of better quality than those reported for the parent mononuclear complex MnIIIL(OAc). We note that the previous HFEPR studies of di-MnIII complexes also exhibited very high quality spectra.8,10,28 These investigations taken together show that a reliable treatment of both the single-ion ZFS interaction and extraction of weak exchange interactions between paramagnetic MnIII (3d4) centres are possible.
Experimental
Materials
The complex [MnL(OAc)]·0.15H2O, where H2L is a tetradentate Schiff base with a tetramethyldisiloxane spacer, was prepared according to the procedure described previously.31 Fumaric acid (trans-HOOCCH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CHCOOH), benzene-1,4-dicarboxylic acid (terephthalic acid, C6H4-1,4-(CO2H)2), and biphenyl-4,4′-dicarboxylic acid, 97% (HO2CC6H4C6H4CO2H) were all from Aldrich.
CHCOOH), benzene-1,4-dicarboxylic acid (terephthalic acid, C6H4-1,4-(CO2H)2), and biphenyl-4,4′-dicarboxylic acid, 97% (HO2CC6H4C6H4CO2H) were all from Aldrich.
Synthesis of complexes
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/b_char_e001.gif) CHCOO)MnL·H2O (1).
A solution of MnL(OAc)·0.15H2O (0.16 g, 0.2 mmol) in methylene chloride (20 ml) in a Schlenk tube was overlayered with a solution of fumaric acid (0.01 g, 0.1 mmol) in dimethylformamide (4 ml). The content was allowed to stand at room temperature. Brown sticks formed within one month and were separated by filtration, washed with diethyl ether and dried at room temperature. Yield: 0.11 g, 69.4%. Anal. Calcd (%) for C84H136Mn2N4O11Si4 (Mr 1645.26): C, 61.32, H, 8.64, N, 3.41. Found: C, 61.31, H, 8.40, N, 3.42. IR spectrum (KBr pellet), selected bands, νmax (cm–1): 3442w, 2956vs, 2868s, 1676vs, 1618vs, 1550s, 1440s, 1355m, 1298m, 1255vs, 1174m, 1066s, 977w, 921w, 885m, 840s, 785s, 746m, 698m, 634w, 565s, 509w, 468vw, 441w. X-ray diffraction quality crystals were grown from a mixture of CH3OH
CHCOO)MnL·H2O (1).
A solution of MnL(OAc)·0.15H2O (0.16 g, 0.2 mmol) in methylene chloride (20 ml) in a Schlenk tube was overlayered with a solution of fumaric acid (0.01 g, 0.1 mmol) in dimethylformamide (4 ml). The content was allowed to stand at room temperature. Brown sticks formed within one month and were separated by filtration, washed with diethyl ether and dried at room temperature. Yield: 0.11 g, 69.4%. Anal. Calcd (%) for C84H136Mn2N4O11Si4 (Mr 1645.26): C, 61.32, H, 8.64, N, 3.41. Found: C, 61.31, H, 8.40, N, 3.42. IR spectrum (KBr pellet), selected bands, νmax (cm–1): 3442w, 2956vs, 2868s, 1676vs, 1618vs, 1550s, 1440s, 1355m, 1298m, 1255vs, 1174m, 1066s, 977w, 921w, 885m, 840s, 785s, 746m, 698m, 634w, 565s, 509w, 468vw, 441w. X-ray diffraction quality crystals were grown from a mixture of CH3OH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CH2Cl2 (∼3
CH2Cl2 (∼3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1). ESI-MS (positive ion mode): m/z 733.42 [MnIIIL]+.
1). ESI-MS (positive ion mode): m/z 733.42 [MnIIIL]+.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CH2Cl2 (∼4
CH2Cl2 (∼4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1). ESI-MS (positive ion mode): m/z 733.42 [MnIIIL]+.
1). ESI-MS (positive ion mode): m/z 733.42 [MnIIIL]+.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) methanol 1
methanol 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (4 ml) at about 60 °C. The content was allowed to stand at room temperature. Brown sticks formed within one month and were separated by filtration, washed with diethyl ether and dried at room temperature. Yield: 0.02 g, 91.0%. Anal. Calcd (%) for C94H142Mn2N4O11Si4 (Mr 1726.37): C, 65.40, H, 8.29, N, 3.25. Found: C, 65.61, H, 8.19, N, 3.41. IR spectrum (KBr pellet), selected bands, νmax (cm–1): 3437m, 2956vs, 2910s, 2868s, 1676s, 1616vs, 1581m, 1541s, 1436s, 1396vs, 1355m, 1307m, 1253vs, 1174s, 1132w, 1064s, 972w, 921vw, 885m, 842vs, 777s, 694m, 636w, 567m, 509w, 439w. ESI-MS (positive ion mode): m/z 733.42 [MnIIIL]+.
1 (4 ml) at about 60 °C. The content was allowed to stand at room temperature. Brown sticks formed within one month and were separated by filtration, washed with diethyl ether and dried at room temperature. Yield: 0.02 g, 91.0%. Anal. Calcd (%) for C94H142Mn2N4O11Si4 (Mr 1726.37): C, 65.40, H, 8.29, N, 3.25. Found: C, 65.61, H, 8.19, N, 3.41. IR spectrum (KBr pellet), selected bands, νmax (cm–1): 3437m, 2956vs, 2910s, 2868s, 1676s, 1616vs, 1581m, 1541s, 1436s, 1396vs, 1355m, 1307m, 1253vs, 1174s, 1132w, 1064s, 972w, 921vw, 885m, 842vs, 777s, 694m, 636w, 567m, 509w, 439w. ESI-MS (positive ion mode): m/z 733.42 [MnIIIL]+.
| Compound | 1·6CH2Cl2 | 2·4CH2Cl2 | 3·4.5H2O |
|---|---|---|---|
| a R 1 = Σ| |Fo| − |Fc| |/Σ|Fo|. b wR2 = {Σ[w(Fo2 − Fc2)2]/Σ[w(Fo2)2]}1/2. c GOF = {Σ[w(Fo2 − Fc2)2]/(n − p)}1/2, where n is the number of reflections and p is the total number of parameters refined. | |||
| Empirical formula | C90H146Cl12Mn2N4O10Si4 | C92H144Cl8Mn2N4O10Si4 | C94H151Mn2N4O15.5Si4 |
| F w | 2091.75 | 1971.95 | 1807.43 |
| T [K] | 100 | 100 | 100 |
| Crystal system | Triclinic | Triclinic | Monoclinic |
| Space group |
P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) |
P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) |
P21/c |
| a [Å] | 13.7007(7) | 11.8837(17) | 15.790(2) |
| b [Å] | 14.7166(7) | 12.7755(19) | 14.221(2) |
| c [Å] | 15.9617(8) | 18.564(3) | 23.958(3) |
| α [°] | 67.7592(16) | 73.414(5) | |
| β [°] | 66.1603(17) | 81.359(5) | 106.126(5) |
| γ [°] | 79.2085(17) | 72.378(5) | |
| V [Å3] | 2722.5(2) | 2568.1(6) | 5168.3(13) |
| ρ calcd [g cm−3] | 1.276 | 1.275 | 1.161 |
| Z | 1 | 2 | 4 |
| μ [mm−1] | 0.622 | 0.555 | 0.350 |
| Crystal size [mm] | 0.528 × 0.523 × 0.485 | 0.32 × 0.14 × 0.04 | 0.41 × 0.096 × 0.072 |
| 2Θ range | 4.88 to 60.22 | 4.62 to 50.06 | 4.56 to 50.06 |
| Reflections collected | 61![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 020 020 |
8962 | 64![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 669 669 |
| Independent reflections | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 855 [Rint = 0.0461] 855 [Rint = 0.0461] |
8962 [Rint = 0.045] | 9090 [Rint = 0.0576] |
| Data/restraints/parameters | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 855/6/605 855/6/605 |
8962/0/558 | 9090/3/567 |
| R 1 | 0.0539 | 0.0765 | 0.0779 |
| wR2b | 0.1653 | 0.2270 | 0.2170 |
| GOFc | 1.040 | 1.061 | 1.030 |
| Largest diff. peak/hole/e Å−3 | 1.04/−2.08 | 1.25/−1.15 | 1.88/−0.98 |
Multifrequency HFEPR data obtained for 1 and 2 were fitted using the following spin Hamiltonian:
| H = βeBgŜ + D[Ŝz2 − S(S + 1)/3] + E(Ŝx2 − Ŝy2) | (1) |
(a) Theoretical calculations based on both an ab initio method, namely the Complete Active Space (CAS) multi-configurational method, as well as at the DFT level using the PBE functional,45 on the full MnIIIGaIII dinuclear complexes of 1–3 were performed for determining the MnIII single-ion ZFS. These calculations were carried out using the TZVP basis set proposed by Ahlrichs46–48 and the auxiliary TZV/C Coulomb fitting basis sets.49–51 The second order contributions to ZFS were evaluated for the five quintet and 30 triplet excited states generated from an active space with four electrons in five d orbitals. Furthermore, to estimate the dynamic electron correlation effects on ZFS parameters, mononuclear models built from a truncation of the original molecules were carried out by the CAS method and subsequent second-order N-electron valence state perturbation theory (NEVPT2).52
(b) For the sake of comparison with the previous studies on [MnL(NCS] and [MnL(OAc)],31,33 additional calculations have been performed using the BLYP functional53 and 6-311G*54 basis set using the CASSCF and Multi-Reference Configuration Interaction (MRCI) approaches. These calculations used the crystal structure geometries of 1–3 with the entire second MnIII-containing moiety removed (refer to ESI† for further details). In addition, the effect of the solvent molecules present in the crystal structure has been studied for brevity at the BLYP/6-311G* level. The spin–spin interaction has been accounted via the MRCI55 approach for the state-averaged quintet CASSCF(4,5) wave function.
(c) In addition, the multi-centre (i.e., both MnIIIL moieties and the bridging ligand) CASSCF(8,10) ZFS parameters have been compared to CAS(8,10)-CI results (automatic auxiliary fitting basis set was used) for 1–3. The L-CASCI approach has followed consistently the protocol as described in the literature.56 The L-CASCI calculations accounted both for spin–orbit and spin–spin couplings (SOC and SSC, respectively).
For an additional comparison to spectroelectrochemistry studies, B3LYP53/6-311G*54 geometry optimisations of neutral (nonet), single (octet) and doubly (septet) charged species of 1–3 have been performed using the Gaussian09 software suite.57 Subsequently, electronic transitions of all the B3LYP/6-311G* optimised structures were evaluated using the TD-DFT method.58 Herein, the 40, 60, and 80 lowest excited states were taken into account for the neutral, single and doubly charged species, respectively, to approach transition energies corresponding to λ ≥ 300 nm. Spin densities were visualised using Molekel59 software suite.
To extend further the computations used to assess the EPR parameters in the single-ion models, the possibility of a magnetic exchange interaction between the two MnIII ions was studied at the DFT level of theory. These calculations were performed with the CAM-B3LYP hybrid functional using the Gaussian 09 package,57 the quadratic convergence approach, and a guess function generated with the fragment tool of the same program.53,60 Triple-ζ and double-ζ all-electron basis sets proposed by Ahlrichs et al. were respectively employed for the Mn ions and the remaining atoms.47,48 The magnetic coupling states were obtained from the relative energies of the broken-symmetry (BS) singlet spin state from the high-spin state with parallel local spin moments.61–63 A polarisable continuum model (PCM) was introduced in the calculations with the parameters corresponding to acetonitrile.64 To assure that the precision of the results was higher than the magnitude of the estimated J values, a triple-ζ basis set, adding an extra p polarisation function for all atoms, together with restricted conditions in the self-consistent convergence of the wave-function and in the evaluation of the bi-electronic integrals (very tight and ultrafine, respectively) were also employed.
Results and discussion
Synthesis
Complexes 1–3 were prepared by reaction of MnL(OAc)·0.15H2O with fumaric acid, terephthalic acid, and biphenyl-4,4′-dicarboxylic acid in DCM/DMF or DCM/DMF/MeOH mixtures after long standing of the reaction mixture at room temperature. Recrystallisation of the crude products from DCM/MeOH 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 afforded single crystals of X-ray diffraction quality.
1 afforded single crystals of X-ray diffraction quality.
X-ray diffraction
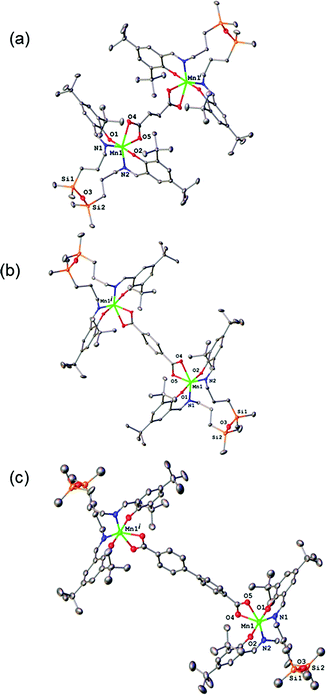
The results of X-ray diffraction studies for 1–3 are shown in Fig. 2. All three dinuclear molecules exhibit similar molecular structure with each exhibiting its own crystallographically imposed inversion symmetry and show the presence of a half of dimeric molecule co-crystallised with 3CH2Cl2, 2CH2Cl2, and 2.25H2O, respectively, in the asymmetric part of the unit cell. Each Mn atom is coordinated by N2O2 set of atoms originating from tetradentate, doubly deprotonated Schiff base ligand and two oxygen atoms provided by the dicarboxylato anion in strongly distorted octahedral geometry. Further analysis of the coordination polyhedra indicates that the equatorial plane comprises N1 and N2 atoms of the tetradentate ligand and two oxygen atoms of the dicarboxylato ion. The axial positions are occupied by the phenolato oxygen atoms. The axial bond lengths Mn–O1 and Mn–O2 are in the range of 1.849(1)–1.870(1) Å. These are significantly shorter than the equatorial interatomic distances Mn–O and Mn–N in the range of 2.342(3)–2.077(3) Å, which indicates an axial compression in the distorted octahedron. The same coordination at the Mn site has been earlier reported for mononuclear compound [MnL(OAc)],31 where H2L is N,N-bis(3,5-di-tert-butyl-2-hydroxybenzaldehyde) 1,3-bis(3-aminopropyl)tetramethyldisiloxane. The average angle within the plane O4–Mn1–O5 is of 59.3(3)°, while N1–Mn1–N2 angle is of 120.5(3)° for 1–3, respectively, reflects also the distortion of the octahedral geometry. The Mn–Mn distances in 1–3 are 8.736, 10.912 and 15.103 Å, respectively.The analysis of the crystal structure packing revealed that all the compounds are associated in the crystal only through the C–H⋯π interactions to form either supramolecular chains or ribbon-like aggregates. Thus, the crystal structures of 1 and 3 are built up from the parallel packing of one-dimensional chains, as shown in Fig. S1a and S1b (ESI†), respectively. The crystal packing of 3 shows the presence of the supramolecular ribbons (Fig. S2, ESI†).
Electrochemistry and spectroelectrochemistry
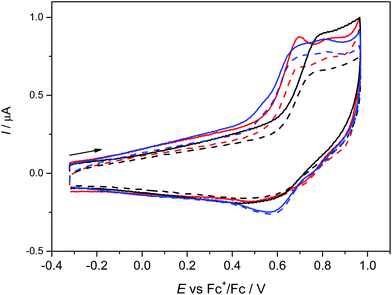
The anodic oxidation of complexes 1–3 is irreversible as shown in Fig. 3 and is similar to the monomeric MnL(OAc) analogue.31 Only a small, broad, cathodic peak can be observed upon the voltammetric scan reversal, even at low scan rates, indicating subsequent irreversible chemical reactions of the oxidised dimeric complexes.A small additional peak is seen behind the first one for 1 and 3 which height varies from scan to scan indicating the follow up reactions of the oxidised state (see also Fig. S3a, ESI†). No reduction processes were observed in cathodic region (see Fig. S3b, ESI†) as also noted for MnL(OAc). After electrolysis of 1–3 in the region of the first irreversible oxidation peak, no X-band EPR signal was observed even at 77 K further indicating a low stability of the oxidised form of 1–3. Although a negative EPR result at 77 K is not proof of the inability to electrochemically generate MnIV species in solution, we note that a variety of bona fide MnIV coordination complexes exhibit EPR spectra (even in some cases as magnetically undiluted solids) at temperatures as high as ambient.65–67 However, there are small differences in the voltammetric responses found for 1–3. The highest oxidation potential was found for 2 with only one oxidation peak demonstrating the (electro)chemical equivalence of the two MnIII sites and the lack of measurable interaction between them, consistent with the magnetometry and HFEPR. For 3 the lowest oxidation potential was found with two overlapping oxidation peaks again indicating two almost equal MnIII redox centres.
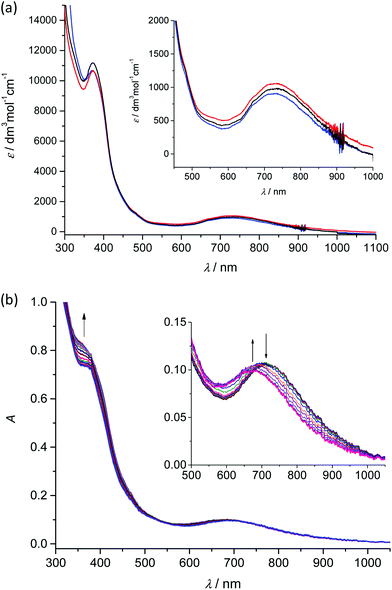
Analogously to the voltammetric studies, the optical spectra of 1–3 are very similar with low-intensity bands at 480, 670 and at around 730 nm (Fig. 4a).
Taking into account our previous works31,33 on mononuclear MnIIIL(OAc) and MnIIIL(NCS), the first low-energy electronic transition at 730 nm can be assigned to LMCT from phenolate moieties to manganese(III) with a strong charge transfer from phenolic moieties to the central Mn atom and the corresponding coordination polyhedron. The in situ UV-vis-NIR spectroelectrochemical experiments confirmed irreversible changes upon anodic oxidation of 1–3 in the region of the first oxidation peak (from +0.2 V to +0.9 V vs. Fc+/Fc) as illustrated for 2 in Fig. 4b. A new optical band at 360 nm emerged upon oxidation and simultaneously the maximum of the low-energy band shifted from 720 nm to 675 nm (see inset in Fig. 4b). However in contrast to the recently studied MnIIIL(NCS) complex,34 upon scan reversal the products that are formed upon oxidation are not reoxidised and no recovery of the initial optical bands upon the voltammetric reverse scan occurred, confirming the low stability of MnIV state as also reported for the MnIIIL(OAc).31
Magnetometry
The direct current (dc) magnetic properties of 1–3 were measured per dinuclear complex and are presented in the form of plots of χMT vs. T and M vs. H/T, as shown in Fig. 5. The χMT values at room temperature (6.02, 6.20, and 6.07 cm3 K mol−1 for 1–3, respectively) are close to that expected for two isolated S = 2 centres (6.0 cm3 K mol−1, g = 2.0). When cooling down, the χMT value remains constant until 40 K and then decreases abruptly to reach a value at 2 K of 4.29, 4.02, and 3.99 cm3 K mol−1 for 1–3, respectively. The isothermal magnetisation curves do not superimpose, and the magnetisation values at 5 T and 2 K (6.62, 6.54, and 6.49Nβ for 1–3) are below the saturation limit of 8Nβ for two S = 2 with g = 2. This behaviour could be due to the presence either of magnetic exchange coupling68 or single-ion zero-field splitting (ZFS). The distance between the two MnIII ions, is quite large (8.736 Å, 10.912 Å, and 15.102 Å for 1, 2, and 3, respectively), so the electron dipole–dipole coupling would be very small (−0.008 cm−1 for 1 and −0.004 cm−1 for 2, see below). Moreover, MnIII in such a coordination geometry has been amply demonstrated to exhibit ZFS.27,69 Consequently, only ZFS would be responsible for the drop of χMT at low temperature. Evidence for weak exchange coupling between the Mn–Mn ions will be described below, along with computational studies probing this phenomenon. The best-fit obtained parameters are: g = 2.004, D = +3.07 cm−1, E/D = 0.000 (F = 7.7 × 10−5) for 1; g = 2.033, D = +3.45 cm−1, E/D = 0.009 (F = 4.4 × 10−6) for 2; and g = 2.019, D = + 3.63 cm−1, E/D = 0.002 (F = 6.6 × 10−5) for 3. The low values of the E/D ratio are not in agreement with those obtained by HFEPR spectroscopy, but this is caused by the poor sensitivity of dc susceptibility to this parameter. More importantly, the positive D values agree with the axial compression observed in the octahedral coordination sphere.69a,f,70,71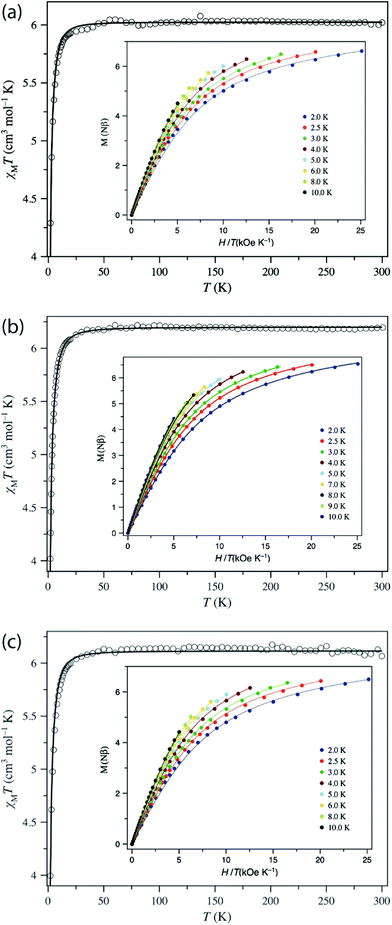 | ||
| Fig. 5 Plots of χMT vs. T in the range 2–300 K in a 0.025 (T < 20 K) and 0.5 T (T ≥ 20 K) applied field and M vs. H/T (inset) for (a) 1, (b) 2, and (c) 3 in the 2–10 K temperature range. The solid lines are the best-fit curves, with the fit parameters given in Table 2. | ||
HFEPR
Complex 1 when measured as is, i.e. unconstrained, produced strong spectra that showed symptoms of field-induced torquing. We did not try to interpret them, but proceeded to experiments on an n-eicosane pellet. Typical low-temperature spectra of 1 as a pellet are shown in Fig. 6 (top part), accompanied by simulations assuming a perfect powder distribution of the crystallites in space. Spectra at two lower frequencies are shown as Fig. S4 and S5, ESI.† The agreement between the simulations and experiments can be described as very good, assuming a spin state S = 2 characteristic for an individual (not coupled) MnIII ion and under the condition of D > 0.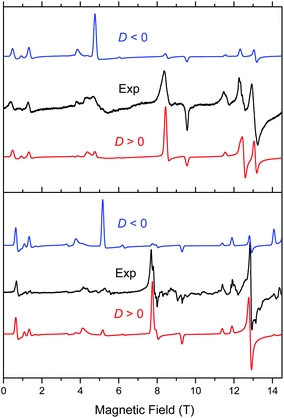 | ||
| Fig. 6 Low-temperature HFEPR spectra of 1 at 422.4 GHz and 15 K (top) and 2 and 406.4 GHz and 10 K (bottom, both represented as black traces) accompanied by simulations using S = 2 spin Hamiltonian parameters as in Table 2. Blue traces: simulations using negative D; red traces: positive D. | ||
Complex 2 was visibly more crystalline than 1. This required extensive grinding prior to pressing it into a pellet. A typical low-temperature pellet spectrum is shown in Fig. 6 (bottom), accompanied by simulations assuming a perfect powder distribution of the crystallites in space. Additional spectra at two different frequencies are shown in Fig. S6 and S7, ESI.† The spectral quality was somewhat lower than that for 1 because of the sample crystallinity, yet the agreement between the simulations and experiments can be also described as very good, assuming again an S = 2 spin state, and under the condition of D > 0. The spin Hamiltonian parameters are similar but not identical to those of 1.
Both complexes produced HFEPR spectra at any temperature between liquid helium and ambient. Fig. 7 shows their room-temperature spectra, again with simulations. In complex 1, the axial ZFS parameter D is almost unchanged between liquid helium and room temperature (Table 2), but |E| strongly decreases, the ZFS tensor becoming almost axial. In 2, both parameters slightly decrease from low to high temperature.
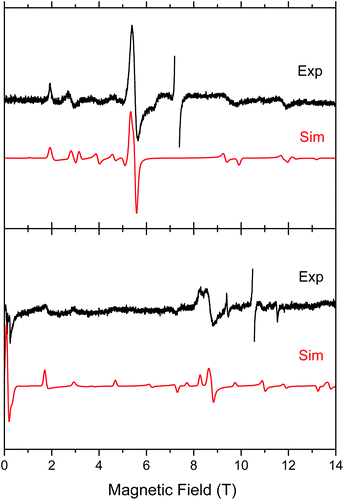 | ||
| Fig. 7 Room-temperature HFEPR spectra of 2 at 203.2 GHz and 280 K (top) and 2 at 295.2 GHz and 277 K (bottom, black traces) accompanied by simulations using spin Hamiltonian parameters as in Table 2. At these temperatures, there is no difference between negative and positive D reflected in the spectra, thus the simulation (red trace) used positive D only. The MnII impurity resonances at g = 2.00 were left out of the experimental spectra and are not simulated. | ||
| Complex | T (K) | D (cm−1) | |E| (cm−1) | |E/D| | g x | g y | g z |
|---|---|---|---|---|---|---|---|
| a The magnetic fits used an isotropic g value which is given only in this column. b Compound 3 was investigated only by magnetometry due to material limitations. c The room temperature HFEPR parameters are of lower precision (not specified) and are provided primarily to demonstrate that the electronic structures of 1 and 2 remain essentially unchanged over a wide temperature range. | |||||||
| 1 | 15 | +3.246(5) | 0.425(3) | 0.13 | 1.991(4) | 2.003(4) | 2.015(5) |
| 1 | 280c | 3.27 | 0.10 | 0.03 | 1.98 | 1.98 | 2.00 |
| 1 (magn.) | NA | +3.07 | 0 | 0.000 | — | — | 2.004 |
| 2 | 10 | +2.997(3) | 0.530(1) | 0.18 | 1.991(5) | 1.991(5) | 1.991(5) |
| 2 | 277c | 2.88 | 0.44 | 0.15 | 1.99 | 1.99 | 1.99 |
| 2 (magn.) | NA | +3.45 | 0.03 | 0.009 | — | — | 2.033 |
| 3 (magn.) | NA | +3.63 | 0.007 | 0.002 | — | — | 2.019 |
A careful inspection of certain turning points in the low-T HFEPR spectra of both 1 and 2 reveals spectral regions at any frequency >200 GHz that show a fine but not quite regular structure with a period of ca. 60–80 mT (Fig. 8). The average value of 70 mT corresponds to 0.065 cm−1, which is very small on the HFEPR scale as it corresponds to ∼2 GHz (∼1% of the frequency used in Fig. 8, right), but is still well within spectral resolution present. Yet, this energy is one order of magnitude more than that from 55Mn hyperfine coupling, which could (potentially) be expected to appear in the spectra.70 We postpone a discussion of this observation noting qualitatively that this could be a symptom of a very weak (<0.1 cm−1) exchange taking place between the two MnIII ions in the dimer.
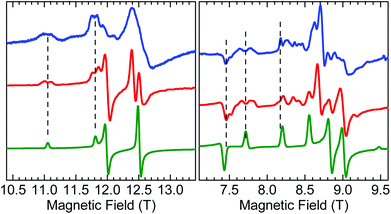 | ||
| Fig. 8 Fragments of HFEPR spectra of 1 at 406.4 GHz and 10 K (left) and 2 at 203.2 GHz and 10 K (right). Blue: Experimental. Red: Calculated using spin Hamiltonian 2 (dimer model, eqn (2)). Green: Calculated using spin Hamiltonian 1 (monomer model, eqn (1)). The indicated splittings appear also in other regions of the spectra, and at different frequencies. | ||
The low-T spin Hamiltonian parameters used in the simulations shown in Fig. 6 were not deduced from the single-frequency spectra, but from the 2-D maps of turning points as a function of frequency/energy according to the principle of tuneable-frequency EPR.72 These maps are shown in Fig. 9. The parameters are listed in Table 2. The room temperature parameters, to the contrary, were obtained from single-frequency spectra only and because of the poor S/N are estimates only.
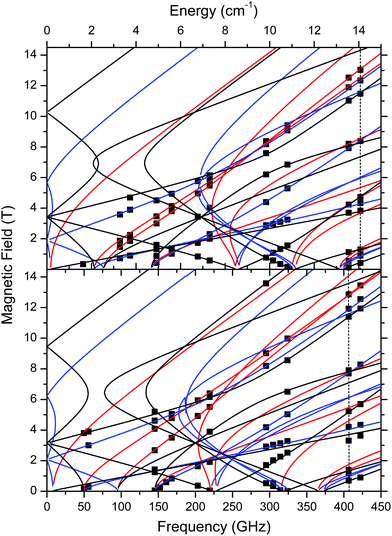 | ||
| Fig. 9 Field vs. frequency/energy map of turning points in complexes 1 (top) and 2 (bottom) at 10–15 K. Squares are experimental points; curves were simulated using spin Hamiltonian parameters as in Table 2. Red curves: turning points with magnetic field B0 parallel to the x-axis of the ZFS tensor; blue: B0 || y; black: B0 || z. The two dashed vertical lines indicate the frequencies at which spectra shown in Fig. 6 were recorded. | ||
To explore the effect of the interactions between the MnIII ions, the spin Hamiltonian in eqn (1) must be replaced by eqn (2) which operates within the space of 25 microstates in a system of two ions with S1 = S2 = 2:
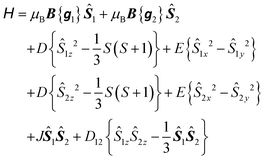 | (2) |
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) D (thus D, E are as in eqn (1)) and are coaxial as well.74 In the present case, D12 is most likely due only to the magnetic dipole–dipole interaction, which depends on the crystallographically-determined inter-ion distance R and can be estimated from:
D (thus D, E are as in eqn (1)) and are coaxial as well.74 In the present case, D12 is most likely due only to the magnetic dipole–dipole interaction, which depends on the crystallographically-determined inter-ion distance R and can be estimated from: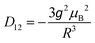 | (3) |
The largest component of the dipolar tensor is along the Mn–Mn direction which is almost perpendicular to the expected direction of the largest component of the ZFS tensor on each MnIII ion, which is along the O(phenolato)–Mn–O(phenolato) axis (i.e., the axial compression axis; see discussion below and Fig. S9, ESI†). Eqn (3) results in D12 values of −0.008 cm−1 for 1 and −0.004 cm−1 for 2. These magnitudes should be treated as an upper estimation as delocalisation effects of the MnIII spins are not taken into account, but are even so much too small to account for the observed splitting of at least ∼60 mT. Nevertheless, for completeness, the EPR simulations for both 1 and 2 included these D12 values.
In contrast, for systems with single atom bridges, such as μ-oxido10,11 or -fluorido,8 the crystallographically-determined distances of ∼3.16 Å and 4.10 Å, would give a maximum direct dipole–dipole coupling some 20 times larger: −0.16 cm−1 and −0.075 cm−1, respectively. Even in the phenolato/diketonato-linked complex, the Mn–Mn distance of 5.26 Å would give D12 ≈ −0.036 cm−1.
However, in each of these three complexes previously studied by HFEPR, a direct covalent pathway between the MnIII ions leads to an isotropic exchange interaction (eqn (2)) that overwhelms the dipolar effect. Use of the JS1S2 formalism (as opposed to −2J or other variants) yields J (in cm−1) = −2.3, +33.0(2), and +1.70, as respectively reported for each.8,10,11,28 The linear MnIII-(μ-F)-MnIII leads to a strong antiferromagnetic “bonding-like” interaction, but in the other complexes the anti- or ferromagnetic nature of the exchange coupling is not obvious. As explored by Retegan et al.,10 and others24,75 for di-MnIII, by Morsing et al. for di-CrIII,76 and by Weihe and Güdel for di-FeIII,77 the specific geometry of the M-(μ-O[X])-M moiety (X = none, H, R) has a profound effect on the exchange coupling parameter.
In our systems, wherein the Mn–Mn distances are much greater and the covalent pathways more convoluted, simulations nevertheless show that the isotropic exchange interaction is indeed responsible for the observed spectral effects. The J (and D12, if it were larger) terms split the energy levels of a monomer which results in splitting of the single-ion resonances calculated using eqn (1) each into several components (Fig. 10 and S8, ESI†). Since powder spectra are superpositions of a very large number of single-crystal spectra, these splittings are mostly blurred and are recognisable only in certain magnetic field ranges allowing only a rough estimation of J.
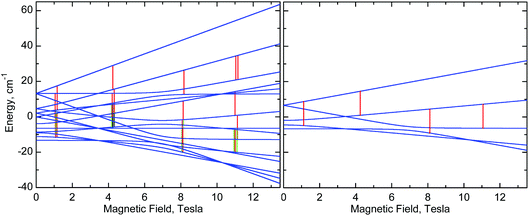 | ||
| Fig. 10 Right: Energy levels of a monomer, calculated at the “z” orientation, using eqn (1) with parameters of 1 (Table 2). Left: Energy levels of a dimer, calculated using eqn (2) with the same single-ion g, D and E parameters of 1 and with J = −0.025 cm−1. The vertical lines represent EPR transitions expected at ν = 406.4 GHz. Only transitions with substantial probability are drawn. Colours are used to distinguish very close transitions. See also Fig. S8, ESI.† | ||
Nevertheless, one can see that in 1, an isotropic exchange term with J = −0.025 cm−1 (ferromagnetic), which is some 100 times smaller than D, is sufficient to split a “z” transition in 1, which in a monomer occurs at 11.16 T, so that the outermost components are 180 mT apart (Fig. 6, 8, 10, and S8, ESI†). Spectra of 2 appear to simulate better with positive J of +0.035 cm−1. It is clear that exchange interactions of such small energy cannot be detected by magnetic measurements, nor would they affect the electrochemistry. The J magnitudes above must be treated as estimations, but single-crystal EPR experiments may provide accurate J values. Interestingly, some of us have recently observed similar effects in HFEPR of very different systems.78 It should also be noted that NMR can be used to probe exchange couplings as shown by the linear correlation between μ-acetato methyl proton chemical shifts and J values that was established for a series of dimanganese(III) complexes containing {Mn2O(μ-O2CCH3)2}2+ cores.22
Computational studies
The magnetic EPR parameters assessment has been performed in three different approaches (a)–(c) (see Computational methods section, ESI†) to test the quality and robustness of the different models, options and choice of approximation, i.e. choice of method (ab initio vs. DFT/functional), basis set, integral treatment and single vs. multicentre approach. The results from the different ab initio methods are collected in Table 3.| Method | |||||||
|---|---|---|---|---|---|---|---|
| Complex | CASa | NEVPT2a | CAS (SOC)b | L-CASCI (SOC)b | MRCI (SOC + SSC)b | L-CASCI (SOC)c | L-CASCI (SOC + SSC)c |
| a Calculated for single-centre geometries from a second order perturbative spin–orbit coupling Hamiltonian applied to the CAS MnGa model and NEVPT2 wavefunctions of the single Mn centre (using TZVP basis set) of model (a). b Calculated for single-centre geometries (using 6-311G* basis set) of model (b). c Calculated for two-centre (using 6-311G* basis set and the autoaux density fitting basis set) using model (c). | |||||||
| 1 | +3.44 (0.234) | +3.57 (0.227) | +2.94 (0.228) | +2.93 (0.227) | +3.64 (0.136) | +2.62 (0.224) | +3.47 (0.234) |
| 2 | +3.55 (0.159) | +3.64 (0.154) | +3.03 (0.154) | +3.03 (0.155) | +3.52 (0.159) | +2.71 (0.151) | +3.58 (0.163) |
| 3 | +3.67 (0.151) | +3.87 (0.147) | +3.14 (0.133) | +3.14 (0.132) | +3.41 (0.232) | +2.81 (0.129) | +3.69 (0.137) |
The obtained results lead to a positive D value (Table 3) which is consistent with the axial (tetragonal) compression observed experimentally in the three complexes (Table 2), but with a significant rhombic distortion, in agreement with HFEPR spectroscopy. This similar axial distortion in 1–3 leads to close D values. However, the trend in the SOC CAS results is also corroborated by DFT calculations (Tables S2 and S3, ESI†), although this method underestimates the D values in manganese(III) complexes.32,34,55b Generally, the SOC CAS results lead to an increase of D parameter with the size of the bridging ligand (see Table 3), which correlates well with the susceptibility fit in Table 2. On the contrary, the inclusion of SSC via MRCI reverses this trend in the single centre calculations of model (b) (see Table 3), which is in accordance with HFEPR (see Table 2) for 1 and 2. HFEPR of powders or solutions does not provide the orientation of the ZFS. However, this can be calculated, and in Fig. S9 (ESI†) are displayed the orientations of the principal axes of the D tensors of 1–3 in the molecular coordinate system obtained in model (a). As expected, the principal z-axis (“hard” axis) points at the oxygen atoms of the coordinated phenolato groups, i.e., along the axis of compression. Lastly, the g-tensors for 1–3 calculated from the NEVPT2 method and using an effective Hamiltonian for the spin–orbit coupling (Table S4, ESI†) agree moderately well with those obtained by HFEPR spectroscopy, with the calculated values being slightly below 2.0 which agrees with the high temperature HFEPR fit in Table 2, and is expected from classical theory for a less than half-filled dn system.
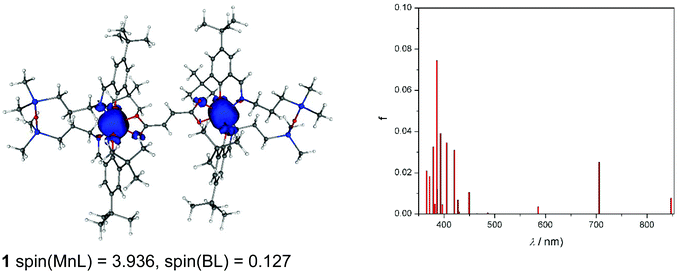
As can be seen from Fig. 11, spin density is localised almost exclusively in the vicinity of the two MnIII ions in the case of the neutral complex 1. Upon oxidation to 1+, part of the spin (about 0.5e) vanishes from these ions (Fig. S10a†). Finally, the doubly charged species, 12+ (septet), has the spin population decreased by one, hence both centres are oxidised to MnIV (Fig. S10b†). The calculated TD-DFT transitions (Fig. 11a) of 1 are in qualitative agreement with the experimental UV-vis spectra (Fig. 4). Comparison of singly and doubly oxidised species with the measured difference spectra are not useful due to irreversible chemical changes of 1–3 upon oxidation.
Finally, CAM-B3LYP DFT calculations on 1–3 showed that the intramolecular magnetic coupling in 1 is ferromagnetic (i.e., J exchange coupling constant is negative: H = JS1S2) and weak, J = −0.007 cm−1, while in 2 and 3 it is antiferromagnetic with J of 0.004 and 0.022 cm−1, respectively. The magnetic communication in an extended pathway can occur only through a π-pathway. A loss of its planarity causes a notable decrease in the aromaticity and the magnetic coupling. In 1–3, the privation of this planarity comes mainly from a twist between the carboxylate groups and the vinyl (in 1: 11.3° twist) or phenyl rings (2: 26.2° and 3: 17.4–20.0°), and between phenyl rings in 3 (≈38°). Neither these structural distortions nor electronic effects such as accidental orthogonality of magnetic orbitals can explain the trend found for the J constants for 1–3. Hence, speculation as to the structural/electronic basis for the opposite type of exchange coupling in 1versus2 and 3 is unwarranted given the very small magnitude of these interactions and the challenges of understanding exchange interactions even in singly bridged systems.10,24,68,75,79 Nevertheless, the DFT results for 1 and 2 are in qualitative agreement with the EPR data.
Conclusions
By using the ability of manganese(III) to form a six-coordinate complex with a salen type ligand bearing a disiloxane unit and an acetate as bidentate co-ligand described previously, three dimanganese(III) complexes have been synthesised and characterised by standard analytical and spectroscopic techniques, X-ray crystallography, as well as by spectroelectrochemistry and magnetic and EPR techniques. The three complexes differ by the bridging dicarboxylato group between two six-coordinate axially compressed high-spin d4 MnIII ions. The Mn⋯Mn separation is 8.736, 10.912, and 15.103 Å in LMn(OOCCH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CHCOO)MnL (1), LMn(OOCC6H4COO)MnL (2), and LMn(OOCC6H4C6H4COO)MnL (3), respectively. The anodic oxidation of these complexes is irreversible and is similar to the monomeric MnL(OAc) analogue. Complex 3 exhibited the lowest oxidation potential with two overlapping oxidation peaks indicating a slightly different oxidation potential for the two MnIII redox centres. By using temperature dependent magnetic susceptibility and variable temperature-variable field (VTVH) magnetisation measurements and high-frequency and -field EPR (HFEPR) spectroscopy, the single-ion spin Hamiltonian parameters (g values, ZFS parameters D and E) were obtained and reproduced successfully by ab initio calculations. The quality of HFEPR spectra of 1 and 2 was superior to that of the analogous mononuclear complex MnL(OAc). This allowed identification of characteristic signatures in high-resolution spectra which presumably indicate very weak exchange interactions between the paramagnetic ions and estimation of the exchange coupling constant, |J| ≈ 0.03(5) cm−1, (JS1S2 formalism) which was in reasonable agreement with DFT calculations for 1 and 2. This result suggests that magnetic exchange interactions can occur in di-MnIII systems over relatively long distances (as much as ∼11 Å), which may be the case in biological di- and multi-Mn systems as well.
CHCOO)MnL (1), LMn(OOCC6H4COO)MnL (2), and LMn(OOCC6H4C6H4COO)MnL (3), respectively. The anodic oxidation of these complexes is irreversible and is similar to the monomeric MnL(OAc) analogue. Complex 3 exhibited the lowest oxidation potential with two overlapping oxidation peaks indicating a slightly different oxidation potential for the two MnIII redox centres. By using temperature dependent magnetic susceptibility and variable temperature-variable field (VTVH) magnetisation measurements and high-frequency and -field EPR (HFEPR) spectroscopy, the single-ion spin Hamiltonian parameters (g values, ZFS parameters D and E) were obtained and reproduced successfully by ab initio calculations. The quality of HFEPR spectra of 1 and 2 was superior to that of the analogous mononuclear complex MnL(OAc). This allowed identification of characteristic signatures in high-resolution spectra which presumably indicate very weak exchange interactions between the paramagnetic ions and estimation of the exchange coupling constant, |J| ≈ 0.03(5) cm−1, (JS1S2 formalism) which was in reasonable agreement with DFT calculations for 1 and 2. This result suggests that magnetic exchange interactions can occur in di-MnIII systems over relatively long distances (as much as ∼11 Å), which may be the case in biological di- and multi-Mn systems as well.
Conflicts of interest
The authors declare no competing interest.Acknowledgements
This work was supported by a grant of Romanian Ministry of Research and Innovation, CNCS – UEFISCDI, project number PN-III-P4-ID-PCE-2016-0642, within PNCDI III (Contract 114/2017). The financial support of the Austrian Agency for International Cooperation in Education and Research (OEAD) (grant no. SK01/2018). This work was supported by the Science and Technology Assistance Agency under the contract no. APVV-15-0053 and APVV-15-0079 and SK-AT-2017-0017, by the Slovak Grant Agency VEGA under contract no. 1/0598/16, 1/0416/17 and 1/0466/18 and by the Ministry of Education, Science, Research and Sport of the Slovak Republic for funding within the scheme “Excellent research teams”. We thank the HPC centre at the Slovak University of Technology in Bratislava, which is a part of the Slovak Infrastructure of High Performance Computing (SIVVP Project, ITMS code 26230120002, funded by the European Region Development Funds), for computing facilities. A portion of this work was performed at the National High Magnetic Field Laboratory, which is supported by National Science Foundation Cooperative Agreements No. DMR-1157490 and DMR-1644779 and the State of Florida. This work was also supported by the Ministerio Español de Ciencia e Innovación (Projects CTQ2016-75068P and CTQ2016-75671P and Unidad de Excelencia María de Maetzu MDM-2015-0538).References
- A. J. Wu, J. E. Penner-Hahn and V. L. Pecoraro, Chem. Rev., 2004, 104, 903–938 CrossRef CAS PubMed.
- V. V. Barynin, M. M. Whittaker, S. V. Antonyuk, V. S. Lamzin, P. M. Harrison, P. J. Artymiuk and J. W. Whittaker, Structure, 2001, 9, 725–738 CrossRef CAS PubMed.
- S. V. Antonyuk, V. R. Melik-Adamyan, A. N. Popov, V. S. Lamzin, P. D. Hempstead, P. M. Harrison, P. J. Artymiuk and V. V. Barynin, Crystallogr. Rep., 2000, 45, 105–116 CrossRef.
- J. A. Cotruvo and J. Stubbe, Biochemistry, 2010, 49, 1297–1309 CrossRef CAS PubMed.
- N. Cox, H. Ogata, P. Stolle, E. Reijerse, G. Auling and W. Lubitz, J. Am. Chem. Soc., 2010, 132, 11197–11213 CrossRef CAS PubMed.
- (a) L. R. Scolnick, Z. F. Kanyo, R. C. Cavalli, D. E. Ash and D. W. Christianson, Biochemistry, 1997, 36, 10558–10565 CrossRef CAS PubMed; (b) Y. Hai and D. W. Christianson, Acta Crystallogr., Sect. F: Struct. Biol. Commun., 2016, 72, 300–306 CrossRef CAS PubMed.
- R. Cammack, A. Chapman, W.-P. Lu, A. Karagouni and D. P. Kelly, FEBS Lett., 1989, 253, 239–243 CrossRef CAS.
- K. S. Pedersen, M. Sigris, H. Weihe, A. D. Bond, C. Aa. Thuesen, K. P. Simonsen, T. Birk, H. Mutka, A.-L. Barra and J. Bendix, Inorg. Chem., 2014, 53, 5013–5019 CrossRef CAS PubMed.
- D. Tétard, A. Rabion, J.-B. Verlhac and J. Guilhem, J. Chem. Soc., Chem. Commun., 1995, 531–532 RSC.
- M. Retegan, M.-N. Collomb, F. Neese and C. Duboc, Phys. Chem. Chem. Phys., 2013, 15, 223–234 RSC.
- C. Bolm, N. Meyer, G. Raabe, T. Weyhermüller and E. Bothe, Chem. Commun., 2000, 2435–2436 RSC.
- (a) P. Mathur, M. Crowder and G. C. Dismukes, J. Am. Chem. Soc., 1987, 109, 5227–5233 CrossRef CAS; (b) E. J. Larson and V. L. Pecoraro, J. Am. Chem. Soc., 1991, 113, 7809–7810 CrossRef CAS; (c) A. Gelasco and V. L. Pecoraro, J. Am. Chem. Soc., 1993, 115, 7928–7929 CrossRef CAS; (d) D. R. Gamelin, M. L. Kirk, T. L. Stemmler, S. Pal, W. H. Armstrong, J. E. Penner-Hahn and E. I. Solomon, J. Am. Chem. Soc., 1994, 116, 2392–2399 CrossRef CAS.
- I. Romero, L. Dubois, M.-N. Collomb, A. Deronzier, J.-M. Latour and J. Pécaut, Inorg. Chem., 2002, 41, 1795–1806 CrossRef CAS PubMed.
- (a) S. Ménage, J.-J. Girerd and A. Gleizes, J. Chem. Soc., Chem. Commun., 1988, 431–433 RSC; (b) J. B. Vincent, H.-L. Tsai, A. G. Blackman, S. Wang, P. D. W. Boyd, K. Folting, J. C. Huffman, E. B. Lobkovsky, D. N. Hendrickson and G. Christou, J. Am. Chem. Soc., 1993, 115, 12353–12361 CrossRef CAS; (c) P. J. Pessiki, S. V. Khangulov, D. M. Ho and G. C. Dismukes, J. Am. Chem. Soc., 1994, 116, 891–897 CrossRef CAS; (d) L. Dubois, D.-F. Xiang, X.-S. Tan, J. Pécaut, P. Jones, S. Baudron, L. Le Pape, J.-M. Latour, C. Baffert, S. Chardon-Noblat, M.-N. Collomb and A. Deronzier, Inorg. Chem., 2003, 42, 750–760 CrossRef CAS PubMed.
- L. Escriche-Tur, M. Corbella, M. Font-Bardia, I. Castro, L. Bonneviot and B. Albela, Inorg. Chem., 2015, 54, 10111–10125 CrossRef CAS PubMed.
- C. Palopoli, N. Bruzzo, C. Hureau, S. Ladeira, D. Murgida and S. Signorella, Inorg. Chem., 2011, 50, 8973–8983 CrossRef CAS PubMed.
- V. Solís, C. Palopoli, V. Daier, E. Rivière, F. Collin, D. M. Moreno, C. Hureau and S. Signorella, J. Inorg. Biochem., 2018, 182, 29–36 CrossRef PubMed.
- S. Signorella, C. Palopoli and G. Ledesma, Coord. Chem. Rev., 2018, 365, 75–102 CrossRef CAS.
- (a) D. Moreno, C. Palopoli, V. Daier, S. Shova, L. Vendier, M. González Sierra, J.-P. Tuchagues and S. Signorella, Dalton Trans., 2006, 5156–5166 RSC; (b) V. Daier, H. Biava, C. Palopoli, S. Shova, J.-P. Tuchagues and S. Signorella, J. Inorg. Biochem., 2004, 98, 1806–1817 CrossRef CAS PubMed; (c) H. Blava, C. Palopoli, C. Duhayon, J.-P. Tuchagues and S. Signorella, Inorg. Chem., 2009, 48, 3205–3214 CrossRef PubMed; (d) H. Biava, C. Palopoli, S. Shova, M. De Gaudio, V. Daier, M. González-Sierra, J.-P. Tuchagues and S. Signorella, J. Inorg. Biochem., 2006, 100, 1660–1671 CrossRef CAS PubMed.
- L. A. Berben and J. C. Peters, Inorg. Chem., 2008, 47, 11669–11679 CrossRef CAS PubMed.
- F.-J. Wu, D. M. Kurtz Jr., K. S. Hagen, P. D. Nyman, P. G. Debrunner and V. A. Vankai, Inorg. Chem., 1990, 29, 5174–5183 CrossRef CAS.
- D. V. Wright, H. J. Mok, C. E. Dubé and W. H. Armstrong, Inorg. Chem., 1998, 37, 3714–3718 CrossRef CAS PubMed.
- (a) K. Wieghardt, U. Bossek, D. Ventur and J. Weiss, J. Chem. Soc., Chem. Commun., 1985, 347–349 RSC; (b) K. Wieghardt, U. Bossek, B. Nuber, J. Weiss, J. Bonvoisin, M. Corbella, S. E. Vitols and J. J. Girerd, J. Am. Chem. Soc., 1988, 110, 7398–7411 CrossRef CAS; (c) U. Bossek, K. Wieghardt, B. Nuber and J. Weiss, Inorg. Chim. Acta, 1989, 165, 123–129 CrossRef CAS.
- T. C. Brunold, D. R. Gamelin and E. I. Solomon, J. Am. Chem. Soc., 2000, 122, 8511–8523 CrossRef CAS.
- J. E. Sheats, R. S. Czernuszewicz, G. C. Dismukes, A. L. Reingold, V. Petrouleas, J. Stubbe, W. H. Armstrong, R. H. Beer and S. J. Lippard, J. Am. Chem. Soc., 1987, 109, 1435–1444 CrossRef CAS.
- M. Hirotsu, N. Ohno, T. Nakajima, C. Kushibe, K. Ueno and I. Kinoshita, Dalton Trans., 2010, 39, 139–148 RSC.
- G. Aromi, P. Gamez, O. Roubeau, P. C. Berzal, K. Kooijman, A. L. Spek, W. L. Driessen and J. Reedijk, Inorg. Chem., 2002, 41, 3673–3683 CrossRef CAS PubMed.
- J. Liu, J. Krzystek, S. Hill, L. Barrios and G. Aromi, Inorg. Chem., 2013, 52, 718–723 CrossRef CAS PubMed.
- N. N. Gerasimchuk, A. Gerges, T. Clifford, A. Danby and K. Bowman-James, Inorg. Chem., 1999, 38, 5633–5636 CrossRef CAS PubMed.
- S. J. Brudenell, L. Spiccia, A. M. Bond, G. D. Fallon, D. C. R. Hockless, G. Lazarev, P. J. Mahon and E. R. T. Tiekink, Inorg. Chem., 2000, 39, 881–892 CrossRef CAS PubMed.
- A. Soroceanu, M. Cazacu, S. Shova, C. Turta, J. Kožišek, M. Gall, M. Breza, P. Rapta, T. C. O. Mac Leod, A. J. L. Pombeiro, J. Telser, A. Dobrov and V. B. Arion, Eur. J. Inorg. Chem., 2013, 1458–1474 CrossRef CAS.
- M. Cazacu, S. Shova, A. Soroceanu, P. Machata, L. Bucinsky, M. Breza, P. Rapta, J. Telser, J. Krzystek and V. B. Arion, Inorg. Chem., 2015, 54, 5691–5706 CrossRef CAS PubMed.
- S. Shova, M. Cazacu, G. Novitchi, G. Zoppellaro, C. Train and V. B. Arion, Dalton Trans., 2017, 46, 1789–1793 RSC.
- S. Shova, A. Vlad, M. Cazacu, J. Krzystek, L. Bucinsky, M. Breza, D. Darvasiová, P. Rapta, J. Cano, J. Telser and V. B. Arion, Dalton Trans., 2017, 46, 11817–11829 RSC.
- C. Teutloff, K.-O. Schäfer, S. Sinnecker, V. Barynin, R. Bittl, K. Wieghardt, F. Lendzian and W. Lubitz, Magn. Reson. Chem., 2005, 43, S51–S64 CrossRef CAS PubMed.
- K.-O. Schäfer, R. Bittl, F. Lendzian, V. Barynin, T. Weyhermüller, K. Wieghardt and W. Lubitz, J. Phys. Chem. B, 2003, 107, 1242–1250 CrossRef.
- L. Rapatskiy, W. M. Ames, M. Pérez-Navarro, A. Savitsky, J. J. Griese, T. Weyhermüller, H. S. Shafaat, M. Högbom, F. Neese, D. A. Pantazis and N. Cox, J. Phys. Chem. B, 2015, 119, 13904–13921 CrossRef CAS PubMed.
- A. Constantatos, R. Bewley, A.-L. Barra, J. Bendix, S. Piligkos and H. Weihe, Inorg. Chem., 2016, 55, 10377–10382 CrossRef PubMed.
- SAINT-Plus, v. 7.06a, Bruker-Nonius AXS Inc., Madison, WI, 2004 Search PubMed; APEX2, Bruker-Nonius AXS Inc., Madison, WI, 2004 Search PubMed.
- O. V. Dolomanov, L. J. Bourhis, R. J. Gildea, J. A. K. Howard and H. Puschmann, J. Appl. Crystallogr., 2009, 42, 339–341 CrossRef CAS.
- G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Crystallogr., 2008, 64, 112–122 CrossRef CAS PubMed.
- J. Cano, VPMAG Package, University of València, Spain, 2003 Search PubMed.
- A. K. Hassan, L. A. Pardi, J. Krzystek, A. Sienkiewicz, P. Goy, M. Rohrer and L. C. Brunel, J. Magn. Reson., 2000, 142, 300–312 CrossRef CAS PubMed.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1327 Search PubMed.
- (a) J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396 CrossRef CAS; (b) J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- A. Schäfer, C. Huber and R. Ahlrichs, J. Chem. Phys., 1994, 100, 5829–5835 CrossRef.
- A. Schafer, H. Horn and R. Ahlrichs, J. Chem. Phys., 1992, 97, 2571–2577 CrossRef.
- A. Schäfer, C. Huber and R. Ahlrichs, J. Chem. Phys., 1994, 100, 5829–5835 CrossRef.
- K. Eichkorn, O. Treutler, H. Ohm, M. Haser and R. Ahlrichs, Chem. Phys. Lett., 1995, 240, 283–290 CrossRef CAS.
- K. Eichkorn, O. Treutler, H. Ohm, M. Haser and R. Ahlrichs, Chem. Phys. Lett., 1995, 242, 652–660 CrossRef CAS.
- K. Eichkorn, O. Treutler, H. Ohm, M. Haser and R. Ahlrichs, Theor. Chem. Acc., 1997, 97, 119–124 Search PubMed.
- (a) C. Angeli, R. Cimiraglia, S. Evangelisti, T. Leininger and J.-P. Malrieu, J. Chem. Phys., 2001, 114, 10252 CrossRef CAS; (b) C. G. Werncke, E. Suturina, P. C. Bunting, L. Vendier, J. R. Long, M. Atanasov, F. Neese, S. Sabo-Etienne and S. Bontemps, Chem. – Eur. J., 2016, 22(5), 1668–1674 CrossRef CAS PubMed.
- (a) A. D. Becke, Phys. Rev. A, 1988, 38, 3098–3100 CrossRef CAS; (b) C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS.
- (a) R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650–654 CrossRef CAS; (b) A. D. McLean and G. S. Chandler, J. Chem. Phys., 1980, 72, 5639–5648 CrossRef CAS.
- (a) F. Neese, J. Am. Chem. Soc., 2006, 128, 10213–10222 CrossRef CAS PubMed; (b) C. Duboc, D. Ganyushin, K. Sivalingam, M. N. Collomb and F. Neese, J. Phys. Chem. A, 2010, 114, 10750–10758 CrossRef CAS PubMed.
- (a) M. Retegan, N. Cox, D. A. Pantazis and F. Neese, Inorg. Chem., 2014, 53, 11785–11793 CrossRef CAS PubMed; (b) H. Fliegl, K. Fink, W. Klopper, C. E. Anson, A. K. Powell and R. Clerac, Phys. Chem. Chem. Phys., 2009, 11, 3900–3909 RSC.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. V. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann., O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, D. Cioslowski and D. J. Fox, Gaussian, Inc., Wallingford, CT, 2009.
- R. Bauernschmitt and R. Ahlrichs, Chem. Phys. Lett., 1996, 256, 454–464 CrossRef CAS.
- P. Flükiger, H. P. Lüthi, S. Sortmann and J. Weber, MOLEKEL 4.3, Swiss Center for Scientific Computing, Manno, Switzerland, 2002.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- E. Ruiz, A. Rodríguez-Fortea, J. Cano, S. Alvarez and P. Alemany, J. Comput. Chem., 2003, 24, 982–989 CrossRef CAS PubMed.
- E. Ruiz, J. Cano, S. Alvarez and P. Alemany, J. Comput. Chem., 1999, 20, 1391–1400 CrossRef CAS.
- E. Ruiz, J. Cano, S. Alvarez and P. Alemany, J. Am. Chem. Soc., 1998, 120, 11122–11129 CrossRef CAS.
- J. Tomasi, B. Mennucci and E. Cancès, J. Mol. Struct.: THEOCHEM, 1999, 464, 211–226 CrossRef CAS.
- M. K. Chan and W. H. Armstrong, Inorg. Chem., 1989, 28, 3777–3779 CrossRef CAS.
- V. C. Quee-Smith, L. DelPizzo, S. H. Jureller, J. L. Kerschner and R. Hage, Inorg. Chem., 1996, 35, 6461–6465 CrossRef CAS.
- M. Zlatar, M. Gruden, O. Yu. Vassillyeva, E. A. Buvaylo, A. N. Ponomarev, S. A. Zvyagin, J. Wosnitza, J. Krzystek, P. Garcia-Fernandez and C. Duboc, Inorg. Chem., 2016, 55, 1192–1201 CrossRef CAS PubMed.
- A. Ceulemans, L. F. Chibotaru, G. A. Heylen, K. Pierloot and L. G. Vanquickenborne, Chem. Rev., 2000, 100, 787–806 CrossRef CAS PubMed.
- (a) S. Romain, C. Duboc, F. Neese, E. Riviere, L. R. Hanton, A. G. Blackman, C. Philouze, J.-C. Lepretre, A. Deronzier and M.-N. Collomb, Chem. – Eur. J., 2009, 15, 980–988 CrossRef CAS PubMed; (b) G. A. Craig, J. J. Marbey, S. Hill, O. Rubeau, S. Parsons and M. Murrie, Inorg. Chem., 2015, 54, 13–15 CrossRef CAS PubMed; (c) J. Telser, J. Krzystek and A. Ozarowski, J. Biol. Inorg. Chem., 2014, 19, 297–318 CrossRef CAS PubMed; (d) J. Krzystek and J. Telser, Dalton Trans., 2016, 45, 16751–16763 RSC; (e) J. Valejo, A. Pascual-Alvarez, J. Cano, I. Castro, M. Julve, F. Lloret, J. Krzystek, G. De Munno, D. Armentano, W. Wernsdorfer, R. Ruiz-Garcia and E. Pardo, Angew. Chem., Int. Ed., 2013, 52, 14075–14079 CrossRef PubMed; (f) Q. Scheifele, C. Riplinger, F. Neese, H. Weihe, A.-L. Barra, F. Juranyi, A. Podlesnyak and P. L. W. Tregenna-Piggott, Inorg. Chem., 2008, 47, 439–447 CrossRef CAS PubMed; (g) C. Mantel, H. Chen, R. H. Crabtree, C. W. Brudwig, J. Pécaut, M.-N. Collomb and C. Duboc, ChemPhysChem, 2005, 6, 541–546 CrossRef CAS PubMed; (h) B. Albela, R. Carina, C. Policar, S. Poussereau, J. Cano, J. Guilhem, L. Tchertanov, G. Blondin, M. Delroisse and J.-J. Girerd, Inorg. Chem., 2005, 44, 6959–6966 CrossRef CAS PubMed.
- H. J. Gerritsen and E. S. Sabisky, Phys. Rev., 1963, 132, 1507–1512 CrossRef CAS.
- I. Krivokapic, C. Noble, S. Klitgaard, P. Tregenna-Piggott, H. Weihe and A.-L. Barra, Angew. Chem., Int. Ed., 2005, 44, 3613–3616 CrossRef CAS PubMed.
- J. Krzystek, S. A. Zvyagin, A. Ozarowski, S. Trofimenko and J. Telser, J. Magn. Reson., 2006, 178, 174–183 CrossRef CAS PubMed.
- F. T. de Oliveira, E. L. Bominaar, J. Hitst, J. A. Fee and E. Münck, J. Am. Chem. Soc., 2004, 126, 5338–5339 CrossRef PubMed.
- The inversion symmetry of the complexes means that sources of anisotropic coupling other than magnetic dipole-dipole (e.g., Dzialoshinskii-Moriya)73 can be disregarded.
- N. Berg, T. Rajeshkumar, S. M. Taylor, E. K. Brechin, G. Rajaraman and L. F. Jones, Chem. – Eur. J., 2012, 18, 5906–5918 CrossRef CAS PubMed.
- T. J. Morsing, J. Bendix, H. Weihe and A. Døssing, Inorg. Chem., 2014, 53, 2996–3003 CrossRef CAS PubMed.
- (a) H. Weihe and H. U. Güdel, J. Am. Chem. Soc., 1997, 119, 6539–6543 CrossRef CAS; (b) H. Weihe and H. U. Güdel, J. Am. Chem. Soc., 1998, 120, 2870–2879 CrossRef CAS.
- (a) O. V. Nesterova, D. S. Nesterov, J. Jezierska, A. J. L. Pombeiro and A. Ozarowski, Inorg. Chem., 2018, 57, 12384–12397 CrossRef CAS PubMed; (b) A. Switlicka, B. Machura, M. Penkala, A. Bienko, D. C. Bienko, J. Titis, C. Rajnak, R. Boca, A. Ozarowski and M. Ozerov, Inorg. Chem., 2018, 57, 12740–12755 CrossRef CAS PubMed.
- G. David, F. Wennmohs, F. Neese and N. Ferré, Inorg. Chem., 2018, 57, 12769–12776 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Computational details and discussion of theoretically determined EPR properties; packing features of 1, 3 (Fig. S1) and 2 (Fig. S2), cyclic voltammograms of 1 and 2 (Fig. S3), HFEPR spectra of 1 and 2 (Fig. S4–S7), fragment of the experimental HFEPR spectrum of 1 and energy levels of a dimer with and without exchange interaction between MnIII ions (Fig. S8), relative orientations of the experimental coordination sphere geometry of 1–3 and the calculated D tensor (Fig. S9); theoretical spin densities and electronic transitions of 1+ and 12+ (Fig. S10); bond distances and angles 1–3 (Table S1), estimated values of the D and E/D ratio for 1–3 (Tables S2 and S3), calculated g-tensor components for 1–3 (Table S4), L-CASCI reference space used (Table S5). CCDC 1875357–1875359. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c8dt04596h |
| This journal is © The Royal Society of Chemistry 2019 |