Open Access Article
Open Access ArticleThe interaction of aluminum with catecholamine-based neurotransmitters: can the formation of these species be considered a potential risk factor for neurodegenerative diseases?†
Gabriele
Dalla Torre
 ab,
Jon I.
Mujika
ab,
Jon I.
Mujika
 a,
Joanna Izabela
Lachowicz
c,
Maria J.
Ramos
a,
Joanna Izabela
Lachowicz
c,
Maria J.
Ramos
 b and
Xabier
Lopez
*a
b and
Xabier
Lopez
*a
aKimika Fakultatea, Euskal Herriko Unibertsitatea (UPV/EHU), and Donostia International Physics Center (DIPC), P.K. 1072, 20080 Donostia, Euskadi, Spain. E-mail: xabier.lopez@ehu.es
bUCIBIO/REQUIMTE, Departamento de Química e Bioquímica, Faculdade de Ciências, Universidade do Porto, Rua do Campo Alegre, s/n, Porto, Portugal
cUniversity of Cagliari, Department of Chemical and Geological Sciences, Cittadella Universitaria, 09042 Monserrato, CA, Italy
First published on 28th January 2019
Abstract
The potential neurotoxic role of Al(III) and its proposed link with the insurgence of Alzheimer's Disease (AD) have attracted increasing interest towards the determination of the nature of bioligands that are propitious to interact with aluminum. Among them, catecholamine-based neurotransmitters have been proposed to be sensitive to the presence of this non-essential metal ion in the brain. In the present work, we characterize several aluminum–catecholamine complexes in various stoichiometries, determining their structure and thermodynamics of formation. For this purpose, we apply a recently validated computational protocol with results that show a remarkably good agreement with the available experimental data. In particular, we employ Density Functional Theory (DFT) in conjunction with continuum solvation models to calculate complexation energies of aluminum for a set of four important catecholamines: L-DOPA, dopamine, noradrenaline and adrenaline. In addition, by means of the Quantum Theory of Atoms in Molecules (QTAIM) and Energy Decomposition Analysis (EDA) we assessed the nature of the Al–ligand interactions, finding mainly ionic bonds with an important degree of covalent character. Our results point at the possibility of the formation of aluminum–catecholamine complexes with favorable formation energies, even when proton/aluminum competition is taken into account. Indeed, we found that these catecholamines are better aluminum binders than catechol at physiological pH, because of the electron withdrawing effect of the positively-charged amine that decreases their deprotonation penalty with respect to catechol. However, overall, our results show that, in an open biological environment, the formation of Al–catecholamine complexes is not thermodynamically competitive when compared with the formation of other aluminum species in solution such as Al-hydroxide, or when considering other endogenous/exogenous Al(III) ligands such as citrate, deferiprone and EDTA. In summary, we rule out the possibility, suggested by some authors, that the formation of Al–catecholamine complexes in solution might be behind some of the toxic roles attributed to aluminum in the brain. An up-to-date view of the catecholamine biosynthesis pathway with sites of aluminum interference (according to the current literature) is presented. Alternative mechanisms that might explain the deleterious effects of this metal on the catecholamine route are thoroughly discussed, and new hypotheses that should be investigated in future are proposed.
Introduction
The possible toxicity of aluminum is a highly controversial issue.1 Although scientific literature on the adverse health effects of aluminum is extensive,2–4 the exact molecular mechanisms of aluminum toxicity are not sufficiently understood.5,6 Among the possible detrimental effects of aluminum, we can mention the promotion of oxidative stress,7–9 the inhibition of the normal function of several enzymes (such as hexokinase,10 glutamate dehydrogenase,11–13etc.), the interference with several key cell metabolism cycles,14–16 and also alteration of the structure and chemistry of important metabolites13,17 and cofactors.18 Moreover, since it has been pointed out that aluminum can cross the blood–brain barrier and accumulate in cerebral tissues,19 special concerns have been raised on the possibility of local toxic effects caused by the presence of the aluminum ion. In fact, aluminum is widely recognized as a potential neurotoxic element.20 Early studies supported this hypothesis, linking aluminum to the formation of neurofibrillary tangles (NFTs),21 and more recent experimental and theoretical studies have underlined the ability of aluminum to bind to phosphorylated peptides22,23 and to promote hyperphosphorylation of normal neurofilaments.24 In addition, the ability of aluminum to contribute to Aβ-amyloid aggregation has been recently demonstrated,4,25,26 and growing evidence is linking aluminum to be a decisive contributing factor in Alzheimer's Disease (AD).3,27Another proposed route for aluminum neurotoxicity is the alteration of signaling processes in which neurotransmitters are somehow affected by the presence of this exogenous metal. Due to the possibility of aluminum binding catechols,28 that bear two of the hardest Lewis base oxygen donors to Al(III), an obvious target would be catecholamine-based neurotransmitters.29–32 As a matter of fact, it has been shown that aluminum affects the signaling process mediated by these neurotransmitters,33 altering their content in animal models,29 and interfering with enzymatic activities in which these neurotransmitters34 are involved.
In particular, some authors suggested that catecholamines may become primary Al(III) binders in citrate-low tissues.30,32
Catechol–aluminum interactions have been extensively studied in the framework of aluminum chelation therapy,28,35–37 because of their strong binding affinity towards high valence metals and their low molecular mass. Although several experimental efforts have been made in this sense, the clear and complete understanding of the properties and behavior of these metal–ligand complexes is still a challenging task. Accordingly, computational chemistry is a very powerful tool to complement the available experimental data and help towards their rationalization and clear understanding. The use of state-of-the-art theoretical approaches can provide fundamental knowledge and valuable insights into the properties of these systems, unattainable by other means. In this sense, we have recently proposed and applied a validated computational protocol38 to account for the binding affinity of a wide set of catecholates and salicylates towards Al(III), finding a good qualitative agreement with respect to experimental stability constants. Moreover, the use of the Bader's Quantum Theory of Atoms in Molecules (QTAIM) and the Energy Decomposition Analysis (EDA) allowed us to characterize the physico-chemical features of the Al–O bonds and rationalize the effects of different substituents towards the modulation of the binding affinities. In this sense, we have stressed how electron withdrawing/donating effects can modulate the strength of the Al–O bonds by means of their efficient transmission through the aromatic rings of these compounds.38
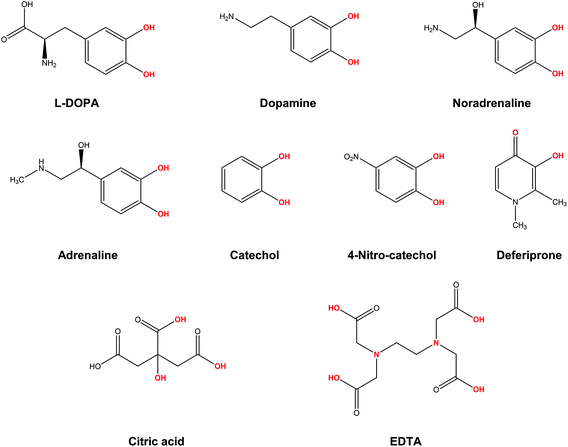
In the present work, we apply a similar methodology to investigate the stability of metal–ligand complexes formed by aluminum and catecholamine-based neurotransmitters (Fig. 1). Four catecholamines are considered in different metal–ligand stoichiometries: L-DOPA, dopamine, noradrenaline (norepinephrine) and adrenaline (epinephrine). Furthermore, and more importantly, we carefully analyze the proton/aluminum ion competition for binding to these neurotransmitters, comparing our results with those previously published for catechol and 4-nitrocatechol38 and with other known low-molecular-mass (LMM) Al(III) chelators such as citrate, deferiprone (1,2-dimethyl-3-hydroxy-4(1H)-piridinone) and ethylenediaminetetraacetic acid (EDTA) (Fig. 1). In particular, citrate was chosen as a reference compound of endogenous aluminum chelators because of its well established high affinity for Al(III) in human serum;39–41 deferiprone was chosen as a reference of exogenous Al(III) chelators since it is the most efficient LMM drug currently employed in aluminum and iron chelation therapy.37,42 Finally, the choice of EDTA as a reference compound is due to its high affinity for trivalent and divalent metal ions, which is also the reason for its controversial role in chelation therapy.43,44 It is important to note that these polydentate ligands span different binding modes (tridentate for citrate, bidentate for deferiprone and hexadentate for EDTA, Fig. 1), leading to different stoichiometric complexes with different entropic contributions, and therefore are very suitable choices to compare the thermodynamics of formation of catecholamines.
Our results show that, although the formation of different Al–catecholamine complexes shows favourable complexation energies compared to catechol, due to the electron withdrawing (EW) effect of the positively charged amino group, the overall stability is not competitive with the formation of other species in solution. Indeed, Al–catecholamine complexes can only barely compete, from a thermodynamic point of view, with the formation of Al(OH)4− species in solution, in agreement with the available experimental data. Al-Hydroxide is widely recognized as the most stable Al(III) hydrolytic species at physiological pH.32,45 Moreover, in an open biological environment, the formation of Al–catecholamine complexes is not as stable as the formation of other metal–ligand complexes such as Al-citrate, Al-deferiprone and Al-EDTA.
In summary, we rule out the possibility that the interaction of aluminum with these neurotransmitters, in an open biological environment, could explain the experimentally assessed toxic effects of Al(III) with neuronal processes involving catechol-based neurotransmitters. Other possibilities are examined and discussed in light of an up-to-date view of the catecholamine biosynthesis pathway.
Methods
Cluster-continuum approach
In order to investigate the thermodynamics of these Al–catecholamine complexes, a cluster-continuum approach is employed.17,46,47 The first coordination shell of aluminum is surrounded by explicit water molecules in an octahedral fashion; the effect of the remaining solvent is treated using the self-consistent reaction field (SCRF) method with the polarized continuum model (PCM), using the integral equation formalism variant (IEFPCM).48 All geometrical optimizations were carried out in the aqueous phase using the Gaussian 16 Rev. A03 suite of programs,49 the B3LYP functional50,51 and 6-31++G(d,p) basis set. Additionally, we added Grimme's D3 dispersion correction,52 along with the Becke–Johnson (BJ) damping function,53 that was shown to further increase the accuracy of non-covalent interactions.54–56To confirm that the optimized structures were real minima on the potential energy surfaces, frequency calculations were carried out at the same B3LYP-D3(BJ)/6-31++G(d,p) – IEFPCM level of theory. All structures showed positive force constants for all the normal modes of vibration. The frequencies were then used to evaluate the zero-point vibrational energy (ZPVE) and the thermal (T = 298 K) vibrational corrections to the enthalpies and Gibbs free energies within the harmonic oscillator approximation. To calculate the entropy, the different contributions to the partition function were evaluated using the standard statistical mechanics expressions in the canonical ensemble and the harmonic oscillator and rigid rotor approximation.
The electronic energies were refined by single-point energy calculations at the B3LYP-D3(BJ)/6-311++G(3df,2p) level of theory. Single point calculations with other dispersion corrected DFT functionals as well as MP2 were also performed to validate the methodology, with similar results (see the ESI†).
Moreover, considering the importance of a proper treatment of solvation energies using implicit solvation models,57,58 we repeated the calculations using the SMD solvation model59 and compared the results with IEFPCM calculations and experimental stability constants (ESI Table S6 and Fig. S3†), finding very similar correlation coefficients.
Definition of binding affinities
We characterized Al(III)–Lig complexes with 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 1
1, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 and 1
2 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 stoichiometries. The formation stability of these complexes was studied following the ligand substitution reaction shown in (1):
3 stoichiometries. The formation stability of these complexes was studied following the ligand substitution reaction shown in (1):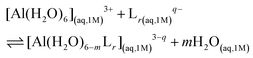 | (1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 1
1, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 and 1
2 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 complexes, respectively. Notice that we consider the ligand's coordinating groups in their unprotonated form, which is the state considered when evaluating experimental log β.
3 complexes, respectively. Notice that we consider the ligand's coordinating groups in their unprotonated form, which is the state considered when evaluating experimental log β.
The enthalpy in solution corresponding to the binding of the ligand to Al(III) is therefore calculated as:
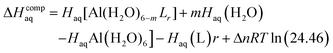 | (2) |
Since the enthalpies are determined using an ideal gas at 1 atm as the standard state, the last term in eqn (2) corresponds to the volume change due to the transformation from 1 atm to 1 M in solution, where Δn refers to the change in the number of species in the reaction.60 In a similar way, the free energy of the complexes is determined as:
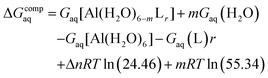 | (3) |
In order to take into account the influence of the protonation constants at the coordination site, we also define free energy at physiological pH values that takes into account the energy penalty associated with the deprotonation of the two phenoxide groups of these catechol-based ligands at physiological pH (7.4), defined as:
| ΔGPhysaq = ΔGcompaq + ΔGdeprotaq | (4) |
The last term in eqn (4) corresponds to the free energy of deprotonation of a given ligand at physiological pH (7.4). This is calculated according to the experimental values for the titratable groups (phenolate) of the ligands. pKa values for catechol and 4-nitrocatechol were taken from ref. 36; for L-DOPA, dopamine, noradrenaline and adrenaline from ref. 30.
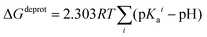 | (5) |
Al–ligand formation energies
A strategy to take into account the aluminum ion/proton competition for the ligand's binding site is presented. Formation energies for aluminum–ligand complexes of different stoichiometries were considered according to the general equilibria: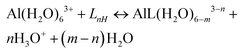 | (6) |
As pointed out by Jensen,57 the calculation of binding energies in solution is a challenging task from a computational point of view. This is mainly due to the inaccurate prediction of solvation energies of small charged ions with continuum solvation models such as IEFPCM. In order to alleviate this problem, the Gibbs free energies of the hydronium and hydroxide ions were calculated as:
| Gaq(H3O+) = Ggas(H3O+) + ΔGsolv(H3O+) | (7) |
| Gaq(OH−) = Ggas(OH−) + ΔGsolv(OH−) | (8) |
Moreover, a correction term57 in the free energies is introduced to account for the pH as:
GpH = m(−pH)RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(10) ln(10) | (9) |
In the case of the calculation of the formation free energy of Al(OH)4− hydrolytic species a similar correction term was introduced to account for pOH:
GpOH = m(−pOH)RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(10) ln(10) | (10) |
pAl calculation
Experimental pAl values of L-DOPA, dopamine, noradrenaline and adrenaline were calculated by means of the Hyperquad simulation and speciation (HySS) program62 using speciation data from ref. 30.Chemical bond analysis
Delocalization Indices (D.I.) are a measure of the covariance between the population of two atoms A and B and, consequently, a measure of the number of electrons simultaneously fluctuating between these atoms,68,69
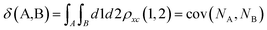 | (11) |
The AIMAll v11.08.23 program72 was used to carry out the QTAIM analysis on the previously optimized structures at the B3LYP-D3(BJ)/6-311++G(3df,2p) level of theory.
Energy decomposition analysis (EDA)
The energy decomposition analysis (EDA) is a state-of-the-art tool for a quantitative interpretation of chemical bonds. The EDA scheme73 based on the theory developed by Ziegler and Rauk74 and by Morokuma75 was carried out using the ADF201776–78 suite of programs. In order to perform the EDA analysis, all 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 Al–ligand complexes previously optimized at the B3LYP-D3(BJ)/6-31++G(d,p) IEFPCM level with Gaussian16 were split into two fragments: the aluminum ion surrounded by four water molecules and the unprotonated ligand. Single-point energies for the EDA analysis were calculated using the B3LYP-D3(BJ) functional and the very robust full electron even-tempered quadruple-ζ basis set79,80 (ET-QZ3P-1DIFFUSE) provided by ADF2017. All EDA calculations were performed in the gas phase.
1 Al–ligand complexes previously optimized at the B3LYP-D3(BJ)/6-31++G(d,p) IEFPCM level with Gaussian16 were split into two fragments: the aluminum ion surrounded by four water molecules and the unprotonated ligand. Single-point energies for the EDA analysis were calculated using the B3LYP-D3(BJ) functional and the very robust full electron even-tempered quadruple-ζ basis set79,80 (ET-QZ3P-1DIFFUSE) provided by ADF2017. All EDA calculations were performed in the gas phase.
The EDA decomposes the instantaneous interaction energy ΔEint between two fragments A and B in a molecule A–B into three well defined terms that can be interpreted in chemically meaningful ways:
| ΔEint = ΔEelstat + ΔEPauli + ΔEoi | (12) |
These terms are (1) the quasi-classical electrostatic interaction energy between the charge densities of the fragments, ΔEelstat (2) the exchange/repulsion between the fragments due to Pauli's principle, ΔEPauli, and (3) the energy gain due to orbital mixing of the fragments, ΔEoi.
Considering that EDA calculations are usually carried out in the framework of density functional theory, if an explicit correction term for dispersion interaction is employed (such as Grimme's D3 method), then EDA numerical results remain unchanged but the dispersion correction appears as an extra term:
| ΔEint = ΔEelstat + ΔEPauli + ΔEoi + ΔEdisp | (13) |
Results and discussion
Binding affinities of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) 1, 1
1, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) 2 and 1
2 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) 3 Al–catecholamine complexes with respect to reference catechol
3 Al–catecholamine complexes with respect to reference catechol
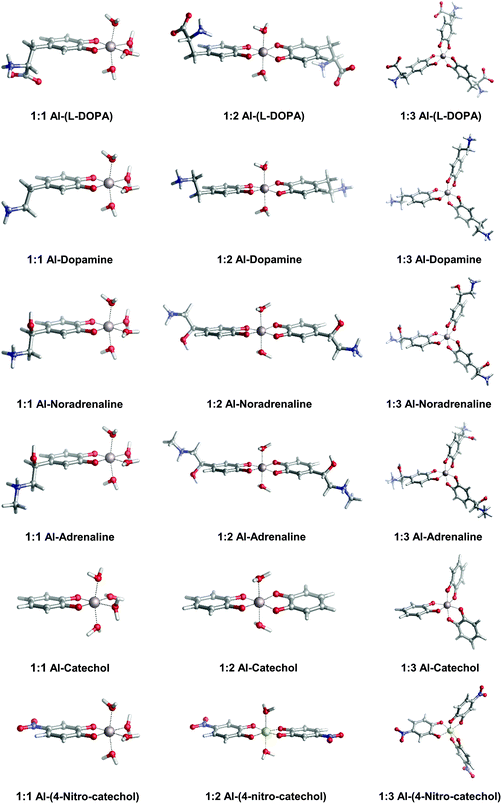
In Fig. 2, we depict the structures characterized in the present work for 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 1
1, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 and 1
2 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 aluminum–catecholamine complexes along with our previously determined structures for catechol and 4-nitrocatechol ligands.38 Very similar structures are obtained with respect to catechol, indicating that the different amine substituents have a little effect on the coordination mode of aluminum to the catechol moiety.
3 aluminum–catecholamine complexes along with our previously determined structures for catechol and 4-nitrocatechol ligands.38 Very similar structures are obtained with respect to catechol, indicating that the different amine substituents have a little effect on the coordination mode of aluminum to the catechol moiety.
In Table 1, we can find the binding energies of catecholamines compared to catechol and 4-nitrocatechol chosen as reference structures of our previous work.38 Two states have been considered for the amino group: protonated and unprotonated. Although the estimation of Kiss et al.30 is that at physiological pH these amines will be protonated, we have decided to consider both possibilities in order to gain more insights into the thermodynamics of binding energies and the role played by the positively charged amino group. It is worth emphasizing that the theoretical methodology employed in this work has been recently thoroughly validated for a wide dataset of catecholates and salicylates using different density functionals, the MP2 method and experimental data.38 In Fig. 3, we compare the binding free energies, ΔGcompaq, of the catecholamines along with the previously obtained values for catechol and 4-nitrocatechol with respect to experimental stability constants (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β), finding a remarkable good correlation coefficient of 0.9909, which confirms the validity of our approach. It is important to mention, at this stage, that experimental log
β), finding a remarkable good correlation coefficient of 0.9909, which confirms the validity of our approach. It is important to mention, at this stage, that experimental log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β values were taken from two different sources: those of catecholamines from an old paper by Kiss et al.30 and those of catechol and 4-nitrocatechol from a more recent paper by Nurchi et al.36 Binding energies with different functionals (M06-2X82 and ωB97X-D83) as well as the MP2 method84,85 can be found in the ESI (Tables S1–S3†), giving very similar correlation coefficients when compared with experimental stability constants (ESI Fig. S1†).
β values were taken from two different sources: those of catecholamines from an old paper by Kiss et al.30 and those of catechol and 4-nitrocatechol from a more recent paper by Nurchi et al.36 Binding energies with different functionals (M06-2X82 and ωB97X-D83) as well as the MP2 method84,85 can be found in the ESI (Tables S1–S3†), giving very similar correlation coefficients when compared with experimental stability constants (ESI Fig. S1†).
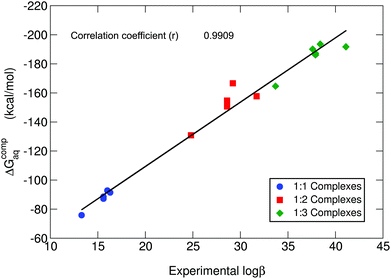 | ||
Fig. 3 B3LYP-D3(BJ) binding energies (ΔGcompaq) versus experimental stability constants (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β).30,36 A correlation coefficient of 0.9909 is obtained. All amino groups are considered in their protonated state. β).30,36 A correlation coefficient of 0.9909 is obtained. All amino groups are considered in their protonated state. | ||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β, log
β, log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βCond.) and pAl data for the whole dataset of catechol-based ligands. Note that cumulative stability constants (log
βCond.) and pAl data for the whole dataset of catechol-based ligands. Note that cumulative stability constants (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β) are comparable with ΔGcompaq, while conditional stability constants (log
β) are comparable with ΔGcompaq, while conditional stability constants (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βCond.) are comparable with ΔGphysaq, since the last two quantities take into account the influence of protonation constants
βCond.) are comparable with ΔGphysaq, since the last two quantities take into account the influence of protonation constants
| Ligands | Theoretical thermodynamics | Experimental parametersa | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| ΔHcompaq | ΔGcompaq | ΔGPhysaq | ΔHcompaq | ΔGcompaq | ΔGPhysaq | log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β β |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βCond. βCond. |
pAl | ||
| Protonated amine | Unprotonated amine | |||||||||
| a Experimental pKa and parameter values for L-DOPA, dopamine, noradrenaline and adrenaline are taken and calculated (pAl) using data from ref. 81; for catechol and 4-nitrocatechol are taken from ref. 36. All energies in kcal mol−1 are calculated at the B3LYP-D3(BJ)/6-311++G(3df,2p) – IEFPCM level of theory. | ||||||||||
| L-DOPA | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
−88.3 | −92.8 | −82.7 | −91.8 | −95.2 | −81.9 | 16.0 | 8.1 | 10.8 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 2 |
−160.0 | −166.6 | −146.4 | −160.3 | −165.6 | −138.8 | 29.2 | 13.3 | ||
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 3 |
−182.8 | −193.5 | −163.3 | −187.7 | −195.7 | −155.5 | 38.4 | 14.5 | ||
| Dopamine | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
−85.7 | −88.6 | −78.8 | −89.5 | −92.8 | −78.9 | 15.6 | 8.0 | 10.8 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 2 |
−148.4 | −154.7 | −135.1 | −153.6 | −161.6 | −133.8 | 28.6 | 13.4 | ||
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 3 |
−181.8 | −190.0 | −160.6 | −186.2 | −195.2 | −153.5 | 37.6 | 14.7 | ||
| Noradrenaline | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
−83.1 | −87.2 | −77.8 | −88.3 | −91.8 | −79.8 | 15.6 | 8.3 | 11.4 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 2 |
−143.0 | −150.7 | −131.8 | −148.5 | −157.0 | −133.0 | 28.6 | 14.0 | ||
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 3 |
−177.5 | −186.1 | −157.7 | −179.2 | −189.8 | −153.8 | 37.9 | 16.0 | ||
| Epinephrine | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
−83.0 | −87.2 | −78.1 | −88.2 | −91.5 | −78.7 | 15.6 | 8.2 | 11.3 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 2 |
−143.0 | −150.7 | −132.5 | −146.4 | −154.6 | −129.3 | 28.6 | 13.9 | ||
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 3 |
−176.4 | −187.2 | −159.2 | −178.4 | −186.3 | −148.0 | 37.9 | 15.8 | ||
| Catechol | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
−88.4 | −91.4 | −79.6 | 16.3 | 8.2 | 10.1 | |||
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 2 |
−151.8 | −157.7 | −134.1 | 31.7 | 13.2 | |||||
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 3 |
−183.1 | −191.7 | −156.6 | 41.1 | 13.5 | |||||
| 4-Nitrocatechol | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
−71.6 | −75.8 | −71.2 | 13.3 | — | 14.2 | |||
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 2 |
−124.0 | −130.8 | −121.7 | 24.8 | — | |||||
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 3 |
−183.1 | −164.6 | −150.8 | 33.7 | — | |||||
We first discuss the results for N-protonated catecholamines, as this is the most likely situation at physiological pH. In general, catecholamines show lower ΔGcompaq (in absolute values) than catechol, in agreement with the lower experimental stability constants (Table 1). However these binding affinities are higher than the ones of 4-nitrocatechol; this compound was chosen as a reference system to evaluate the electron withdrawing (EW) effect of substituents in the catechol ring. Accordingly, the introduction of a positively charged amino tail in catecholamines has an EW effect, which is smaller than the one provoked by the 4-nitro substituent. This can be explained considering that, as assessed in our previous work,38 the strong EW effect of the NO2 group added to a catecholate ring is mediated through both resonance and inductive mechanisms of action. On the other hand, the EW effect of the protonated amino group of catecholamines is mediated only by the electron attracting behavior of the positive charge. Among catecholamines, L-DOPA and dopamine show, in general, higher ΔGcompaq than adrenaline and noradrenaline. In this sense, we should bear in mind that protonated L-DOPA has a higher total negative charge (−2) than the rest of the catecholamines (−1) due to the presence of the carboxylate group (Fig. 1); therefore, its interaction with the trivalent aluminum ion is expected to be stronger. Besides, the higher Al(III) affinity of dopamine compared to noradrenaline and adrenaline can be explained considering that the latter two compounds contain a hydroxyl group in the alkyl chain, which has an EW effect. These aspects will be discussed in detail in the “Analysis of Al–O bonds” section.
In order to check the effect of the positive charge of the amine towards binding affinities, we re-evaluated ΔGcompaq values considering the unprotonated amino groups. In all cases, there is an increase of absolute ΔGcompaq values (Table 1), which is due to the higher total negative charge of N-unprotonated catecholamines. Interestingly, now L-DOPA and dopamine show larger binding energies than catechol. Again, L-DOPA bears a higher total negative charge (−3) than catechol (−2) and the other catecholamines (−2), that explains its stronger aluminum affinity. However, in the case of dopamine, the presence of the alkyl tail acts as an electron donating group (ED) by induction, although such an effect is weakened by the presence of the EW effect (by induction) of NH2. Moreover, when a second EW group is added to the alkyl chain, namely, –OH in noradrenaline and adrenaline, the overall EW effect prevails over the ED one, lowering the binding ability of these two catecholamines with respect to catechol (Table 1).
In summary, the positive charge at the amino group plays a major role in the modulation of the binding affinities in these aluminum–ligand complexes, although the presence of other substituents also influences the overall stability.
In order to confirm these speculations and to obtain a more physically sound picture of the substituent effects, as well as to investigate the bonding nature of these complexes, we decided to perform a detailed chemical bond analysis based on both QTAIM and EDA analysis which is presented in the next section.
Analysis of Al–O bonds
Bader's Quantum Theory of Atoms in Molecules (QTAIM, Table S4 and Fig. S2†) allows us to gain more insight into the physico-chemical properties of these Al–ligand interactions. For simplicity, we will focus our discussion on 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexes, considering both N-protonated and N-unprotonated catecholamines. Similarly as reported in our previous work on the interaction of aluminum with substituted catechols and salicylic acids,38 we find positive values of the Laplacian of the electron density, ∇2ρ(rBCP), and small but negative values of the energy density, H(rBCP), consistently for all Al–O bond critical points. According to the Bader's criteria, positive values of ∇2ρ(rBCP) and H(rBCP) are indicative of closed-shell interactions (i.e. ionic or electrostatic bonds), while negative values for both quantities indicate the presence of shared (covalent) interactions. The mixed situation present in our results, previously reported for bonds involving metals,65 suggests that although Al–O bonds are mainly of ionic nature, they also contain a small degree of covalency, due to their dative nature. To provide a more accurate analysis of these aluminum–ligand interactions, Al–O delocalization indices (D.I.Al–O) were also calculated. Delocalization indices are a measure of the average number of electron pairs shared between two atoms, therefore they have been related to the measure of the covalent character of a given bond.71
1 complexes, considering both N-protonated and N-unprotonated catecholamines. Similarly as reported in our previous work on the interaction of aluminum with substituted catechols and salicylic acids,38 we find positive values of the Laplacian of the electron density, ∇2ρ(rBCP), and small but negative values of the energy density, H(rBCP), consistently for all Al–O bond critical points. According to the Bader's criteria, positive values of ∇2ρ(rBCP) and H(rBCP) are indicative of closed-shell interactions (i.e. ionic or electrostatic bonds), while negative values for both quantities indicate the presence of shared (covalent) interactions. The mixed situation present in our results, previously reported for bonds involving metals,65 suggests that although Al–O bonds are mainly of ionic nature, they also contain a small degree of covalency, due to their dative nature. To provide a more accurate analysis of these aluminum–ligand interactions, Al–O delocalization indices (D.I.Al–O) were also calculated. Delocalization indices are a measure of the average number of electron pairs shared between two atoms, therefore they have been related to the measure of the covalent character of a given bond.71
As previously hypothesized, the results seem to confirm the electron withdrawing effect mediated by the positively charged amino group (Table S4 and Fig. S2†) that decreases the electron density from the two Al–O bonds; a more detailed albeit speculative analysis of the D.I.Al–O values is presented and thoroughly discussed in the ESI.†
In summary, Bader's analysis confirmed the hybrid nature of the Al–O interactions, and has been proven to be a powerful tool to rationalize the effects that the different chemical environments of these catechol-based compounds have on their binding affinity trend.
The EDA approach was also used to characterize the degree of the ionic/covalent character of the Al–O bonds (Table S5†) by splitting the total interaction energy (ΔEInt) into the electrostatic (ΔEelstat), orbital interaction (ΔEoi) and Pauli repulsion (ΔEPauli) terms. EDA results confirm the previous QTAIM analysis, pointing to a mainly ionic bond with a smaller but significant covalent character. As expected, there are pronounced differences in the electrostatic contributions to the bond depending on the total charge of the ligand. In this sense, unprotonated catecholamines show higher ΔEelstat values than protonated ones (Table S5†). Moreover, N-protonated L-DOPA, catechol and 4-nitrocatechol show larger electrostatic energies than protonated dopamine, noradrenaline and adrenaline, in agreement with their higher negative charge. One has to take into account that a lower ΔEelstat will be compensated with a lower de-solvation energy when forming the complex, and therefore the big differences in ΔEelstat and ΔEint shown in Table S5† are not reflected in the actual ΔGcompaq trend (Table 1), due to the lack of solvation effects in EDA analysis. Also, this puts a word of caution in the use of EDA with no-solvation effects when comparing ligands of different total charges.
In general, protonated catecholamines show lower orbital interaction energies (ΔEoi) than the protonated counterparts, in agreement with the previous delocalization indices analysis (Fig. S2†), indicating a lower covalent contribution. However, among different compounds a clear trend in orbital and interaction energies with respect to binding energies (ΔGcompaq) could not be established. Therefore, we remark again that EDA results should be taken only with caution, since no solvation is introduced in this energy decomposition scheme; we already reported the paramount importance of considering solvation effects when dealing with charged complexes in solution.86
Aluminum ion/proton competition for ligand binding
Unlike log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β, conditional (apparent) stability constants (log
β, conditional (apparent) stability constants (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βcond) are weighted by taking into account the influence of the protonation constants of a given ligand.87 That is, their calculation considers the ligand in all of its possible forms in solution;87 accordingly, log
βcond) are weighted by taking into account the influence of the protonation constants of a given ligand.87 That is, their calculation considers the ligand in all of its possible forms in solution;87 accordingly, log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βcond takes into account the proton/aluminum ion competition for ligand's coordination site. This is due to the fact that both Al(III) and H+ are hard Lewis acids and, therefore, compete for the binding of hard Lewis bases, coherently with the Pearson's Hard and Soft Acids and Bases (HSAB) principle.88
βcond takes into account the proton/aluminum ion competition for ligand's coordination site. This is due to the fact that both Al(III) and H+ are hard Lewis acids and, therefore, compete for the binding of hard Lewis bases, coherently with the Pearson's Hard and Soft Acids and Bases (HSAB) principle.88
A comparison between the experimental values of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β and log
β and log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βcond points to a change in chelation performance between catechol and catecholamines (Table 1). Thus, whereas in general higher values of log
βcond points to a change in chelation performance between catechol and catecholamines (Table 1). Thus, whereas in general higher values of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β are found for catechol with respect to catecholamines, the opposite is true when considering conditional stability constants, indicating that when proton competition is taken into account catecholamines are better aluminum chelators than catechol. The reason relies on the lower pKa values of the two hydroxyl groups of the catechol ring of catecholamines30 compared with those of catechol.36 In Table 1, we report the values of physiological binding energies (ΔGPhysaq), calculated by taking into account the energetic penalty that Al(III) has to pay in order to deprotonate the ligands, based on their experimental pKa values (see the Methods section). In agreement with the experimental log
β are found for catechol with respect to catecholamines, the opposite is true when considering conditional stability constants, indicating that when proton competition is taken into account catecholamines are better aluminum chelators than catechol. The reason relies on the lower pKa values of the two hydroxyl groups of the catechol ring of catecholamines30 compared with those of catechol.36 In Table 1, we report the values of physiological binding energies (ΔGPhysaq), calculated by taking into account the energetic penalty that Al(III) has to pay in order to deprotonate the ligands, based on their experimental pKa values (see the Methods section). In agreement with the experimental log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βcond data, we also observe a change in the trend between ΔGPhysaq and ΔGcompaq, with catecholamines showing slightly higher ΔGPhysaq values than catechol but smaller ΔGcompaq (Table 1).
βcond data, we also observe a change in the trend between ΔGPhysaq and ΔGcompaq, with catecholamines showing slightly higher ΔGPhysaq values than catechol but smaller ΔGcompaq (Table 1).
The estimation of ΔGPhysaq is a first approach to understand the chelation performance towards Al(III). However, the fact that both theoretical and experimental information are combined in the evaluation of ΔGPhysaq partially jeopardize the usefulness of this approach; both contributions to the final binding energy are not evaluated at the same level and the procedure depends on the availability of experimental pKa values for the ligands. In order to overcome these limitations, we decided to calculate the binding energies of Al–ligand complexes departing from protonated ligands. In this way, the proton/aluminum ion competition for ligand binding is intrinsically considered in the definition of the corresponding reaction equilibria (see the Methods section). We will refer to these free energies as ΔGPhysaq,LnH, where the subscript LnH stands for the protonation state of a given ligand L at physiological pH. Results can be found in Table 2; we have considered that both hydroxyl groups of the catechol moiety in all compounds are protonated and that the amino groups of catecholamines are also in their protonated state. We have observed that, irrespective of the stoichiometry and of the catecholamine, we obtain in all cases substantial negative ΔGphysaq,LnH values. This suggests that, in all cases, aluminum is able to displace the protons from the catechol moieties and form stable Al–ligand complexes.
| Ligands | Reaction equilibria | ΔHcompaq,LnH | ΔGcompaq,LnH | ΔGPhysaq,LnH | ΔΔGPhysaq,LnH | pAl |
|---|---|---|---|---|---|---|
| a Data taken from ref. 32. b Calculated with the HySS program using data from ref. 81. c Data taken from ref. 36. d Calculated with the HySS program using data from ref. 89 All energies in kcal/mol are obtained at the B3LYP-D3(BJ)/6-311++(3df,2p) – IEFPCM level of theory. | ||||||
| Hydroxide | Al(H2O)63+ + 4OH− → Al(OH)4− + 6H2O | −82.0 | −94.9 | −59.0 | 0 | 12.1a |
| L-DOPA | Al(H2O)63+ + L2H0 → AlL(H2O)4+ + 2H3O+ | −10.8 | −19.9 | −40.1 | 18.9 | |
| Al(H2O)63+ + 2L2H0 → AlL2(H2O)2− + 4H3O+ | −4.9 | −20.7 | −61.1 | −2.1 | 10.8b | |
| Al(H2O)63+ + 3L2H0 → AlL33− + 6H3O+ | 48.6 | 28.6 | −31.9 | 27.1 | ||
| Dopamine | Al(H2O)63+ + L2H+ → AlL(H2O)42+ + 2H3O+ | −10.8 | −18.9 | −39.0 | 20.0 | |
| Al(H2O)63+ + 2L2H+ → AlL2(H2O)2+ + 4H3O+ | 1.5 | −15.2 | −55.5 | 3.4 | 10.8b | |
| Al(H2O)63+ + 3L2H→+ → AlL30 + 6H3O+ | 43.1 | 19.2 | −41.3 | 17.7 | ||
| Adrenaline | Al(H2O)63+ + L2H+ → AlL(H2O)42+ + 2H3O+ | −12.4 | −21.2 | −41.3 | 17.7 | |
| Al(H2O)63+ + 2L2H+ → AlL2(H2O)2+ + 4H3O+ | −1.7 | −18.6 | −59.0 | 0 | 11.3b | |
| Al(H2O)63+ + 3L2H+ → AlL30 + 6H3O+ | 34.5 | 12.0 | −48.5 | 10.5 | ||
| Noradrenaline | Al(H2O)63+ + L2H+ → AlL(H2O)42+ + 2H3O+ | −12.6 | −21.9 | −42.1 | 16.9 | |
| Al(H2O)63+ + 2L2H+ → AlL2(H2O)2+ + 4H3O+ | −2.2 | −20.2 | −60.6 | −1.6 | 11.4b | |
| Al(H2O)63+ + 3L2H+ → AlL30 + 6H3O+ | 34.8 | 8.5 | −52.1 | 6.9 | ||
| Catechol | Al(H2O)63+ + L2H0 → AlL(H2O)4+ + 2H3O+ | −10.6 | −19.4 | −39.6 | 19.4 | |
| Al(H2O)63+ + 2L2H0 → AlL2(H2O)2− + 4H3O+ | 3.8 | −13.7 | −54.0 | 5.0 | 10.1c | |
| Al(H2O)63+ + 3L2H0 → AlL33− + 6H3O+ | 50.0 | 24.4 | −36.2 | 22.8 | ||
| 4-Nitrocatechol | Al(H2O)63+ + L2H0 → AlL(H2O)4+ + 2H3O+ | −15.2 | −25.0 | −45.2 | 13.8 | |
| Al(H2O)63+ + 2L2H0 → AlL2(H2O)2− + 4H3O+ | −11.1 | −30.0 | −70.4 | −11.4 | 14.2c | |
| Al(H2O)63+ + 3L2H0 → AlL33− + 6H3O+ | 14.5 | −14.0 | −74.6 | −15.6 | ||
| Deferiprone | Al(H2O)63+ + LH0− → AlL(H2O)42+ + H2O + H3O+ | −26.8 | −33.3 | −43.4 | 15.6 | |
| Al(H2O)63+ + 2LH0− → AlL2(H2O)2+ + 2H2O + 2H3O+ | −39.7 | −51.0 | −71.2 | −12.2 | 15.4d | |
| Al(H2O)63+ + 3LH0− → AlL30 + 3H2O + 3H3O+ | −28.8 | −53.7 | −84.0 | −25.0 | ||
| Citrate | Al(H2O)63+ + LH3− → AlL(H2O)3− + 2H2O + H3O+ | −58.5 | −70.0 | −80.0 | −21.0 | 14.4a |
| Al(H2O)63+ + 2LH3− → AlL5− + 4H2O + 2H3O+ | −46.7 | −71.7 | −91.8 | −32.8 | ||
| EDTA | Al(H2O)63+ + LH3− → AlL− + 5H2O + H3O+ | −79.2 | −111.8 | −121.9 | −62.9 | 16.4a |
In summary, both experimental and theoretical results point to the importance of considering properly the effect of ligand deprotonation in order to evaluate the overall performance of a given ligand towards aluminum binding. In fact, the order in relative binding affinity can be altered when deprotonation energies of the ligands are taken into account. Nevertheless, the interaction between aluminum and catechol/catecholamines is strong enough to displace the protons from the ligand, leading to potentially stable complexes.
Comparison between different ligands towards aluminum binding and aluminum hydroxide formation in solution
In an open biological environment, in order to bind to a given ligand, the aluminum ion has to compete not only with the protons, but also with other endogenous (and eventually exogenous) chelators. Moreover, the speciation of the Al(III) ion in solution is a complex task;32 indeed, at physiological pH, there exist several Al(III)-hydroxide species, with Al(OH)4− being the most stable one.30,32 Accordingly, we also need to consider the possibility of the hydroxide binding competition, in order to evaluate the chelation performance of a given ligand.In this sense, the main shortcoming in the use of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βcond as a criterion to evaluate the chelation properties is the fact that conditional stability constants depend on the stoichiometries of the corresponding metal–ligand complexes.42,87 For this reason, stability constant values of ligands displaying different denticities (e.g. bidentate, tridentate, hexadentate etc.) cannot be directly compared because of different entropic contributions of their chelate effect.42
βcond as a criterion to evaluate the chelation properties is the fact that conditional stability constants depend on the stoichiometries of the corresponding metal–ligand complexes.42,87 For this reason, stability constant values of ligands displaying different denticities (e.g. bidentate, tridentate, hexadentate etc.) cannot be directly compared because of different entropic contributions of their chelate effect.42
In order to overcome such limitations, the pM parameter has been introduced as a general criterion to compare the chelation performance between different ligands.90 This is defined as −log[MF] usually taken at [MT] = 1 × 10–6 M and [LT] = 1 × 10–5 M at pH 7.4, where [MF] is the concentration of free metal in solution (in this case aluminum), and [MT] and [LT] are the total concentrations of the metal and the ligand, respectively.87 Such an experimental parameter is very useful to assess the potential competitiveness of different ligands towards Al(III) in an open biological environment, and it will be used in this section for the discussion of the Al(III) binding efficiency of different ligands (see Table 2 and Fig. 5).
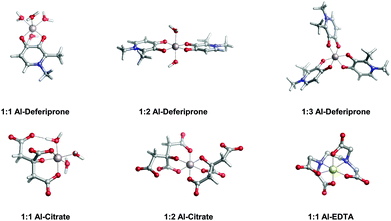
In Table 2 and Fig. 5, we compare the formation energies of the catechol-based ligands with those of some reference compounds displaying different denticities, namely: citrate, the main biochelator of aluminum in blood serum;39–41 deferiprone, one of the main drugs used in Al(III) chelation therapy;37,42,91 EDTA, one of the most powerful Al(III) chelating agents43,44 (Fig. 4). As in the previous section, all ligands are considered at their most likely protonation states at physiological pH (Table 2): citrate with a hydroxy group protonated and the three carboxylates unprotonated; deferiprone with the hydroxy group protonated, and EDTA with one amine protonated and the four carboxylates unprotonated. In addition, relative formation energies (ΔΔGphysaq,LnH) for each ligand are calculated with respect to the formation energy of Al(OH)4− hydrolytic species, which represents the competition of hydroxide for aluminum binding in solution (Table 2). We depict both theoretical and experimental (pAl) data in Fig. 5. Note that the vertical line at pAl = 12.1 indicates the threshold for an efficient competition with aluminum hydroxide formation; the same is true for the horizontal line at ΔGphysaq,LnH = −59.0 kcal mol−1, which marks the theoretical limit for a given ligand to be able to compete with hydroxide formation at physiological pH.
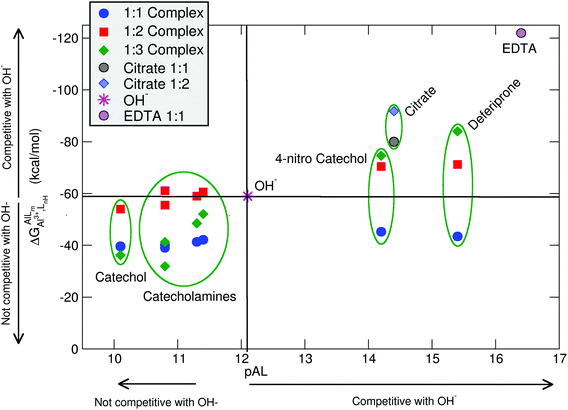 | ||
| Fig. 5 Proton versus aluminum ion competition for different ligands at different stoichiometries. On the x-axis, experimental pAl values. On the y-axis, DFT formation energies. Aluminum hydroxide [Al(OH)4−] formation is used as a threshold for positive/negative Al–ligand competition. All Al–ligand reaction equilibria are presented in Table 2. | ||
In Fig. 5 we see that, although all catecholamines and catechol compounds show negative formation energies, only 4-nitrocatechol at 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 and 1
2 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 stoichiometries is able to clearly outcompete hydroxide at physiological pH (Fig. 5). This is coherent with an experimental pAl of 14.2 for 4-nitrocatechol, similar to the 14.4 value of citrate. Similarly, citrate, deferiprone and EDTA lie in the top-right region of Fig. 5, the region where they can form more stable complexes than Al(OH)4− according to both theoretical and experimental data. The ΔGphysaq,LnH values of catechol, irrespective of the stoichiometry, are lower (in absolute values) than −59.0 kcal mol−1, the calculated formation free energy of Al(OH)4− hydrolytic species (Table 2). This is in agreement with the lower pAl value of Al-catechol, 10.2, than that of Al-hydroxide, 12.1. Catecholamines lie in an intermediate situation between that of catechol and 4-nitrocatechol, but both theoretical and experimental results restrain them in an area of low competitiveness with respect to hydroxide formation (Fig. 5). Indeed, only 1
3 stoichiometries is able to clearly outcompete hydroxide at physiological pH (Fig. 5). This is coherent with an experimental pAl of 14.2 for 4-nitrocatechol, similar to the 14.4 value of citrate. Similarly, citrate, deferiprone and EDTA lie in the top-right region of Fig. 5, the region where they can form more stable complexes than Al(OH)4− according to both theoretical and experimental data. The ΔGphysaq,LnH values of catechol, irrespective of the stoichiometry, are lower (in absolute values) than −59.0 kcal mol−1, the calculated formation free energy of Al(OH)4− hydrolytic species (Table 2). This is in agreement with the lower pAl value of Al-catechol, 10.2, than that of Al-hydroxide, 12.1. Catecholamines lie in an intermediate situation between that of catechol and 4-nitrocatechol, but both theoretical and experimental results restrain them in an area of low competitiveness with respect to hydroxide formation (Fig. 5). Indeed, only 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 Al-L-DOPA and Al–noradrenaline seem to be barely competitive with Al-hydroxide, showing ΔGPhysaq,LnH values of −61.1 and −60.6 kcal mol−1, respectively (Table 2). Interestingly, among bidentate compounds, all Al–catecholamine complexes, as well as all Al–catechol ones (but not Al-4-nitrocatechol nor Al-deferiprone) show a preference towards the formation of the 1
2 Al-L-DOPA and Al–noradrenaline seem to be barely competitive with Al-hydroxide, showing ΔGPhysaq,LnH values of −61.1 and −60.6 kcal mol−1, respectively (Table 2). Interestingly, among bidentate compounds, all Al–catecholamine complexes, as well as all Al–catechol ones (but not Al-4-nitrocatechol nor Al-deferiprone) show a preference towards the formation of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 metal–ligand complex (Fig. 5). This is in agreement with the speciation diagram for Al–adrenaline depicted by Kiss et al.,30 where they found that the 1
2 metal–ligand complex (Fig. 5). This is in agreement with the speciation diagram for Al–adrenaline depicted by Kiss et al.,30 where they found that the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 Al–adrenaline complex is the prevalent one in the 5–8 pH range.
2 Al–adrenaline complex is the prevalent one in the 5–8 pH range.
The overall low competitive situation of all catecholamines is reflected by their pAl values around 10 and 11, that we calculated using the speciation data of Kiss et al.30 They are close but lower than the pAl value of Al-hydroxide, 12.1 (Table 2), although Martin32 has reported a generic and single pAl value for all catecholamines of 12.8, which seems to be only barely competitive compared with Al-hydroxide formation.
In summary, despite that catecholamines display in principle favorable proton/aluminum ion competition with an enhanced affinity with respect to catechol, this is not sufficient to transform them into potential strong aluminum binders in aqueous solution at physiological pH; they can only barely compete with aluminum-hydroxide formation. Moreover, as demonstrated by our calculations and by the available experimental data, other well known aluminum chelators such as citrate, deferiprone and EDTA, are much more prompt to bind to Al(III) than catecholamines in an open biological environment. Accordingly, we can classify these neurotransmitters as overall poor aluminum binders; the impact of these findings in light of the catecholamine biosynthesis pathway will be discussed in the next section.
Discussion and biological implications of the results
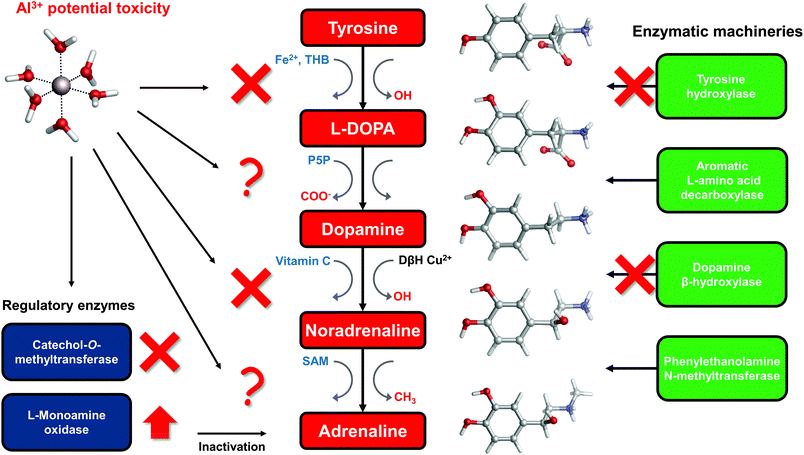
The catechol moiety is the building block of catecholamines, a class of neurotransmitters and hormones of fundamental importance for the correct homeostasis and function of both the central (CNS) and peripheral (PNS) nervous systems, where they exert a wide range of tasks.92–94 Within the CNS, these neurotransmitters are involved in many cognitive, motor, emotional, neuronal plasticity and memory-related functions. In the PNS, as hormones they find their way in the correct behavior of both the sympathetic and parasympathetic systems, where they play an important role in the fight-or-flight response and, in general, in the body's response to stress.95L-DOPA, dopamine, noradrenaline (norepinephrine) and adrenaline (epinephrine) are synthesized from the aminoacid L-tyrosine (Fig. 6); the resulting catecholamine biosynthesis pathway involves several enzymes, substrates, cofactors, metal ions and regulatory mechanisms that are highly interjoined with other metabolic pathways, leading to a complex and finely controlled network.93 Hence, the perturbation, interference or impairment of such an intricate network is associated with the development of severe clinical phenotypes and neurometabolic disorders.93As introduced in the beginning, Al(III) is believed to play a role in the insurgence of neurodegenerative diseases (in particular Alzheimer's Disease27) as well as in the impairment of several key neuronal processes.3 Indeed, it has been shown that this exogenous metal affects the signaling process mediated by catecholamines,33 it alters their content in animal models,29 and interferes with enzymatic activities that involve these neurotransmitters.34,96–98 Moreover, it has been demonstrated that the ingestion of aluminum affects catecholamine levels in different brain tissues.99,100
Therefore, a relationship between the presence of aluminum in the brain and interferences with the metabolic routes involving catecholamines has been established. Does the interaction of aluminum with catecholamines, and the resulting metal–neurotransmitter complexes, play a direct and crucial role that could be considered a potential risk factor for neurodegenerative phenotypes? Our calculations clearly support the formation of stable complexes between aluminum and catecholamines, with favorable complexation energies even when proton displacement is taken into account. However, in solution the resulting complexes are only barely competitive with the formation of Al(OH)4− hydrolytic species at physiological pH. Additionally, both theoretical and available experimental data point to a highly unfavored competition of all Al–neurotransmitter complexes with respect to other endogenous biochelators such as citrate, or with respect to other ligands like deferiprone and EDTA.
As a consequence, the direct interaction of free aluminum ions in solution with catecholamines does not seem to be a likely factor that could interfere with these metabolic pathways. Based on our thermodynamic data, the formation of strong aluminum–catecholamine complexes must fulfill two conditions: (i) a solvent-free environment that protects from hydroxide attack or prevents hydroxide formation, and (ii) the absence of other efficient aluminum chelators. Some authors have already suggested that the formation of aluminum–catecholamine complexes requires a citrate-free environment,30,32 although they did not discuss carefully the effect of hydroxide molecules.
In light of these considerations, what is the experimentally assessed detrimental role of aluminum within the catecholamine route?
To answer this question, in the rest of the section we will collect and discuss (to the best of our knowledge) the literature regarding Al(III) and catecholamines, and evaluate some other possible mechanisms of Al(III) interference that could be assessed in future. For that purpose, an up-to-date representation of the catecholamine biosynthesis pathway with sites of aluminum influence (according to the literature) is proposed in Fig. 6.
There are three enzymes whose activity has been reported to be inhibited by the presence of aluminum: tyrosine hydroxylase (TH),97,98 dopamine β-hydroxylase (DBH)34,96 and catechol-O-methyltransferase (COMT).101,102 Tyrosine hydroxylase is responsible for the synthesis of L-DOPA using the aminoacid L-tyrosine as a substrate and Fe(II) and tetrahydrobiopterin (THB) as cofactors. Dopamine β-hydroxylase, an enzyme that contains Cu(II) metal ions in its active site, converts dopamine to noradrenaline using vitamin C as a cofactor. Finally, catechol-O-methyltransferase is involved in the regulation (inactivation) of catecholamine levels by methylation of their hydroxyl groups, using Mg(II) and S-adenosyl methionine (SAM) as cofactors (Fig. 6).
Interestingly, all of these three enzymes make use of divalent metal ions (iron, copper and magnesium) in order to perform the redox reactions required by their active sites. Al(III) is well known for being a non-redox metal,7,8,103 therefore it can have a direct and strong influence on the reaction mechanisms catalyzed by these enzymes. Aluminum has been shown to be able to bind to Fe(III)-loaded transferrin.104–107 Accordingly, aluminum might be able to displace the copper ion from the active site of DBH and, due to its different ionic radius, conformationally impair the activity of that enzyme. Alternatively, another possibility is that the non-redox behavior of Al(III) alters the reaction mechanism of DBH leading to its inactivation.
Similarly, Al(III) might compete with Fe(II) and Mg(II) being utilized as a cofactor by TH and COMT, respectively, thus affecting their normal behavior.
Quite interestingly, Al(III) inhibits O-methylation (COMT) but not N-methylation (phenylalanine N-methyltransferase, PNMT)101,102 of catecholamines. PNMT is the enzyme in charge of the synthesis of adrenaline through N-methylation of noradrenaline (Fig. 6). These findings were interpreted in terms of the formation of strong and stable Al–catecholamine complexes, in which the methylation at the oxygen atoms of the catecholate would be affected by the binding of the metal, whereas the methylation at the terminal amino group of noradrenaline would be unaffected since this group is not directly bound to aluminum.101,102 In line with this interpretation, authors showed that the use of a potent chelating agent such as deferoxamine (DFO) is able to reverse the Al(III)-induced inhibition of COMT,102 in agreement with the much higher Al(III) affinity of EDTA and deferiprone characterized in this work. They also reported that an excess of DFO inhibits again COMT, because of the removal of magnesium ions that are required as cofactors.102
Our results would further support this hypothesis, since in COMT, contrary to PNMT, there is a well-defined Mg(II) binding site that can protect aluminum from hydroxide formation, due to the lack of solvent molecules. Therefore, such an environment could favor the formation of a strong aluminum–catecholamine complex that, ultimately, impairs the normal functioning of COMT. In this sense, Sparta and Alexandrova investigated the effects of various divalent and trivalent metal ions towards the enzymatic activity of COMT by means of QM/MM simulations.108 They found that trivalent metal ions such as Fe(III) impair the reaction mechanism by increasing the activation energy needed for the methyl transfer reaction; this is due to the higher electrophilic nature of Fe(III) that reduces the basicity of the oxygen donors of the catechol-based substrate, rather than to an iron-induced conformational change of the enzyme.108 Aluminum could certainly play a similar role since it also shows a strong electrophilic nature according to its high charge and small size.
Regarding the non-inhibition of PNMT, it is important to note that while COMT requires metal ions as cofactors, PNMT does not rely on metal ions.109 The unfavourable competition of Al–adrenaline complexes with respect to Al-hydroxide formation in the absence of a protective metal ion binding site might explain its non-sensitivity to the presence of Al(III) reported in the literature.101,102
The catecholamine pathway contains two main enzymatic regulators that ensure the correct homeostasis of the levels of these neurotransmitters: one is the previously discussed catechol-O-methyltransferase, and the second one is monoamine oxidase (MAO, Fig. 6). MAO enzymes catalyze the oxidative deamination of biological monoamines using flavin adenine dinucleotide (FAD) as cofactors, thus leading to their inactivation. Different mechanisms of action (at least four) have been proposed for MAO catalytic activity, although the exact one is still not well understood.110 Interestingly, while Al(III) inhibits COMT, some authors reported, by means of kinetic studies in rat brain, that this metal is instead able to increase the activity of MAO, in particular the B isotype.111,112 Hyperactivation of monoamine oxidase enzymatic activity is one of the hallmarks of both Alzheimer's113 and Parkinson's114 diseases. However, it is hard to hypothesize what could be the role of aluminum in the overactivation of MAO, considering the lack of a clear reaction mechanism.
So far we have discussed the role that aluminum might have with respect to the enzymatic machineries acting on the catecholamine pathway. However, there are many low-molecular-mass organic cofactors that are pivotal for the correct behavior of these enzymes and therefore could be important targets of this metal (Fig. 6).
In this sense, there is evidence that aluminum affects the metabolism of tetrahydrobiopterin (THB).115–118 THB is an essential cofactor employed by many enzymes, including tyrosine hydroxylase. Impaired THB metabolism by aluminum has been related in particular to dialysis dementia.116 One hypothesis that has been made is that Al(III) might interfere with the activity of dihydrobiopterin reductase,118 an enzyme that employs the nicotinamide adenine dinucleotide phosphate (NADPH) cofactor to catalyze the production of tetrahydrobiopterin from dihydrobiopterin. However, such an hypothesis was not further investigated. Quite interestingly, computational studies proved the ability of Al(III) to alter the conformation of NADH,18 a cofactor closely related to NADPH. Although still unclear, Al(III) interference with THB metabolism might be another possibility to explain the metal-induced inhibition of TH.
Vitamin C, also known as ascorbic acid, is an essential vitamin required as a cofactor by DBH for the conversion of dopamine into noradrenaline (Fig. 6). Perturbation of vitamin C metabolism in the brain has been related to the occurrence of severe neurodegenerative diseases.119 Moreover, several studies highlight the chelation properties of vitamin C and its interaction with aluminum has been investigated.120–123 In this sense, the structure and binding mode of the Al-ascorbate complexes in solution have been unveiled and clarified by means of both experimental and DFT computations.123 Therefore, vitamin C might be a potential Al(III) target, and the resulting complex might be involved in the impairment of DHB activity (Fig. 6).
Conclusions
We have investigated the possible formation of complexes between aluminum and an important class of catecholamine-based neurotransmitters: L-DOPA, dopamine, noradrenaline (norepinephrine) and adrenaline (epinephrine). Chemical bond analyses confirmed the main ionic nature of the Al–O interactions, but with a significant degree of covalent character. Then, we have determined that aluminum can clearly displace the protons of the hydroxyl groups of the catechol moiety forming stable aluminum–catecholamine complexes. However, in solution, the estimated binding affinities are lower than the formation energies of aluminum-hydroxide, and much lower than the Al(III) affinities of other ligands such as citrate, deferiprone and EDTA. According to these results, we can rule out the hypothesis that the formation of aluminum–catecholamine complexes, in an open biological environment, might be behind the detrimental role attributed to this metal within the catecholamine biosynthesis pathway. Other possible mechanisms are discussed; aluminum could interfere/compete with the homeostasis of other metal ions required as cofactors of enzymes involved in the catecholamine route. Moreover, it could bind within the active site of these metal-dependent enzymes, where the presence of a protective metal-ion binding site, like in the case of COMT, would provide the necessary conditions for the formation of strong aluminum–catecholamine complexes. Finally, it could also bind to other organic cofactors such as vitamin C and it could interfere with the upstream metabolic routes of other cofactors (THB). Again, it is worth emphasizing that little-to-nothing is known about the molecular basis of aluminum's behavior in these biochemical pathways; therefore, much more basic knowledge in this sense must be gained in future, and the present paper encourages further theoretical and experimental studies.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors would like to thank the technical and human support provided by the SGI/IZO (SGIker) of the UPV/EHU. Financial support comes from the European Commission, Horizon 2020 Research and Innovation Programme (grant agreement number 642294 TCCM). Additional financial support comes from the European Union (FEDER funds POCI/01/0145/FEDER/007728) and National Funds (Fundação para a Ciência e Tecnologia and Ministério da Educação e Ciência FCT/MEC) UID/MULTI/04378/2013, under the Partnership Agreement PT2020; NORTE-01-0145-FEDER-000024, supported by Norte Portugal Regional Operational Programme (NORTE 2020), under the PORTUGAL 2020 Partnership Agreement, through the European Regional Development Fund (ERDF).References
- C. Exley, Front. Neurol., 2014, 5, 1–6 CrossRef PubMed.
- C. C. Willhite, N. A. Karyakina, R. A. Yokel, N. Yenugadhati, T. M. Wisniewski, I. M. F. Arnold, F. Momoli and D. Krewski, Crit. Rev. Toxicol., 2014, 44, 1–80 CrossRef CAS PubMed.
- M. Kawahara and M. Kato-Negishi, Int. J. Alzheimers Dis., 2011, 2011, 276393 Search PubMed.
- C. Exley, Coord. Chem. Rev., 2012, 256, 2142–2146 CrossRef CAS.
- V. B. Gupta, S. Anitha, M. L. Hegde, L. Zecca, R. M. Garruto, R. Ravid, S. K. Shankar, R. Stein, P. Shanmugavelu and K. S. Jagannatha Rao, Cell. Mol. Life Sci., 2005, 62, 143–158 CrossRef CAS PubMed.
- L. Tomljenovic, J. Alzheimers Dis., 2011, 23, 567–598 CAS.
- C. Exley, Free Radicals Biol. Med., 2004, 36, 380–387 CrossRef CAS PubMed.
- J. I. Mujika, F. Ruipérez, I. Infante, J. M. Ugalde, C. Exley and X. Lopez, J. Phys. Chem. A, 2011, 115, 6717–6723 CrossRef CAS PubMed.
- F. Ruipérez, J. I. Mujika, J. M. Ugalde, C. Exley and X. Lopez, J. Inorg. Biochem., 2012, 117, 118–123 CrossRef PubMed.
- C. Exley, N. C. Price and J. D. Birchall, J. Inorg. Biochem., 1994, 54, 297–304 CrossRef CAS PubMed.
- P. Zatta, E. Lain and C. Cagnolini, Eur. J. Biochem., 2000, 267, 3049–3055 CrossRef CAS PubMed.
- S. J. Yang, J. W. Huh, J. E. Lee, S. Y. Choi, T. U. Kim and S. W. Cho, Cell. Mol. Life Sci., 2003, 60, 2538–2546 CrossRef CAS PubMed.
- J. I. Mujika, J. M. Ugalde and X. Lopez, J. Phys. Chem. B, 2014, 118, 6680–6686 CrossRef CAS PubMed.
- J. Lemire, C. Auger, R. Mailloux and V. D. Appanna, J. Neurosci. Res., 2014, 92, 464–475 CrossRef CAS PubMed.
- J. Lemire, R. Mailloux, S. Puiseux-Dao and V. D. Appanna, J. Neurosci. Res., 2009, 87, 1474–1483 CrossRef CAS PubMed.
- R. J. Mailloux, R. Hamel and V. D. Appanna, J. Biochem. Mol. Toxicol., 2006, 20, 198–208 CrossRef CAS PubMed.
- J. I. Mujika, E. Rezabal, J. M. Mercero, F. Ruipérez, D. Costa, J. M. Ugalde and X. Lopez, Comput. Struct. Biotechnol. J., 2014, 9, e201403002 CrossRef PubMed.
- E. Formoso, J. I. Mujika, S. J. Grabowski and X. Lopez, J. Inorg. Biochem., 2015, 152, 139–146 CrossRef CAS PubMed.
- R. A. Yokel, J. Alzheimers Dis., 2006, 10, 223–253 Search PubMed.
- V. Kumar and K. D. Gill, Arch. Toxicol., 2009, 83, 965–978 CrossRef CAS PubMed.
- I. Klatzo, H. Wisniewski and E. Streicher, J. Neuropathol. Exp. Neurol., 1965, 24, 187–199 CrossRef CAS PubMed.
- T. Kiss, K. Gajda-Schrantz and P. F. Zatta, Neurodegenerative Diseases and Metal Ions, John Wiley & Sons, Ltd, 2006, ch. 13, pp. 371–393 Search PubMed.
- R. Grande-Aztatzi, J. M. Mercero and J. M. Ugalde, Phys. Chem. Chem. Phys., 2016, 18, 11879–11884 RSC.
- M. Abdel-ghany, A. Khalek and D. Shalloway, J. Biol. Chem., 1993, 268, 11976–11981 CAS.
- J. I. Mujika, J. Rodríguez-Guerra, X. Lopez, J. M. Ugalde, L. Rodríguez-Santiago, M. Sodupe and J.-D. Maréchal, Chem. Sci., 2017, 8, 5041–5049 RSC.
- D. Drago, M. Bettella, S. Bolognin, L. Cendron, J. Scancar, R. Milacic, F. Ricchelli, A. Casini, L. Messori, G. Tognon and P. Zatta, Int. J. Biochem. Cell Biol., 2008, 40, 731–746 CrossRef CAS PubMed.
- C. Exley, J. Alzheimers Dis. Rep., 2017, 1, 23–25 Search PubMed.
- A. E. Martell, R. D. Hancock, R. M. Smith and R. J. Motekaitis, Coord. Chem. Rev., 1996, 149, 311–328 CrossRef CAS.
- T. Kaur, R. K. Bijarnia and B. Nehru, Drug Chem. Toxicol., 2009, 32, 215–221 CrossRef CAS PubMed.
- T. Kiss, I. Sovago and R. B. Martin, J. Am. Chem. Soc., 1989, 111, 3611–3614 CrossRef CAS.
- T. Kiss, Arch. Gerontol. Geriatr., 1995, 21, 99–112 CrossRef CAS PubMed.
- R. B. Martin, Acc. Chem. Res., 1994, 27, 204–210 CrossRef CAS.
- A. C. Miu and O. Benga, J. Alzheimers Dis., 2006, 10, 179–201 CAS.
- A. J. Cross, T. J. Crow, E. K. Perry, R. H. Perry, G. Blessed and B. E. Tomlinson, Br. Med. J. (Clin. Res. Ed.), 1981, 282, 93–94 CrossRef CAS.
- R. A. Yokel, Coord. Chem. Rev., 2002, 228, 97–113 CrossRef CAS.
- V. M. Nurchi, T. Pivetta, J. I. Lachowicz and G. Crisponi, J. Inorg. Biochem., 2009, 103, 227–236 CrossRef CAS PubMed.
- G. Crisponi, V. M. Nurchi, V. Bertolasi, M. Remelli and G. Faa, Coord. Chem. Rev., 2012, 256, 89–104 CrossRef CAS.
- G. Dalla Torre, J. I. Mujika, E. Formoso, E. Matito, M. J. Ramos and X. Lopez, Dalton Trans., 2018, 47, 9592–9607 RSC.
- J. I. Mujika, J. M. Ugalde and X. Lopez, Phys. Chem. Chem. Phys., 2012, 14, 12465–12475 RSC.
- P. Rubini, A. Lakatos, D. Champmartin and T. Kiss, Coord. Chem. Rev., 2002, 228, 137–152 CrossRef CAS.
- R. Milacic, S. Murko and J. Scancar, J. Inorg. Biochem., 2009, 103, 1504–1513 CrossRef CAS PubMed.
- G. Crisponi and M. Remelli, Coord. Chem. Rev., 2008, 252, 1225–1240 CrossRef CAS.
- G. Crisponi, V. M. Nurchi, J. I. Lachowicz, M. Crespo-Alonso, M. A. Zoroddu and M. Peana, Coord. Chem. Rev., 2015, 284, 278–285 CrossRef CAS.
- A. Fulgenzi, D. Vietti and M. E. Ferrero, BioMed. Res. Int., 2014, 2014, 758323 Search PubMed.
- T. Kiss, J. Inorg. Biochem., 2013, 128, 156–163 CrossRef CAS PubMed.
- J. R. Pliego and J. M. Riveros, J. Phys. Chem. A, 2001, 105, 7241–7247 CrossRef CAS.
- D. Riccardi, H. B. Guo, J. M. Parks, B. Gu, L. Liang and J. C. Smith, J. Chem. Theory Comput., 2013, 9, 555–569 CrossRef CAS PubMed.
- J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3093 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian16 Revision A.03 Search PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648 CrossRef CAS.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- E. R. Johnson and A. D. Becke, J. Chem. Phys., 2005, 123, 174104 CrossRef PubMed.
- L. Goerigk, H. Kruse and S. Grimme, ChemPhysChem, 2011, 12, 3421–3433 CrossRef CAS PubMed.
- R. Sedlak, T. Janowski, M. Pitonak, J. Rezac, P. Pulay and P. Hobza, J. Chem. Theory Comput., 2013, 9, 3364–3374 CrossRef CAS PubMed.
- S. Grimme, A. Hansen, J. G. Brandenburg and C. Bannwarth, Chem. Rev., 2016, 116, 5105–5154 CrossRef CAS PubMed.
- J. H. Jensen, Phys. Chem. Chem. Phys., 2015, 17, 12441–12451 RSC.
- J. Ho, Phys. Chem. Chem. Phys., 2015, 17, 2859–2868 RSC.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396 CrossRef CAS PubMed.
- J. Alí-Torres, L. Rodríguez-Santiago and M. Sodupe, Phys. Chem. Chem. Phys., 2011, 13, 7852–7861 RSC.
- M. W. Palascak and G. C. Shields, J. Phys. Chem. A, 2004, 108, 3692–3694 CrossRef CAS.
- L. Alderighi, P. Gans, A. Ienco, D. Peters, A. Sabatini and A. Vacca, Coord. Chem. Rev., 1999, 184, 311–318 CrossRef CAS.
- R. F. W. Bader, Atoms in Molecules: A Quantum Theory, Oxford Univ. Press, Oxford, 1990 Search PubMed.
- B. Silvi and C. Gatti, J. Phys. Chem. A, 2000, 104, 947–953 CrossRef CAS.
- G. Gervasio, R. Bianchi and D. Marabello, Chem. Phys. Lett., 2004, 387, 481–484 CrossRef CAS.
- E. Matito, J. Poater, F. M. Bickelhaupt and M. Solà, J. Phys. Chem. B, 2006, 110, 7189–7198 CrossRef CAS PubMed.
- S. J. Grabowski, Chem. Rev., 2011, 111, 2597–2625 CrossRef CAS PubMed.
- R. F. W. Bader and M. E. Stephens, J. Am. Chem. Soc., 1975, 97, 7391–7399 CrossRef CAS.
- X. Fradera, M. A. Austen and R. F. W. Bader, J. Phys. Chem. A, 1999, 103, 304–314 CrossRef CAS.
- K. Ruedenberg, Rev. Mod. Phys., 1962, 34, 326–376 CrossRef CAS.
- E. Matito, M. Solà, P. Salvador and M. Duran, Faraday Discuss., 2007, 135, 325–345 RSC.
- T. A. Keith, AIMAll (Version 14.11.23), 2014 Search PubMed.
- L. Zhao, M. von Hopffgarten, D. M. Andrada and G. Frenking, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, 1–37 Search PubMed.
- T. Ziegler and A. Rauk, Theor. Chim. Acta, 1977, 46, 1–10 CrossRef CAS.
- K. Kitaura and K. Morokuma, Int. J. Quantum Chem., 1976, 10, 325–340 CrossRef CAS.
- G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. Fonseca Guerra, S. J. A. van Gisbergen, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931–967 CrossRef CAS.
- C. Fonseca Guerra, J. G. Snijders, G. Te Velde and E. J. Baerends, Theor. Chem. Acc., 1998, 99, 391–403 Search PubMed.
- E. J. Baerends, T. Ziegler, A. J. Atkins, J. Autschbach, D. Bashford, O. Baseggio, A. Bérces, F. M. Bickelhaupt, C. Bo, P. M. Boerritger, L. Cavallo, C. Daul, D. P. Chong, D. V. Chulhai, L. Deng, R. M. Dickson, J. M. Dieterich, D. E. Ellis, M. van Faassen, A. Ghysels, A. Giammona, S. J. A. van Gisbergen, A. Goez, A. W. Götz, S. Gusarov, F. E. Harris, P. van den Hoek, Z. Hu, C. R. Jacob, H. Jacobsen, L. Jensen, L. Joubert, J. W. Kaminski, G. van Kessel, C. König, F. Kootstra, A. Kovalenko, M. Krykunov, E. van Lenthe, D. A. McCormack, A. Michalak, M. Mitoraj, S. M. Morton, J. Neugebauer, V. P. Nicu, L. Noodleman, V. P. Osinga, S. Patchkovskii, M. Pavanello, C. A. Peeples, P. H. T. Philipsen, D. Post, C. C. Pye, H. Ramanantoanina, P. Ramos, W. Ravenek, J. I. Rodríguez, P. Ros, R. Rüger, P. R. T. Schipper, D. Schlüns, H. van Schoot, G. Schreckenbach, J. S. Seldenthuis, M. Seth, J. G. Snijders, M. Solà, S. M. M. Swart, D. Swerhone, G. te Velde, V. Tognetti, P. Vernooijs, L. Versluis, L. Visscher, O. Visser, F. Wang, T. A. Wesolowski, E. M. van Wezenbeek, G. Wiesenekker, S. K. Wolff, T. K. Woo and A. L. Yakovlev, ADF2017, SCM, Theoretical Chemistry, Vrije Universiteit, Amsterdam, The Netherlands, https://www.scm.com Search PubMed.
- R. C. Raffenetti, J. Chem. Phys., 1973, 59, 5936 CrossRef CAS.
- D. P. Chong, E. van Lenthe, S. Van Gisbergen and E. J. Baerends, J. Comput. Chem., 2004, 25, 1030–1036 CrossRef CAS PubMed.
- T. Kiss, I. Sovago and R. Martin, J. Inorg. Biochem., 1989, 36, 348 CrossRef.
- Y. Zhao and D. G. Truhlar, J. Chem. Theory Comput., 2007, 3, 289–300 CrossRef CAS PubMed.
- J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC.
- C. Moller and M. S. Plesset, Phys. Rev., 1934, 46, 618–622 CrossRef CAS.
- M. Head-Gordon, J. A. Pople and M. J. Frisch, Chem. Phys. Lett., 1988, 153, 503–506 CrossRef CAS.
- J. I. Mujika, G. Dalla Torre, E. Formoso, R. Grande-Aztatzi, S. J. Grabowski, C. Exley and X. Lopez, J. Inorg. Biochem., 2018, 181, 111–116 CrossRef CAS PubMed.
- C. Bazzicalupi, A. Bianchi, C. Giorgi, M. P. Clares and E. García-España, Coord. Chem. Rev., 2012, 256, 13–27 CrossRef CAS.
- R. G. Pearson, J. Am. Chem. Soc., 1963, 85, 3533–3539 CrossRef CAS.
- D. J. Clevette, W. O. Nelson, A. Nordin, C. Orvig and S. Sjoeberg, Inorg. Chem., 1989, 28, 2079–2081 CrossRef CAS.
- W. R. Harris, K. N. Raymond and F. L. Weitl, J. Am. Chem. Soc., 1981, 103, 2667–2675 CrossRef CAS.
- V. M. Nurchi, G. Crisponi, T. Pivetta, M. Donatoni and M. Remelli, J. Inorg. Biochem., 2008, 102, 684–692 CrossRef CAS PubMed.
- T. Flatmark, Acta Physiol. Scand., 2000, 168, 1–17 CrossRef CAS PubMed.
- M. A. Kurian, P. Gissen, M. Smith, S. J. R. Heales and P. T. Clayton, Lancet Neurol., 2011, 10, 721–733 CrossRef CAS PubMed.
- G. Eisenhofer, Pharmacol. Rev., 2004, 56, 331–349 CrossRef CAS PubMed.
- D. Purves, Neuroscience, Sinauer Associates, Sunderland, Mass, 2012 Search PubMed.
- M. Milanese, M. I. Lkhayat and P. Zatta, J. Trace Elem. Med. Biol., 2001, 15, 139–141 CrossRef CAS.
- J. R. Hofstetter, I. Vincent, O. Bugiani, B. Ghetti and J. A. Richter, Neurochem. Pathol., 1987, 6, 177–193 CrossRef CAS PubMed.
- H. Erazi, S. Ahboucha and H. Gamrani, Neurosci. Lett., 2011, 487, 8–11 CrossRef CAS PubMed.
- G. L. Wenk and K. L. Stemmer, Neurotoxicology, 1981, 2, 347–353 CAS.
- A. A. Moshtaghie, P. Malekpouri, M. Moshtaghie, M. Mohammadi-nejad and M. Ani, Neurol. Sci., 2013, 34, 1639–1650 CrossRef PubMed.
- P. Zatta and A. C. Alfrey, Aluminium Toxicity in Infants’ Health and Disease, World Scientific, 1998 Search PubMed.
- L. Mason and C. Weinkove, Ann. Clin. Biochem., 1983, 20, 105–111 CrossRef CAS PubMed.
- F. Ruipérez, J. I. Mujika, J. M. Ugalde, C. Exley and X. Lopez, J. Inorg. Biochem., 2012, 117, 118–123 CrossRef PubMed.
- W. R. Harris and L. Messori, Coord. Chem. Rev., 2002, 228, 237–262 CrossRef CAS.
- J. I. Mujika, X. Lopez, E. Rezabal, R. Castillo, S. Marti, V. Moliner and J. M. Ugalde, J. Inorg. Biochem., 2011, 105, 1446–1456 CrossRef CAS PubMed.
- J. I. Mujika, B. Escribano, E. Akhmatskaya, J. M. Ugalde and X. Lopez, Biochemistry, 2012, 51, 7017–7027 CrossRef CAS PubMed.
- R. A. Yokel and P. J. McNamara, Pharmacol. Toxicol., 2001, 88, 159–167 CrossRef CAS.
- M. Sparta and A. N. Alexandrova, PLoS One, 2012, 7, e47172 CrossRef CAS PubMed.
- P. Georgieva, Q. Wu, M. J. McLeish and F. Himo, Biochim. Biophys. Acta, 2009, 1794, 1831–1837 CrossRef CAS PubMed.
- H. Gaweska and P. F. Fitzpatrick, Biomol. Concepts, 2011, 2, 365–377 CAS.
- J.-W. Huh, M.-M. Choi, J. H. Lee, S.-J. Yang, M. J. Kim, J. Choi, K. H. Lee, J. E. Lee and S.-W. Cho, J. Inorg. Biochem., 2005, 99, 2088–2091 CrossRef CAS PubMed.
- P. Zatta, P. Zambenedetti and M. Milanese, NeuroReport, 1999, 10, 3645–3648 CrossRef CAS PubMed.
- S. Schedin-Weiss, M. Inoue, L. Hromadkova, Y. Teranishi, N. G. Yamamoto, B. Wiehager, N. Bogdanovic, B. Winblad, A. Sandebring-Matton, S. Frykman and L. O. Tjernberg, Alzheimers Res. Ther., 2017, 9, 1–19 CrossRef PubMed.
- P. Riederer and G. Laux, Exp. Neurobiol., 2011, 20, 1 CrossRef PubMed.
- J. D. Cowburn and J. A. Blair, Lancet, 1987, 2, 105 CrossRef CAS.
- I. Bone and M. Thomas, Lancet, 1979, 1, 782 CrossRef CAS.
- C. Exley, Aluminium and Alzheimer's Disease, Elsevier, 2001 Search PubMed.
- R. J. Leeming and J. A. Blair, Lancet, 1979, 313, 556 CrossRef.
- J. Kocot, D. Luchowska-Kocot, M. Kiełczykowska, I. Musik and J. Kurzepa, Nutrients, 2017, 9, 659 CrossRef PubMed.
- T. P. Kruck, J. G. Cui, M. E. Percy and W. J. Lukiw, Cell. Mol. Neurobiol., 2004, 24, 443–459 CrossRef CAS PubMed.
- J. Domingo, M. Gomez, J. Llobet and C. Richart, Lancet, 1991, 338, 1467 CrossRef CAS.
- A. E. Martell, in Chelates of Ascorbic Acid, Americal Chemical Society, 1982, vol. 200, ch. 7, pp. 153–178 Search PubMed.
- D. Cesario, E. Furia, G. Mazzone, A. Beneduci, G. De Luca and E. Sicilia, J. Phys. Chem. A, 2017, 121, 9773–9781 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8dt04216k |
| This journal is © The Royal Society of Chemistry 2019 |