Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Neptunium(IV)-hydroxamate complexes: their speciation, and kinetics and mechanism of hydrolysis
S.
Edwards
a,
F.
Andrieux
a,
C.
Boxall
 *a,
M. J.
Sarsfield
b,
R. J.
Taylor
b and
D.
Woodhead
b
*a,
M. J.
Sarsfield
b,
R. J.
Taylor
b and
D.
Woodhead
b
aEngineering Department, Lancaster University, Lancaster, Lancashire LA1 4YW, UK. E-mail: c.boxall@lancaster.ac.uk
bNational Nuclear Laboratory, Central Laboratory, Sellafield, Cumbria CA20 1PG, UK
First published on 3rd December 2018
Abstract
Simple hydroxamic acids such as acteohydroxamic acid (AHA) have been identified as suitable reagents for the control of Pu and Np in advanced separation processes for nuclear fuel reprocessing such as the Advanced PUREX or UREX based recycle processes, due to their ability to strip the tetravalent form of Pu and Np from tri-butyl phosphate into nitric acid. However, both free and metal bound hydroxamates are known to undergo acid catalysed hydrolysis at low pH, the kinetics of which must be characterised before implementation of PUREX/UREX based reprocessing flowsheets. In support of this implementation, a comprehensive thermodynamic and kinetic model that describes both the complex speciation and hydrolysis of AHA in the presence of Np(IV) has been developed. The model has two unique features: (i) in the case of the hydrolysis reaction kinetics, the model includes the hydrolysis of not only free AHA but also both the mono- and bishydroxamato-Np(IV) complexes; (ii) for the associated speciation calculations, the model explicitly includes the ionic strength dependence of not only the mono- and bishydroxamato-Np(IV) complexes but also the mono- and bisnitrato neptunium(IV) and monohydroxoneptunium(IV) complexes. For the latter three species, respective SIT coefficients of Δε1,NO3 = −0.13 ± 0.03 kg mol−1,  , Δε2,NO3 = −0.37 ± 0.13 kg mol−1,
, Δε2,NO3 = −0.37 ± 0.13 kg mol−1,  Δε1,OH = −0.36 kg mol−1 and log10
Δε1,OH = −0.36 kg mol−1 and log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K01,OH = −1.23 were also determined. Using experimental data from a series of kinetic studies on the Np(IV)–AHA system, this model has been used to determine the rate constants for hydrolysis of mono– and bis–acetohydroxamatoneptunium(IV) at 25 °C for the first time. These were found to be 3.5 × 10−5 ± 2.5 × 10−5 dm3 mol−1 s−1 and 1.9 × 10−3 ± 1.3 × 10−3 dm3 mol−1 s−1, respectively. Comparison of these values with the rate constants for hydrolysis of free AHA indicates that complexation of AHA with Np(IV) increases the rate of hydroxamate hydrolysis – an observation that we attribute to the electron withdrawing effect of the metal centre within the Np(IV)–AHA complex increasing the susceptibility of the AHA carbonyl carbon to nucleophilic attack, the accepted first step in its mechanism of hydrolysis.
K01,OH = −1.23 were also determined. Using experimental data from a series of kinetic studies on the Np(IV)–AHA system, this model has been used to determine the rate constants for hydrolysis of mono– and bis–acetohydroxamatoneptunium(IV) at 25 °C for the first time. These were found to be 3.5 × 10−5 ± 2.5 × 10−5 dm3 mol−1 s−1 and 1.9 × 10−3 ± 1.3 × 10−3 dm3 mol−1 s−1, respectively. Comparison of these values with the rate constants for hydrolysis of free AHA indicates that complexation of AHA with Np(IV) increases the rate of hydroxamate hydrolysis – an observation that we attribute to the electron withdrawing effect of the metal centre within the Np(IV)–AHA complex increasing the susceptibility of the AHA carbonyl carbon to nucleophilic attack, the accepted first step in its mechanism of hydrolysis.
Introduction
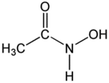
Neptunium-237, formed during the irradiation of uranium-235 based fuels in thermal nuclear reactors, is found in waste streams of the industrial PUREX (Plutonium URanium EXtraction) process that is currently used to reprocess such fuels.1 Typically, ca. 60% of neptunium is co-extracted with uranium and plutonium in the first extraction stage of the PUREX process with the remainder routed to the highly active waste stream. Control of neptunium thus adds significantly to complexity and waste volumes of PUREX reprocessing.2 Np-237 can also be a useful resource, as target material for Pu-238 production for use as a power source in space missions.Simple hydroxamic acids (XHAs) such as formo- and aceto-hydroxamic acids (FHA and AHA, example structure in Scheme 1), are salt-free, hydrophilic organic compounds, which act as bidentate O,O donor ligands with affinities for ‘hard’ cations such as Fe3+, Np4+ and Pu4+ with which they form 5-membered chelate rings.3–6 They have been used as enzyme inhibitors,7 soil enhancers,8 antimicrobials,9 DNA cleavers,10 spectrophotometric reagents for the determination of metal ions11 as well as in drug delivery systems12 and ion exchange applications.13 In the environment, hydroxamates are used by fungi in the sequestration of iron from soil.14–18
These ligands are also redox active capable of rapidly reducing Np(VI) to Np(V)19,20 and we have observed the slow reduction of Pu(IV) ions by FHA and AHA.21,22 Their ability to efficiently strip tetravalent actinides from the PUREX solvent (30% tributyl phosphate in odourless kerosene – TBP/OK), however, is due to the strong hydrophilic complexes formed.23,24 Consequently, these simple reagents have been identified for use in advanced nuclear fuel cycles based on e.g. Advanced PUREX or UREX reprocessing, wherein recycling of neptunium and other minor actinides for transmutation or as fuel has been suggested.25
FHA and AHA are known to undergo acid catalysed hydrolysis in nitric acid to form hydroxylamine and the parent carboxylic acid, XCOOH, in accordance with:22,26
The hydrolysis of free hydroxamates in acidic solution is well characterized, their kinetics obeying the Arrhenius relationship given below27 where for FHA and AHA, respectively, A, the pre-exponential factor, is 9.09 × 109 and 3.22 × 109 dm3 mol−1 s−1 and EA, the activation energy, is 77.3 and 79.9 kJ mol−1.
 | (1) |
Hydrolysis of metal bound hydroxamates occurs at different rates, which may impact negatively on an Advanced PUREX process by decomposing the ligand during the process, so diminishing achievable separation factors. Previous work has shown that at 25 °C hydrolysis of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 iron(III)–AHA and 1
1 iron(III)–AHA and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 Np(IV)–FHA complexes occurs with second order rate parameters of 5.0 × 10–4 and 1.0 × 10–5 dm3 mol−1 s−1 respectively. Preliminary studies of the Pu(IV)–XHA system show that the 1
1 Np(IV)–FHA complexes occurs with second order rate parameters of 5.0 × 10–4 and 1.0 × 10–5 dm3 mol−1 s−1 respectively. Preliminary studies of the Pu(IV)–XHA system show that the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex is slowly reduced to free Pu(III) by hydroxylamine.21,22 An understanding of these processes is vital if they are to be controlled within the design of any Advanced PUREX and/or UREX process.
1 complex is slowly reduced to free Pu(III) by hydroxylamine.21,22 An understanding of these processes is vital if they are to be controlled within the design of any Advanced PUREX and/or UREX process.
To this end, we have used UV–visible and near-IR electronic absorption spectrophotometry to both study experimentally and model for the first time the kinetics of the hydrolysis of the Np(IV)–AHA system in nitrate media. As well as hydroxamate complexes, neptunium(IV) is known to form nitrato complexes in the presence of nitrate ions, the formation of which may influence Np(IV)–AHA complexation and thus the rate of hydrolysis of the hydroxamate. Therefore, both Np(IV)–AHA and Np(IV)–nitrate complexation needed to be incorporated into our kinetic model. However, the thermodynamic stability constants for the mono- and bis-hydroxamatoneptunium(IV) complexes are unavailable whilst the conditional stability constants are only known under one set of ionic strength conditions (specifically I = 2 mol dm−3 at 295 K)23,28 – thus requiring us to work with conditional stability and equilibrium constants throughout. Whilst the dependencies of the conditional stability constants on ionic strength for the Np(IV)–AHA complexes are unavailable, a review of available literature data has allowed us to derive such dependencies for the nitrato neptunium(IV) complexes using Specific ion Interaction Theory (SIT theory).29 Such an approach was also used by Lemire et al. in their critical review and analysis of log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β data for, inter alia, Np(IV)–F−, Np(IV)–NO3−, Np(VI)–CO32−, Pu(IV)–Cl− and Pu(IV)–NO3− complexes.30 For consistency, we have employed the same approach here. Therefore, our kinetic model includes not only the Np(NO3)3+ and Np(NO3)22+ complexes but also, again for the first time, the effect of ionic strength on the concentrations of these complexes.
β data for, inter alia, Np(IV)–F−, Np(IV)–NO3−, Np(VI)–CO32−, Pu(IV)–Cl− and Pu(IV)–NO3− complexes.30 For consistency, we have employed the same approach here. Therefore, our kinetic model includes not only the Np(NO3)3+ and Np(NO3)22+ complexes but also, again for the first time, the effect of ionic strength on the concentrations of these complexes.
Thus, in this paper, we have built a numerical model in the process modelling software, gPROMS, to determine rates of hydrolysis of the mono- and bis-hydroxamatoneptunium(IV) complexes. We have included ionic strength dependent concentrations of NpNO33+ and Np(NO3)22+ using SIT theory.
Experimental
Np(IV) aqueous stock solutions were prepared as described previously.31 Specifically, neptunium stock solutions in nitric acid were prepared from dissolution of NpO2 in strong nitric acid under reflux. Concentrations of total neptunium in the resultant stock were confirmed by gamma spectroscopy, calibrated against a neptunium standard. Valence conditioning to form a Np(IV) stock was then achieved by electrochemical conditioning (−0.35 V vs. Ag/AgCl using a platinum gauze working electrode) or by addition of a substantial excess of Fe(II) (FeCl2). In the latter case, Np(IV) solution was purified from Fe and Cl ions by solvent extraction into 30% tributyl phosphate (TBP) in odourless kerosene and backwashing into HNO3. In such solutions, Np is predominantly present as Np(IV) with small amounts of Np(V), the exact proportions being dependent on factors including acidity and standing time. With Np(V), its characteristic bands at 979 nm and 1100 nm in its UV-visible, near-infra-red (near IR) electronic absorption spectrum (EAS) (ε = 369 dm3 mol−1 cm−1 and 24 dm3 mol−1 cm−1 respectively in nitric acid media32) enable sub-millimolar Np(V) concentrations to be accurately resolved by spectrophotometry. Thus, Np(V) was quantified using EAS throughout the experiments described below and, from an averaging of the concentrations calculated using the bands at both 979 nm and 1100 nm, was found to be ∼11% of total Np present. The implications of this for the speciation and kinetic run studies presented herein are considered during the discussion of Fig. 9 and 10 below.All other reagents including HNO3 (70%, AnalaR, BDH Chemicals Ltd, UK) and AHA (Sigma–Aldrich Ltd, UK) were obtained from suppliers at the highest available purity and used as received. AHA was stored at 4 °C to prevent decomposition; solutions were prepared immediately prior to use in order to prevent hydrolysis, by room temperature dissolution of a weighed portion into distilled water.
UV–visible, near IR EAS were recorded using PerkinElmer Lambda 19 or 900 spectrophotometers coupled by fibre optics to an external sample compartment for remote safe analysis of the α-active radioisotope 237Np. Both instruments had a spectral resolution/data interval of 1 nm. Note that in all figures containing neptunium spectra, the individual spectra have been offset for clearer comparison.
Solutions for the kinetic experiments of Np(IV)–AHA complex stability were prepared by mixing aliquots of Np(IV) stock, HNO3 and AHA directly into an optical cuvette of pathlength 1 cm; the complexant was added last. During the kinetic absorbance measurements, the spectrometer was set to scan the range 600–1300 nm at variable time intervals. All kinetic runs were recorded in the narrow temperature range of 297–298 K with the temperature being maintained by a water flow controlled Ocean Optics fibre optic cell holder. The temperature of the solution was checked using a thermocouple at the end of each experiment.
The main peaks of interest in the spectra reported below are those due to Np(V) at 979 and 1100 nm (vide supra) and the compound feature centred at 732 nm associated with the Np(IV)–hydroxamate complexes.4 All three peaks were corrected to account for baseline shifts between experiments. For the strong Np(V) peak at 979 nm and the weaker peak at 1100 nm, this simply involved measuring the absorbances at 979 and 1100 nm with respect to an extrapolated baseline drawn between two reference points: the absorbance values at 640 and 1050 nm where the molar absorptivities due to free Np(IV), free Np(V) and Np(IV)–AHA are near zero.
Due to the more complex nature of the feature at 732 nm, we used the same baseline correction methodology reported in an earlier communication4 and a subsequent paper by Taylor et al.23 This involved drawing a line between the absorbances at two reference points much closer to the feature maximum and measuring the absorbance at 732 nm with respect to that line. In this case, the two points used were the absorbance values at 640 nm and 775 nm.
As discussed above, the molar absorptivities of Np(IV), Np(V) and Np(IV)–AHA complexes are near zero at 640 nm and so do not change as the speciation changes between the free Np, Np–nitrate and Np–AHA species. In contrast, both the Np(IV)–HNO3 and Np(IV)–AHA systems studied here exhibit non-zero, but small, absorptivities at 775 nm. For freshly made solutions of these systems, absorptivities were found to depend principally on [HNO3]; specifically the absorbance at 775 nm, measured with respect to that at 640 nm, was found to be 0.011 ± 0.001 and 0.016 ± 0.003 at 1 and 3 mol dm−3 HNO3 respectively. This gives rise to a small uncertainty in baseline between acidities of 0.003 absorbance units at 732 nm, which translates to an average uncertainty in the baseline-subtracted peak absorbance at 732 nm of just 2.3% – justifying the use of this baseline correction for the speciation studies described later where the 732 nm peak absorbance is measured from freshly made solutions.
Consequently, and again for reasons of consistency with previous studies,4,23 the same baseline correction method was also used for the 732 nm peak absorbance during kinetic run studies of Fig. 10 below. In this instance, we compare the absorbances measured at 775 nm, again with respect to that at 650 nm, at the start and end of the runs. In this instance, the absorbance at 775 nm, measured with respect to that at 650 nm, was found to change by an average of 0.009 ± 0.012 over all kinetic runs. This gives rise to a small uncertainty in baseline from the beginning to the end of a run of 0.006 absorbance units at 732 nm, which translates to an average uncertainty in the baseline-subtracted peak absorbance at 732 nm of just 5.6% of the absorbance value at the end of each run – justifying the use of this baseline correction for the kinetic runs described later.
Two different software packages have been used to generate and model the results presented in this paper. Firstly, HySS is free software that is widely used for simulating titration curves and calculating speciation diagrams (available at http://www.hyperquad.co.uk/hyss.htm). When calculating speciation diagrams, stability constants for each species and the added reagent concentration ranges are entered into the user interface. HySS performs a mass balance on each of the reagents solving a set of linear equations written in a Fortran subroutine called by the HySS program.33 The software is capable of performing calculations for an unlimited number of reagents and equilibria, as well as when solid precipitate is present in solution. The calculated results can be copied to Microsoft Excel to plot customised diagrams, such as those presented in Fig. 5–8, vide infra.
Secondly, gPROMS (General PROcess Modelling System, Process Systems Enterprise, UK) is an industry standard software platform for creating first principles process models coupled with experimental data. It has been used to determine reaction kinetics from experimental data for a wide range of chemical processes both heterogeneous (e.g. solvent extraction,34 solid–liquid adsorption35 and crystallization36) and homogeneous (e.g. enzyme catalyzed addition reactions37). Here we employed gPROMs to determine the reaction kinetics of the homogeneous complexation/hydrolysis reactions in the Np(IV)–AHA system from speciation and kinetic run data. Rate constants were determined using the parameter estimation facility of gPROMS. This facility uses a maximum likelihood formulation to determine parameter values and performs statistical analysis on the results.38 Experimental results are imported into gPROMS in order to perform parameter estimation.
The gPROMS objective function for finding parameters is the maximum likelihood formulation39 given by the equation below. In this, N is the total number of measurements taken during all the experiments; θ is the set of model parameters to be estimated; NE is the number of experiments performed; NVi is the number of variables measured in the ith experiment; NMij is the number of measurements of the jth variable in the ith experiment; σ2ijk is the variance of the kth measurement of variable j in experiment i;  is the kth measured value of variable j in experiment I; zijk is the kth predicted value of variable j in experiment i.
is the kth measured value of variable j in experiment I; zijk is the kth predicted value of variable j in experiment i.
This objective function has the advantage of being able to determine multiple parameters simultaneously and give statistical analysis of the results. Minimisation of the maximum likelihood formulation is achieved using the MAXLKHD solver of gPROMS. Note that the fitting parameters must be given pre-determined bounds found by preliminary investigation.
Results and discussion
The dynamics of hydrolysis of the metal–AHA system in acidic media such as HNO3 and HClO4 are complicated by metal–AHA complex speciation and competitive complexation with NO3− and – potentially at some of the lower acidities employed in this study (see Fig. 9 below) – OH− anions. Thus in this section, we extend metal-hydroxamate-pH speciation diagrams from our previous paper investigating Np(IV)–FHA hydrolysis4 to include ionic strength dependent concentrations of Np(IV) mono and bisnitrato and monohydroxide complexes.Sarsfield et al. have published a model of the extraction of Np(IV)–AHA complexes into TBP.28 In this, they note that no evidence has yet been reported for Np(IV) mixed ternary complexes of AHA in the aqueous phase with either nitrate or OH− ions, even though such ternary complexes seem probable. Consequently, they ignore ternary complexes in their model and assume that all aquo-species can be modelled in terms of individual nitrate, hydroxyl, and AHA complexes of Np(IV). Here we adopt a similar approach for the same reasons.
The conditional stability constants for the formation of the Np(IV)–AHA complexes in non-complexing perchlorate media are only available at one temperature and ionic strength, 295 K and 2.0 mol kg−1.23 Similarly, conditional stability constant values for the hydroxyl complexes of Np(IV) are also only available at one temperature, 298 K, although at a slightly wider range of ionic strengths, 1 and 2 mol kg−1.30 In contrast, values are available at a range of ionic strengths for the AHA acid dissociation constant28 (required to convert the Np(IV)–AHA complex stability constants into stepwise equilibrium constants Np(IV)–AHA complex formation) and the stability constants for the formation of the Np(IV)–NO3 complexes,30 thus allowing SIT theory to be used to derive relationships describing the dependencies of these constants on ionic strength. However, none of these constants have significantly large numbers of values reported at a single temperature – values of the AHA dissociation constant are also reported over a temperature range of 295–298 K, whilst those of the Np(IV)–nitrate complex stability constants are reported at two closely placed temperatures, 293 and 298 K. So as to maximize the number of data points used in SIT analyses of the AHA dissociation constant and the mononitrato neptunium(IV) complex stability constant, Sarsfield et al.28 and Lemire et al.30 respectively use all dissociation/stability constants reported in the temperature ranges just cited. This results in SIT relationships describing the ionic strength dependencies for these constants that can be considered to apply at 295–298 K for the AHA dissociation constant and at 293–298 K for the mononitrato neptunium(IV) complex stability constant. Advantageously, these temperature ranges encompass the temperatures at which the conditional stability constants for the formation of the Np(IV)–AHA and Np(IV)–OH− complexes are reported, 295 and 298 K respectively. Accordingly, we have used these data to calculate metal-hydroxamate-nitrate-pH speciation diagrams for all binary complexes formed in the Np(IV)–AHA–HNO3 system – said diagrams explicitly accounting for the ionic strength dependent concentrations of the Np(IV) mono- and bisnitrato and monohydroxide complexes. Within the constraints of available data, these diagrams may be considered to be valid only for 295–298 K; consequently, all experimental kinetic runs reported here (Fig. 9–11, vide infra) were also recorded in this temperature range.
The metal-hydroxamate-nitrate-pH speciation diagrams presented in this paper are then calculated as follows. First, speciation diagrams are calculated for the Np(IV)–NO3 system in the absence of AHA in the temperature range 293–298 K as a function of total nitric concentration using HySS (hyperquad simulation and speciation) software package. Calculations are then extended to calculate the speciation of the Np(IV)–AHA–NO3 system at 295 K as a function of total AHA concentration expressed as pHL where pHL = −log10[AHA]. The process is described in detail in the next section.
Speciation and kinetic modelling of metal-hydroxamic acid systems
Np(IV) forms hydroxamate complexes in ratios 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 to 3
1 to 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, AHA
1, AHA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) metal.4 Conditional stability constants have been obtained at 295 K in non-complexing perchlorate media at an ionic strength, I, of 2.0 mol kg−1 for the equilibria given in eqn (2a)–(2c).23 These conditional stability constants are as follows:
metal.4 Conditional stability constants have been obtained at 295 K in non-complexing perchlorate media at an ionic strength, I, of 2.0 mol kg−1 for the equilibria given in eqn (2a)–(2c).23 These conditional stability constants are as follows: | (2a) |
 | (2b) |
 | (2c) |
where HL is AHA; L− is the deprotonated conjugate base. As discussed above, literature values for β1 to β3 are limited to those given in eqn (2a)–(2c) – meaning that the dependence on ionic strength, I, of these stability constants is currently unavailable. Also as discussed above, in contrast the ionic strength dependence of the acid dissociation constant for AHA, Ka,AHA, can be calculated using SIT Theory.35 This is of relevance as it determines the availability of L− to participate in the complex formation reactions given in eqn (2a)–(2c). Sarsfield et al. have obtained such a dependence by performing a SIT theory-based fit to literature data reported in the temperature range 295–298 K:28
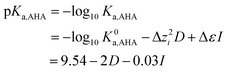 | (3a) |
 | (3b) |
 | (3c) |
 | (4a) |
 | (4b) |
 | (4c) |
For the experiments presented later, the ionic strength is predominantly determined by the concentration of nitric acid, present in vast excess. Thus, Table 1 reports values for Ka,AHA, K1, K2 and K3 at 295 K at the nitric acid concentrations of 0.5, 1 and 3 mol dm−3 used in those experiments.
| [HNO3]/mol dm−3 | pKa,AHA | K a,AHA | K 1 | K 2 | K 3 |
|---|---|---|---|---|---|
| 0.5 | 9.17 | 6.76 × 10−10 | 4570 | 9.12 | 0.0085 |
| 1 | 9.1 | 7.94 × 10−10 | 5370 | 10.71 | 0.01 |
| 3 | 8.96 | 1.1 × 10−9 | 7413 | 14.79 | 0.0138 |
Neptunium(IV) forms a range of weak inner sphere complexes with nitrate ions of which the mono- and bis-nitrato species are the most important in the HNO3 concentration range used in these experiments.41–44 These complexes, for which the stability constants β1,NO3 and β2,NO3 are given by eqn (5) and (6), would form during PUREX/UREX-based reprocessing, limiting the availability of neptunium(IV) to complex with the hydroxamate ligand. Literature values for β1,NO3 and β2,NO3 are given in logarithmic form in Tables 2 and 3 as reported in the critical review of Lemire et al.30
 | (5) |
 | (6) |
| β2,NO3 = [Np(NO3)22+]/[Np4+][NO3−]2 |
| Method | Ionic medium | Temp./K | Log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β1,NO3 β1,NO3 |
Ref. |
|---|---|---|---|---|
| Distribution, TTA | 0.5 mol dm−3 HClO4 | 293 | 0.45 | 40 |
| Distribution, TTA | 1 mol dm−3 HClO4 | 293 | 0.34 | 40 |
| Distribution, TTA | 1.5 mol dm−3 HClO4 | 293 | 0.36 | 40 |
| Distribution, TTA | 2 mol dm−3 HClO4 | 293 | 0.30 | 40 |
| Spectroscopic, Kinetic | 2 mol dm−3 HClO4 | 298 | 0.34 | 41 |
| Distribution, TTA | 4 mol dm−3 (Na,H)ClO4 | 298 | –0.15 | 42 |
| Spectroscopic | 9 mol dm−3 HClO4 | 298 | 0.9 | 43 |
| Method | Ionic Medium | Temp./K | Log10β2,NO3 | Reference |
|---|---|---|---|---|
| Distribution, TTA | 1 mol dm−3 HClO4 | 293 | 0.080 | [40] |
| Distribution, TTA | 2 mol dm−3 HClO4 | 293 | 0.18 | [40] |
| Distribution, TTA | 4 mol dm−3 (Na,H)ClO4 | 298 | –0.74 | [42] |
| Spectroscopic | 9 mol dm−3 HClO4 | 298 | 2.06 | [43] |
Furthermore, again as mentioned above, neptunium(IV) forms NpOH3+, Np(OH)22+, Np(OH)3+ and Np(OH)4 complexes. Preliminary speciation diagrams (not shown) indicate that the formation of hydroxide complexes higher than NpOH3+ is unlikely at pH < 2 and so can be neglected under the conditions used in PUREX/UREX-based reprocessing. However, the same may not be true for the HNO3 concentrations used here (0.5–3 mol dm−3 HNO3, see Table 1 and Fig. 9 below). This is in agreement with a recent paper by Yusov et al.44 that arrives at the same conclusion. Thus, of the Np(IV)–OH species studied only the NpOH3+ complex may be present in significant quantities under the conditions studied here; the equilibrium constant, K1,OH, for the formation of the monohydroxide complex by Np4+ hydrolysis is given in eqn (7).
 | (7) |

As described above, our previous speciation and kinetic modelling of the Np(IV)–FHA system only considered formation of the NpNO33+ complex using a conditional equilibrium constant determined in 4.0 mol dm−3 HClO4.4 Improving upon this, the models presented here have been extended to include the ionic strength dependence of the degree of complexation of the mono- and bis-nitrato and monohydroxide complexes.
To enable this, we have derived the dependencies on ionic strength of the stability constants for the neptunium(IV) mono- and bis-nitrato complexes by applying SIT theory to literature data. This has involved adapting the approach of eqn (3a), where for complex stability constants the term Δzi2 is now the difference in the squared charge of the complex and the complex's constituent ions, the SIT equations for  and
and  are then given by:
are then given by:
 | (8) |
 | (9) |
 and
and  are the stability constants of mono- and bis-nitrato complexes at infinite dilution, Δε1,NO3 and Δε2,NO3 are the respective ion interaction correction coefficients, and all other terms take their usual meanings. An analogous equation can be written for the ionic strength dependence of the formation of the neptunium(IV) monohydroxide complex:
are the stability constants of mono- and bis-nitrato complexes at infinite dilution, Δε1,NO3 and Δε2,NO3 are the respective ion interaction correction coefficients, and all other terms take their usual meanings. An analogous equation can be written for the ionic strength dependence of the formation of the neptunium(IV) monohydroxide complex:log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K1,OH = log10 K1,OH = log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K01,OH − IΔε1,OH −6D K01,OH − IΔε1,OH −6D | (10) |
Values of Δε and log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β0 for the Np(IV)–nitrate complexes were obtained by plotting values of (log10
β0 for the Np(IV)–nitrate complexes were obtained by plotting values of (log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βi − Δz2D), derived from the literature data of Tables 2 and 3, against ionic strength as per eqn (8) and (9); the plot gradient is equal to Δε and log10
βi − Δz2D), derived from the literature data of Tables 2 and 3, against ionic strength as per eqn (8) and (9); the plot gradient is equal to Δε and log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β0 can be obtained from its y axis intercept. Thus, Fig. 1 and 2 show plots of log10
β0 can be obtained from its y axis intercept. Thus, Fig. 1 and 2 show plots of log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β1,NO3 + 8D and log10
β1,NO3 + 8D and log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β2,NO3 + 14D vs. I for the data of Tables 2 and 3 respectively.
β2,NO3 + 14D vs. I for the data of Tables 2 and 3 respectively.
 | ||
| Fig. 1 Plot of literature values of log10(β1,NO3) + 8D vs. ionic strength for NpNO33+ complex, plotted using the data of Table 2 in the temperature range 293–298 K. | ||
 | ||
| Fig. 2 Plot of literature values of log10(β2,NO3) + 14D vs. ionic strength for Np(NO3)22+ complex, plotted using the data of Table 3 in the temperature range 293–298 K. | ||
As can be seen from Tables 2 and 3, there are comparatively little log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β data for the nitrate–neptunium(IV) complexes with data for the bis-nitrato neptunium(IV) complex being particularly sparse. Thus, as described at the beginning of section 3, so as to maximize the number of data points used in the SIT extrapolation of Fig. 2 we have used log10
β data for the nitrate–neptunium(IV) complexes with data for the bis-nitrato neptunium(IV) complex being particularly sparse. Thus, as described at the beginning of section 3, so as to maximize the number of data points used in the SIT extrapolation of Fig. 2 we have used log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β2,NO3 data recorded at 293 and 298 K, and at ionic strengths higher than those normally employed in SIT theory-based analyses – an approach also used by Lemire et al. in their analysis of log10
β2,NO3 data recorded at 293 and 298 K, and at ionic strengths higher than those normally employed in SIT theory-based analyses – an approach also used by Lemire et al. in their analysis of log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β data for nitrate and halide complexes of Np(IV) and Pu(IV).30 For consistency, we have also employed the same approach for the log10
β data for nitrate and halide complexes of Np(IV) and Pu(IV).30 For consistency, we have also employed the same approach for the log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β1,NO3 data of Fig. 1. The linear trends observed in Fig. 1 and 2 suggest that this approach is reasonable.
β1,NO3 data of Fig. 1. The linear trends observed in Fig. 1 and 2 suggest that this approach is reasonable.
The slope and intercept of the plot in Fig. 1 give values of Δε1,NO3 = −0.13 ± 0.03 kg mol−1 and  respectively in the temperature range 293–298 K. Despite the data point at an ionic strength of 4 mol kg−1 being an apparent outlier, these values are in good agreement with values of Δε1,NO3 = −0.09 ± 0.05 kg mol−1 and
respectively in the temperature range 293–298 K. Despite the data point at an ionic strength of 4 mol kg−1 being an apparent outlier, these values are in good agreement with values of Δε1,NO3 = −0.09 ± 0.05 kg mol−1 and  obtained by Lemire et al. at 298 K using data over a slightly narrower ionic strength range30 – again suggesting that the approach of Fig. 1 and 2 is reasonable. The values of Δε1,NO3 and
obtained by Lemire et al. at 298 K using data over a slightly narrower ionic strength range30 – again suggesting that the approach of Fig. 1 and 2 is reasonable. The values of Δε1,NO3 and  obtained from Fig. 1 are also consistent with analogous values for the mono-nitrato complexes of uranium(IV), for which Δε1,NO3 = −0.21 kg mol−1 and β01,NO3 = 1.4745,46 and plutonium(IV), for which Δε1,NO3 = −0.17 kg mol−1 and
obtained from Fig. 1 are also consistent with analogous values for the mono-nitrato complexes of uranium(IV), for which Δε1,NO3 = −0.21 kg mol−1 and β01,NO3 = 1.4745,46 and plutonium(IV), for which Δε1,NO3 = −0.17 kg mol−1 and  .47 From these values, it appears that
.47 From these values, it appears that  increases across the actinide series whereas Δε1,NO3 shows no visible trend.
increases across the actinide series whereas Δε1,NO3 shows no visible trend.
The slope and intercept of the plot in Fig. 2 give values of Δε2,NO3 = −0.37 ± 0.13 kg mol−1 and  respectively in the temperature range 293–298 K, which are consistent with analogous values for uranium(IV), for which Δε2,NO3 = −0.41 kg mol−1 and
respectively in the temperature range 293–298 K, which are consistent with analogous values for uranium(IV), for which Δε2,NO3 = −0.41 kg mol−1 and 
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 45 and plutonium(IV), for which Δε2,NO3 = −0.36 kg mol−1 and
45 and plutonium(IV), for which Δε2,NO3 = −0.36 kg mol−1 and 
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 47 – once again suggesting that the approach of Fig. 1 and 2 is reasonable.
47 – once again suggesting that the approach of Fig. 1 and 2 is reasonable.
Using the Δε and β0 values obtained above, log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β vs. I plots can be constructed for the mono and bisnitrato Np(IV) complexes using eqn (8) and (9), Fig. 3. Both plots in Fig. 3 have forms typical of a SIT curve: a decrease in stability constant with increasing I at low ionic strength due to the attenuation of long range electrostatic attractions, and an increase in stability constant with increasing I at high ionic strength due to the increasing dominance of non-electrostatic short range attractive interactions.29
β vs. I plots can be constructed for the mono and bisnitrato Np(IV) complexes using eqn (8) and (9), Fig. 3. Both plots in Fig. 3 have forms typical of a SIT curve: a decrease in stability constant with increasing I at low ionic strength due to the attenuation of long range electrostatic attractions, and an increase in stability constant with increasing I at high ionic strength due to the increasing dominance of non-electrostatic short range attractive interactions.29
 | ||
Fig. 3 Graph of log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β versus ionic strength for NpNO33+ and Np(NO3)22+ complexes calculated using eqn (8) & (9) in the temperature range 293–298 K. β versus ionic strength for NpNO33+ and Np(NO3)22+ complexes calculated using eqn (8) & (9) in the temperature range 293–298 K. | ||
As discussed above, of the Np(IV)–hydroxide complexes, only the monohydroxide is expected to be present under conditions studied here.44 The literature gives Np(IV) monohydroxide complex SIT coefficient values at 298 K of −0.36 kg mol−1 and −1.23 for Δε1,OH and log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K01,OH, respectively.44,48 Accordingly, Fig. 4 shows a graph of log10
K01,OH, respectively.44,48 Accordingly, Fig. 4 shows a graph of log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K1,OHvs. I from 0.10–1.0 mol kg−1 HNO3 calculated using eqn (10). The upper limit of I derives from uncertainties from ionic strength corrections in the calculation of Δε1,OH and log10
K1,OHvs. I from 0.10–1.0 mol kg−1 HNO3 calculated using eqn (10). The upper limit of I derives from uncertainties from ionic strength corrections in the calculation of Δε1,OH and log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K01,OH in the source literature – which make the use of the derived parameters at I > 1.0 mol kg−1 unreliable.48 Thus, in subsequent speciation calculations, values of K01,OH at I < 1.0 mol kg−1 are calculated as per Fig. 4; at I > 1 mol kg−1, the stability constants calculated at 1.0 mol kg−1 are used as default.
K01,OH in the source literature – which make the use of the derived parameters at I > 1.0 mol kg−1 unreliable.48 Thus, in subsequent speciation calculations, values of K01,OH at I < 1.0 mol kg−1 are calculated as per Fig. 4; at I > 1 mol kg−1, the stability constants calculated at 1.0 mol kg−1 are used as default.
 | ||
Fig. 4 Graph of log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K1,OHversus ionic strength at 298 K for the NpOH3+ complex calculated using eqn (10). K1,OHversus ionic strength at 298 K for the NpOH3+ complex calculated using eqn (10). | ||
Modelling HNO3 partial dissociation (eqn (11)) in solutions at high [HNO3] improves both speciation and kinetic model accuracy by accounting for the effect of (i) proton concentration on ligand hydrolysis rates and Np(IV) hydroxamate concentration; and (ii) free nitrate ion concentration on nitrato complex speciation and concentration.49
 | (11) |
Thus, Fig. 5 shows a speciation diagram for the Np(IV)–NO3 system as a function of total HNO3, calculated to allow for both HNO3 partial dissociation (eqn (11)) and ionic strength derived variations in stability/formation constant values for NpOH3+, NpNO33+ and Np(NO3)22+ (viaeqn (8)–(10) and Fig. 4). Two observations can be made.
 | ||
| Fig. 5 Speciation diagram of 0.0019 mol dm−3 Np(IV) in solutions of 0.10–3.0 mol dm−3 HNO3, T = 293–298 K. | ||
(i) It can be seen from Fig. 5 that under the conditions employed in the kinetic experiments described below i.e. [HNO3] > 0.50 mol dm−3, the NpOH3+ concentration is negligible compared to that of free Np4+ and the two Np(IV)–NO3 complexes, so validating our decision above to ignore the higher hydroxide complexes of Np(IV) in our speciation calculations.
(ii) Not unexpectedly, Fig. 5 shows that at [HNO3] > ∼0.30 mol dm−3, Np(IV) solution speciation is dominated by nitrate complexes. In particular, the concentration of the Np(NO3)3+ complex dominates at [HNO3] > ∼0.2 mol dm−3 and quickly rises to a maximum value at [HNO3] = ∼1 mol dm−3. The apparent abruptness of this rise is likely due to the speciation in Fig. 5 being reported not as a function of [H3O+] or [NO3−] individually, but rather as a function of increasing total [HNO3] – for which both [H3O+] and [NO3−] increase at the same time. Consequently, the equilibrium positions of the reactions given by eqn (5) (NpOH3+ formation) and eqn (7) (mono-nitrato complex formation) both move simultaneously: eqn (7) to the left and eqn (5) to the right. The combined effect of these two concurrent shifts in equilibrium with increasing [HNO3] is to synergistically increase the concentration of Np(NO3)3+ in the manner observed at [HNO3] < 1 mol dm−3.
With these two observations in mind, calculations can now be extended to include Np(IV) complexation by AHA. Accordingly, Fig. 6–8 shows speciation diagrams, calculated using the data of Table 1 and eqn (8)–(11), for the Np(IV)–AHA–HNO3 system showing Np(IV) speciation as a function of pHL at total HNO3 concentrations relevant to the kinetic experiments described below i.e. [HNO3] = 0.50, 1.0 and 3.0 mol dm−3. Whilst the hydrolysis of the Np(IV) ions to form the monohydroxide complex is explicitly included in our model viaeqn (10), it is noteworthy that NpOH3+ is negligibly near-zero in the speciation diagrams of Fig. 6–8, even at the lowest total [AHA] of 1 × 10−3 mol dm−3 (pHL = 3) and lowest total [HNO3] of 0.5 mol dm−3 used in the computation of Fig. 6. The latter is especially surprising as Fig. 5 shows that, in the absence of AHA and at the total Np(IV) concentrations of 1.93 × 10−3 mol dm−3 under discussion here, NpOH3+ is present at a concentration of <2 × 10−5 mol dm−3 in 0.5 mol dm−3 nitric acid. This suggests that Np(IV) ion hydrolysis is effectively suppressed by AHA complexation under the conditions studied here, an observation that is in agreement with the work of Sarsfield et al. on the extraction of Np(IV)–AHA complexes into TBP and who likewise conclude that hydrolysis is suppressed, except at very low AHA and HNO3 concentrations of 0.01 and 0.1 mol dm−3 respectively.28
It is widely held that hydrolysis of free hydroxamic acids and hydroxamate ligands in mono- and bishydroxamate complexes occurs via nucleophilic attack on the carbonyl carbon,43 ultimately producing carboxylic acid and hydroxylamine. Previously, we have applied this mechanism to analysis of the hydrolysis of the monoformohydroxamate–neptunium(IV) complex.4 Here we extend this approach to the hydrolysis of the acetohydroxamate ligand in the Np(IV) mono- and bisacetohydroxamate complexes for the first time. In this analysis, the newly developed speciation diagrams of Fig. 6–8 are used to define the initial concentrations of the kinetic runs analysed. This is the subject of the next section.
Kinetic studies of the Np(IV) AHA system
The equations for the hydrolysis of free AHA and hydroxamate ligands in the mono- and bis-hydroxamate-neptunium(IV) complexes at 25 °C are as follows: | (12) |
 | (13) |
 | (14) |
Given that the pKa,AHA of AHA varies from 9.54 to 8.96 for ionic strength values from 0 to 3 mol kg−1 (see Table 1 and the data of ref. 21 and 50 then under the conditions employed in the experiments described below, pH ≤ 0, I ≥ 0.5 mol kg−1), the dominant form of the free ligand will be the acid rather than the depronated conjugate base. Thus, direct hydrolysis of the free hydroxamate anion may be neglected. However, the hydrolysis of the free hydroxamic acid itself, and the associated decrease in total AHA concentration with time, must be included and this is accounted for viaeqn (12).
The hydrolysis of free AHA and bound hydroxamate both occur via a second order process in which free acid and bound hydroxamate are protonated during the rate determining step to form the reducible intermediate,4,7 yielding the following rate equations
 | (15) |
 | (16) |
 | (17) |
The main purpose of this work then, is to determine values of k1 and k2 from experimental kinetic hydrolysis data in the context of the reaction scheme of eqn (13) and (14). Parameter estimation is the process of determining a set of unknown model (fitting) parameters by optimisation of computed fits to experimental data. Here, the experimental data are a series of kinetic runs for the Np(IV)–AHA system during which the concentrations of the hydrolysing complexes were followed by UV–vis spectrophotometry, Fig. 9 and 10. The gPROMS software package contains a parameter estimation function which can then be used to compute fits for absorbance vs. time data extracted from Fig. 10 and so determine values of the chosen (model) fitting parameters.
For the spectrophotometric data of Fig. 10, the fitting parameters used were the rate constants k1 and k2, and the UV-vis extinction coefficients for the mono and bis complexes, which were unknown a priori in the first instance, the extinction coefficients of Np4+, NpNO33+, Np(NO3)22+ and NpOH3+ were determined either from the work of Yusov et al.44 or from the UV–visible, near-IR EAS of solutions of Np(IV) in AHA-free HNO3 shown in Fig. 9. The total Np concentration used in each EAS was in the range 2.2 to 3.1 mmol dm−3; the majority of this was present as Np(IV) (see Experimental section above), although the bands seen at 979 and 1100 nm in all spectra of Fig. 9 indicates the presence of some Np(V). Quantification of these bands using their molar absorptivities of 369 and 24 dm3 mol−1 cm−1 respectively32 (vide supra) indicates that the concentration of Np(V) in these experiments has a mean value of 0.3 mmol dm−3, no more than 13% of total Np and nearly an order of magnitude less than the majority constituent, Np(IV). The log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β values for the formation of the mononitrato complex of Np(V) at an ionic strength of 2 mol dm−3 is reported to be in the range −0.25 to −1.6; that for the formation of the bisnitrato complex is reported to be −1.37. Comparison of these values with log10
β values for the formation of the mononitrato complex of Np(V) at an ionic strength of 2 mol dm−3 is reported to be in the range −0.25 to −1.6; that for the formation of the bisnitrato complex is reported to be −1.37. Comparison of these values with log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β values, calculated in Fig. 3, of +0.21 and −0.21 for the formation of mono and bisnitrato complexes of Np(IV) at an ionic strength of 2 mol dm−3 indicates that, thermodynamically, formation of the mononitrato neptunium(IV) complex is at least 3 and potentially 70 times more likely than formation of the mononitrato neptunium(V) complex; formation of the bisnitrato neptunium(IV) complex is similarly 15 times more likely than that of the bisnitrato neptunium(V) complex. Given that the concentration of Np(IV) in the experiments of Fig. 9 is nearly 10 times that of Np(V), these figures indicate that the concentration of the mononitrato neptunium(V) complex is at most 3.3% that of the mononitrato neptunium(IV) complex in these systems, whilst that of the bisnitrato neptunium(V) complex is <0.7% that of the bisnitrato neptunium(IV) species. It is, therefore, reasonable to conclude that the experiments of Fig. 9 are dominated by the speciation of the Np(IV)–nitrate complexes and that, once the total Np(IV) concentration in each experiment has been corrected for the total Np(V) concentration, the effect of Np(V) can be ignored.
β values, calculated in Fig. 3, of +0.21 and −0.21 for the formation of mono and bisnitrato complexes of Np(IV) at an ionic strength of 2 mol dm−3 indicates that, thermodynamically, formation of the mononitrato neptunium(IV) complex is at least 3 and potentially 70 times more likely than formation of the mononitrato neptunium(V) complex; formation of the bisnitrato neptunium(IV) complex is similarly 15 times more likely than that of the bisnitrato neptunium(V) complex. Given that the concentration of Np(IV) in the experiments of Fig. 9 is nearly 10 times that of Np(V), these figures indicate that the concentration of the mononitrato neptunium(V) complex is at most 3.3% that of the mononitrato neptunium(IV) complex in these systems, whilst that of the bisnitrato neptunium(V) complex is <0.7% that of the bisnitrato neptunium(IV) species. It is, therefore, reasonable to conclude that the experiments of Fig. 9 are dominated by the speciation of the Np(IV)–nitrate complexes and that, once the total Np(IV) concentration in each experiment has been corrected for the total Np(V) concentration, the effect of Np(V) can be ignored.
Thus, Fig. 9 shows the spectra of 1.9 and 2.6 mmol dm−3 solutions of Np(IV) in 1.0 mol dm−3 and 3.0 mol dm−3 HNO3 in the presence of an effectively silent ∼0.3 mmol dm−3 of Np(V). For each of the spectra of Fig. 9, the concentrations of Np4+, NpNO33+ and Np(NO3)22+ for each solution were calculated using SIT theory-based speciation diagrams of the type shown in Fig. 5. Using Beer's law, these concentrations were then equated to the background-corrected absorbance (see section 2) at 732 nm by the unknown extinction coefficients for NpNO33+ and Np(NO3)22+ and a value for the extinction coefficient of Np4+ at 732 nm of 31 dm3 mol−1 cm−1 – the latter value obtained from data reported by Yusov et al.44
From Fig. 5, it can be seen that there are insignificant quantities of NpOH3+ in solution under the acid conditions used in the experiments of Fig. 9 and 10 below; therefore, we took the view that this species does not require fitting in the remainder of the work described here. The resultant simultaneous equations for the absorbances at 732 nm of NpNO33+ and Np(NO3)22+ were then solved using Microsoft equation solver, yielding extinction coefficient values of 55.1 and 24.5 dm3 mol−1 cm−1, respectively.
Kinetic hydrolysis experiments were then conducted on the Np(IV)–AHA system as a function of HNO3 concentration at fixed AHA concentration and as a function of AHA concentration at fixed HNO3 concentration, results shown in Fig. 10 which itself is a summary of a much larger data set.
Whilst the focus of these experiments is the hydrolysis kinetics of the Np(IV)–AHA system, the spectra of Fig. 10 exhibit similar absorption bands at 979 and 1100 nm to those seen in Fig. 9, indicating the presence of Np(V). Analysis of these band at t = 0 as per Fig. 9 indicates that this again corresponds to initial concentrations of Np(V) in the range 0.26 to 0.3 mmol dm−3i.e. 12% of total neptunium present.
Taylor et al. have reported log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β values of 4.83 and 8.09 for the formation of the mono- and bisacetohydroxamato complexes of Np(V) in 2 mol dm−3 perchlorate media at 293 K.23 As per Table 1, these can be converted to conditional equilibrium constants for mono- and bisacetohydroxamato Np(V) complex formation of 6.4 × 10−5 and 1.7 × 10−6 respectively. Comparison of these with the values for the analogous parameters for Np(IV), K1 and K2, given in Table 1 shows that, thermodynamically, formation of Np(V)–AHA complexes is at least seven orders of magnitude less likely than Np(IV)–AHA complexes. Np(V)–AHA complex formation can therefore be ignored in the experiments of Fig. 10. Further, comparison of the 979 and 1100 nm bands obtained at the start and end of the runs shown in Fig. 10 indicates that the Np(V) concentration is nearly invariant during each run; typically it is found to change by ∼23 μmol dm−3, corresponding to an uncertainty in the total Np(IV) concentration of only 1% which, given that Np(IV) is the focus of these experiments, can be safely neglected. Thus, as in the treatment of the data of Fig. 9, it is reasonable to conclude that the data of Fig. 10 are dominated by the hydrolysis behaviour of the Np(IV)–AHA system and that, once the total Np(IV) concentration in the each experiment has been corrected for the total Np(V) concentration, the effect of Np(V) can be ignored.
β values of 4.83 and 8.09 for the formation of the mono- and bisacetohydroxamato complexes of Np(V) in 2 mol dm−3 perchlorate media at 293 K.23 As per Table 1, these can be converted to conditional equilibrium constants for mono- and bisacetohydroxamato Np(V) complex formation of 6.4 × 10−5 and 1.7 × 10−6 respectively. Comparison of these with the values for the analogous parameters for Np(IV), K1 and K2, given in Table 1 shows that, thermodynamically, formation of Np(V)–AHA complexes is at least seven orders of magnitude less likely than Np(IV)–AHA complexes. Np(V)–AHA complex formation can therefore be ignored in the experiments of Fig. 10. Further, comparison of the 979 and 1100 nm bands obtained at the start and end of the runs shown in Fig. 10 indicates that the Np(V) concentration is nearly invariant during each run; typically it is found to change by ∼23 μmol dm−3, corresponding to an uncertainty in the total Np(IV) concentration of only 1% which, given that Np(IV) is the focus of these experiments, can be safely neglected. Thus, as in the treatment of the data of Fig. 9, it is reasonable to conclude that the data of Fig. 10 are dominated by the hydrolysis behaviour of the Np(IV)–AHA system and that, once the total Np(IV) concentration in the each experiment has been corrected for the total Np(V) concentration, the effect of Np(V) can be ignored.
Rates of hydrolysis of AHA within the Np(IV)–AHA system were then determined from the data for Fig. 10 (and its associated larger dataset) by first measuring the absorbance of free Np(IV), mono- and bis-hydroxamato and mono- and bisnitrato complexes at 732 nm as a function of time. The resultant absorbance vs. time plots are shown in Fig. 11a–h. gPROMS-modelled absorbance–time curves, also shown in Fig. 11a–h, were then computed as described above by using the (previously unknown) Beer–Lambert extinction coefficients for the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 2
1 and 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 Np(IV)–AHA complexes and the kinetic rate parameters k1 and k2 as fitting parameters. In contrast, the values of extinction coefficients of the Np4+, NpNO33+, Np(NO3)22+ complexes (vide supra) and the conditional equilibrium constants K1, K2, K3, (given by eqn (4a)–(4c) and Table 1) β1,NO3, β2,NO3 (given by SIT calculations using eqn (8) and (9)) and the pKA,HNO3 value for nitric acid (given by eqn (11)) were fixed. The value of k0, the rate constant for the hydrolysis of the free AHA ligand was also fixed by taking the average of the values of 2.7 × 10–5 dm3 mol−1 s−1 and 3.2 × 10–5 dm3 mol−1 s−1 computed using the Arrhenius data of Chung and Lee26 and Taylor et al.27 respectively.
1 Np(IV)–AHA complexes and the kinetic rate parameters k1 and k2 as fitting parameters. In contrast, the values of extinction coefficients of the Np4+, NpNO33+, Np(NO3)22+ complexes (vide supra) and the conditional equilibrium constants K1, K2, K3, (given by eqn (4a)–(4c) and Table 1) β1,NO3, β2,NO3 (given by SIT calculations using eqn (8) and (9)) and the pKA,HNO3 value for nitric acid (given by eqn (11)) were fixed. The value of k0, the rate constant for the hydrolysis of the free AHA ligand was also fixed by taking the average of the values of 2.7 × 10–5 dm3 mol−1 s−1 and 3.2 × 10–5 dm3 mol−1 s−1 computed using the Arrhenius data of Chung and Lee26 and Taylor et al.27 respectively.
 | ||
| Fig. 11 Plots of experimental and modelled absorbance of the Np(IV)–AHA system at 732 nm, data of (a–h) taken from the corresponding figures (and respective associated larger spectral data sets) in Fig. 10. For the avoidance of doubt, initial total acid, AHA and Np(IV) concentrations are shown as insets on each figure. | ||
Fig. 11a–h show good agreement between experimental and modelled absorbance data, with the gPROMS-estimated values of the rate parameters k1 and k2 used to obtain the model-to-experiment data fits being summarised in Table 4. The mean values for the rate constants for the hydrolysis of the mono- and bis-hydroxamate complexes are found to be k1 = 3.5 × 10−5 ± 2.5 × 10−5 dm3 mol−1 s−1 and k2 = 1.9 × 10−3 ± 1.3 × 10−3 dm3 mol−1 s−1 respectively at 298 K. These are both more than the value of k0 of 3 × 10−5 dm3 mol−1 s−1 used in the gPROMs fitting procedure of Fig. 11 and Table 4, the value for k2 substantially so. This indicates a progression of order:
| k2 > k1 > k0 | (18) |
| Experiment of Fig. 10 and 11 | [HNO3]/mol dm−3 | [Np4+]/mol dm−3 | [AHA]0/mol dm−3 | % Np initially as NpL22+ | Fitted k1/dm3 mol−1 s−1 | Fitted k2/dm3 mol−1 s−1 | Fitted extinction coefficient for NpL3+ at 732 nm/dm3 mol−1 cm−1 | Fitted extinction coefficient for NpL22+ at 732 nm/dm3 mol−1 cm−1 |
|---|---|---|---|---|---|---|---|---|
| A | 1.0 | 0.0028 | 0.00526 | 2.5 | 4.6 × 10−5 | 58 | ||
| B | 1.0 | 0.0026 | 0.010 | 6.8 | 4.9 × 10−5 | 65 | ||
| C | 1.0 | 0.00195 | 0.050 | 33 | 6.9 × 10−5 | 5.3 × 10−5 | 77 | 85 |
| D | 1.0 | 0.00193 | 0.10 | 50 | 2.6 × 10−5 | 4.5 × 10−4 | 74 | 87 |
| E | 3.0 | 0.0026 | 0.0375 | 14 | 6.9 × 10−5 | 1.8 × 10−3 | 45 | 89 |
| F | 3.0 | 0.00193 | 0.050 | 19 | 1.9 × 10−6 | 3.0 × 10−3 | 52 | 74 |
| G | 3.0 | 0.00193 | 0.10 | 34 | 1.3 × 10−5 | 2.2 × 10−3 | 55 | 74 |
| H | 3.0 | 0.00193 | 0.25 | 52 | 1.0 × 10−5 | 3.8 × 10−3 | 61 | 74 |
| Mean values of fitted parameters | 3.5 × 10−5 ± 2.5 × 10−5 | 1.9 × 10−3 ± 1.3 × 10−3 | 61 ± 10 | 81 ± 6.6 | ||||
That is, acetohydroxamate in the 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 AHA–Np(IV) complex hydrolyses much faster than acetohydroxamate in the 1
1 AHA–Np(IV) complex hydrolyses much faster than acetohydroxamate in the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex which hydrolyses faster than free AHA. This is consistent with the findings of our earlier studies of the Fe(III)–AHA system wherein the rate of hydrolysis of the ligand within the monohydroxamato–iron(III) complex was greater than that of the free hydroxamate, this complexation induced enhancement in hydrolysis rate becoming more pronounced with increasing temperature.3,51
1 complex which hydrolyses faster than free AHA. This is consistent with the findings of our earlier studies of the Fe(III)–AHA system wherein the rate of hydrolysis of the ligand within the monohydroxamato–iron(III) complex was greater than that of the free hydroxamate, this complexation induced enhancement in hydrolysis rate becoming more pronounced with increasing temperature.3,51
This was explained in the context of a quantum mechanical calculation-based analysis which showed that the hydrolysis of the free hydroxamic acid proceeds via the energetically favoured protonation of the carbonyl group followed by nucleophilic attack of a water molecule on the carbonyl carbon. This leads to the cleavage of the C–N bond, and the formation of NH2OH as the leaving group.51 The same calculations suggest that, for hydroxamic acids bound to metal centres, it is protonation of the less favourable nitrogen site that results in a weakening of the C–N bond, which enables the hydrolysis to proceed via the ejection of a NHOH–M leaving group, with the electron withdrawing effect of the metal centre making the nucleophilic attack by water on the carbonyl carbon more likely. It is the latter effect which is principally responsible for the greater rate of hydrolysis of the bound hydroxamate compared to the free AHA.
That a similar trend in rate parameters to that seen in the Fe(III)–AHA system is also observed in the Np(IV)–AHA system suggests that a similar mechanism of hydrolysis enhancement is in operation with the electron withdrawing effect of the neptunium(IV) metal centre increasing the susceptibility of the carbonyl carbon to nucleophilic attack, thus explaining why k1 > k0.
A value of k1 for the monohydroxamato–iron(III) complex of 5.3 × 10−5 dm3 mol−1 s−1 at 298 K can be obtained using the Arrhenius data of our earlier study. This is larger than the value of 3.8 × 10−5 dm3 mol−1 s−1 obtained here for the analogous k1 parameter for the monohydroxamato–neptunium(IV) complex at the same temperature (see Table 4). This hierarchy of k1 values can be simply understood on the basis of the charge densities of the two ions. Using Shannon–Prewitt effective ionic radii values, charge densities of 427 and 162 C mm−3 can be calculated for high spin Fe3+ and 8-coordinate Np4+ respectively. Fe(III) will therefore have a stronger electron withdrawing effect than Np(IV) when complexed to the O atom of the hydroxamate carbonyl, with a consequent greater enhancement in the rate of nucleophilic attack of water on the C atom of the carbonyl.
Table 4 and eqn (18) also indicate that the rate constant for the hydrolysis of the hydroxamate ligand on the bishydroxamato-Np(IV) complex, k2, is greater than that for the same ligand on the monohydroxamato-Np(IV) complex, k1. Since protonation of the hydroxamate nitrogen leads to hydrolysis of the complex, this could be explained simply in terms of there being two hydroxamate ligands attached to the metal centre in the bishydroxamato complex – with the likelihood of protonation and subsequent nucleophilic attack on a carbonyl carbon consequently increased with respect to the monohydroxamato complex.
However, k2 is almost two orders of magnitude greater than k1, compared to k1 being only ∼20% greater than k0. Whilst this unambiguously demonstrates that complexation with Np(IV) increases the rate of hydrolysis of AHA, the size of the difference between k2 and k1 compared to that between k1 and k0 suggests other factors are in play beyond a simple mass action effect derived from having two ligand per bishydroxamato versus one per monohydroxamato complex. One possible source of the increased value of k2versus k1 is the charge on the complex to which the hydrolyzing ligand is attached. The monohydroxamato complex has a net charge of +3, whilst the bishydroxamato complex has a lower net charge of +2. Given that a key step in the hydrolysis of the bound ligand is protonation of the hydroxamate nitrogen site, coulombic repulsion issues may arise from the positive charges on the protonating H+ ion and the complex. With its lower net charge, the bishydroxamato complex might be expected to protonate more easily than the monohydroxamato complex and thus hydrolyse more quickly, so leading to the observed increase in k2 over k1.
It is worth discussing one final point with regards to eqn (18). That k1 is greater than k0 for the Np(IV)–AHA system is the opposite of the trend we have previously reported for the analogous rate parameters in the Np(IV)–FHA system.4 This is most likely due to the fact that, in the then-absence of stability constant data for the Np(IV)–FHA system, Np(IV)–AHA speciation diagrams were used to inform the design of the Np(IV)–FHA kinetic run experiments and the subsequent interpretation of the results. Here, not only have Np(IV)–AHA speciation diagrams been used to inform interpretation of Np(IV)–AHA kinetic run data – those diagrams have also been calculated using ionic strength dependent conditional stability constants; the approach adopted here is thus more self-consistent and the results, therefore, more reliable.
Returning to Table 4, the extinction coefficient values for NpL3+ and NpL22+ at 732 nm are currently unknown and these were also used as model fitting parameters for the data of Fig. 11a–h (vide supra) – the so-obtained values also being shown in Table 4. Mean values of these extinction coefficients obtained using the whole data set of Table 3 are 61.2 ± 10 (16% variation) and 80.5 ± 6.6 (8% variation) dm3 mol−1 cm−1 for NpL3+ and NpL22+ respectively.
Closer inspection of the data reveals that different mean extinction coefficients for both NpL3+ and NpL22+ may be calculated at the two HNO3 concentrations employed in the kinetic run experiments. At 1.0 mol dm−3 HNO3, mean extinction coefficients of 68.5 ± 7.5 (11% variation) and 86 ± 1 (1.1% variation) dm3 mol−1 cm−1 may be calculated for NpL3+ and NpL22+ respectively, whilst at 3.0 mol dm−3 HNO3 mean extinction coefficients of 53.25 ± 5.7 (11% variation) and 77.75 ± 6.5 (8.3% variation) dm3 mol−1 cm−1 may be calculated for NpL3+ and NpL22+ respectively.
This observed difference in the mean extinction coefficients calculated for each complex at these two acidities is almost certainly due to the effect of ionic strength on the conditional equilibrium constants K1 and K2. Similar nitric acid concentration-dependent variations in the extinction coefficients for Am(III), Am(V) and Am(VI) at 503, 718 and 996 nm respectively are reported by Grimes et al.52 using values previously reported by Zalupski et al.53 Mean values over a nitric acid concentration range of 1 to 6.5 mol dm−3 are found to be 342 ± 46 (13.5% variation), 40 ± 4.2 (11% variation) and 85 ± 6 (7% variation) dm3 mol−1 cm−1 for the Am(III), Am(V) and Am(VI) peaks respectively – variations that are consistent with those reported here. Grimes et al. attribute their observed acid dependent variations in extinction coefficients to the media effects of increasing or decreasing background electrolyte concentrations when [HNO3] is varied.
Such an effect for Np(IV)–AHA complexes can also be expected on the basis of the variations with ionic strength of β1 and β2 for Np(IV)–nitrate complexes shown in Fig. 3. However, whilst we were able to account for the ionic strength-derived variations in stability constants for the Np(IV)–nitrate system by use of the SIT relationships of eqn (11) and (12), there is no available analogous SIT data for the acetohydroxamate complexes of Np(IV). This is due to the limited number of acidities at which K1 and K2 have been measured. Thus, full correction of the extinction coefficients reported in Table 4 in the context of SIT theory is not currently possible.
Conclusions
We propose a new, coupled thermodynamic and kinetic model for the hydrolysis of AHA in the Np(IV)–AHA system. This model is used to fit hydrolytic kinetic run data for the Np(IV)–AHA system using the custom modelling software package, gPROMS. The model includes not only the hydrolysis of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 2
1 and 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 AHA–Np(IV) complexes, but also the ionic strength dependent concentrations of NpNO33+, Np(NO3)22+ and NpOH3+ determined using SIT theory. In doing this, we have calculated speciation diagrams for the same Np(IV)–nitrate and Np(IV)–OH complexes as a function of total nitric acid concentration (i.e. simultaneous variation of both the H+ and NO3− concentration), the first time that this has been done.
1 AHA–Np(IV) complexes, but also the ionic strength dependent concentrations of NpNO33+, Np(NO3)22+ and NpOH3+ determined using SIT theory. In doing this, we have calculated speciation diagrams for the same Np(IV)–nitrate and Np(IV)–OH complexes as a function of total nitric acid concentration (i.e. simultaneous variation of both the H+ and NO3− concentration), the first time that this has been done.
Speciation diagrams for the Np(IV)–HNO3–AHA system indicate that at pH ≤ 0, only Np4+, NpL3+, NpL22+, NpNO33+ and Np(NO3)22+ are present in significant quantities under the experimental conditions studied here. Modelling of kinetic run experiments using the extinction coefficients and hydrolysis rate constants, k1 and k2 for the mono- and bis-hydroxamato complexes as fitting parameters gives excellent fits that are self-consistent and give average values of k1 = 3.5 × 10−5 ± 2.5 × 10−5 dm3 mol−1 s−1 and k2 = 1.9 × 10−3 ± 1.3 × 10−3 dm3 mol−1 s−1 respectively at 298 K – the first time that these have been reported.
These values indicate a hierarchy of AHA hydrolysis rate constants in the order k2 > k1 > k0, indicating that complexation of Np(IV) with AHA increases the rate of ligand hydrolysis. Subsequent extension of these modelling approaches to Pu(IV) ions would then provide a sound basis to understand fully the stability of hydroxamic acids and their actinide complexes in, inter alia, advanced PUREX and UREX process flow sheets. This will be the subject of our next communication.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors wish to thank the Engineering and Physical Science Research Council UK for provision of an EngD award to support Scott Edwards, The National Nuclear Nuclear Laboratory, Sellafield Ltd and The Lloyds Register Foundation for additional financial support. The Lloyds Register Foundation is an independent charity that supports the advancement of engineering-related education, and funds research and development that enhances safety of life at sea, on land and in the air.Notes and references
- P. D. Wilson, The Nuclear Fuel Cycle: From Ore to Wastes, Oxford University Press, 1996 Search PubMed.
- R. J. Taylor, C. R. Gregson, M. J. Carrott, C. Mason and M. J. Sarsfield, Solvent Extr. Ion Exch., 2013, 31, 442–462 CrossRef CAS.
- F. P. L. Andrieux, C. Boxall and R. J. Taylor, J. Solution Chem., 2007, 36, 1201–1217 CrossRef CAS.
- F. P. L. Andrieux, C. Boxall, I. May and R. J. Taylor, J. Solution Chem., 2008, 37(2), 215–232 CrossRef CAS.
- R. J. Taylor, I. May, A. L. Wallwork, I. S. Denniss, N. J. Hill, B. Y. Galkin, B. Y. Zilberman and Y. S. Fedorov, J. Alloys Compd., 1998, 271–273, 534–537 CrossRef CAS.
- P. Tkac and A. Paulenova, Sep. Sci. Technol., 2008, 43(9–10), 2670–2683 CrossRef CAS.
- K. K. Ghosh, Indian J. Chem., Sect. B: Org. Chem. Incl. Med. Chem., 1997, 36, 1089–1102 Search PubMed.
- S. N. Gray, Biochem. Soc. Trans., 1998, 26, 666–670 CrossRef CAS PubMed.
- S. Pepelinjak, B. Zorc and I. Butula, Acta Pharm., 2005, 55, 401–408 Search PubMed.
- P. Chittari, V. R. Jadhav, K. N. Ganesh and S. Rajappa, J. Chem. Soc., Perkin Trans. 1, 1998, 1319–1324 RSC.
- R. R. Nanewar and U. Tandon, Talanta, 1978, 25(6), 352–353 CrossRef CAS PubMed.
- el-R. Kenawy, M. el-Newehy, F. Abdel-Hay and R. M. Ottenbrite, Biomacromolecules, 2007, 8(1), 196–201 CrossRef CAS PubMed.
- F. Vernon, Pure Appl. Chem., 2009, 54, 2151–2158 Search PubMed.
- K. N. Raymond, G. E. Freeman and M. J. Kappel, Inorg. Chim. Acta, 1984, 94, 193–204 CrossRef CAS.
- J. C. Renshaw, G. D. Robson, A. P. J. Trinci, M. G. Wiebe, F. R. Livens, D. Collison and R. J. Taylor, Mycol. Res., 2002, 106, 1123–1142 CrossRef CAS.
- B. Monzyk and A. L. Crumbliss, J. Am. Chem. Soc., 1979, 101, 6203–6213 CrossRef CAS.
- A. L. Crumbliss and J. M. Harrington, in Advances in Inorganic Chemistry, ed. R. van Eldik and C. D. Hubbard, Academic Press, 2009, vol. 61, pp. 179–250 Search PubMed.
- A. M. Albrecht-Gary and A. L. Crumbliss, Met. Ions Biol. Syst., 1998, 35, 239–327 CAS.
- B. Colston, G. R. Choppin and R. J. Taylor, Radiochim. Acta, 2000, 88, 329–334 CAS.
- E.-H. L. Dong-Yong Chung, Bull. Korean Chem. Soc., 2005, 26(11), 1692–1694 CrossRef.
- R. J. Taylor, C. Mason, R. Cooke and C. Boxall, J. Nucl. Sci. Technol., 2002, 39(sup3), 278–281 CrossRef.
- M. J. Carrott, O. D. Fox, G. LeGurun, C. J. Jones, C. Mason, R. J. Taylor, F. P. L. Andrieux and C. Boxall, Radiochim. Acta, 2009, 96, 333–343 Search PubMed.
- R. J. Taylor, S. Sinkov, G. R. Choppin and I. May, Solvent Extr. Ion Exch., 2008, 26(1), 41–61 CrossRef CAS.
- M. J. Carrott, O. D. Fox, C. J. Maher, C. Mason, R. J. Taylor, S. I. Sinkov and G. R. Choppin, Solvent Extr. Ion Exch., 2007, 25(6), 723–745 CrossRef CAS.
- Advanced Separation Techniques for Nuclear Fuel Reprocessing and Radioactive Waste Treatment, ed. K. L. Nash and G. J. Lumetta, Woodhead Publishing Ltd., 2011 Search PubMed.
- D. Y. Chung and E. H. Lee, J. Ind. Eng. Chem., 2006, 12(6), 962–966 CAS.
- R. J. Taylor and I. May, Czech. J. Phys., 1999, 49(1), 617–621 CrossRef CAS.
- M. J. Sarsfield, H. E. Sims and R. J. Taylor, Solvent Extr. Ion Exch., 2011, 29, 49–71 CrossRef CAS.
- I. Grenthe, F. Mompean, K. Spahiu and H. Wanner, Guidelines For The Extrapolation To Zero Ionic Strength, OECD Nuclear Energy Agency, 2013 Search PubMed.
- R. J. Lemire, et al., Chemical Thermodynamics of Neptunium and Plutonium, OECD Nuclear Energy Agency, Elsevier, 2001 Search PubMed.
- M. J. Sarsfield, R. J. Taylor and C. J. Maher, Radiochim. Acta, 2009, 95(12), 677–682 Search PubMed.
- H. A. Friedman and L. M. Toth, J. Inorg. Nucl. Chem., 1980, 42, 1347–1349 CrossRef CAS.
- L. Alderighi, P. Gans, A. Ienco, D. Peters, A. Sabatini and A. Vacca, Coord. Chem. Rev., 1999, 184(1), 311–318 CrossRef CAS.
- A. I. Alonso, A. M. Urtiaga, S. Zamacona, A. Irabien and I. Ortiz, J. Membr. Sci., 1997, 130(1–2), 193–203 CrossRef CAS.
- L. T. Markouska, V. D. Meshko and M. S. Marinkouski, J. Serb. Chem. Soc., 2006, 71(8–9), 957–967 CrossRef.
- M. I. Ali and P. A. Schneider, Chem. Eng. Sci., 2008, 63(13), 3514–3525 CrossRef CAS.
- T. Suau, G. Álvaro, M. D. Benaiges and J. López-Santin, Biochem. Eng. J., 2008, 41(1), 95–103 CrossRef CAS.
- PSE: gPROMS technologies, Model validation and model-based data analysis http://www.psenterprise.com/gproms/technologies/model_validation.html (accessed Mar 4, 2016).
- Process Systems Enterprise Limited , gPROMS Documentation v3.7. 2013.
- I. V. Shilin and V. K. Nazarov, Radiokhimiya, 1966, 8, 514–519 CAS.
- A. G. Rykov and G. N. Yakovlev, Sov. Radiochem., 1966, 8, 26–30 Search PubMed.
- P. R. Danesi, R. Chiarizia, G. Scibona and G. D'Alessandro, J. Inorg. Nucl. Chem., 1971, 33(10), 3503–3510 CrossRef CAS.
- Y. A. Barbanel and L. P. Murav'eva, Sov. Radiochem., 1972, 14(3), 498–501 Search PubMed.
- A. B. Yusov, A. M. Fedosseev and C. H. Delegard, Radiochim. Acta, 2004, 92(12), 869–881 CAS.
- I. Grenthe, et al., Chemical Thermodynamics of Uranium, OECD Nuclear Energy Agency, 2004 Search PubMed.
- N. A. Smith and K. R. Czerwinski, J. Radioanal. Nucl. Chem., 2013, 298(3), 1777–1783 CrossRef CAS.
- J. M. Berg, D. K. Veirs, R. B. Vaughn, M. A. Cisneros and C. A. Smith, J. Radioanal. Nucl. Chem., 1998, 235(1–2), 25–29 CrossRef CAS.
- V. Neck and J. I. Kim, Radiochim. Acta, 2001, 89(1), 1–16 CAS.
- E. Wiberg and N. Wiberg, Inorganic Chemistry, Academic Press, 2001 Search PubMed.
- The Chemistry of Hydroxylamines, Oximes and Hydroxamic Acids, ed Z. Rappoport and J. F. Liebman, John Wiley & Sons, 2008 Search PubMed.
- F. P. L. Andrieux, C. Boxall, H. M. Steele and R. J. Taylor, J. Solution Chem., 2014, 43(3), 608–622 CrossRef CAS.
- T. S. Grimes, G. P. Horne, C. J. Dares, S. M. Pimblott, S. P. Mezyk and B. J. Mincher, Inorg. Chem., 2017, 56(14), 8295–8301 CrossRef CAS PubMed.
- P. R. Zalupski, T. S. Grimes and C. R. Heathman, Appl. Spectrosc., 2017, 21(12), 2608–2615 CrossRef PubMed.
| This journal is © The Royal Society of Chemistry 2019 |