Investigation of solvent effects on the hydrodeoxygenation of guaiacol over Ru catalysts†
Abstract
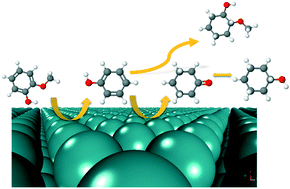
The effects of a liquid phase environment on the hydrodeoxygenation of guaiacol, a prototypical lignin derived compound, have been investigated over a Ru catalyst from first principles. A microkinetic reactor model with parameters obtained from density functional theory and implicit solvation schemes was developed to study the effects of condensed phases on the reaction mechanism and kinetic parameters. Phenol was found to be the major aromatic product across all reaction environments. Our model predicts that less protic solvents such as 1-butanol, diethyl ether, and n-hexane have a positive effect on the reaction kinetics for the production of phenolics relative to vapor and aqueous reaction environments. The dominant reaction mechanism for aromatics production remains unchanged across all reaction media. Next, we investigated the possibility of cycloalkane production through hydrogenation of phenol in vapor and liquid phase environments. Our calculations indicated that the reaction pathway for cycloalkane production from phenol will most likely follow an initial dehydrogenation of the hydroxyl group. Based on the vapor phase density functional theory calculations, we proposed a probable reaction pathway and calculated the condensed phase effects along this reaction route. We observed that an aqueous phase has a more favorable effect for cycloalkane production from phenol relative to vapor phase and other less protic solvent environments.
- This article is part of the themed collection: 2019 Catalysis Science & Technology HOT Articles


 Please wait while we load your content...
Please wait while we load your content...
