The consequences of surface heterogeneity of cobalt nanoparticles on the kinetics of CO methanation†
Abstract
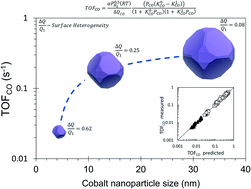
The CO hydrogenation reaction was studied under methanation conditions (H2/CO >3, 250–300 °C) on Co/SiO2 catalysts with different mean Co nanoparticle size (dp = 4 nm, 13 nm and 33 nm). The catalysts were prepared by incipient wetness impregnation; the cobalt loading and reduction conditions were suitably selected in order to produce catalysts with different dp. Operando FTIR and kinetic measurements provided consistent data for the heat of CO adsorption at low and full coverage. The results confirm the structural sensitivity of the CO hydrogenation reaction on supported cobalt catalysts and demonstrate the energetic heterogeneity of the cobalt surface. A model derived from the Temkin formalism accurately fits the kinetic data and renders the heterogeneity of the cobalt surface by capturing the change in the heat of CO adsorption with the CO coverage. This change is normalized by the heat of CO adsorption at high coverage (ΔQCO/Q1) in order to quantify and compare the heterogeneity of cobalt surfaces. The CO hydrogenation turnover rates are lower on the catalyst with smaller nanoparticles. This surface shows higher heterogeneity and lower apparent activation energy, which is attributed to a larger amount of the more active B5-B sites in this catalyst.
- This article is part of the themed collection: 2019 Catalysis Science & Technology HOT Articles


 Please wait while we load your content...
Please wait while we load your content...