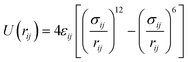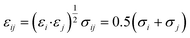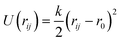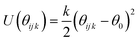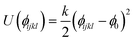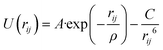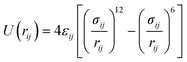Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Molecular behaviour of phenol in zeolite Beta catalysts as a function of acid site presence: a quasielastic neutron scattering and molecular dynamics simulation study†
Carlos
Hernandez-Tamargo
 a,
Alexander
O'Malley
a,
Alexander
O'Malley
 *bc,
Ian P.
Silverwood
*bc,
Ian P.
Silverwood
 d and
Nora H.
de Leeuw
d and
Nora H.
de Leeuw
 *a
*a
aSchool of Chemistry, Cardiff University, Main Building, Park Place, Cardiff, CF10 3AT, UK. E-mail: deleeuwn@cardiff.ac.uk
bThe Centre for Sustainable Chemical Technologies (CSCT), Department of Chemistry, University of Bath, Claverton Down, Bath, BA2 7AY, UK. E-mail: a.o'malley@bath.ac.uk
cUK Catalysis Hub, Research Complex at Harwell, Science and Technology Facilities Council Rutherford Appleton Laboratory, Harwell Science and Innovation Campus, Oxon OX11 0QX, UK
dISIS Pulsed Neutron and Muon Facility, Science and Technology Facilities Council Rutherford Appleton Laboratory, Harwell Science and Innovation Campus, Oxon OX11 0QX, UK
First published on 4th November 2019
Abstract
Quasielastic neutron scattering (QENS) experiments complemented by classical molecular dynamics (MD) simulations at 393–443 K were employed in a study of the mobility and interactions of phenol in acidic zeolite H-Beta, to understand systems relevant to potential routes for the depolymerization and hydrodeoxygenation of lignin. QENS experiments observed isotropic phenol rotation with a fraction of static molecules, yielding rotational diffusion coefficients between 2.60 × 1010 and 3.33 × 1010 s−1 and an activation energy of rotation of 7.2 kJ mol−1. The MD simulations of phenol in the acidic and all-silica zeolite corroborate the experimental results, where molecules strongly adsorbed to the acidic sites behave as an immobile fraction with minimal contribution to the rotational diffusion, and the mobile molecules yield similar rotational diffusion coefficients to experiment. Translational diffusion is too slow to be detected in the instrumental time window of the QENS experiments, which is supported by MD-calculated activation energies of translation larger than 25 kJ mol−1. The study illustrates the effect of active sites in potential catalyst structures on the dynamical behaviour of molecules relevant to biomass conversion.
1 Introduction
Lignin, which is one of the main components of biomass has an extraordinary potential as a renewable source of fuels and valuable chemicals.1 However, the transformation of lignin is hampered by its complex polymeric structure, i.e. a three-dimensional polymer constituted of phenolic building blocks, with many points of unsaturation and multiple links among the phenolic monomers. Consequently, appropriate catalysts are needed for the effective and efficient conversion of lignin.1–3 The dehydration and hydrogenation capacity of the catalyst are the features of interest with regard to promoting the conversion of compounds derived from the depolymerisation of lignin. The hydrodeoxygenation (HDO) process assists the further depolymerisation of lignin to its simple molecular forms and increases the H![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C and C
C and C![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) O ratios, thus enhancing the energy content of the final products intended to be used as fuels. In this regard, bifunctional catalysts consisting of metal nanoparticles supported on solid acids have shown remarkable performance towards the conversion of lignin-derived compounds.4–7 Zeolites, owing to their versatility as microporous solid acids and their hydrothermal stability,8–11 are a common choice to act as supports of the metal nanoparticles. For instance, recent studies have reported the deposition of Ru, Ni, Pd and Pt on zeolites ZSM-5, Beta and HY, where the hydrogenation is controlled by the metal clusters, whilst the acid sites of the support govern the dehydration and alkylation of the hydrogenation products.4–7
O ratios, thus enhancing the energy content of the final products intended to be used as fuels. In this regard, bifunctional catalysts consisting of metal nanoparticles supported on solid acids have shown remarkable performance towards the conversion of lignin-derived compounds.4–7 Zeolites, owing to their versatility as microporous solid acids and their hydrothermal stability,8–11 are a common choice to act as supports of the metal nanoparticles. For instance, recent studies have reported the deposition of Ru, Ni, Pd and Pt on zeolites ZSM-5, Beta and HY, where the hydrogenation is controlled by the metal clusters, whilst the acid sites of the support govern the dehydration and alkylation of the hydrogenation products.4–7
Phenolic monomers, such as phenol and cresols, constitute the simplest molecular forms obtained after the depolymerisation of lignin,12,13 and thus they constitute a suitable starting model for the study of the HDO of lignin-derived compounds.14–19 These low-molecular weight phenols may be hydrogenated and deoxygenated at the metal nanoparticle to form monocycloalkanes and aromatics, or remain inside the micropore system of the zeolite, where further coupling reactions transform the phenols into bicycloalkanes.3 Hence, the dynamical behaviour of the sorbate as dictated by both the micropore size and composition (mainly through active site-sorbate interactions) of the zeolite is an important feature in determining the product selectivity during the upgrading of lignin. Only zeolites with relatively large micropores, such as zeolite Beta, will allow the diffusion of phenols and the subsequent coupling reactions, while frameworks with smaller pores will influence the pathway towards monocycloalkanes.4,20,21 Therefore, a detailed analysis of the dynamical behaviour of phenolic monomers inside the micropores will provide a more complete understanding of the HDO of lignin-derived compounds using bifunctional catalysts.
Techniques based on neutron spectroscopy are of growing significance in the field of heterogeneous catalysis,22 both in the study of the catalyst itself,23,24 and investigation of the relevant molecular species upon adsorption.25,26 Quasielastic neutron scattering (QENS) is particularly effective in the study of microporous catalysts,27 allowing the measurement of molecular movements taking place over timescales of 2 ps–100 ns depending on the instrument, and thus it may be employed to measure both nanoscale diffusion,28–30 and also local motions such as rotation.31–34 Crucially, this technique can be employed on sub-micron crystals, in contrast to other methods, such as PFG-NMR, which have timescales from micro- to milliseconds and hence need crystal sizes in the order of micrometres or larger to be able to measure intra-crystalline diffusion.
Details of the dynamical behaviour on the molecular and nanoscale are provided by molecular dynamics (MD) simulations using classical interatomic potentials, which are capable of modelling sizable crystal systems (2–100 nm) and time ranges of up to hundreds of nanoseconds, allowing us to observe self-diffusive motion. The dynamical characteristics derived from the MD analysis are an essential complement to the QENS experiments, as shown in previous reports on a range of zeolite-sorbate systems.35–39 QENS observables such as the intermediate scattering function and its temporal Fourier transform, the dynamic structure factor, may be calculated directly to compare simulation results with experiment.40,41
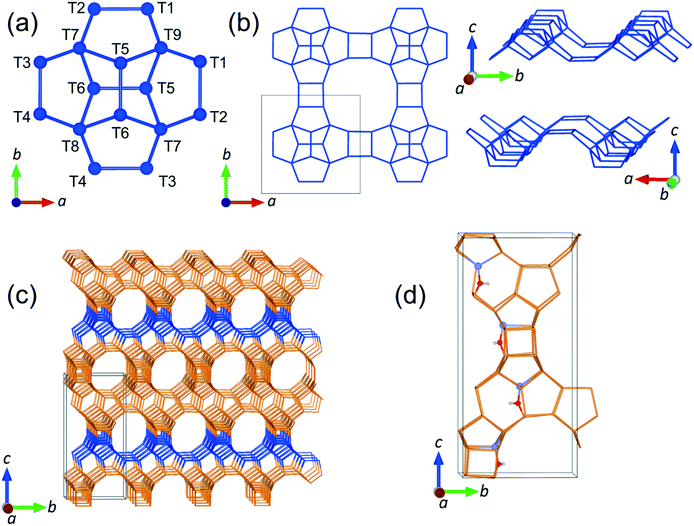
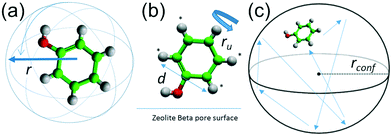
In the present work, we have studied the mobility of phenol in zeolite Beta using QENS experiments complemented by density functional theory (DFT) calculations and classical MD simulations. We are particularly interested in the behaviour of phenol since it is the simplest representation of the set of phenolic monomers derived from the depolymerisation and upgrading of lignin. In addition, zeolite Beta with framework type BEA (see Fig. 1), was chosen on account of its extensive use as a support for metal nanoparticles during the catalysis of HDO reactions,42–44 and also because this zeolite has pore openings of 12 T-sites, which allows for diffusion of phenol into the zeolite.20
2 Methods
2.1 Quasielastic neutron scattering experiments
The commercial zeolite Beta samples used in the present work were obtained from Zeolyst International (CP814E*, Si/Al = 12.5), and received originally in the NH4 form. These samples were activated into the catalytic H-Beta form by heating from room temperature to 798 K for 4 hours, with a heating rate of 5 K min−1, and then dried for 10 hours under vacuum at 170 °C. Next, the samples were ground using a pestle and mortar with 10% weight of phenol (approximately 4 molecules per unit cell) in a glovebox under argon. Finally, the samples (4.4 grams in total for phenol mixed samples) were transferred to thin walled aluminium cans of annular geometry, where a 1 mm annulus was used to avoid multiple scattering from the sample.QENS experiments were carried out using the time-of-flight backscattering neutron spectrometer OSIRIS45 at the ISIS Pulsed Neutron and Muon Source. The cells were placed in a top-loading closed cycle refrigerator. Initially the samples were heated to 333 K in order to melt the phenol and ensure its adsorption into the zeolite pores. The samples were then cooled to a base temperature of 10 K and a resolution measurement was taken, before being heated to 393, 418 and 443 K where the QENS spectra were measured. This range of temperatures has been selected by considering the temperatures used during the hydroprocessing of phenolic compounds,21,43,46 and also to avoid any molecular decomposition associated with pyrolytic processes.47
The 002 reflection from the pyrolytic graphite analyser was used, giving an energy resolution of 24.5 μeV at full width at half maximum (FWHM) with energy transfers measured in a window of ±0.55 meV; the detector covered measurements over a Q range of 0.2–1.6 Å−1. We measured the neutron scattering of the empty zeolite Beta samples (which contain a small amount of hydrogen compared to the dosed samples) and the signal was then subtracted from that of the phenol loaded Beta, so that only the signal from the phenol could be extracted. In this way any scattering from the aluminium container, which is very low in comparison with the zeolite is also subtracted. No further corrections were necessary. All QENS spectra were fitted using the neutron scattering analysis software packages DAVE48 and Mantid.49
2.2 Computational simulations
The interatomic potentials (IP) and density functional theory (DFT) calculations were employed to analyse the interaction of phenol with the Brønsted acid site and its mobility in the pore system of the zeolite. The IP calculations involved both geometry optimizations and molecular dynamics simulations, which were performed by the codes General Utility Lattice Program (GULP)50,51 and DL_POLY,52 respectively. The DFT calculations were carried out by the planewave code Vienna Ab initio Simulation Package (VASP).53–56 The analysis of the aluminium substitution at the intra-framework position of zeolite Beta was achieved by the code Site Occupancy Disorder (SOD).57| Buckingham | |||
|---|---|---|---|
| A (eV) | ρ (Å) | C (eV Å6) | |
| a The same three-body potential was used for the four triads O2−⋯Si4+⋯O2−, O2−⋯Al3+⋯O2−, O2−⋯Si4+⋯O1.426− and O2−⋯Al3+⋯O1.426−. It is important to note that a cut-off of 2.5 Å was necessary for the triads O2−⋯Si4+⋯O1.426− and O2−⋯Al3+⋯O1.426− during the MD simulations with the DL_POLY code. Energy and temperature drifts are observed if the cut-off is shorter or larger than 2.5 Å by 0.5 Å. | |||
| O2−⋯O2− | 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 764.0000 764.0000 |
0.14900 | 27.88000 |
| O2−⋯O1.426− | 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 764.0000 764.0000 |
0.14900 | 27.88000 |
| O2−⋯H1.426+ | 311.9700 | 0.25000 | 0.00000 |
| O2−⋯Si4+ | 1283.9070 | 0.32052 | 10.66158 |
| O2−⋯Al3+ | 1460.3000 | 0.29912 | 0.00000 |
| O1.426−⋯Si4+ | 983.5566 | 0.32052 | 10.66158 |
| O1.426−⋯Al3+ | 1142.6775 | 0.29912 | 0.00000 |
| Morse U(rij) = D0{1 − exp[−k(rij − r0)]}2 − D0 | |||
|---|---|---|---|
| D 0 (eV) | k (Å−1) | r 0 (Å) | |
| O1.426−⋯H1.426+ | 7.0525 | 2.1986 | 0.9485 |
| Three body harmonic | |||
|---|---|---|---|
| k (eV rad−2) | θ 0 (°) | ||
| O⋯T⋯Oa | 2.09724 | 109.47 | |
We have adapted the parametrization reported by Mooney et al. to define the intra- and inter-molecular interactions of phenol.65 These parameters have been designed to reproduce the pure liquid properties of phenol over a range of temperatures, spanning from 333.15 to 523.15 K. The original parametrization keeps the phenol bond lengths fixed during the simulation, while employing harmonic and torsional potentials for the bond angles and dihedrals. In the present work, we have allowed the C–C and C–H bond lengths to change according to the harmonic parameters reported by Sastre and collaborators.66 The C–O and O–H bond lengths were kept fixed as originally proposed by Mooney et al.65 using the SHAKE algorithm.67 The full set of potentials is listed in Table 2.
| Torsion U(ϕijkl) = A[1 + cos(mϕijkl − δ)] | |||
|---|---|---|---|
| A (eV) | δ (°) | m | |
| Caro:2 or 6–Caro:1–O–H | 0.054412 | 180.0 | 2 |
The interaction of the oxygen atom of phenol with the silicon and aluminium atoms of the zeolite was modelled based on the Buckingham potentials reported for the framework pairs (Si4+, O2−) and (Al3+, O2−),62,63 but rescaling the repulsion parameter A following a procedure similar to the protocol used by Schröder and collaborators.64 We have employed the same inter-molecular parameters reported by Mooney et al. to describe the interaction between the acidic proton of the zeolite and the oxygen atom of phenol.65 We defined the remaining interactions between the zeolite framework and phenol by introducing the Lennard-Jones parameters reported by Vetrivel and co-workers.68 The full set of potentials is listed in Table 3.
| Buckingham | |||
|---|---|---|---|
| A (eV) | ρ (Å) | C (eV Å6) | |
| a The asterisk denotes atoms of phenol. | |||
| Si⋯O* | 410.8502 | 0.32052 | 10.66158 |
| Al⋯O* | 467.2960 | 0.29912 | 0.00000 |
The unit cell of zeolite Beta was optimized at constant pressure using the IP method, yielding the lattice parameters a = 12.465 Å and c = 26.224 Å, which are in good agreement with the experimental values of a = 12.5 Å and c = 26.6 Å.70 We observed that the most stable substitution of a single Al atom at the intra-framework positions of zeolite Beta preferred the site T6 (Fig. 1 for numeration). The analysis with two Al substitutions, which generates a total of 273 structures, also identified two T6 sites located in different parallel pores along the [100] direction and separated by 14 Å, as the most probable positions for the double Al substitution. Note that for the single and double Al-substituted systems, the negative charge introduced by the incorporation of Al was not counterbalanced by adding protons H+ to the system, but by diluting it among the framework O atoms, as this protocol decreased considerably the otherwise prohibitively large number of configurations that would need to be simulated.71
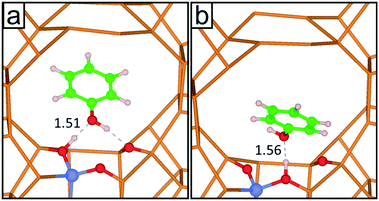
In order to approach the Si/Al ratio used in experiment, we replaced four Si atoms with Al (Si/Al = 15). Unfortunately, this number of substitutions still produces an exceedingly high number of unique combinations by the SOD code, which it is not feasible to examine. Therefore, using the evidence of the single and double substitutions, we placed the four Al atoms at T6 sites, each in a different pore out of four that exist in the unit cell of zeolite Beta. Once the four Al atoms were added to the structure, we inspected all the possible configurations to counterbalance the charge with protons, leading to the most stable structure shown in Fig. 1d, where the proton is bound to the oxygen atom numbered 12 (O12), that bridges the sites T4 and T6.
The method of multiple initial times was employed to average the trajectory over the 6 ns of production run into 1 ns, shifting the initial time every 25 ps. We observed that 1 ns was enough to obtain mean-squared displacement (MSD) plots with acceptable linearity to calculate the self-diffusivity of phenol throughout the pore system of zeolite Beta.38,39 The MSD was calculated from the variation in the coordinates of the centre of mass of the molecules. The self-diffusion coefficients were derived from the Einstein relationship:
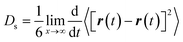 | (1) |
The optimization of the unit cell of zeolite Beta proceeded by a set of fixed-volume calculations, allowing only the relaxation of the atomic positions and the shape of the cell. The correlation between energy versus cell volume was then fitted with the Birch-Murnaghan equation of state.84 This procedure provided an optimized volume for the unit cell of 4189 Å,3 lattice parameters a = 12.589 Å and c = 26.428 Å and a predicted isotropic bulk modulus of 33.4 GPa.
We then performed short MD simulations in order to validate the classical MD simulations regarding the interaction between phenol and the Brønsted acid sites. A single molecule of phenol was loaded in zeolite Beta, which was represented by a single unit cell. The acid site consisted of an aluminium atom at the position T6, with the proton at O12. The structure obtained after the geometry optimization was annealed for 2.5 ps from 0 to 443 K, followed by 2.5 ps of equilibration at 443 K with a time step of 0.5 fs; in both cases the temperature was scaled every 50 steps. Afterwards, the production run consisted of 7.5 ps of a NVT ensemble, where the temperature was controlled by a Nosé-thermostat.85–87
3 Results and discussion
3.1 Quasielastic neutron scattering experiments
QENS spectra as a function of the momentum transfer vector Q at 393 K are shown for phenol in zeolite Beta in Fig. 2, (the QENS spectra for 418 and 443 K are shown in the ESI,† section S1). The QENS spectra at Q = 0.56 Å−1 were omitted due to the presence of a Bragg peak in zeolite Beta at this Q value, which caused issues upon subtraction of the empty zeolite spectrum from that of the loaded zeolite. The spectra were fitted to a delta function convoluted with the resolution measurement taken at 10 K, a single Lorentzian function (which was enough to describe the data satisfactorily) and a flat background function to account for any motions too fast for the instrumental window and the Debye–Waller factor. The figure contains the data points, the total fit (black), and the quasielastic component of the spectra (red) given by a Lorentzian function.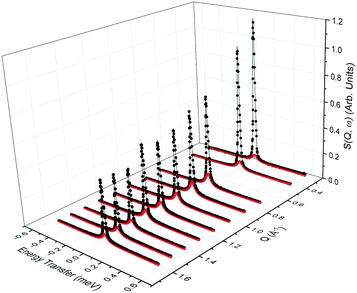 | ||
Fig. 2 QENS spectra as a function of Q for phenol in zeolite Beta at 393 K. (−) is the total fit to the data points, ( ) is the quasielastic Lorentzian component. ) is the quasielastic Lorentzian component. | ||
We note that the Lorentzian component is very small, particularly at low Q values, and the elastic component is very large at all Q values. This suggests that we are either observing localised motions (rotation or confined diffusion), or that a large proportion of the molecules are static on the timescales probed by the instrument. The fact that only one Lorentzian function is required to fit the broadening of the spectra suggests that only one dominant mode of motion is observed on the timescale of the instrument. The contribution from the Lorentizan component increases with temperature, suggesting more movement is observed in the system as the temperature increases.
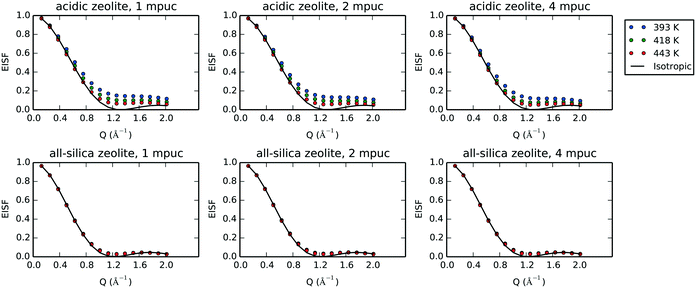
Given the large elastic component throughout the spectra, we now analyse the possible localised motions present, which can be characterised using the elastic incoherent structure factor (EISF), which is given by
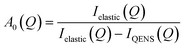 | (2) |
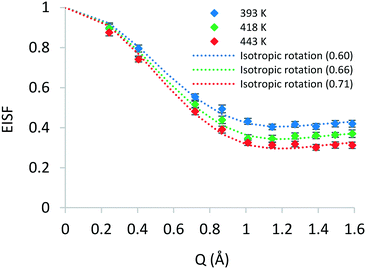
A number of models are available to characterise the localised motions of phenol, related to the geometries of motion of the protons in the molecule. The models used to fit the experimental EISF at 393 K are detailed in section S2 of the ESI† and are depicted in Fig. 4. They include the isotropic rotation model derived by Sears,88 the 2-site jump rotation model, the uniaxial rotation model and the model of translational diffusion confined to a sphere as derived by Volino and Dianoux.89 It was found that the best fit to the experimental data was the model of isotropic rotation with a fraction of immobile molecules. Good fits were also achieved with the model of diffusion confined to a sphere, however the widths of the Lorentzian component of the QENS spectra were found to be independent of Q, as opposed to exhibiting a Q-dependence associated with confined diffusion, similar to previous work90 (further detail on the broadenings can be found in the ESI†).
Having reached this conclusion, we next proceed to fit the experimental EISF at 418 and 443 K with the isotropic rotational models with the same radius of rotation, but a varying mobile fraction, as shown in Fig. 3. We find that mobile fractions of 0.66 and 0.71 fit 418 and 443 K respectively, and we therefore conclude that the motion observable in our temperature range is the isotropic rotation of phenol with a temperature-dependent mobile fraction of 0.60 to 0.71, and that a static population of molecules persists over this temperature range but decreases with increasing temperature.
After identifying the type of motion observed from the EISF, we may now calculate the rates of rotation using the broadenings of the Lorentzian component. The broadenings as a function of Q at all temperatures are plotted in Fig. 5, and the isotropic rotational diffusion coefficient may be calculated as outlined in ref. 33.
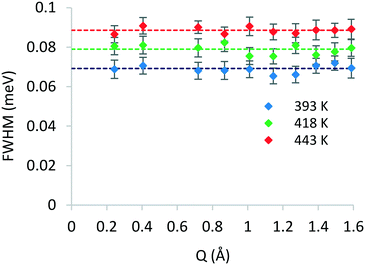 | ||
| Fig. 5 Q-Dependence of the FWHM broadening of the Lorentzian components of QENS spectra of phenol in zeolite Beta at different temperatures. | ||
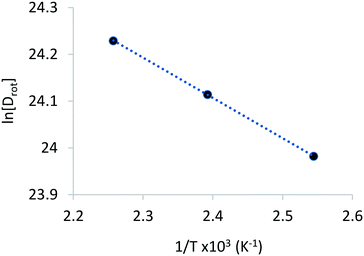
The rotational diffusion coefficients yielded values of 2.60 × 1010, 2.97 × 1010 and 3.33× 1010 s−1 for the temperatures 393, 418 and 443 K, respectively. The activation energy for rotational diffusion was calculated from the Arrhenius plot in Fig. 6 as 7.2 kJ mol−1.
3.2 Molecular dynamics simulations
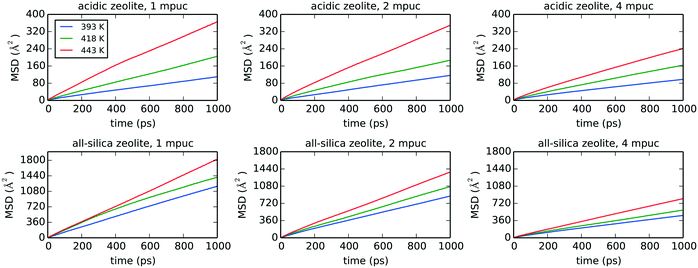
Fig. 8 shows the MSD graphs for the three different temperatures, phenol loadings and zeolite frameworks used in the classical MD simulations, with the self-diffusion coefficients and diffusion activation energies compiled in Table 4. The diffusion of phenol in the acidic zeolite is much slower compared to the all-silica framework, as expected from the strong H-bond interaction established between phenol and the Brønsted acid site. The comparison of the diffusion coefficients calculated for the acidic and all-silica frameworks indicates that the largest difference is observed for the lowest temperature with a loading of 1 mpuc, where the all-silica coefficient is 10.7 times higher compared to the value derived for the acidic zeolite. This difference decreases when the temperature is raised, and more molecules are loaded into the system, with the all-silica coefficient being 3.1 times larger compared to the acidic framework for a simulation carried out at 443 K and with a loading of 4 mpuc. The presence of strong H-bond interactions and high concentration of acid sites, although in principle beneficial for the catalytic performance, increase the retention time of the reactants and consequently the probabilities of secondary reactions, thereby reducing the overall efficiency of the catalysts.3 This is emphasised by the observed reduction in diffusion in going from an all-silica to acidic zeolite and highlights the need of a thorough optimization of the Si/Al ratio in order to maximise yield and selectivity, and decrease coke formation.91
| T (K) | Acidic zeolite | All-silica zeolite | ||||
|---|---|---|---|---|---|---|
| 1 mpuc | 2 mpuc | 4 mpuc | 1 mpuc | 2 mpuc | 4 mpuc | |
| 393 | 1.88 | 1.98 | 1.72 | 20.15 | 14.80 | 8.04 |
| 418 | 3.44 | 3.26 | 2.84 | 25.05 | 18.07 | 9.88 |
| 443 | 6.29 | 5.98 | 4.20 | 29.48 | 22.82 | 13.85 |
| E a | 35 | 32 | 26 | 11 | 13 | 16 |
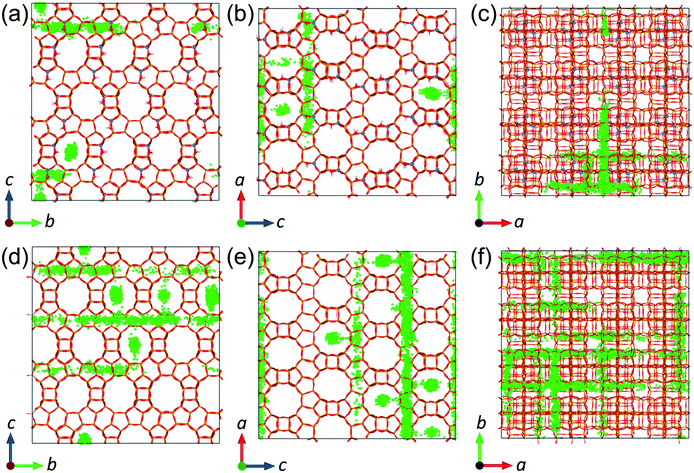
The reduction of molecular diffusion as a consequence of agglomeration is stronger in the all-silica structure, but less significant in the acidic structure, as long as the acid sites are not oversaturated by the number of phenol molecules. In the all-silica zeolite, the diffusion coefficients are reduced on average by 26 and 43% when the loadings are increased from 1 to 2 mpuc and from 2 to 4 mpuc, respectively. In comparison, the diffusion in the acidic zeolite remains approximately constant from 1 to 2 mpuc, showing an average decrease of only 2%, although the variation is more noticeable from 2 to 4 mpuc, with a reduction of 19%. We can explain these trends by observing the progression of the diffusion of phenol through the pore system of the zeolites over time. In the case of all-silica zeolite, the phenol molecules do not preferentially interact with any site of the framework and thus their movement covers practically the entire structure, as shown in Fig. 9, taking the MD trajectory of one of the molecules at 443 K and 1 mpuc as an example. Therefore, the increase of the number of molecules in the all-silica pore will more easily reduce the average molecular diffusion, because of agglomeration and inter-molecular H-bond interactions. In contrast, the presence of Brønsted acid sites introduces preferential adsorption centres in the framework, where the phenol molecule will spend most of the simulation time (see Fig. 9). The volume of the supercell covered is therefore much lower compared to the all-silica structure, and the loading of additional molecules will not significantly reduce diffusion, which is already hindered by H-bond interactions between the phenol molecules and the acidic protons.
As listed in Table 4, the activation energies of translational diffusion obtained from our MD simulations for the acidic H-Beta zeolite can be as high as 35 kJ mol−1 for a loading of 1 mpuc, which steadily decreases with loading down to a value of 26 kJ mol−1 for 4 mpuc. As expected, the energy barriers are lower, by at least a factor of 1.6, for the all-silica framework under similar simulation conditions, although they show the opposite trend: higher concentrations produce larger activation energies, which is an anticipated outcome as the agglomeration increases (see Table 4). Note that we have used a Si/Al ratio of 15 in the simulations, which places 4 Al atoms in each unit cell. At a concentration of 1 mpuc, each molecule loaded into the acidic zeolite experiences four times the effect of a number of acid sites per unit cell. Therefore, if a molecule gathers enough energy to escape the strong H-bond interaction with the current acidic proton, it may immediately re-adsorb on a neighbouring acid centre. This will inevitably decrease the diffusivity of the molecule, being reflected in a high activation energy of diffusion. However, if the number of phenol molecules is increased, the number of free acid centres will decrease; hence, a molecule that breaks apart from the H-bond interaction with an acidic proton will be less likely to establish a new interaction with surrounding acid centres that are already progressively saturated by the addition of new phenol molecules. For this reason, the energy barrier of diffusion in the acidic zeolite decreases in our simulations when more molecules are loaded into the pore system. We should also note that the maximum loading employed was 4 mpuc, which signifies full saturation of acid sites by phenol molecules. We suggest that a further increase above 4 mpuc may produce a similar trend as observed for all-silica zeolite, since the effects of molecular agglomeration will play a more prominent role once the acid sites are fully saturated.
Translational diffusion is not detected in the present QENS experiments, which could be tentatively justified considering the increment in energy barrier when the translational diffusion of phenol in all-silica zeolite is compared to acidic zeolite. We therefore consider the interaction between phenol and the Brønsted acid sites slows down the molecules, making translation to go undetected in experiment. Supporting this analysis, we have included more information at the end of the present section by comparing the timescales of rotational and translational motions.
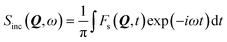 | (3) |
In order to extract information from the MD simulations to be compared with the experiment, it is more convenient to retain the time-domain of the data and work with the function Fs(Q,t). Owing to the polycrystallinity of the zeolite samples used in experiment, we derived the powder average of the function Fs(Q,t) (the modulus |Q|, represented by Q, replaces Q hereafter) from the MD simulations for a suitable comparison to the QENS data:41,92
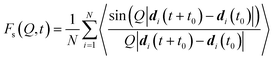 | (4) |
We have initially applied eqn (4) to the rotational part of the intermediate scattering function, Frots(Q,t), since it is the movement detected in experiment, leaving the analysis of the translational part, Ftranss(Q,t), for a later comparison between the timescales of rotation and translation.
We need two exponential decays to properly fit the calculated Frots(Q,t) (a single exponential function provides a poor fit for the ISF), with each exponential representing a motion in a specific frequency domain.40 In the present case, the first decay within below the experimental window of 0.55 meV, while the second is above the 0.55 meV mark, which is an indication of a motion too fast to be observed by the experiment:
| F s(Q,t) = C1(Q)e−Γ1t + C2(Q)e−Γ2t + B(Q) | (5) |
The Ci parameter is a pre-exponential factor that weights the contribution of the rotational motion represented by the respective exponential. The decay constant Γi can be treated in the same way as the half-width at half-maximum of a Lorentzian used to fit the quasielastic part of an experimental QENS signal.40 The constant B(Q) can be considered as an exponential where t = ∞, and thus it represents the final atomic arrangement in Q space; the relation of B(Q) with Q will provide the rotation symmetry of the molecule.41 Hence, the constant B(Q) is equivalent to the EISF, which is given by eqn (2). The EISFs thus derived from the MD simulations are fitted with an isotropic rotation model given by:
| A0(Q) = j02(Qr) | (6) |
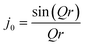 | (7) |
Fig. 10 shows the EISF plot derived from our MD simulations for each temperature, molecular loading and framework, with the isotropic fitting for the highest temperature serving as lower bound of the plots. The radii of gyration for the fitting with the isotropic model are listed in Table 5.
| Acidic zeolite | All-silica zeolite | |||||
|---|---|---|---|---|---|---|
| T (K) | 1 mpuc | 2 mpuc | 4 mpuc | 1 mpuc | 2 mpuc | 4 mpuc |
| 393 | 2.07 | 2.12 | 2.17 | 2.53 | 2.52 | 2.53 |
| 418 | 2.24 | 2.26 | 2.33 | 2.55 | 2.53 | 2.53 |
| 443 | 2.37 | 2.39 | 2.41 | 2.56 | 2.55 | 2.55 |
We observe the most hindered rotational diffusion of phenol in H-Beta at the temperature of 393 K, since the calculated EISF minimum for this temperature lies farthest above the isotropic model (see Fig. 10), which is a direct consequence of the strong H-bond interaction between phenol and the Brønsted acid site. Upon increasing the temperature, a steady decrease of the EISF minimum towards the full isotropic rotation model is observed, indicating a breaking of the interaction between phenol and the acid site as more molecules are able to freely rotate. Notably, the EISF calculated for phenol in the all-silica system matches the full isotropic diffusion model very well at all three temperatures and concentrations, with radii of gyration that fluctuate within a narrow range of 2.52 to 2.56 Å, showing that the movement is far less inhibited by the Van der Waals interactions with the wall of the micro-pores, due to the lack of Brønsted acid sites.
We note that, although the MD simulations include all possible forms of proton motion in the sampled time, and thus the EISF would be a complicated mixture of all such different motions, the isotropic rotation should be predominant as suggested by experiment. In addition, considering that the isotropic model fits the MD data at lower Q values for all systems, we can therefore feel confident to use the isotropic model to directly fit the Frots(Q,t) decays derived from the MD simulation over the range of lower Q values, thus allowing us to calculate rotational diffusion coefficients:41
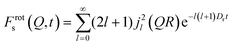 | (8) |
Fig. 11 shows the Q-dependence of the calculated Dr values for the first five Q points of the MD data obtained for phenol in the H-Beta system (4 mpuc), revealing the invariability of Dr with Q. Table 6 lists the values of Dr for each zeolite framework, phenol loading and temperature, together with the activation energies of rotation.
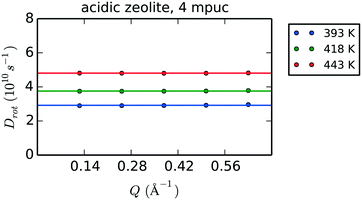 | ||
| Fig. 11 Q-Dependence of the rotational diffusion coefficients Dr evaluated after fitting with eqn (8) the exponential decays obtained using eqn (4) on the MD simulation of 4 mpuc in acidic zeolite. The horizontal solid line sets the average over the Dr values calculated for the first five Q points of the data. | ||
| Acidic zeolite | All-silica zeolite | QENS | |||||
|---|---|---|---|---|---|---|---|
| T (K) | 1 mpuc | 2 mpuc | 4 mpuc | 1 mpuc | 2 mpuc | 4 mpuc | |
| 393 | 2.60 | 2.80 | 2.92 | 7.55 | 6.60 | 5.60 | 2.60 |
| 418 | 3.44 | 3.56 | 3.76 | 9.80 | 8.88 | 7.30 | 2.97 |
| 443 | 4.70 | 4.83 | 4.81 | 11.52 | 10.58 | 9.05 | 3.33 |
| E a | 17.1 | 15.7 | 14.4 | 12.3 | 13.7 | 14.0 | 7.2 |
We obtained rotational diffusion coefficients from the MD simulations of phenol in H-Beta zeolite within the range of 2.60 × 1010 to 4.83 × 1010 s−1. These values are in good agreement with the QENS-derived Dr values, although tending to overestimate experimental coefficients which are in the range of 2.60 × 1010 to 3.33 × 1010 s−1. This overestimation may be caused by a number of phenomena, such as the slight difference in loading between experiment and simulation, the use of interatomic potentials not specifically parameterised for phenol in acidic zeolites, and the neglect of structural defects in the zeolite framework for the models employed in the MD simulations, thereby reducing the strength of the overall interaction between phenol and zeolite, and thus increasing the freedom of movement of the adsorbed molecules. We can also observe from Table 6 that a more rapid variation of the diffusion coefficients with temperature leads to MD-derived activation energies of rotation twice as large as the experimental estimates. Along with the previous reasons outlined, we suggest that higher concentrations of defects in the real systems cause a lower sensitivity of the rotational diffusion to the variation in temperature; in the MD simulations, only the interaction between phenol and the Brønsted acid site through an H-bond may be broken, allowing the molecule to rotate more freely. However, if defects are also present in the structure, a molecule that breaks apart from the acid site could re-adsorb on the defects, consequently reducing the effect of the additional thermal energy introduced in the system by the rise in temperature.
The absence of Brønsted acid sites in the all-silica structure increases the range of rotational diffusion coefficients to 5.60 × 1010–11.52 × 1010 s−1. However, in contrast to the translational diffusion, the activation energies of rotation for phenol in all-silica (12.3–14.0 kJ mol−1) are only marginally smaller than the calculated values in the acidic zeolite (14.4–17.1 kJ mol−1). Therefore, we could consider that the most significant proportion of the rotational dynamics observed for phenol in the acidic zeolite comes from molecules that periodically break apart from the H-bonds with the Brønsted acid sites (again supporting the observations of the QENS experiments). We observed earlier, during the analysis of the translational diffusion, that the higher loading of phenol reduces the frequency of re-adsorption to the Brønsted acid sites, and thus the activation energy of translation consequently decreases (see Table 4). This trend is also observed for the rotational diffusion, with a barrier of 17.1 kJ mol−1 for 1 mpuc reducing to 14.4 kJ mol−1 for 4 mpuc, which contributes to the argument that molecules, which are not strongly interacting with the zeolite framework, are responsible for the observed rotational dynamics (suggesting again that isotropic free rotation is the dominant motion). If we consider that the real system is not ideal, presenting different defects where strong adsorption can occur in addition to the Brønsted sites, the number of molecules contributing to the observed rotational dynamics would further decrease, supporting the model of the immobile fraction used to fit the experimental EISF curves.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) t), replacing di with the coordinates of the center of mass of the phenol molecule i,40,93 allowing us to analyse translational motion independent from molecular rotation. Following the same procedure employed for rotation, the exponential decays derived from eqn (4) are fitted with eqn (5), providing the values of Γ1 and Γ2, which are equivalent to the HWHM of Lorentzians characteristic of a quasielastic scattering. Similar to the rotational part of Fs(Q,t), only Γ1 is taken into account, since the value of Γ2 lies above the present experimental window of 0.55 meV.
t), replacing di with the coordinates of the center of mass of the phenol molecule i,40,93 allowing us to analyse translational motion independent from molecular rotation. Following the same procedure employed for rotation, the exponential decays derived from eqn (4) are fitted with eqn (5), providing the values of Γ1 and Γ2, which are equivalent to the HWHM of Lorentzians characteristic of a quasielastic scattering. Similar to the rotational part of Fs(Q,t), only Γ1 is taken into account, since the value of Γ2 lies above the present experimental window of 0.55 meV.
Fig. 12 shows the plots of Γ1 over the range of Q values smaller than 1.0 Å−1 for the rotation and translation of phenol in acidic and all-silica zeolites with a concentration of 4 mpuc at 393, 418 and 443 K. Considering that the timescale of the motion is proportional to the inverse of its Γ value, we can compare the relative speed of rotation and translation by analysing their Γ1 values. Further comparison to the experimental HWHM shows that rotation is the most likely form of motion detected by QENS, as the rotational broadening calculated from the MD simulations for acidic zeolite is far closer to the experimental value than the broadening simulated for translation, motion that is likely too close to the resolution limit of the instrument to be detected. The values of Γ1 for both rotation and translation in the all-silica zeolite increase compared to the acidic framework, corresponding to motions occurring in a shorter timescale, which is expected from the absence of strong H-bond interactions between phenol and the zeolite; this suggests that we might observe translation in QENS experiments of all-silica zeolites with similar instrumental configuration.
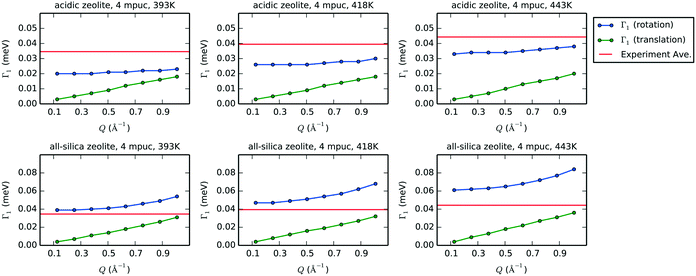 | ||
| Fig. 12 Values of Γ1 after fitting with eqn 5 the exponential decays that represent the intermediate structure factors Fs(Q,t) for rotation (blue) and translation (green) for each value of Q smaller than 1.0 Å−1. In the case of translation, the coordinates of the center of mass are used in eqn (4) to obtain the exponential decays. The plots show acidic zeolite (first row) and all-silica zeolite (second row), with a concentration of 4 mpuc, at the temperatures 393, 418 and 443 K. The horizontal red line in each graph indicates the experimental average of the HWHM at the corresponding temperature. | ||
4 Conclusions
The dynamical behaviour of phenol was measured in zeolite Beta (Si/Al = 12.5) using quasielastic neutron scattering, to probe the behaviour of phenolic monomers of lignin in potential biomass conversion catalysts. The significant elastic component in all spectra at all temperatures, and subsequent fitting of the EISF to the relevant models of localised motion, suggest that on the instrumental timescale we are observing isotropic rotation of the phenol molecule in the zeolite pores, with rotational diffusion coefficients of 2.60 × 1010–3.33 × 1010 s−1. The EISF also showed that at each temperature there is a population of molecules which remain static, and this population decreases with increasing temperature; we can consider this population to be phenol molecules bound to the Brønsted acid sites or other defects in the acidic zeolite catalyst.Molecular dynamics simulations of phenol in zeolite Beta were performed to complement the QENS experiments. The activation energies of translation derived from the MD calculations, with values between 26 and 35 kJ mol−1, support the idea that phenol translational diffusion is likely to be too slow to be observed in the instrumental time window. Calculation of the EISF, and subsequent calculation of rotational diffusion coefficients gave values of 2.60 × 1010 to 4.83 × 1010 s−1, which are in close agreement with the experimental values, although overestimating slightly the freedom of mobility, as is common in such studies. The comparison of the activation energies of rotation in the acidic and all-silica zeolites indicates that molecules not bound to the acidic sites are responsible for the observed rotational dynamics in the MD simulations, supporting the experimental observations that a fraction of phenol is immobile (due to H-bonding to the acidic sites), while the rest undergo isotropic rotation in the H-Beta catalyst pores.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was performed using the computational facilities of the Advanced Research Computing @ Cardiff (ARCCA) Division, Cardiff University, and HPC Wales. Via our membership of the UK's HEC Materials Chemistry Consortium, which is funded by EPSRC [grant number: EP/L000202], this work used the ARCHER UK National Supercomputing Service (http://www.archer.ac.uk). The authors acknowledge EPSRC [grant number: EP/K009567/2] and NERC [grant number: NE/R009376/1] for funding. C. H. T. thanks Dr. S. E. Ruiz-Hernandez for valuable consultations. A. J. O. M. acknowledges the Ramsay Memorial Trust for the provision of a Ramsay Memorial Fellowship, and Roger and Sue Whorrod for the funding of the Whorrod Fellowship. The STFC Rutherford Appleton Laboratory is thanked for access to neutron beam facilities; the data from our experiment RB1720221 can be found at DOI:10.5286/ISIS.E.87772570. All computer simulation data created during this research is openly available from the University of Cardiff Research Portal at http://doi.org/10.17035/d.2019.0082440884.References
- R. Rinaldi and F. Schüth, Energy Environ. Sci., 2009, 2, 610–626 RSC.
- C. Li, X. Zhao, A. Wang, G. W. Huber and T. Zhang, Chem. Rev., 2015, 115, 11559–11624 CrossRef CAS PubMed.
- T. Ennaert, J. Van Aelst, J. Dijkmans, R. De Clercq, W. Schutyser, M. Dusselier, D. Verboekend and B. F. Sels, Chem. Soc. Rev., 2016, 45, 584–611 RSC.
- D. Y. Hong, S. J. Miller, P. K. Agrawal and C. W. Jones, Chem. Commun., 2010, 46, 1038–1040 RSC.
- W. Zhang, J. Chen, R. Liu, S. Wang, L. Chen and K. Li, ACS Sustainable Chem. Eng., 2014, 2, 683–691 CrossRef CAS.
- C. Zhao and J. A. Lercher, ChemCatChem, 2012, 4, 64–68 CrossRef CAS.
- S. Kasakov, H. Shi, D. M. Camaioni, C. Zhao, E. Baráth, A. Jentys and J. A. Lercher, Green Chem., 2015, 17, 5079–5090 RSC.
- C. Costa, I. P. Dzikh, J. M. Lopes, F. Lemos and F. R. Ribeiro, J. Mol. Catal. A: Chem., 2000, 154, 193–201 CrossRef CAS.
- M. Hunger, Catal. Rev.: Sci. Eng., 1997, 39, 345–393 CrossRef CAS.
- K. Tanabe and W. F. Hölderich, Appl. Catal., A, 1999, 181, 399–434 CrossRef CAS.
- A. Galadima and O. Muraza, Microporous Mesoporous Mater., 2017, 249, 42–54 CrossRef CAS.
- B. Güvenatam, E. H. Heeres, E. A. Pidko and E. J. Hensen, Catal. Today, 2016, 269, 9–20 CrossRef.
- B. Güvenatam, E. H. Heeres, E. A. Pidko and E. J. Hensen, J. Mol. Catal. A: Chem., 2015, 410, 89–99 CrossRef.
- J. Lu, S. Behtash, O. Mamun and A. Heyden, ACS Catal., 2015, 5, 2423–2435 CrossRef CAS.
- L. Nie, P. M. De Souza, F. B. Noronha, W. An, T. Sooknoi and D. E. Resasco, J. Mol. Catal. A: Chem., 2014, 388–389, 47–55 CrossRef CAS.
- Q. Tan, G. Wang, L. Nie, A. Dinse, C. Buda, J. Shabaker and D. E. Resasco, ACS Catal., 2015, 5, 6271–6283 CrossRef CAS.
- L. Nie and D. E. Resasco, J. Catal., 2014, 317, 22–29 CrossRef CAS.
- C. Hernandez-Tamargo, A. Roldan and N. H. de Leeuw, J. Phys. Chem. C, 2019, 123, 7604–7614 CrossRef CAS.
- C. E. Hernandez-Tamargo, A. Roldan and N. H. de Leeuw, Mol. Catal., 2017, 433, 334–345 CrossRef CAS.
- C. Zhao, D. M. Camaioni and J. A. Lercher, J. Catal., 2012, 288, 92–103 CrossRef CAS.
- C. Zhao, S. Kasakov, J. He and J. A. Lercher, J. Catal., 2012, 296, 12–23 CrossRef CAS.
- A. J. O'Malley, S. F. Parker and C. R. A. Catlow, Chem. Commun., 2017, 53, 12164–12176 RSC.
- D. T. Lundie, A. R. McInroy, R. Marshall, J. M. Winfield, P. Jones, C. C. Dudman, S. F. Parker, C. Mitchell and D. Lennon, J. Phys. Chem. B, 2005, 109, 11592–11601 CrossRef CAS PubMed.
- M. E. Potter, S. Chapman, A. J. O'Malley, A. Levy, M. Carravetta, T. M. Mezza, S. F. Parker and R. Raja, ChemCatChem, 2017, 9, 1897–1900 CrossRef CAS.
- R. F. Howe, J. McGregor, S. F. Parker, P. Collier and D. Lennon, Catal. Lett., 2016, 146, 1242–1248 CrossRef CAS.
- A. J. O'Malley, S. F. Parker, A. Chutia, M. R. Farrow, I. P. Silverwood, V. García-Sakai and C. R. A. Catlow, Chem. Commun., 2016, 52, 2897–2900 RSC.
- H. Jobic and D. N. Theodorou, Microporous Mesoporous Mater., 2007, 102, 21–50 CrossRef CAS.
- H. Jobic, J. Mol. Catal. A: Chem., 2000, 158, 135–142 CrossRef CAS.
- H. Jobic and D. N. Theodorou, J. Phys. Chem. B, 2006, 110, 1964–1967 CrossRef CAS PubMed.
- H. Paoli, A. Méthivier, H. Jobic, C. Krause, H. Pfeifer, F. Stallmach and J. Kärger, Microporous Mesoporous Mater., 2002, 55, 147–158 CrossRef CAS.
- S. Mitra, A. Tripathy, N. Gupta and R. Mukhopadhyay, Appl. Phys. A: Mater. Sci. Process., 2002, 74, s1308–s1310 CrossRef CAS.
- H. Jobic, M. Bée and A. J. Dianoux, J. Chem. Soc., Faraday Trans. 1, 1989, 85, 2525 RSC.
- S. K. Matam, A. J. O'Malley, C. R. A. Catlow, S. Suwardiyanto, P. Collier, A. P. Hawkins, A. Zachariou, D. Lennon, I. Silverwood, S. F. Parker and R. F. Howe, Catal. Sci. Technol., 2018, 8, 3304–3312 RSC.
- H. Jobic, A. Renouprez, M. Bee and C. Poinsignon, J. Phys. Chem., 1986, 90, 1059–1065 CrossRef CAS.
- V. K. Sharma, S. Gautam, S. Mitra and R. Mukhopadhyay, Z. Phys. Chem., 2010, 224, 133–152 CrossRef CAS.
- A. J. O'Malley, I. Hitchcock, M. Sarwar, I. P. Silverwood, S. Hindocha, C. R. A. Catlow, A. P. E. York and P. J. Collier, Phys. Chem. Chem. Phys., 2016, 18, 17159–17168 RSC.
- B. J. Borah, H. Jobic and S. Yashonath, J. Chem. Phys., 2010, 132, 144507 CrossRef PubMed.
- A. J. O'Malley, C. R. A. Catlow, M. Monkenbusch and H. Jobic, J. Phys. Chem. C, 2015, 119, 26999–27006 CrossRef.
- A. J. O'Malley, V. García Sakai, I. P. Silverwood, N. Dimitratos, S. F. Parker and C. R. A. Catlow, Phys. Chem. Chem. Phys., 2016, 18, 17294–17302 RSC.
- A. Sayeed, S. Mitra, A. V. Anil Kumar, R. Mukhopadhyay, S. Yashonath and S. L. Chaplot, J. Phys. Chem. B, 2003, 107, 527–533 CrossRef CAS.
- R. Mukhopadhyay, A. Sayeed, S. Mitra, A. V. Anil Kumar, M. N. Rao, S. Yashonath and S. L. Chaplot, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 66, 061201 CrossRef CAS PubMed.
- X. Zhu, L. L. Lobban, R. G. Mallinson and D. E. Resasco, J. Catal., 2011, 281, 21–29 CrossRef CAS.
- C. Zhao, W. Song and J. A. Lercher, ACS Catal., 2012, 2, 2714–2723 CrossRef CAS.
- X. Zhu, L. Nie, L. L. Lobban, R. G. Mallinson and D. E. Resasco, Energy Fuels, 2014, 28, 4104–4111 CrossRef CAS.
- M. T. F. Telling and K. H. Andersen, Phys. Chem. Chem. Phys., 2005, 7, 1255–1261 RSC.
- X. Wang and R. Rinaldi, Angew. Chem., Int. Ed., 2013, 52, 11499–11503 CrossRef CAS PubMed.
- Z. Ma, V. Custodis and J. A. Van Bokhoven, Catal. Sci. Technol., 2014, 4, 766–772 RSC.
- R. T. Azuah, L. R. Kneller, Y. Qiu, P. L. Tregenna-Piggott, C. M. Brown, J. R. Copley and R. M. Dimeo, J. Res. Natl. Inst. Stand. Technol., 2009, 114, 341–358 CrossRef CAS PubMed.
- O. Arnold, J. Bilheux, J. Borreguero, A. Buts, S. Campbell, L. Chapon, M. Doucet, N. Draper, R. Ferraz Leal, M. Gigg, V. Lynch, A. Markvardsen, D. Mikkelson, R. Mikkelson, R. Miller, K. Palmen, P. Parker, G. Passos, T. Perring, P. Peterson, S. Ren, M. Reuter, A. Savici, J. Taylor, R. Taylor, R. Tolchenov, W. Zhou and J. Zikovsky, Nucl. Instrum. Methods Phys. Res., Sect. A, 2014, 764, 156–166 CrossRef CAS.
- J. D. Gale and A. L. Rohl, Mol. Simul., 2003, 29, 291–341 CrossRef CAS.
- J. D. Gale, Z. Kristallogr., 2005, 220, 552–554 CAS.
- I. T. Todorov, W. Smith, K. Trachenko and M. T. Dove, J. Mater. Chem., 2006, 16, 1911–1918 RSC.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS PubMed.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251–14269 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- R. Grau-Crespo, S. Hamad, C. R. A. Catlow and N. H. De Leeuw, J. Phys.: Condens. Matter, 2007, 19, 256201 CrossRef.
- M. Born and K. Huang, Dynamical Theory of Crystal Lattices, Oxford University Press, Oxford, 1988 Search PubMed.
- P. P. Ewald, Ann. Phys., 1921, 369, 253–287 CrossRef.
- J. E. Jones, Proc. R. Soc. London, Ser. A, 1924, 106, 463–477 CrossRef CAS.
- R. A. Buckingham, Proc. R. Soc. London, Ser. A, 1938, 168, 264–283 CrossRef CAS.
- M. J. Sanders, M. Leslie and C. R. Catlow, J. Chem. Soc., Chem. Commun., 1984, 1271–1273 RSC.
- C. R. Catlow, R. James, W. C. MacKrodt and R. F. Stewart, Phys. Rev. B, 1982, 25, 1006–1026 CrossRef CAS.
- K. P. Schröder, J. Sauer, M. Leslie, C. Richard, A. Catlow and J. M. Thomas, Chem. Phys. Lett., 1992, 188, 320–325 CrossRef.
- D. A. Mooney, F. Müller-Plathe and K. Kremer, Chem. Phys. Lett., 1998, 294, 135–142 CrossRef CAS.
- G. Sastre, N. Raj, C. R. A. Catlow, R. Roque-Malherbe and A. Corma, J. Phys. Chem. B, 1998, 102, 3198–3209 CrossRef CAS.
- J. P. Ryckaert, G. Ciccotti and H. J. Berendsen, J. Comput. Phys., 1977, 23, 327–341 CrossRef CAS.
- R. Vetrivel, C. R. A. Catlow and E. A. Colbourn, J. Chem. Soc., Faraday Trans. 2, 1989, 85, 497–503 RSC.
- International Zeolite Association, http://www.iza-structure.org/databases/ModelBuilding/BEA.pdf Search PubMed.
- J. M. Newsam, M. M. J. Treacy, W. T. Koetsier and C. B. D. Gruyter, Proc. R. Soc. London, Ser. A, 1988, 420, 375–405 CrossRef CAS.
- A. R. Ruiz-Salvador, R. Grau-Crespo, A. E. Gray and D. W. Lewis, J. Solid State Chem., 2013, 198, 330–336 CrossRef CAS.
- H. J. C. Berendsen, J. P. M. Postma, W. F. van Gunsteren, A. DiNola and J. R. Haak, J. Chem. Phys., 1984, 81, 3684–3690 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133–A1138 CrossRef.
- P. E. Blöchl, Phys. Rev. B, 1994, 50, 17953–17979 CrossRef PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B, 1999, 59, 1758–1775 CrossRef CAS.
- H. Monkhorst and J. Pack, Phys. Rev. B, 1976, 13, 5188–5192 CrossRef.
- K. M. Ho, C. L. Fu, B. N. Harmon, W. Weber and D. R. Hamann, Phys. Rev. Lett., 1982, 49, 673–676 CrossRef CAS.
- C. L. Fu and K. M. Ho, Phys. Rev. B, 1983, 28, 5480–5486 CrossRef CAS.
- M. Methfessel and A. T. Paxton, Phys. Rev. B, 1989, 40, 3616–3621 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- W. H. Press, S. A. Teukolsky, W. T. Vetterling and B. P. Flannery, The Art of Scientific Computing, Cambridge University Press, New York, 3rd edn, 2007 Search PubMed.
- F. Birch, Phys. Rev., 1947, 71, 809–824 CrossRef CAS.
- S. Nosé, J. Chem. Phys., 1984, 81, 511–519 CrossRef.
- S. Nosé, Prog. Theor. Phys. Suppl., 1991, 103, 1–46 CrossRef.
- D. M. Bylander and L. Kleinman, Phys. Rev. B, 1992, 46, 13756–13761 CrossRef PubMed.
- V. F. Sears, Can. J. Phys., 1966, 44, 1279–1297 CrossRef CAS.
- F. Volino and A. Dianoux, Mol. Phys., 1980, 41, 271–279 CrossRef CAS.
- A. J. O'Malley, M. Sarwar, J. Armstrong, C. R. A. Catlow, I. P. Silverwood, A. P. E. York and I. Hitchcock, Phys. Chem. Chem. Phys., 2018, 20, 11976–11986 RSC.
- S. C. Wiedemann, A. Muñoz-Murillo, R. Oord, T. van Bergen- Brenkman, B. Wels, P. C. Bruijnincx and B. M. Weckhuysen, J. Catal., 2015, 329, 195–205 CrossRef CAS.
- K. W. Herwig, Z. Wu, P. Dai, H. Taub and F. Y. Hansen, J. Chem. Phys., 1997, 107, 5186–5196 CrossRef CAS.
- S. Gautam, T. Le, A. Striolo and D. Cole, Phys. Chem. Chem. Phys., 2017, 19, 32320–32332 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9cy01548e |
| This journal is © The Royal Society of Chemistry 2019 |