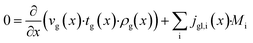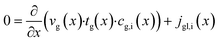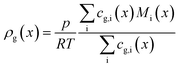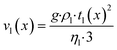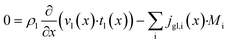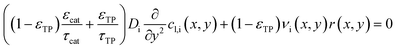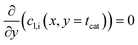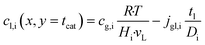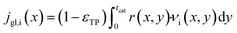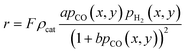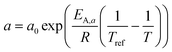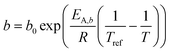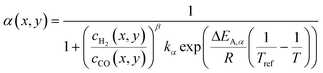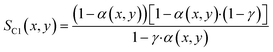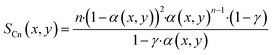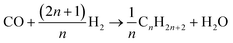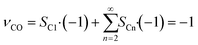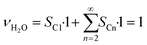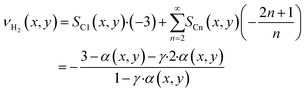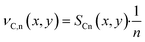Performance of diffusion-optimised Fischer–Tropsch catalyst layers in microchannel reactors at integral operation†
Received
7th March 2019
, Accepted 29th March 2019
First published on 1st April 2019
Abstract
Microchannel reactors offer a solution to utilize highly active catalysts for the Fischer–Tropsch process. The use of a wall-coated catalyst improves temperature control and prevents the negative correlation between pressure drop and catalyst efficiency. Diffusion limitations are, however, still a concern as a high reactor productivity demands a large catalyst layer thickness, to increase catalyst holdup while using as few channels as possible. Utilizing transport pores is one way of optimising the catalyst and achieving greater layer thicknesses while maintaining a good product selectivity. In this publication, we describe an isothermal and isobaric microchannel-reactor with a novel product film formation model and an improved selectivity description for accurate calculation of the product distribution. The optimisation of catalyst layers by defining ideal thicknesses and transport pore fraction is tested within realistic integral operation of the catalyst layers. Because the catalysts selectivity is strongly affected by the local syngas ratio the interplay of diffusion effects and convection in the gas phase is of major importance for the accurate prediction of catalyst behaviour. Non-optimised layers with great layer thickness and strong impact of diffusion limitations improve their performance with increasing conversion. Optimised layers with ideal amounts of transport pores and very thin layers, for which diffusion restrictions are less significant, on the other hand, exhibit an opposite behaviour and do not benefit from high conversions. These findings can also improve the interpretation of experimental results, which are often conducted at different conversion levels.
Introduction
The Fischer–Tropsch (FT) synthesis is a well-known process for the conversion of different carbon feedstocks, from fossil or renewable sources, to liquid fuels and waxes. The so-called low temperature FT synthesis is an exothermic reaction conducted on cobalt based supported catalysts. At reaction conditions the gaseous reactants are converted to liquid products within the porous catalyst. Various reactor concepts have been employed to accommodate the reaction, with fixed bed reactors and slurry bubble columns being commercially established,1–3 whereas CSTRs, monolithic reactors and microchannel reactors are widely used in lab scale.
Conventional fixed bed reactors offer a high catalyst hold-up but are limited in terms of heat removal capacity and internal diffusion restrictions may occur when large catalyst particles are used. Different pathways to define the structure of the catalyst can help to overcome these restrictions.4 By employing cross flow structures, the radial heat transfer within the reactor tubes can be enhanced and allows for higher productivities.5–7 Microreactors with randomly packed catalyst beds exhibit an even further enhanced heat transfer resulting in almost isothermal operation and can handle highly active catalysts.8–11 The smaller channel dimensions, however, require smaller particle sizes that avoid diffusion limitations but also increase the pressure drop significantly,9,11,12 thus limiting the potential reactor length. Open channels with catalyst layers on the channel walls break up this negative coupling of the pressure drop and diffusion length and have been tested in washcoated monoliths, foams and microchannels. Ceramic monoliths are often operated with a product recycle to limit the temperature rise, due to the low thermal conductivity of the support material.13–15 Metallic monoliths on the other hand have been used in single-pass tubular reactors, due to their higher heat conductivity,16–19 though these structures still pose the risk of significant temperature gradients.19 Microchannels with a wall-coated catalyst do not suffer from these heat distribution problems and have been tested experimentally.17,20–23 For both types of microreactors, packed beds and wall coatings, the variation of catalyst thickness has shown lower selectivities of desired long chain products when the catalyst layer thickness is increased. Using a maximal layer thickness is of paramount interest to operate commercial reactors with as few channels as possible for a given reactor size. An upper boundary for the layer thickness exists because the internal mass transport limits the maximum exploitable catalyst thickness, which is analogue to the diffusion limitation of catalyst particles.24–26
By using transport pores the internal diffusion is enhanced and can improve the observed selectivities, as shown in the group of Montes18,27 and also by our previous work.22 Our existing simulation work28 predicts the improved selectivity but also predicts an improved total productivity, which does not agree well with the experimental evidence. This can be a result of the simplified model, not taking axial convection into account. Thus, the effect of integral reactor operation is addressed within this publication.
Despite an abundance of simulation work on the FT process, to the authors' knowledge, there is no work satisfyingly describing and comparing the behaviour of catalysts under integral operation for different diffusion lengths or for employment of transport pores. Simulation work with differential reactors was either only focusing on pore optimisation in general29,30 or elaborating specifically on the relation between diffusion, selectivity and pore filling degree28,31–34 or FT kinetics.35,36 When complete reactors were considered often fluidized catalyst systems have been used,37–39 which are useful for kinetic studies but not directly applicable to fixed bed reactors. In cases where fixed bed reactors were simulated, diffusion effects were often neglected because the interest was on describing product selectivities,40,41 the transient deactivation42–44 or combining FTS with hydroprocessing.45 Jess and Kern46,47 made detailed simulations with a model combining effects of mass and heat diffusion and convection, but chose a constant selectivity model. For milli-fixed-beds and larger reactors significant temperature profiles develop7,48,49 making a comparison with microchannel reactor data difficult. Based on their experimental data Almeida et al.21 developed a reactor model for microchannel reactors, though diffusion effects were not implemented. Similarly, Ostadi et al.50 tested various kinetics in a reactor model against experimental data from a microreactor and explored possible effects of conversion and the effect of water on selectivity. But, internal mass transport was again not considered.
The present paper focuses on a model that combines an improved, variable selectivity model with internal diffusion and gas and liquid convection for a wall coated reactor set-up. This allows detailed evaluation of the impact of diffusion restrictions on syngas ratios, product selectivities and reactor performance during integral operation of reactors that utilize catalysts with and without transport pores.
Model description
The simulations conducted for this publication are based on the model as described in our previous publications. A few changes to the employed kinetics were applied to allow for a more accurate representation of the real system. Because methane selectivity is typically not in line with the value expected from a strict Anderson–Schulz–Flory distribution, an additional parameter was used, as described by Förtsch et al.51 Our previous simulation work considered differential reactors only. For the simulation of more realistic integral reactors the axial dimension in which the convective transport occurs was added. Based on work of Nusselt on the film condensation of water52 an analogue approach was adapted for the reactive film formation of liquid products to estimate the effect of external mass transport. Because our previous work has shown only very minor temperature gradients due to the heat generation, heat balances were not included in the model. Also neglected was all time-dependent behaviour. The catalyst does not deactivate, which occurs over a long-term period, and after start-up all pores are completely filled with only liquid hydrocarbons, which is estimated to be completed in several hours.
A schematic overview of the model is provided with Fig. 1 illustrating the different phases, simulation domains and general terms for the reactor dimensions.
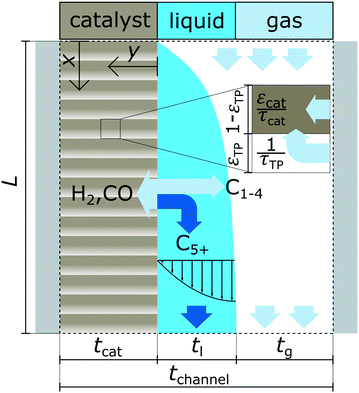 |
| | Fig. 1 Graphical illustration of the reactor model with the three phases, overall dimensions and simulation domains; “x” indicates axial coordinate and “y” indicates coordinate for the lateral direction. | |
Transport in gas phase
The dominating transport along the axial direction is governed by the convection in the gas phase. Therefore, the total mass transport is described with eqn (1) taking the variable gas density, its velocity and the open gas channel thickness into account for the convective term and adding the cumulative mass exchange flux with the liquid phase. For each species the concentration profile is described with eqn (2), being analogously build to eqn (1). The known inlet gas velocity and gas composition serve as the required boundary conditions, eqn (3) and (4). Eqn (5) completes the gas phase description by linking the gas density with the gas composition assuming ideal gas behaviour.| | 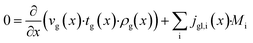 | (1) |
| | 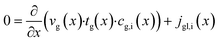 | (2) |
| | 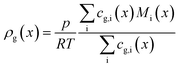 | (5) |
Transport in liquid phase
Purpose of the modelling of the liquid film formation is to assess its impact on external mass transport and layer performance, thus prediction of film thickness is the aim. In literature different attempts to include the liquid phase are based on equilibrium calculations41,53 or complex multidimensional simulations54 or the equations used are of empirical origin.7,55,56 For ease of simulation a simplistic, non-empirical model of the formation of a liquid film on top of the catalyst layer is applied. It is analogue to the “water film theory” as published by Nusselt on the condensation of water on a vertical surface.52 The assumptions to create the model are no momentum transport from the gas to the liquid phase and an ideal laminar flow on a smooth surface. The model allows to express the average liquid velocity as function of the liquid film thickness, eqn (6). This in turn allows to solve the partial differential of eqn (7) when the boundary condition, eqn (8), at the inlet is applied and provides the axial profile of the liquid film thickness. As the liquid film forms, the volume for the gas phase decreases, eqn (9).| | 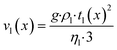 | (6) |
| | 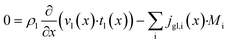 | (7) |
| | | tg(x) = tchannel − tl(x) − tcat | (9) |
These equations do not describe any axial transport of the reactants or products within the liquid phase and only account for the formation of a liquid film generated by accumulating liquid products. This accumulation of products in the liquid phase is the opposite of the sink term in eqn (1) and requires the molar fluxes from the gas to the liquid phase of each species. These fluxes are solved by describing the reaction in the catalyst phase.
Diffusion and reaction in catalyst
For each point along the axial direction of the channel the reaction-diffusion equation is solved, eqn (10). This expression is as used in our previous works.28,34 It contains the modification of the effective diffusivity to include diffusion in transport pores. This modification is valid for sufficiently small transport pores to ensure a homogeneous concentration profile. Initial estimation lead to upper limits for transport pore diameters of 1–2 μm under all circumstances.28 For transport pore fractions exceeding 10% the limit can increase to 10 μm; later 3D simulations confirmed this.57 Thus, transport pores can be about three orders of magnitude larger than the typical mesopores of catalysts. Additionally, the concentration of the reactants, the stoichiometric coefficients and the reaction rate are now also dependent on the axial coordinate.| | 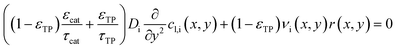 | (10) |
| | 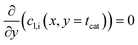 | (11) |
| | 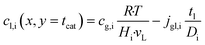 | (12) |
It is worth noting that eqn (10) needs to be computed only for the reactants in order to obtain the reaction rate and the selectivity profile. The two boundary conditions for either species are built on the assumption of no flux through the reactor wall and a linear concentration profile within the liquid film, eqn (11) and (12). The latter ignores the parabolic velocity profile within the liquid film and any axial transport of reactants inside it. This is required to avoid a true multidimensional simulation approach, with its higher computational efforts, and is justified by the magnitudes lower axial transport in the liquid film. Due to the much lower liquid holdup, compared with the gas holdup, and further due to the lower concentration of reactants in the liquid than in the gas phase, reactants are typically over three magnitudes more efficiently transported in the gas than in the liquid (see ESI,† Fig. S3). Finally, to complete the set of transport equations the aforementioned molar flux of species needs a description by integrating the reaction rate and the stoichiometric coefficients throughout the layer at a given position along the axial direction, eqn (13).
| | 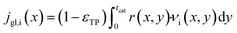 | (13) |
Eqn (13) is evaluated for CO, H2 and for the alkanes from C1 to C4. For all higher hydrocarbons the molar flux from the gas to the liquid phase is set to zero. This simplifies the system and defines the C1 to C4 hydrocarbons as purely gaseous and all other hydrocarbons as completely non-volatile and lumped together in the liquid phase. Though Visconti and Mascellaro41 have shown that there is a distribution of hydrocarbons between gas and liquid phase up to triacontane, simple balancing leads to a total C5+ hydrocarbon molar fraction of only up to 4% – in the worst case. Thus, only minor changes to gas concentration could be expected from a more realistic model, at the cost of severe computational efforts. Hence, the simplified model seems justified.
Kinetics
A kinetic model of Langmuir–Hinshelwood type is used, as described by Yates and Satterfield,58eqn (14), to calculate the distribution of the reaction rate. Despite the many kinetics being proposed for the FT reaction, this type was chosen because it is widely used in literature.6,7,31–33,43,45,48,49,59 The frequency factor and the sorption coefficient are complemented with a temperature dependency,37eqn (15) and (16). To allow for an easy adjustment of overall activity an additional activity factor F was also added to eqn (14).| | 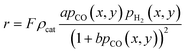 | (14) |
| | 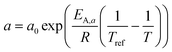 | (15) |
| | 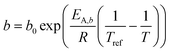 | (16) |
The product distribution is calculated assuming an ASF-distribution with an α-model based on works of Vervloet et al.,31eqn (17). This computes the value of the chain growth probability at each point along the axial and the lateral direction as function of the H2–CO ratio and temperature.
| | 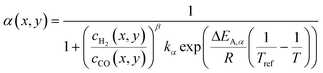 | (17) |
With the ASF-distribution alone a common behaviour of FT catalyst to exhibit an overly high methane selectivity, also observed in our previous experimental work,22 cannot be predicted and a modification is required. A simple, yet rigorous modification comes by Förtsch et al.,51 which introduces only one further constant that describes the enhanced termination probability for methane. With this the selectivity for methane and all other hydrocarbons can be written as shown by eqn (18) and (19).
| | 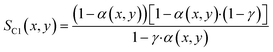 | (18) |
| | 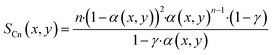 | (19) |
These equations are useful for detailed analysis, yet for computing the stoichiometric coefficients need to be defined using the selectivities. The general reaction, eqn (20), is valid for alkanes of all chain lengths.
| | 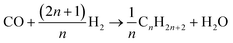 | (20) |
As the species CO, H2 and H2O are the same for each reaction to an alkane of a certain carbon number, cumulation of their stoichiometric coefficients over all carbon numbers results in their coefficients for the total reaction, eqn (21) to (23). For the hydrocarbons the coefficient is calculated for each individual species, eqn (24).
| | 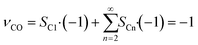 | (21) |
| | 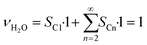 | (22) |
| | 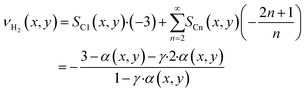 | (23) |
| | 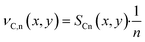 | (24) |
All simulation work was done using the same values and physical property models60,61 as hitherto used, only the liquid viscosity necessitated amendments to the models.62 For calculation of the values the average carbon number of the liquid product was kept constant at a value of 28 to allow best comparability with previous results. This is also close to the average molar number reported by Visconti and Mascellaro41 based on experimental and simulation data. The kinetics also remained unchanged with the exemption of the modification to the ASF distribution by adding a parameter for increased methane formation probability. This additional parameter required a value, which was assigned to 0.5. This is exactly in the middle between the two limits and close to the result from initial fitting on experimental data (see ESI,† Fig. S2). However, the scope of this publication is not parameter estimation but rather a simulation study to understand the behaviour of diffusion limited catalyst layers in integral reactors, justifying the reasonable guess for that parameter. Physical properties and kinetic parameters are shown in Tables 1 and 2, respectively. The calculations were conducted for conditions as stated in Table 3. Because the H2–CO ratio, inert fraction, activity factor and channel length were varied, their range is also included in the tables. The model was implemented in and computed with gPROMS ModelBuilder, version 4.2.
Table 1 Physical properties of the liquid products
| Parameter |
Value |
Unit |
|
D
CO
|
1.430 × 10−8 |
m2 s−1 |
|
D
H2
|
3.605 × 10−8 |
m2 s−1 |
|
H
CO
|
363.7 |
bar |
|
H
H2
|
458.6 |
bar |
|
η
l
|
0.7399 × 10−3 |
Pa s |
|
v
L
|
0.5818 × 10−3 |
mol m−3 |
|
ρ
l
|
678.5 |
kg m−3 |
Table 2 Default kinetic parameters for reaction rate and selectivity equations; for parameter variation range in parenthesis
| Parameter |
Value |
Unit |
|
F
|
1(…10) |
— |
|
ρ
cat
|
1000 |
kg m−3 |
|
a
0
|
8.853 × 10−3 |
mol s−1 kg−1 bar−2 |
|
b
0
|
2.226 |
bar−1 |
|
E
A,a
|
37.37 |
kJ mol−1 |
|
E
A,b
|
−68.48 |
kJ mol−1 |
|
k
α
|
0.0567 |
— |
|
β
|
1.76 |
— |
| ΔEA,α |
120.4 |
kJ mol−1 |
|
T
ref
|
493.15 |
K |
|
γ
|
0.5 |
— |
Table 3 Reaction conditions and structural parameters of the catalyst and reactor; for parameter variation range in parenthesis
| Parameter |
Value |
Unit |
|
T
|
493.15 |
K |
|
p
|
21 |
bar |
| H2/CO |
2(0.01…5) |
mol/mol |
|
x
inert
|
0(…0.95) |
mol/mol |
|
τ
cat
|
3 |
— |
|
τ
TP
|
1 |
— |
|
L
|
0.05(…1) |
m |
|
t
channel
|
0.001 |
m |
Simulation results
Typical behaviour and expectations
The intention of this paper is, first, to evaluate the differences between differential and the more complex integral operation of catalyst layers. Secondly, it is of interest whether any changes exist and to which extent these changes affect the optimisation of catalyst layers by using transport pores. As a standard comparison for further simulations the behaviour of differentially operated catalyst layers is shown in Fig. 2. It repeats the results of our previous work with the most recent model, where only the sink or source term in eqn (1), (2) and (7) are set to zero changing the integral model into a differential one, where there are no axial gradients. The results illustrate the objective of the simulation, the ATY, which is the molar flux of C5+ products at the catalyst surface (for definition see ESI†). It is a better-suited variant of the more commonly used space time yield, STY, but instead of catalyst volume the surface area is used as reference because only the latter is constant for the wall coated reactors. Comparison of ATY is done for so-called “dense” and “ideal” layers of varying thicknesses. Dense layers have no additional transport pores, thus from a thickness of 140 μm and onwards strong diffusion limitations set in and reduce the maximum utilization of the catalyst, leading to a distinctive maximum in the ATY. This is mainly caused by a sudden drop in C5+-selectivity and only marginally delayed by the slightly further increasing catalyst efficiency. At around 160 μm of layer thickness, the catalyst efficiency has reached its maximum with almost 140% and starts to decline for even thicker layers. The peculiar behaviour of the efficiency is a result of the kinetics with CO as a reaction inhibiting species and the slower diffusion of CO compared to H2. Introducing an ideal fraction of transport pores in the catalyst layer prevents the drop in ATY by finding the optimal trade-off between improved diffusive mass transport and not excluding to much active phase from the reaction. Because diffusion restrictions change with layer thickness, the ideal fraction of transport pores is also dependent on the layer thickness. For layers up to 140 μm no transport pores are necessary and from that point on an ever-increasing ideal fraction of transport pores is needed. As the beneficial effect of transport pores is limited, the highest ATY can be obtained at a thickness of 353 μm with 42% transport pores in the layer. Depending on how to calculate the improvement, by either comparing the total maximum for both layer types or comparing the improvement for every single layer thickness a gain in ATY of 50% or up to almost 100% can be achieved, respectively.
 |
| | Fig. 2 Catalyst efficiency, C5+-selectivity and ATY as function of layer thickness for layers without (“dense”) and with “ideal” fraction of transport pores for a differentially operated catalyst layer. | |
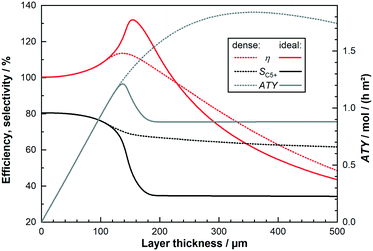
When considering the effect integral reactor operation on the optimization of diffusion limited catalyst layers will have, the predominant question is how a change in reactant concentration affects the reaction rates and selectivities. To answer this, rather than discussing the concentration values themselves, the H2–CO ratio and the fraction of inert components, representing true inert gases and products, is used – the model treats the latter as unreactive. This provides plots that are streamlined to illustrate the behaviour of catalyst layers with and without diffusion limitations, before integral reactors are discussed. Using just conversion as a parameter is a futile approach because the differing initial selectivity will change the relative consumption of H2 and CO leading to different concentration profiles even if the conversion were the same. Fig. 3a shows the simulation results of a thin layer of 25 μm thickness as function of the H2–CO ratio and for different fractions of inert components, again under differential operation. Fig. 3b does the same for a much thicker layer of 200 μm to allow for the comparison of a heavily diffusion restricted catalyst layer with the thin layer, for which diffusion limitations are almost non-existent. For ease of orientation the vertical line indicates a syngas ratio of two, which is a commonly used value and chosen here as feed ratio for subsequent integral reactor simulations. The overall reaction rate for the thin layer exhibits the well-known behaviour of the kinetic expression. Within the observed range the rate increases in H2-richer atmospheres and decreases when the atmosphere is lean of H2. When greater fractions of inert gases displace the reactants, the reaction decelerates and the trend of increasing rate for larger H2–CO ratios also disappears. The picture for the thick layer is quite different. Only the inert component fraction acts similarly as it reduces the rate by doing so to the reactant concentration. But the influence of a varying H2–CO ratio has changed, especially for values exceeding two, where different ratios hardly have an impact on the resulting rate and the overall rate is much lower compared with the thin layer. Interestingly, for ratios of about two and lower the rate is higher than for the thin layer before again falling below the rate of the thin layer for syngas ratios of about 1.1 and lower. This can be explained by the diffusion limitations as indicated by the catalyst efficiency. The thin layer deviates only slightly from an efficiency of 100% under all circumstances, thus displaying the “true” kinetic behaviour. However, the thicker layer is deviating substantially from this. As the intrinsic reaction rate is accelerated by greater H2 fractions, diffusion limitations become more prominent and lead to generally reduced efficiencies with increasing syngas ratios. For very low H2–CO ratios the rate is slowed down enough to get the efficiency back to almost the intrinsic level. But, due to the difference in diffusivities for CO and H2 there is a range in which the concentration loss, caused by diffusion, also shifts the H2–CO ratios inside the layer to much higher values, that overcompensates the loss in reaction rate by lowered reactant concentration. This leads to a distinctive maximum in the catalyst efficiency, exceeding 100%, at a ratio of about 1.8 for 0% inert gas fraction. With increasing inert fraction, the rate is slowed down and the response to changes in the syngas ratio is lessened. This flattens out the curves, lowers the catalyst efficiency and eventually leads to the disappearance of the observable maximum. For the C5+-selectivity, starting with the thin layer, there is hardly any influence by dilution of the reactants leading to a distinctive s-shaped curve over the H2–CO ratio on the y-axis. For very low hydrogen levels the C5+-selectivity approaches 100%, it is reduced to about 80% for a ratio of two and drops further down to 20% with increasing syngas ratio. This is basically a direct result of the selectivity describing equations. But, for the thick layer, in which diffusion restrictions change the internal concentration profile, this is no longer the case. The line starts with an almost constant value of 100% at very low syngas ratios before the s-shaped curve is much more pronounced with a very steep drop and eventually followed by an asymptotic approach of 0% for rising H2–CO ratios. Dilution is again less important than for the rate but especially in the middle, where the drop is the steepest for pure reactants, any dilution increases the selectivity towards longer chained products. Because integral reaction rate and selectivity have opposing tendencies and both factor in the calculation of the ATY, the ATY displays a maximum. This holds for either layer depicted, albeit the absolute values are quite different, which is merely a result of the eightfold difference in thickness. Nonetheless, there is a crucial difference for both layers, that is the position of the maximum. For the thin layer it is located above a syngas ratio of two, whereas the thick layer reaches its highest ATY values below the ratio of two. This is of importance when considering the consumption ratio, which exhibits almost a mirrored curve to the C5+-selectivity and exceeds a value of two all the time. This means that the consumption ratio is always higher than the feed ratio of two and will inevitably lead to a substoichiometric syngas ratio within the entire reactor. Because the maximum ATY for thick layers lies below the feed ratio, these layers should benefit from integral operation, whereas the performance of thin layers will deteriorate. The extent of this is of course dependent on conversion and also on the volume of gaseous products that dilute the reactants in the gas phase. This means that a catalyst layer with a higher C5+-selectivity, e.g. a thin layer with little diffusion limitations, will create lesser amounts of C1–4 species than a thick layer. To illustrate this interplay the trajectories of integrally operated reactors are added to Fig. 3a and b as red lines, together with numbers indicating the gas fraction of inert species at the inlet, 0%, and at the outlet, where the CO conversion is kept constant at 80%. These trajectories are based on the results of the subsequent section, where the axial profiles during integral operation for two layers as examples for thick and thin layers are shown. Here, instead, the data is plotted as function of the local syngas ratio. The 25 μm layer reaches a final inert gas fraction of 66.1% and the 200 μm layer a higher value of 77.0%. Furthermore, because the consumption ratio of the thick layer is much higher, at least initially, its trajectory sweeps over a wider range of the H2–CO ratio, ending at a value of about 0.6 compared with 1.25 for the thin layer. It is also notable that the thin layer, despite also undergoing dilution of the reactants, does not strongly deviate from the curve of no inert gas fraction. The thicker layer, however, is quite significantly impacted by dilution of the reactants. This can most notably be seen for the catalyst efficiency and the ATY. Both would exhibit a significant improvement without dilution, but for the real calculation the efficiency drops directly with only a slight bulge where the maximum could have been. For the ATY the obtainable gain upon reducing the syngas ratio is much larger, therefore there is still a temporary improvement visible before the final decline occurs. Especially when looking at the ATY it is easy to conceive that if maximizing productivity by changing the syngas ratio is the objective, thicker layers would require syngas ratios below a value of two, whereas thin layers would benefit from adopting values above two. However, optimising operation conditions is not within the scope of this work. The plot of neither layer shows the actual spatial distribution of the local ATY nor the total ATY of a reactor during integral operation. Thus, it does not allow for the evaluation of the reactor performance under varying feed conditions.
 |
| | Fig. 3 a: Effect of varying H2–CO ratios (x-axis) and inert gas molar fraction (chart series) on performance parameters of a differential catalyst layer with a thickness of 25 μm and no transport pores; added overlay of a trajectory from an integral reactor operating at 80% CO conversion in red. b: Effect of varying H2–CO ratios (x-axis) and inert gas molar fraction (chart series) on performance parameters of a differential catalyst layer with a thickness of 200 μm and no transport pores; added overlay of a trajectory from an integral reactor operating at 80% CO conversion in red. | |
Effects of integral operation
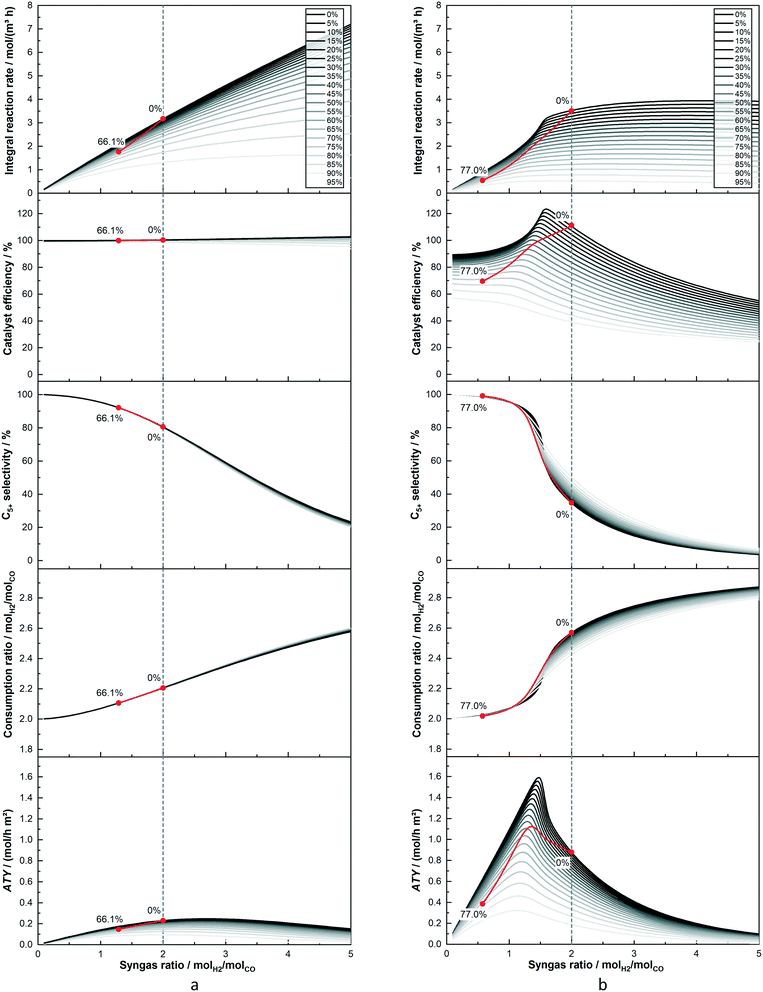
For a better understanding of the integral reactor behaviour, Fig. 4 displays the axial profiles of the cases already used for the trajectories in the previous figures. Two layers of 25 μm and 200 μm are compared when the total conversion for both is kept at 80%. The identical feed composition and the constant conversion lead to the inlet concentrations as well as the concentration of CO at the outlet to be constant. Nonetheless, the concentration of H2 and CO for the layer of 200 μm, with the exemptions at inlet and outlet, is always lower than for the reactor with the thin layer. This is a result of the initially much lower C5+-selectivity of the thick layer, leading to a higher formation rate of the gaseous C1–4-products. This dilutes the reactants to a greater extent and also consumes relatively more hydrogen. Due to the higher usage ratio of the thick layer, its syngas ratio drops faster than for the thin layer. This has in turn a strong positive effect on the C5+-selectivity, which increases and exceeds the value of the 25 μm layer just after half-way down the reactor. At about the same point does the consumption ratio of the thick layer fall below the value of the thin one. Nevertheless, for the 200 μm layer the syngas ratio has almost reached a value of one, compared with still just under two for the thin layer. Thus, the difference of the ratios between consumption and provision is much greater for the thick layer. This leads to a continuously high drop of the local syngas ratio, despite the lowered consumption ratio in the last part of the reactor. The substantially decreased syngas ratio, although having led to the maximum possible gain for selectivity, has a significant negative effect on the integral reaction rate. This is also illustrated by the steep decline of the local molar flux of CO for the thick layer along the axial direction, ending up at only about 15% of its initial value. When the C5+-selectivity is factored in, to yield the ATY, a clear maximum of the local ATY-profile is visible at about 55% downstream of the channel, caused by the almost tripled C5+-selectivity. The thin layer, in comparison to the thick one, exhibits a much lower initial usage ratio and higher C5+-selectivity due to negligible diffusion limitations. Therefore, the drop in the syngas ratio is considerably lower and the gradient getting steeper along the axial direction is just a result of the increased difference between the local usage and the local H2–CO ratio. With much shallower profiles of selectivity and molar flux of CO, though again with opposing tendencies, the thin layer does not lead to the build-up of a distinct maximum in ATY, instead the ATY profile shows a constant decline. This is caused by the too low gain in selectivity of just 12% at the outlet, that cannot compensate the almost halved CO flux. Despite improving upon productivity by operation at 80% CO conversion the 200 μm layer still does not perform proportionally better than the 25 μm layer, inasmuch as the area beneath its ATY profile is not eight times larger than for the thin layer.
 |
| | Fig. 4 Comparison of axial profiles of gas concentration, H2–CO ratios, local selectivity, efficiency and local molar flux of CO and C5+ (ATY) for layers of 25 μm and 200 μm thickness. 80% CO conversion, no liquid film. | |
How diffusion limited layers potentially benefit from integral operation can be further answered when looking at the lateral profiles at different sections of the reactor, as shown in Fig. 5. For the thin layer the concentration profiles show hardly any change along the lateral profile, confirming the lack of diffusion limitations. When comparing inlet, middle and outlet the concentration shows a decline, with a larger drop for H2 as it reaches the initially lower level of CO at the very end of the reactor. The reaction rate decreases accordingly for the different axial locations but does not change along the lateral direction. Similarly, the chain growth probability exhibits no lateral gradient but mildly gains along the axial direction. The 200 μm layer, instead, shows a quite severe change in performance along the axial direction. As a thick layer it exhibits at the middle and at the end of the channel a considerably lowered syngas ratio. The gradient in the lateral concentration profiles of H2 and CO is remarkably similar but due to the similar surface concentrations of CO and H2 the local H2–CO ratio does not drop as much as at the inlet. This is caused by the diffusivity of H2 being about 2.5 times higher than the diffusivity of CO and so equalling almost exactly the consumption ratio. Moreover, at the outlet the surface concentration of H2 is below the one of CO and the local syngas ratio decreases due to the relatively parallel decline in both curves. Despite this, the chain growth probability seems very constant, as it has already approached unity and cannot benefit from a lowered syngas ratio any further. For the middle part the lowered syngas ratio and its limited lateral change also help to improve selectivity. The changing syngas ratio has a less beneficial effect on the reaction rate. With decreasing reactant concentrations and thus slower reaction rate the catalyst efficiency could be expected to improve. This is not the case as a result of the change of the lateral profile for the reaction rate. At the inlet a maximum in the profile occurs together with two inflexion points. This allows for an efficiency larger than 100%. The middle profile is already much shallower and misses a maximum in the middle, therefore having a catalyst efficiency of less than 100%. Yet, it still exhibits one inflexion point, which retards the rate drop to some extent. At the rate profile for the outlet position, there is no longer any inflexion point visible and the efficiency is even lower.
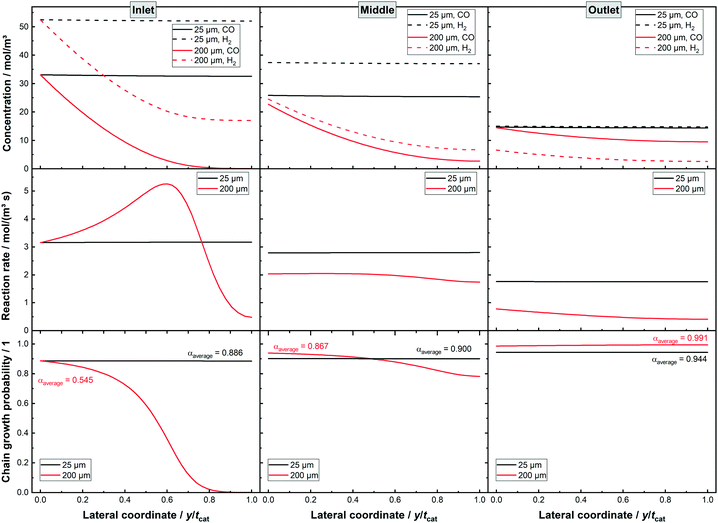 |
| | Fig. 5 Lateral profiles of liquid concentration, local reaction rate and alpha values for two dense layers with thicknesses of 25 and 200 μm, respectively, 80% CO conversion, no liquid film. | |
This behaviour of thick layers, for which diffusion limitations play a crucial role and eventually cause the selectivity to improve while the rate exacerbates, give rise to the fact that these thick layers benefit from integral operation whilst thin layers do not. Nevertheless, whether this difference can cause a significant change in the performance can only be answered by assessing the total productivity of each layer. It also depends on the conditions chosen to make a judgment on the performance. Within this publication the total productivity is deemed as the axial integral of the local ATY. Fig. 6 displays the axial ATY profiles along with the axial conversion profiles for catalyst layers of different thickness operated at 80% conversion. The depicted thin layers of 25 μm, 100 μm and 140 μm show a maximum ATY right at the inlet of the reactor and exhibit a profile with a negative gradient that is getting increasingly steeper along the axial direction. Hence, their ideal operating conversion is 0%, as indicated by the vertical lines. In contrast to this the thicker layers of 200 μm and 250 μm, for which diffusion limitations play an important role, comprise a maximum somewhere in the middle of the reactor with a corresponding CO conversion of 58.6% and 63.3%.
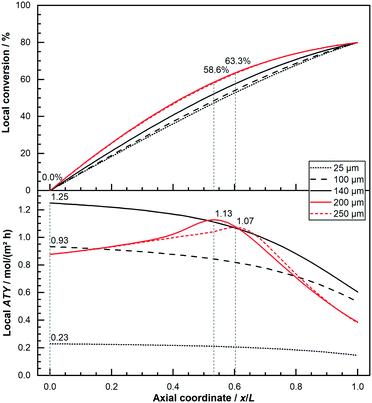 |
| | Fig. 6 Comparison of axial profiles of conversion and local productivity for dense layers of different thickness (25 μm, 100 μm, 146 μm, 200 μm and 250 μm); local maximum indicated with vertical lines and value readings, 80% CO conversion, no liquid film. | |
At its maximum, the local ATY is between 20% to almost 30% higher, compared with the inlet value, before the inevitable drop sets in. The maximum for the 200 μm layer occurs earlier and the rise is higher, indicating a vanishing gain as the layers get too thick. This behaviour of thick layers does not mean that thick layers should be operated at the conversion at which the local maximum occurs nor that thick layers are beneficial for integral operation of reactors. To make this decision instead of the local ATY the integral reactor performance, measured as total ATY, needs to be evaluated for various catalyst thicknesses and conversion levels. This is done in Fig. 7 for a couple of dense thin and thick layers as well as some thick layers with ideal fraction of transport pores. The ideal fraction of transport pores is kept constant from the optimisation conducted for differential reactor operation. To aid clearness and comparability of the results the thin layers are used as background for the other two types. The results for the thin layers are illustrated at the top. Starting with the lowest thickness of 25 μm one can see a shallow curve over the entire conversion range up to 80%. The next thicker layer of 50 μm matches nicely the expected twice as high values at each conversion point. With further increasing thickness, the total ATY profiles increase proportionally. But with growing thickness the drop at the right end of the plot also becomes more pronounced. This reflects the fact that layers with limited diffusion restrictions do not benefit from integral operation. The thick layers, as shown in the middle of the figure, with thicknesses of 150 μm and higher, where diffusion limitations have a relevant effect, exhibit a different pattern.
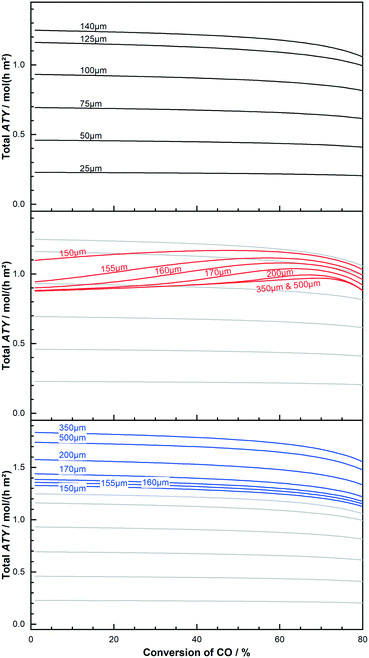 |
| | Fig. 7 Effect of conversion on total productivity (ATY) of layers of different thickness and kind; thin layers with limited diffusion effects (top); layers with significant mass transport restrictions (middle); thick layers with added, ideal fraction of transport pores (bottom). | |
The effective total ATY is dropping with increased layer thickness, and the extent of this drop is varying for different CO conversion levels. At low conversion the 150 μm layer already shows a significant loss in ATY but this drop only continues to layer thicknesses of up to about 160 μm after which the drop stabilizes and constant values for the ATY are obtained. For mediocre conversion levels the loss by increased layer thickness is reduced even further. In this middle and the high conversion range layers of 200 μm and thicker exhibit almost identical profiles, where the total ATY increases with conversion, forms a maximum before it drops again for conversion values of 70% and higher. However, though thick layers benefit from integral operation at high conversion levels, the total improvement cannot outreach the ATY obtained for an optimal layer thickness of about 140 μm. But the difference is getting smaller and a layer of 155 μm to 160 μm is performing almost as good as the 140 μm layer at around 60% conversion. Moreover, at a conversion of 80% the thin layers tend to lose about 10% of the initial ATY, whereas the thick layers of 200 μm and above achieve the same performance as at 0% conversion. For layers with added ideal fractions of transport pores the results are shown at the bottom of the figure. The shape of their profile plot compares to what is seen for the thin layers. Only the total level is increased due to the optimisation, allowing for more active catalyst phase being effectively utilized. This optimisation also avoids the presence of strong diffusion limitations, thus the similar profiles to the thin layers, for which diffusion restrictions also do not play an important role. The absence of diffusion limitations makes these layers again more susceptible to be hampered by integral operation. Nonetheless, the productivity is still higher than for the thick, dense layers. Besides total production the selectivity towards long chained products is often also of interest. The corresponding C5+ profiles analogues to Fig. 7 are shown in the ESI.† When changing the conversion from 0% to 80%, all layer types improve upon integral operation, but the thick layers without transport pores are substantially inferior to the thin layers or the “ideal” layers. The majority of thick layers exhibit C5+-selectivities between 35% and 60%, while the thin layers spread between 85% and 65% and the optimized layers are relatively narrow distributed between 65% and 70% (see ESI,† Fig. S4 and S5). This favours again the thin and the optimized layers over the thick, dense layers.
Finally, Fig. 8 allows for a direct comparison of the previous results, like obtained from a differential model, with the integral operation at 80% conversion. Depicted is the ATY as function of layer thickness for “dense” and “ideal” layers for 1% conversion and for 80% conversion. Up to layer thicknesses of about 140 μm a straight line indicates the region of negligible diffusion resistance and the operation at 80% conversion leads to an obvious drop in productivity. With increasing layer thickness without introducing transport pores, a flat plateau is reached after a sudden drop. This is due to the occurrence of a limit in the exploitable depth of the layers, after which no further added layer thickness contributes to the reaction. This heavily diffusion limited region shows no drop at all, and in a small range between 160 μm and 200 μm even a slight gain is reached by operating at 80% CO conversion. For layers with ideal transport pore fraction, however, a significant loss due to integral operation is observable over the entire range. This loss is again a result of the absence of relevant diffusion limitations. But, when comparing the relation of the total maximum of ideal to dense layers at either 1% or 80% CO conversion it seems that integral operation does not affect the efficacy of layer optimisation. At 1% conversion the maximum of the “ideal” layer is 47% higher than the maximum of the “dense” one. And at 80% conversion the maximum of the “ideal” one is still 47% above the maximum of the “dense”. This similarity occurs because the absolute maximum of ATY for “dense” or “ideal” layers is in either case at a point where diffusion limitations are still of negligible effect. As these limitations, with their negative impact on selectivity and consumption ratio and an according penalty on productivity, are a prerequisite to allow for a benefit from integral operation, a lack of diffusion restrictions for both types results in similar behaviour with increasing conversion. This similarity in the results for a variety of CO conversions is further shown in the ESI† (Table S1). The shift in the optimal thickness for varying conversion levels is also very minor. Hence, integral operation seems as indiscriminative towards the global productivity optimization of catalyst layers but in detail may still substantially affect potential gain if only catalyst layers of certain thicknesses are examined.
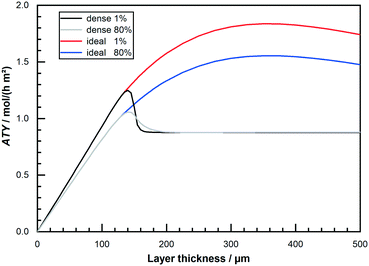 |
| | Fig. 8 Comparison of obtainable total productivity from “dense” and “ideal” layers of different thickness at 1% and 80% CO conversion, no liquid film. | |
Film formation – effects of external mass transfer
All results shown up to this point do not include the formation of a liquid film. But the formation of a superficial liquid product layer may cause additional restrictions to the diffusive flow of the reactants. This may hamper the catalyst layer productivity, thus warranting a further investigation. The model includes a simplistic approach, that does not take turbulent flow of the film nor momentum transport from the gas to the liquid film into account. Both effects would increase the average speed of the liquid film and thereby lowering its thickness. This makes the simplistic model overly pessimistic. Fig. 9 repeats the results of Fig. 8 with a thickness variation for “dense” and “ideal” layers at 1% and 80% CO conversion for the simulation with and without film formation. At the top, hardly any differences are visible for the two different instances and the typical curves are shown. The graph in the middle of Fig. 9 plots the maximum calculated layer thickness. Because the liquid film accumulates all liquid products formed in the catalyst layer, the maximum film thickness occurs at the outlet of the reactor. Here the thickness is also proportional to the cubic root of the total volume flow,52 thus to the total ATY. The plot of the maximum film thicknesses exhibits therefore a more bulged profile, similar to the ATY but with smaller differences between the 1% and the 80% conversion results. The maximum film thicknesses for the “dense” and the “ideal” layer types lie between almost 5 μm and 5.5 μm. With this as the maximum film thickness, compared with layer thicknesses of up to several hundred μm, in which only a small fraction of pores is available for diffusion, only a marginal loss due to film formation can be expected. This percentage loss in total ATY is depicted in the bottom row of Fig. 9. For all layers with thicknesses up to about 100 μm the liquid film formation has almost no effect. “Dense” layers are affected most in the range from 140 μm to about 170 μm, where the loss spikes to levels exceeding 2% for 1% CO conversion before returning to a constant level of 0.5% for even thicker layers. For the high conversion the spike is much less pronounced with a maximum of just above 0.5% and eventually the line levels out at 0.4% loss. The “ideal” layers differ from the “dense” ones only from 140 μm onwards, but there is no distinct spike and the loss slowly and constantly increases, in accordance with the climb in total productivity, to levels of 0.5% and 0.7% for 80% and 1% CO conversion, respectively. Overall, the film formation has little to no impact on the productivity. Neglecting external mass transport limitations, therefore, appears justified. However, the simulation cases only take the activity from the original works of Yates and Satterfield58 into account, but modern catalysts should be multiple times more active.9,11,31 This higher activity also increases productivity and hence the ability to form a larger liquid film, with a consequential higher impact of external mass transport. Because previous simulation work has also shown that external mass transport, albeit on a low level, scales almost linear with the activity,63 a variation of the activity factor was conducted. To evaluate maximum possible effects only the optimum layer thickness, for which the highest ATY is achieved for each activity factor, was chosen for comparison. For activity factors starting from one and increasing up to 10 the results are shown in Fig. 10. At the top the plots of the ATY for “dense” and “ideal” layers and for each layer type one with and one without the liquid film are depicted. To some extent it confirms results of previous work, indicating a rise of the ATY approximately with the square root of the activity factor and the known performance gap between “dense” and “ideal” layers. The difference between the simulations with and without liquid film formation is still relatively small, but it becomes more and more apparent the higher the activity gets. The growing difference is not just because of the higher productivity and the accordingly larger film thickness. To get the best productivity from a catalyst of higher activity the optimum layer thickness needs to be decreased (Fig. 10 top centre) because the diffusion inside the catalyst layer reduces the maximum exploitable thickness with increasing reaction rates. This is the main cause of the non-linear correlation between ATY and activity factor. It also means that layers of higher activity and productivity, with an increased liquid film thickness (Fig. 10 bottom centre), achieve this with a lower catalyst layer thickness. Therefore, the impact of external diffusion in the liquid product film gets more and more pronounced. This is shown at the bottom of Fig. 10, where the percentage loss in ATY is calculated by comparing the results of the no film simulation with the calculated values from the simulation with liquid film formation. The dense layers can serve as an example, when relating the results for an activity factor of one and 10. Despite a relatively small shift of the maximum liquid film thickness from 4.7 μm to 6.8 μm, the loss in ATY goes up more than four times, from 0.3 to 1.4%. A very similar result is obtained when looking at the data for the “ideal” layers. With less than 2.5% loss in productivity, the overall impact of the liquid film is not too severe, even at a much higher catalyst activity.
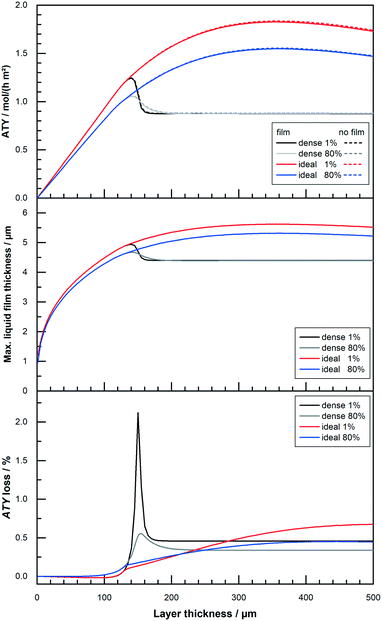 |
| | Fig. 9 Profiles of total ATY (top), max. liquid film thickness (middle) and percentage of ATY loss due to external film diffusion (bottom) as function of layer thickness for layers of different CO conversion. | |
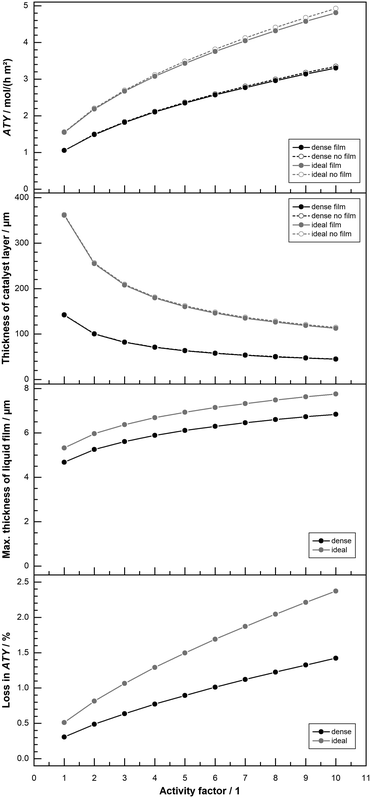 |
| | Fig. 10 Profiles of total ATY (top), catalyst layer thickness (top centre), max. liquid film thickness (bottom centre) and percentage of ATY loss due to external film diffusion (bottom) as function of activity factor for dense layers and layers with ideal pore fraction, CO conversion of 80%. | |
The standard length of the reactor channel in this work is 50 mm and based on the size of our lab scale reactors.22 For reactors of industrial scale this is likely to be substantially too short64 and scenarios with longer channel length have been computed as well. With greater channel length the total accumulation of liquid product in the liquid film is higher, so is the film thickness and eventually its negative effect on productivity. For a variation of channel length from 50 mm up to 1 m the ATY, the maximum liquid film thickness and the loss due to the film are shown in Fig. 11. When the film is neglected in the simulation a variation of the channel length does not change the ATY. But when film formation is taken into account a fair drop in ATY occurs, that deteriorates with increasing channel length. The maximum film thickness rises from about 7 μm to 18 μm and liquid product in the liquid film is higher, so is the film thickness and eventually its negative effect on productivity. For a variation of channel length from 50 mm up to 1 m the ATY, the maximum liquid film thickness and the loss due to the film are shown in Fig. 11. When the film is neglected in the simulation a variation of the channel length does not change the ATY. But when film formation is taken into account a fair drop in ATY occurs, that deteriorates with increasing channel length. The maximum film thickness rises from about 7 μm to 18 μm and 20 μm for the “dense” and “ideal” layers, respectively. Despite the rather small difference in liquid film thickness the percentage loss in ATY is much more severe for the “ideal” layers than for the “dense” ones. The layers with transport pores exceed 8% loss, whereas the “dense” layers lose just about 4% at the maximum channel length of 1 m. These results illustrate that external diffusion limitations, estimated with this simple yet overly pessimistic model, are of minor concern when considering the overall restrictions for such reactors. However, if highest accuracy is sought, especially for high-performing optimized catalysts, the film formation should be incorporated. In that instance further efforts to include the momentum of the gas phase, laminar–turbulent transition of the film and variable physical properties of the liquid may be required.
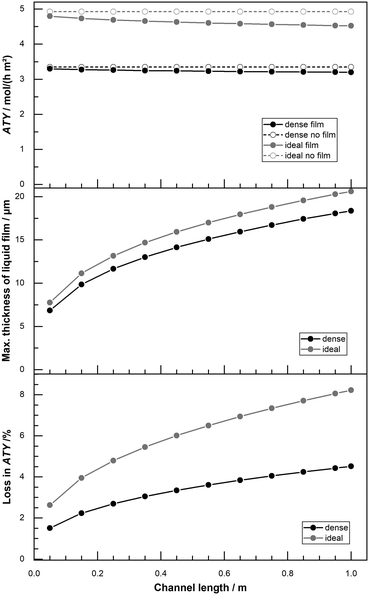 |
| | Fig. 11 Profiles of total ATY (top), max. liquid film thickness (middle) and percentage of ATY loss due to external film diffusion (bottom) as function of channel length for dense layers and layers with ideal pore fraction; CO conversion of 80%, activity factor of 10. | |
Conclusions
An isothermal plug-flow reactor model for catalyst layers, including internal diffusion and external film formation, was used to explore the effects of mass transport at higher conversions. Integral operation establishes axial concentration profiles that exhibit a shift of the local syngas ratio to lower values with proceeding axial position as the consumption was higher than the feed ratio. This declining ratio has a positive effect on the product distribution leading to higher C5+-selectivities and lower methane formation at higher conversions, which agrees with experimental data8–10,19,35,65,66 and is in line with simulation results.50 Some sources report opposite tendencies for conventional fixed bed reactors with wide tube diameters48 or for microreactors with catalysts coated on the channel walls.21,23 Mass transport limitations affected by GHSV were proposed as a root-cause. This could not be found in our simulation work. Elevated temperature profiles48 and lack of efficient convective external fluid cooling23 seem also likely as a cause. However, a suggested formation of a, possibly stagnant, liquid film is still conceivable, especially as experimental work was conducted in narrow annular channels were surface tension can stabilise liquid droplets. For our assumed geometry with wide, flat channels the surface tension is irrelevant.52 Moreover, the model overestimates film thickness because of a simplified vapour liquid distribution and because of the neglection of momentum transfer from the gas to the liquid phase. The model only includes alkanes up to butane in the gas phase and all alkanes with higher carbon numbers are exclusive to the liquid phase. This is a simplification overestimating the total amount of the liquid phase because under process conditions an overlap between gas and liquid phase up to triacontane can be found.41 When the momentum transfer from the gas to the liquid phase is included the liquid velocity would increase and therefore the film thickness would drop.
Apart from an effect on the selectivity higher conversions also affect the total productivity. Thin layers and layers with ideal amount of transport pores exhibit a lower productivity with higher conversion levels. Thick layers instead, for which strong diffusion effects are observed, significantly benefit from increased conversion levels. These opposing behaviours can reduce the optimisation potential, when the ATY values for layers of the same thickness with or without transport pores move closer together. However, when only the optimal points of layers with and without transport pores are compared the conversion has almost no effect. This indifference is because the best performing layers are those with still a sufficiently low impact of diffusion and thus a comparable decline in productivity with increasing conversion, irrespective of layer type.
The prediction of a liquid film formation has shown only a marginal impact of less than 2.5% on lab scale reactors even when tenfold higher activities are considered. In these cases, even the maximum film thickness is less than 10 μm. For larger reactor dimensions of up to 1 m in length, there is a more relevant effect of more than 8% loss in productivity for the optimised catalyst layers. This is a pessimistic scenario because in long channels the high gas velocity would accelerate the liquid phase and reduce film thickness, which is neglected in the current model. Lab scale reactors should be well described with the current version of the model, but a more sophisticated modelling of the liquid film might be required for the design of commercial microchannel reactors. Of particular interest are experiments and simulations that would focus on the conditions that lead to the formation of stagnant liquids, where capillary effects, momentum transfer from the gas flow and possibly liquid recirculation are considered. Though this might be more relevant for fixed bed reactors than for the wall coated reactor, the open gas channel dimension as one key parameter for reactor design would require evaluation. Furthermore, the wall coated reactor provides a simpler design basis to allow for direct optical measurement of the liquid hold-up.
Notations
Latin
|
a
| Reaction rate constant, mol s−1 kg−1 bar−2 |
|
a
0
| Frequency factor for reaction rate constant, mol s−1 kg−1 bar−2 |
| ATY | Areal time yield of desired products, mol s−1 m−2 |
|
b
| Absorption constant, bar−1 |
|
b
0
| Frequency factor for absorption constant, bar−1 |
|
c
0,i
| Concentration of species i in the gas phase at the inlet, mol m−3 |
|
c
g,i
| Concentration of species i in the gas phase, mol m−3 |
|
D
i
| Diffusion coefficient of species i (H2 or CO), m2 s−1 |
|
E
A,a
| Activation energy for reaction rate constant, J mol−1 |
|
E
A,b
| Activation energy for absorption constant, J mol−1 |
|
E
A,α
| Activation energy, J mol−1 |
|
F
| Activity factor, dimensionless |
|
j
gl,i
| Molar flux between gas and liquid phase for species i, mol s−1 m−2 |
|
k
α
| Selectivity coefficient, dimensionless |
|
L
| Total length of catalyst layer, m |
|
M
i
| Molar mass of species i, g mol−1 |
|
P
| Pressure, bar |
|
R
| Universal gas constant, J mol−1 K−1 |
|
r
| Reaction rate, mol s−1 m−3 |
|
S
C1
| Methane selectivity, dimensionless |
|
S
Cn
| Selectivity for alkanes with carbon number n, dimensionless |
|
T
| Temperature, K |
|
t
channel
| Total thickness of the reactor channel, m |
|
t
g
| Thickness of the open gas channel, m |
|
t
l
| Thickness of the liquid film, m |
|
t
cat
| Thickness of the catalyst layer, m |
|
T
ref
| Reference temperature (493.15 K), K |
|
v
g
| Velocity of the gas phase, m s−1 |
|
v
g,0
| Velocity of the gas phase at the inlet, m s−1 |
|
v
l
| Velocity of the liquid film, m s−1 |
|
v
L
| Molar volume of the liquid, mol m−3 |
|
x
| Axial dimension coordinate, m |
|
x
inert
| Molar fraction of inerts in gas feed, dimensionless |
|
y
| Dimension coordinate inside the catalyst layer, m |
Greek
|
α
| Chain growth probability, dimensionless |
|
ρ
g
| Density of the gas phase, kg m−3 |
|
ρ
l
| Density of the liquid phase, kg m−3 |
|
ρ
cat
| Apparent density of the catalyst, kg m−3 |
|
η
l
| Dynamic viscosity of the liquid phase, Pa s |
|
η
| Catalyst efficiency, dimensionless |
|
ε
cat
| Porosity of the catalyst, dimensionless |
|
ε
TP
| Volume fraction of transport pores, dimensionless |
|
τ
cat
| Tortuosity inside the catalyst phase, dimensionless |
|
τ
TP
| Tortuosity inside the transport pores, dimensionless |
|
ν
i
| Stoichiometric coefficient of species i (CO, H2, H2O), dimensionless |
|
ν
C,n
| Stoichiometric coefficient for alkanes with carbon number n, dimensionless |
|
γ
| Termination probability factor, dimensionless |
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
The authors gratefully thank Deutsche Forschungsgemeinschaft (DFG) for financial support through SPP 1570 (grant number TU89/9).
References
- B. H. Davis, Catal. Today, 2002, 71, 249–300 CrossRef CAS.
- E. Rytter and A. Holmen, Catal. Today, 2016, 275, 11–19 CrossRef CAS.
- R. Guettel, U. Kunz and T. Turek, Chem. Eng. Technol., 2008, 31, 746–754 CrossRef CAS.
- R. Güttel, Chem. Ing. Tech., 2015, 87, 694–701 CrossRef.
- K. Pangarkar, T. J. Schildhauer, J. R. van Ommen, J. Nijenhuis, J. A. Moulijn and F. Kapteijn, Catal. Today, 2009, 147, 2–9 CrossRef.
- D. Vervloet, F. Kapteijn, J. Nijenhuis and J. R. van Ommen, Catal. Today, 2013, 216, 111–116 CrossRef CAS.
- B. Kaskes, D. Vervloet, F. Kapteijn and J. R. van Ommen, Chem. Eng. J., 2016, 283, 1465–1483 CrossRef CAS.
- C. Cao, J. Hu, S. Li, W. Wilcox and Y. Wang, Catal. Today, 2009, 140, 149–156 CrossRef CAS.
- R. Myrstad, S. Eri, P. Pfeifer, E. Rytter and A. Holmen, Catal. Today, 2009, 147S, S301–S304 CrossRef.
-
J. Yang, S. Boullosa Eiras, R. Myrstad, H. J. Venvik, P. Pfeifer and A. Holmen, in Catalysts and Catalysis: Advances and Applications, ed. B. H. Davis and M. L. Occelli, CRC Press, 2016, pp. 259–266 Search PubMed.
- H. J. Robota, L. A. Richard, S. Deshmukh, S. LeViness, D. Leonarduzzi and D. Roberts, Catal. Surv. Asia, 2014, 1–6 Search PubMed.
- C. Knobloch, R. Güttel and T. Turek, Chem. Ing. Tech., 2013, 85, 455–460 CrossRef CAS.
- R. M. de Deugd, R. B. Chougule, M. T. Kreutzer, F. M. Meeuse, J. Grievink, F. Kapteijn and J. A. Moulijn, Chem. Eng. Sci., 2003, 58, 583–591 CrossRef CAS.
- R. Güttel, J. Knochen, U. Kunz, M. Kassing and T. Turek, Ind. Eng. Chem. Res., 2008, 47, 6589–6597 CrossRef.
- A. M. Hilmen, E. Bergene, O. A. Lindvåg, D. Schanke, S. Eri and A. Holmen, Catal. Today, 2005, 105, 357–361 CrossRef CAS.
- C. G. Visconti, E. Tronconi, L. Lietti, G. Groppi, P. Forzatti, C. Cristiani, R. Zennaro and S. Rossini, Appl. Catal., A, 2009, 370, 93–101 CrossRef CAS.
- L. C. Almeida, F. J. Echave, O. Sanz, M. A. Centeno, G. Arzamendi, L. M. Gandía, E. F. Sousa-Aguiar, J. A. Odriozola and M. Montes, Chem. Eng. J., 2011, 167, 536–544 CrossRef CAS.
- D. Merino, O. Sanz and M. Montes, Fuel, 2017, 210, 49–57 CrossRef CAS.
- D. Merino, O. Sanz and M. Montes, Chem. Eng. J., 2017, 327, 1033–1042 CrossRef CAS.
- L. C. Almeida, O. Sanz, J. D'olhaberriague, S. Yunes and M. Montes, Fuel, 2013, 110, 171–177 CrossRef CAS.
- L. C. Almeida, O. Sanz, D. Merino, G. Arzamendi, L. M. Gandía and M. Montes, Catal. Today, 2013, 215, 103–111 CrossRef CAS.
- H. Becker, R. Güttel and T. Turek, Catal. Today, 2016, 275, 155–163 CrossRef CAS.
- X. Ying, L. Zhang, H. Xu, Y.-L. Ren, Q. Luo, H.-W. Zhu, H. Qu and J. Xuan, Fuel Process. Technol., 2016, 143, 51–59 CrossRef CAS.
- M. F. M. Post, A. C. Vanthoog, J. K. Minderhoud and S. T. Sie, AIChE J., 1989, 35, 1107–1114 CrossRef CAS.
- E. Iglesia, S. C. Reyes, R. J. Madon and S. L. Soled, Adv. Catal., 1993, 39, 221–302 CAS.
- E. Iglesia, S. L. Soled, J. E. Baumgartner and S. C. Reyes, J. Catal., 1995, 153, 108–122 CrossRef CAS.
- D. Merino, I. Pérez-Miqueo, O. Sanz and M. Montes, Top. Catal., 2016, 59, 207–218 CrossRef CAS.
- H. Becker, R. Güttel and T. Turek, Catal. Sci. Technol., 2016, 6, 275–287 RSC.
- F. J. Keil and C. Rieckmann, Chem. Eng. Sci., 1994, 49, 4811–4822 CrossRef CAS.
- T. Doğu, Ind. Eng. Chem. Res., 1998, 37, 2158–2171 CrossRef.
- D. Vervloet, F. Kapteijn, J. Nijenhuis and J. R. van Ommen, Catal. Sci. Technol., 2012, 2, 1221–1233 RSC.
- K. D. Kruit, D. Vervloet, F. Kapteijn and J. R. van Ommen, Catal. Sci. Technol., 2013, 3, 2210–2213 RSC.
- F. Pöhlmann and A. Jess, Catal. Today, 2016, 275, 172–182 CrossRef.
- H. Becker, R. Güttel and T. Turek, Chem. Ing. Tech., 2014, 86, 544–549 CrossRef CAS.
- F. Fazlollahi, M. Sarkari, A. Zare, A. A. Mirzaei and H. Atashi, J. Ind. Eng. Chem., 2012, 18, 1223–1232 CrossRef CAS.
- K. Keyvanloo, S. J. Lanham and W. C. Hecker, Catal. Today, 2016, 270, 9–18 CrossRef CAS.
- C. Maretto and R. Krishna, Catal. Today, 1999, 52, 279–289 CrossRef CAS.
- B. Xu, Y. Fan, Y. Zhang and N. Tsubaki, AIChE J., 2005, 51, 2068–2076 CrossRef CAS.
- B. Todic, T. Bhatelia, G. F. Froment, W. Ma, G. Jacobs, B. H. Davis and D. B. Bukur, Ind. Eng. Chem. Res., 2013, 52, 669–679 CrossRef CAS.
- C. G. Visconti, E. Tronconi, L. Lietti, R. Zennaro and P. Forzatti, Chem. Eng. Sci., 2007, 62, 5338–5343 CrossRef CAS.
- C. G. Visconti and M. Mascellaro, Catal. Today, 2013, 214, 61–73 CrossRef CAS.
- M. Sadeqzadeh, J. Hong, P. Fongarland, D. Curulla-Ferré, F. Luck, J. Bousquet, D. Schweich and A. Y. Khodakov, Ind. Eng. Chem. Res., 2012, 51, 11955–11964 CrossRef CAS.
- M. Sadeqzadeh, S. Chambrey, S. Piché, P. Fongarland, F. Luck, D. Curulla-Ferré, D. Schweich, J. Bousquet and A. Y. Khodakov, Catal. Today, 2013, 215, 52–59 CrossRef CAS.
- M. Sadeqzadeh, S. Chambrey, J. Hong, P. Fongarland, F. Luck, D. Curulla-Ferre, D. Schweich, J. Bousquet and A. Y. Khodakov, Ind. Eng. Chem. Res., 2014, 53, 6913–6922 CrossRef CAS.
- K. Pabst, M. I. González, B. Kraushaar-Czarnetzki and G. Schaub, Ind. Eng. Chem. Res., 2013, 52, 8978–8987 CrossRef CAS.
- A. Jess and C. Kern, Chem. Eng. Technol., 2012, 35, 369–378 CrossRef CAS.
- A. Jess and C. Kern, Chem. Eng. Technol., 2012, 35, 379–386 CrossRef CAS.
- M. H. Rafiq, H. A. Jakobsen, R. Schmid and J. E. Hustad, Fuel Process. Technol., 2011, 92, 893–907 CrossRef CAS.
- G. Chabot, R. Guilet, P. Cognet and C. Gourdon, Chem. Eng. Sci., 2015, 127, 72–83 CrossRef CAS.
- M. Ostadi, E. Rytter and M. Hillestad, Chem. Eng. Res. Des., 2016, 114, 236–246 CrossRef CAS.
- D. Förtsch, K. Pabst and E. Groß-Hardt, Chem. Eng. Sci., 2015, 138, 333–346 CrossRef.
- W. Nusselt, Zeitschrift des Vereins Deutscher Ingenieure, 1916, 60, 541–546 Search PubMed.
- G. Haarlemmer and T. Bensabath, Comput. Chem. Eng., 2016, 84, 281–289 CrossRef CAS.
- I. V. Derevich, V. S. Ermolaev, V. Z. Mordkovich and D. D. Galdina, Theor. Found. Chem. Eng., 2012, 46, 8–19 CrossRef CAS.
- I. Iliuta, F. Larachi, B. P. A. Grandjean and G. Wild, Chem. Eng. Sci., 1999, 54, 5633–5645 CrossRef CAS.
- M. A. Latifi, A. Naderifar and N. Midoux, Chem. Eng. Sci., 1997, 52, 4005–4011 CrossRef CAS.
- A. Bufe, M. Klee, G. Wehinger, T. Turek and G. Brenner, Chem. Ing. Tech., 2017, 89, 1385–1390 CrossRef CAS.
- I. C. Yates and C. N. Satterfield, Energy Fuels, 1991, 5, 168–173 CrossRef CAS.
- P. Kaiser, F. Pöhlmann and A. Jess, Chem. Eng. Technol., 2014, 37, 964–972 CrossRef CAS.
- J. J. Marano and G. D. Holder, Ind. Eng. Chem. Res., 1997, 36, 1895–1907 CrossRef CAS.
- C. Erkey, J. B. Rodden and A. Akgerman, Can. J. Chem. Eng., 1990, 68, 661–665 CrossRef CAS.
- J. J. Marano and G. D. Holder, Ind. Eng. Chem. Res., 1997, 36, 2409–2420 CrossRef CAS.
- R. Guettel and T. Turek, Chem. Eng. Sci., 2009, 64, 955–964 CrossRef CAS.
- S. R. Deshmukh, A. L. Y. Tonkovich, K. T. Jarosch, L. Schrader, S. P. Fitzgerald, D. R. Kilanowski, J. J. Lerou and T. J. Mazanec, Ind. Eng. Chem. Res., 2010, 49, 10883–10888 CrossRef CAS.
- J. Yang, W. Ma, D. Chen, A. Holmen and B. H. Davis, Appl. Catal., A, 2014, 470, 250–260 CrossRef CAS.
- Ø. Borg, N. Hammer, S. Eri, O. A. Lindvåg, R. Myrstad, E. A. Blekkan, M. Rønning, E. Rytter and A. Holmen, Catal. Today, 2009, 142, 70–77 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9cy00457b |
|
| This journal is © The Royal Society of Chemistry 2019 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article a,
Robert
Güttel
a,
Robert
Güttel
 b and
Thomas
Turek
b and
Thomas
Turek
 *a
*a