Preparation of highly active phosphated TiO₂ catalysts via continuous sol–gel synthesis in a microreactor

Abstract

Microreactors, featuring μm-sized tubes, offer greater flexibility and precise control of chemical processes compared to conventional large-scale reactors, due to their elevated surface-to-volume ratio and modular construction. However, their application in catalyst production has been largely neglected. Herein, we present the development of a microreactor process for the one-step sol–gel preparation of phosphated TiO₂ – a catalyst which has been recently demonstrated to be an eco-friendly material for the selective synthesis of the platform chemical 5-hydroxymethylfurfural (5-HMF) from bio-derived glucose. In order to establish catalyst preparation–property–performance relationships, 18 samples were prepared according to a D-optimal experimental plan with a central point. The key properties of these samples (porosity, crystallite size, mole bulk fraction of P) were correlated, using quadratic and interaction models, with the catalytic performance (conversion, selectivity, reaction rate) of 5-HMF synthesis as a test reaction. The optimal calculated catalyst features were set as target parameters to optimise catalyst synthesis applying quadratic correlation functions. An optimal catalyst was obtained, validating the models employed, with a yield of almost 100% and a space–time yield of ca. 3 orders of magnitude higher than that of a conventional batch process (26.8 vs. 0.07 g_cat h⁻¹ cm_reactor⁻³). The high yield could be mainly attributed to the optimal hydrolysis ratio and temperature. Controlling the TiO₂ crystallite size and surface acidity in conjunction with fine-tuning of the porous properties in the microreactor led to increased glucose conversion (95.6 vs. 78.7%), surface based formation rates of 5-HMF (0.047 vs. 0.008 g_5-HMF h⁻¹ m_cat⁻²), and selectivity towards 5-HMF (55.5 vs. 50.0%) of the optimal catalyst in relation to the batch-prepared material.

---

Introduction

There has recently been a significant increase in interest in process intensification, as it promises to improve efficiency of industrial processes and lower their ecological impact.¹ One notable approach is the use of continuous microreactors featuring μm-sized tubes. Their high surface-to-volume ratio results in fast heat exchange and very short mixing times, which enables precise process control, enhancing both efficacy and safety compared to processes performed in batch and/or large-scale reactors.^2–7 Furthermore, microreactors render the time and cost intensive scale-up of both the catalyst and process redundant. In addition, their modular design is of unrivalled flexibility. Their scalability to industrial production rates through parallelization has been recently proven for both pharmaceuticals and fine chemicals.⁸

Numerous catalysed reactions in microreactors have been reported,^9–16 and Torrente-Murciano et al.^17–19 highlighted the benefits of applying microreactors with specific geometries to tune the size and size distribution of Ag and Ag–Pd nanoparticles. However, the use of such reactors in the preparation of heterogeneous catalysts has been greatly overlooked, even though the controlled synthesis of catalysts is key for improving efficiency and sustainability of catalysed processes.²⁰ Fouling of the small reactor channels has impeded their long-term use in the industrial production of solids in microreactors.^21–25 However, a recent study by Riedlberger et al.²⁶ on the synthesis of phosphated TiO₂ in such systems demonstrated that fine-tuning of nucleation kinetics and mixing times could diminish this issue.

TiO₂ nanoparticles are widely applied in sunscreens, paints, toothpastes, solar cells, electrochemical electrodes, capacitors, and heterogeneous catalysts, amongst others.^27,28 Recently, Beltramini et al.^29–31 discovered that phosphate modified TiO₂ anatase nanoparticles almost fully convert glucose selectively into 5-hydroxymethylfurfural (5-HMF). This reaction offers a sustainable access to 5-HMF, a platform chemical for functionalised materials useful for polymers, fuels, etc.,^32,33 since glucose can be retrieved from industrially amenable bio sources.^33,34 Hence, there is a need for efficient catalysts for this reaction: phosphated TiO₂ features an activation energy ca. 40 kJ mol⁻¹ lower compared to common mineral acids.³⁶ The improved catalytic activity of this material was attributed to the beneficial role of the phosphorus incorporated into the crystal lattice of TiO₂, which decreases its crystallite size upon synthesis.^30,37 In addition, this dopant prevented sintering of the TiO₂ crystals and stabilised them in their anatase phase even under elevated temperatures (873–1173 K)^30,38–42 at which rutile formation usually becomes predominant.⁴³ Besides, the presence of phosphate groups increases Lewis acidity and introduces Brønsted acid sites.^29–31 It was concluded that a balanced amount of Lewis and Brønsted acid centres are required to efficiently isomerise glucose to fructose over the first sites and to quickly dehydrate the intermediate to 5-HMF over the latter ones, which was realised at an optimal phosphate content of 15 wt%. This is in line with earlier results in the literature demonstrating the beneficial role of bifunctional acid catalysts (like solid heteropoly acid salts⁴⁴ or Sn-beta zeolite)⁴⁵ in this reaction. In addition to 5-HMF production, phosphorus doped TiO₂ has also proved its capability in photodegradation reactions of various organic compounds,^{37,40,46–49} dehydration of isopropanol to propene,^39,41 and nitration of toluene,³⁸ which has further raised our interest in this catalytic material.

Preparation methods for phosphated TiO₂ in the aforementioned studies included impregnation^46,49 and solid–solid kneading³⁸ of pre-formed TiO₂ nanoparticles, hydrothermal synthesis,⁴⁸ and sol–gel synthesis.^{29–31,37,39–41,47,48} The latter offers many advantages over the other processes due its mild reaction conditions resulting in better product homogeneity, minimising sintering of the particles, and facilitating functionalisation of the resultant material.^50,51 Upon this preparation route, a metal–organic precursor like titanium butoxide (TB) is typically hydrolysed in an H₂O containing organic solvent, which results in instantaneous formation of sub-nanometer sized sol particles. Subsequently, a 3D gel network is formed by progressive concurrent particle growth and agglomeration, which usually leads to highly porous solids, once organic residues have been removed. Conventionally, this process has been performed in a batch reactor, which may impose several drawbacks compared to continuous reactors, such as lower space–time yields and less well-defined catalyst properties due to inhomogeneity of the reaction solution. Furthermore, it is also more difficult to control the various reaction steps involved.^52,53

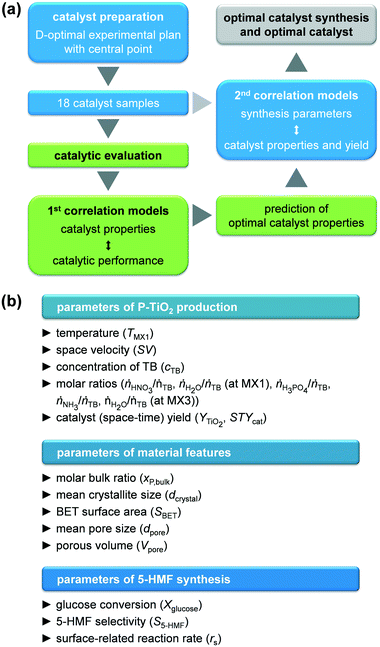
Therefore, we aimed at combining the advantages of both sol–gel synthesis and microflow reactors to achieve controlled and optimised preparation of phosphated TiO₂ in a modular Ehrfeld system involving three mixing steps for i) hydrolysis of the Ti precursor, ii) phosphate functionalisation of the sol particles, and iii) final gelation–precipitation. In order to rationalise both synthesis of the catalyst and catalysed 5-HMF formation from glucose, a design of experiments (DoE) software was employed that provided models to correlate catalyst synthesis conditions (temperature, space velocity, concentrations and molar feed ratios of reactants), catalyst yield, catalyst properties (porosity, crystallite size, molar P/Ti bulk ratio determined by N₂ physisorption, X-ray powder diffraction (XRPD), X-ray fluorescence spectroscopy (XRF), respectively), and catalytic performance upon 5-HMF synthesis from glucose. Structural insights of selected samples were gathered by various spectroscopic, temperature-programmed, or imaging techniques. Based on these models, the optimal microreactor process provided a superior (space–time) yield than the batch process resulting in an optimal catalyst with improved catalytic performance compared to the batch sample because of its well-tuned structure.

Materials and methods

Catalyst preparation

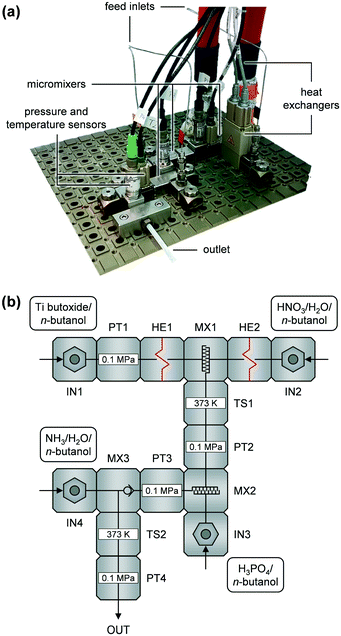
Continuous catalyst syntheses were carried out in an Ehrfeld Modular Microreactor System (MMRS, i.d. 3.00 mm) controlled by HitecZang LabVision software and based on the set-up previously described.²⁶ A photograph and a simplified piping & instrumentation diagram (PID) of the set-up are depicted in Fig. 1a and b, respectively. The volumetric flows of the four feeds containing TB (Sigma-Aldrich, 97%), HNO₃(aq) (Carl Roth, ≥65%) + deionised H₂O, H₃PO₄ (Sigma-Aldrich, ≥99.999%), and NH₃(aq) (Sigma-Aldrich, 25%) + deionised H₂O, all in n-butanol (Sigma-Aldrich, ≥99.7%) are denoted as F_TB, F_HNO3, F_H3PO4, and F_NH3, respectively. These solutions were mixed consecutively in the three micromixers (Fig. 1, MX1–MX3). The nominal volumetric ratio was kept constant at F_TB/F_HNO3/F_H3PO4/F_NH3 = 1/1/1.3/1.6 during all syntheses, based on former investigations,²⁶ while temperature (T_MX1), space velocity (SV), concentration of TB (c_TB), and molar flow ratios of each reactant (HNO₃, H₂O at MX1, H₃PO₄, NH₃, and H₂O at MX3) in relation to TB (ṅ_HNO3/ṅ_TB, ṅ_H2O/ṅ_TB (at MX1), ṅ_H3PO4/ṅ_TB, ṅ_NH3/ṅ_TB, ṅ_H2O/ṅ_TB (at MX3), respectively) were varied. The temperature in MX1 was adjusted utilising the two heat exchangers (HE1 and HE2) in the TB and H₃PO₄ feeds, respectively. The space velocity, based on the flow of pure TB and a total reactor volume of V_r = 2.24 cm³, was varied through the total flow of the TB solution while the other reactant flows were set according to the flow ratio given above. Molar flow ratios were tuned by modifying the concentrations of the reactants in the feed solutions. Ca. 200 cm³ of the resulting slurry were collected in a stirred beaker upon each experiment. The catalyst precursor was separated from the slurry without further ageing by centrifugation at 10 000 rpm for 10 min and subsequent washing i) two times with ca. 200 cm³ of acetone + 0.75 cm³ NH₃(aq) and ii) with ca. 200 cm³ of n-hexane + 0.75 cm³ NH₃(aq). The materials obtained were dried at 338 K in vacuum for 15 h and finally they were calcined at 873 K (5 K min⁻¹) for 3 h in static air. A table detailing all reaction solutions and synthesis parameters applied is given in the ESI† (Table S1). These samples are denoted as P-TiO₂-mr-x, where x is the number of the experimental run. The optimised phosphated TiO₂ and the pure TiO₂ catalyst both prepared under the same conditions are labelled P-TiO₂-mr and TiO₂-mr, respectively. A phosphated TiO₂ benchmark catalyst and a pure TiO₂ material (denoted as P-TiO₂-b and TiO₂-b, respectively) were synthesised in a batch reactor using the same c_TB and molar ratios of reactants (n_HNO3/n_TB, n_H2O/n_TB, n_H3PO4/n_TB, n_NH3/n_TB) as for the synthesis of P-TiO₂-mr and TiO₂-mr, respectively. In case of P-TiO₂-b, 1.27 g of H₃PO₄ were dissolved in a mixture containing 74.12 g of n-butanol and 31.03 g of deionised water in a round-bottom flask. Subsequently, 42.54 g of TB and 4.26 g of NH₃(aq) were added dropwise to this solution under vigorous stirring and heating to 318 K. After the addition of all reactants, the slurry was stirred for a further hour. Afterwards, all solvents were removed by centrifugation and the solid was washed, dried, and calcined as previously elaborated. The TiO₂-b sample was synthesised in the same way by omitting H₃PO₄. Apparent reaction rate (r_c), catalyst yield (Y_cat), and space–time yield (STY_cat) were calculated according to eqn (S1)–(S3),† respectively.

Fig. 1 (a) Photograph and (b) piping & instrumentation diagram (PID) of the modular Ehrfeld system (MMRS) utilised in this study for the continuous preparation of the catalysts. The four reaction solutions were fed into the inlets (IN) by HPLC pumps (not visualized) and mixed together in the three micromixers (MX). Feed 1 and 2 were temperature controlled by heat exchangers (HE) prior to mixing in MX1. The microreactor was monitored by four pressure transducers (PT) and two temperature sensors (TS).

Characterisation

The bulk elemental composition of the calcined samples was determined by XRF spectroscopy applying a Thermo ARL ADVANT'XP spectrometer equipped with a Rh source (60 kV, 40 mA) and a flow proportional counter (FPC) detector. Mole fraction of phosphorus in the bulk catalyst was determined by eqn (S4).† Semi-quantitative analysis was performed using Uniquant software. XRPD was carried out utilising a Bruker D8 Advance instrument, applying Ni-filtered Cu-Kα radiation, an angular step size of 0.009° 2θ, and a counting time of 0.5 s per step. The average TiO₂ particle size was estimated from the largest reflection of each individual phase using the Scherrer equation. Nitrogen sorption was measured at 77 K in a Quantachrome NOVA 3000e instrument, after evacuating the samples at 573 K for 3 h. The total surface area and average pore size were determined by applying Brunauer–Emmett–Teller (BET) and Barrett–Joyner–Halenda (BJH) models, respectively. Temperature-programmed desorption of NH₃ (NH₃-TPD) analysis was performed at a Quantachrome Autosorb iQ TPX unit equipped with a thermal conductivity detector (TCD). For this measurement, a sample of ca. 100 mg was first pretreated in He (50 cm³ STP min⁻¹) at 773 K (50 K min⁻¹) for 2 h followed by an adsorption step in 10 mol% NH₃ in N₂ (25 cm³ STP min⁻¹) at 373 K for 30 min, a subsequent purging step in N₂ (25 cm³ STP min⁻¹) at 373 K for 2 h, and finally a desorption step in which the temperature was increased from 373 to 1073 K at a heating rate of 10 K min⁻¹ in N₂ (25 cm³ STP min⁻¹). Fourier transform infrared spectroscopy (FT-IR) of pyridine adsorbed was conducted in a Bruker Vertex 70 spectrometer (400–4000 cm⁻¹, co-addition of 32 scans). Self-supporting wafers of catalyst (5 ton m⁻², 30 mg, 1 cm²) were degassed under vacuum (10⁻³ mbar) for 4 h at 573 K, prior to adsorbing pyridine at room temperature. Gaseous and weakly adsorbed molecules were subsequently removed by evacuation at room temperature (15 min) and 473 K, 573 K, and 673 K (30 min). The total concentrations of Brønsted and Lewis acid sites were calculated from the band area of pyridine adsorbed at 1545 and 1454 cm⁻¹, using previously determined extinction coefficients of ε_Brønsted = 1.67 cm mmol⁻¹ and ε_Lewis = 2.94 cm mmol⁻¹.⁵⁴ Temperature-programmed surface reaction (TPSR) of n-propylamine to propene and ammonia was studied using a Micromeritics Autochem II chemisorption analyzer coupled with a Pfeiffer Vacuum OmniStar quadrupole mass spectrometer. Following in situ pretreatment in flowing He (50 cm³ min⁻¹) at 773 K for 2 h, the samples were saturated with n-propylamine at 473 K. Physisorbed amine was removed by purging with He. The decomposition of n-propylamine was monitored in the range 473–773 K using a heating rate of 10 K min⁻¹. Diffuse reflectance ultraviolet-visible spectroscopy (UV-vis) spectroscopy was carried out at a PerkinElmer Lambda 650 spectrometer with an integrating sphere (150 mm in diameter, Spectralon) and an R955 photomultiplier tube (PMT) detector. Samples and blank (Spectralon) were scanned between 200 and 800 nm using monochromatised light from tungsten halogen and deuterium lamps (switching at 319.2 nm) at steps of 1 nm s⁻¹. The measured reflectance was converted to Kubelka–Munk intensity and the band gaps were calculated from the wavelength λ, given by the intersection of the two tangents, applying the following equation: E_bandgap/eV = 1239.8 nm λ⁻¹.⁴⁶ Solid-state magic angle spinning nuclear magnetic resonance (MAS NMR) spectroscopy with high-power proton decoupling spectra of ³¹P were recorded at a spinning speed of 10 kHz on a Bruker Avance 700 MHz spectrometer featuring a 2.5 mm probe head and 2.5 mm ZrO₂ rotors. ³¹P MAS NMR spectra were collected using 1024 accumulations at pulses of 7.2 ms and a relaxation time of one second, and NH₄H₂PO₄ as reference.

Catalytic evaluation

All samples were tested for their catalytic performance during 5-HMF synthesis from glucose based on the method reported by Beltramini et al.²⁹ In brief, α-D-glucose (520 mg, Sigma-Aldrich, 96%), NaCl (400 mg, Sigma-Aldrich, ≥99.8%), and the catalyst (125 mg) were mixed together with deionised water (2.0 cm³), tetrahydrofuran (THF, 6.0 cm³, Acros Organics, 99.99%), and 1-methyl-2-pyrrolidinone (NMP, 2.0 cm³, Sigma-Aldrich, 99.5%) in a sealed 20 cm³ glass vial equipped with a magnetic stirrer bar. The reaction was performed in a Biotage Initiator microwave reactor at 423 K for 105 min at autogenous pressure (ca. 1.0 MPa). After cooling-down, the reaction mixture was decanted to remove any solids and the resulting two phases were isolated in a separation funnel. Both liquids were analysed individually by high-performance liquid chromatography (HPLC) using an Agilent 1200 Series instrument with an evaporative light scattering detector (ELSD) to analyse glucose and fructose concentrations. A diode array detector (DAD) was applied to analyse the 5-HMF. All measurement solutions were further purified through a 0.45 μm syringe filter. For calibration purposes, α-D-glucose (vide supra), α-D-fructose (Alfa Aesar, 99%), and 5-HMF (Sigma-Aldrich, ≥98.0%) were utilised. Glucose conversion (X_glucose), 5-HMF selectivity (S_5-HMF), and the catalyst surface-based rate of 5-HMF formation (r_s) were calculated by eqn (S5)–(S7),† respectively. For examining catalyst stability, sample P-TiO₂-mr was filtered from the reaction mixture after the 5-HMF reaction, washed three times with 10 cm³ of acetone each and finally it was calcined as described above. Amounts of chemicals applied in the mixture for the 5-HMF reaction were adapted, due to the small loss of catalytic material upon each regeneration step, to keep the weight ratio constant with respect to the catalyst.

Design of experiments (DoE)

GlobalOptimize 2.1 software was employed to create the experimental plan, to calculate correlation models, and to optimise the catalyst synthesis and properties. All parameters used as well as all models and results obtained can be found in the ESI† (Tables S1–S4 and Fig. S1 and S2). Input parameters were selected based on literature findings, mainly in order to influence sol–gel process or 5-HMF synthesis. The developed approach is schematically presented in Fig. 2. A D-optimal experimental plan with a central point was defined for the catalyst synthesis, resulting in 18 experiments in which T_MX1, SV, c_TB, ṅ_HNO3/ṅ_TB, ṅ_H2O/ṅ_TB (at MX1), ṅ_H3PO4/ṅ_TB, ṅ_NH3/ṅ_TB, and ṅ_H2O/ṅ_TB (at MX3) were varied simultaneously. First, the BET surface area, the mean pore size, the total pore volume, the mean crystallite size, and the mole bulk fraction of P of the resulting calcined catalysts were correlated with the glucose conversion, the 5-HMF selectivity, and the surface related reaction rate of 5-HMF applying a linear combination of either interaction and quadratic models, which provided the best fit for the data. These models were used to predict optimal catalyst properties, at which the conversion, selectivity, and reaction rate should be maximised. The resulting properties were finally used as target parameters to optimise the catalyst synthesis, while simultaneously targeting maximum catalyst (space–time) yield, employing a linear combination of quadratic models.

Fig. 2 (a) Schematic representation of the two-stage DoE approach developed in this study for the simultaneous optimization of both catalyst preparation in the microreactor process (blue) and catalytic performance (green) in correlation with the catalyst properties. (b) Overview on the influence and target parameters of catalyst production, catalyst properties, and catalytic performance used for the DoE herein.

Results and discussion

Sol–gel synthesis of phosphated TiO₂ in a microreactor

The microreactor set-up was developed based on the conventional batch process for synthesising phosphated TiO₂via sol–gel reported by Beltramini et al.^29–31 We thought the three reaction steps, i.e., i) hydrolysis and sol formation, ii) phosphatisation, and iii) gelation–precipitation, could be better controlled by using a continuous microreactor featuring three micromixers (Fig. 1b, MX1–3). We utilised two narrow slit plate mixers for the first two mixing steps, during which sol particles below 2–3 nm in size were expected to form according to earlier investigations.²⁶ The first step mixed the solutions containing the Ti precursor (TB) and H₂O (MX1) and the second one blended the resulting mixture with the H₃PO₄ containing feed (MX2). In addition, we added HNO₃ to the H₂O containing feed during the first mixing step, prior to the phosphorus incorporation step, to investigate the catalytic role of mineral acids on hydrolysis upon TiO₂ sol formation.³⁷ Since generation of nm–μm-sized aggregates was anticipated during gelation–precipitation, i.e., when NH₃ was added to the reaction mixture (MX3), we decided to use a valve mixer, which prevents fouling because of its advantageous dimensions.²⁶

A D-optimal experimental plan with a central point for synthesising the phosphated TiO₂ catalysts in the microreactor was defined based on the boundaries of the input parameters (Table S1†), which were either given based on technical limitations (e.g., for the temperature in the heaters, HE1 and HE2) or established through preliminary experiments (e.g., miscibility of H₂O and n-butanol). This provided a set of a minimum of 18 experiments in which all eight input parameters (Fig. 2b) were altered simultaneously. Since the DoE software allows the suggested parameters to be varied, the plan was adapted if necessary, e.g., when the H₂O concentration in one of the feed solutions would have been too high in order to completely mix with n-butanol. It was observed that under all conditions applied, there was no severe fouling of the microreactor, i.e., the pressure in the system did not exceed 0.7 MPa during catalyst production. This result corroborates the theory that using TB as precursor for this synthesis appears to be a promising way to avoid clogging of the narrow microchannels of the slit plate mixers as a result of the slower hydrolysis kinetics of this compound compared to other alkoxides, e.g., Ti isopropoxide.²⁶ However, it should be noted that the largest increase in pressure occurred at high concentrations of TB (c_TB) and small space velocities. Since our microreactor set-up only ran for between 5 and 60 min (depending on c_TB and SV), long-term tests will be required in the future to evaluate fouling behaviour on industrially-relevant production time scales of several days and longer.

TiO₂ based yields (Y_TiO2) and catalyst space–time yields (STY_cat) achieved for the microreactor prepared samples ranged between 21.2–99.2% and 0.7–26.7 g_cat h⁻¹ cm_reactor⁻³, respectively (Table S2†). In the batch reactor, comparable Y_TiO2 values of 89.6 and 91.7% (Table 1) could be achieved for pure (TiO₂-b) and phosphated TiO₂ (P-TiO₂-b), respectively, but at only STY_cat of 0.07 g_cat h⁻¹ cm_reactor⁻³, i.e., ca. 1–3 orders of magnitude lower than all samples prepared in the microreactor. This can be explained by the larger reactor volume in the batch system (ca. 170 vs. 2.24 cm³). In addition, the STY_cat as defined in this work (eqn (S3))† does not take into account the unavoidable time of repetitive shut-downs, emptying, refilling, and restarting of the batch system, which would further lower its effective space–time yield over the long term. Considering the microreactor prepared samples only, STY_cat increases almost linearly with ascending space velocity (Fig. S3†), which is generally expected in continuous reactors. In contrast, a broad distribution of Y_TiO2 (21.2–87.9%) was observed at SV < 40 h⁻¹, while above this limit Y_TiO2 remained between 80.6 and 99.2% when plotting the yield against space velocity (Fig. 3a, red and blue symbols, respectively). This distribution indicates that catalyst yield is heavily influenced by reaction kinetics at low SV. Replotting Y_TiO2 as a function of apparent reaction rates of TB (r_c) reveals a monotonically increasing relationship between both (Fig. 3b). Interestingly, the lowest reaction rates were observed for the samples synthesised at low SV and, in fact, both groups appear to follow different reaction kinetics according to r_c–T_MX1 correlations (Fig. 3c): i) samples prepared at SV > 40 h⁻¹ show a steady increase in r_c as T_MX1 increases and ii) the ones synthesised at SV < 40 h⁻¹ show an r_c which is almost invariant in relation to T_MX1. The lower yield of the latter samples might be therefore partially explained by the slower reaction rates. Eventually, the reaction network is controlled by thermodynamics for long residence times, e.g., by favouring hydrolysis ↔ hydroxylation over condensation.

Table 1 Catalyst synthesis parameters, catalyst properties, and catalytic performance for TiO₂ and P-TiO₂ prepared via batch or microreactor, respectively. The optima of catalyst preparation and 5-HMF synthesis for the P-TiO₂-mr sample are also shown based on the models derived from DoE (vide Tables S3 and S4)

Parameters	P-TiO2-mr^a	Catalyst preparation optimum^b	5-HMF synthesis optimum^b	P-TiO2-b	TiO2-mr	TiO2-b
a Values are given with the standard deviations calculated from the triple determination of the optimal catalyst (Tables S1 and S2). b As predicted by the DoE software. c Calculated from the concentration of the reactants in the feed solutions and the volumetric flows of the latter. In case of the batch-prepared samples the values were directly determined from the concentration ratio in the reaction solution. d The nH2O/nTB ratio upon batch synthesis accounts for the total H2O present in the batch reactor, i.e., the sum of ṅH2O/ṅTB at MX1 and MX3 in the case of the catalysts prepared in the microreactor.
T MX1 (K)	317 ± 1	318	—	317	317	318
SV (h^−1)	105 ± 2	110	—	—	105	—
c TB (mol l^−1)	0.85 ± 0.01	0.85	—	0.74	0.85	0.74
ṅ HNO3/ṅTB^c (—)	0	0	—	0	0	0
ṅ H2O/ṅTB (at MX1)^c (—)	2.1 ± 0.2	2.0	—	15.2^d	2.2	15.2^d
ṅ H3PO4/ṅTB^c (—)	0.26 ± 0.01	0.27	—	0.10	0.00	0.00
ṅ NH3/ṅTB^c (—)	0.50 ± 0.02	0.5	—	0.50	0.54	0.50
ṅ H2O/ṅTB (at MX3)^c (—)	12.6 ± 0.4	12.1	—	0.0^d	13.5	0.0^d
Y TiO2 (%)	98.9 ± 0.3	99.9	—	89.6	82.9	91.7
STYcat (gcat h^−1 cmreactor^−3)	26.8 ± 0.4	25.7	—	0.07	20.5	0.07
x P,bulk (—)	0.053 ± 0.005	0.046	0.040	0.049	0	0
d crystal (nm)	7.5 ± 0.1	7.0	6.3	8.6	29.2	45.1
S BET (m^2 gcat^−1)	28 ± 9	18	17	118	15	4
d pore (nm)	6.9 ± 1.0	5.2	5.4	9.6	3.6	3.6
V pore (cm^3 gcat^−1)	0.05 ± 0.02	0.03	0.03	0.40	0.04	0.01
X glucose (%)	95.6 ± 1.2	—	100.0	78.7	21.4	5.6
S 5-HMF (%)	55.5 ± 0.8	—	52.8	50.0	42.4	24.5
r s (g5-HMF h^−1 mcat^−2)	0.047 ± 0.013	—	0.037	0.008	0.014	0.008

---

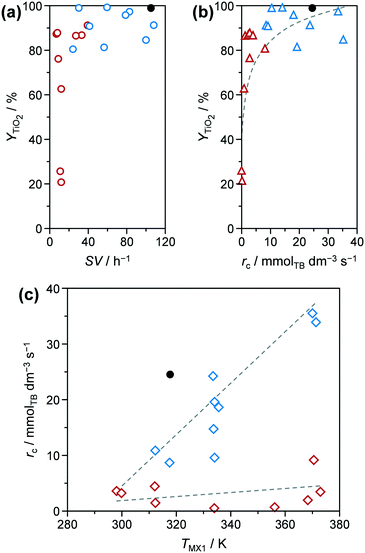Fig. 3 Y _TiO2 as a function of (a) space velocity (SV) and (b) apparent reaction rate regarding TB (r_c). (c) Apparent reaction rate as function of temperature in mixer MX1 (T_MX1). Symbols of the same colour in these plots correspond to the same samples. Solid symbols represent the results of P-TiO₂-mr synthesised under optimal conditions (Table 1).

In order to identify possible correlations between input and target parameters, Y_TiO2, STY_cat, x_P,bulk, d_crystal, S_BET, and V_pore from all 18 of the DoE samples were fitted by quadratic models as functions of synthesis input parameters (models are summarised in Table S3†). Limitations in these models become obvious when either certain conditions in the reactor are not practically feasible (e.g., too high hydrolysis ratios which would lead to biphasic mixtures) or the resulting target parameters would not have a physical meaning (e.g., yields higher than 100%). For our investigations, we varied a single parameter from the corresponding models and kept all other seven parameters constant at the values used for the preparation of the optimal catalyst P-TiO₂-mr (vide infra). For instance, Fig. 4 visualises Y_TiO2 as a modelled function of temperature T_MX1 (blue line). According to the model, catalyst yield is maximum at low temperatures of around 320 K and reaches a minimum at ca. 345 K. Subsequently, it increases again as T_MX1 increases up to 370 K but attaining a lower level with respect to Y_TiO2 at 320 K (∼80 vs. 100%). One plausible explanation for this behaviour could be that at lower temperatures a higher degree of supersaturation can be achieved. This is corroborated by the fact that P-TiO₂-mr-13 and -16 samples synthesised under similar conditions (Table S1†) at T_MX1 = 312.8 and 356.5 K, respectively, resulted in Y_TiO2 of 62.8 and 21.2% (Table S2†). At T_MX1 > 345 K, it appears that reaction kinetics is accelerated and might partially compensate for deficient supersaturation.

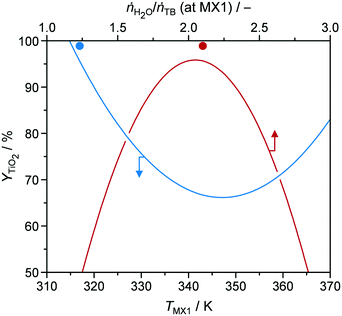Fig. 4 Y _TiO2 as a function of temperature (T_MX1) and hydrolysis ratio ṅ_H2O/ṅ_TB (at MX1) at mixer MX1. Solid symbols represent the results of P-TiO₂-mr synthesised under optimal conditions (Table 1).

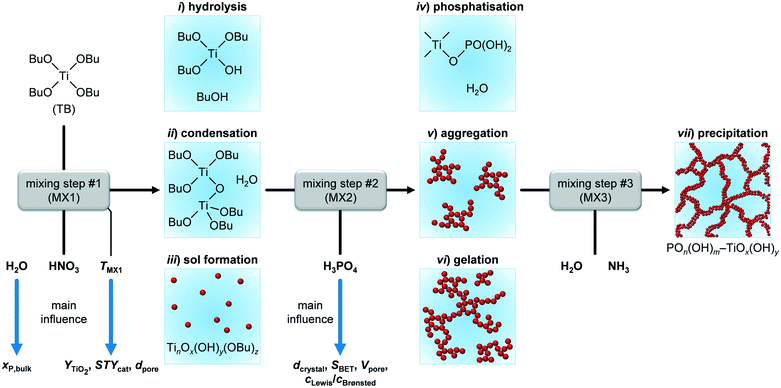
Focusing on the hydrolysis ratio ṅ_H2O/ṅ_TB (at MX1) (red line in Fig. 4), an optimal ratio of 2.1 was observed at which Y_TiO2 is maximised in the model with fixed parameters. According to stoichiometry, formation of 1 mole of Ti–O–Ti bridges would require 1 mole of H₂O (Fig. 5), corresponding to ṅ_H2O/ṅ_TB = 0.5. The higher hydrolysis ratio found optimal for a high Y_TiO2 could be partially explained by the fact that, from a kinetic perspective, 2 hydroxylated Ti species are required for condensation. Furthermore, H₂O interacts strongly with mineral acids such as HNO₃ or H₃PO₄, leading to protolysis.³⁷ We initially thought that this effect may catalyse the hydrolysis step. However, if we consider that the P-TiO₂-mr-3 sample, which was synthesised at a high SV of 100 h⁻¹ without the use of HNO₃, resulted in a good Y_TiO2 of 84.7% (Tables S1 and S2†), demonstrating that a residence time below 0.5 s was sufficient to effectively hydrolyse the TB agent and that hydrolysis does not appear to be the rate-determining step. We therefore deduced that neither HNO₃ or any additional catalysts may be necessary for optimal catalyst synthesis of P-TiO₂. This hypothesis is further elaborated in section 3.1 of the ESI.† With respect to the decrease of Y_TiO2 at hydrolysis ratios above 2.1 it appears that such excess of H₂O shifts condensation equilibrium towards hydroxylated Ti species.

Fig. 5 Reaction scheme of the sol–gel synthesis process of phosphated TiO₂ from TB precursor in the microreactor set-up used herein. Blue arrows mark the main influence parameters on catalyst (space–time) yield and on catalyst properties derived from the DoE evaluation.

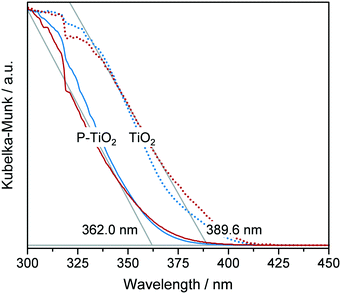
Although hydrolysis does not seem to be the bottle neck in the reaction network, the added H₂O was observed to play a significant role in the incorporation of the phosphate species (Fig. 6a) in addition to the expected global trend of x_P,bulk (i.e., mole bulk fraction of P in the resulting catalyst) to ascend as H₃PO₄ content increased in the feed (ṅ_H3PO4/ṅ_TB, Fig. S4†). Following the quadratic correlation for x_P,bulk as a function of ṅ_H2O/ṅ_TB (at MX1) (Table S3†), while keeping the other parameters constant, provided an inverse trend to the one described for Y_TiO2 as a function of ṅ_H2O/ṅ_TB (at MX1) (vide supra). x_P,bulk is minimised at a similar hydrolysis ratio of ca. 2.1, at which Y_TiO2 is maximised. This corroborates the strong interaction of H₂O and H₃PO₄ with TB, which we attempted to better understand by conducting UV-vis of the calcined TiO₂ and P-TiO₂ catalysts (Fig. 7). In accordance with earlier findings in the literature,^37,40,46 phosphate modification of TiO₂ leads to a blue-shifted O2p → Ti3d transition within the UV-vis spectra, corresponding to an enlargement of the band gap from 3.2 to 3.4 eV (TiO₂-mr and P-TiO₂-mr, respectively). This effect was partially explained by the smaller crystallite size (d_crystal), caused by the presence of the phosphorus dopant, which was also the case for our samples substantiated by the peak broadening in XRPD patterns of the phosphated catalysts (Fig. S5,† Scherrer derived d_crystal is given in Table 1). Hence, one may conclude that linking phosphate groups to hydrolysed TiO_x(OH)_y sol particles impedes further crystal growth, an effect that has also been previously observed.^30,37 In addition to shifts in the O1s and Ti2p_3/2 X-ray photoelectron spectroscopy (XPS) spectra to higher binding energies,^30,46,53 peak broadening and loss of intensity in XRPD patterns³⁰ were used to explain the incorporation of phosphorus into the TiO₂ crystal lattice, which is in line with our observations (see Fig. S5–S8†).

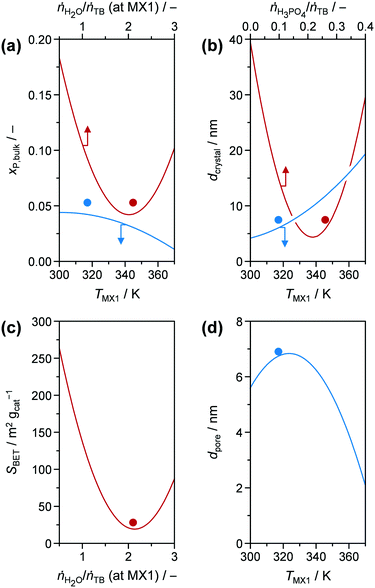Fig. 6 (a) x_P,bulk, (b) d_crystal, (c) S_BET, and (d) d_pore as modelled functions (obtained from DoE) of (a, b and d) T_MX1, (a and c) ṅ_H2O/ṅ_TB (at MX1), and (b) ṅ_H3PO4/ṅ_TB, respectively. Other input parameters were fixed at the optimal values for P-TiO₂-mr (Table 1). Solid symbols represent the results for P-TiO₂-mr synthesised under optimal conditions.

Fig. 7 UV-vis spectra of TiO₂ and P-TiO₂ prepared in the batch (blue lines) or in the microreactor (red lines), respectively. Grey lines represent the method of determining the band gap of TiO₂ from the observed wavelengths of the O2p → Ti3d transition. For the sake of clarity, this is shown for the microreactor synthesised samples only.

The presence of H₃PO₄ in the reaction mixture greatly influenced d_crystal. Even for very low amounts of H₃PO₄ in the feed (ṅ_H3PO4/ṅ_TB ∼ 0.05, corresponding to x_P,bulk ∼ 0.01), the crystallite size decreased from 29.9 nm in pure TiO₂ to 12.2 nm (vide P-TiO₂-mr-18 and -11 samples in Tables S1 and S2,† respectively). This effect was visualised by TEM images of pure and phosphated TiO₂ (Fig. S9†). These results also revealed that addition of phosphoric acid to the synthesis mixture leads to almost monodisperse crystals hinting that phosphate already is incorporated into the TiO₂ lattice at an early stage upon crystal growth. According to the conclusion given above, this is explained by the reaction of H₃PO₄ with hydrolysed TB hampering the extended crystal growth of TiO₂. Both measured data (Fig. S10†) and quadratic model (Fig. 6b, red line) point to a minimum of the crystallite size for medium ṅ_H3PO4/ṅ_TB ∼ 0.23 and x_P,bulk ∼ 0.09, respectively. Based on the model, d_crystal became larger for higher ratios, a fact that was also proven using samples prepared under similar conditions, e.g.: P-TiO₂-mr-1, -5, and -15 synthesised at ṅ_H3PO4/ṅ_TB ∼ 0.05, 0.43, and 0.10 (Table S1†) resulting in crystallite sizes of 13.4, 10.4, and 7.3 nm, respectively (Table S2†). This entire effect has not been previously observed, since former studies investigated samples with a maximum mole bulk fraction of phosphorus ≤0.15.^{30,37,40,42,55,56} In case of the first and latter samples (ṅ_H3PO4/ṅ_TB = 0.05 and 0.10), ca. 47 mol% of phosphorus in the feed solution was incorporated into the resulting solid while only 41 mol% were found in P-TiO₂-mr-5 (high ṅ_H3PO4/ṅ_TB), indicating a limit to phosphate uptake in the TiO₂ sol–gel framework. We further concluded that hydrolysis and condensation, and the resulting crystallite growth were accelerated and favoured over P incorporation at high acid-to-TB ratios.

Porous properties, i.e., S_BET, d_pore, and V_pore, of the calcined samples were mainly influenced by ṅ_H2O/ṅ_TB (at MX1), ṅ_H3PO4/ṅ_TB, and T_MX1 (Fig. 6c and d), according to the DoE models (Table S3†); a simple global correlation between experimental results and input parameters was not observed, indicating a more complex dependency between porosity and synthesis conditions. In the following discussion, V_pore is not further investigated, since it generally increased linearly with S_BET (Fig. S11†). A relationship between both properties can usually be anticipated; however, a peculiar feature in our case was that two groups emerged in this correlation. A steeper rise of V_pore was detected as S_BET increased for high mole bulk fractions of phosphorus (x_P,bulk > 0.15), indicating a different porous structure in the samples containing less phosphorus. The correlation S_BET model as a function of hydrolysis ratio in MX1 (Fig. 6c) reveals a similar shape compared to the x_P,bulk model (Fig. 6a) and its minimum at ṅ_H2O/ṅ_TB (at MX1) ∼ 2.2 is only slightly higher than the one of the latter model (2.0, vide supra). Thus, it could be concluded that surface area and phosphorus content in the catalysts are tuned by the same mechanistic steps during sol–gel formation, which makes sense when considering phosphate is incorporated into the TiO₂ crystal lattice. One aspect of this dependency relates to the observation that S_BET increases as d_crystal decreases (Fig. S12†). However, this correlation comprises huge distributions and hence, crystallite size is one but not the only parameter that influences the porous properties of our samples. Based on experimental evidence and models, we deduced that i) phosphorus incorporation into the titanium oxide framework upon sol formation and ii) the arrangement of the resulting crystallites within the mesoporous agglomerates during gelation were governed by the hydrolysis ratio (ṅ_H2O/ṅ_TB (at MX1)).

5-HMF synthesis over phosphated TiO₂

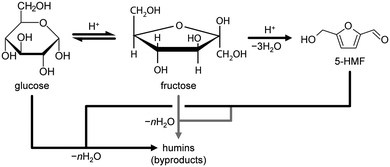
Conversion of glucose to 5-HMF via fructose as an intermediate (Scheme 1) was chosen as a model reaction since it has previously been shown that phosphated TiO₂ catalysts exhibit promising activity and selectivity for this reaction when conducted in biphasic systems.^29–31 Under optimised conditions, low glucose concentration (2 wt%), high catalyst-to-substrate ratios (m_cat/m_glucose = 1/3), biphasic systems (like THF/H₂O), medium temperatures (448 K), and ca. 3 h of reaction time lead to 94% glucose conversion and 83% 5-HMF yield.²⁹ The addition of NMP as an additive was also found to significantly improve selectivity, explained by i) suppressing the formation of polycondensation humin byproducts from the substrate, intermediate, and product (Scheme 1), and ii) facilitated partitioning of 5-HMF into the organic layer.⁵⁷ For the purpose of the investigations presented herein, we utilised the synthesis approach by Beltramini et al.²⁹ However, since the focus of our study was on the optimisation of the catalyst and its synthesis, conditions for 5-HMF synthesis were, for the sake of comparison, fixed to maintain conversion levels below 100% by applying a lower reaction temperature (423 K) and a larger substrate concentration (5.5 wt%). Furthermore, reactions were performed in microwave irradiated batch reactors, enabling fast heating rates and high energy efficiency.³⁵ In line with results from the literature, we also obtained an increase in both activity and selectivity towards 5-HMF for comparable catalysts synthesised in a batch reactor when phosphate is present in the TiO₂ framework (Fig. 8). Glucose conversion (X_glucose, green bars) improved from 2.7% in the reaction without a catalyst to 5.6% for the TiO₂-b sample and finally, to 78.7% for the P-TiO₂-b sample, while selectivity for 5-HMF (S_5-HMF, blue bars) increased from 17.5 to 24.5 to 50.0%, respectively, and selectivity to fructose (S_fructose) declined likewise.

Scheme 1 5-HMF synthesis from glucose via fructose intermediate.

Fig. 8 Glucose conversion (X_glucose, green bars), selectivities towards 5-HMF (S_5-HMF, blue bars) and fructose (S_fructose, red bars) and surface related reaction rate (r_s, grey bars) upon 5-HMF synthesis from glucose without catalyst (blank) as well as over pure TiO₂ and P-TiO₂ prepared in batch mode (‘b’) or in the microreactor (‘mr’). Reaction conditions: 5.5 wt% of glucose, m_cat/m_glucose = 1/4, 4.3 wt% of NaCl, V_H2O/V_THF/V_NMP = 2/6/2, T = 423 K, P = 1.0 MPa, and t = 105 min.

The change in activity can be explained by the different amounts and types of catalytically active acid sites present on TiO₂-b and P-TiO₂-b. The total concentrations of Brønsted (c_Brønsted) and Lewis (c_Lewis) acid sites and their evolution upon increasing the evacuation temperature were quantified by infrared spectroscopic analysis of chemisorbed pyridine (Fig. 9, blue symbols). The absence of Brønsted acidity was evidenced for the TiO₂ sample and was accompanied by a minor concentration of Lewis acid sites that was almost vanished after evacuation at 573 K. Phosphorus incorporation led to the appearance of Brønsted acidity and the higher concentration of stronger Lewis acid sites than the pure TiO₂ sample. In the case of the phosphated catalyst (P-TiO₂-b), 50% and 11% of the Lewis acid sites present at 473 K are retained after evacuation at 573 K and 673 K, respectively. Contrarily, in the absence of phosphorus, TiO₂-b sample only preserved 75% at 573 K and the complete disappearance of Lewis acid sites was detected after evacuation at 673 K, which suggests the presence of stronger acid sites on the P-TiO₂-b sample (Fig. 9b). These results are in line with the observations by NH₃-TPD (Fig. S14,† blue lines). Brønsted sites were further investigated by TPSR of n-propylamine (Fig. 10a, blue lines): primary amines, which can be adsorbed in stoichiometric quantities on Brønsted acid sites, decompose upon heating via the Hofmann elimination to alkenes and ammonia. The relative evolutions of n-propylamine, propene, and ammonia between 473 K and 773 K are provided in Fig. S15b and d.† In the case of the TiO₂-b sample, the mass spectra of these compounds are barely constant, which could be due to the negligible adsorption of n-propylamine, in line with the absence of Brønsted acid sites on these catalysts (Fig. 9a, blue diamonds). For the phosphated TiO₂ sample (Fig. S15d†), only unreacted n-propylamine was detected in appreciable amounts between 473 K and 525 K. A single broad desorption peak was observed, which is attributed to the loss of weakly bound molecules, e.g., associated to Lewis acid sites, hydroxyl defects or hydrogen bonded to protonated amines at the Brønsted sites that are unable to catalyze the Hofmann elimination.⁵⁸ Above 525 K, propene and ammonia were also evolved. As shown in Fig. 10a, two well-resolved peaks can be distinguished in the propene spectra (blue line). The first peak is characteristic of the surface reaction of n-propylamine adsorbed on Brønsted acid sites.⁵⁸ The temperature of the peak maximum and the associated amount of propene desorbed can be used as an alternative mean to quantify the strength and bulk concentration of Brønsted acid sites, respectively. In contrast to the first peak, the origin of the second peak is still a subject of debate. Its appearance has been linked with the presence of a weaker type of acid sites⁵⁹ and with the interaction with Lewis acid centers.⁶⁰ Readsorption and subsequent reaction of the desorbed n-propylamine on Brønsted acid sites vacated at lower temperatures that could give rise to additional propene desorption at higher temperatures seems unfeasible since no ammonia desorption was detected in this temperature range (Fig. S15d†). The latter suggests the possible formation of dialkylamines and their subsequent decomposition into the alkene and the primary amine at temperatures above 650 K.⁶¹

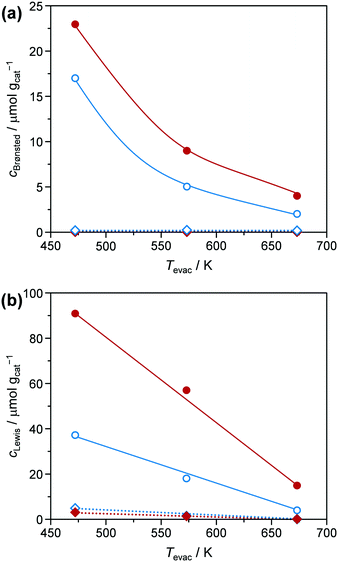Fig. 9 Evolution of the concentration of (a) Brønsted (c_Brønsted) and (b) Lewis (c_Lewis) acid sites of the TiO₂ (diamonds) and P-TiO₂ (circles) catalysts prepared in the batch (blue symbols) or in the microreactor (red symbols), respectively, with the evacuation temperature (T_evac) determined by infrared spectroscopy of pyridine adsorbed (see Fig. S13†).

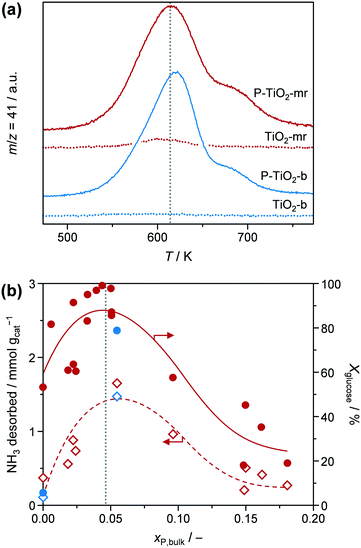Fig. 10 (a) Propene evolution upon TPSR of n-propylamine over TiO₂ (dashed lines) and P-TiO₂ (straight lines) catalysts prepared in the batch (blue lines) or in the microreactor (red lines), respectively. Evolution of n-propylamine and ammonia is given in Fig. S15 in the ESI.† (b) Total amount of NH₃ desorbed during NH₃-TPD analysis (diamonds) and glucose conversion (X_glucose, circles) of (selected) P-TiO₂ samples, prepared in the batch (‘b’, blue symbols) or in the microreactor (‘mr’, red symbols), as a function of mole bulk fraction of P. Dotted line represents optimal x_P,bulk.

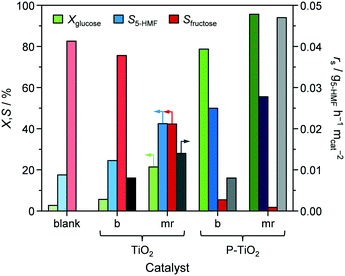
In view of these evidences, which are in line with various studies,^29,30,39,41 it is clear that phosphatisation of TiO₂ enhances the number of Lewis and Brønsted sites; however, only the optimal balance between both centres in such bifunctional catalysts correlated with elevated 5-HMF formation compared to systems featuring only one type of acid site.^{29–31,44,45} According to the observations and conclusions of these studies, fructose isomerisation is supposed to mainly take place over Lewis sites while Brønsted centres are likely to catalyse dehydrogenation of a cyclic enol intermediate^62,63 into 5-HMF. The low activity and 5-HMF selectivity determined in our experiments when a catalyst was absent and the observation of decreasing fructose concentrations as X_glucose increases in favour of 5-HMF formation (Fig. 8) corroborate earlier hypotheses claiming fructose isomerisation to be the rate determining step in this reaction.^29,31

In order to gain a deeper understanding of the interplay between catalyst properties and catalytic performance, we evaluated all microreactor prepared samples (P-TiO₂-mr-1–18) under the same reaction conditions as the batch catalysts. Their individual catalytic results are summarised in Table S2.† We found an optimal value for the phosphorus bulk concentration of x_P,bulk ∼ 0.05 at which X_glucose, ranging from 18.0 to 99.1%, is maximised (Fig. 10b, circles) in line with the results obtained by Beltramini et al.³⁰ However, in the correlation presented herein, strong local deviations were also observed, hinting that more than one single catalyst property might influence the activity. This relation can be partly explained by the number of catalytically active surface acid sites present in our samples since the total amount of NH₃ desorbed shows a similar trend for x_P,bulk, featuring a slight shift of the maximum to higher bulk phosphorus concentrations of 0.07 (Fig. 10b, diamonds). This result substantiates that not only the number of acid sites but also the balanced presence of both Lewis and Brønsted sites is relevant to the efficient conversion of glucose to 5-HMF over P-TiO₂ based catalysts. In terms of the correlation between mole surface and bulk fraction of phosphorus (Fig. S16†), all samples had slightly more phosphorus on the surface compared to the bulk. From this we deduced that the surface of the samples exhibiting x_P,bulk > 0.05 may already be enriched with Brønsted acid sites at the expense of Lewis centres and hence, resulting in lower activity of glucose–fructose isomerisation, but enhanced dehydrogenation of fructose to 5-HMF. In fact, selectivity towards 5-HMF was highest (S_5-HMF > 44.7%, Table S2†) for the samples containing most phosphorus (x_P,bulk > 0.09). Besides, the change in selectivity could also be explained by the ca. 10% higher acid site density in these samples compared to the ones featuring less phosphorus (Fig. S17b†). The same explanations hold for the TiO₂ catalysts without phosphate loading: the microreactor prepared sample, P-TiO₂-mr-18, had a significantly higher number of surface acid sites (0.38 vs. 0.10 mmol g_cat⁻¹) and hence, exhibited greatly improved activity of 56.2% compared to its batch prepared counterpart (TiO₂-b) with only 5.6% conversion (vide points of X_glucose at x_P,bulk = 0 in Fig. 10b). The local fine structure of the X_glucose–x_P,bulk correlation in Fig. 10b is likely due to other catalyst properties influencing their activity. It can be generally stated that as S_BET increases, conversion also increases to almost 100%, which could be explained by the likely higher absolute number of active sites exposed. Interestingly, the two groups of microreactor prepared samples that showed a different correlation for V_porevs. S_BET (Fig. S11† and vide supra) also exhibited a distinct activity when correlating X_glucose and S_BET (Fig. S18a†). Understanding the different porous features of these two groups will require a deeper structural analysis in an upcoming investigation.

In contrast to X_glucose, S_5-HMF was only slightly affected (changing between 34.7 and 49.8%, Table S2 and Fig. S18b†) by catalyst properties of the samples of this study. In view of this result and based on the literature,^{19,29–31,34,35,57,62–69} we concluded that reaction conditions (i.e., reaction or residence time, temperature, pressure and partitioning of 5-HMF into the organic layer) play a more significant role on selectivity than catalyst features. In all cases, the resulting reaction mixtures in our experiments became medium to dark brown solutions, which probably caused the unresolved peaks observed in the HPLC analysis. Several side reactions have been identified in 5-HMF synthesis from sugar sources combining in a network of isomerisation, dehydration, fragmentation, and/or condensation steps,^62,63,65e.g.: 5-HMF, likely adsorbed on strong Brønsted acid sites,^70,71 and H₂O can undergo polymerisation reactions and/or form levulinic acid.⁶⁴ Furthermore, the glucose substrate, the fructose intermediate, and the 5-HMF product can be involved in polycondensation, creating cross-linked humin compounds.^65,67–69 In order to achieve high selectivity to 5-HMF, it was necessary i) to quickly isomerise glucose into fructose, thus avoiding the formation of reactive glucose oligosaccharides^31,65 and ii) to partition 5-HMF into the organic layer to separate it from the sugars and H₂O.^34,35,56 Despite the use of NMP as a phase transfer mediator for 5-HMF,²⁹ the average product concentration in our system was only 1.5-times higher in the organic phase than in the aqueous layer. The high glucose concentration (i.e., 5.5 wt%) is prone to result in excessive oligomer formation, triggering the side reactions described above.⁶⁵

Finally, we assessed the catalyst efficiency expressed as surface based reaction rate (r_s), i.e., formation rate of 5-HMF per BET surface area of calcined, fresh catalyst, for all the developed materials (Tables 1 and S2†). For the bulk prepared catalysts, there was no improvement when comparing TiO₂-b and P-TiO₂-b, resulting in a r_s of 0.008 g_5-HMF h⁻¹ m⁻². In contrast, samples synthesised in the microreactor (P-TiO₂-mr-1–18) exhibited higher catalyst efficiencies (0.007–0.047 g_5-HMF h⁻¹ m⁻²) compared to the bulk. Plotting r_svs. a single catalyst property did not allow simple correlations to be identified, hinting that catalyst efficiency is affected by an interplay of porosity, crystallite size, and molar P/Ti bulk ratio (i.e., acidity). Fig. 11 highlights the correlations between r_s and x_P,bulk and d_crystal when the other catalyst properties are kept fixed. According to these models (Table S4†), the most efficient catalyst should possess small d_crystal and low x_P,bulk. Hence, 5-HMF synthesis over P-TiO₂ catalysts appears to be particle size dependent. This was attributed to the fact that the proportion of crystallographic facets of TiO₂ crystallites, as present in our samples, is usually different for crystals of different sizes, which is likely to impact the active sites.⁷² The second maximum found for small d_crystal and high x_P,bulk is likely due to enhanced surface acid site concentration, which was found beneficial for 5-HMF synthesis activity (vide supra and Fig. S17b†). The third maximum for large d_crystal and low x_P,bulk stems from including the P-TiO₂-mr-18 sample (pure TiO₂) in the DoE which showed very large crystals (29.9 nm), a x_P,bulk of 0, but a high r_s of 0.032 g_5-HMF h⁻¹ m⁻² (Table S2†). We interpreted this outlier in the correlation as evidence that the reaction mechanism over pure TiO₂ differs from that using the phosphated catalysts and is probably due to the presence of different types of acid sites in both groups of materials (Fig. 9, 10, and S14†). The fourth maximum shown for large d_crystal and large x_P,bulk (Fig. 11) unveils the limitation of the models applied since it appears difficult to prepare huge TiO₂ crystallites at high phosphate concentrations. Samples exhibiting x_P,bulk between 0.148 and 0.180 only contained TiO₂ crystals of 10.4–14.5 nm in size (Table S2†). However, as it will be demonstrated below, the accuracy of the models was sufficient to tune catalyst preparation and performance at the same time.

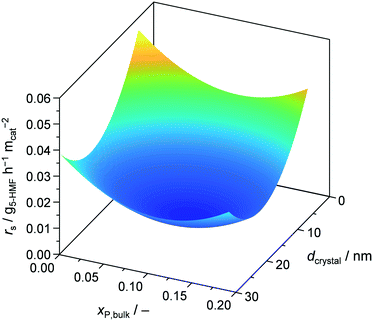Fig. 11 Reaction rate of 5-HMF as a function of mole bulk fraction of P and TiO₂ crystallite size at fixed S_BET = 17 m² g_cat⁻¹, d_pore = 5.4 nm, and V_pore = 0.03 cm³ g_cat⁻¹.

Optimisation of catalyst synthesis and catalytic performance

Combination of DoE models for catalyst synthesis (Table S3†) and catalytic reaction (Table S4†) were exploited to simultaneously relate parameters that influence catalyst preparation, catalyst yield, catalyst properties, and catalytic performance (Fig. 2). Optimal catalyst properties (x_P,bulk, d_crystal, S_BET, d_pore, and V_pore) were achieved with the aid of the DoE software by optimising the 5-HMF synthesis models for maximal X_glucose, S_5-HMF, and r_s. The resulting catalyst properties were subsequently used as target values for optimising catalyst synthesis and obtaining maximal Y_TiO2 and STY_cat. The results of both optimisations (columns ‘optimum’), the synthesis parameters effectively applied, the resulting catalyst properties, and the catalytic performance are summarised in Table 1 (sample ‘P-TiO₂-mr’). Synthesis parameters were used to predict resulting catalyst (space–time) yield and catalyst properties. The same was done for the 5-HMF synthesis values (Table 1). It turned out that the DoE models generally underestimated the target parameters by 1.4–25%, which is still, however, a good approximation of the correlations discussed here. The deviation even reached 60% in the case of V_pore; however, we would like to stress that the standard deviation and experimental error were in a similar range. The synthesis of the optimal catalyst P-TiO₂-mr was repeated three times and delivered reproducible results, based on a maximal relative standard deviation of ca. 30% for each parameter (except for V_pore; Table 1). This emphasises that a stable process could be established, pointing to a validation of the correlation models in this work, even though the models would benefit from further refinement to better reflect local effects as already mentioned above.

From Fig. 12, it can be seen that applying optimal synthesis conditions for P-TiO₂ catalysts in the microreactor simultaneously resulted in the highest Y_TiO2 and STY_cat values (98.9% and 26.8 g_cat h⁻¹ cm_reactor⁻³, respectively) of all the batch and microreactor prepared samples (Tables 1 and S2†). For comparison purposes, a second phosphate-free TiO₂ catalyst (TiO₂-mr) was prepared under the conditions that were found to be optimal for the P-TiO₂-mr system. Y_TiO2 and STY_cat from this sample were slightly lower (82.9% and 20.5 g_cat h⁻¹ cm_reactor⁻³) compared to its phosphate containing counterpart, emphasising that both systems have different optimal synthesis conditions. This appears plausible since we had already discovered that even a small concentration of phosphate was likely to alter the mechanism of the sol–gel process (Fig. 5).

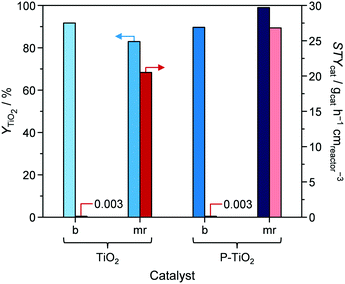Fig. 12 Yield (Y_TiO2) and space–time yield (STY_cat) of pure (TiO₂) and phosphated titania (P-TiO₂) prepared in batch mode (b) or in the microreactor (mr), respectively.

Surprisingly, the TiO₂-mr material featured X_glucose = 21.4%, S_5-HMF = 42.4%, and r_s = 0.014 g_5-HMF h⁻¹ m⁻² upon 5-HMF synthesis, which is a considerable improvement compared to the TiO₂-b sample (5.6%, 24.5%, 0.008 g_5-HMF h⁻¹ m⁻², respectively, Fig. 8 and Table 1). We deduced from this result that the microreactor prepared catalyst partially benefitted from catalyst properties which were found to boost catalytic performance, such as lower crystallite size, low porosity (Table 1), and higher acidity (as evidenced by the small propene evolution upon TPSR of n-propylamine, Fig. 10, red dashed line). However, glucose conversion, 5-HMF selectivity, and catalyst efficiency could be maximised towards 95.6%, 55.5%, 0.047 g_5-HMF h⁻¹ m⁻², respectively, only in case of the optimised P-TiO₂-mr sample in relation to the catalytic performance of the batch catalyst P-TiO₂-b (X_glucose = 78.7%, S_5-HMF = 50.0%, and r_s = 0.008 g_5-HMF h⁻¹ m⁻², Fig. 8 and Table 1). The effect upon phosphorus incorporation into the TiO₂ framework on the acid properties elaborated above with respect to the batch samples also applies to the microreactor catalysts; however, a clear difference in the amount and nature of acid centres in the resulting materials could be unravelled based on the catalyst synthesis protocol. Comparison of the phosphated TiO₂ samples by FT-IR of pyridine adsorbed (Fig. 9) evidenced a higher concentration of both Brønsted and Lewis acid sites and also a significantly higher ratio of Lewis-to-Brønsted sites in the case of the sample prepared by the microreactor route (P-TiO₂-mr). Additionally, the latter also exhibited stronger acid centres as the amount of pyridine adsorbed upon temperature increase on both types of sites was preserved to a larger extent over this sample. This is corroborated by the results from TPSR of n-propylamine (Fig. 10a) since the main peak shifts to higher temperatures for the phosphated TiO₂ sample prepared in the batch reactor in comparison to the P-TiO₂-mr catalyst. Additionally, higher concentration of Brønsted acid sites are also derived by TPSR (20 mmol_C3H6 g_cat⁻¹ and 23 mmol_C3H6 g_cat⁻¹ for P-TiO₂-b and P-TiO₂-mr, respectively) in line with the infrared analysis. Furthermore, the shift of the band gap in the UV spectra (Fig. 7) and the different shapes of propene evolution upon TPSR (Fig. 10a) as well as of NH₃-TPD curves (Fig. S14†) point to distinct microstructural features in both microreactor and batch reactor prepared materials. The ³¹P NMR spectra of the phosphated samples are given in Fig. 13. The spectra showed a broad signal between ca. 5 ppm and ca. −25 ppm that can be ascribed to the presence of a number of species with different protonation degree.⁷³ The major signal appeared at ca. −4 ppm and corresponds to orthophosphate species in which the degree of P oxidation is +5, followed by contributions from titanium hydrogen phosphate phases, i.e., HPO₄²⁻ (ca. −10.5 ppm) and H₂PO₄⁻ (ca. −18 ppm), formed during the synthesis. In the case of the P-TiO₂-b sample, the appearance of an additional peak at ca. −9 ppm was observed. Even though the origin of this peak is unclear, the lower acidity of this sample in comparison to that of the P-TiO₂-mr catalyst (Fig. 9) made the assignment of this peak to the presence of the Ti(HPO₄)₂ phase unfeasible but rather due to the occurrence of both titanium phosphate and condensed phosphate species or to the titanium pyrophosphate phase formed by dehydration of adjacent P–OH groups during calcination.⁷⁴ Thus, catalyst synthesis in the microreactor only appears to favour the formation of phosphorus species providing the necessary amount and ratio of Lewis and Brønsted sites to efficiently catalyse the glucose-to-5-HMF reaction. In addition, TEM (Fig. S9†) and STEM-EDXS (Fig. S19†) revealed a uniform distribution of Ti and P in both samples and they confirm the formation of smaller nanoparticles in the microreactor prepared material. Hence, it appears evident that the well-controlled environment in the channels of the microreactor results in an optimal catalyst which was ca. six times more efficient in catalysing the 5-HMF reaction than the batch catalyst.

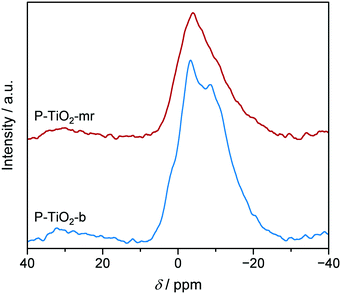Fig. 13 ³¹P MAS NMR spectra of P-TiO₂ catalysts prepared in the batch (blue) or in the microreactor (red), respectively.

Reusability of the optimal P-TiO₂-mr catalyst was demonstrated by repeating the 5-HMF reaction ten times with the same sample. A filtration–washing–calcination procedure was applied after each run to regenerate the catalytic material. After ten runs both glucose conversion and 5-HMF selectivity were preserved (X_glucose = 92.1 vs. 95.6% and S_5-HMF = 53.2 vs. 55.5%, vide Fig. S20†).

Conclusions

In this study, we established a novel one-step sol–gel method for the preparation of a highly active phosphated TiO₂ catalyst in a microreactor. Precise control of catalyst synthesis parameters in conjunction with DoE enabled us to identify key parameters that impact catalyst preparation, its properties and performance. The catalyst yield was mainly affected by thermodynamics (i.e., supersaturation) and the hydrolysis ratio. We unravelled that the hydrolysis step was crucial for incorporating the phosphorus into the TiO₂ crystals. Furthermore, it influenced the way in which the crystal aggregates were formed, impacting the resulting surface area. The size of the TiO₂ crystallites was mainly adjusted by the amount of H₃PO₄ added: molar flow ratios of ṅ_H3PO4/ṅ_TB ≤ 0.2 impeded crystal growth while at ratios above 0.2 a pronounced increase in crystal size was observed, explained by a catalytic effect due to the excessive amounts of acid present. Testing the obtained materials for their catalytic performance upon 5-HMF synthesis in a microwave reactor revealed that selectivity was mainly influenced by reaction conditions rather than by catalyst properties. The interplay of small TiO₂ crystallites and low mole bulk fractions of phosphorus (x_P,bulk ∼ 0.05) were key to achieve a high activity. Through global optimisation the final catalyst synthesis in the microreactor approached a yield of 98.9% and a space–time yield of 26.8 g_cat h⁻¹ cm_reactor⁻³ compared to 89.6% and 0.07 g_cat h⁻¹ cm_reactor⁻³ in the batch reactor. The optimal microreactor catalyst featured a significantly higher glucose conversion of 95.6%, a slightly improved selectivity towards 5-HMF of 55.5% and a substantially increased catalytic efficiency of 0.047 g_5-HMF h⁻¹ m⁻² compared to a batch material (78.7%, 50.0%, 0.008 g_5-HMF h⁻¹ m⁻²) which was attributed to the well-controlled size distribution of the TiO₂ crystallites, the larger acid site density, and the enhanced molar Lewis-to-Brønsted centre ratio in the first. This approach is likely applicable to other functionalised solid materials, enabling reproducible and quickly adaptable synthesis, fast optimisation of the targeted product, and providing useful hints in terms of correlations between synthesis and performance parameters.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors thank Dr. R. Hauert (EMPA) for conducting XPS analysis, C. Simon (FHS St. Gallen) for his valuable input on DoE evaluation, Dr. A. Armutlulu (ETH Zurich) for TEM/STEM-EDXS microscopy as well as our collaborators from ZHAW Dr. T. Franken for NH₃ TPD measurements, Dr. N. Zucchetto for N₂ physisorption characterization, Dr. R. Kontic for XRPD analysis, S. Ammann and S. Mühlemann for XRF investigations, and Dr. M. Rothensteiner for experimental support and discussions.

Notes and references

1. V. Hessel, S. Hardt and H. Löwe, Chemical Micro Process Engineering, Wiley-VCH, Weinheim, 2004, p. 674.
2. D. M. Roberge, M. Gottsponer, M. Eyholzer and N. Kockmann, Chim. Oggi, 2009, 27, 8–11.
3. N. Kockmann, M. Gottsponer, B. Zimmermann and D. M. Roberge, Chem. – Eur. J., 2008, 14, 7470–7477.
4. W. Ehrfeld, Chimia, 2002, 56, 598–604.
5. R. Wohlgemuth, I. Plazl, P. Žnidaršič-Plazl, K. V. Gernaey and J. M. Woodley, Trends Biotechnol., 2015, 33, 1–13.
6. V. Kumar and K. D. P. Nigam, Green Process. Synth., 2012, 1, 79–107.
7. R. Porta, M. Benaglia and A. Puglisi, Org. Process Res. Dev., 2016, 20, 2–25.
8. N. Kockmann, M. Gottsponer and D. Roberge, Chem. Eng. J., 2011, 167, 718–726.
9. P. Anastas and J. Warner, Green Chemistry: Theory and Practice, Oxford University Press, New York, 2000, p. 30.
10. J. Bolivar, J. Wiesbauer and B. Nidetzky, Trends Biotechnol., 2011, 29, 333–342.
11. P. Riedlberger and D. Weuster-Botz, Bioresour. Technol., 2012, 106, 138–146.
12. J. M. Köhler and B. P. Cahill, Micro-Segmented Flow Applications in Chemistry and Biology, Springer, Heidelberg, 2014.
13. H. P. L. Gemoets, Y. Su, M. Shang, V. Hessel, R. Luque and T. Noel, Chem. Soc. Rev., 2016, 45, 83–117.
14. A. Gavriilidis, A. Constantinou, K. Hellgardt, K. Kuok Hii, G. J. Hutchings, G. L. Brett, S. Kuhn and S. P. Marsden, React. Chem. Eng., 2016, 1, 595–612.
15. D. Jussen, H. Soltner, B. Stute, W. Wiechert, E. von Lieres and M. Pohl, J. Biotechnol., 2016, 231, 174–182.
16. Y. Muranaka, H. Nakagawa, R. Masaki, T. Maki and K. Mae, Ind. Eng. Chem. Res., 2017, 56, 10998–11005.
17. K.-J. Wu, G. M. De Varine Bohan and L. Torrente-Murciano, React. Chem. Eng., 2017, 2, 116–128.
18. K.-J. Wu, Y. Gao and L. Torrente-Murciano, Faraday Discuss., 2018, 208, 427–441.
19. K.-J. Wu and L. Torrente-Murciano, React. Chem. Eng., 2018, 3, 267–276.
20. H. Jacobsen, in Handbook of Green Chemistry, ed. T. Anastas and R. H. Crabtree, Wiley-VCH, Weinheim, 2013, vol. 2, p. 93.
21. M. Schoenitz, L. Grundemann, W. Augustin and S. Scholl, Chem. Commun., 2015, 51, 8213–8228.
22. M. Mayer, J. Bucko, W. Benzinger, R. Dittmeyer, W. Augustin and S. Scholl, Exp. Heat Transfer, 2014, 28, 222–243.
23. K. Wu and S. Kuhn, Chim. Oggi, 2014, 32, 62–66.
24. R. L. Hartman, Org. Process Res. Dev., 2012, 16, 870–887.
25. H. Wang, A. Mustaffar, A. N. Phan, V. Zivkovic, D. Reay, R. Law and K. Boodhoo, Chem. Eng. Process., 2017, 118, 78–107.
26. M. Hochstrasser, D. Jussen and P. Riedlberger, Chem. Eng. Process., 2017, 121, 15–23.
27. P. V. Kamat, J. Phys. Chem. C, 2007, 111, 2834–2860.
28. D. P. MacWan, P. N. Dave and S. Chaturvedi, J. Mater. Sci., 2011, 46, 3669–3686.
29. L. Atanda, A. Shrotri, S. Mukundan, Q. Ma, M. Konarova and J. Beltramini, ChemSusChem, 2015, 8, 2907–2916.
30. L. Atanda, S. Mukundan, A. Shrotri, Q. Ma and J. Beltramini, ChemCatChem, 2015, 7, 781–790.
31. L. Atanda, M. Konarova, Q. Ma, S. Mukundan, A. Shrotri and J. Beltramini, Catal. Sci. Technol., 2016, 6, 6257–6266.
32. P. Y. Dapsens, C. Mondelli and J. Pérez-Ramírez, ACS Catal., 2012, 2, 1487–1499.
33. T. Wang, M. W. Nolte and B. H. Shanks, Green Chem., 2014, 16, 548–572.
34. A. A. Rosatella, S. P. Simeonov, R. F. M. Frade and C. A. M. Afonso, Green Chem., 2011, 13, 754–793.
35. A. Mukherjee, M.-J. Dumont and V. Raghavan, Biomass Bioenergy, 2015, 72, 143–183.
36. B. Girisuta, L. Janssen and H. Heeres, Ind. Eng. Chem. Res., 2007, 46, 1696–1708.
37. C. Castañeda, F. Tzompantzi, R. Gómez and H. Rojas, J. Chem. Technol. Biotechnol., 2016, 91, 2170–2178.
38. S. K. Samantaray and K. Parida, Appl. Catal., A, 2001, 220, 9–20.
39. E. Ortiz-Islas, R. Gomez, T. López, J. Navarrete, D. H. Aguilar and P. Quintana, Appl. Surf. Sci., 2005, 252, 807–812.
40. L. Kőrösi and I. Dékány, Colloids Surf., A, 2006, 280, 146–154.
41. E. Ortiz-Islas, T. López, R. Gomez and J. Navarrete, J. Sol-Gel Sci. Technol., 2006, 37, 165–168.
42. L. Kőrösi, S. Papp, I. Bertóti and I. Dékány, Chem. Mater., 2007, 19, 4811–4819.
43. N. Wetchakun, B. Incessungvorn, K. Wetchakun and S. Phanichphant, Mater. Lett., 2012, 82, 195–198.
44. C. Y. Fan, H. Y. Guan, H. Zhang, J. H. Wang, S. T. Wang and X. H. Wang, Biomass Bioenergy, 2011, 35, 2659–2665.
45. E. Nikolla, Y. Román-Leshkov, M. Moliner and M. E. Davis, ACS Catal., 2011, 1, 408–410.
46. G.-S. Shao, F.-Y. Wang, T.-Z. Ren, Y. Liu and Z.-Y. Yuan, Appl. Catal., B, 2009, 92, 61–67.
47. T.-Y. Ma, X.-Z. Lin and Z.-Y. Yuan, Stud. Surf. Sci. Catal., ed. E. M. Gaigneaux, M. Devillers, S. Hermans, P. Jacobs, J. Martens and P. Ruiz, Elsevier, Burlington, 2010, vol. 175, pp. 571–574.
48. P. Goswami and J. N. Ganguli, Bull. Mater. Sci., 2012, 35, 889–896.
49. E. Iravani, S. A. Allahyari and M. Torab-Mostaedi, J. Braz. Chem. Soc., 2016, 27, 1766–1773.
50. S. M. Gupta and M. Tripathi, Cent. Eur. J. Chem., 2012, 10, 279–294.
51. S. Dervin and S. C. Pillai, Sol-Gel Materials for Energy, Environment and Electronic Applications, ed. S. C. Pillai and S. Hehir, Springer, Cham, 2017, pp. 1–22.
52. S. Kaluza, M. K. Schröter, R. Naumann d'Alnoncourt, T. Reinecke and M. Muhler, Adv. Funct. Mater., 2008, 18, 3670–3677.
53. S. Kaluza, M. Behrens, N. Schiefenhövel, B. Kniep, R. Fischer, R. Schlögl and M. Muhler, ChemCatChem, 2011, 3, 189–199.
54. C. A. Emeis, J. Catal., 1993, 141, 347–354.
55. K. J. A. Raj, R. Shanmugam, R. Mahalakshmi and B. Viswanathan, Indian J. Chem., Sect. A: Inorg., Bio-inorg., Phys., Theor. Anal. Chem., 2010, 49, 9–17.
56. K. M. Parida, M. Acharya, S. K. Samantaray and T. Mishra, J. Colloid Interface Sci., 1999, 217, 388–394.
57. Y. Román-Leshkov, J. N. Chheda and J. A. Dumesic, Science, 2006, 312, 1933–1937.
58. R. J. Gorte, Catal. Lett., 1999, 62, 1–13.
59. G. Caeiro, P. Magnoux, J. M. Lopes, F. Ramôa Ribeiro, S. M. C. Menezes, A. F. Costa and H. S. Cerqueira, Appl. Catal., A, 2006, 314, 160–171.
60. V. Kanazirev, K. M. Dooley and G. L. Price, J. Catal., 1994, 146, 228–236.
61. L. M. Parker, D. M. Bibby and R. H. Meinhold, Zeolites, 1985, 5, 384–388.
62. M. J. Antal, W. S. L. Mok and G. N. Richards, Carbohydr. Res., 1990, 199, 91–109.
63. J. Lewkowski, ARKIVOC, 2001, 2, 17–54.
64. J. Horvat, B. Klaić, B. Metelko and V. Šunjić, Tetrahedron Lett., 1985, 26, 2111–2114.
65. B. F. M. Kuster, Starch/Staerke, 1990, 42, 314–321.
66. C. V. McNeff, D. T. Nowlan, L. C. McNeff, B. Yan and R. L. Fedie, Appl. Catal., A, 2010, 384, 65–69.
67. S. De, S. Dutta and B. Saha, Green Chem., 2011, 13, 2859–2868.
68. S. J. Dee and A. T. Bell, ChemSusChem, 2011, 4, 1166–1173.
69. J. Wang, J. Ren, X. Liu, J. Xi, Q. Xia, Y. Zu, G. Lu and Y. Wang, Green Chem., 2012, 14, 2506–2512.
70. V. V. Ordomsky, J. van der Schaaf, J. C. Schouten and T. A. Nijhuis, J. Catal., 2012, 287, 68–75.
71. J. S. Kruger, V. Choudhary, V. Nikolakis and D. G. Vlachos, ACS Catal., 2013, 3, 1279–1291.
72. Y.-K. Peng, Y. Hu, H.-L. Chou, Y. Fu, I. F. Teixeira, L. Zhang, H. He and S. C. E. Tsang, Nat. Commun., 2017, 8, 675–687.
73. L. Djafera, A. Ayral, B. Boury and R. M. Laine, J. Colloid Interface Sci., 2013, 393, 335–339.
74. Y. Bereznitski, M. Jaroniec, A. I. Bortun, D. M. Poojary and A. Clearfield, J. Colloid Interface Sci., 1997, 191, 442–448.

---

Footnote

† Electronic supplementary information (ESI) available: Details of catalyst preparation; equations used herein; details of DoE parameters and results; catalyst synthesis–properties–performance correlation plots; XPS graphs; XRPD patterns; TEM images; FT-IR spectra; NH₃-TPD graphs; STEM-EDXS images. See DOI: 10.1039/c8cy02574f

---