A dimer path for CO dissociation on PtSn

Abstract

Density functional theory calculations are used to investigate CO adsorption, dissociation and SnO_X formation on Pt₃Sn. We find that direct CO dissociation is prevented by high activation energies. An energetically feasible path is instead CO dimer formation followed by C–O bond cleavage. Dimers are formed in the presence of Sn adatoms which effectively stabilize anionic OCCO⁻ species. The presence of Sn adatoms is crucial as dimers are unstable on Pt-only systems. The proposed mechanism may explain recent experimental observations of SnO_X and C–C formation as Pt_xSn is exposed to CO.

---

Introduction

Nanoalloys represent an important materials class, with a wide range of applications as catalysts, electrodes and sensors.^1–3 Amongst them, PtSn nanoalloys have been applied as CO oxidation catalysts^4–7 and anodes in hydrogen and direct alcohol fuels cells.^8–13 The mixing pattern of bimetallic alloy particles differs typically from the corresponding bulk and is generally complex depending both on the constituent metals and the synthesis method.^14–16 Exposure of reactants to alloy nanoparticles adds complexity. For example, PtSn nanoalloys are prone to segregation, forming SnO_X, under typical CO oxidation conditions. In fact, the formation of SnO_X/Pt interfaces explains the low temperature CO oxidation behavior of Pt₃Sn,^17,18 which in contrast to regular Pt, remains active at low temperatures.

The degree of segregation is determined by the reaction conditions and can experimentally be monitored by, for example, following the Sn 3d core level binding energies with XPS^6,19,20 or the CO stretch vibration with IR spectroscopy.^{4–7,20–22} Recently, these methods were used to monitor SnO_X formation upon exposure of CO to PtSn nanoparticles.¹⁹ The conclusion was based on the comparison of Sn 3d and C 1s XPS peaks after reduction in H₂ at 723 K and after 90 min CO exposure (2% CO/He) at 498 K. In addition to the formation of SnO_X, the formation of C–C bonds was detected.¹⁹

The observation in ref. 19 is interesting as it implies that CO dissociates on PtSn nanoparticles. CO dissociation is usually highly activated on Pt(111), and does not occur below 673 K even at high CO pressures.²³ However, CO dissociation is structure sensitive, and the required temperature for the reaction is lowered on Pt(557) and Pt(100) surfaces, where CO dissociation starts at 548 K and 500 K respectively.^23–27 The temperature for CO dissociation was in these studies determined by absence of the C–O stretch vibration (sum frequency generation) and presence of elemental carbon on the surface (Auger electron spectroscopy). The mechanism of CO dissociation was in ref. 23 suggested to proceed via the Boudouard reaction, in which CO dissociates with the formation of CO₂ and elemental carbon. CO dissociation is unlikely to happen via the Boudouard reaction on PtSn nanoparticles because SnO_X is formed instead of CO₂.

Herein, CO dissociation is investigated on Pt₃Sn using density functional theory (DFT) calculations. We find that direct CO dissociation is prevented by high activation energies and that C–O bond cleavage can appear after CO dimer formation. The dimers may form in the presence of Sn adatoms which effectively stabilize anionic OCCO⁻ species.

Computational methods

DFT calculations are performed using the Vienna ab initio Simulation Package (VASP 5.4.1)^28–31 within the generalized gradient approximation (GGA), employing the PBE exchange-correlation functional.^32,33 The projector augmented wave approximation (PAW)³⁴ is used to describe the interaction between the valence electrons and the atom cores. The surfaces are constructed with the Atomistic Simulation Environment (ASE)³⁵ from optimized bulk lattices using (12 × 12 × 12) k-point grids for Pt₃Sn and Pt.§ Structures are optimized using a plane wave kinetic energy cut-off of 450 eV. The convergence criterion for the electronic self-consistent field (SCF) loop is set to 10⁻⁵ eV and structures are relaxed until all forces are below 0.05 eV Å⁻¹. Calculations of the reaction barriers are obtained initially with the climbing image nudged elastic band^36–38 and further refined with the dimer method.³⁹ A partial hessian vibrational analysis of the CO dissociation transition states including the top layer of Pt-atoms was used to confirm that they are saddle points and local minima.

CO dissociation is studied on (111), (100) and (211) surfaces for Pt and Pt₃Sn, assuming bulk composition and ordering. In this way, dissociation on terrace as well as step sites is explored. The (111) surface is considered using (4 × 2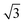)_rect and p(4 × 4) surface cells for Pt and Pt₃Sn, respectively. The (100) surfaces are treated with a 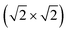R45° surface cell. The (111) surfaces are modelled with 5 layers, whereas 6 layers are used for the (100) systems. For the (211) system, a 6-layered non-orthorhombic periodic slab is used with 24 surface atoms. The Pt₃Sn(100) and Pt₃Sn(211) can be constructed with different amounts of Sn in the top-most layer. To study the effect of Sn, we consider the surface terminations that have the highest concentration of Sn. The periodic surface cells are shown in the ESI.† The effect of Sn adatoms is investigated in a (4 × 2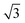)_rect surface cell for the (111) surface. The surface slabs are separated by a vacuum of, at least, 16 Å. In all calculations, the bottom two surface layers are fixed to the corresponding bulk positions. Integration over the Brillouin zone is approximated by finite sampling using the Monkhorst-Pack scheme⁴⁰ with k-point grids of 3 × 3 × 1 for (111) and (100) and 3 × 5 × 1 for (211). Methfessel Paxton smearing of the Fermi discontinuity is applied with a smearing width of 0.05 eV.⁴¹ In terms of number of metal layers and vacuum thickness and cut-off, the systems are sufficiently converged.^42,43

Results and discussion

Direct CO dissociation routes are investigated on different surfaces and at different coverages in section A. The possibility of Sn ad atoms is discussed in section B. The effect of ad atoms on CO dissociation is explored in sections C and D. Finally, alternative CO dissociation routes, such as the Boudouard reaction on pure Pt-systems are discussed in section E.

A. Direct CO dissociation on Pt and Pt₃Sn surfaces

Direct CO dissociation is studied on the (111), (100) and (211) surfaces of Pt and Pt₃Sn. The reaction is initially investigated in the low CO coverage limit of 1/16 ML (111), 1/8 ML (100) and 1/24 ML (211). Dissociation is considered from CO adsorbed in the stable position which is hollow hcp for (111) and bridge for (100) and (211). For Pt(111), it is well known that this adsorption site does not correspond to the experimentally observed low coverage position which is atop.⁴³ Nevertheless, the applied methodology is still able to predict adsorption energies and reaction barriers with reasonable accuracy to obtain qualitative trends.⁴⁴

The results for the direct dissociation are shown in Fig. 1 and Table 1. The reported product state is close the transition state and would be stabilized by subsequent separation of O and C. On Pt(111), the dissociation proceeds from CO on the hcp hollow site, followed by a CO bond elongation over a bridge site, to yield C and O in hcp and fcc sites, respectively. On Pt(100), the CO molecule is initially in a bridge position, it dissociates over the hollow position and the product state include C in hollow and O in bridge positions. On Pt(211), CO is adsorbed in a bridge position and dissociates over the four-fold hollow position at the step. The product state is in this case O in a hollow position above the step and C in a bridge position at the step. The barriers for dissociation are in all cases high. From the initial state they are 3.52 eV [Pt(111)], 3.14 eV [Pt(100)], and 3.36 eV [Pt(211)]. To compare the CO dissociation barriers independently from the adsorbed state, the barriers can be expressed with respect to a gas phase CO molecule. With this reference, the barriers amount to 1.64 eV [Pt(111)], 0.99 eV [Pt(100)], and 1.64 eV [Pt(211)]. The value for dissociation on Pt(111) reported here is lower than the value obtained by Liu et al.⁴⁵ (2.21 eV) with a p(2 × 2) surface cell. The difference can in part be attributed to the possibility of more extensive relaxations in the larger surface cell.

Fig. 1 Potential energy diagram for CO dissociation on the considered surfaces, Pt (black) and Pt₃Sn (red). Zero energy corresponds to a bare metal surface with CO in the gas-phase. The atomic models show the transition states. Atomic colour codes: O (red), C (gray), Sn (yellow) and Pt (blue).

Table 1 Calculated CO adsorption energy (ΔE_ads,CO), reaction barrier from gas phase CO (ΔE^{‡,gas phase CO}), reaction barrier from adsorbed state (ΔE^‡), and reaction energy (ΔE_r) for the direct CO dissociation. d(C–O)_TS is the calculated C–O bond distance in the transition state. Differential adsorption energies are reported for CO at coverages (θ) higher than the lowest for each facet. Energies and distances are reported in eV and Å, respectively

Surface	θ (ML)	ΔEads,CO	ΔE^‡,gas phase CO	ΔE^‡	ΔEr	d(C–O)TS
ΔEads,CO = (ER − ECO,gas − EBare surface).ΔE^‡,gas phase CO = (ETS − ECO,gas − EBare surface).ΔE^‡ = (ETS − ER).ΔEr = (EP − ER).ER, ETS, EP: energies of reactant state, transition state and product state.ECO,gas: energy of gas phase CO.EBare surface: energy of surface slab.
Pt(111)	1/16	−1.88	1.64	3.52	2.42	1.65
Pt(111)	1/4	−1.73	2.29	4.02	2.64	1.64
Pt(111)	1/2	−1.52	2.55	4.07	3.36	2.18
Pt(100)	1/8	−2.15	0.99	3.14	1.69	2.00
Pt(211)	1/24	−1.73	1.64	3.36	3.34	2.06
Pt3Sn(111)	1/16	−1.87	1.86	3.72	2.93	2.04
Pt3Sn(111)	1/4	−1.80	1.94	3.74	2.32	1.95
Pt3Sn(111)	1/2	−1.59	2.19	3.78	2.81	1.81
Pt3Sn(100)	1/8	−0.54 (bridge)	2.05	2.60 (bridge)	1.98	2.13
		−1.79 (top)		3.85 (top)
Pt3Sn(211)	1/24	−0.37	2.07	2.44	2.11	2.19
Sn–Pt(100)	1/8	−2.13	1.21	3.34	2.17	2.02
2Sn–Pt(100)	1/8	−3.19	0.28	3.46	2.63	2.04

---

Pt(100) is the only surface for which the CO dissociation is exothermic (−0.47 eV) with respect to a CO molecule in gas phase. This, together with the 0.99 eV barrier for dissociation from the gas-phase is consistent with the experimental results by Somorjai and co-workers showing CO dissociation on Pt(100) at 500 K.^23,24 Considering entropy, it is, however, clear that the product state needs to be further stabilized by, for example, C–C bond formation.

On Pt₃Sn(111), CO adsorbs in an hcp hollow position with a Sn atom directly below the adsorption site. Dissociation proceeds with a barrier of 3.72 eV over a bridge site and the product state has O and C in hollow positions. The adsorption energy is low on Pt₃Sn(100) for the local minimum closest to the transition state, where CO occupies a long-bridge site between two Pt atoms. The low adsorption energy is a consequence of Sn in the top most layer. Dissociation proceeds over this position with a barrier of 2.60 eV. The on top site, which is further from the transition state, has a stronger adsorption energy (−1.79 eV) owing to charge transfer effects from Sn. From the on top adsorption site, the dissociation barrier becomes 3.85 eV.

The adsorption energy is low also on Pt₃Sn(211) and the molecule occupies a bridge position. The dissociation occurs in this case over a hollow position with a barrier of 2.44 eV. The barriers with respect to gas-phase CO are on the alloy surfaces 1.87 eV [Pt₃Sn(111)], 2.05 eV [Pt₃Sn(100)], and 2.07 eV [Pt₃Sn(211)].

We find that the barriers for direct CO dissociation at low coverage are high on Pt as well as on Pt₃Sn surfaces. The low stability of adsorbed CO on Pt₃Sn(100) and Pt₃Sn(211) renders the barrier with respect to this state lower than on the Pt-only surfaces. The barriers from CO in the gas-phase are, however, in all cases higher for the alloy surfaces.

It is possible that CO coverage affects the CO dissociation barrier. In fact, on Pt(111), a coverage between 0.30 ML and 0.60 ML is reasonable at the experimental conditions where CO dissociation has been observed, i.e. CO pressures (20 mbar) and temperatures (498–548 K).^19,46 To investigate this, we studied dissociation at Pt₃Sn(111) and Pt(111) with CO coverages of 1/16 ML and 4/16 ML and 8/16 ML (Table 1). It is found that the barriers in this regime are nearly independent of the coverage. This is consistent with previous results for NO dissociation on Pt(111).⁴⁷ The high barriers, independent of coverage, suggest that the observed CO dissociation on PtSn nanoparticles¹⁹ does not proceed along this type of reaction path.

B. Alternative surfaces – the possibility of Sn adatoms

Given the high barriers for direct CO dissociation, we considered alternative structural models for the alloy. The mixing in alloy nanoparticles (NP) is often complex, and it has been shown that Pt₃Sn NP have a partial segregation with an enrichment of Sn in the surface region.⁴⁸ This is expected as the Pt–Pt bonds are stronger than are the Pt–Sn bonds.⁴⁹ The segregation could, furthermore, be enhanced by the presence of adsorbates such as CO.⁵ For Pt₃Sn NP, this is likely given the preferential adsorption of CO on Pt-sites. This is exemplified in Fig. 1 where the adsorption energy is reduced by more than 1 eV if CO occupies a site close to Sn. To maximize the CO–Pt interaction, it is possible that Sn in the surface layer is replaced by Pt, forming instead Sn adatoms. In the following we have considered CO dissociation on such systems modeled as Sn adatoms on a Pt-skin. Model systems with different Sn adatom concentration are investigated on Pt(100) and Pt(111)/Pt₃Sn to study how they affect the CO dissociation barriers.

C. CO dissociation in the presence of Sn adatoms

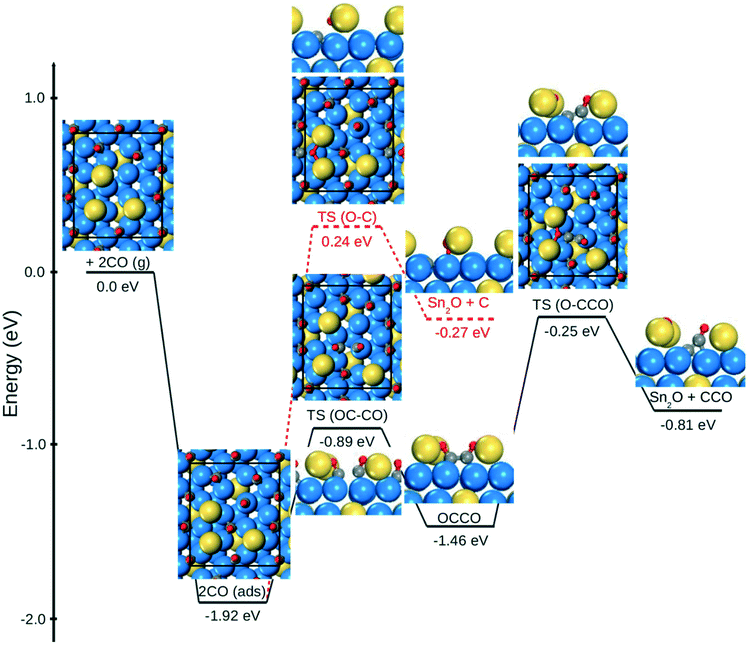
On regular Pt(100), the adsorption energy of CO is −2.15 eV, with a CO dissociation barrier of 3.14 eV. If one Sn ad-atom is added onto Pt(100), the calculated adsorption energy remains approximately the same −2.13 eV (Table 1), while the reaction barrier increases to 3.34 eV. Moreover, with two Sn adatoms the adsorption energy increases in magnitude to −3.19 eV and the barrier increases to 3.46 eV. However, the barrier, with respect to CO in gas phase is lowered to 0.28 eV. Sn adatoms onto Pt(100) do not lead to decreased intrinsic CO dissociation barriers, rendering direct CO dissociation unlikely onto Pt(100) even when assisted by Sn. On a model of Pt(111)/Pt₃Sn, the effect of up to three Sn adatoms is investigated at a CO coverage of 0.50 ML. From the adsorbed state, the direct CO dissociation barrier from the adsorbed state decreases from 3.78 eV (0 Sn adatoms), 2.93 eV (1 Sn ad-atom), 2.35 eV (2 Sn adatoms) to 2.16 eV in the presence of 3 Sn adatoms (see Table S1 and Fig. S1, ESI†).

For the systems with two and three Sn adatoms respectively, Sn₂O is formed upon direct CO dissociation.

D. Dimer route for CO dissociation with Sn adatoms

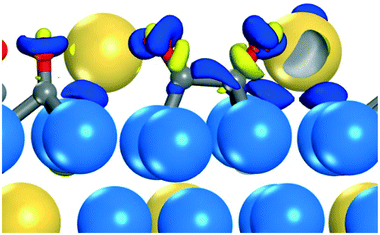
Although presence of Sn adatoms lowers the barrier for direct CO dissociation, the reaction is still highly activated and alternative pathways could be in operation. A possible alternative path would be the formation of CO dimers, which has been discussed within the field of electrocatalysis.^50–54 In ref. 51 it was suggested that a CO dimer can be stabilized via a positively charged environment. We consider the scenario of dimer formation on Sn₃/Pt(111)/Pt₃Sn with a coverage of ½ ML in CO. The activation barrier to form (CO)₂ over an fcc site is 1.03 eV, and the formation is endothermic by 0.45 eV (Fig. 2). This could be compared with the similar process on Pt(111) where the reaction is endotherm by 1.42 eV with an activation barrier of 1.44 eV, see Fig. S7 in ESI.† Thus, the presence of Sn adatoms stabilizes CO dimer formation. The stabilization of the (CO)₂ originates form electrostatic stabilization via the 3 Sn adatoms. The Bader charge analysis of the dimer, reveals a total charge of −0.91e on (CO)₂, corresponding to an anionic OCCO⁻ species. As adsorbed CO on regular Pt(111) has a charge of −0.13e it is clear that additional charge is provided by Sn. Such a process is not possible on Pt(111), where the charge on the dimer is only −0.10e. The charge accumulation on the dimer is shown by a charge density difference analysis in Fig. 3. The analysis reveals charge accumulation in a π-type orbital with bonding character between the two CO molecules. Additional stabilization is provided by charge accumulation on the oxygen atoms which are coordinate to the positively charge Sn-atoms. The average Bader charges on the three Sn adatoms is +1.07e. The stabilization of an anionic CO dimer is similar in character to the well-known formation of neutral NO dimers.⁵⁵ The subsequent C–O bond cleavage from the dimer state has a barrier of 1.22 eV forming SnOSn. The overall barrier for dissociation via dimer formation is 1.67 eV which is clearly lower than the global barrier for direct CO dissociation (2.16 eV). The stabilization of the dimer can be further enhanced by considering Sn atoms in the topmost metal layer (Fig. S4†). The barrier for dimer formation is for this case decreased to 0.85 eV and the dimer state is endothermic by only 0.15 eV. In this way, the overall CO dissociation barrier is lowered to 1.08 eV.

Fig. 2 CO dissociation on Pt(111)/Pt₃Sn with 3 Sn adatoms. Zero energy corresponds to a bare metal surface with CO in the gas-phase. The C–C distance of the CO dimerization transition state is 1.95 Å, and the O–C distance in the subsequent C–O bond cleavage is 2.11 Å. The C–O distance during direct CO dissociation is 1.98 Å. Atomic colour codes: C (gray), O (red), Sn (yellow) and Pt (blue).

Fig. 3 Analysis of the bonding in the CO dimer via a charge density difference map. The charge density difference is calculated as Δρ = ρ_full − ρ_Sn3 − ρ_{full without Sn3} and the iso-surfaces are visualized at ±0.04 e Å⁻³. Dark blue (yellow) iso-surface represent accumulation (depletion) of charge with respect to the system without Sn adatoms. Atomic color codes: O (red), C (gray), Sn (yellow) and Pt (blue).

The experimentally determined apparent activation barrier for CO dissociation of PtSn NP was in ref. 19 estimated to be −0.39 eV. Comparison with this value would require the construction of a micro-kinetic model. At this point we do not know the degrees of rate control for the different steps which make a simple estimate of the apparent barrier difficult.⁵⁶ However, our calculations show that direct CO dissociation is highly unlikely.

The stabilization of the dimer requires electropositive adatoms such as Sn. Using Pt adatoms, the barrier for dimer formation is 2.21 eV and the process is endothermic by 2.07 eV, rendering this path highly unlikely on Pt-only systems.

E. Other reaction routes for CO on pure Pt-systems

We note that CO dissociation has been observed experimentally over Pt-only systems.^23–25 It was suggested to occur according to the Boudouard reaction (CO + CO → CO₂ + C). Therefore, we have, in addition to direct CO dissociation, explored different possibilities including the Boudouard reaction. For this route we find that the barriers at 0.5 ML are 3.05 eV and 3.15 eV on Pt(111) and Pt(100), respectively. Thus, the barrier for the Boudouard reaction is lower than the direct CO dissociation path on Pt(111) and similar for Pt(100). A variant of the Boudouard reaction with the dimer is calculated to have global barrier of 3.63 eV. We refer to the ESI† and Fig. S5–S7 for a full description of the investigated CO dissociation routes on Pt-only systems. As the investigated routes are highly activated. We speculate that the experimental observations^23–25 could be caused by other mechanistic features such as impurities.

Conclusions

We have used density functional theory calculations to investigate different routes for CO dissociation on Pt₃Sn. Direct dissociation is found to be prevented by high activation energies. An energetically feasible path is instead C–O bond cleavage from a CO dimer. We find that dimers can be formed in the presence of Sn adatoms which effectively supply charge for the formation of anionic OCCO⁻ species. The positively charged Sn adatoms provide an additional electrostatic stabilization. Our results provide an explanation for the experimentally observed SnO_X and C–C bond formation as PtSn nanoparticles are exposed to CO. The presented mechanism for CO dimer formation is expected to be active for other Pt-alloys where Pt is mixed with metals having a low electronegativity.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

M. V. acknowledges funding from the Scientific Research-Foundation Flanders (FWO) for a postdoctoral fellowship and a travel grant to visit Chalmers (02/2016-09/2016). Initial computational resources and services used for this work were provided by VSC (Flemish Supercomputer Center), funded by the Hercules foundation and the Flemish Government – department EWI. The calculations were finalized at C3SE (Göteborg) and Uppmax (Uppsala) via a SNIC grant. We acknowledge financial support from the Swedish Research Council (2016-05234) and Chalmers Area of Advance Materials. The Competence Centre for Catalysis is hosted by Chalmers University of Technology and financially supported by the Swedish Energy Agency and the member companies AB Volvo, ECAPS AB, Johnson Matthey AB, Preem AB, Scania CV AB, Umicore Denmark ApS and Volvo Car Corporation AB.

Notes and references

1. L. M. Liz-Marzan, C. J. Murphy and J. Wang, Chem. Soc. Rev., 2014, 43, 3820–3822.
2. A. K. Singh and Q. Xu, ChemCatChem, 2013, 5, 652–676.
3. M. B. Cortie and A. M. McDonagh, Chem. Rev., 2011, 111, 3713–3735.
4. A. Moscu, L. Veyre, C. Thieuleux, F. Meunier and Y. Schuurman, Catal. Today, 2015, 258, 241–246.
5. A. Moscu, Y. Schuurman, L. Veyre, C. Thieuleux and F. Meunier, Chem. Commun., 2014, 50, 8590–8592.
6. W. D. Michalak, J. M. Krier, S. Alayoglu, J. Y. Shin, K. An, K. Komvopoulos, Z. Liu and G. A. Somorjai, J. Catal., 2014, 312, 17–25.
7. M. M. Schubert, M. J. Kahlich, G. Feldmeyer, M. Huttner, S. Hackenberg, H. A. Gasteiger and R. J. Behm, Phys. Chem. Chem. Phys., 2001, 3, 1123–1131.
8. Y.-J. Leng, X. Wang and I. M. Hsing, J. Electroanal. Chem., 2002, 528, 145–152.
9. V. K. Puthiyapura, D. J. L. Brett, A. E. Russell, W.-F. Lin and C. Hardacre, ACS Appl. Mater. Interfaces, 2016, 8, 12859–12870.
10. Y. J. Wang, N. N. Zhao, B. Z. Fang, H. Li, X. T. T. Bi and H. J. Wang, Chem. Rev., 2015, 115, 3433–3467.
11. E. Antolini and E. R. Gonzalez, Catal. Today, 2011, 160, 28–38.
12. S. García-Rodríguez, F. Somodi, I. Borbáth, J. L. Margitfalvi, M. A. Peña, J. L. G. Fierro and S. Rojas, Appl. Catal., A, 2009, 91, 83–91.
13. X. Lu, Z. Deng, C. Guo, W. Wang, S. Wei, S.-P. Ng, X. Chen, N. Ding, W. Guo and C.-M. L. Wu, ACS Appl. Mater. Interfaces, 2016, 8, 12194–12204.
14. R. Ferrando, J. Jellinek and R. L. Johnston, Chem. Rev., 2008, 108, 845–910.
15. K. D. Gilroy, A. Ruditskiy, H. C. Peng, D. Qin and Y. N. Xia, Chem. Rev., 2016, 116, 10414–10472.
16. B. Roldan Cuenya and F. Behafarid, Surf. Sci. Rep., 2015, 70, 135–187.
17. M. Vandichel, A. Moscu and H. Gronbeck, ACS Catal., 2017, 7, 7431–7441.
18. M. Vandichel and H. Grönbeck, Top. Catal., 2018, 61, 1458–1464.
19. A. Moscu, C. Theodoridi, L. Cardenas, C. Thieuleux, D. Motta-Meira, G. Agostini, Y. Schuurman and F. Meunier, J. Catal., 2018, 359, 76–81.
20. Y. Jugnet, D. Loffreda, C. Dupont, F. Delbecq, E. Ehret, F. Aires, B. S. Mun, F. A. Akgul and Z. Liu, J. Phys. Chem. Lett., 2012, 3, 3707–3714.
21. C. Dupont, Y. Jugnet, F. Delbecq and D. Loffreda, J. Catal., 2010, 273, 211–220.
22. C. Dupont, D. Loffreda, F. Delbecq and Y. Jugnet, J. Phys. Chem. C, 2007, 111, 8524–8531.
23. K. McCrea, J. Parker and G. Somorjai, in Surface Chemistry and Catalysis, ed. A. F. Carley, P. R. Davies, G. J. Hutchings and M. S. Spencer, Springer US, Boston, MA, 2002,  DOI:10.1007/978-1-4757-6637-0_4, pp. 55–78.
24. K. R. McCrea, J. S. Parker and G. A. Somorjai, J. Phys. Chem. B, 2002, 106, 10854–10863.
25. Y. Iwasawa, R. Mason, M. Textor and G. A. Somorjai, Chem. Phys. Lett., 1976, 44, 468–470.
26. Y. O. Park, R. I. Masel and K. Stolt, Surf. Sci., 1983, 131, L385–L389.
27. X. Q. D. Li, T. Radojicic and R. Vanselow, Surf. Sci., 1990, 225, L29–L32.
28. G. Kresse and J. Furthmuller, Phys. Rev. B: Condens. Matter Mater., 1996, 54, 11169–11186.
29. G. Kresse and J. Furthmuller, Comput. Mater. Sci., 1996, 6, 15–50.
30. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558.
31. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251.
32. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
33. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396.
34. P. E. Blochl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
35. S. R. Bahn and K. W. Jacobsen, Comput. Sci. Eng., 2002, 4, 56–66.
36. G. Mills, H. Jonsson and G. K. Schenter, Surf. Sci., 1995, 324, 305–337.
37. G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901–9904.
38. G. Henkelman and H. Jónsson, J. Chem. Phys., 2000, 113, 9978–9985.
39. G. Henkelman and H. Jónsson, J. Chem. Phys., 1999, 111, 7010–7022.
40. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192.
41. M. Methfessel and A. T. Paxton, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 40, 3616–3621.
42. V. Nilsson, M. Van den Bossche, A. Hellman and H. Gronbeck, Surf. Sci., 2015, 640, 59–64.
43. P. J. Feibelman, B. Hammer, J. K. Nørskov, F. Wagner, M. Scheffler, R. Stumpf, R. Watwe and J. Dumesic, J. Phys. Chem. B, 2001, 105, 4018–4025.
44. J. K. Nørskov, F. Abild-Pedersen, F. Studt and T. Bligaard, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 937.
45. Z.-P. Liu and P. Hu, J. Chem. Phys., 2001, 114, 8244–8247.
46. M. Jørgensen and H. Grönbeck, ACS Catal., 2017, 7, 5054–5061.
47. E. C. Adams, L. R. Merte, A. Hellman, M. Skoglundh, J. Gustafson, E. C. Bendixen, P. Gabrielsson, F. Bertram, J. Evertsson, C. Zhang, S. Carlson and P.-A. Carlsson, Phys. Chem. Chem. Phys., 2016, 18, 10850–10855.
48. A. Neitzel, G. Kovács, Y. Lykhach, S. M. Kozlov, N. Tsud, T. Skála, M. Vorokhta, V. Matolín, K. M. Neyman and J. Libuda, Top. Catal., 2016, 60, 522–532.
49. The cohesion energy of fcc Pt₄ is calculated to be 0.70 eV higher than that of fcc Pt₃Sn .
50. H. Xiao, W. A. Goddard, T. Cheng and Y. Liu, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 6685–6688.
51. J. H. Montoya, C. Shi, K. Chan and J. K. Nørskov, J. Phys. Chem. Lett., 2015, 6, 2032–2037.
52. Y. Yang, P. Cheng, S. Zhang and S. Huang, RSC Adv., 2016, 6, 4354–4364.
53. E. Pérez-Gallent, M. C. Figueiredo, F. Calle-Vallejo and M. T. M. Koper, Angew. Chem., Int. Ed., 2017, 56, 3621–3624.
54. S. Hedstrom, E. C. dos Santos, C. Liu, K. Chan, F. Abild-Pedersen and L. G. M. Pettersson, J. Phys. Chem. C, 2018, 122, 12251–12258.
55. A. Hellman, I. Panas and H. Grönbeck, J. Chem. Phys., 2008, 128, 104704.
56. M. Jorgensen and H. Gronbeck, Catal. Sci. Technol., 2017, 7, 4034–4040.

---

Footnotes

† Electronic supplementary information (ESI) available: The ESI contains atomic structure files and detailed description of alternative C–O dissociation routes. See DOI: 10.1039/c8cy01989d

‡ Present address: Department of chemistry and material science (School of Chemical Engineering) and Department of Applied Physics, Aalto University, 02150 Espoo, Finland.

§ Only orthorhombic structures are considered (α = β = γ = 90.0). The optimized cell parameters (a = b = c) for the metal(alloy)s Pt, and Pt₃Sn are 3.97 Å and 4.06 respectively.

---