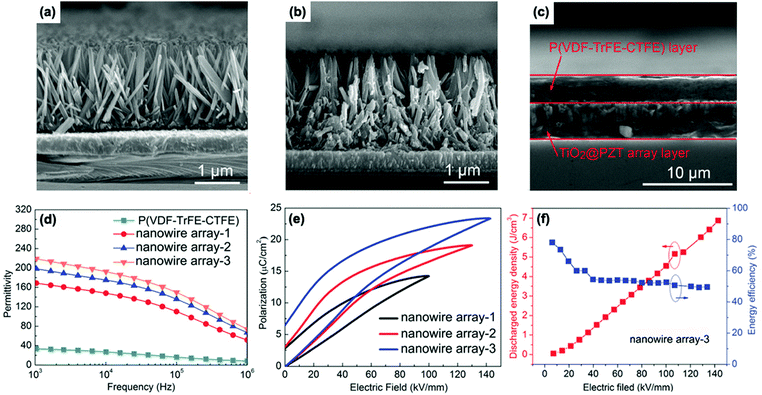
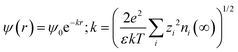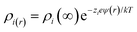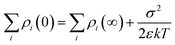Open Access Article
Open Access ArticleInterface design for high energy density polymer nanocomposites
Hang
Luo†
a,
Xuefan
Zhou†
a,
Christopher
Ellingford
 b,
Yan
Zhang
b,
Yan
Zhang
 ac,
Sheng
Chen
d,
Kechao
Zhou
a,
Dou
Zhang
ac,
Sheng
Chen
d,
Kechao
Zhou
a,
Dou
Zhang
 *a,
Chris R.
Bowen
*a,
Chris R.
Bowen
 *c and
Chaoying
Wan
*c and
Chaoying
Wan
 *b
*b
aState Key Laboratory of Powder Metallurgy, Central South University, Changsha, Hunan 410083, China. E-mail: dzhang@csu.edu.cn
bInternational Institute for Nanocomposites Manufacturing (IINM), WMG, University of Warwick, CV4 7AL, UK. E-mail: chaoying.wan@warwick.ac.uk
cDepartment of Mechanical Engineering, University of Bath, Bath, BA2 2ET, UK. E-mail: c.r.bowen@bath.ac.uk
dKey Laboratory of Polymeric Materials and Application Technology of Hunan Province, College of Chemistry, Xiangtan University, Xiangtan 411105, Hunan Province, China
First published on 4th July 2019
Abstract
This review provides a detailed overview on the latest developments in the design and control of the interface in polymer based composite dielectrics for energy storage applications. The methods employed for interface design in composite systems are described for a variety of filler types and morphologies, along with novel approaches employed to build hierarchical interfaces for multi-scale control of properties. Efforts to achieve a close control of interfacial properties and geometry are then described, which includes the creation of either flexible or rigid polymer interfaces, the use of liquid crystals and developing ceramic and carbon-based interfaces with tailored electrical properties. The impact of the variety of interface structures on composite polarization and energy storage capability are described, along with an overview of existing models to understand the polarization mechanisms and quantitatively assess the potential benefits of different structures for energy storage. The applications and properties of such interface-controlled materials are then explored, along with an overview of existing challenges and practical limitations. Finally, a summary and future perspectives are provided to highlight future directions of research in this growing and important area.
1. Introduction
Polymers are a key element in energy harvesting and storage devices due to their unique properties in comparison with traditional ceramic and metallic materials, such as high breakdown strength, mechanical flexibility, low density, ease of processing and low cost.1–6 Today, functional polymer composites are attracting interest in an increasing number of applications, including polymer based dielectric capacitors which are widely employed in the areas of power transmission, hybrid electric vehicles, high power weapons, radar, wind power generation, and microelectronic systems; these sectors are summarized in Fig. 1. As an example, a converter valve is used for the conversion of an alternating current (AC) into a direct current (DC) in high voltage direct current (HVDC) transmission engineering, and in such a system the dielectric capacitors occupy over 50% of the volume. Polymers are preferred due to their advantages in terms of excellent electrical properties and ease of forming in continuous and large area dielectric films with a tailored thickness in the micrometer range. Table 1 provides a summary for a variety of current dielectrics in polymeric and ceramic form.3,7–14 The dielectric material often employed in commercially available capacitors is biaxially oriented polypropylenes (BOPP). However, the mismatch between ambient temperature (∼140 °C) and the maximum operating temperature (∼105 °C) of BOPP can become a limitation to its application.15 In this case, high-temperature dielectric materials, such as polyethylene naphthalate (PEN), polyphenylene sulfide (PPS), poly(ethylene terephthalate) (PET) and polyimide (PI) have been developed.7 Another important commercially available capacitor system is the multi-layer ceramic capacitor (MLCC), where the mainstream dielectric is the BaTiO3 or doped-BaTiO3 ceramics.16 Compared with the capacitors formed from bulk ceramics, MLCC possesses high capacitance (e.g. 1–100 μF), small volume (e.g. 0.6 by 0.3 mm2), high reliability, and excellent high-frequency characteristics.17 In addition, MLCCs can endure a relatively high electric field due to the small thickness of the individual layers, of the order of several microns, compared with bulk ceramic capacitors whose dimensions are several hundred microns.18 Recently, electroactive polymers with high relative permittivity, such as ferroelectric poly(vinylidenefluoride) (PVDF) and its co/ter-polymers, and ceramic/polymer composites have been intensively studied due to their high permittivity and high breakdown strength. A comparison to show the ranges for different energy storage devices are summarized in Table 2, where the advantages of polymer based dielectric capacitors include high power density, high efficiency, stability and low cost compared with other energy storage devices such as lithium ion batteries and supercapacitors.7,19–27| Dielectrics for capacitors | Relatively permittivity (1 kHz) | Dielectric loss (1 kHz) | Breakdown strength (kV mm−1) | Max. operating temperature (°C) | Thermal conductivity (W (m K)−1) | Energy density (J cm−3) |
|---|---|---|---|---|---|---|
| BOPP | 2.2 | ∼0.0002 | ∼640 | 105 | 2.1–2.35 | 1–1.2 |
| PEN | 3.2 | ∼0.0015 | ∼550 | 125 | ∼0.26 | 1–1.5 |
| PPS | 3.0 | ∼0.0003 | ∼550 | 200 | ∼0.3 | 1–1.5 |
| PET | 3.6 | ∼0.005 | ∼570 | 125 | 0.29 | 1–1.5 |
| PI | 3.5 | 0.04 | ∼238 | ∼200 | 6.58–11.7 | 1.4 |
| PVDF and its co/ter-polymer | ∼>10 | ∼0.02–0.2 | ∼200–600 | 125 | ∼0.24 | ∼>4 |
| Ceramics/polymer composites | ∼50 | ∼0.02–0.08 | ∼300–500 | ∼150 | — | ∼10–30 |
| MLCC | ∼100–3000 | — | — | ∼125 | — | ∼10 |
| Bulk ceramics | ∼102–4 × 103 | — | ∼10–50 | ∼200 | — | ∼1–7 |
| Energy storage devices | Power density (W kg−1) | Energy density (W h kg−1) | Efficiency | Stability | Cost |
|---|---|---|---|---|---|
| Dielectric capacitor | ∼104–107 | ∼10−2–10−1 | High | Good | Low |
| Supercapacitor | ∼>104 | ∼<10 | Low | Good | High |
| Lithium-ion batteries | ∼<1000 | ∼150–250 | High | Low | Low |
In order to enhance polymer properties for applications, such as those in Fig. 1, a wide variety of polymer based composite systems are being explored. These are based on a polymer matrix that contains organic, ceramic, and carbon-based fillers that can be either randomly dispersed, aligned or ordered in a multi-layer form.28–32 The properties of polymer composites do not solely rely on the structure and properties of the individual components, since we will see in this review that interfacial interactions between the matrix and filler has an important role in determining the overall performance.33–35 In such composite systems, an additional third phase, namely the interfacial region is introduced and due to the high specific surface area of nanoscale fillers, the volume ratio of the interfacial phase can be as high as 50–70 vol%. As a consequence, the interfacial properties can have a significant impact on the overall performance of nanocomposites and their devices.
For a linear dielectric capacitor, the energy stored is related to the working voltage (V) and the capacitance (C): ½CV2, the “energy density” is therefore given by eqn (1):
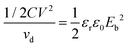 | (1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ = ε′′/ε′. The dielectric displacement as a function of applied electric field should also be considered in order to account for material non-linearities, which are often observed at high electric field, and avoid the above simplification of assuming a linear dielectric response.16,37–39
δ = ε′′/ε′. The dielectric displacement as a function of applied electric field should also be considered in order to account for material non-linearities, which are often observed at high electric field, and avoid the above simplification of assuming a linear dielectric response.16,37–39
For polymer based nanocomposite systems, the surface modification of inorganic fillers using organic modifiers is often employed to enhance the interfacial interaction, material compatibility, and dispersion of the filler in a polymer matrix. However, the mismatch of relative permittivity or electrical conductivity between the inorganic fillers and polymer matrix often leads to the development of an inhomogeneous electric field distribution throughout the composite, and generally leads to a significant reduction of the breakdown strength of dielectric composites. We will see later in this review that this is due to the electric field being concentrated in the low permittivity phase as a consequence of Gauss’ law.40,41 This field concentration can be overcome to some extent by constructing an inorganic shell layer, grafting multifunctional organic shell layers, using multiple hierarchical shells on the surface of the fillers and building topological structures, including sandwiched or multi-layered structures.
The aim of this review is to overview the important role of the interface and interphase to allow tailoring of the properties of nanocomposite dielectrics. Polymer nanocomposites for energy storage applications continues to be a growing area that has attracted increasing discussion via a variety of existing reviews. These include a wide variety of key topics, which include an examination of PVDF and its copolymers, and their nanocomposites for high energy density capacitor applications;7,8,11,22,42–45 high-temperature dielectric nanocomposites;10,15 high-κ dielectrics;18,46,47 recent achievements on BaTiO3 nanomaterials and their synthesis, dielectric and ferroelectric properties;48 dielectric and energy storage properties of polymers and multilayered dielectrics films;3,49,50 ceramic films and bulk ceramics for energy storage capacitors;12,16,25,32,51 the effects of fillers on the dielectric and energy storage properties of polymer composites;2,52 carbon based polymer composites for energy storage;9,53,54 polymer based nanodielectric design for advanced capacitors;45,55,56 interface engineering in polymer nanocomposites to improve energy storage;36,57 and the strategies for engineering the surfaces of fillers.58
This review will cover methods of interface design by introducing the range of interface layers and structures. Examples include the creation of core–shell structures that use organic, insulating ceramic (dielectric) and electrically conductive outer-layers on nano-fillers; including sandwich and multi-layer architectures (Section 2). The efforts to create multiple shells with hierarchical and controlled graded structures to further improve nanocomposite performance are discussed (Section 3). The effect of the interface on polarization mechanisms, breakdown strength and growth of defects is then discussed. There is an in-depth examination of the influence of filler morphology, such as filler dimensionality, aspect ratio and volume fraction, along with an overview of the variety of models being developed for prediction of properties and understand effective properties (Section 4). Specific examples of interfacial design strategies and its impact for high performance energy storage capacitors are discussed (Section 5). Finally, an outlook and future perspectives of high-performance polymer composite capacitors are proposed.
2. Architectures for interface design
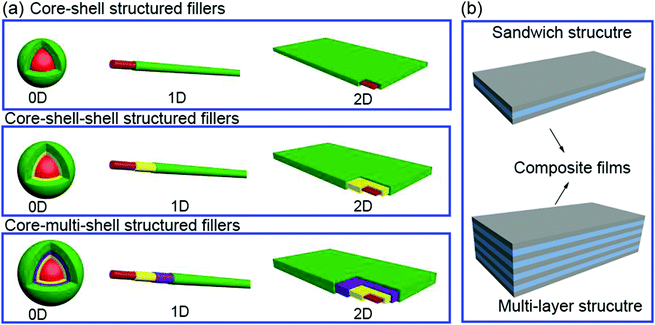
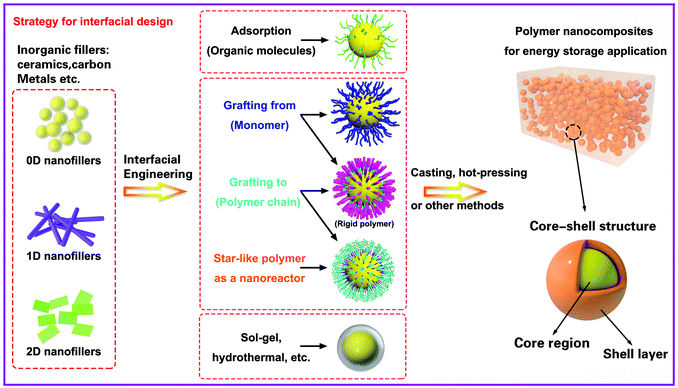
In this section we will provide an overview of the interface types observed in dielectric nanocomposites, as shown in Fig. 2. The fillers can be considered at a range of dimensions,59–61 namely zero dimensional (0D) nanofillers which include spherical nanoparticles, nanocubes and nanoparticles with irregular morphologies, one dimensional (1D) nanofillers which include nanowires, nanofibers, nanotubes and nanoribbons, and two dimensional (2D) nanofillers which include nanosheets and nanoplatelet, as shown in the left column of Fig. 3. The outer surface of the fillers can be coated with a range of materials, as seen in the center column of Fig. 3, which can be used to tune the interface between filler and matrix; see right column of Fig. 3.The strategies of core shell synthesis including adsorption, grafting from, grafting to, star-like nanoreactors and sol–gel/hydrothermal approaches will now be described based on organic or inorganic shells, hierarchical outer layers (Fig. 2a), and multi-layer structures (Fig. 2b). As a representative structure, 0D nanofillers will be firstly covered used to describe the processes of interfacial engineering and nanocomposite preparation.
2.1 Theory of surface energies
Ceramic fillers such as Pb1−xZrxTiO3 (PZT), BaTiO3, TiO2, Ba1−xSrxTiO3 (BST), and carbonaceous particles such as graphene and carbon nanotubes (CNT) are often incompatible with the polymer matrix due to the significant difference in surface energy compared to the matrix and poor polymer–particle interfacial interactions.62 Inorganic fillers therefore tend to form agglomerates within polymer matrices which results in phase separation and poor properties.Nano-scale fillers can readily agglomerate easily due to their high surface energy, high van der Waals forces or high electrostatic forces, resulting in the poor dispersity in the polymer matrix. The surface energy of a material is defined as the excess energy per unit area due to the existence of a free surface; it can also be the thermodynamic work done per unit area of surface extension. When the filler material possess a high surface energy, they tend to agglomerate in order to form a more stable lower energy state. Generally, high-surface energy materials include metals, metal oxides, and inorganic compounds (such as sapphire, nitrides, oxides, silica, and diamond), which exhibit dense, refractory, and hard properties, where the surface energy values of such materials is approximately 200–5000 dyn cm−1. Organic polymers, which act as the composite matrix, are typically low surface energy materials, where the surface energy is approximately 10 and 50 dyn cm−1. The reader is referred to the work of the Menachem Lewin group for a summary of surface tensions and surface energy values of these materials,63 where the values of a range of polymers, minerals, oxides and clays based on theoretical calculations or empirical equations were also presented. In order to account for the difference of surface energy between the polymer-based matrix and inorganic fillers, the high-energy surfaces of inorganic fillers are often coated with low-energy surface materials, such as siloxane coupling reagents or polymers, whereby a thin layer can reduce the surface energy of inorganic fillers. Therefore, the design and construction of an interfacial layer using modifiers with different function properties is an attractive approach to enhance the dispersion properties of inorganic nano-scale fillers. Additional approaches to increase the compatibility between the filler and polymer matrix can be to exploit electrostatic interactions, hydrogen bonding or dipole–dipole interactions, which is summarized in Fig. 4.
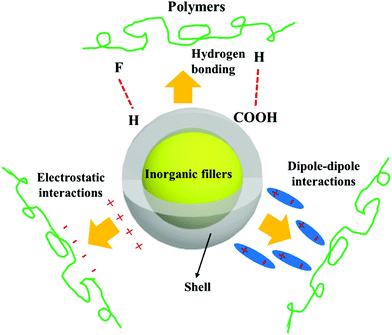 | ||
| Fig. 4 Schematic of the range of interactions between the core–shell structured filler and polymers matrix. | ||
2.2 Core–shell structure
To date, core–shell structured nanoparticles have been explored in depth for surface modification and multi-functional applications.64–67 In polymer based nanocomposites, the ability to enhance dispersion of nanofillers and tailor the interfacial properties remain important technical challenges to be addressed68–70 and the surface modification of fillers with a variety of organic modifiers is an effective approach to overcome these issues.71,72 Organic modifiers can be physically adsorbed onto the filler surface through electrostatic interactions or by hydrogen bonding. A variety of modifiers have been used, as shown in Fig. 5, which include dopamine,73,74 silanes,75 phosphonic acid,76 ethylene diamine,77 polyvinyl alcohol,78 and paraffin.79 These organics have been utilized to modify the surfaces of inorganic fillers and are of interest due to their simple treatment process, for example by solution mixing. Alternatively, the organic shell can be chemically grafted onto the filler surfaces via “grafting to” or “grafting from” approaches through living/controlled free radical polymerization or click-chemistry reactions. The “grafting from” approach relies on the formation of a core–shell structure by the in situ polymerization of monomers on initiator-functionalized nanoparticle surfaces. In contrast, the “grafting to” approach leads to the formation of a core–shell structure by grafting the pre-prepared polymer chains onto the nanoparticle surface via a reaction between the polymer end-groups and the functional groups on the nanoparticle surface. Moreover, an additional strategy for the creation of a well-defined nanoparticle/polymer core–shell structure was developed using star-like polymers as nanoreactors; see central column of Fig. 3. These three methods will be examined in more detail in Section 3.1.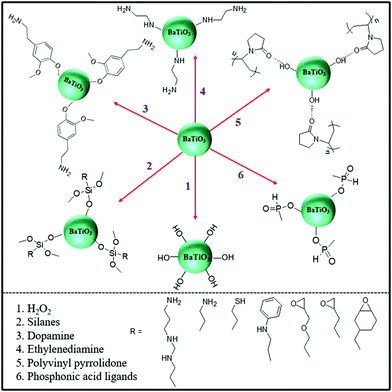 | ||
| Fig. 5 Examples of organic modifiers for surface engineering of a ceramic filler particle, in this case BaTiO3.73–79 | ||
Table 3 summarizes the range of organic modifiers that have been employed to date for improving filler dispersion and compatibility in dielectric nanocomposites. The development of an organic shell not only improves interface compatibility between the polymer matrix and inorganic fillers, it can also prevent the inner core from agglomerating and thus improve filler dispersion. As an example, dopamine has been used for surface modification of a variety of filler particles80 due to its versatile “adhesive” properties and its ability to readily form a polydopamine layer via self-polymerization at ambient conditions. Dopamine modified BaTiO3 nanofibers have an amorphous layer with a thickness of ∼5 nm, which have resulted in an improvement of relative permittivity by ∼20% and breakdown strength by ∼100% compared to epoxy composites with BaTiO3 nanofibers.73 The use of physically adsorbed organic modifiers leads to the presence of free residual species in the composite, which can lead to increased leakage currents and increased dielectric loss.75,81 In contrast, chemically grafted polymer layers may overcome this problem due to its covalently bonded nature.82,83
| Filler | Morphology of the fillers | Polymer matrix | Modifier | Method | Ref. |
|---|---|---|---|---|---|
| BaTiO3 | 0D | P(VDF–HFP) | Phosphonic acid | Surface absorption | 76 |
| BaTiO3 | 0D | PVDF | Carboxylic acids | Surface absorption | 96 |
| BaTiO3 | 0D | Poly(vinyl alcohol) (PVA) | Gallic acid (GA) | Surface absorption | 97 |
| BaTiO3 | 0D | PVDF | Polyvinylprrolidone (PVP) | Surface absorption | 98 |
| BaTiO3 | 0D | PVDF | Titanate coupling agent | Surface absorption | 99 |
| BaTiO3 | 0D | PVDF | PVP | Surface absorption | 100 |
| Ba(Fe0.5Ta0.5)O3 | 0D | PVDF | Dopamine | Polycondensation | 101 |
| BaTiO3 | 0D | Poly(vinylidene fluoride-co-chlorotrifluoroethylene) (P(VDF–CTFE)) | GA | Polycondensation | 102 |
| BaTiO3 | 0D | PVDF | Polydopamine | Polycondensation | 73 |
| SiO2 | 0D | P(VDF–HFP) | Fluoride 1H,1H,2H,2H-perfluorooctyltriethoxy-silane | Grafting to | 103 |
| BaTiO3 | 0D | P(VDF–HFP) | Hydantoin epoxy | Grafting to | 104 |
| BaTiO3 | 0D | Glycidyl methacrylate functionalized P(VDF–HFP) | Amino-terminated silane molecules | Grafting to | 105 |
| Al2O3 | 0D | Polypropylene | Phosphonic acid-terminated poly(ethylene-co-1-butene) | Grafting to | 106 |
| BaTiO3 | 0D | Poly(vinylidene fluoride-trifluoroethylene-chlorotrifluoroethylene (P(VDF–TrFE–CTFE)) | Poly(2,5-bis[(4-trifluoromethoxyphenyl) oxycarbonyl]styrene) (PTFMPCS) | Grafting from | 107 |
| BaTiO3 | 0D | Poly(methyl methacrylate) (PMMA) | PMMA | Grafting from | 108 |
| BaTiO3 | 0D | Poly(2-hydroxylethyle methacrylate) (PHEMA)@PMMA | PHEMA@PMMA or poly(acrylate)sodium@PHEMA | Grafting from | 109 |
| BaTiO3 | 0D | PMMA | PMMA | Grafting from | 110 |
| BaTiO3 | 0D | Poly(vinylidene fluoride-trifluoroethylene-chlorofluoroethylene) (P(VDF–TrFE–CFE)) | Hyperbranched aromatic polyamide (HBP) | Grafting from | 111 |
| BaTiO3 | 0D | HBP@PMMA | HBP@PMMA | Grafting from | 83 |
| BaTiO3 | 0D | P(VDF–HFP) | Poly(trifluoroethyl acrylate) (PTFEA) | Grafting from | 86 |
| BaTiO3 | 0D | Polystyrene | Polystyrene | Grafting from | 112 |
| SrTiO3 | 1D | PVDF | PVP | Surface absorption | 113 |
| BaTiO3 | 1D | P(VDF–HFP) | Fluoro-polydopamine | Surface absorption | 114 |
| Ba0.8Sr0.2TiO3 | 1D | PVDF | Ethylenediamine | Surface absorption | 115 |
| BaTiO3 | 1D | P(VDF–TrFE–CFE) | Ethylenediamine | Surface absorption | 116 |
| SrTiO3 | 1D | PVDF | Dopamine | Polycondensation | 117 |
| 0.5Ba(Zr0.2Ti0.8)O3–0.5(Ba0.7Ca0.3)TiO3 | 1D | PVDF | Polydopamine | Polycondensation | 118 |
| Ba0.6Sr0.4TiO3 | 1D | PVDF | H2O2 | Oxidation | 119,120 |
| MWCNT | 1D | Polypropylene | Poly(ethylene-co-butylene)–OH | Grafting to | 121 |
| MWCNT | 1D | P(VDF–HFP) | Methoxypolyethylene glycol (mPEG) | Grafting to | 122 |
| NaNbO3 | 1D | PVDF | Polydopamine | Polycondensation | 123 |
| BaTiO3 | 1D | P(VDF–HFP) | PMPCS | Grafting from | 124 |
| Na2Ti3O7 | 1D | P(VDF–HFP) | PMPCS | Grafting from | 125 |
| Reduced graphene oxide (RGO) | 2D | PVDF | PVA | Surface absorption | 126 |
| BaTiO3/graphene | 2D | P(VDF–HFP) | Polydopamine | Polycondensation | 127 |
| Graphene oxide | 2D | Nitrile butadiene rubber | γ-Aminopropyl triethoxysilane | Condensation reaction | 128 |
| Boron nitride | 2D | PVDF | Hydroxyl groups | Oxidation | 71 |
| Graphene-oxide | 2D | PI | p-Phenylenediamine | Grafting to | 129 |
| Graphene | 2D | Poly(p-phenylene benzobisoxazole) | Hyperbranched aromatic polyamide | Grafting from | 130 |
Fluoro-polymers, such as PVDF and its copolymers, are generally immiscible with a number of inorganic fillers due to their low surface energy. Although a number of strategies have been used to modify nanofillers using a hydrocarbon modifier, this continues to result in filler agglomeration and the creation of voids and defects in the nanocomposite films which can initiate dielectric breakdown.84 To overcome this challenge, a fluoro-phosphonic acid has been used to engineer the surface of BaTiO3 nanoparticles, and effectively reduce its surface energy. This resulted in a good dispersion of the nanoparticles in poly(vinylidene fluoride-co-hexafluoro propylene) (P(VDF–HFP)) based composites.85 In addition, a series of core–shell structured BaTiO3@fluoro-polymer hybrid nanoparticles with a variety of shell structures and thicknesses were prepared via a surface-initiated Reversible Addition–Fragmentation Chain Transfer Polymerization (RAFT) polymerization, which led to uniformly dispersed BaTiO3 nanoparticles in the polymer matrix and thereby improved the electrical properties of the nanocomposites.86 These reports demonstrate that the use of a fluoro-polymer is a promising route to modify and engineer the surface of ceramic fillers. The fluorine atoms from the modifier and matrix can reduce the mismatch of interfacial properties, and since fluorine atoms possess a high electronegativity they can easily form hydrogen bonds with hydrogen atoms from the modifiers and polymer matrix.
The organic modifiers described above with long hydrocarbon chains generally possess a lower relative permittivity compared to ceramic fillers and the PVDF homopolymer or copolymer matrix. It has been shown that a large difference in relative permittivity between an inorganic ceramic filler and the polymer matrix leads to an inhomogeneous electric field distribution, since electric fields tends to concentrate in phases of low permittivity.40,41 Therefore, the introduction of a high-permittivity inorganic filler will lead to a decrease in the composite breakdown strength as a result of an electric field concentration formed in the interfacial region. Therefore, the ability to decrease the permittivity contrast between the filler and polymer matrix of a nanocomposite is potentially an effective route to enhance the breakdown strength and energy storage density; see eqn (1). This can be achieved by introducing a low-permittivity ceramic shell layer on the surface of the high-permittivity nanofiller to mitigate the permittivity mismatch between the filler particle and polymer matrix. A number of examples are shown in Table 4, which demonstrate that TiO2,87 Al2O3,88,89 and SiO2,90–93 have been often chosen as the buffer layer due to their intermediate relative permittivity which is of a magnitude between that of the high-permittivity filler and low-permittivity polymer matrix. Fig. 6 shows the microstructure of 2D Bi2Te3@Al2O3 nanoplates, where a uniform Al2O3 shell has been successfully formed on the surface.89 The materials selected also exhibit a low dielectric loss; for example Al2O3, εr ∼ 10,94 SiO2, tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ ∼ 0.0002.95
δ ∼ 0.0002.95
| Core | Morphology of the filler | Shell | Matrix | Method | Ref. |
|---|---|---|---|---|---|
| BaTiO3 | 0D | TiO2 | P(VDF–HFP) | Hydrothermal | 131 |
| Ag | 0D | TiO2 | Polytetrafluoroethylene | Sol–gel | 133 |
| BaTiO3 | 0D | Al2O3 | PVDF | Heterogeneous nucleation | 88 |
| Ceramic | 0D | Al2O3 | Polyolefin | Metallocene polymerization | 134 |
| BaTiO3 | 0D | Fe3O4 | PVDF | Chemical precipitation | 135 |
| BaTiO3 | 0D | Fe3O4 | PVDF | Chemical precipitation | 136 |
| CCTO | 0D | Fe3O4 | PI | Hydrothermal | 137 |
| BaTiO3 | 0D | SiO2 | PVDF | Hydrolysis reaction | 91 |
| BaTiO3 | 0D | SiO2 | PVDF | Stöber method | 95 |
| Zn | 0D | ZnO | PVDF | Calcination | 138 |
| BaTiO3 | 1D | TiO2 | PVDF | Hydrothermal | 139 |
| BaTiO3 | 1D | TiO2 | PVDF | Electrospinning | 140 |
| BaTiO3 | 1D | TiO2 | PVDF/P(VDF–HFP) | Electrospinning | 141 |
| BaTiO3 | 1D | TiO2 | P(VDF–HFP) | Kinetics-controlled coating | 142 |
| BaTiO3 | 1D | Al2O3 | PVDF | Electrospinning | 143 |
| BaTiO3 | 1D | Al2O3 | PVDF | Electrospinning | 94 |
| SiC | 1D | SiO2 | PVDF | Sol–gel | 144 |
| Bi2S3 | 1D | SiO2 | PVDF | Sol–gel | 145 |
| BZT–BCT | 1D | CoFe2O4 | PVDF | Sol–gel and electrospinning | 146 |
| BaTiO3 | 1D | SiO2 | PI | Electrospinning | 147 |
| BaTiO3 | 1D | SiO2 | PVDF | Hydrolysis reaction | 92 |
| Bi2Te3 | 2D | Al2O3 | PVDF | Sol–gel | 89 |
| Bi2Te3 | 2D | SiO2 | P(VDF–HFP) | Sol–gel | 90 |
| BaTiO3 | 0D | C | P(VDF–HFP) | CVD | 148 |
| SiO2 | 0D | RGO | Epoxy | Electrostatic assembly | 149 |
| BaTiO3 | 0D | Ag | PVDF | Deposition | 150 |
| Ag | 1D | C | PVDF | Hydrothermal | 151 |
| BaTiO3 | 0D | Ag@polydopamine | P(VDF–HFP) | Chemical precipitation and absorb | 152 |
| TiO2 | 1D | C@SiO2 | PVDF | CVD and sol–gel | 153 |
| BaTiO3 | 1D | TiO2@Al2O3 | PVDF | Electrospinning | 154 |
| BaTiO3 | 1D | Polydopamine–Pt | P(VDF–HFP) | Polycondensation and reduction reaction | 155 |
 | ||
| Fig. 6 (a) SEM image of 2D Bi2Te3 nanoplates; (b) TEM image, and (c) HRTEM image of 2D Bi2Te3@Al2O3 nanoplates. Reproduced from ref. 89 with permission from the Royal Society of Chemistry. | ||
Rahimabady et al.87 prepared P(VDF–HFP) based nanocomposites using TiO2 coated BaTiO3 nanoparticles (BaTiO3@TiO2). The relative permittivity, εr, of the P(VDF–HFP) nanocomposite with 50 vol% BaTiO3@TiO2 at 1 kHz was increased to εr ∼ 110, which is over three times higher than BaTiO3/P(VDF–HFP) nanocomposites due to the strong interfacial interaction and space charge accumulation at interfaces. The enhanced polarization was attributed to a highly interactive interface between the multiple dielectric materials due to the introduction of an intermediate TiO2 layer. The results showed that nanocomposites with a core–shell structured filler achieved a higher breakdown strength compared to BaTiO3/P(VDF–HFP) nanocomposites. The reasons for the improved breakdown strength include the introduction of an inorganic TiO2 shell with an intermediate relative permittivity between the BaTiO3 filler and P(VDF–HFP) matrix, which reduced the local electric field concentration. The TiO2 shell was also thought to tightly adhere to the polymer matrix and both factors can act to enhance the breakdown strength of the nanocomposites. As an alternative approach, a graded dielectric filler was proposed by Huang et al.131 to overcome the paradox of attempting to achieve an improved breakdown strength and increased relative permittivity in nanocomposite systems. This included the use of a shell layer with an intermediate relative permittivity (such as TiO2, εr ∼ 40), a high-permittivity core (BaTiO3, εr ∼ 1000) and a polymer matrix (e.g. P(VDF–HFP), εr ∼ 10). The use of a gradient of dielectric fillers resulted in not only an enhanced interfacial polarization induced by the TiO2 nanowire layer grown on the BaTiO3 nanoparticles, but also improved the breakdown strength by smoothing the inhomogeneous electric field distribution within the composite.
In addition to inorganic dielectrics at the interface, inorganic conductive materials, such as carbon, have been considered as a novel interfacial modifier to modulate the performance of dielectric nanocomposites. Yang et al. prepared a novel core–shell structure including TiO2 nanowires that acted as a core and a conductive carbon layer as the shell which was formed by a hydrothermal reaction and chemical vapor deposition (CVD) processes, as shown in Fig. 7.132 From the SEM image of the TiO2@C, it was found that the carbon layer on the surface of TiO2 nanowires was compact and smooth, and the interface thickness could be precisely modulated by controlling the duration of the CVD process. It is of interest to note that this work discovered a novel strategy to tailor the dielectric properties of PVDF based nanocomposites by tuning the carbon shell thickness. In addition, a novel percolative dielectric nanocomposites was formed with enhanced relative permittivity by introducing a small loading level of TiO2@C nanowires; for example, the highest relative permittivity achieved was to εr ∼ 2171 at 1 kHz, which was 80 times higher than the composite fillers with untreated TiO2 nanowires at the same filler loading level.
 | ||
| Fig. 7 (a) SEM image of TiO2 nanowires, (b) TEM image, (c) high-angle annular dark field (HAADF) pattern of a TiO2 nanowire coated by C layer, (d–f) Mapping images of Ti, O, and C elements. Reproduced from ref. 132 with permission from the Royal Society of Chemistry. | ||
2.3 Building hierarchical interfaces
Interfacial polarization is a dominant factor affecting the performance of polymer nanocomposites,57,156 due to the mismatch in relative permittivity and electric conductivity of the interfacial layer between the polymer matrix and filler particles.129,130 As discussed in Sections 2.2 and 2.3, simple core–shell structures formed using organic or inorganic modifiers are effective routes to improve energy storage performance. This core–shell approach can be enhanced by the use of multiple-shells to provide a hierarchical functional interface layer. Such as structure, as shown in Fig. 2, can further assist in the dispersion, polarization, buffering, or shielding. For example, the use of an outer dispersion layer can contribute to the dispersion and interfacial interaction of the ceramic fillers in the polymer nanocomposites, while an inner polarization layer can act to increase the relative permittivity of the nanocomposites. Additional buffer layers can relieve the local electric field concentrations due to a permittivity mismatch, and a shielding layer can also act to prevent the mobility of free electrons, resulting in suppression of the dielectric loss and electric conductivity in the polymer nanocomposites.157 Therefore, the design and manufacture of hierarchical interfaces can provide novel core–shell architectures with multi-functional roles in polymer nanocomposites.Recently, a core–multi-shell structure BaTiO3@TiO2@Al2O3 nanowire has been developed to improve the performance of nanocomposites, whereby the individual shells possess a different relative permittivity or electric conductivity.110 Due to the decrease in relative permittivity between the BaTiO3 (εr ∼ 1000), TiO2 (εr ∼ 110), Al2O3 (εr ∼ 10), and PVDF (εr ∼ 8), the composites incorporated with BaTiO3@TiO2@Al2O3 nanofibers exhibited a decreased dielectric loss, enhanced relative permittivity, and enhanced breakdown strength compared with composites with only BaTiO3 nanofibers or BaTiO3@TiO2 nanofibers.143,158 In addition, a novel structure with hierarchical interfaces based on NaNbO3@dopamine–Ag nanofibers were employed in PVDF based nanocomposites, as shown in Fig. 8. Compared with composite with NaNbO3 or NaNbO3@dopamine nanofibers, the composite with NaNbO3@dopamine–Ag nanofibers achieved an enhanced energy density (16.04 J cm−3 at 485 MV m−1) and suppressed energy loss.159 In addition, Gupta et al. designed polydopamine functionalized core@double-shell nanoparticles which included a TiO2 nanoparticle core and a BaTiO3–TiO2 double-shell (defined as TiO2–BaTiO3–TiO2@dopamine) as fillers to incorporate into a polymer matrix. Due to the mismatch of electrical conductivity and relative permittivity between TiO2 and BaTiO3, each TiO2–BaTiO3–TiO2@dopamine nanoparticle acted as an individual capacitor. This resulted in the core/outer TiO2 shells acting as capacitor plates because of their high electrical conductivity (∼10−4 S m−1) and the BaTiO3 layer acting as a dielectric due to its high permittivity (εr > 200). The use of a double shell configuration aided in tailoring the interface, and resulted in enhanced polarization, breakdown strength and suppressed leakage currents for the composites employing TiO2–BaTiO3–TiO2@dopamine nanoparticles.160
 | ||
| Fig. 8 TEM images of (a) NaNbO3@dopamine nanofibers, and (b) NaNbO3@dopamine–Ag nanofibers. Reproduced from ref. 160 with permission from the Royal Society of Chemistry. | ||
A novel percolative nanocomposite with high relative permittivity and low dielectric loss was formed by introducing multi-phase hierarchical fillers, including dopamine modified barium strontium titanate (BST) nano-cuboid decorated functionalized graphene sheets.161 The dopamine acted as an adhesion layer to improve the interfacial bonding between the fillers and the polymer matrix, while the BST nano-cuboid layer acted as an isolation layer to prevent the graphene from making contact with each other to minimise electrical conductivity and dielectric loss. In addition, due to increased interfacial polarization of the hierarchical interfaces between the BST, graphene, dopamine, and P(VDF–HFP), the nanocomposites achieved a high relative permittivity of εr ∼ 170.4 and low dielectric loss of 0.114 at 1 kHz.
2.4 Sandwich- and multi-layer structures
The above sections have indicated that a variety of core–shell structures that are created at a range of dimensions, see Fig. 2 and 3, can enhance the performance of dielectric nanocomposites due to an improved dispersivity and compatibility of the fillers in polymer matrix. However, the breakdown strength of the nanocomposites is often reduced with an increase of inorganic filler loading level. This is particularly true in 0–3 type nanocomposites (namely zero dimensionally connected filler particles in a three-dimensionally connected polymer matrix), where the filler loading levels can be as high as 50–60 vol%. Recently, the building of topological-structures including sandwich or multi-layer structures has been considered in the form of 2–2 type composite, where two dimensional connected fillers are dispersed in a two dimensional connected polymer matrix, by introducing an additional insulating layer into the composites; see Fig. 2. This approach provides an intriguing new strategy to enhance or maintain breakdown strength, while increasing relative permittivity.162–165Pristine polymers, such as P(VDF–HFP),166 PVDF,167–169 P(VDF–TrFE–CFE),170 and PMMA, and acrylic rubber (EDs)171 have been selected as the insulating layer, which is due to their inherent high dielectric strength and low loss. Zhang et al.166 prepared sandwich-structured composites that consisted of a pure poly(vinylidene fluoride-co-hexafluoropropylene) (P(VDF–HFP)) central layer and BaTiO3/P(VDF–HFP) upper and lower layers formed by spin-coating, and the three individual layers were stacked to form a sandwich-structure. The thickness of the central layer was modulated to investigate the effects of central layer thickness on the effective properties of the composites. However, this type of sandwich-structured composite often suffers from a low relative permittivity and polarization due to the central polymer layer being of low relative permittivity, which limits the overall energy density. To overcome this issue, a small amount of ceramic nanofiller, such as NaNbO3 platelets,172 (Na0.5Bi0.5)0.93Ba0.07TiO3 platelets,78 BaTiO3 nanoparticles,173 BaTiO3 nanofibers,162 boron nitride nanosheets (BNNs),174,175 and BaSrTO3 (BST) nanofibers,115 have been incorporated into the polymer central layer to create an insulating layer with enhanced relative permittivity. As an example, Wang et al.176 presented a trilayer-structured nanocomposite prepared by hot pressing. The three individual layers were PVDF/BNNs, PVDF/BST, and PVDF/BNNs nanocomposites, respectively. A small amount of BaSrTO3 nanofibers was introduced to the PVDF polymer matrix in the central layer and compared to a sandwich structure with a pure PVDF central layer. The BST/PVDF nanocomposite exhibited improved relative permittivity from εr ∼ 9.3 to εr ∼ 14.2. As a result, a discharge energy density of 20.5 J cm−3 was achieved due to the contributions of an enhanced breakdown strength by the BNNs/PVDF outer layer and improved relative permittivity of the BST/PVDF central layer.
Recently, a layered-structure was designed in order to achieve a large electric displacement and high breakdown strength.173 This three-tiered PVDF-based nanocomposite was prepared by gradually increasing the BaTiO3 nanoparticle loading level layer-by-layer, as shown in Fig. 9. Due to the graded BaTiO3 nanoparticle loading level, a weak electric field region was formed that acted as an efficient insulating barrier, which effectively increased the breakdown strength of the nanocomposite compared with a nanocomposite containing homogeneously dispersed BaTiO3 nanoparticles.
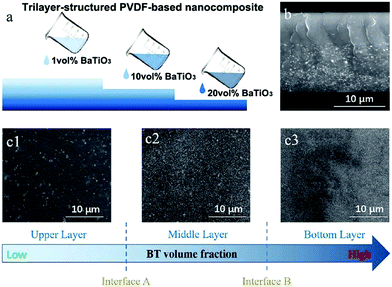 | ||
| Fig. 9 (a) Fabrication process of the trilayer-structured nanocomposite, (b) cross-sectional SEM image of the nanocomposite, (c1–c3) SEM images of the upper, middle and bottom layers with different BaTiO3 nanoparticle loading levels. Reproduced from ref. 173 with permission from the Royal Society of Chemistry. | ||
3. Methods to control the interfacial layer in nanocomposites
The previous section has described the range of architectures used to tailor the interface such as core–shells, hierarchical core–shells and sandwich or multi-layer structures. This section overviews the processing methods used to create and control such interfaces.3.1 Preparation of core–shell structures by organic flexible polymer shells
Many modifiers are coated on the surface of inorganic fillers simply via physical adsorption due to the lack of functional groups. A physical coating can be achieved by mixing the modifiers and fillers in solvents while under the action of mechanical stirring or ultrasonication.146 Deng and co-workers reported a ternary PVDF nanocomposite with dopamine modified BaTiO3 nanoparticles and γ-aminopropyl triethoxysilane (KH550) modified Bi2S3 nanorods.177 The dopamine surfactant and KH550 were diluted in deionized water and potassium hydrogen phthalate buffer solution, respectively, then mixed with the ceramic filler by simple stirring. The processed hybrid fillers were incorporated into the polymer matrix to prepare PVDF composites by a casting method, as shown in Fig. 10.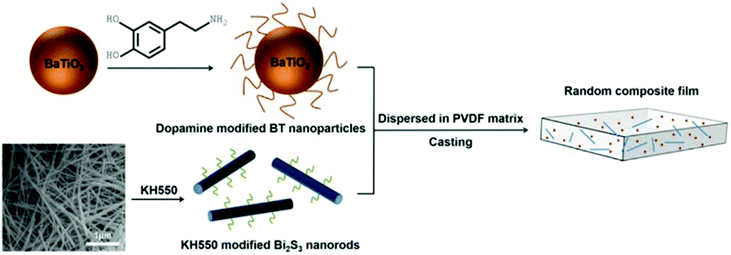 | ||
| Fig. 10 Schematic of processing procedure of PVDF nanocomposite with dopamine modified BaTiO3 nanoparticles and KH550 modified Bi2S3 nanorods. Reprinted from ref. 177, Copyright (2018), with permission from Elsevier. | ||
As discussed in Section 2.2, physically adsorbed surfactants often leave free residual species in the composites, resulting in a high leakage current and dielectric loss. To solve this problem, covalently bonding organic modifiers via “grafting to” or “grafting from” approaches have been studied.178 The “grafting to” approach is particularly suitable for preparing polymer based nanocomposites with a high loading level of ceramic fillers since the shell layer can also be utilized as the polymer matrix.105 To realise a “grafting to” strategy, active groups of the modifier and the surface of inorganic fillers are both essential elements. Huang et al. prepared PS and PMMA with active thiol-terminated end groups by a RAFT polymerization method, which was directly reacted with vinyl-functionalized BaTiO3 nanoparticles to form a core–shell structure.57 As another example, in the process of preparing a BaTiO3@hydantoin epoxy resin,104 the epoxy group from the hydantoin epoxy resin was able to react with hydroxyl ions on the surface of BaTiO3 nanoparticles through a ring-opening reaction, and was further cross-linked by a curing agent, namely dipropylenetriamine. The hydantoin epoxy resin modified BaTiO3 nanoparticles exhibited a homogeneous dispersion and strong interfacial adhesion with the P(VDF–HFP) matrix.
Recently, a number of successful processing methods were reported, such as a methoxypolyethylene glycol (mPEG) graft on the surface of carbon nanotubes (CNT) by esterification between the –OH from mPEG and –COOH from CNT. Due to the tight encapsulation of CNT by the mPEG, a high relative permittivity of εr ∼ 69.7 and a low dielectric loss of 0.042 were simultaneously achieved in a P(VDF–HFP) nanocomposite.122 Core–shell structured BaTiO3@PS and BaTiO3@PMMA nanocomposites with high relative permittivity and low dielectric loss were prepared by Jiang et al.,82 using a “grafting to” method and thiol–ene click reaction. It was shown that the organic shell layer, including grafting density and molecular weight, can be easily tailored which contributed to a detailed understanding of the structure–dielectric property relationships of the core–shell structured nanocomposites.
The main features of the “grafting from” strategy is to build a shell layer via an in situ polymerization of monomers via the initiating sites on the nanoparticle surface.109,112,179 Atom Transfer Radical Polymerization (ATRP) and reversible RAFT methods are usually employed in the “grafting from” strategy process. As shown in Fig. 11, poly(2-hydroxylethyle methacrylate) (PMMA), poly(hydroxyethyl methacrylate) (PHEMA) and sodium polyacrylate (PANa) were coated on the surfaces of BaTiO3 nanoparticles by ATRP method, respectively, and core@double-shell structured BaTiO3 nanoparticles were prepared by grafting PHEMA-block-PMMA and PANa-block-PHEMA block copolymer using ATRP method. For RAFT method, the process is outlined in Fig. 12. Firstly, the RAFT reagent e.g. 4-cyanopentanoic acid dithiobenzoate (CPDB) is introduced on the surface of any modified nanoparticles, then the monomer of the modifier polymer initiates in situ polymerization by the RAFT reagent. In this method, the thicknesses of the polymer shell can be tailored by varying the molecular weight of the grafted polymer. Core–shell structured BaTiO3 nanoparticles with either different shell thickness or different molecular structures were prepared by grafting two types of fluoroalkyl acrylate monomers via RAFT polymerization. It was shown that a high energy density and low dielectric loss could be successfully realized in the nanocomposites. Moreover, the energy storage densities of the P(VDF–HFP)-based nanocomposites could be tailored by adjusting the structure and thickness of the fluoro-polymer shell.86 As an example, nanocomposites with a thick fluoro-polymer shell were prepared using fluoroalkyl acrylate monomers with short side groups, which exhibited a high breakdown field and enhanced energy storage capability in comparison with the pure P(VDF–HFP); for example 6.23 J cm−3 for a nanocomposite with 50% BaTiO3–PTFEA2 and 4.10 J cm−3 for P(VDF–HFP).
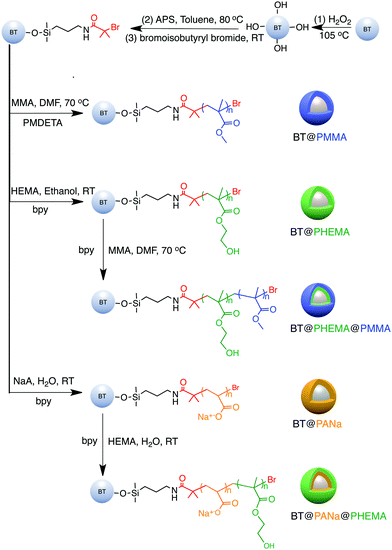 | ||
| Fig. 11 Synthesis of functionalized BaTiO3 nanoparticles using a “grafting from” strategy. Reprinted with permission from ref. 109. Copyright (2016) American Chemical Society. | ||
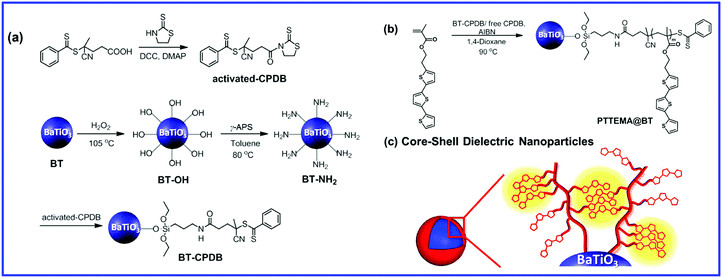 | ||
| Fig. 12 Synthesis of functionalized BaTiO3 nanoparticles using “grafting from” strategy. Reprinted figure with permission from ref. 179. Copyright (2014) American Chemical Society. | ||
Recently, the reduction of nanoparticle agglomeration and improving their dispersibility in nanocomposites via strong bonding,48,180–191 has led to the development of a viable route to prepare organic–inorganic nanocomposites composed of monodisperse ferroelectric nanoparticles, which were directly bonded with polymers utilizing rationally designed amphiphilic star-like diblock copolymer as nanoreactors. Star-like diblock copolymers, such as poly(acrylic acid)-block-poly(vinylidene fluoride) (PAA-b-PVDF), were prepared by sequential ATRP and copper-catalysed azide–alkyne cyclo additions. The precursors were selectively incorporated into the space occupied by the inner PAA blocks and converted into BaTiO3 nanoparticles directly and were stably capped with PVDF chains, as shown in Fig. 13. The PVDF-capped BaTiO3 nanoparticles were highly uniform and after hot-pressing the chemically synthesized PVDF-capped BaTiO3 nanoparticles, homogeneous PVDF/BaTiO3 nanocomposites were fabricated. It was found that the PVDF/BaTiO3 nanocomposite filled with 84.7 wt% nanoparticles (∼16 nm) possessed a high relative permittivity of εr ∼ 85 (at 2 MHz) and dielectric loss of ∼0.028. In comparison, pristine PVDF exhibits a relative permittivity of εr ∼ 10 and dielectric loss of ∼0.16. This improvement can be attributed to the large interfacial areas and strong interfacial interactions in the PVDF/BaTiO3 nanocomposite which promote interfacial exchange coupling through a dipolar interface layer, thereby leading to the enhanced polarization, improved relative permittivity and reduced dielectric loss.
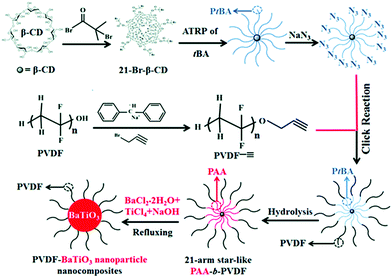 | ||
| Fig. 13 Synthetic route to amphiphilic 21-arm, star-like PAA-b-PVDF diblock copolymer and subsequent conversion into PVDF-capped BaTiO3 nanoparticles and PVDF/BaTiO3 nanocomposites. Reproduced from ref. 48 with permission from the Royal Society of Chemistry. | ||
3.2 Tailoring the interfacial thickness by organic rigid liquid crystalline polymers
The interfacial region can be considered as a shell of a certain thickness on the nanoparticle surface, as shown in Fig. 14a.36 The volume fraction of the interfacial region (finterface) of a spherical nanocomposite filler can be calculated by eqn (2): | (2) |
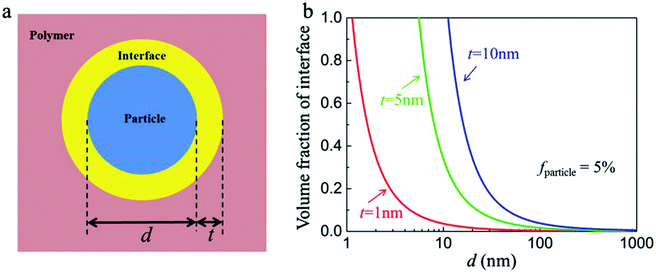 | ||
| Fig. 14 (a) Schematic of the ceramic/polymer interface structure in a nanocomposite. (b) Volume fraction of interface in the nanocomposites with the diameter of nanoparticles and interface thicknesses. Reproduced with permission from ref. 36. Copyright 2018, John Wiley and Sons. | ||
As discussed in Section 3.1, many of the polymers employed as interfacial modifiers are flexible organics, which generally have a random walk or Gaussian coil chain shape due to the flexibility of their molecular backbone.58,193,194 The interfacial thickness tends to be proportional to the molecular weight of polymer, however, it cannot be precisely calculated via the average degree of polymerization of the polymer. Rigid chain structures, i.e. π-conjugation along the polymer backbone (semiconducting polymers), helical secondary structures (biomolecules), aromatic groups (aramid and aromatic polyester high-performance resins) or mesogen-jacketed liquid crystalline polymers, all lead to the adoption of extended and rigid chain conformations. Among them, the mesogen-jacketed liquid crystalline polymers can be synthesized by a living radical polymerization and the polymer-chain length can be tailored by controlling the degree of polymerization, thereby resulting in an interfacial modified thickness that can be accurately controlled by design of the degree of polymerization of the mesogen-jacketed liquid crystalline polymers; as shown in Fig. 15.193,195
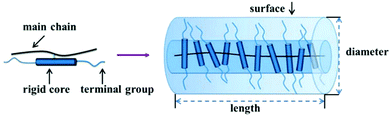 | ||
| Fig. 15 Schematic of a rod-like mesogen-jacketed liquid crystalline polymers (MJLCP). Reproduced from ref. 193 with permission from the Royal Society of Chemistry. | ||
Kuang and Xie et al.196 successfully grafted a liquid crystalline polymer with azobenzene mesogens as the side chain to golden nanoparticles by the two-phase Brust–Schiffrin method. In addition, Luo et al.125 utilized a liquid-crystalline polymer, PMPCS to design and tailor the interfacial region, and focused on the effects of the interfacial layer thickness between a Na2Ti3O7 nanofiber filler and the polymer matrix on the performance of the nanocomposites, as shown in Fig. 16. PMPCS is a rigid polymer with crowded, and bulky side groups connected with the main chain through a short spacer or with a single covalent bond.197,198 These interesting features lead to the PMPCS forming a rigid polymer structure, and when the molecular weight of the PMPCS is greater than 104, the main chain is constrained to form a straight conformation. The size of the straight conformation unit can be calculated by eqn (3):199,200
Lrod = 0.154 (nm) × 2Nrod × sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 52° ≈ 0.24Nrod (nm) 52° ≈ 0.24Nrod (nm) | (3) |
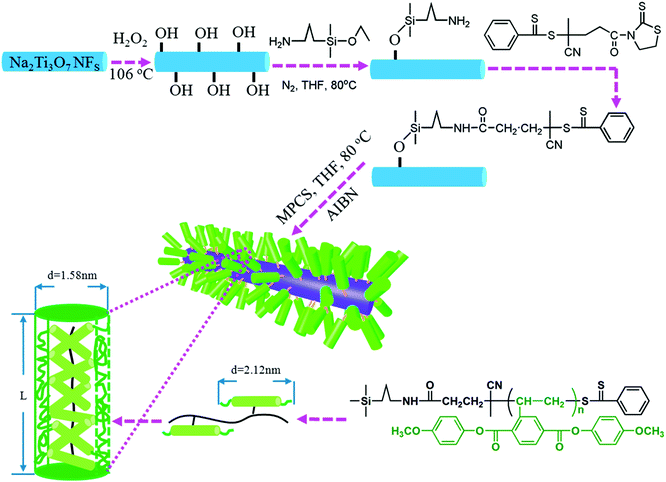 | ||
| Fig. 16 Modulation of the interfacial layer thickness on Na2Ti3O7 nanofibers by rigid polymer PMPCS. Reprinted with permission from ref. 125. Copyright (2017) American Chemical Society. | ||
A novel liquid-crystalline polymer PTFMPCS was also investigated by introducing fluoro-atoms into the PMPCS to engineer the surfaces of BaTiO3 nanoparticles.107,201,202 As a result, a significantly improved energy density was achieved by accurate interfacial control using this fluoro-polymer in a polymer nanocomposite. Subsequently, a series of fluoro-liquid-crystalline polymers with three to seven fluoro-atoms were prepared, which were used to engineer the surface of BaTiO3 platelets and nanoparticles and modulate the performance of the composites.
3.3 Formation of a controllable inorganic ceramic shell layer
A number of routes have been used for the preparation of core–shell structures with an inorganic ceramic shell layer of moderate to high relative permittivity to mitigate electric field concentrations at the interface between the filler and matrix.203 The methods used included sol–gel,87 hydrothermal,204 hydrolysis reaction,205 coaxial electrospinning,206 CVD,153 and the Stöber method.95 Coaxial electrospinning is a method recently employed; firstly, a homogeneous precursor solution with a designed molar ratio of the raw target nanofibers was prepared by a solution method.207–210 Secondly, the viscosity of the solution is modulated using polymers, such as poly(vinyl pyrrolidone). Thirdly, the solution is transferred to the syringe of the electrospinning instrument and an appropriate electric field is applied. Finally, the core–shell structured ceramic nanofibers are obtained after an annealing treatment.Although efforts on preparing core–shell structured fillers with different ceramic shell layers have been made to improve the dielectric and energy storage performance, the effects of ceramic shell layer thickness on the performance of polymer based dielectric nanocomposites is less well explored. Huang et al.142 prepared BaTiO3 nanowires encapsulated by TiO2 shells of variable thickness by a kinetically-controlled coating method, as shown in Fig. 17. Two kinds of materials with shell layer thickness dimensions of 50 and 110 nm were obtained by tailoring the tetrabutyl orthotitanate content. The performance of the P(VDF–HFP) polymer nanocomposites with BaTiO3@TiO2 and bare BaTiO3 nanowires were investigated. The results showed that the nanocomposites with BaTiO3@TiO2 nanofibers achieved significantly improved performance, including higher breakdown strength and energy storage density due to the more uniform electric field distribution and enhanced polarization in the nanocomposites by the moderate TiO2 buffer layer compared with nanocomposites containing only uncoated BaTiO3 nanofibers. For example, a high energy density of 9.53 J cm−3 at 440 kV mm−1 was obtained for nanocomposites with core–shell structured nanowires compared to a lower energy density of 5.60 J cm−3 at 360 kV mm−1 for nanocomposites with 5 wt% uncoated fibers.
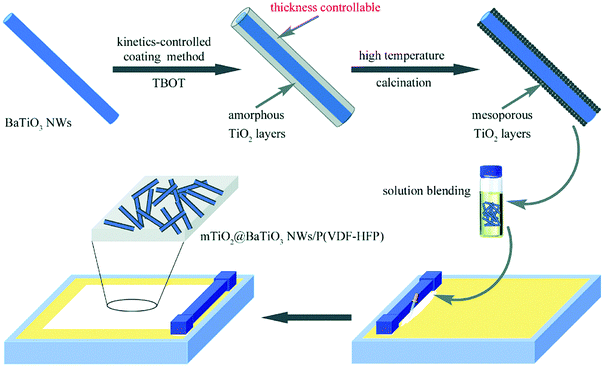 | ||
| Fig. 17 Preparation process of BaTiO3@TiO2 nanowires by a kinetics-controlled coating method. Reproduced from ref. 142 with permission from the Royal Society of Chemistry. | ||
It is of interest to note that the energy storage density of nanocomposites can be modulated by the TiO2 shell thickness. To reveal how the thickness of the TiO2 buffer layer can affect the properties of the composites, Hu et al.211 prepared BaTiO3@TiO2 nanoparticles with a modulated TiO2 shell layer thickness from 0–10 nm. The core–shell structured nanoparticles were prepared via a surface coating approach in solution and, following heat treatment, the thickness of the TiO2 shell layer could be tailored by modulating the amount of the titanate coupling agent employed in the preparation process. The core–shell fillers were incorporated into a PVDF polymer matrix and used for energy storage applications where the dielectric properties, breakdown strength, and energy storage performance of the nanocomposites were strongly related to the thickness of the TiO2 shell layer. Nanocomposites with a TiO2 shell layer thickness of 1–3 nm achieved the highest relative permittivity and breakdown strength compared with the nanocomposites with other TiO2 shell layer thickness. The authors proposed that the introduction of a TiO2 shell layer on the surface of the BaTiO3 nanoparticle induced a two-charged interface and therefore more electronic charge was captured in the interfacial region to enhance interfacial polarization.
Recently, TiO2 nanowires with multiple shells including carbon and SiO2 layers have been prepared.153 The detailed synthesis procedure is shown in Fig. 18. As shown, TiO2 nanowires was synthesized by a hydrothermal and calcination method using a raw material of TiO2 nanoparticles, and the carbon layer was formed on the surface of TiO2 nanowires using a CVD treatment; the outer shell SiO2 layer was formed by a sol–gel synthesis method. The composite with TiO2@C nanowires showed the typical characteristics of a composite containing conductive fillers, where the permittivity and dielectric loss sharply increased with an increase of TiO2@C nanowire loading level, see Fig. 18d and e. The percolation response disappeared when the TiO2@C nanowires were coated with an insulating SiO2 layer. As a result, the composites with 30 wt% TiO2@C@SiO2 nanowires achieved an enhanced permittivity of εr ∼ 41 and suppressed dielectric loss of 0.05 at 1 kHz, which were superior to the composites containing only TiO2 nanowires.
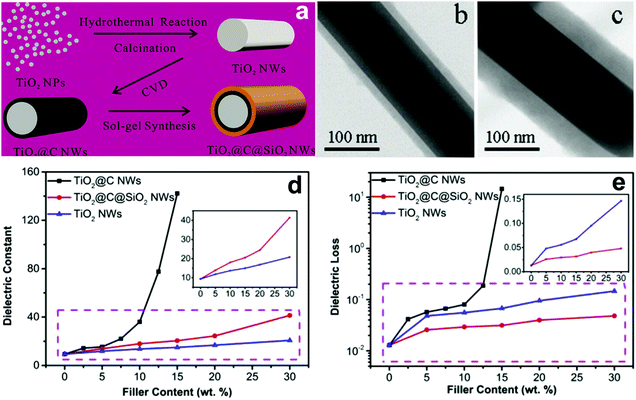 | ||
| Fig. 18 (a) Schematic of the synthesis of TiO2@C@SiO2 nanowires starting with TiO2 nanoparticles and TEM images of the core–shell structured (b) TiO2@C and (c) TiO2@C@SiO2 nanowire. Relative permittivity (d) and dielectric loss (e) of PVDF-based nanocomposites loaded with TiO2 nanowires, TiO2@C nanowires, and TiO2@C@SiO2 nanowires as a function of filler content. Reprinted from ref. 153, Copyright (2018), with permission from Elsevier. | ||
3.4 Characterization of interfaces in polymer nanocomposites
It is well-known that the interfacial region between the nanoparticles and the polymer matrix plays an important role in the electric polarization, mechanical, thermal, and optical properties of nanocomposites. However, it remains a challenge to characterize the interfacial region and its electric properties since the interfacial region cannot be isolated from nanocomposites based on the existing characterization methods, such as dipolar polarization, space charge density and electric field distribution. At present, there are two important methods to study the interfacial region: indirect analysis techniques (theoretical simulation based on experiment results) and direct analysis techniques. For the former, the interphase bonding, interphase density, and thickness can be quantified using Fourier transform infrared spectroscopy (FTIR), transmission electron microscopy (TEM)/thermal gravimetric analysis (TGA). However, FTIR is applicable only to metal–polymer composites in which the interfacial interactions generate considerable changes in the infrared spectrum of the polymer arising from bonding between the two moieties at the interface.212 Using the data gleaned from TGA/TEM or FTIR and subsequent analysis, the interphase density and thickness could be calculated via the number of anchoring points per chain. For the latter, there are limited reported on efforts to directly observe the interface structure and assess their physical properties. For example, Li and He et al. have recently detected the local polarization properties at the matrix/particle interface in ferroelectric nanocomposites via a modified Kelvin Probe Force Microscopy (KPFM) method with nanoscale spatial resolution. In principle, the surface potential of ferroelectric polymers can be influenced by dipolar polarization and KPFM can be effective in measuring nanoscale variations in the local surface potential at the interface. Compared with the standard KPFM approach, the main features of the modified KPFM include open-loop control and PeakForce Tapping mode imaging; Fig. 19 shows such a setup. The results indicated that the electric polarization in the matrix/particle interfacial region was higher than the polymer matrix under the application of an electric field.213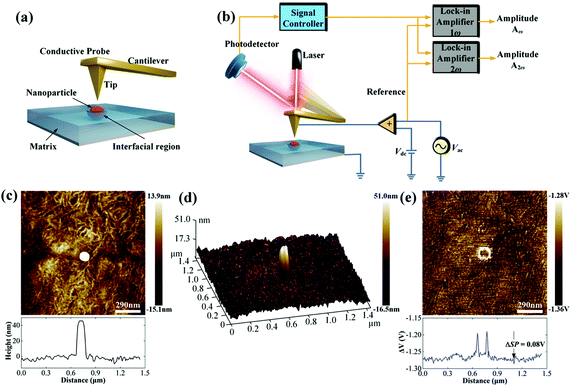 | ||
| Fig. 19 (a) Schematic of the Kelvin Probe Force Microscopy (KPFM) testing process. (b) Schematic of the working principle. (c) Topography signal near an embedded nanoparticle. (d) 3D image of the surface topography near an embedded nanoparticle. (e) The ΔV signal near an embedded nanoparticle. With permission from ref. 213. Copyright 2019, John Wiley and Sons. | ||
4. Interfacial models, polarization mechanism and simulations
We have seen that nano-sized ceramic fillers embedded in a polymer matrix lead to the formation of a large interfacial region area, which plays an important role in determining the properties of the nanocomposites since the interface has a significant impact on the physicochemical properties of materials.214–217 In general, the interfacial region in polymer nanocomposites is characterized as a region that extends from the surface of the nanoparticle, through the modification layer and interfacial polymer layers (with modified chain structures), and finally to the host matrix polymer.36 This section reviews the interfacial models, polarization mechanisms and simulations to examine polymer based nanocomposites.4.1 Interface models
Usually, ceramic–polymer nanocomposites consist of three regions, the polymer matrix, the ceramic filler and the interfacial layer. It is a challenge to fully characterize and understand the interfacial regions, such as nanoparticle surface states, polymer chain configurations, inorganic/organic compatibility and local interfacial electrical and dielectric behaviour. The development of interface models can enable an improved understanding of interface effects on the electrical and dielectric properties of such nanocomposites. According to previous studies,218,219 the interface can change the distribution and motion of space charges, resulting in improved polarization, and act as scattering points to prolong carrier path length, thereby improving breakdown strength. Moreover, interfaces often serve as traps for charges and can result in regulated local charge mobility and conductivity. In addition, the modified electronic states of interfaces can create traps or change the depth of traps, which is closely related to the space-charge (interfacial) polarization and breakdown behaviour. Interfaces can also induce a change in the polymer molecular structure that initiates from the interfacial region to the matrix (free volume fraction, mobility, crystallinity, and configuration of polymer chains), which affects the dielectric properties of the polymer matrix.A variety of interface models have been proposed to describe the interfacial interactions in dielectric nanocomposites, the mode of charge transportation and its effect on electrical properties.220–222 Tanaka developed a multi-core model to describe the interactions between the polymer and spherical ceramic nanoparticles.221 In this model, the interfacial layer includes three layers: (i) the bonded layer, (ii) the bound layer and (iii) the loose layer, as seen in Fig. 20a.4 The bonded layer is based on polymer chains, which are bonded tightly to both the inorganic filler and the polymer network. The interactions holding these chains in place are electrostatic, covalent, hydrogen bonding or van der Waals forces. The bound layer is considered to be ∼1 nm thickness and prevents the formation of polar dipoles, reducing the relative permittivity of the composite. The middle layer of the model is the bound layer. In this layer, the polymer chains interact strongly with the bonded layer and the surface of the filler. Typically, the thickness of the layer ranges from 2 nm to 9 nm, which depend on the interfacial interaction strength of the bonded layer. The polymer chains in the bound layer form structures around the filler nanoparticle that affect chain folding, mobility and conformation. The final layer is termed the loose layer which loosely interacts with the bound layer, leading to a different conformation and mobility to the polymer matrix and can span tens of nanometres. This layer is attributed to the contribution of the reduction in the free volume of the composite. At high filler levels, the loose layers can overlap and this results in an area with combined effects from individual filler particles, thereby increasing the impact that the fillers have on the macroscopic properties of the composites.
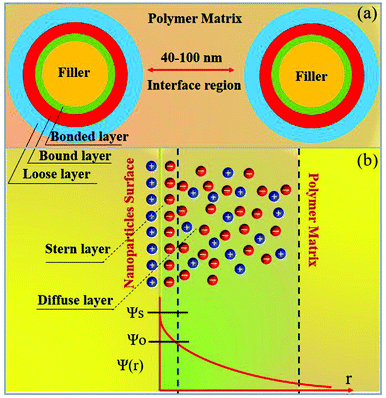 | ||
| Fig. 20 (a) The multi-core model for polymer nanocomposites, (b) charge distribution of a diffuse electrical double layer. | ||
Lewis proposed a diffuse electrical double layer model for describing polymer nanocomposites.220 As shown in Fig. 20b the surface of the nanoparticle becomes charged due to the difference in Fermi levels or chemical potential of the nanoparticles and polymer matrix. This results in screening of ionic charges in the surrounding polymer, which in turn suppresses charge accumulation on the nanoparticles. An electrical double layer consisting of a Stern layer and a Gouy–Chapman diffused layer are formed. When the nanoparticle is positively charged inside the nanocomposite, a layer exhibiting a positive potential ψs is formed by the surface states related with immobile charged impurities, trapped carriers, mobile electrons, and holes in the nanoparticle. The negatively charged Stern layer is formed on the nanoparticle surface, which contains small molecules, special absorbed ions, and solvated ions, and cannot move freely. Outside this layer is the Helmholtz plane (OHP) with an electrical potential of ψo. Taking TiO2–BaTiO3–TiO2@dopamine/PVDF nanocomposite as an example, the Fermi level difference between TiO2 and BaTiO3 is above 0.5 eV, which results in accumulated space charges on TiO2 and BaTiO3. The surface charge densities (σ′) in different layers of TiO2–BaTiO3–TiO2 nanoparticles follow the trend of σ′ (TiO2) core > σ′ (BaTiO3) middle layer >σ′ (TiO2) outer layer to maintain charge neutrality. The positive charges in the TiO2 layer in turn develop negative charges on the dopamine layer due to polar interaction. The interfacial charges present in the polymer matrix form a Gouy–Chapman–Stern layer at the interface of TiO2–BaTiO3–TiO2 nanoparticles, and the interfacial polarization and permittivity is enhanced.160
An extension of the OHP into the polymer matrix is the Gouy–Chapman diffused layer, which is formed around the Stern layer by a distribution of negative and positive ions. This layer potentially works as an “interaction zone” to affect the dielectric and electrical properties of the nanocomposite. The distribution of charges in this layer is related to the electrical potential ψ(r) across the interface region. The magnitude of ψ(r) changes with the distance (r) from the particle surface and can be described with a combined Poisson–Boltzmann equation, and the ψ(r) function is shown as follows:
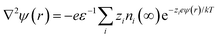 where ε is the relative permittivity of the medium, k is the Boltzmann constant, zi and ni(∞) are the ion valency and concentration of ion species i in the bulk matrix, respectively. When the potential is small, the ψ(r) can be reduced to the simple Debye–Hückel form, as shown below:
where ε is the relative permittivity of the medium, k is the Boltzmann constant, zi and ni(∞) are the ion valency and concentration of ion species i in the bulk matrix, respectively. When the potential is small, the ψ(r) can be reduced to the simple Debye–Hückel form, as shown below:
The charge density (ρi) in the double layer is expressed as follows:
and is associated with the surface conductivity (σ) of the nanoparticles. This equation implies that the charge density, ρi, in the double layer can be increased by increasing the σ, which is useful to induce polarization at opposite ends of nanoparticles under an applied electric field since charges at the interfaces are efficiently transferred.
The multi-core model of Fig. 20 and 21a was later modified by Li et al.223 to produce a multi-regional structure model, as shown in Fig. 21b. The bonded region was considered to be rich in charge traps with the deep traps replaced by shallower traps as the distance away from the filler increased. The deep traps prevent charge mobility, reduce space charge and increase the breakdown strength of the nanocomposite.91
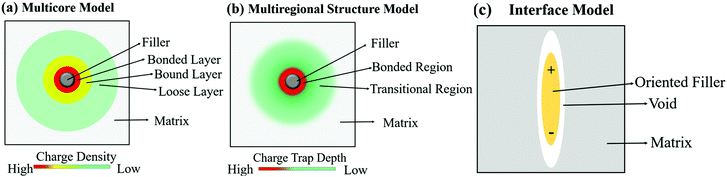 | ||
| Fig. 21 Schematic visualising the difference in how the (a) multi-core model, (b) multi-regional structure model and (c) interface model treat the interface between filler and matrix. | ||
A different approach to the interface model was developed by Ezzat et al.224 who considered the composite interfaces as a three-phase system, namely filler, polymer matrix and a void between both regions. The model, known as the interphase model, considered the shape and orientation of the filler, rather than assuming a spherical morphology; this is shown in Fig. 21c. The model considered that as the filler concentration increased, the concentration of void spaces also increased in the composite.225,226 The voids are important since they contribute to the enhancement of mobile charge interference from charge trapping, charge distribution and molecular and ionic relaxation processes at the filler interface.227
A bipolar charge-transport model has been used to describe the mode of charge transport when an electric field is applied to the system. It has successfully shown that increasing the charge trap depths and densities increases the breakdown strength of a composite. However, this model makes a number of assumptions,228,229 where it treats the energy barriers for trapping and detrapping for electrons and holes as being of the same energy.230,231 Macroscopically, the model fails to take into account ion transport or Maxwell–Wagner–Sillars polarization and its impact of relative permittivity or electrical conductivity. In addition, an induced dipole moment model has been used to describe the polymer–filler interface. The approach assumes that polar groups are permanent dipoles and that the nanoparticles have induced dipoles under an electric field.232 The fillers result in the formation of deep charge traps, which vary based on the relative permittivity, shape and size of the filler. The traps led to a reduction in space charge, when the particle size was below 200 nm and when its relative permittivity increased. The interfacial models have been discussed, experimental efforts to understand polarization are now described, along with polarization mechanisms.
4.2 Polarization mechanism
There are four principle types of polarization, which include electronic polarization, interfacial polarization, dipolar polarization and ionic polarization. Electronic polarization relates to when an atom or molecule is located in electric field and its electrons are displaced slightly toward the positive direction of the electric field and form impermanent polarizations. Electronic polarization is present in all materials and persists over the entire frequency range, which can contribute to the permittivity, while it does not contribute to conductivity or dielectric loss in most dielectrics. Ionic polarization is the result of the displacement of cations and anions in an electric field, which is the main contributor of permittivity to the dielectrics and present as predominant polarization in inorganic crystals, glasses and ceramics. Dipolar polarization is a result of dipole orientation in the direction of the electric field and which occurs in polar dielectrics, such as polar polymers and ceramics. Interfacial polarization was recognized before 1900, and Maxwell–Wagner–Sillars (MWS) is a well-known mechanism for interfacial polarization. Interfacial polarization is observed at relatively low frequencies and formed in dielectric composites with two or more compositions, which associate with permittivity, dielectric loss and conductivity.233–237 Usually, the formation of interfacial polarization will lead to the enhancement of relative permittivity in a nanocomposite. However, under the application of a high electric field, space charges are blocked at the interface and trapped due to the long relaxation process of interfacial polarization in the discharge cycle, which leads to low energy storage efficiency as a result of an inefficient energy discharge. The increased local electric field may also create AC conduction and result in increased dielectric loss and decreased breakdown strength. Therefore, numerous approaches have been utilized to achieve dielectric enhancement with suppressed dielectric loss and improved breakdown strength in nanocomposites.To study the polarization mechanism in detail, Niu et al.192 modified BaTiO3 with different aromatic modifiers in a PVDF matrix. The range of modifiers acted to vary the number of carboxylic acid groups bound to the surface of BaTiO3 and the number of fluorine atoms attached to the benzene ring. In all cases, the chemically modified BaTiO3 showed a lower relative permittivity compared to pure BaTiO3, which was attributed to polar groups promoting a stronger dipole interaction with the PVDF matrix, thus reducing the interfacial polarization and increasing the dispersion. In addition, the modifiers on the BaTiO3 surface acted as charge traps which reduced space charge polarization and minimized the conduction pathways in the polymer film. A high breakdown strength, high energy displacement, high energy density and high efficiency was achieved when the modifier was from a single carboxylic acid linkage to BaTiO3 with four fluorines attached to the ring. This was attributed to the ability of the aromatic ring to orientate under an electric field, while the rings with two carboxylic acid linkages were severely restricted from any movement.238 Dual modification of BaTiO3 with partial modification with OH groups and a titanate coupler (D-h-BaTiO3) is shown in Fig. 22a.239 The hydroxyl groups improved the compatibility of the nanoparticles with PVDF and resulted in amorphous regions whilst the oligomeric chains on DN-101 re-introduced a crystalline structure to the PVDF matrix. Compared with pure PVDF, the increased relative permittivity and reduced dielectric loss at low frequencies was achieved for D-h-BaTiO3 in PVDF, which was attributed to the OH groups on BaTiO3 acting as charge traps to minimize charge conduction pathways in the film.240 The discharged energy density and stored energy density were enhanced upon inclusion of the filler into the PVDF film. The OH groups act as free electron traps for the BaTiO3 and thus lead to an increased negative charge build-up on the surface of the nanoparticle. This increased the interfacial polarization between the nanoparticles and PVDF matrix, thereby increasing the overall polarization in the composite, as shown in Fig. 22b.
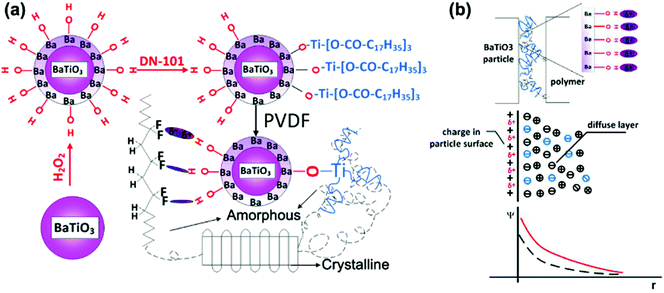 | ||
| Fig. 22 (a) Diagrams of the modification of BaTiO3 particles and interaction in D-h-BaTiO3/PVDF. (b) Charge distribution in D-h-BaTiO3/PVDF interface. Reprinted with permission from ref. 239. Copyright (2014) American Chemical Society. | ||
Liu et al.92 studied the correlation between the interfacial polarization and discharged energy density in dielectric nanocomposites that consisted of core–shell structured BaTiO3@SiO2 nanofibers in a PVDF polymer matrix. The results showed that coating SiO2 layers on the surface of BaTiO3 nanofibers can act to block the movement of charge carriers through the nanocomposite by providing a shielding role on the charge-rich inter layer, which resulted in weak Maxwell–Wagner–Sillars interfacial polarization and thus reduced the energy loss and improved the energy discharged density of the nanocomposite. As shown in Fig. 23, without any interfacial polarization, there is no significant gain in the charge and discharge process and all stored charges can be completely released during the discharge process. With a high interfacial polarization, the polarization charges are stored in the charging process and trapped in the discharge process, resulting in a lower discharge and lower energy storage efficiency.
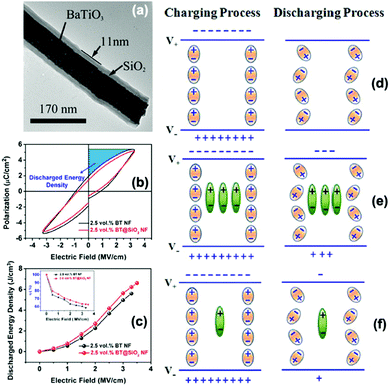 | ||
| Fig. 23 (a) TEM of the morphology of core–shell structured BaTiO3@SiO2 nanofibers. (b and c) Polarisation–electric field loops, discharged energy density and energy storage efficiency of nanocomposites with BaTiO3 nanofibers and BaTiO3@SiO2 nanofibers. Schematic of charge and discharge mechanism under an electric field across a nanocomposite: (d) without interfacial polarization, (e) with high interfacial polarization, and (f) with low interfacial polarization. Interfacial polarization charges are represented by green dipoles. Charges completely released in discharge process are represented by orange dipoles. Reprinted from ref. 92 with permission of AIP Publishing. | ||
Rahimabady et al.87 obtained a higher relative permittivity in PVDF–HFP based nanocomposites with TiO2 coated BaTiO3 nanoparticles compared to unmodified BaTiO3. The enhancement was attributed to the build-up of interfacial polarization between the BaTiO3/TiO2 interface and the TiO2/PVDF–HFP interface as well as an increase in the charge trapping by the TiO2 shell. More specifically, Rahimabady et al. indicated that the increase in interfacial polarization was the result of the high density of oxygen vacancies that act as n-type semiconductors on TiO2, resulting in a Fermi level difference of 0.5 eV between TiO2 and BaTiO3 so that the TiO2 exhibits positive space charge and BaTiO3 exhibits negative space charge. PVDF–HFP is electronegative and therefore formed a negatively charged layer at the interface.
TiO2 with an organic dopamine core–shell that was decorated with silver nanoparticles (nAg) have been introduced into a nitrile-butadiene-rubber (NBR) matrix by Yang et al. with a view to introducing a Coulomb blockade effect from enhanced quantum confinement of the silver nanoparticles, as shown in Fig. 24.241 The mechanism of the Coulomb blockade effect is a result of the nanoparticles having a higher energy barrier to allow tunneling electrons to pass compared to micro-scale particles. This higher energy barrier typically prevents a second electron from tunneling, in this case from TiO2,241 which prevents space charge accumulation, as free electrons from TiO2 are quantum confined to the filler. The Coulomb blockade effect has been used to reduce the leakage current and increase the breakdown strength of composites.242 In this case, the nAg reduced the space charge polarization and prevented electron migration243 since the nAg introduced a barrier that required more energy than the thermal motion of an electron to overcome and thus prevented a second electron passing through. The nAg particles can be thought of as a “Coulomb island”. In the work, ten parts per hundred parts of rubber of modified nAg–dopamine–TiO2 filler was added. However, this resulted in degradation of the dielectric properties compared to the addition of dopamine–TiO2 into NBR, with a lower relative permittivity, higher dielectric loss tangent and lower breakdown strength. The explanation was that the decoration of the nAg particles on the surface of the filler increased interfacial polarization, leading to the introduction of ions, which could lead to breakdown of the composite at a lower electric field.244 In addition, the nAg particles reduced the space charge through the Coulomb blockade effect.245
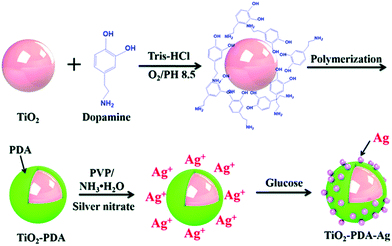 | ||
| Fig. 24 Schematic of dopamine coated TiO2 with silver nanoparticles to introduce the Coulomb blockade effect. Reproduced from ref. 241 with permission from the Royal Society of Chemistry. | ||
In the case of multi-layer structured composites, the interfacial polarization at the interface between layers plays an important role in the electric and dielectric properties of nanocomposites. For multi-layer structured composites with PVDF-based ferroelectric polymer layers, its enhanced electric displacement often results from the C–F bonds and the spontaneous alignment of dipoles in the crystalline phases of its PVDF based ferroelectric polymer layers (with a low relative permittivity) at a largely enhanced local electric field. Importantly, in addition to the polarization from the PVDF ferroelectric layer, interfacial polarization can also build up at the interface of multi-layer structured composites in response to the application of an electric field and plays an important role in the electric and dielectric properties of composites. Chen et al.246 developed a multi-layer film comprised of PVDF and polycarbonate (PC) with either 32 layers or 256 layers, but maintained the same total polymer thickness by reducing the thickness of the individual polymer layers; a schematic is shown in Fig. 25. The breakdown strength of the 32-layer multi-layer film was greater than the multi-layer film with 256 layers. This was attributed to the inability of the space charges to penetrate the PC, resulting in greater interfacial polarization. However, in the 256-layer multi-layer film, space charges could penetrate more easily leading to a lower interfacial polarization and a lower breakdown strength and higher DC conductivity.
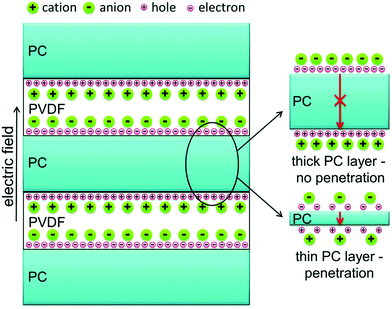 | ||
| Fig. 25 Schematic of interfacial polarization of space charges in polycarbonate (PC)/PVDF multi-layer films under an applied electric field. A thick PC layer prevents space charges from penetrating through the film to increase interfacial polarization, whereas a thin PC layer allows space charges to penetrate. Reproduced from ref. 246 with permission from the Royal Society of Chemistry. | ||
Xie et al.247 developed a linear/ferroelectric bilayer-heterostructured polymer nanocomposite with an ultra-high discharged energy which exhibited an enhanced breakdown strength and a large difference between the maximum dielectric displacement and remnant polarization (Dmax–Pr). The enhancement was attributed to the interfacial barrier and the interfacial polarization effect at the interface of two layers. A linear PI was employed as the bottom insulating layer to provide high breakdown strength, while ferroelectric P(VDF–CTFE) with dispersed BaTiO3 nanoparticles was used as the top layer to provide a high relative permittivity, as shown in Fig. 26a and b. In this structure, both the PI single or a BaTiO3/P(VDF–CTFE) single layer exhibited a lower breakdown strength compared with the bilayer composite. The polarization in the BaTiO3/P(VDF–CTFE) layer (PBP, polarization associated with an electric field, such as dipole orientation polarization, interfacial polarization between the filler and the polymer matrix) was weakened with a decrease of the local electric field, as shown in Fig. 26c. Thus, although the overall applied electric field of the BaTiO3/P(VDF–CTFE)–PI nanocomposite was improved, the contribution of the BaTiO3/P(VDF–CTFE) layer to the overall polarization was limited. The contribution to the overall polarization enhancement was attributed to the interface of the bilayer films. Due to the large contrast in relative permittivity and conductivity between the linear and ferroelectric layer, a higher Maxwell–Wagner–Sillars interfacial polarization builds up at the PI/PVDF interfaces in response to the application of an electric field. Hence, space charges that include free electrons, ions in the BaTiO3/P(VDF–CTFE) layer and bound charges near the PI layer result in an additional enhancement of polarization at BaTiO3/P(VDF–CTFE)/PI interface, as shown in Fig. 26c.
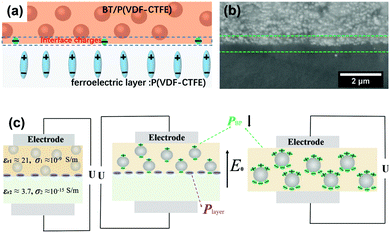 | ||
| Fig. 26 (a) Schematic and (b) cross-section SEM image of bilayer heterostructure BaTiO3/P(VDF–CTFE)–polyimide (PI) nanocomposite. (c) Schematic of two-layer dielectric considered in the Maxwell–Wagner–Sillars model for interfacial polarization and the poling mechanism of the bilayer heterostructure BaTiO3/P(VDF–CTFE)–PI. Reprinted from ref. 247, Copyright (2018), with permission from Elsevier. | ||
In addition to experimental methods, computational methods have also been employed to understand the factors that affect the performance of dielectric nanocomposites. In polymer nanocomposites, it is a challenge to predict the relative permittivity and electric field distribution due to the large numbers of factors that should be considered in any model. Finite element simulation is an effective theoretical approach to examine the interface charge density distribution and spatial potential distribution in nanocomposites.248,249 The method is based on microstructure-specific space discretization, whereby discrete meshes are used that coincide with the interfaces of the multi-phase microstructure of a nanocomposite. However, for the range of microstructures to be considered, different meshes are needed, and the numerical complexity significantly increases with increasing complexity of the composite structure. To overcome this challenge, phase field simulation has been developed,250 which solves electrostatic equations in terms of a polarization vector field in reciprocal space using a fast Fourier transform technique and a parallel computing algorithm.251 For this method, the interphase boundary conditions are automatically satisfied without explicitly tracking the inter-phase interfaces when calculating the effective permittivity, local electric field distribution, and charge density in the nanocomposite. In Sections 4.3 and 4.4, respectively, we discuss the use of finite element simulation and phase field simulation in nanocomposites to assess their properties.
4.3 Finite element simulation
Shen et al. utilized the finite-element method to investigate the space charge effects on the dielectric response of polymer nanocomposites.252 In this model system, two kinds of polymer nanocomposites with randomly distributed and aggregated SrTiO3 nanoparticle fillers in the polyethylene matrix were developed, as shown in Fig. 27a and b. The equilibrium distributions of space charge in these two polymer composites are respectively shown in Fig. 27c and d. Fig. 27e and f provide the space charge distribution along the A–A and B–B cross sections. It was found that the positively charged ions concentrate at the interfaces and gradually reduced into the bulk matrix if the nanoparticles in the polymer composite were negatively charged. The results were consistent with the electric double layer model, as described in Section 4.1. Moreover, the high density of charges can lead to high local electrical conductivity. Space charge has a significant contribution to the increase of relative permittivity and to the dielectric loss, especially when the nanofillers aggregate and the ion concentration in the bulk polymer is high. Preventing the nanoparticles from aggregating is beneficial to the increase of relative permittivity without increasing the loss significantly. Using the present model, Fig. 27g shows the calculated relative permittivity as a function of the volume fraction of the nanoparticle filler for the P(VDF–HFP)/TiO2 polymer composite. It was noted that the relative permittivity exhibited a slow increase with increasing filler volume fraction without consideration of the space-charge contribution. However, after taking space-charge effects into account, the relative permittivity increased to a large extent, which was in better agreement with the experimental results. The computational results demonstrated that the dielectric response is largely determined by space charges accumulating at interfaces.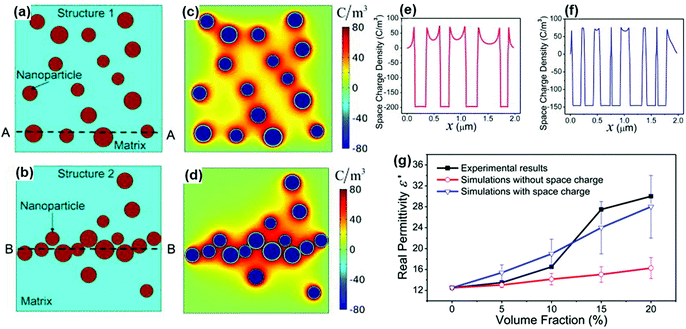 | ||
| Fig. 27 (a and b) Schematics of polymer nanocomposites with 12% volume fraction of randomly distributed and aggregated SrTiO3 nanoparticles with radii ranging from 70 to 120 nm. (c and d) Corresponding equilibrium distributions of space charge and (e and f) cross section profiles along A–A and B–B. (g) Effects of the nanoparticle volume fraction on the relative permittivity of P(VDF–HFP)/TiO2 nanocomposites predicted from the model and by experiment. Reprinted from ref. 252 with permission of AIP Publishing. | ||
Roscow et al.253 used finite element modelling to examine the electric field distribution and dielectric properties of composites containing conductive fillers at a range of aspect ratios and orientations. Electric field maps for an aspect ratio of eight are shown in Fig. 28a where they investigated the influence of filler angle with respect to applied electric field and the aspect ratio of a filler on the normalized breakdown strength (Eb*), εr and energy density (eqn (1); εr.(Eb*)2). The data is shown in Fig. 28b–d, respectively, where the data was normalized with respect to the filler-free matrix which is indicated by the dotted line. Fig. 28b shows that high aspect ratio inclusions aligned perpendicular to the applied field provided the highest breakdown strength, since this orientation led to the lowest electric field concentrations, as seen in Fig. 28a. The lowest breakdown strength occurred when the high aspect ratio particles were parallel to the applied electric field. The model indicated that for the wide range of filler orientations and aspect ratios, the breakdown strength is always lower than that the filler-free matrix in which the field is homogenous at all points in the matrix. An opposing trend was observed for the relative permittivity since electric field concentrations benefit relative permittivity, but are detrimental to dielectric strength. Since energy density depends on the square of the breakdown strength, the inclusion of conductive fillers of any orientation or aspect ratio reduces the energy storage capabilities of the composite compared to the matrix material, as shown in Fig. 28d. However, the model does not include ion transport, in particular at interfaces, and the impact of filler on the polymer materials, but nevertheless explains the challenge of using filler materials to increase relative permittivity, while not degrading the breakdown strength. Fillers with high aspect ratio were also modeled using a finite element approach in Luo et al.254
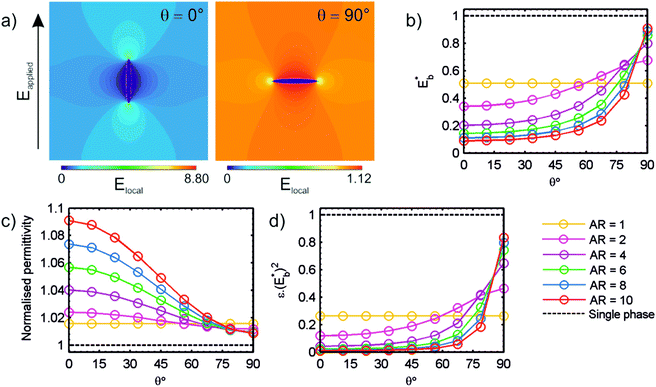 | ||
| Fig. 28 (a) Contour maps of electric field distribution for an individual conductive inclusion with high aspect ratio (AR = 8), and angle with respect to applied field (φ = 0° (left) and 90° (right)) contained within a dielectric matrix; and variation of (b) effective breakdown strength, Eb2, (c) relative permittivity and (d) energy density, εr·(Edielectric)2 with changing angle and aspect ratio of single inclusion. Reprinted with permission from ref. 253. Copyright (2017) American Chemical Society. | ||
Finite element simulations were also successfully used to examine the electric field distribution and dielectric properties of nanocomposites with a core–shell or hierarchical structured fillers. Pan and Zhai et al. used finite element simulations to analyse the electric field and electric current density distribution in the PVDF-based nanocomposites filled with dopamine coated BaTiO3 nanoparticles and dopamine coated BaTiO3@Al2O3 nanofibers.143 For the BaTiO3@Al2O3 nanofibers, BaTiO3 nanoparticles were homogeneously embedded in the Al2O3 nanofibers, as shown in Fig. 29. In both the experiment method and simulation, the majority of nanofillers were located along the in-plane-oriented direction of the polymer matrix. The experimental results revealed that the dopamine coated BaTiO3@Al2O3 nanofibers improved the dielectric performance and breakdown strength of the nanocomposites, leading to an enhanced energy density. In terms of the simulation results, it was found that the local electric field strength in the nanocomposites with dopamine coated BaTiO3 nanoparticles was significantly higher than the nanocomposites with dopamine coated BaTiO3@Al2O3 nanofibers located between the adjacent fillers, as indicated by the intensified pink region in Fig. 29. As a result of the larger permittivity contrast between the matrix and nanofillers, the local electric field strength is traceable to charge agglomeration at the interface. In addition, the nanocomposites with dopamine coated BaTiO3@Al2O3 nanofibers also exhibited a significantly lower local electric current density than the nanocomposites with dopamine coated BaTiO3 nanoparticles. It is known that the difference of the electric current density is attributed to the contrast of local electric resistivity between the matrix and nanofillers. The Al2O3 insulated layer was considered to be effective in restricting charge carrier migration in the space between the matrix and nanofillers. Moreover, in the nanocomposites with dopamine coated BaTiO3 nanoparticles, the local electric field or electric current density at adjacent nanoparticles tended to form a channel along the electric field direction, exhibited by the intensified yellow region in Fig. 29, which can lead to a greater probability of breakdown. As a result, the dopamine coated BaTiO3@Al2O3 nanofibers were more attractive in energy storage applications.
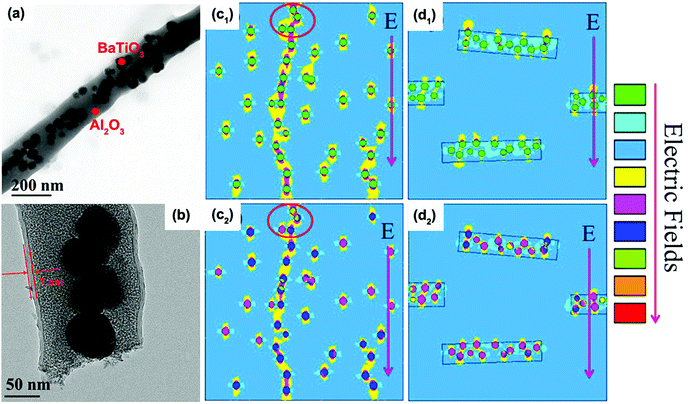 | ||
| Fig. 29 TEM images of (a) BaTiO3@Al2O3 nanofiber and (b) dopamine coated BaTiO3@Al2O3 nanofiber. Distributions of electric field and electric current density simulated for the nanocomposites with dopamine coated BaTiO3 nanoparticles (c1 and c2), and the nanocomposites with dopamine coated BaTiO3@Al2O3 nanofibers (d1 and d2). Reprinted with permission from ref. 143. Copyright (2017) American Chemical Society. | ||
Sandwich/multi-layer structured nanocomposites have been widely studied for the high performance they can achieve, such as improved breakdown strength and high energy density. The formation of a weak electric field and incomplete breakdown are the key factors for achieving high performance. Wang et al.167 used finite element simulations to prove that the improvement in energy density of sandwich-structured BaTiO3/PVDF nanocomposites was attributed to the favourable electric field redistribution. Electric tree growth theory was used to explore the electric breakdown mechanism in sandwich structured nanocomposites. As can be seen in Fig. 30a, the spacing of adjacent equi-potential lines were used to show the heterogeneous distribution of electric field.255 It is clear that the BaTiO3/PVDF nanocomposite layer can endure higher electric field when it is formed as a sandwich structure, compared to a monolayer nanocomposite. In addition, the electric field of the BaTiO3/PVDF layer with 1 vol% BaTiO3 in the sandwich-structured nanocomposites is smaller than that on the single-layer composite with 20 vol% BaTiO3. The weak internal electric field is formed to block the development of electrical trees in the interface of the adjacent layers in the sandwich BaTiO3/PVDF nanocomposites, which was considered to be the main reason for the enhanced breakdown strength; see Fig. 30c. After introducing BaTiO3 nanoparticles into the PVDF matrix, the electric field is increased in the regions above and below the BaTiO3 nanoparticles, while it weakens the field on the left and right side of the ceramic fillers (perpendicular to applied field) and the authors indicate that the incomplete breakdown theory can explain the simulation results. It was thought that an incomplete breakdown path is formed only in the high electric field region when the local electric field is higher than its intrinsic breakdown strength, and the path will not grow through the whole composite film to achieve complete breakdown.256 The functional region of low electric field can only be formed when the BaTiO3 loading in the middle layer was at an optimal value, which was 20 vol% in this work. If the BaTiO3 content is reduced, the distance between adjacent BaTiO3 nanoparticles will be too far to form a low electric field region.
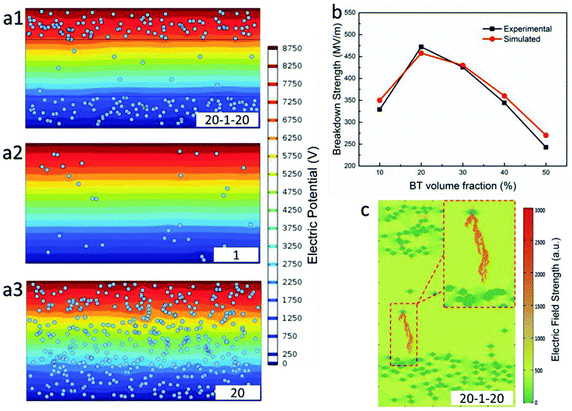 | ||
| Fig. 30 Simulation of electric field in (a1) sandwich structured nanocomposite with 20 vol% BaTiO3 nanoparticles in the outer layers and 1 vol% BaTiO3 nanoparticles in the central layer, (a2) single PVDF nanocomposite with 1 vol% BaTiO3 nanoparticles, (a3) single PVDF nanocomposite with 20 vol% BaTiO3 nanoparticles, (b) comparison of the breakdown strength for experimental data and simulated results, (c) simulation of incomplete breakdown process in the sandwich structured nanocomposite. With permission from ref. 167. Copyright 2015, John Wiley and Sons. | ||
4.4 Phase field simulation
The electrostatic breakdown propagation of dielectric materials is complex, however, the use of a phase-field model is a good approach to understand the breakdown behaviour arising from electrostatic stimuli.257 For the phase field model, it is considered that the complete breakdown path of the composite is similar to the process of crack propagation, although a clear difference is that it incorporates electric energy, gradient energy, and phase separation energy. The calculation process was described in detail by Shen groups.258 Through a continuum phase-field model, the microstructural effects on the effective relative permittivity, breakdown strength, and the energy density of polymer nanocomposites can be systematically studied, including the shape, the orientation and volume fraction of the nanofiller. Taking the PVDF–BaTiO3 nanocomposite as an example, they performed a 2D simulation to predict the breakdown phase evolution under applied electric fields and the simulated results. The polymer nanofiber composites exhibited a shorter breakdown path than the nanoparticle based composites, suggesting that the breakdown phase tended to penetrate through the nanofiber rather than around the nanofiber. In addition, the electric field distribution indicated that the electric field concentrates at the two shoulders along the electric field direction for the polymer nanoparticle composite, which makes it easy to form a breakdown path. In comparison, the electric field concentrates at the vertices of the nanofibers for the polymer nanofiber composites. Therefore, the nanofiber composite exhibited a higher breakdown strength compared with the nanoparticle based composite, proving that phase-field model results coincided with the experimental results; this is also in agreement with observations in Fig. 28.In subsequent work, the breakdown phase evolution of polymer based 3D nanocomposites with 10 vol% of nanofiller was examined by high throughput computation; see Fig. 31a. The structures examined included vertical nanofibers (S1), vertical nanosheets (S2), random nanoparticles (S3), parallel nanofibers (S4), parallel nanosheets (S5) and ellipsoidal nanoparticles (S6). In the simulation, the aspect ratio of the nanofiber was 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 and the length scale of the nanosheet was 1
20 and the length scale of the nanosheet was 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6
6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6. The growth behaviour of the breakdown phase in these nanocomposites under applied electric fields along the z-direction is shown in Fig. 31b. The breakdown strength of nanocomposites were 230, 151, 195, 216, 223 and 310 kV mm−1 respectively from S0 to S5, as shown in Fig. 31c, revealing that the nanocomposites with vertical nanofibers exhibited the lowest breakdown strength, while the nanocomposites with parallel aligned nanosheets showed the highest breakdown strength, as highlighted also in Fig. 28. Fig. 31d defines the microstructure dataset for the high throughput computation by assigning different length ratios of the nanofillers. Based on the microstructure dataset, the breakdown strength, the effective relative permittivity, and the energy density were calculated by phase-field modelling, as shown in Fig. 31e–g. As the nanofiller changes from S1 to S5, the breakdown strength of nanocomposites gradually increases from 0.56 to 1.35 times that of polymer matrix breakdown strength while the effective relative permittivity decreases from 2.24 to 1.08 times that of the polymer matrix relative permittivity. The nanocomposites with parallel nanosheets possess the highest energy density, which is about 1.97 times that of the polymer matrix.
6. The growth behaviour of the breakdown phase in these nanocomposites under applied electric fields along the z-direction is shown in Fig. 31b. The breakdown strength of nanocomposites were 230, 151, 195, 216, 223 and 310 kV mm−1 respectively from S0 to S5, as shown in Fig. 31c, revealing that the nanocomposites with vertical nanofibers exhibited the lowest breakdown strength, while the nanocomposites with parallel aligned nanosheets showed the highest breakdown strength, as highlighted also in Fig. 28. Fig. 31d defines the microstructure dataset for the high throughput computation by assigning different length ratios of the nanofillers. Based on the microstructure dataset, the breakdown strength, the effective relative permittivity, and the energy density were calculated by phase-field modelling, as shown in Fig. 31e–g. As the nanofiller changes from S1 to S5, the breakdown strength of nanocomposites gradually increases from 0.56 to 1.35 times that of polymer matrix breakdown strength while the effective relative permittivity decreases from 2.24 to 1.08 times that of the polymer matrix relative permittivity. The nanocomposites with parallel nanosheets possess the highest energy density, which is about 1.97 times that of the polymer matrix.
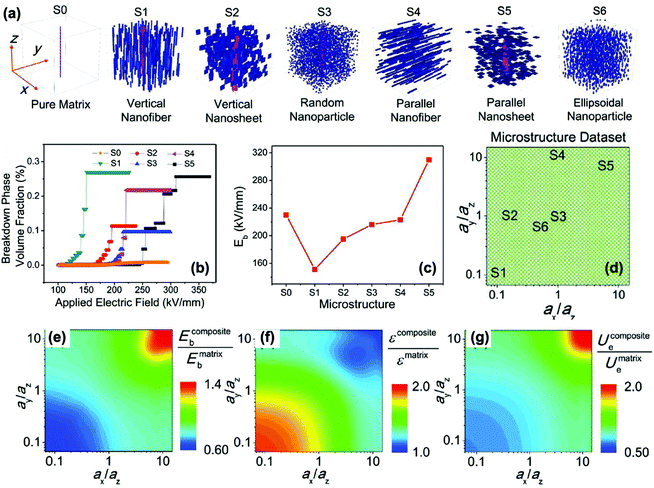 | ||
| Fig. 31 (a) Simulations of nanocomposites with various 3D-microstructures and corresponding breakdown phase morphology. (b) Evolution of breakdown phase volume fraction with electric field and (c) extracted breakdown strengths. (d) Definition of the microstructure dataset. The datasets of (e) the breakdown strength, (f) the effective relative permittivity, and (g) the energy density from the high throughput calculation. With permission from ref. 257. Copyright 2017, John Wiley and Sons. | ||
Further, according to the high throughput calculation results, the Shen group searched for dielectric materials with a higher energy density by forming polymer nanocomposite with sandwich structures (Section 2.4). For example, a sandwich nanocomposite which was filled with parallel nanosheets at the upper and lower layers, and with vertical nanofibers at the middle layer, was designed and the energy density for this designed microstructure is 2.42 times higher than the polymer matrix.
Phase field simulation was also employed to study the nanocomposites with core–shell structured nanofillers for energy storage applications. Wang et al. investigated the electric field distribution in nanocomposites filled with high-permittivity core–shell structured nanofillers, as shown in Fig. 32.251 In this simulation approach, a graded permittivity distribution was achieved by setting the dielectric susceptibility of core (χc), shell (χs), and matrix (χm) from a high level to a low level. The core–shell structured nanofillers were optimized by regulating the shell thickness (t) and χs for a given core size (r), and dielectric susceptibilities of χc and χm. Firstly, the electric field distributions in nanocomposites were simulated for nanofillers with and without a core–shell structure, as shown in Fig. 32c and d respectively. The core–shell structure was shown to be able to effectively reduce both the local electric field concentration and distortion at the interface region. Then, the effects of χs and shell thickness (t) were further investigated, which showed that the optimal χs was confirmed as χs![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) χm
χm![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) χc = 1.81
χc = 1.81![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100, and the χc had little effect on the optimal χs, as shown in Fig. 32e. In addition, a thicker shell was beneficial to reduce the electric field concentration, as shown in Fig. 32f. The results theoretically confirmed that constructing a dielectric gradient in nanocomposites by core–shell structure is an effective approach to mitigate the field concentration and improve the breakdown strength.
100, and the χc had little effect on the optimal χs, as shown in Fig. 32e. In addition, a thicker shell was beneficial to reduce the electric field concentration, as shown in Fig. 32f. The results theoretically confirmed that constructing a dielectric gradient in nanocomposites by core–shell structure is an effective approach to mitigate the field concentration and improve the breakdown strength.
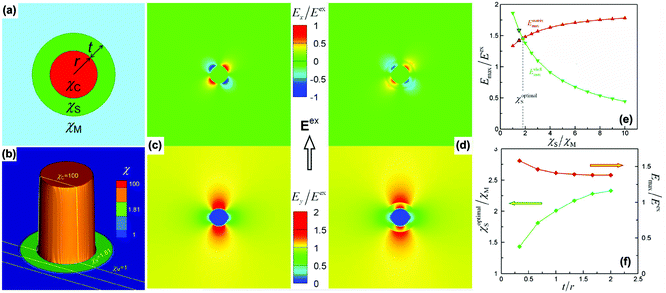 | ||
Fig. 32 (a) Schematic of the design variables in nanocomposite with core–shell structured nanofiller embedded in the matrix. (b) Three-dimensional visualization of dielectric susceptibility distribution in nanocomposite, where χm![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) χs χs![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) χc = 1 χc = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.81 1.81![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 and t/r = 2 100 and t/r = 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3. Local electric field concentration in nanocomposite for nanofillers (c) without and (d) with core–shell structure. (e) Effect of χs on local electric field concentration in nanocomposite with χm 3. Local electric field concentration in nanocomposite for nanofillers (c) without and (d) with core–shell structure. (e) Effect of χs on local electric field concentration in nanocomposite with χm![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) χc = 1 χc = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 and t/r = 2 100 and t/r = 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3. (f) Effects of t on optimal χs and maximum local electric field magnitude in nanocomposite with χm 3. (f) Effects of t on optimal χs and maximum local electric field magnitude in nanocomposite with χm![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) χc = 1 χc = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100. Reprinted from ref. 251 with permission of AIP Publishing. 100. Reprinted from ref. 251 with permission of AIP Publishing. | ||
In the case of sandwich/multi-layer structured nanocomposites, phase field simulation has also been used effectively to analyse the spatial distribution of electric field in the nanocomposites, Zeng and Nan et al. prepared a series of single-layer and multi-layer structured nanocomposites using P(VDF–HFP) as the matrix and parallel boron nitride nanosheets as the filler.259 The detailed structures of nanocomposites are shown in Fig. 33a. The parallel boron nitride nanosheets can limit electron tunnelling through the matrix/filler interfaces and suppress the growth of electrical trees during breakdown, as shown in Fig. 33. Here, the main concern was the effect of different multi-layer structures on the electric field distribution in the nanocomposites. The results of phase field simulation, as shown in Fig. 33b, indicated that the 12L (12 layer) structured nanocomposites exhibited the most homogeneous spatial distribution of electric field compared with other structured nanocomposites, which was beneficial for the suppression of dielectric loss. The multi-layer structured nanocomposites containing a multi-interfacial region can effectively block the growth of electrical trees, and thus improve the breakdown strength and energy density. These results indicate that developing phase-field models and performing high throughput calculations is an important approach to discover polymer nanocomposites with high storage properties and design potential architectures.
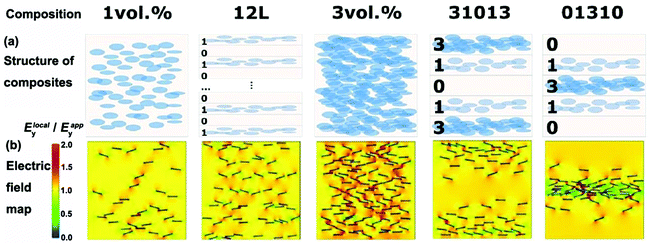 | ||
| Fig. 33 (a) Composition and structure of nanocomposites with parallel boron nitride nanosheets. (b) Phase-field simulation of electric field distribution in corresponding nanocomposites. Reprinted from ref. 259 with permission of AIP Publishing. | ||
5. Strategies for high energy storage application of the composites
As discussed in above sections, interfacial design has been successfully applied to improve the performance of polymer composites. With the aid of some specific focussed examples, this section discusses the strategies to create new materials for high energy storage applications. This includes optimizing the morphologies of the fillers (type and dimensionality), filler orientation and structural design.5.1 Optimization the morphologies of the ceramic fillers
The present section focuses on the morphology of ceramic fillers and corresponding performance of polymer composites where 0D, 1D and 2D ceramic fillers are taken into account.In general, 0D ceramic fillers embedded in a polymer matrix were mostly studied and discussed by researchers. Linear dielectric nanoparticles with low relative permittivity and high breakdown strength, such as TiO2, ZrO2 and SiO2, have been used to improve the breakdown strength of corresponding polymer composites. However, to improve the dielectric properties, ferroelectric ceramic nanoparticles, such as PZT, BaTiO3, PMN-PT, and BST, have been intensively studied due to their high permittivity. Combined with the interfacial design strategies, enhanced dielectric and energy storage properties can be achieved in 0D filler based polymer composites. Recently, Chen et al.107 achieved a significantly improved energy density in a BaTiO3 nanoparticle based polymer composite by accurate interfacial tailoring using a novel rigid-fluoro-polymer. As discussed in Section 3.2, the interfacial thickness can be tailored using rigid liquid crystalline polymers. In this study, RAFT polymerization was used to prepare the core–shell structured BaTiO3@rigid-fluoro-polymer nanoparticles with different shell thicknesses. The dielectric performance and energy storage properties of BaTiO3@rigid-fluoro-polymer/P(VDF–TrFE–CTFE) nanocomposites were investigated in detail. As shown in Fig. 34, the rigid-fluoro-polymer shell effectively improved the compatibility and the shell thickness had significant effects on the performance of nanocomposites. The unmodified BaTiO3/P(VDF–TrFE–CTFE) nanocomposites exhibited higher relative permittivity and lower breakdown strength because of the strong interfacial polarization arising from the presence of voids and aggregation. In contrast, the BaTiO3@rigid-fluoro-polymer/P(VDF–TrFE–CTFE) nanocomposites produced lower relative permittivity resulting from the high dispersion, compatibility and insulating nature of the material. However, with an increase of shell thickness, the breakdown strength of nanocomposites was improved. The highest breakdown strength of 514 kV mm−1 and discharged energy density of 16.18 J cm−3 were achieved in nanocomposites containing 5 vol% fillers, when the shell thickness was approximately 11 nm.
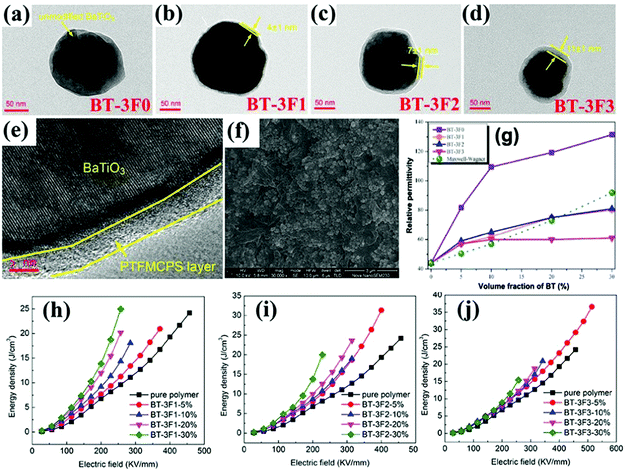 | ||
| Fig. 34 TEM images of (a) BaTiO3-3F0, (b and e) BaTiO3-3F1, (c) BaTiO3-3F2 and (d) BaTiO3-3F3 nanoparticles. (f) SEM image of the freeze-fractured cross section of nanocomposite with 30 vol% BaTiO3-3F3 nanoparticles. (g) Relative permittivity of nanocomposites with BaTiO3-3F0, BaTiO3-3F1, BaTiO3-3F2 and BaTiO3-3F3 nanoparticles at 1 kHz. (h–j) Energy density of pure polymer and nanocomposites. Reproduced from ref. 107 with permission from the Royal Society of Chemistry. | ||
For 0D ceramic filler based polymer composites, a high volume fraction (>50 vol%) of nanoparticles is often necessary to achieve high relative permittivity, which is often at the expense of breakdown strength and mechanical flexibility of the composites. As a result, 1D ceramic fillers are found to be more attractive for the preparation of high performance polymer composites.260–262 1D fillers achieve percolation more easily, leading to a higher relative permittivity and thermal conductivity. Their lower surface area compared with spherical nanoparticles is also beneficial for preventing filler agglomeration and the large dipole moment of 1D fillers facilitates the dielectric enhancement of polymer composites at a lower loading compared to 0D fillers.2 Following this strategy, a number of 1D ceramic fillers, such as TiO2,260 BaTiO3,263 PZT,264 CaCu3Ti4O12,265 0.5Ba(Zr0.2Ti0.8)O3–0.5(Ba0.7Ca0.3)TiO3,118 SrTiO3 nanofibers,266 have been used to fabricate high performance nanocomposites. For example, Shen and Nan et al. prepared BaTiO3@TiO2 nanofibers where BaTiO3 nanoparticles were embedded in TiO2 nanofibers using a modified electrospinning process.141,207 After dopamine modification, the nanofibers were incorporated into the PVDF and P(VDF–HFP) polymer matrix, respectively. In these systems, in addition to the nanofiber/polymer interfaces, further interfaces between the BaTiO3 and TiO2 were introduced into the nanocomposites without increasing the total volume fraction of nanofibers. Percolation of the BaTiO3/TiO2 interfaces gave rise to enhanced interfacial polarization of the BaTiO3@TiO2, leading to substantially increased relative permittivity of the nanocomposites at a low volume fraction of nanofibers. An improved breakdown strength was also achieved by taking advantages of the large aspect ratio of the nanofibers and dopamine modification, which resulted in an ultrahigh energy density. The dopamine coated BaTiO3@TiO2/PVDF nanocomposites with 3 vol% nanofibers showed a high breakdown strength of 646 kV mm−1 and energy density of ∼20 J cm−3. For BaTiO3@TiO2/P(VDF–HFP) nanocomposites with 3 vol% nanofibers, the breakdown strength was ∼797.7 kV mm−1 and energy density reached ∼31.2 J cm−3. Importantly, a high discharge efficiency of ∼78% was also achieved at a high electric field of ∼800 kV mm−1.
2D ceramic fillers have also been introduced into the polymer matrix and proven to be effective in improving the energy density due to their ultrahigh specific surface area and superior mechanical flexibility, such as BNNs,71,267 (Na0.5Bi0.5)0.93Ba0.07TiO3,78 NaNbO3,172 TiO2,268 Bi2Te3,89,90 and (Ba0.6Sr0.4)TiO3 plate-like particles.269 The high aspect ratio 2D fillers also build up efficient conduction barriers that limit charge migration toward the electrodes and hinder the growth of electric trees during breakdown, resulting in an enhanced breakdown strength. As shown in Fig. 35a and b, the BNNs were homogeneously dispersed in the polymer matrix without chemical surface modification, which was attributed to the polar surface of the BNNs with a large specific surface area. A uniform and dense insulating network of BNNs was formed in the polymer matrix, creating a robust scaffold to hinder the onset of electromechanical failure and functioning as an efficient barrier against the leakage current and the space-charge conduction. With the addition of BNNs, the Weibull Eb value was greatly improved and reached the highest value of 610 kV mm−1 at a filler content of 12 wt%, which increased by 70% compared with the pristine terpolymer. The value of shape parameter β, which is the Weibull modulus associated with the linear regressive fit of the distribution and indicate the concentration of data distribution,270 also increased from 8.44 in pristine terpolymer to 15.8. A further increase of BNNs content would degrade performance due to aggregation of BNNs. The suppressed conduction loss also leaded to the reduction in remnant displacement. Moreover, the BNNs were thought to serve as nucleating agents to promote the population density of the nucleation centers for PVDF crystallization and result in increased crystallinity and decreased crystal size of polymer in the nanocomposites, which facilitated the reversal of dipoles within ferroelectric crystalline domains and thereby decreased the hysteresis loss. As a result, a high discharged energy density of 20.3 J cm−3 and efficiency of ∼80% was achieved in polymer composites with 12 wt% BNNs at 650 kV mm−1. Importantly, the polymer composites exhibited considerably improved thermal conductivity with the addition of BNNs, beneficial for the breakdown stability and lifetime of polymer capacitors. Similarly, Wen and Guo et al.268 obtained thin flexible PVDF based nanocomposites with a high energy density (21.1 J cm−3) by adding 1 wt% 2D monolayer titania. The nanocomposites showed enhanced relative permittivity of εr ∼ 12 at 1 kHz and a breakdown strength of 650 kV mm−1 compared with pure PVDF (εr ∼ 10.5 at 500 kV mm−1).
 | ||
| Fig. 35 (a) Large-scale and (b) zoom-in cross-section SEM images of the BNNs/P(VDF–TrFE–CFE) polymer composites with 12 wt% BNNs. (c) Weibull breakdown strength and shape parameter as a function of filler content. (d) Comparison of dielectric displacement-electric field (D–E) loops of pristine P(VDF–TrFE–CFE) and polymer composites with different filler contents at an electric field of 300 kV mm−1. Insert: Remnant displacement as a function of filler content. (e) Comparison of discharged energy density and charge–discharge efficiency of pristine P(VDF–TrFE–CFE) and polymer composites with 12 wt% BNNs at different electric fields. (f) Thermal conductivity of polymer composites with different filler contents. Reproduced from ref. 267 with permission from The Royal Society of Chemistry. | ||
5.2 Orientation of the fillers
In addition to the filler morphology and filler volume fraction, the filler orientation relative to the applied electric field also plays an important role in achieving high performance of polymer composites, as highlighted by the finite element simulation and phase field simulation discussions (Sections 4.3 and 4.4). Tang and Sodano et al.264,271 experimentally investigated the effects of aspect ratio of PZT nanowires and their alignment in the PVDF matrix on the dielectric and energy storage performance of polymer composites. It was demonstrated that polymer composites with nanowires aligned in the axis of the electric field have higher relative permittivity than that with randomly dispersed nanowires while maintaining the breakdown strength. The alignment of the nanowires led to energy densities up to 51.6% greater than polymer composites with random alignment at 20% volume fraction.It has been accepted that ceramic nanowires aligned perpendicular to the electric field in a polymer matrix benefits the enhancement of breakdown strength, while the ceramic nanowires aligned in the axis of the electric field can induce large electric polarization, as indicated in Fig. 31. Recently, Xie and Jiang et al.272 fabricated P(VDF–CTFE) based nanocomposites with BaTiO3 nanowires aligned perpendicular to the applied electric field BaTiO3 nanowires⊥E, denoted as X–Y-aligned nanocomposites) and aligned in the direction of the applied electric field (BaTiO3 nanowires ‖E, denoted as Z-aligned nanocomposite), as shown in Fig. 36a and c. The nanocomposites under two different orientations with 3 vol% BaTiO3 nanowires showed distinct electrical properties. The relative permittivity and electrical conductivity of the Z-aligned nanocomposite are higher than those of the X–Y-aligned nanocomposite. The difference of relative permittivity due to filler orientation can be explained by the effective medium theory,273 which indicated that the effective relative permittivity of the Z-aligned nanocomposite is larger than that of the X–Y-aligned nanocomposite. However, the breakdown strength of X–Y-aligned nanocomposite was higher than that of pristine P(VDF–CTFE), because the BaTiO3 nanowires⊥E led to increased path tortuosity in the electrical treeing process during breakdown; this also has agreement with Modelling of Fig. 31b. However, the Z-aligned nanocomposite exhibited a reduced breakdown strength, which was attributed to that of the BaTiO3 nanowires‖E increased the path connection in the electrical treeing process during breakdown; as is also in agreement with the model in Fig. 28. In terms of the D–E loops, the Z-aligned nanocomposite has larger Dmax and (Dmax–Pr) values even at a lower electric field. The larger polarization achieved by BaTiO3 nanowires‖E and large relative permittivity were responsible for the enhanced dielectric displacement. As a result, the highest discharged density of 10.8 J cm−3 and efficiency of 61.4% were obtained in the Z-aligned nanocomposite at a lower electric field of 240 kV mm−1.
 | ||
| Fig. 36 Cross-sectional SEM images of the (a) X–Y-aligned and (b) Z-aligned nanocomposites. (c) Schematic of the poling mechanism for BaTiO3 nanowires under different orientations. (d) The relative permittivity, (e) electrical conductivity, (f) breakdown strength, (g) D–E loops, (h) discharge energy density and (i) charge–discharge efficiency for the pure P(VDF–CTFE) and nanocomposites under different orientations. Reproduced from ref. 272 with permission from The Royal Society of Chemistry. | ||
The application of a nanowire array was also an effective way to achieve the alignment of nanowires in polymer composites and obtain enhanced dielectric and energy storage performance. Zhang and Luo et al.274,275 successfully synthesized titanium dioxide/lead zirconate titanate (TiO2–PZT) nanowire arrays by a simple two-step method, and demonstrated their ability to achieve high discharge energy density in P(VDF–TrFE–CTFE) based polymer composites under low operating voltage applications, as shown in Fig. 37. The orientation and density of nanowire arrays were important for the enhancement of dielectric properties and dielectric displacement. Nanowire array-1 to array-3 correspond to an intensified density of the nanowire array in polymer composites. The polymer composite with nanowire array-3 possessed the highest relative permittivity, breakdown strength, and dielectric displacement. As a result, a high discharge energy density of 6.9 J cm−3 was achieved at a low electric field of 143 kV mm−1, which was attributed to the high relative permittivity of εr ∼ 218.9 at 1 kHz and high polarization of 23.35 μC cm−2 at this electric field. The enhancement of relative permittivity and polarization was attributed to the different components of the composite and the interfaces between them. PZT has a high relative permittivity of εr ∼ 1800 and the P(VDF–TrFE–CTFE) also has a relatively high relative permittivity of εr ∼ 40.276 The system consists of two large interfacial regions, namely the TiO2/PZT and PZT/P(VDF–TrFE–CTFE) interfaces. Interfacial polarizations also contribute to the enhanced relative permittivity of the system, as discussed in Sections 4.1 and 4.2, and the discharge energy density obtained in this work is the highest known for a ceramic/polymer nanocomposite at such a low electric field. The filler orientation along the applied electric field direction therefore provides a promising strategy for high-energy density capacitors at a low operating voltage.
5.3 Structural design
As discussed in Sections 2–4, the use of fillers with core–shell or hierarchical structures help to improve interfacial interaction, compatibility, dispersion, breakdown strength, and interfacial polarization.277,278 For example, Su and Yang et al.278 successfully synthesized BaTiO3@sheet-like TiO2 core–shell nanoparticles with hierarchical interfaces, as shown in Fig. 38. The PVDF based nanocomposites with 2.5 vol% BaTiO3@ sheet-like TiO2 possessed a higher electric displacement (6.0 μm cm−2) compared to that with 2.5 vol% BaTiO3 (5.1 μm cm−2) at 350 kV mm−1, this was ascribed to the hierarchical interfacial polarization induced by the large surface area of the TiO2 sheet assembled on BaTiO3 nanoparticles in the nanocomposites. Moreover, an enhanced breakdown strength of 490 kV mm−1 was also achieved in 2.5 vol% BaTiO3@TiO2/PVDF nanocomposites compared to that of the 2.5 vol% BaTiO3/PVDF nanocomposites (350 kV mm−1). As a result, the energy storage density of the nanocomposites with 2.5 vol% BaTiO3@TiO2 nanoparticles attained 17.6 J cm−3. | ||
| Fig. 38 (a) Frequency-dependent relative permittivity, (b) dielectric loss, (c) observed energy density of PVDF based nanocomposites embedded with BaTiO3@TiO2, BaTiO3 nanoparticles and pure PVDF. (d) TEM image of BaTiO3@TiO2 nanoparticles and schematic of the origin of the ultrahigh energy density for BaTiO3@TiO2/PVDF nanocomposite. Reprinted with permission from ref. 278. Copyright (2016) American Chemical Society. | ||
In terms of composite structures, sandwich or multi-layer structures have been shown to maintain a high dielectric strength.279,280 Specifically, a layer with a higher breakdown strength, such as a pure polymer or a composite with a small amount of filler, is introduced into the multi-layer structured polymer composites which can improve the overall breakdown strength. The remaining nanocomposite layers contain a larger amount of fillers, which are beneficial in enhancing the electric displacement, as discussed in Section 2.4. Wang et al.167 designed a sandwich-structured nanocomposite where the interfacial regions of the structure block the growth of electrical trees, thus enhancing the breakdown strength and energy density. In this structure, 1 vol% BaTiO3 nanoparticles was introduced into the central layer (polymer matrix: PVDF) as the “hard layer” to ensure a high effective breakdown strength. The outer layers were based on 10–50 vol% BaTiO3 nanoparticles/PVDF nanocomposites as “soft layers” to provide a high relative permittivity. The highest breakdown strength of 470 kV mm−1 and energy density of 18.8 J cm−3 were obtained when the BaTiO3 loading in the soft layers was 20 vol%. Recently, a newly designed sandwich-structured BaTiO3 nanoparticle/P(VDF–HFP) nanocomposite was presented where a high content of BaTiO3 was introduced into the central layer to provide a high relative permittivity, while the two outer layers contained small amounts of BaTiO3 to provide a favorable breakdown strength, as shown in Fig. 39a.281 The nanocomposites with 9 wt% BaTiO3 in the central layer and 1 wt% BaTiO3 in the outer layers (abbreviated as 1-9-1) exhibited an ultra-high discharged energy density of 26.4 J cm−3 and a superior discharged efficiency of 72% at 526 kV mm−1, which were the highest values achieved in sandwich-structured nanocomposites. Importantly, the performance of sandwich-structured nanocomposites 1-9-1 were better than sandwich-structured nanocomposites 9-1-9, pure P(VDF–HFP) and a single layer nanocomposite with 5 wt% BaTiO3 nanoparticles, as shown in Fig. 39b–d, which indicated that the structure and filler contents of nanocomposites have a significant influence on their properties.
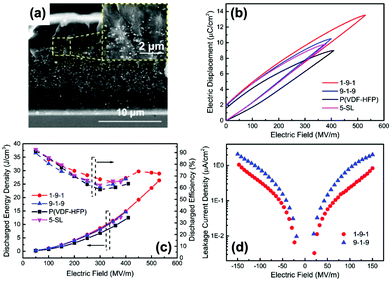 | ||
| Fig. 39 (a) Cross-section SEM image of sandwich-structured BaTiO3 nanoparticles/P(VDF–HFP) nanocomposites 1-9-1. Inset: SEM image of the interface between adjacent layers, scale bar 2 μm. (b) D–E loops, (c) discharged energy density and discharged efficiency of nanocomposites 1-9-1, 9-1-9, pure P(VDF–HFP), and single layer nanocomposite with 5 wt% BaTiO3 nanoparticles. (d) Leakage current density-electric field curves of nanocomposites 1-9-1 and 9-1-9. Reprinted from ref. 281, Copyright (2018), with permission from Elsevier. | ||
1D or 2D fillers have also been intensively employed in sandwich- and multi-layer structured nanocomposites. Shen and Nan et al.162 successfully prepared sandwich structured nanocomposites consisting of a central BaTiO3 nanofiber/PVDF nanocomposite layer and two outer layers based on BaTiO3 nanoparticles/PVDF nanocomposites. In the central layer, the BaTiO3 nanofibers were in the preferred orientations of being perpendicular to the applied electric field direction. The sandwich structured nanocomposites with 2 vol% BaTiO3 nanofibers loaded in the central layer (thickness of 3–4 μm) and 10 vol% BaTiO3 nanoparticles loaded in the outer layers (thickness of 5–6 μm) achieved the highest breakdown strength of 453 kV mm−1 and thereby the highest discharged energy density of 9.72 J cm−3, in comparison with pure PVDF (258 kV mm−1, 3.70 J cm−3), 10 vol% BaTiO3 nanoparticles/PVDF single layer nanocomposite (228 kV mm−1, 4.23 J cm−3) and 2 vol% BaTiO3 nanofibers/PVDF single layer nanocomposite (347 kV mm−1, 5.86 J cm−3). Subsequently, they fabricated sandwich-structured nanocomposites with a GO–TiO2/PVDF central layer and Ba0.6Sr0.4TiO3 nanofibers/PVDF out layers.282 The thickness of each layer was ∼5 μm and the GO–TiO2 indicates that the graphene oxide nanosheets were coated by TiO2 nanoparticles. A high energy density of 14.6 J cm−3 was achieved at an electric field of 450 kV mm−1 in the sandwich-structured nanocomposites with 10 wt% GO–TiO2 loading in the central layer and 3 vol% Ba0.6Sr0.4TiO3 nanofibers loading in the outer layers. Jiang and Zhang et al.78 utilized 2D (Na0.5Bi0.5)0.93Ba0.07TiO3 (NBBT) platelets with a size of up to 5 μm and a thickness of 0.2–0.5 μm to fabricate single layered, sandwich-structured and multi-layered NBBT@PVP/P(VDF–HFP) nanocomposites. The results indicated that five-layered nanocomposites containing three central hard layers (1 vol% NBBT loading) and neighbouring soft layers (30 vol% NBBT) showed a maximum energy storage density of 14.95 J cm−3 at 258 kV mm−1. The energy efficiency remained 0.9 at 200 kV mm−1.
Furthermore, modulation of the nanostructure of polymer composites in three dimensions has been developed in recent years to achieve a high performance. As an example, Zhang and Shen et al.258,283 proposed a nonequilibrium processing method that combined electrospinning, hot-pressing and thermal etching. They fabricated several 10-layer nanocomposite films by collecting through a layer-by-layer process and simultaneously tuning the concentration and orientation of BaTiO3 nanofillers in each layer, including the nanocomposites with small-large-small and large-small-large BaTiO3 nanoparticles composition gradients (respectively denoted as sphere-SLS and sphere-LSL), as well as the nanocomposites with parallel and orthotropic oriented BaTiO3 nanofibers (respectively denoted as fiber-parallel and fiber-orthotropic). For comparison, nanocomposites with randomly distributed BaTiO3 nanospheres and nanofibers were also prepared (denoted as sphere-random and fiber-random), as shown in Fig. 40a. The out-of-plane Young's modulus and characteristic breakdown strength are shown in Fig. 40b and c, along with the shape parameter of the different nanocomposites. As can be seen, the introduction of BaTiO3 nanofillers can provide an improved Young's modulus compared with the pure polymer matrix. In terms of breakdown strength, only the sphere-SLS, fiber-parallel and fiber-orthotropic configurations show a higher breakdown strength compared to the polymer. Moreover, the sphere-random nanocomposites exhibited the lowest breakdown strength while the fiber-orthotropic nanocomposites showed highest breakdown strength. The enhancement of breakdown strength was attributed to the fibers impeding the propagation of breakdown paths along the out-of-plane directions and a substantial widening of breakdown paths. This was proven by a phase-field model, which simulated the initiation and real-time evolution of the electrical treeing process under an electric field along the out-of-plane direction of nanocomposite films. The relative permittivity of the nanocomposites showed an improvement compared with the pure polymer matrix, but the difference between the nanocomposite types was slight, as shown in Fig. 40d and e. Therefore the breakdown strength dominated the energy storage performance. As a result, the fiber-orthotropic nanocomposite delivered the highest energy density of 25.5 J cm−3 at 690 kV mm−1 with a discharged efficiency of 76.3%, which is an enhancement of 45.8% over that of the pure polymer (≈17.8 J cm−3 at 640 kV mm−1), as shown in Fig. 40e.
 | ||
| Fig. 40 (a) Schematic and cross-sectional SEM images of P(VDF–HFP)/BaTiO3 nanocomposites with configurations of sphere-SLS, sphere-LSL, sphere-random, fiber-parallel, fiber-orthotropic and fiber-random. (b) The out-of-plane Young's modulus, (c) characteristic breakdown strength as well as shape parameter, (d) dielectric and (e) energy storage properties of different nanocomposites. With permission from ref. 258. Copyright 2018, John Wiley and Sons. | ||
6. Summary and outlook
The state-of-the-art designs of interfaces in polymer based dielectric nanocomposites for energy storage applications have been overviewed. A wide range of interface structures have been investigated; these include the creation of core–shell structures that use (i) organic shells to improve the dispersion and compatibility with the polymeric matrix, (ii) dielectric inorganic ceramic shells to reduce electric field concentrations and mitigate the permittivity contrast between the filler and matrix; and (iii) inorganic conductive shells in an attempt to exploit the high permittivity of the system near percolation. In addition to single-phase shells, the building of hierarchical and controlled gradient structures have also been examined for multi-scale control of properties. Sandwich and multi-layer architectures have been considered to tailor the electric field distribution in layers of different relative permittivity and thereby influence the breakdown field. The influence of the morphology of additives on the interface such as filler dimension, aspect ratio, orientation with respect to applied electric field and volume fraction has been described. The impact of such interface structures on composite polarization and the energy storage capability have been discussed, along with an overview of existing models to understand the polarization mechanism and quantitatively assess the potential benefits for energy storage applications.A detailed comparison of composites based on a variety of components, modifiers, performance and their benefits/limitations are summarized in Table 5. In summary, ceramic/polymer nanocomposites are potential dielectrics to obtain high performance, such as improved permittivity, high breakdown strength, high energy density, low density and flexibility. With regards to the use of a ceramic filler, ferroelectric ceramics with high permittivity, such as BaTiO3 and (Ba,Sr)TiO3 are typical choices. One-dimensional structured fillers, such as BaTiO3 nanowires, with high aspect ratio is an attractive filler since introducing a low loading level (e.g. <10 vol%) of such one-dimensional structured fillers can allow the nanocomposites to obtain a high relative permittivity and maintain a high breakdown strength. Any fillers dispersed in a polymer matrix should be modified using organic materials before being incorporated into the polymer matrix, and the fluorine–polymer is an excellent modifier to improve the surface properties of the fillers, and living polymerization methods including ATRP and RAFT can obtain dense and tailored shell layers. The thicknesses and electric conductivity of the shell layers play an important role in determining the performance of the nanocomposites. Rigid polymers, such as liquid crystal polymers can be utilized to accurately control the thicknesses of the shell layers and a low electrical conductivity is needed to obtain a high breakdown strength. Generally, optimized hierarchically layered composites, such as sandwich/multilayer structures is a feasible method to balance the paradox between high permittivity and high breakdown strength in single-layered composites and their performance can be controlled by varying the interface, chemical structure and ratios of the constituent layers.
| Ceramic | Polymer matrix | Modifier | Modifier thickness (nm) | Molecular weight of modifier | Permittivity (at 1 kHz) | Breakdown strength (kV mm−1) | Discharged energy density (J cm−3) | Benefits | Limitations | Ref. |
|---|---|---|---|---|---|---|---|---|---|---|
| BaTiO3 | P(VDF–HFP) | Phosphonic acid | — | — | 32 (50 vol%) | ∼215 | 3.2 | Effectively improve dispersion using simple process | Improved dielectric loss and leakage current from residual modifiers | 76 |
| BaTiO3 | PVDF | Carboxylic acids | — | — | 28 (50 vol% F4CBT-1) | ∼325 | 9.89 | Permittivity of the nanocomposite can be adjusted by varying the coverage level of the modifiers | Modifiers do not form strong interaction with the fillers | 96 |
| BaTiO3 | PVA | Gallic acid (GA) | 1.6 | — | 51 (40%BT@ GA) | 144 | 0.554 (at 50 kV mm−1) | Well-dispersed nanocomposites by strengthened interfacial interaction | Limited breakdown strength and energy density due to the residual modifier (GA) | 97 |
| BaTiO3 | PVDF | Titanate coupling agent | 2–3 | — | ∼11.3 (4 vol% mBT-2) | 517 | 11.27 | Breakdown strength of nanocomposites was enhanced by the improved compatibility between BT nanoparticles and PVDF matrix | The shell layer is not dense and designable | 99 |
| BaTiO3 | PVDF | PVP | — | — | ∼14 (10 vol%) | 336 | 6.8 | Dielectric permittivity of the nanocomposites was enhanced by a simple surface treatment | Limited breakdown strength and energy density due to the residual modifiers PVP | 100 |
| BaTiO3 | P(VDF–HFP) | Hydantoin epoxy | 2–3 | — | ∼49.5 (50 vol%) | ∼187 | 7.9 (calculated value) | Environmental-friendly modifier with simple process | Limited breakdown strength and energy density due to the residual modifiers | 104 |
| BaTiO3 | (P(VDF–TrFE–CTFE)) | (PTFMPCS) | 11 ± 1 |
M
n = 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 800 |
∼55 (5 vol%) | 514 | 16.18 | Thickness of shell layer can be controlled, with large effect on the performance of nanocomposites | Mismatch between the designed theoretical and practical values of shell thicknesses due to the polydispersity of modifiers | 107 |
| BaTiO3 | PMMA | PMMA | 10 | — | 14.6 (76.88 wt%) | — | — | Composites with low dielectric loss due to the dense shell layer with low dielectric loss | Limited permittivity of the nanocomposite due to the low permittivity of PMMA matrix | 110 |
| BaTiO3 | P(VDF–TrFE–CFE) | Hyperbranched aromatic polyamide (HBP) | — | — | 1484.5 (40 vol%) | 17.1 | — | Super-high permittivity due to enhanced interfacial polarization from the hyperbranched aromatic polyamide modifier | Limited energy density due to the low breakdown strength | 111 |
| BaTiO3 | HBP@PMMA | HBP@PMMA | ∼15 | — | 39.3 (56.7 wt%) | — | — | Enhanced permittivity by the double-shell modifier, which also acted as the matrix | Limited energy density due to the HBP@PMMA matrix | 83 |
| BaTiO3 | P(VDF–HFP) | PTFEA | 2–3 | M n = 4100 | ∼45 (50 vol%) | — | — | Improved dispersion and compatibility of BaTiO3 nanoparticles in P(VDF–HFP) matrix by the dense and controllable shell layer | Modifier layer has limited effect on the permittivity of composites | 86 |
| BaTiO3 | Polystyrene | Polystyrene | 7 | — | 24.51 (47.69 vol%) | — | — | Low dielectric loss and controllable by design of shell layer thickness | Low permittivity of the PS shell is not beneficial for enhancement of the nanocomposites | 112 |
| SrTiO3 | PVDF | PVP | 7 | Mw = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 300![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
∼10 (2.5 vol%) | 380 | 6.8 | Improved dispersion and compatibility of SrTiO3 nanofibers in PVDF matrix | Limited energy density by the existing residual modifier PVP | 113 |
| BaTiO3 | P(VDF–HFP) | Fluoro-polydopamine | ∼10 | — | ∼14 (5 vol%) | 480 | 12.87 | Prevention of nanofiller agglomeration in the polymer matrix is more effective than dopamine functionalization | Existing residual fluoro-polydopamine in the nanocomposite due to the weak bonding force | 114 |
| Ba0.8Sr0.2TiO3 | PVDF | Ethylenediamine | — | — | ∼17.5 (7.5 vol%) | 450 | 14.86 | High energy density by the functionalized high aspect ratio Ba0.8Sr0.2TiO3 nanowires | Residual ethylenediamine will increase dielectric loss of the nanocomposites and it is not beneficial for obtaining high energy efficiency | 115 |
| BaTiO3 | P(VDF–TrFE–CFE) | Ethylenediamine | — | — | 69.5 (17.5 vol%) | 300 | 10.48 | Improved dispersion and compatibility of BaTiO3 nanofibers | Relatively low breakdown strength and limited energy density by residual ethylenediamine and ternary-PVDF matrix | 116 |
| SrTiO3 | PVDF | Polydopamine | ∼10 | — | ∼13 (5 vol%) | 360 | 9.12 | Improved the dispersion and compatibility of SrTiO3 nanofibers | Relatively low breakdown strength and limited energy density due to residual dopamine | 117 |
| 0.5Ba(Zr0.2Ti0.8)O3–0.5(Ba0.7Ca0.3)TiO3 | PVDF | Polydopamine | — | — | ∼12 (3 vol%) | 310 | 7.87 | Improved dispersivity and compatibility between BZT–BCT nanofibers and PVDF matrix | Decreased breakdown strength and energy density with the increase of filler loading by the residual modifiers | 118 |
| Ba0.6Sr0.4TiO3 | PVDF | –OH | — | — | ∼12 (2.5 vol%) | 398 | 6.4 | Simple process to achieve enhanced breakdown strength and energy density | Cannot form a dense shell layer, therefore enhancement of energy density is limited | 119 |
| BaTiO3 | P(VDF–HFP) | (PMPCS) | 33.3 |
M
n = 65![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
22.5 (7.5 vol%) | 300 | 7.5 | Dense and controllable shell layer | Enhanced interfacial polarization, relatively low energy density | 124 |
| Na2Ti3O7 | P(VDF–HFP) | PMPCS | 25 ± 1.5 |
M
n = 60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 200 |
69.6 (7.5 vol%) | — | — | Improvement in permittivity by the controllable shell layers thicknesses | High dielectric loss by the Na2Ti3O7 fillers with high conductivity, enhanced interfacial polarization, limitation to energy storage | 125 |
| BaTiO3/graphene | P(VDF–HFP) | Polydopamine | 1–2 | — | 66.2 (10 vol% BaTiO3 + 1.2 vol graphene) | 40 | — | High permittivity and low dielectric loss with conductive filler | Low breakdown strength and limitation of energy storage | 127 |
| Boron nitride | PVDF | Hydroxyl groups | 5.1 | — | 11.1 (6 wt%) | 517 | 13.1 | Simple process to achieve enhanced breakdown strength and energy density | Cannot form a dense shell layer to effectively improve the dispersivity | 71 |
In terms of simulation tools, finite element and phase field approaches are effective methods to theoretically describe the electric field distribution and the breakdown process in the layered composites. In addition, the oriented distribution of the fillers in polymer matrix exhibit the advantages of being able to achieve high performance, such as high breakdown strength and energy density when the aligned fillers are perpendicular to the direction of electric field; the permittivity and polarization can be enhanced when the aligned fillers are parallel to the direction of electric field.
Based on the review, a number of points can be highlighted for future research avenues on interfacial design for energy storage;
(i) The introduction of a filler of high electrical conductivity or high permittivity into a low permittivity polymer leads to electric field concentrations, in particular around the filler. While this leads to an increased relative permittivity, it also acts to increase the probability of dielectric breakdown. This technical challenge can be tackled by the fabrication of sandwich structures, but further work is required to understand the mechanisms for their intriguing properties.
(ii) Models often consider either single particle and the influence of charge transport and mobility in the composites, or the distribution of electric field in the composite structure. It would be of interest to combine such approaches to develop a unified model that considers such aspects. There is a need to examine whether an enhanced polarization at an interface, which enhances relative permittivity, is also likely to lead to dielectric breakdown.
(iii) Greater experimental characterization of the dielectric properties and phase structure of the filler–polymer interface, this can also inform modelling studies.
(iv) The impact of nanofillers on the crystallisation behaviour of the matrix and enhancing the properties of the interface and matrix is of interest; further work would be of interest to explore the mechanical and dielectric properties of such interfacial regions to understand the composite properties and also inform modelling studies.
(v) The use of rigid polymers is an interesting approach, such as the use of liquid crystalline polymer to design the interface and interfacial layer thickness in a wide range of nanostructured composites for applications related to energy storage.
(vi) A high breakdown strength is extremely important for achieving a high energy density. Electric breakdown often occurs in composites with high leakage current and accumulated heat. It is of interest to further develop simulation methods, such as phase field simulations, to explore the breakdown mechanisms in such composites. Models that takes into account both the electric field concentrations, which initiates breakdown, and the subsequent breakdown path would provide a more detailed of the impact of composite architecture of dielectric strength and failure.
(vii) There is a need for the development of high-permittivity dielectric materials and high energy storage capacitors applied over a wide temperature range to meet the challenges and limitations of electronic devices with high-temperature working requirements; this can involve the use of high thermal stability polymers which brings new challenges in dielectric loss and conductivity.
(viii) Specific examples of demonstrator energy storage devices and systems related to the polymer nanocomposite dielectrics and their application is worthy of considering in future work in order to truly demonstrate the potential of these complex materials; for example applications related to Fig. 1.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
Dr H. Luo would like to acknowledge the funding from Hunan Natural Science Foundation (2019JJ40349), China Postdoctoral Science Foundation (2017M620353), Special Funding for the Postdoctoral Science Fund of China (2018T110840), and State Key Laboratory of Powder Metallurgy, Central South University, Changsha, China; Prof. D. Zhang would like to acknowledge the funding from National Natural Science Foundation of China (51672311), Science and Technology Project of Hunan Province, China (2016WK2022).References
- S. Luo, J. Yu, S. Yu, R. Sun, L. Cao, W.-H. Liao and C.-P. Wong, Adv. Energy Mater., 2019, 9, 1803204 CrossRef.
- X. Huang, B. Sun, Y. Zhu, S. Li and P. Jiang, Prog. Mater. Sci., 2019, 100, 187–225 CrossRef CAS.
- Y. Qiao, X. Yin, T. Zhu, H. Li and C. Tang, Prog. Mater. Sci., 2018, 80, 153–162 CAS.
- Z. Pan, L. Yao, J. Zhai, X. Yao and H. Chen, Adv. Mater., 2018, 30, 1705662 CrossRef PubMed.
- Q. Li, L. Chen, M. R. Gadinski, S. Zhang, G. Zhang, H. Li, A. Haque, L.-Q. Chen, T. N. Jackson and Q. Wang, Nature, 2015, 523, 576–579 CrossRef CAS PubMed.
- Y. Yang, J. He, Q. Li, L. Gao, J. Hu, R. Zeng, J. Qin, S. X. Wang and Q. Wang, Nat. Nanotechnol., 2019, 14, 151–155 CrossRef CAS PubMed.
- Prateek, V. K. Thakur and R. K. Gupta, Chem. Rev., 2016, 116, 4260–4317 CrossRef CAS PubMed.
- Q. Chen, Y. Shen, S. Zhang and Q. M. Zhang, Annu. Rev. Mater. Res., 2015, 45, 433–458 CrossRef CAS.
- Z.-M. Dang, M.-S. Zheng and J.-W. Zha, Small, 2016, 12, 1688–1701 CrossRef CAS PubMed.
- J. S. Ho and S. G. Greenbaum, ACS Appl. Mater. Interfaces, 2018, 10, 29189–29218 CrossRef CAS PubMed.
- X. Hu, K. Yi, J. Liu and B. Chu, Energy Technol., 2018, 6, 849–864 CrossRef CAS.
- L. Yang, X. Kong, F. Li, H. Hao, Z. Cheng, H. Liu, J.-F. Li and S. Zhang, Prog. Mater. Sci., 2019, 102, 72–108 CrossRef CAS.
- J. R. Laghari and W. J. Sarjeant, IEEE Trans. Power Electron., 1992, 7, 251–257 CrossRef.
- H. Qi and R. Zuo, J. Mater. Chem. A, 2019, 7, 3971–3978 RSC.
- Q. Li, F.-Z. Yao, Y. Liu, G. Zhang, H. Wang and Q. Wang, Annu. Rev. Mater. Res., 2018, 48, 219–243 CrossRef CAS.
- Z. Yao, Z. Song, H. Hao, Z. Yu, M. Cao, S. Zhang, M. T. Lanagan and H. Liu, Adv. Mater., 2017, 29, 1601727 CrossRef PubMed.
- H. Kishi, Y. Mizuno and H. Chazono, Jpn. J. Appl. Phys., 2003, 42, 1–15 CrossRef CAS.
- H. Du, X. Lin, H. Zheng, B. Qu, Y. Huang and D. Chu, J. Alloys Compd., 2016, 663, 848–861 CrossRef CAS.
- B. Chu, X. Zhou, K. Ren, B. Neese, M. Lin, Q. Wang, F. Bauer and Q. M. Zhang, Science, 2006, 313, 334–336 CrossRef CAS PubMed.
- P. Khanchaitit, K. Han, M. R. Gadinski, Q. Li and Q. Wang, Nat. Commun., 2013, 4, 2845 CrossRef PubMed.
- Q. M. Zhang, H. Li, M. Poh, F. Xia, Z. Y. Cheng, H. Xu and C. Huang, Nature, 2002, 419, 284–287 CrossRef CAS PubMed.
- H. Li, F. Liu, B. Fan, D. Ai, Z. Peng and Q. Wang, Small Methods, 2018, 2, 1700399 CrossRef.
- S. Guan, H. Li, S. Zhao and L. Guo, Compos. Sci. Technol., 2018, 158, 79–85 CrossRef CAS.
- Y. Qiao, M. S. Islam, K. Han, E. Leonhardt, J. Zhang, Q. Wang, H. J. Ploehn and C. Tang, Adv. Funct. Mater., 2013, 23, 5638–5646 CrossRef CAS.
- X. Hao, J. Adv. Dielectr., 2013, 3, 1330001 CrossRef.
- M. S. Whittingham, MRS Bull., 2008, 33, 411–419 CrossRef CAS.
- D. Han, J. Zhang, Z. Weng, D. Kong, Y. Tao, F. Ding, D. Ruan and Q. H. Yang, Mater. Today Energy, 2019, 11, 30–45 CrossRef.
- H. Deng and Q. Fu, Macromol. Rapid Commun., 2017, 38, 1700444 CrossRef PubMed.
- J. Yuan, Chin. Chem. Lett., 2017, 28, 2036–2044 CrossRef CAS.
- Y. Wu, Z. Wang, X. Shen, X. Liu, N. M. Han, Q. Zheng, Y.-W. Ma and J.-K. Kim, ACS Appl. Mater. Interfaces, 2018, 10, 26641–26652 CrossRef CAS PubMed.
- J. Chen, Y. Wang, H. Li, H. Han, X. Liao, R. Sun, X. Huang and M. Xie, Chem. Mater., 2018, 30, 1102–1112 CrossRef CAS.
- Z. Liu, T. Lu, J. Ye, G. Wang, X. Dong, R. Withers and Y. Liu, Adv. Mater. Technol., 2018, 3, 1800111 CrossRef.
- C. Yang, H. Wei, L. Guan, J. Guo, Y. Wang, X. Yan, X. Zhang, S. Wei and Z. Guo, J. Mater. Chem. A, 2015, 3, 14929–14941 RSC.
- Z.-M. Dang, J.-K. Yuan, J.-W. Zha, T. Zhou, S.-T. Li and G.-H. Hu, Prog. Mater. Sci., 2012, 57, 660–723 CrossRef CAS.
- S. Cho, J. S. Lee and J. Jang, ACS Appl. Mater. Interfaces, 2015, 7, 9668–9681 CrossRef CAS PubMed.
- X. Zhang, B.-W. Li, L. Dong, H. Liu, W. Chen, Y. Shen and C.-W. Nan, Adv. Mater. Interfaces, 2018, 5, 1800096 CrossRef.
- Y. Zhang, C. Zhang, Y. Feng, T. Zhang, Q. Chen, Q. Chi, L. Liu, G. Li, Y. Cui, X. Wang, Z. Dang and Q. Lei, Nano Energy, 2019, 56, 138–150 CrossRef CAS.
- L. Wu, K. Wu, C. Lei, D. Liu, R. Du, F. Chen and Q. Fu, J. Mater. Chem. A, 2019, 7, 7664–7674 RSC.
- B. Zhao, M. Hamidinejad, C. Zhao, R. Li, S. Wang, Y. Kazemi and C. B. Park, J. Mater. Chem. A, 2019, 7, 133–140 RSC.
- X. Hao, Y. Wang, J. Yang, S. An and J. Xu, J. Appl. Phys., 2012, 112, 114111 CrossRef.
- B. Chu, M. Lin, B. Neese, X. Zhou, Q. Chen and Q. M. Zhang, Appl. Phys. Lett., 2007, 91, 122909 CrossRef.
- S. Li, S. Yu and Y. Feng, High Voltage, 2016, 1, 122–129 CrossRef.
- P. Martins, A. C. Lopes and S. Lanceros-Mendez, Prog. Mater. Sci., 2014, 39, 683–706 CAS.
- H. Tran Doan, S. Boggs, G. Teyssedre, C. Laurent, M. Cakmak, S. Kumar and R. Ramprasad, Prog. Mater. Sci., 2016, 83, 236–269 CrossRef.
- S. L. Zhong, Z. M. Dang, W. Y. Zhou and H. W. Cai, IET Nanodielectr., 2018, 1, 41–47 CrossRef.
- Z. M. Dang, J. K. Yuan, S. H. Yao and R. J. Liao, Adv. Mater., 2013, 25, 6334–6365 CrossRef CAS PubMed.
- L. Zhu, J. Phys. Chem. Lett., 2014, 5, 3677–3687 CrossRef CAS PubMed.
- B. Jiang, J. Iocozzia, L. Zhao, H. Zhang, Y.-W. Harn, Y. Chen and Z. Lin, Chem. Soc. Rev., 2019, 48, 1194–1228 RSC.
- E. Baer and L. Zhu, Macromolecules, 2017, 50, 2239–2256 CrossRef CAS.
- Y. Wang, J. Chen, Y. Li, Y. Niu, Q. Wang and H. Wang, J. Mater. Chem. A, 2019, 7, 2965–2980 RSC.
- H. Palneedi, M. Peddigari, G.-T. Hwang, D.-Y. Jeong and J. Ryu, Adv. Funct. Mater., 2018, 28, 1803665 CrossRef.
- K. B. N. Balasubramanian and T. Ramesh, Polym. Adv. Technol., 2018, 29, 1568–1585 CrossRef.
- M. H. Al-Saleh, Nanotechnology, 2019, 30, 062001 CrossRef CAS PubMed.
- U. O. Uyor, A. P. Popoola, O. Popoola and V. S. Aigbodion, Adv. Polym. Technol., 2018, 37, 2838–2858 CrossRef CAS.
- Y. Niu and H. Wang, ACS Appl. Nano Mater., 2019, 2, 627–642 CrossRef CAS.
- D. Q. Tan, Adv. Funct. Mater., 2019, 1808567 CrossRef.
- X. Huang and P. Jiang, Adv. Mater., 2015, 27, 546–554 CrossRef CAS PubMed.
- F. Caruso, Adv. Mater., 2001, 13, 11–22 CrossRef CAS.
- G. Cao, Nanostructures & Nanomaterials-Synthesis, Properties & Applications, Imperial College Press, 2004 Search PubMed.
- S. Ramakrishna, An Introduction to Electrospinning and Nanofibers, World Scientific Publishing Co. Pte. Ltd, 2005 Search PubMed.
- P. J. Burke, Nanotubes and Nanowires, World Scientific Publishing Co. Pte. Ltd., 2005 Search PubMed.
- X. Han, S. Chen, X. Lv, H. Luo, D. Zhang and C. R. Bowen, Phys. Chem. Chem. Phys., 2018, 20, 2826–2837 RSC.
- M. Lewin, A. Mey-Marom and R. Frank, Polym. Adv. Technol., 2005, 429–441 CrossRef CAS.
- W. Schaertl, Nanoscale, 2010, 2, 829–843 RSC.
- R. G. Chaudhuri and S. Paria, Chem. Rev., 2012, 112, 2373–2433 CrossRef PubMed.
- M. B. Gawande, A. Goswami, T. Asefa, H. Guo, A. V. Biradar, D.-L. Peng, R. Zboril and R. S. Varma, Chem. Soc. Rev., 2015, 44, 7540–7590 RSC.
- H. Heinz, C. Pramanik, O. Heinz, Y. Ding, R. K. Mishra, D. Marchon, R. J. Flatt, I. Estrela-Lopis, J. Llop, S. Moya and R. F. Ziolo, Surf. Sci. Rep., 2017, 72, 1–58 CrossRef CAS.
- W. Xu, G. Yang, L. Jin, J. Liu, Y. Zhang, Z. Zhang and Z. Jiang, ACS Appl. Mater. Interfaces, 2018, 10, 11233–11241 CrossRef CAS PubMed.
- Z. Li, F. Liu, G. Yang, H. Li, L. Dong, C. Xiong and Q. Wang, Compos. Sci. Technol., 2018, 164, 214–221 CrossRef CAS.
- H. Feng, X. Fang, X. Liu, Q. Pei, Z.-K. Cui, S. Deng, J. Gu and Q. Zhuang, Composites, Part A, 2018, 109, 578–584 CrossRef CAS.
- L. Wu, K. Wu, D. Liu, R. Huang, J. Huo, F. Chen and Q. Fu, J. Mater. Chem. A, 2018, 6, 7573–7584 RSC.
- H. Ye, T. Lu, C. Xu, M. Zhong and L. Xu, Nanotechnology, 2018, 29, 095702 CrossRef PubMed.
- Y. Song, Y. Shen, H. Liu, Y. Lin, M. Li and C.-W. Nan, J. Mater. Chem., 2012, 22, 8063–8068 RSC.
- H. Luo, C. Chen, K. Zhou, X. Zhou, Z. Wu and D. Zhang, RSC Adv., 2015, 5, 68515–68522 RSC.
- Z.-M. Dang, H.-Y. Wang and H.-P. Xu, Appl. Phys. Lett., 2006, 89, 112902 CrossRef.
- P. Kim, N. M. Doss, J. P. Tillotson, P. J. Hotchkiss, M.-J. Pan, S. R. Marder, J. Li, J. P. Calame and J. W. Perry, ACS Nano, 2009, 3, 2581–2592 CrossRef CAS PubMed.
- J. Li, J. Claude, L. E. Norena-Franco, S. Il Seok and Q. Wang, Chem. Mater., 2008, 20, 6304–6306 CrossRef CAS.
- C. Jiang, D. Zhang, K. Zhou, X. Zhou, H. Luo and I. Abrahams, J. Mater. Chem. A, 2016, 4, 18050–18059 RSC.
- D. Zhang, Z. Wu, X.-F. Zhou, A.-Q. Wei, C. Chen and H. Luo, Sens. Actuators, A, 2017, 260, 228–235 CrossRef CAS.
- H. Lee, S. M. Dellatore, W. M. Miller and P. B. Messersmith, Science, 2007, 318, 426–430 CrossRef CAS PubMed.
- Z.-M. Dang, T. Zhou, S.-H. Yao, J.-K. Yuan, J.-W. Zha, H.-T. Song, J.-Y. Li, Q. Chen, W.-T. Yang and J. Bai, Adv. Mater., 2009, 21, 2077–2082 CrossRef CAS.
- K. Yang, X. Huang, M. Zhu, L. Xie, T. Tanaka and P. Jiang, ACS Appl. Mater. Interfaces, 2014, 6, 1812–1822 CrossRef CAS PubMed.
- L. Xie, X. Huang, Y. Huang, K. Yang and P. Jiang, J. Phys. Chem. C, 2013, 117, 22525–22537 CrossRef CAS.
- K. Yang, X. Huang, L. Fang, J. He and P. Jiang, Nanoscale, 2014, 6, 14740–14753 RSC.
- P. Kim, S. C. Jones, P. J. Hotchkiss, J. N. Haddock, B. Kippelen, S. R. Marder and J. W. Perry, Adv. Mater., 2007, 19, 1001–1005 CrossRef CAS.
- K. Yang, X. Huang, Y. Huang, L. Xie and P. Jiang, Chem. Mater., 2013, 25, 2327–2338 CrossRef CAS.
- M. Rahimabady, M. S. Mirshekarloo, K. Yao and L. Lu, Phys. Chem. Chem. Phys., 2013, 15, 16242–16248 RSC.
- D. He, Y. Wang, X. Chen and Y. Deng, Composites, Part A, 2017, 93, 137–143 CrossRef CAS.
- J. Chen, X. Wang, X. Yu, L. Yao, Z. Duan, Y. Fan, Y. Jiang, Y. Zhou and Z. Pan, J. Mater. Chem. C, 2018, 6, 271–279 RSC.
- J. Chen, X. Wang, X. Yu, Y. Fan, Z. Duan, Y. Jiang, F. Yang and Y. Zhou, Appl. Surf. Sci., 2018, 447, 704–710 CrossRef CAS.
- K. Yu, Y. Niu, Y. Bai, Y. Zhou and H. Wang, Appl. Phys. Lett., 2013, 102, 102903 CrossRef.
- S. Liu, S. Xue, B. Shen and J. Zhai, Appl. Phys. Lett., 2015, 107, 032907 CrossRef.
- H. Tang, Z. Zhou, C. C. Bowland and H. A. Sodano, Nano Energy, 2015, 17, 302–307 CrossRef CAS.
- S. Liu, J. Wang, B. Shen, J. Zhai, H. Hao and L. Zhao, J. Alloys Compd., 2017, 696, 136–142 CrossRef CAS.
- K. Bi, M. Bi, Y. Hao, W. Luo, Z. Cai, X. Wang and Y. Huang, Nano Energy, 2018, 51, 513–523 CrossRef CAS.
- Y. Niu, F. Xiang, Y. Wang, J. Chen and H. Wang, Phys. Chem. Chem. Phys., 2018, 20, 6598–6605 RSC.
- Z.-H. Dai, T. Li, Y. Gao, J. Xu, Y. Weng, J. He and B.-H. Guo, Colloids Surf., A, 2018, 548, 179–190 CrossRef CAS.
- J. Fu, Y. Hou, M. Zheng, Q. Wei, M. Zhu and H. Yan, ACS Appl. Mater. Interfaces, 2015, 7, 24480–24491 CrossRef CAS PubMed.
- P. Hu, S. Gao, Y. Zhang, L. Zhang and C. Wang, Compos. Sci. Technol., 2018, 156, 109–116 CrossRef CAS.
- K. Yu, Y. Niu, Y. Zhou, Y. Bai and H. Wang, J. Am. Ceram. Soc., 2013, 96, 2519–2524 CrossRef CAS.
- Z. Wang, T. Wang, C. Wang, Y. Xiao, P. Jing, Y. Cui and Y. Pu, ACS Appl. Mater. Interfaces, 2017, 9, 29130–29139 CrossRef CAS PubMed.
- Z.-H. Dai, J.-R. Han, Y. Gao, J. Xu, J. He and B.-H. Guo, Colloids Surf., A, 2017, 529, 560–570 CrossRef CAS.
- L. Li, R. Feng, Y. Zhang and L. Dong, J. Mater. Chem. C, 2017, 5, 11403–11410 RSC.
- H. Luo, D. Zhang, C. Jiang, X. Yuan, C. Chen and K. Zhou, ACS Appl. Mater. Interfaces, 2015, 7, 8061–8069 CrossRef CAS PubMed.
- L. Xie, X. Huang, K. Yang, S. Li and P. Jiang, J. Mater. Chem. A, 2014, 2, 5244–5251 RSC.
- G. Zhang, Y. Li, S. Tang, R. D. Thompson and L. Zhu, ACS Appl. Mater. Interfaces, 2017, 9, 10106–10119 CrossRef CAS PubMed.
- S. Chen, X. Lv, X. Han, H. Luo, C. R. Bowen and D. Zhang, Polym. Chem., 2018, 9, 548–557 RSC.
- M. Li, X. Huang, C. Wu, H. Xu, P. Jiang and T. Tanaka, J. Mater. Chem., 2012, 22, 23477–23484 RSC.
- Y. Huang, X. Huang, L. S. Schadler, J. He and P. Jiang, ACS Appl. Mater. Interfaces, 2016, 8, 25496–25507 CrossRef CAS PubMed.
- L. Xie, X. Huang, C. Wu and P. Jiang, J. Mater. Chem., 2011, 21, 5897–5906 RSC.
- L. Xie, X. Huang, Y. Huang, K. Yang and P. Jiang, ACS Appl. Mater. Interfaces, 2013, 5, 1747–1756 CrossRef CAS PubMed.
- K. Yang, X. Huang, L. Xie, C. Wu, P. Jiang and T. Tanaka, Macromol. Rapid Commun., 2012, 33, 1921–1926 CrossRef CAS PubMed.
- S. Liu and J. Zhai, J. Mater. Chem. A, 2015, 3, 1511–1517 RSC.
- G. Wang, X. Huang and P. Jiang, ACS Appl. Mater. Interfaces, 2017, 9, 7547–7555 CrossRef CAS PubMed.
- H. Tang and H. A. Sodano, Nano Lett., 2013, 13, 1373–1379 CrossRef CAS PubMed.
- H. Tang, Y. Lin and H. A. Sodano, Adv. Energy Mater., 2013, 3, 451–456 CrossRef CAS.
- L. Yao, Z. Pan, J. Zhai, G. Zhang, Z. Liu and Y. Liu, Composites, Part A, 2018, 109, 48–54 CrossRef CAS.
- Q. Chi, T. Ma, Y. Zhang, Y. Cui, C. Zhang, J. Lin, X. Wang and Q. Lei, J. Mater. Chem. A, 2017, 5, 16757–16766 RSC.
- S. Liu, J. Zhai, J. Wang, S. Xue and W. Zhang, ACS Appl. Mater. Interfaces, 2014, 6, 1533–1540 CrossRef CAS PubMed.
- S. Liu, S. Xue, W. Zhang, J. Zhai and G. Chen, J. Mater. Chem. A, 2014, 2, 18040–18046 RSC.
- A. E. Daugaard, K. Jankova, J. M. R. Marin, J. Bogelund and S. Hvilsted, Eur. Polym. J., 2012, 48, 743–750 CrossRef CAS.
- H. Luo, Z. Wu, C. Chen, C. Ma, K. Zhou and D. Zhang, Composites, Part A, 2016, 86, 57–65 CrossRef CAS.
- Z. B. Pan, L. M. Yao, G. L. Ge, B. Shen and J. W. Zhai, J. Mater. Chem. A, 2018, 6, 14614–14622 RSC.
- D. Zhang, C. Ma, X. Zhou, S. Chen, H. Luo, C. R. Bowen and K. Zhou, J. Phys. Chem. C, 2017, 121, 20075–20083 CrossRef CAS.
- H. Luo, C. Ma, X. Zhou, S. Chen and D. Zhang, Macromolecules, 2017, 50, 5132–5137 CrossRef CAS.
- D. Wang, Y. Bao, J.-W. Zha, J. Zhao, Z.-M. Dang and G.-H. Hu, ACS Appl. Mater. Interfaces, 2012, 4, 6273–6279 CrossRef CAS PubMed.
- H. Luo, Z. Wu, X. Zhou, Z. Yan, K. Zhou and D. Zhang, Compos. Sci. Technol., 2018, 160, 237–244 CrossRef CAS.
- X. Zhi, Y. Mao, S. Wen, Y. Li, L. Zhang, T. W. Chan and L. Liu, Composites, Part A, 2015, 76, 194–202 CrossRef CAS.
- X. Fang, X. Liu, Z.-K. Cui, J. Qian, J. Pan, X. Li and Q. Zhuang, J. Mater. Chem. A, 2015, 3, 10005–10012 RSC.
- H. Feng, W. Ma, Z.-K. Cui, X. Liu, J. Gu, S. Lin and Q. Zhuang, J. Mater. Chem. A, 2017, 5, 8705–8713 RSC.
- Q. Huang, H. Luo, C. Chen, X. Zhou, K. Zhou and D. Zhang, J. Alloys Compd., 2016, 696, 1220–1227 CrossRef.
- M. Yang, H. Zhao, C. Hu, P. Haghi-Ashtiani, D. He, Z.-M. Dang and J. Bai, Phys. Chem. Chem. Phys., 2018, 20, 2777–2786 RSC.
- F. Liang, L. Zhang, W.-Z. Lu, Q.-X. Wan and G.-F. Fan, Appl. Phys. Lett., 2016, 108, 072902 CrossRef.
- Z. Li, L. A. Fredin, P. Tewari, S. A. DiBenedetto, M. T. Lanagan, M. A. Ratner and T. J. Marks, Chem. Mater., 2010, 22, 5154–5164 CrossRef CAS.
- C. Zhang, Q. Chi, J. Dong, Y. Cui, X. Wang, L. Liu and Q. Lei, Sci. Rep., 2016, 6, 33508 CrossRef PubMed.
- X. Huo, W. Li, J. Zhu, L. Li, Y. Li, L. Luo and Y. Zhu, J. Phys. Chem. C, 2015, 119, 25786–25791 CrossRef CAS.
- Q. G. Chi, J. F. Dong, C. H. Zhang, C. P. Wong, X. Wang and Q. Q. Lei, J. Mater. Chem. C, 2016, 4, 8179–8188 RSC.
- Y. Zhang, Y. Wang, Y. Deng, M. Li and J. Bai, ACS Appl. Mater. Interfaces, 2012, 4, 65–68 CrossRef CAS PubMed.
- R. Su, Z. Luo, D. Zhang, Y. Liu, Z. Wang, J. Li, J. Bian, Y. Li, X. Hu and J. Gao, J. Phys. Chem. C, 2016, 120 Search PubMed.
- X. Lin, P. Hu, Z. Jia and S. Gao, J. Mater. Chem. A, 2016, 4, 2314–2320 RSC.
- X. Zhang, Y. Shen, B. Xu, Q. Zhang, L. Gu, J. Jiang, J. Ma, Y. Lin and C. W. Nan, Adv. Mater., 2016, 28, 2055 CrossRef CAS PubMed.
- G. Wang, Y. Huang, Y. Wang, P. Jiang and X. Huang, Phys. Chem. Chem. Phys., 2017, 19, 21058–21068 RSC.
- Z. Pan, L. Yao, J. Zhai, D. Fu, B. Shen and H. Wang, ACS Appl. Mater. Interfaces, 2017, 9, 4024–4033 CrossRef CAS PubMed.
- D. He, Y. Wang, S. Song, S. Liu and Y. Deng, ACS Appl. Mater. Interfaces, 2017, 9, 44839–44846 CrossRef CAS PubMed.
- D. He, Y. Wang, S. Song, S. Liu, Y. Luo and Y. Deng, Compos. Sci. Technol., 2017, 151, 25–33 CrossRef CAS.
- Q. Chi, T. Ma, Y. Zhang, Q. Chen, C. Zhang, Y. Cui, T. Zhang, J. Lin, X. Wang and Q. Lei, ACS Sustainable Chem. Eng., 2018, 6, 403–412 CrossRef CAS.
- J. Wang, Y. Long, Y. Sun, X. Zhang, H. Yang and B. Lin, Appl. Surf. Sci., 2017, 426, 437–445 CrossRef CAS.
- Y. Feng, W. L. Li, J. P. Wang, J. H. Yin and W. D. Fei, J. Mater. Chem. A, 2015, 3, 20313–20321 RSC.
- L. Huang, P. Zhu, G. Li, D. Lu, R. Sun and C. Wong, J. Mater. Chem. A, 2014, 2, 18246–18255 RSC.
- S. Luo, S. Yu, R. Sun and C.-P. Wong, ACS Appl. Mater. Interfaces, 2014, 6, 176–182 CrossRef CAS PubMed.
- Z. Chen, H. Li, G. Xie and K. Yang, RSC Adv., 2018, 8, 1–9 RSC.
- K. Yang, X. Huang, J. He and P. Jiang, Adv. Mater. Interfaces, 2015, 2, 1500361 CrossRef.
- M. Yang, C. Hu, H. Zhao, P. Haghi-Ashtiani, D. He, Y. Yang, J. Yuan and J. Bai, Carbon, 2018, 132, 152–156 CrossRef CAS.
- Z. Pan, J. Zhai and B. Shen, J. Mater. Chem. A, 2017, 5, 15217–15226 RSC.
- L. Wang, X. Huang, Y. Zhu and P. Jiang, Phys. Chem. Chem. Phys., 2018, 20, 5001–5011 RSC.
- D. Yu, N. X. Xu, L. Hu, Q. L. Zhang and H. Yang, J. Mater. Chem. C, 2015, 3, 4016–4022 RSC.
- W. S. Gutowski, J. Adhes., 2003, 79, 445–482 CrossRef CAS.
- Z. Pan, L. Yao, J. Zhai, B. Shen, S. Liu, H. Wang and J. Liu, J. Mater. Chem. A, 2016, 4, 13259–13264 RSC.
- Z. Pan, M. Wang, J. Chen, S. Bo, J. Liu and J. Zhai, Nanoscale, 2018, 10, 16621–16629 RSC.
- Prateek, R. Bhunia, S. Siddiqui, A. Garg and R. K. Gupta, ACS Appl. Mater. Interfaces, 2019, 11, 14329–14339 CrossRef CAS PubMed.
- H. Luo, K. Zhou, C. Bowen, F. Zhang, A. Wei, Z. Wu, C. Chen and D. Zhang, Adv. Mater. Interfaces, 2016, 3, 1600157 CrossRef.
- P. Hu, Y. Shen, Y. Guan, X. Zhang, Y. Lin, Q. Zhang and C.-W. Nan, Adv. Funct. Mater., 2014, 24, 3172–3178 CrossRef CAS.
- P. Hu, J. Wang, Y. Shen, Y. Guan, Y. Lin and C.-W. Nan, J. Mater. Chem. A, 2013, 1, 12321–12326 RSC.
- Y. Feng, M.-L. Li, W.-L. Li, T.-D. Zhang, Y. Zhao and W.-D. Fei, Appl. Phys. Lett., 2018, 112, 022901 CrossRef.
- Y. Zhang, W. Li, S. Xu, Z. Wang, Y. Zhao, J. Li and W. Fei, J. Mater. Chem. A, 2018, 6, 24550–24559 RSC.
- H. Luo, D. Zhang, L. Wang, C. Chen, J. Zhou and K. Zhou, RSC Adv., 2015, 5, 52809–52816 RSC.
- Y. Wang, J. Cui, Q. Yuan, Y. Niu, Y. Bai and H. Wang, Adv. Mater., 2015, 27, 6658–6663 CrossRef CAS PubMed.
- L. L. Sun, B. Li, Y. Zhao, G. Mitchell and W. H. Zhong, Nanotechnology, 2010, 21, 305702 CrossRef CAS PubMed.
- Y. N. Hao, X. H. Wang, S. O'Brien, J. Lombardi and L. T. Li, J. Mater. Chem. C, 2015, 3, 9740–9747 RSC.
- Y. Zhang, Q. Chi, L. Liu, C. Zhang, C. Chen, X. Wang and Q. Lei, APL Mater., 2017, 5, 076109 CrossRef.
- J. Chen, Y. Wang, X. Xu, Q. Yuan, Y. Niu, Q. Wang and H. Wang, J. Mater. Chem. A, 2018, 6, 24367–24377 RSC.
- Z. Pan, B. Liu, J. Zhai, L. Yao, K. Yang and B. Shen, Nano Energy, 2017, 40, 587–595 CrossRef CAS.
- Y. Wang, L. Wang, Q. Yuan, Y. Niu, J. Chen, Q. Wang and H. Wang, J. Mater. Chem. A, 2017, 5, 10849–10855 RSC.
- Q. Li, F. Liu, T. Yang, M. R. Gadinski, G. Zhang, L.-Q. Chen and Q. Wang, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 9995–10000 CrossRef CAS PubMed.
- J. Lao, H. Xie, Z. Shi, G. Li, B. Li, G.-H. Hu, Q. Yang and C. Xiong, ACS Sustainable Chem. Eng., 2018, 6, 7151–7158 CrossRef CAS.
- F. Liu, Q. Li, J. Cui, Z. Li, G. Yang, Y. Liu, L. Dong, C. Xiong, H. Wang and Q. Wang, Adv. Funct. Mater., 2017, 27, 1606292 CrossRef.
- S. Song, Y. Wang, Y. Luo, D. He, A. Abella and Y. Deng, Mater. Des., 2018, 140, 114–122 CrossRef CAS.
- J. O. Zoppe, N. C. Ataman, P. Mocny, J. Wang, J. Moraes and H.-A. Klok, Chem. Rev., 2017, 117, 1105–1318 CrossRef CAS PubMed.
- Y. Qiao, M. S. Islam, L. Wang, Y. Yan, J. Zhang, B. C. Benicewicz, H. J. Ploehn and C. Tang, Chem. Mater., 2014, 26, 5319–5326 CrossRef CAS.
- Y. Chen, Z. Wang, Y. He, Y. J. Yoon, J. Jung, G. Zhang and Z. Lin, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 1391–1400 CrossRef PubMed.
- Y. Chen, D. Yang, Y. J. Yoon, X. Pang, Z. Wang, J. Jung, Y. He, Y. W. Harn, M. He, S. Zhang, G. Zhang and Z. Lin, J. Am. Chem. Soc., 2017, 139, 12956–12967 CrossRef CAS PubMed.
- Y. Chen, Y. J. Yoon, X. Pang, Y. He, J. Jung, C. Feng, G. Zhang and Z. Lin, Small, 2016, 12, 6714–6723 CrossRef CAS PubMed.
- D. Yang, Y. Chen, H. Peng, G. Chen and Z. Lin, Nanoscale, 2018, 10, 22750–22757 RSC.
- Y. Chen, T. Gan, C. Ma, L. Wang and G. Zhang, J. Phys. Chem. B, 2016, 120, 4715–4722 CrossRef CAS PubMed.
- C. Feng, X. Pang, Y. He, Y. Chen, G. Zhang and Z. Lin, Polym. Chem., 2015, 6, 5190–5197 RSC.
- B. Jiang, X. Pang, B. Li and Z. Lin, J. Am. Chem. Soc., 2015, 137, 11760–11767 CrossRef CAS PubMed.
- X. Liu, J. Iocozzia, Y. Wang, X. Cui, Y. Chen, S. Zhao, Z. Li and Z. Lin, Energy Environ. Sci., 2017, 10, 402–434 RSC.
- X. Li, J. Iocozzia, Y. Chen, S. Zhao, X. Cui, W. Wang, H. Yu, S. Lin and Z. Lin, Angew. Chem., Int. Ed., 2018, 57, 2046–2070 CrossRef CAS PubMed.
- X. Pang, Y. He, B. Jiang, J. Iocozzia, L. Zhao, H. Guo, J. Liu, M. Akinc, N. Bowler, X. Tan and Z. Lin, Nanoscale, 2013, 5, 8695–8702 RSC.
- H. Z. Guo, Y. Mudryk, M. I. Ahmad, X. C. Pang, L. Zhao, M. Akinc, V. K. Pecharsky, N. Bowler, Z. Q. Lin and X. Tan, J. Mater. Chem., 2012, 22, 23944–23951 CAS.
- J. Wang, X. Pang, M. Akinc and Z. Lin, J. Mater. Chem., 2010, 20, 5945–5949 RSC.
- Y. Niu, Y. Bai, K. Yu, Y. Wang, F. Xiang and H. Wang, ACS Appl. Mater. Interfaces, 2015, 7, 24168–24176 CrossRef CAS PubMed.
- X. F. Chen, Z. Shen, X. H. Wan, X. H. Fan, E. Q. Chen, Y. Ma and Q. F. Zhou, Chem. Soc. Rev., 2010, 39, 3072–3101 RSC.
- X. Yang, Z. Xiang, S. Chen, H. Luo, D. Zhang and H. Zhang, New J. Chem., 2017, 41, 7553–7561 RSC.
- X. Liang, X. Chen, C. Y. Li, Z. Shen, X. Fan and Q. Zhou, Polymer, 2010, 51, 3693–3705 CrossRef CAS.
- Z. Y. Kuang, Y. J. Fan, L. Tao, M. L. Li, N. Zhao, P. Wang, E. Q. Chen, F. Fan and H. L. Xie, ACS Appl. Mater. Interfaces, 2018, 10, 27269–27277 CrossRef CAS PubMed.
- P. Li, S. Chen, H. Luo, D. Zhang and H. Zhang, J. Polym. Sci., Polym. Chem., 2017, 55, 754–766 CrossRef CAS.
- S. Chen, H. Luo, H. L. Xie and H. L. Zhang, Polymer, 2013, 54, 1794–1802 CrossRef CAS.
- D. Zhang, Y. X. Liu, A. Xinhua Wan and Q. F. Zhou, Macromolecules, 1999, 32, 5183–5185 CrossRef CAS.
- L. Y. Shi, Y. Zhou, X. H. Fan and Z. Shen, Macromolecules, 2013, 46, 5308–5316 CrossRef CAS.
- K. Qian, X. Lv, S. Chen, H. Luo and D. Zhang, Dalton Trans., 2018, 47, 12759–12768 RSC.
- H. Luo, S. Chen, L. Liu, X. Zhou, C. Ma, W. Liu and D. Zhang, ACS Sustainable Chem. Eng., 2019, 7, 3145–3153 CrossRef CAS.
- L. A. Fredin, Z. Li, M. A. Ratner, M. T. Lanagan and T. J. Marks, Adv. Mater., 2012, 24, 5946–5953 CrossRef CAS PubMed.
- D. Kang, G. Wang, Y. Huang, P. Jiang and X. Huang, ACS Appl. Mater. Interfaces, 2018, 10, 4077–4085 CrossRef CAS PubMed.
- X. Zhou, D. Zhong, H. Luo, J. Pan and D. Zhang, Appl. Surf. Sci., 2018, 427, 1183–1192 CrossRef CAS.
- X. Zhang, Y. Shen, Q. Zhang, L. Gu, Y. Hu, J. Du, Y. Lin and C. W. Nan, Adv. Mater., 2015, 27, 819–824 CrossRef CAS PubMed.
- H. Qu, S. Wei and Z. Guo, J. Mater. Chem. A, 2013, 1, 11513–11528 RSC.
- J. Xue, J. Xie, W. Liu and Y. Xia, Acc. Chem. Res., 2017, 50, 1976–1987 CrossRef CAS PubMed.
- J. Yoon, H.-S. Yang, B.-S. Lee and W.-R. Yu, Adv. Mater., 2018, 30, 1704765 CrossRef PubMed.
- J. Xue, T. Wu, Y. Dai and Y. Xia, Chem. Rev., 2019, 119, 5298–5415 CrossRef CAS PubMed.
- P. Hu, Z. Jia, Z. Shen, P. Wang and X. Liu, Appl. Surf. Sci., 2018, 441, 824–831 CrossRef CAS.
- D. Ciprari, K. Jacob and R. Tannenbaum, Macromolecules, 2006, 39, 6565–6573 CrossRef CAS.
- S. Peng, X. Yang, Y. Yang, S. Wang, Y. Zhou, J. Hu, Q. Li and J. He, Adv. Mater., 2019, 1807722 CrossRef PubMed.
- A. J. Bard and L. R. Faulkner, Electrochemical Methods-Fundamentals and Applications, John Wiley & Sons, Inc, 2nd edn, 2001 Search PubMed.
- M. Elimelech, et al., Particle Deposition and Aggregation-Measurement, Modelling and Simulation, Butterworth-Heinemann, 1995 Search PubMed.
- P. Atkins and J. D. Paula, Atkins' Physical Chemistry, Oxford University Press, 8th edn, 2006 Search PubMed.
- H. Ohshima, Electrical Phenomena at Interfaces and Biointerfaces-Fundamentals and Applications in Nano-, Bio-, and Environmental Sciences, John Wiley & Sons, Inc., 2012 Search PubMed.
- Z.-H. Shen, J.-J. Wang, J.-Y. Jiang, Y.-H. Lin, C.-W. Nan, L.-Q. Chen and Y. Shen, Adv. Energy Mater., 2018, 8, 1800509 CrossRef.
- X. Zhang, W. Chen, J. Wang, Y. Shen, L. Gu, Y. Lin and C.-W. Nan, Nanoscale, 2014, 6, 6701–6709 RSC.
- T. J. Lewis, IEEE Trans. Dielectr. Electr. Insul., 2004, 11, 739–753 CrossRef CAS.
- T. Tanaka, M. Kozako, N. Fuse and Y. Ohki, IEEE Trans. Dielectr. Electr. Insul., 2005, 12, 669–681 CrossRef CAS.
- T. Tanaka, IEEE Trans. Dielectr. Electr. Insul., 2005, 12, 914–928 CrossRef CAS.
- S. Li, G. Yin, G. Chen, J. Li, S. Bai, L. Zhong, Y. Zhang and Q. Lei, IEEE Trans. Dielectr. Electr. Insul., 2010, 17, 1523–1535 CAS.
- M. Ezzat, N. A. Sabiha and M. Izzularab, Appl. Nanosci., 2014, 4, 331–338 CrossRef CAS.
- X. He, K. Yao and B. K. Gan, J. Appl. Phys., 2005, 97, 084101 CrossRef.
- J. P. Calame, J. Appl. Phys., 2006, 99, 084101 CrossRef.
- F. A. Pearsall, J. Lombardi and S. O'Brien, ACS Appl. Mater. Interfaces, 2017, 9, 40324–40332 CrossRef CAS PubMed.
- A. M. Pourrahimi, R. T. Olsson and M. S. Hedenqvist, Adv. Mater., 2018, 30, 1703624 CrossRef PubMed.
- S. Li, D. Min, W. Wang and G. Chen, IEEE Trans. Dielectr. Electr. Insul., 2016, 23, 3476–3485 CAS.
- D. Min, W. Wang and S. Li, IEEE Trans. Dielectr. Electr. Insul., 2015, 22, 1483–1491 CAS.
- A. T. Hoang, Y. V. Serdyuk and S. M. Gubanski, Polymers, 2016, 8 Search PubMed , UNSP 103.
- T. Takada, Y. Hayase, Y. Tanaka and T. Okamoto, IEEE Trans. Dielectr. Electr. Insul., 2008, 15, 152–160 CAS.
- K. C. Kao, Dielectric Phenomena in Solids-With Emphasis on Physical Concepts of Electronic Processes, Elsevier, Inc., 2004 Search PubMed.
- C. Kittel, Introduction to Solid State Physics, John Wiley & Sons, 8th edn, 2005 Search PubMed.
- S. O. Kasap, Principles of Electronic Materials and Devices, McGraw-Hill, 3rd edn, 2006 Search PubMed.
- A. J. Dekker, Electrical Engineering Materials, Prentice-Hall, Inc, 1959 Search PubMed.
- Z.-M. Dang, Polymer Nanocomposites with High Permittivity, Nanocrystalline Materials Their Synthesis-Structure-Property Relationships and Applications, Elsevier, 2nd edn, 2014, ch. 9 Search PubMed.
- J. Shen and Y. Q. Ma, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 61, 14279–14282 CrossRef CAS.
- L. Gao, J. He, J. Hu and Y. Li, J. Phys. Chem. C, 2014, 118, 831–838 CrossRef CAS.
- J. Shen and Y. Q. Ma, J. Appl. Phys., 2001, 89, 5031–5035 CrossRef CAS.
- D. Yang, S. Huang, M. Ruan, Y. Wu, S. Li, H. Wang, J. Zhang, H. Ma, W. Guo and L. Zhang, J. Mater. Chem. C, 2017, 5, 7759–7767 RSC.
- X. Xiao, N. Xu, Y. Jiang, Q. Zhang, E. Yu and H. Yang, RSC Adv., 2016, 6, 69580–69585 RSC.
- L. Ren, X. Meng, J.-W. Zha and Z.-M. Dang, RSC Adv., 2015, 5, 65167–65174 RSC.
- S. Nayak, B. Sahoo, T. K. Chaki and D. Khastgir, RSC Adv., 2013, 3, 2620–2631 RSC.
- Y. Yao, N. Ning, L. Zhang, T. Nishi and M. Tian, RSC Adv., 2015, 5, 23719–23726 RSC.
- X. Chen, J.-K. Tseng, I. Treufeld, M. Mackey, D. Schuele, R. Li, M. Fukuto, E. Baer and L. Zhu, J. Mater. Chem. C, 2017, 5, 10417–10426 RSC.
- B. Xie, Q. Zhang, L. Zhang, Y. Zhu, X. Guo, P. Fan and H. Zhang, Nano Energy, 2018, 54, 437–446 CrossRef CAS.
- A. Chen, Y. Zhi, R. Guo and A. S. Bhalla, J. Appl. Phys., 2003, 93, 3475–3480 CrossRef.
- K. Zhou, S. A. Boggs, R. Ramprasad, M. Aindow, C. Erkey and S. P. Alpay, Appl. Phys. Lett., 2008, 93, 325 Search PubMed.
- Y. U. Wang, Appl. Phys. Lett., 2010, 96, 034115 Search PubMed.
- Y. U. Wang, D. Q. Tan and J. Krahn, J. Appl. Phys., 2011, 110, 044103 CrossRef.
- Z.-H. Shen, J.-J. Wang, X. Zhang, Y. Lin, C.-W. Nan, L.-Q. Chen and Y. Shen, Appl. Phys. Lett., 2017, 111, 092901 CrossRef.
- J. I. Roscow, C. R. Bowen and D. P. Almond, ACS Energy Lett., 2017, 2, 2264–2269 CrossRef CAS.
- H. Luo, J. Roscow, X. Zhou, S. Chen, X. Han, K. Zhou, D. Zhang and C. R. Bowen, J. Mater. Chem. A, 2017, 5, 7091–7102 RSC.
- R. K. Bose, J. Koetteritzsch, S. J. Garcia, M. D. Hager, U. S. Schubert and S. van der Zwaag, J. Polym. Sci., Polym. Chem., 2014, 52, 1669–1675 CrossRef CAS.
- D. P. Agoris, I. Vitellas, O. S. Gefle, S. M. Lebedev and Y. P. Pokholkov, J. Phys. D: Appl. Phys., 2001, 34, 3485–3491 CrossRef CAS.
- Z.-H. Shen, J.-J. Wang, Y. Lin, C.-W. Nan, L.-Q. Chen and Y. Shen, Adv. Mater., 2018, 30, 1704380 CrossRef PubMed.
- X. Zhang, J. Jiang, Z. Shen, Z. Dan, M. Li, Y. Lin, C.-W. Nan, L. Chen and Y. Shen, Adv. Mater., 2018, 30, 1707269 CrossRef PubMed.
- Y. Zeng, Z.-H. Shen, Y. Shen, Y. Lin and C.-W. Nan, Appl. Phys. Lett., 2018, 112, 103902 CrossRef.
- H. X. Tang and H. A. Sodano, Appl. Phys. Lett., 2013, 102, 063901 CrossRef.
- G. Wang, X. Huang and P. Jiang, Sci. Rep., 2017, 7, 43071 CrossRef CAS PubMed.
- Y. Wang, X. Huang, T. Li, Z. Wang, L. Li, X. Guo and P. Jiang, J. Mater. Chem. A, 2017, 5, 20737–20746 RSC.
- D. Zhang, X. Zhou, J. Roscow, K. Zhou, L. Wang, H. Luo and C. R. Bowen, Sci. Rep., 2017, 7, 45179 CrossRef CAS PubMed.
- H. Tang, Y. Lin, C. Andrews and H. A. Sodano, Nanotechnology, 2010, 22, 015702 CrossRef PubMed.
- Y. Yang, Z. Wang, Y. Ding, Z. Lu, H. Sun, Y. Li, J. Wei, R. Xiong, J. Shi, Z. Liu and Q. Lei, APL Mater., 2013, 1, 050701 CrossRef.
- B. Xie, Y. Zhu, M. A. Marwat, S. Zhang, L. Zhang and H. Zhang, J. Mater. Chem. A, 2018, 6, 20356–20364 RSC.
- Q. Li, G. Zhang, F. Liu, K. Han, M. R. Gadinski, C. Xiong and Q. Wang, Energy Environ. Sci., 2015, 8, 922–931 RSC.
- R. Wen, J. Guo, C. Zhao and Y. Liu, Adv. Mater. Interfaces, 2018, 5, 1701088 CrossRef.
- L. Wang, F. Gao, J. Xu, K. Zhang, J. Kong, M. Reece and H. Yan, Compos. Sci. Technol., 2018, 158, 112–120 CrossRef CAS.
- V. Tomer, E. Manias and C. A. Randall, J. Appl. Phys., 2011, 11, 154103 Search PubMed.
- H. Tang, Y. Lin and H. A. Sodano, Adv. Energy Mater., 2012, 2, 469–476 CrossRef CAS.
- B. Xie, H. Zhang, Q. Zhang, J. Zang, C. Yang, Q. Wang, M. Li and S. Jiang, J. Mater. Chem. A, 2017, 5, 6070–6078 RSC.
- Z. Wang, J. K. Nelson, H. Hillborg, S. Zhao and L. S. Schadler, Compos. Sci. Technol., 2013, 76, 29–36 CrossRef CAS.
- D. Zhang, W. Liu, L. Tang, K. Zhou and H. Luo, Appl. Phys. Lett., 2017, 110, 133902 CrossRef.
- D. Zhang, W. Liu, R. Guo, K. Zhou and H. Luo, Adv. Sci., 2017, 5, 1700512 CrossRef PubMed.
- X. Zhang, Y. Shen, Z. Shen, J. Jiang, L. Chen and C.-W. Nan, ACS Appl. Mater. Interfaces, 2016, 8, 27236–27242 CrossRef CAS PubMed.
- Prateek, D. Singh, N. Singh, A. Garg and R. K. Gupta, Compos. Sci. Technol., 2019, 174, 158–168 CrossRef CAS.
- R. Su, Z. Luo, D. Zhang, Y. Liu, Z. Wang, J. Li, J. Bian, Y. Li, X. Hu, J. Gao and Y. Yang, J. Phys. Chem. C, 2016, 120, 11769–11776 CrossRef CAS.
- J.-Y. Pei, J.-W. Zha, W.-Y. Zhou, S.-J. Wang, S.-L. Zhong, L.-J. Yin, M.-S. Zheng, H.-W. Cai and Z.-M. Dang, Appl. Phys. Lett., 2019, 114, 103702 CrossRef.
- K. Yin, J. Zhang, Z. Li, J. Feng, C. Zhang, X. Chen, A. Olah, D. E. Schuele, L. Zhu and E. Baer, J. Appl. Polym. Sci., 2019, 136, 47535 CrossRef.
- Y. Wang, L. Wang, Q. Yuan, J. Chen, Y. Niu, X. Xu, Y. Cheng, B. Yao, Q. Wang and H. Wang, Nano Energy, 2018, 44, 364–370 CrossRef CAS.
- Y. Shen, Y. Hu, W. Chen, J. Wang, Y. Guan, J. Du, X. Zhang, J. Ma, M. Li and Y. Lin, Nano Energy, 2015, 18, 176–186 CrossRef CAS.
- J. Jiang, X. Zhang, Z. Dan, J. Ma, Y. Lin, M. Li, C.-W. Nan and Y. Shen, ACS Appl. Mater. Interfaces, 2017, 9, 29717–29731 CrossRef CAS PubMed.
Footnote |
| † These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2019 |