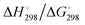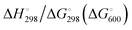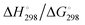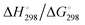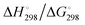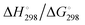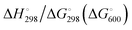The role of polysulfide dianions and radical anions in the chemical, physical and biological sciences, including sulfur-based batteries

Abstract

The well-known tendency of sulfur to catenate is exemplified by an extensive series of polysulfide dianions [S_n]²⁻ (n = 2–9) and related radical monoanions [S_n]˙⁻. The dianions can be isolated as crystalline salts with appropriate cations and structurally and spectroscopically characterized. Although the smaller radical monoanions may be stabilized in zeolitic matrices, they are usually formed in solution via disproportionation or partial dissociation of the dianions as well as by electrochemical reduction of elemental sulfur. An understanding of the fundamental chemistry of these homoatomic species is key to unravelling their behaviour in a broad variety of chemical environments. This review will critically evaluate the techniques used to characterize polysulfide dianions and radical anions both in solution and in the solid state, i.e. Raman, UV-visible, EPR, NMR and X-ray absorption spectroscopy, X-ray crystallography, mass spectrometry, chromatography and high-level quantum-chemical calculations. This is followed by a discussion of recent advances in areas in which these anionic sulfur species play a crucial role, viz. alkali-metal–sulfur batteries, organic syntheses, biological chemistry, geochemical processes including metal transport, coordination complexes, atmospheric chemistry and materials science.

---

Ralf Steudel

Ralf Steudel is emeritus professor of inorganic chemistry at the Technical University Berlin, Germany. He is best known for his many contributions to the chemistry of sulfur and selenium as well as for his textbooks and monographs on various aspects of inorganic chemistry. He spent a one-year sabbatical as visiting professor at the Spectroscopy Laboratory of M.I.T. (Cambridge, Mass.) and since cooperated with organic and inorganic chemists, with spectroscopists, crystallographers, theoreticians, astronomers and microbiologists around the world to explore the rich chemistry of the non-metals. As a former chairman of the 6th International Symposium on Inorganic Ring Systems held in Berlin he is a long-term member of the “IRIS family”.

Tristram Chivers

Tristram Chivers, a native of Bath, England, received his BSc, PhD (with Prof. R. D. Chambers FRS) and DSc degrees all from the University of Durham (UK). He joined the University of Calgary in 1969 and served as Head of the Chemistry Department from 1977 to 1982. He is currently Professor Emeritus of Chemistry. His research interests are in the area of main group element chemistry with emphasis on chalcogen compounds and inorganic ring systems. He is the author of two books: “A Guide to Chalcogen-Nitrogen Chemistry” and (with I. Manners) “Inorganic Rings and Polymers of the p-Block Elements: From Fundamentals to Applications”.

---

1 Introduction

The p-block element sulfur¹ is the tenth most abundant element in the universe. The crown-shaped structure of the most stable allotrope, cyclo-S₈, is well-known as is the fact that elemental sulfur forms an extensive series of other cyclic allotropes, of which 16 have been structurally characterized.² Cyclic frameworks are maintained in dications such as [S₄]²⁺, [S₈]²⁺ and [S₁₉]²⁺, which are formed upon oxidation of elemental sulfur with strong oxidizing agents and can be isolated as crystalline salts with weakly coordinating anions.^2b The radical cation [S₅]˙⁺ produced from the dissociation of [S₈]²⁺ in solution also has a cyclic structure, but it has not been isolated in the solid state.^3,4 However, the synthesis of the bicyclic radical cation [S₈]˙⁺ as the blue salt Cs_0.73Na_0.27[S₈][B₁₂Cl₁₂], which was characterized by X-ray diffraction, was reported in 2017.⁵

In addition, sulfur forms a series of homoatomic polysulfide dianions [S_n]²⁻ (n = 2–9), which have been isolated and structurally characterized as salts often in combination with solvated or chelated group 1 or 2 metal cations or large organic counter-ions, e.g. [R₄N]⁺ (R = alkyl), [Ph₄P]⁺, [(Ph₃P)₂N]⁺.^6,7 With one exception (Section 2) these dianions form catenated, unbranched structures in the solid state. Similar to the behaviour of the dication [S₈]²⁺, some of the long-chain dianionic species (n = 6–9) undergo an entropy-driven partial dissociation or disproportionation in solution to give polysulfide radical anions [S_n]˙⁻ (n = 2–4), the most prevalent of which is the blue trisulfide radical anion (n = 3), which is well-known to be stabilized by entrapment in an aluminosilicate matrix, e.g. in ultramarine blue.⁸ A unique polysulfide radical anion is the cyclic species [S₆]˙⁻, which forms a six-membered ring with two long central S–S bonds (263.3 pm, cf. 205 pm in cyclo-S₈) in the solid state and has been isolated as a [Ph₄P]⁺ salt.⁹ In 2017 a dimeric bismuth(III) complex formally containing the tetrasulfide radical anion [S₄]˙⁻ was isolated and structurally characterized (Section 5.5).¹⁰ Long-chain polysulfide radical anions [S_n]˙⁻ (n = 5–8, 10) have been detected in the laser desorption mass spectra of cyclo-S₈ in the negative ion mode (Section 3.3) and are also considered in computational studies (Section 4).¹¹

Organic polysulfanes R–S_n–R are often called polysulfides although they are derivatives of the covalent sulfanes H–S_n–H. The same holds for the partially substituted polysulfanes R–S_n–H (“hydropolysulfides”). In aqueous solution, these sulfur-rich SH compounds (n > 1) are much stronger acids than H₂S and therefore exist at pH values above 5 as mono- or di-anions, respectively.¹² Their rational nomenclature, which is in line with IUPAC recommendations, can be found in a previous review.¹³

The broad significance of elemental sulfur and many inorganic sulfur compounds in the geo-, bio- and cosmo-spheres, has been recognized for more than thirty-five years.¹⁴ Contemporary interest has been focused on the chemical properties of polysulfide dianions and the radical anions derived from them in part because of their function in alkali metal–sulfur batteries,¹⁵ but also owing to their role in a variety of other environments. The purpose of this article is to provide a critical review of recent advances in the analytical characterization, computational investigations and applications of these catenated, anionic polysulfur species. The discussion will begin with recent developments in the synthesis and structural determinations of polysulfide salts (Section 2). Subsequently, the identification of polysulfide dianions and radical anions by various spectroscopic and chromatographic techniques (Section 3), as well as computational studies (Section 4), will be considered. Finally, the significance and applications of these species in the following areas will be evaluated (Section 5): alkali metal–sulfur batteries (Section 5.1), organic syntheses (Section 5.2), biological chemistry (Section 5.3), geochemical transformations (Section 5.4), coordination complexes (Section 5.5) and atmospheric chemistry (Section 5.6). The conjunction of dianionic and monoanionic polysulfur species in this discussion evolves naturally from the observation that the dianions are in equilibrium with the radical anions, especially in non-aqueous solvents.¹⁶ Biological and geochemical transformations involving polysulfides occur in aqueous media, whereas alkali-metal–sulfur batteries employ non-aqueous solvents or polysulfide melts. The formation of organosulfur compounds or metal complexes of polysulfide dianions and radical anions may take place in either environment.

The coverage is not intended to be comprehensive. Rather, we will attempt to provide a critical overview of the important developments that have appeared since previous reviews on these species.^6–8

2 Novel syntheses and structures

The preparation and structural characterization of polysulfide dianions [S_n]²⁻ with up to nine sulfur atoms has been described in previous reviews.^6,7 Although the direct reaction of sulfur with an alkali metal in liquid ammonia is a well-established approach, the selective preparation of specific sodium oligosulfides is challenging. To this end Takata et al. reported the stoichiometric reactions of a sodium dispersion with sulfur powder in 1,2-dimethoxyethane (DME) at 70 °C to give either Na₂S or Na₂S₂, the yields of which were determined by reaction with benzyl chloride followed by GC-MS analysis of the dibenzylsulfanes so formed (Section 3.4).¹⁷ Aromatic hydrocarbons or ketones were found to be effective catalysts to enhance both the yield and selectivity of individual salts Na₂S_n (n = 1 or 2).¹⁷ In 2016, Mali and co-workers prepared a series of sodium polysulfides from the reaction of sodium metal with elemental sulfur in anhydrous methanol at 45–50 °C in order to obtain ²³Na solid-state NMR spectra (Section 3.6).¹⁸ Whereas the series Na₂S_n (n = 2, 4, 5) were obtained as pure compounds, X-ray diffraction patterns and solid-state ²³Na NMR spectra revealed that the material with a stoichiometry of 2Na:3S crystallizes as a mixture of Na₂S₂ and Na₂S₄ rather than homogeneous Na₂S₃ (Section 3.6).¹⁸ In 2019 Röhr et al. obtained the high-temperature (HT) polymorph of Cs₂S₃ from the reaction of Cs₂S₂ with elemental sulfur at 800 °C followed by cooling to room temperature.¹⁹ The crystal structure of this form of Cs₂S₃ embodies four crystallographically independent trisulfide dianions [S₃]²⁻ of very similar molecular structures;¹⁹ such HT polymorph had been predicted earlier on the basis of Raman spectra (see Section 3.1). The solvation of the alkali-metal cation can stabilize longer chain dianions in the hexasulfide [K(THF)]₂[S₆] and the unique nonasulfide [K₂(THF)][S₉], as demonstrated in 2007 by Lerner and co-workers.^20a However, a few years later the preparation of the unsolvated salt K₂S₆ by the reaction of potassium with stoichiometric amounts of sulfur in liquid ammonia was achieved by Getzschmann and Kaskel.^20b The all-trans conformation of the S₆ chain in K₂S₆ is in contrast with the cis,cis conformation in the solvated analogue.^19,20 Larger alkali-metal cations can also stabilize longer polysulfide dianions in the solid state, e.g. the hexasulfide Cs₂S₆ is well-known and the structure of a new triclinic form, in which the two crystallographically independent cesium atoms adopt ten- and eleven-fold coordination, was disclosed by Pfitzner and co-workers in 2015.²¹ In a study of the influence of the alkali-metal cation on the stabilization of polysulfides in 2018 Lu and co-workers found that in DMSO solution the large cation Rb⁺ exerts a stronger stabilizing effect than the smaller cation Li⁺ on short-chain polysulfide dianions [S_n]²⁻ (n = 3, 4), since the weaker solvation energy of Rb⁺ with respect to DMSO results in stronger cation–anion electrostatic interactions.²²

Lithium polysulfides Li₂S_n (n = 1–8) are of particular interest in view of their role as intermediates in the operation of lithium–sulfur batteries (Section 5.1.3).¹⁵ Seminal work by Rauh and co-workers more than 40 years ago established that the stoichiometric reactions of lithium sulfide with cyclo-S₈ in solvents such as DMSO, DMF or THF are the most efficient synthesis of lithium polysulfides with the nominal composition “Li₂S_n” [eqn (1)],²³ and that method is still used in investigations of these materials during the last few years.^22,24,25 However, these products are comprised of an equilibrium mixture, both in the solid state and in solution, and there is no straightforward procedure for the separation of individual polysulfides (Section 3.4).

Li₂S + (n − 1)/8S₈ → Li₂S_n (n = 3–8) (1)

Although pure Li₂S₈ has not been isolated and structurally characterized, the magnesium salt [Mg(N-MeIm)₆][S₈] (MeIm = methylimidazole) was prepared more than 25 years ago by stirring Mg powder and sulfur in N-methylimidazole at 100 °C and the X-ray structure of a nickel analogue [Ni(N-MeIm)₆][S₈] was determined;^26a the only other known octasulfide is [Et₃NH]₂[S₈].^26b The conformation of chains and rings of two-coordinate sulfur atoms is represented by the signs of the torsion angles, and the order of signs is called the “motif” of the molecule or ion. Most of these angles are near ±90°; thus, a helical chain has the motif +++… (right-handed helix) or −−−… (left-handed helix). The chains of sulfur atoms in [Et₃NH]₂[S₈] do not show the common helical all-trans conformation, but a mixed sequence with the signs of the dihedral angles ++−++ and −−+−− (enantiomers; Fig. 1b). By contrast, the conformation of the central five atoms of the [S₈]²⁻ anion in the nickel(II) complex [Ni(N-MeIm)₆][S₈] shown in Fig. 1a is similar to those of salts of [S₆]²⁻ and [S₇]²⁻.^21,27 The different conformations of the [S₈]²⁻ chains in these two salts may be attributed to hydrogen-bonding between the NH group and terminal S atoms in the case of the triethylammonium salt.

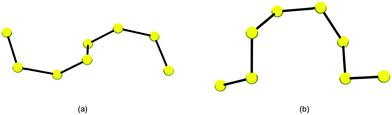Fig. 1 Conformation of the [S₈]²⁻ chain in (a) [Ni(N-MeIm)₆][S₈] and (b) [Et₃NH]₂[S₈] (adapted from Fig. 3 in ref. 26a).

In 2017, prompted by the interest in magnesium–sulfur batteries, Bieker and co-workers²⁸ extended the approach of Rauchfuss et al.^26a to the synthesis of the DMSO analogue [Mg(DMSO)₆][S₈] (DMSO = dimethyl sulfoxide) [eqn (2)]. They found that solutions of magnesium polysulfides undergo disproportionation and dissociation equilibria in a similar manner to the well-established behaviour of lithium polysulfides.²⁸

Mg + S₈ + 6L → [Mg(L)₆][S₈] (L = N-methylimidazole or DMSO) (2)

In order to evaluate the role of polysulfide dianions in alkali metal–sulfur batteries as well as in biological environments, synthetic work in the last 3–4 years has focused on soluble salts. The reaction of an organic salt of the nucleophilic thiolate (hydrosulfide) anion [HS]⁻ with elemental sulfur was first reported more than 30 years ago in the preparation of the heptasulfide [PPN]₂[S₇] {PPN = (PPh₃)₂N} in ethanol.²⁷ In 2015, Pluth and co-workers achieved the synthesis of [Bu₄N][HS] in 53% yield from reaction of pure Na[HS] with [Bu₄N]Cl in acetonitrile.²⁹ In a different approach Sundermeyer et al. showed that the proton-induced decarboxylation of methylcarbonate anions with H₂S, generated in situ from S(SiMe₃)₂ and methanol, produces soluble imidazolium and pyrrolidinium salts [Cat][HS] (Cat = cation) [eqn (3)].³⁰ The reactions of [BMPyr][HS] (BMPyr = N-butyl-N-methylpyrrolidinium) with elemental sulfur in various stoichiometries in methanol, acetonitrile or THF occur rapidly at room temperature to give a series of polysulfides [BMPyr]₂[S_n] (n = 2, 4, 6, 8), but these salts could not be isolated in pure form possibly owing to the presence of odd-numbered polysulfides.^30b However, by using trimethylsilylthiolate ([Me₃SiS]⁻) instead of thiolate ([HS]⁻) salts, pure pyrrolidinium hexasulfides were obtained in essentially quantitative yields (Scheme 1).^30c

[Cat]⁺[MeOCO₂]⁻ + H₂S → [Cat]⁺[HS]⁻ + MeOH + CO₂ (3)

Through a combination of experimental evidence and density functional theory (DFT) calculations, Pluth et al. have demonstrated that polysulfide intermediates [S_n]²⁻ are involved in the biologically significant production of NO from the reaction of persulfides RSSH with nitrite ions (Scheme 2).³¹ This study also invoked the reaction of [Bu₄N][HS] with sulfur to form the hexasulfide [Bu₄N]₂[S₆], which served as a source the trisulfide radical anion [S₃]˙⁻ (via homolytic dissociation) for reaction with NO to generate the unbranched [SSNO]⁻ anion.

Scheme 1 Synthesis of pyrrolidinium hexasulfides.

Scheme 2 Involvement of polysulfides in the formation of NO from persulfides and nitrite.

In 2018 the first structurally characterized example of a branched polysulfide [SS₃]²⁻, the perthio form of the sulfite ion [SO₃]²⁻, was reported by Seff and co-workers.^32a This unique polysulfide was formed via disproportionation of sulfur vapour at 623 K in a zeolite matrix with the equally unusual trisulfur dication [S₃]²⁺ as the counter-ion. The [SS₃]²⁻ and [S₃]²⁺ ions are sequestered in cavities of the matrix with S–S bond lengths of approximately 216(5) and 211(8) pm, respectively, as determined by X-ray diffraction (Fig. 2); the high values of the estimated standard deviations are the result of disorder problems.^32a

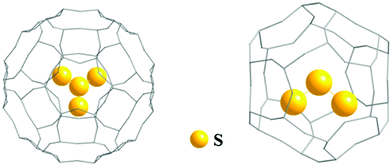Fig. 2 Schematic representation of entrapment of [SS₃]²⁻ and [S₃]²⁺ ions in a zeolite matrix (adapted with permission from the graphical abstract in ref. 32a).

Strong interactions with the surrounding sodium ([SS₃]²⁻) and oxygen atoms ([S₃]²⁺) of the zeolite matrix are thought to stabilize these unusual ions. The trapping of [S₃]²⁺ in this way is reminiscent of the well-known encapsulation of the [S₃]˙⁻ radical ion in sodalite (Section 3.5).⁸ In addition, it is noted that in 2013 the neutral trisulfur molecule S₃ has been selectively sequestered in the pores of a coordination network formed by the polymeric complex [(TPT)₃ZnI₂]_n {TPT = 2,4,6-tris(4-pyridyl)triazine}.³³

3 Characterisation of polysulfide dianions and radical anions

The broad variety of spectroscopic, as well as chromatographic and computational techniques, that are available for the characterization of polysulfide dianions and radical anions in solution or the solid state are discussed in the following sections. In each case the capabilities as well as the limitations of the method are considered. Indeed, as emphasized in a recent book chapter by Prendergast et al.,^15a it is essential to employ several independent techniques before firm conclusions about the identity of a particular species are made. The use of a combination of UV-visible, IR/Raman and EPR spectra to identify the blue species formed in solutions of polysulfide dianions in electron-pair donor solvents as the trisulfide radical anion [S₃]˙⁻ is a cogent example of this dictum.³⁴ Similarly, UV-visible and EPR spectra have been employed to confirm the presence of [S₃]˙⁻ in the recent applications of this species as a reagent in organic synthesis (Section 5.2). The singular ability of Raman spectroscopy for the identification of [S₃]˙⁻ is impressively demonstrated by the use of this technique to establish that the blue mineral recently found in a monastery at Dalheim, Germany, in the dental calculus of a medieval (11th or early 12th century by radiocarbon dating) religious woman is lapis lazuli.³⁵ The characteristic symmetric stretching vibration of [S₃]˙⁻ was observed at 548 cm⁻¹ with an overtone at 1096 cm⁻¹ (Fig. 3) (Section 3.1).⁸ This significant anthropological finding casts doubt on the widely held assumption concerning the limited availability of lapis lazuli in medieval Europe and suggests that the woman was working on valuable illuminated manuscripts.³⁵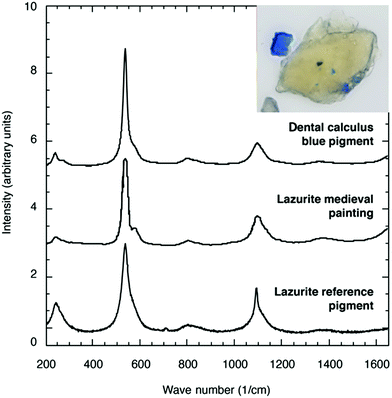

Fig. 3 Comparison of micro-Raman spectra of the blue mineral found in the dental calculus of a medieval woman with reference lazurites. Inset shows the embedded blue mineral and a sample of it freed from the dental calculus (adapted with permission from Fig. 2 and 4 in ref. 35).

The disulfide radical anion [S₂]˙⁻ is also well-characterized by IR/Raman, UV-visible and EPR spectra. However, despite numerous claims for the spectroscopic signature of the tetrasulfide radical anion [S₄]˙⁻ by various techniques, there is still some uncertainty about the identification of this important species (see Discussion in Sections 3.1–3.6).

3.1 Raman spectra

The S–S bonds of polysulfides are strong Raman scatterers due to the high polarizability of the bonding and lone pair electrons at the two-coordinate sulfur atoms. Therefore, laser Raman spectroscopy is a very useful technique for identifying individual polysulfides and polysulfide radical anions. However, assignments of lines in the spectra of polysulfide mixtures may be difficult owing to the coincidence of some lines for different molecular sizes and due to incidental degeneracies within one ion. In addition, the Raman effect is a low intensity phenomenon since only a tiny fraction of the incoming radiation is scattered inelastically. Consequently, a sufficient concentration is needed in solutions since several anion conformations may be present in equilibrium resulting in broad Raman signals from superposition of closely neighbouring lines. Fortunately, for highly coloured species such as some radical anions the enormous enhancement of Raman intensity caused by resonance effects helps to identify such species even at low concentrations. This requires that the wavelength of the laser radiation is close to the wavelength of an absorption band of the species to be detected.

However, it should also be noted that S–S bonds in polysulfur compounds are light-sensitive since homolytic dissociation can be triggered by visible light of suitable wavelengths. Therefore, red or infrared laser radiation is recommended for Raman investigations. Sample cooling helps to reduce the thermal or photochemical decomposition and at the same time decreases the line widths resulting in larger and narrower peaks and hence better spectral resolution.

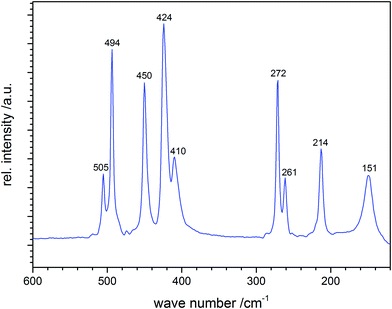
Vibrational wavenumbers of polysulfide anions can be calculated theoretically either from empirical force constants and geometrical parameters adopted from similar molecules and ions (preferred)³⁶ and, with some restrictions, by quantum-chemical calculations (see also Section 4). As an example, the well-resolved Raman spectrum of solid cesium hexasulfide (Cs₂S₆) is shown in Fig. 4.²¹ The sample was prepared by reacting S₈ with cesium carbonate at 120 °C in ethanol and was characterized by X-ray diffraction on single crystals. The helical anion is of C₂ symmetry with SS bond lengths in the range 202.5–206.4 pm. The five stretching modes result in five well-separated lines between 410 and 510 cm⁻¹, while the bending modes occur below 300 cm⁻¹; the torsion modes are to be expected in the region below 100 cm⁻¹, which has not been recorded in this case. The spectrum is in excellent agreement with the earlier Raman data of Ziemann and Bues of 1979;^37a the observed stretching modes also agree very well with the wavenumbers predicted in 1977 for the free helical hexasulfide anion of C₂ symmetry calculated from force constants and geometrical parameters adopted from S₈ and other sulfur compounds such as [NH₄]₂[S₅].³⁶

Fig. 4 Raman spectrum of solid Cs₂S₆ (figure courtesy of A. Pfitzner).

Interestingly, a high-temperature form of Cs₂S₃, which was predicted in 1979 on the basis of the additional Raman lines (splitting of stretching modes) observed when this trisulfide was heated to 125 °C followed by rapid cooling to 25 °C,^37b was prepared from Cs₂S₂ and sulfur and structurally characterized forty years later (Section 2).¹⁹

All reliable Raman spectra of polysulfide dianions recorded with pure samples using red or infrared laser excitation and exclusion of oxygen to avoid autoxidation support the following statements:^6,19

1. The stretching modes of unbranched dianions [S_n]²⁻ occur only in the region 390–510 cm⁻¹ and there are no fundamental modes in the region 300–390 cm⁻¹.

2. The stretching modes are only slightly influenced by the cations or by solvents.

3. All dianions [S_n]²⁻ with n = 3–9 in a large number of alkali-metal, ammonium, phosphonium and telluronium salts form unbranched chains of differing conformations as demonstrated by X-ray diffraction analyses of single crystals (a branched tetrasulfide anion has been identified in a zeolite structure; Section 2, Fig. 2)

4. There is no limitation to the chain-length n of the dianions [S_n]²⁻; in solutions and in melts even-membered as well as odd-membered chains exist in a dynamic equilibrium which is established rapidly (Section 3.4).

5. In organic solvents, but not in water, the alkali-metal polysulfides are also in equilibrium with dissolved S₈ molecules and with radical anions (S₈ is insoluble in water and can be present as a solid only).

6. Some alkali-metal polysulfides dissociate on melting with formation of radical anions which reversibly recombine on cooling and annealing of the melt to regenerate the original phase, provided the temperature has not been so high that elemental sulfur evaporates from the melt (the dissociation in solvents will be discussed below).

7. Autoxidation of polysulfide dianions produces thiosulfate and sulfate ions³⁸ giving rise to novel Raman signals both above 500 cm⁻¹ and below 400 cm⁻¹.³⁹

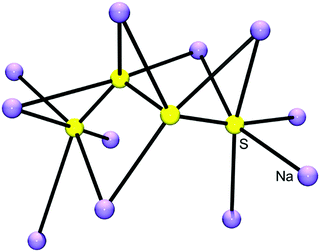
In salts with alkali-metal cations from Na⁺ to Cs⁺, as well as with organic ammonium and phosphonium cations, the polysulfide anions form chains of differing conformations which are located in a cavity formed by surrounding cations⁶ (Fig. 5). However, with lithium cations completely different structures are observed since quasi-molecular ion pairs are formed for n > 2. Besides Li₂S₂ no other binary lithium polysulfide has so far been characterized by X-ray structural analysis since these compounds crystallize from polar solvents with at least one solvent molecule attached to the cations in addition to the polysulfido ligand. The coordination number of Li is always 4. For example, crystals of [Li(TMEDA)]₂[S₆] consist of a bicyclic Li₂S₆ unit with one tetramethylethylenediamine (TMEDA) molecule chelated to each metal atom (see Fig. 6).⁴¹ Due to the small size of the naked Li cation and its high electric field strength, the Li–S interactions can be considered as partly covalent and partly ionic. Consequently, the Raman spectrum contains not only typical SS stretching modes in the region 390–500 cm⁻¹, but also Li–S stretching modes (near and below 390 cm⁻¹) which most probably are coupled to the SS stretching fundamentals of the neighbouring bonds. In addition, Li–N stretching modes are to be expected in the same region. With chelating triamines attached to Li ions the polysulfide unit forms a chain which is end-capped on both sides by the LiN₃ unit.⁴²

Fig. 5 Cationic environment of the tetrasulfide anion (yellow) in the crystal structure of Na₂S₄ calculated from the atomic coordinates of Tegman;⁴⁰ shown are all cations (violet) surrounding the [S₄]²⁻ anion with Na–S_term distances of between 283 and 289 pm. The terminal sulfur atoms of the anion are approximately octahedrally coordinated by five Na and one S atom (figure courtesy of H. Hartl).

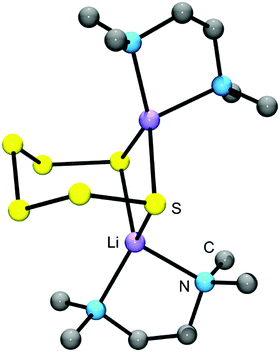Fig. 6 Solid-state structure of [Li(TMEDA)]₂[S₆] determined by X-ray crystallography (bond lengths: Li–S 249 pm, S–S: 204–208 pm; adapted from Tatsumi et al. 1990, ref. 41).

Lithium polysulfides are expected to remain partly undissociated in organic solutions forming ion pairs such as [Li(solvent)S_n]⁻. In this way otherwise unstable, longer polysulfides are stabilized, since all polysulfide dianions are strong S-donor ligands and numerous metal complexes are known.⁴³ The calculated structure of the ion pair [Li(THF)₂S_n]⁻ is shown in Fig. 7. Only ionic polysulfides with large complex cations like [K(crypt-2,2,2)]⁺, [R₄N]⁺ and [R₄P]⁺ (R = alkyl or phenyl group) do not engage in ion pair formation, since the positive charge is distributed over a large number of atoms in those cations. This important issue will be further discussed in Section 5.

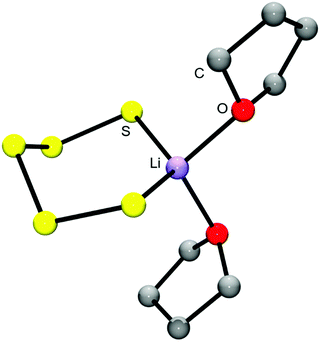Fig. 7 Molecular structure of the ion pair [Li(THF)₂S₅]⁻ in the gas phase, calculated at the B3LYP/6-31G(d) level.⁴⁴ The O₂LiS₅ fragment is approximately of C_s symmetry with bond lengths d_SS = 210.6 and 212.1 pm, d_LiS = 245.5 and 247.4 pm, d_LiO = 204.0 and 205.2 pm. The fundamental vibrations in the region 310–600 cm⁻¹ are all stretching modes of the O₂LiS₅ unit which are predicted as follows (in cm⁻¹): 471 (SS), 463 (SS), 416 (SS), 401 (LiS), 386 (LiO), 363 (LiO/LiS/SS) and 361 (LiO/LiS) (adapted from ref. 44).

The structures, vibrational spectra and thermodynamic properties of polysulfide anions and radical anions can also be predicted by quantum-chemical calculations both for the free ions (gas phase) as well as for the species in a polarizable medium of different dielectric constant simulating the influence of a solvent of a particular polarity (PCM calculations).⁴⁴ However, free polysulfide dianions with up to 8 sulfur atoms are unstable in the gas phase or in vacuum since they either suffer spontaneous electron autodetachment or Coulomb explosion producing one or two radical monoanions, respectively, due to the strong Coulomb repulsion between the two excess electrons.⁴⁵ Therefore, the electrospray mass spectra of sodium trisulfide, tetrasulfide and a mixture of potassium polysulfides, dissolved in ultra-pure water, recorded by Nagy et al. in 2019 in the negative ion mode have been found to be quite similar and showed only peaks due to radical anions with not more than three sulfur atoms (Section 3.3).⁴⁶ However, longer-chain polysulfide ions with up to nine sulfur atoms were detected by negative ion mass spectrometry when the dianions were protonated to [HS_n]⁻ during electrospray using methanolic solutions with ammonium acetate buffer as reported by Gun et al. in 2004.⁴⁷ In that case the overall charge of the gaseous anions is reduced by 50% and Coulomb explosion does not take place.

Penta- and hexasulfide anions are also unstable with respect to homolytic dissociation in solvents of low polarity such as THF (ε ≈ 8). However, all dianions [S_n]²⁻ do become thermodynamically stable with respect to dissociation at one of the central bonds in solvents of higher polarity such as water (ε = 78).⁴⁴ Therefore, solutions of Li₂S₆ in organic solvents of low polarity like tetrahydrofuran (THF), dimethoxyethane (DME) or tetraethyleneglycol dimethylether (TMGME) with dielectric constants of between 7.2 and 7.8 are of pale green to blue colour at low concentrations, while in dimethylacetamide (DMA, ε = 38) the intense blue colour of [S₃]˙⁻ is observed.^48,49 The green colour may be explained by a mixture of [S₂]˙⁻ (yellow) and [S₃]˙⁻ (blue). The higher polarity and larger donor number of DMA (DN = 28) result in stronger cation–solvent interactions reducing the formation of ion pairs such as [LiS₆]⁻ in which the polysulfide dianion is stabilized against homolytic dissociation. Aqueous solutions of lithium polysulfides are yellow to orange-red depending on the chain length and the concentration, indicating a negligible (undetectable) radical concentration.

In general, the dissociation equilibrium of a polysulfide dianion to the corresponding monoanions depends on (a) the thermodynamic properties of the ion, (b) the temperature, (c) the concentration, (d) the dielectric constant of the solvent, (e) the ion strength of the solution, and (f) on the nature of the counterions.

From the most sophisticated calculations⁴⁴ and reliable Raman as well as EPR spectra the following facts can be derived:

1. The small radical ions [S_n]˙⁻ with n = 3–5 are chain-like while larger ions [S_n]˙⁻ with n = 6–9 (and probably beyond) are cyclic but with one or two very long bonds.^44,45

2. The Raman spectra of the polysulfide radical ions [S_n]˙⁻ with n = 3–5 are characterized by fundamental modes in the region 330–600 cm⁻¹.^21,44,50

3. In solution the radical ions are in equilibrium with the corresponding dianions which are by far the dominant species at room temperature, but only in highly polar solvents and not in ether-based solvents as demonstrated by the concentration and temperature-dependence of the UV-vis absorption spectra;⁴⁹ for Gibbs energies ΔG° of the homolytic dissociation reactions, see Section 4.

4. Electron paramagnetic resonance (EPR) spectra of lithium polysulfides dissolved in DMF exhibit a signal assigned to [S₃]˙⁻ and, at high sulfur content, a signal attributed to [S₄]˙⁻ is observed.⁵¹ A radical with an absorption maximum at 617 nm ([S₃]˙⁻) in the UV-visible has also been detected by EPR spectroscopy in ether-based solvents.⁴⁹

5. Low concentrations of the radical anions under equilibrium conditions can best be detected by resonance Raman spectroscopy exploiting their absorption bands near 400 nm ([S₂]˙⁻) and, depending on the matrix, at 595–620 nm ([S₃]˙⁻), respectively.^8,52 Even the overtones 2ν₁, 3ν₁, 4ν₁ and 5ν₁ of [S₃]˙⁻ have been observed by resonance Raman spectroscopy.^53,54

6. Stable concentrations of some of the radical anions can be obtained by matrix-isolation under non-equilibrium conditions, e.g. in ionic crystal structures such as NaI, KI, sodalite and other rigid matrices in which diffusion is not possible at room temperature.⁵⁵

7. In molten alkali-metal polysulfides,⁵⁰ as well as in high-temperature aqueous fluids containing potassium thiosulfate⁵⁶ or other sulfur species under high pressure,⁵³ trisulfide radical anions have been observed by Raman spectroscopy.

Calculated vibrational data for the four smallest polysulfide radical anions are summarized in Table 1 both for gaseous ions and for two solvents characterized by dielectric constants ε of 8 (e.g. tetrahydrofuran, THF) or 78 (e.g. propylene carbonate or water) using the polarizable continuum model (PCM).⁴⁴

Table 1 Harmonic vibrational modes of polysulfide monoanions [S_n]˙⁻ in the gas phase and in a polarizable continuum, calculated at the B3LYP/6-31+G(2df,p) level (wavenumbers in cm⁻¹; symmetry species in parentheses). Stretching modes are separated from bending and torsion modes by the symbol//(adapted from ref. 44)

Ion	Gas phase	PCM8-corrected	PCM78-corrected
[S2]˙^− (D∞h)	570	578	578
[S3]˙^− (C2v)	559(b)/521(a)//222(a)	544(b)/527(a)//222(a)	538(b)/528(a)//222(a)
[S4]˙^− (C2v)	595(a)/570(b)/327(a)//281(b)/93(a)/87(a)	589(a)/542(b)/344(a)//280(b)/109(a)/103(a)	588(a)/533(b)/345(a)//279(b)/113(a)/105(a)
[S5]˙^− (Cs)	556(a′)/535(a′′)/424(a′)/332(a′′)//226(a′)/177(a′′)/155(a′)/60(a′′)/44(a′)	548(a′)/495(a′′)/441(a′)/352(a′′)//244(a′)/176(a′)/175(a′′)/83(a′′)/45(a′)	545(a′)/479(a′′)/444(a′)/356(a′′)//249(a′)/179(a′)/174(a′′)/87(a′′)/52(a′)

---

Anharmonic vibrational frequencies of gaseous [S₃]˙⁻ have been calculated by two different methods at the RCCSD(T) level with the cc-pVQZ basis set as follows (values in cm⁻¹): ν₃ = 595/599(b₂), ν₁ = 543/543(a₁), 2ν₂ = 450/453(a₁), ν₂ = 225/226(a₁).⁵⁷ The calculated data are in excellent agreement with the following experimental wavenumbers (cm⁻¹):

[S₂]˙⁻: 590 (in sodalite⁵⁸), 589 (in NaI) and 594 (in KI).⁶

[S₃]˙⁻: 580–590 (ν₃), 545–550 (ν₁), 220–265 (ν₂) in sodalite^52,58 and in high-temperature high-pressure aqueous fluids;⁵³ 534 (ν₁) in Li–S cells^54,59 (Section 5.1.3).

While the radicals entrapped in natural minerals most probably result from reduction of sulfate ions by some carbon-containing material, the sulfur-doped alkali halides are prepared by strong heating of elemental sulfur with the crystalline halides. In this reaction an electron is transferred from a halide ion to a small sulfur molecule such as S₂ or S₃, which are components of sulfur vapour and of hot sulfur melts and which possess large electron affinities. The sulfur radical anion then takes the site of the former halide anion in the crystal structure.

The radical ion [S₄]˙⁻ has not yet been observed convincingly by Raman spectroscopy, but EPR spectra of [S₄]˙⁻ have been reported (Section 3.5).⁵¹ An absorption band at 520 nm previously assigned to [S₄]˙⁻ is in fact due to the red molecule S₄ which is of C_2v symmetry⁶⁰ and characterized by a Raman line at 678 cm⁻¹ which does not fit any vibrational wavenumber calculated for [S₄]˙⁻ (see Table 1). [S₅]˙⁻ and larger polysulfide radical ions with up to 25 atoms have been observed by mass spectrometry,⁶¹ but only [S₆]˙⁻ has been isolated in a crystal structure, namely with the rather innocent [Ph₄P]⁺ cation⁹ and no vibrational spectra of this cyclic radical anion have been published.

In 2013 Tübke et al. reported vibrational wavenumbers for polysulfide dianions and monoanions with up to 8 sulfur atoms both for the gas phase and for THF solution, calculated at the B3PW91/6-311G(2df,p) level.⁶² Not all of these frequencies agree with well-established experimental data or with the statements given above. For example, the stretching modes of [S₃]˙⁻ have been observed at 584 (ν_as) and 550 cm⁻¹ (ν_s),⁵² while Tübke et al. calculated these modes at 522 (ν_as) and 535 cm⁻¹ (ν_s) which is the incorrect order. Furthermore, intense Raman signals were predicted by these authors for the dianions [S_n]²⁻ (n = 6–8) in the region 300–400 cm⁻¹, which contradicts experimental spectra of pure polysulfides recorded at room temperature as shown above. Since the authors did not publish the calculated geometries of the di- and monoanions, the reason for the deviation from experiments and other theoretical calculations cannot be identified. In Section 4 we will show that certain DFT calculations on thermodynamically unstable (gaseous) polysulfide anions may result in partly unreliable geometries and frequencies.

Since there is a mathematical relationship between SS stretching frequencies and the corresponding S–S bond lengths in polysulfur compounds,⁶³ the geometrical parameters of the polysulfide dianions in crystalline salts⁶ can be used to demonstrate that SS stretching modes below 390 cm⁻¹ are unlikely in chain-like anions [S_n]²⁻ (n = 3–8).

3.2 UV-visible spectra

The colours of polysulfide dianions [S_n]²⁻ range from pale-yellow for the disulfide ion via yellow-orange for the intermediate chain-length species to orange-red for the longer chains. In principle, therefore, UV-visible spectra should be a useful diagnostic tool for the identification of individual dianions. However, in electron-pair donating solvents, e.g. DMSO, DMF, THF and in aqueous solutions these species exist as an equilibrium mixture of various polysulfide dianions formed via disproportionation. The interpretation of the UV-visible spectra of such solutions is further complicated by the generation of highly coloured radical anions upon dilution via partial dissociation of the dianions in non-aqueous solvents. The most prevalent of these is the bright blue trisulfide radical anion [S₃]˙⁻ with a solvent-dependent absorption band in the range 595–620 nm, while the yellow [S₂]˙⁻ has λ_max ≈ 400 nm.⁸ The reported assignment of an absorption band for the red [S₄]˙⁻ radical anion is controversial (vide infra). Consequently, UV-visible spectra of polysulfide solutions should be interpreted cautiously in conjunction with data obtained by other techniques, especially Raman spectra (Section 3.1) and derivatization experiments followed by chromatographic separation (Section 3.4).

This caveat is clearly illustrated by several independent studies of the UV-visible spectra of lithium polysulfides prepared according to eqn (1) during the period 2012–2014.^64–67 The consistent finding of these investigations is that, within the spectral range 300–600 nm, the absorption maxima for long-chain polysulfide dianions occur at higher wavelengths, whereas short-chain polysulfide dianions exhibit absorption bands closer to the UV part of the spectrum. Operando UV-visible spectroscopy has been used by Lu et al. in 2018 as part of an investigation of the redox chemistry that occurs in alkali metal–sulfur batteries with a view to understanding the influence of the alkali-metal cation.²² These authors had previously reported on the basis of a rotating-ring disk electrode study that the initial electrochemical reduction of cyclo-S₈ produces the dianionic [S₈]²⁻ chain.⁶⁸ The reduction was carried out in DMSO containing a M[ClO₄] electrolyte (M = Li⁺, Na⁺, K⁺ or Cs⁺) and monitored by recording the UV-visible spectra. The following assignments of absorption bands for polysulfide dianions and radical anions were invoked based on previous data from the literature:^15a [S₈]²⁻ (492 nm), [S₆]²⁻ (475, 350 nm), [S₄]²⁻ (420 nm), [S₃]²⁻ (340, 270 nm) and [S₃]˙⁻ (617 nm). The odd-membered species [S₇]²⁻ and [S₅]²⁻ were ignored in this study despite the fact that [S₅]²⁻ is a thermodynamically favored polysulfide dianion (Section 4). Interestingly, in contrast to the behaviour of polysulfide dianions in electron-pair donor solvents, Yellowlees and co-workers found that the formation of the blue trisulfide radical anion [S₃]˙⁻ only occurs to a small extent in the ionic liquid [C₄mim][DCA] (C₄mim = 1-butyl-3-methylimidazolium; DCA = dicyanamide).⁶⁹ By contrast, Seddon and co-workers had shown earlier that elemental sulfur produces highly coloured solutions involving an equilibrium between [S₆]²⁻ and [S₃]˙⁻ ions in the ionic liquid tributylethylphosphonium diethylphosphate [Bu₃EtP][(EtO)₂PO₂].^8,70

The formation of the unbranched [SSNO]⁻ anion from the reaction of NO with sulfide is a significant process in biological signaling and may involve the intermediate formation of polysulfide dianions (Section 5.3).⁷¹ A recent study provides a compelling illustration of the capability of UV-visible spectroscopy for monitoring reactions of polysulfide radical anions. In an elegant experiment Pluth and co-workers followed the reaction of the blue trisulfide radical ion [S₃]˙⁻ (617 nm) with NO by UV-visible spectroscopy.³¹ The reagent [S₃]˙⁻ was produced by homolytic dissociation of the polysulfide dianion in [Bu₄N]₂[S₆], which was generated from the reaction of cyclo-S₈ and [Bu₄N][HS] in THF as described in Section 2. The formation of the red [SSNO]⁻ anion (446 nm) in this reaction is depicted convincingly in Fig. 8.

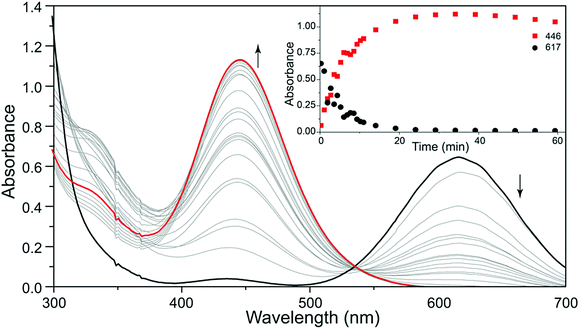Fig. 8 UV-visible spectra of the reaction of [S₃]˙⁻ with NO to give [SSNO]⁻ (red curves). Reproduced from ref. 31 with permission. Copyright 2016, American Chemical Society.

UV-visible spectroscopy has also been used by Akaike, Nagy et al. to estimate the variation in the concentrations of polysulfide radical anions [S_n]˙⁻ (n = 2–4) generated from the reaction of cyclo-S₈ and [Bu₄N][HS] as a function of reaction stoichiometry and temperature. The reaction was carried out in various stoichiometries (1 : 1, 1 : 2, 1 : 3 and 1 : 8) in dilute d₈-THF/CD₃CN solutions for the temperature range 20–60 °C.⁴⁶ The authors concluded that (a) at room temperature [S₄]˙⁻ (490 nm) is the predominant species, (b) as the temperature is increased more [S₃]˙⁻ (610 nm) is formed, and (c) [S₂]˙⁻ (426 nm) is the primary species for the 1 : 8 stoichiometry, but the equilibrium is shifted to [S₃]˙⁻ as the temperature is increased for this stoichiometry. However, these conclusions should be viewed with circumspection owing to a potential overlap of the band attributed to [S₄]˙⁻ (490 nm) with that assigned to the formal dimer [S₈]²⁻ (492 nm) (vide supra). Furthermore, time-dependent DFT calculations by Fabian et al. in 2006 using different hybrid functionals predicted a very weak electronic transition in the visible region with an absorption maximum in the range 562–604 nm for [S₄]˙⁻, whereas the same theoretical study predicted values of 608–617 nm for [S₃]˙⁻ in good agreement with the experimental data (vide supra).⁶⁰

3.3 Mass spectrometry

Electrospray mass spectrometry (ESI-MS) is a powerful, soft ionization tool that can potentially distinguish between polychalcogenides of different chain length in solutions. In 2004, both ion trap and electrospray time-of-flight mass spectrometry were applied to the analysis of aqueous solutions of sodium tetrasulfide Na₂S₄ in the pH range of 6–10 and in the presence of methanol and ammonium acetate for protonation of the gaseous dianions. Remarkably, the most abundant species detected in the negative ion mode was the hexasulfide [HS₆]⁻, although significant amounts of other polysulfides [HS_n]⁻ (n = 4, 5, 7, 8, 9) were also evident. At higher capillary temperatures (>140 °C) disproportionation and redox processes took place in the ESI chamber,⁴⁷ as predicted on the basis of chemical reasoning.⁷² Interestingly, the laser desorption ionization mass spectra of cyclo-S₈ in the negative ion mode gives rise to peaks for the monoanions [S_n]˙⁻ (n = 1–8, 10). The heavier clusters (n = 4–8, 10) appear at relatively low laser power, while [S₃]˙⁻ dominates the spectra at intermediate energies.¹¹

In 2015 high-resolution mass spectrometry was employed by Cortese-Krott et al. to confirm the presence of polysulfide radical anions [S_n]˙⁻ (n = 2–4) in dilute (100 μM) aqueous solutions of Na₂S_n (n = 3, 4).⁷¹ The most abundant species observed was the trisulfide radical anion [S₃]˙⁻ (m/z ≈ 96). In addition, peaks at m/z ≈ 64 and ≈128 indicated the possible presence of [S₂]˙⁻ and [S₄]˙⁻. These tentative assignments were seemingly confirmed by high-resolution mass spectra obtained from triple quadrupole experiments, which gave the following m/z values (calculated masses are given in parentheses): [S₂]˙⁻ 63.9469 (63.9448), [S₃]˙⁻ 95.9170 (95.9168), [S₄]˙⁻ 127.9057 (127.8890). The assignment of these m/z values to polysulfide radical monoanions rather than dianions with twice the number of sulfur atoms was verified by inspection of the isotopic distribution patterns.⁷¹ However, the assignment of the peak at m/z = 127.9057 to [S₄]˙⁻ is probably in error since the almost isobaric ion [S₃O₂]˙⁻ fits the observed mass much better (calcd 127.9060); the latter ion may result from the reaction of [S₃]˙⁻ with O₂, which evidently has not been excluded carefully enough. The peaks observed at m/z 80 and 119 may be assigned to [SO₃]⁻ and [NaS₃]⁻, respectively. The reaction of [S₃]˙⁻ with O₂ will be further discussed in Section 5.3.

3.4 Chromatography and NMR spectra of polysulfide dianions after derivatization

The exact speciation of polysulfide dianions in solutions cannot be determined by vibrational spectroscopy due to the many overlapping signals and due to possible homolytic dissociation (Section 3.1). Since the various anions exist in a rapidly established dynamic equilibrium, direct chromatographic separation by either HPLC or ion chromatography is also not possible. Therefore, indirect analytical methods have been developed using rapid derivatization of the dianions to produce less reactive end-capped polysulfanes R–S_n–R, which then can be identified by liquid chromatography, mass spectrometry or ¹H NMR spectroscopy.

Protonation of aqueous polysulfide anions by cold concentrated hydrochloric acid yields an oily mixture of water-insoluble polysulfanes H₂S_n (n = 1–25) as shown by ¹H NMR spectroscopy.¹² However, it is not always clear during derivatization reactions of this type whether exchange of sulfur atoms between anions or partly protonated ions takes place before full protonation and kinetic stabilization is achieved, e.g.:

[HS_x]⁻ + [S_y]²⁻ → [HS_m]⁻ + [S_n]²⁻ (x + y = m + n) (4)

Therefore, the rate of the derivatization reaction is a decisive factor. In addition, the oily sulfane mixture changes its composition on storage even at low temperatures and H₂S_n molecules with up to 35 sulfur atoms as well as S₈ are formed:¹²

2H₂S_n → H₂S_n−x + H₂S_n+x (5)

H₂S_n → H₂S_n−8 + S₈ (n > 8) (6)

Since the sulfanes are much stronger acids in water than H₂S, full protonation of the polysulfide dianions requires very low pH values. The pK_a values for the first and second dissociation step of the oligosulfanes H₂S₂ to H₂S₈ decrease with increasing number of sulfur atoms and have been estimated as follows: 5.11/10.03, 4.31/7.83, 3.91/6.63, 3.61/6.03, 3.58/5.51, 3.48/5.18, 3.40/4.94 (for comparison H₂S: 7.01/≈16). Consequently, at pH values between 5 and 9.5 the hydrogen disulfide ion [HS₂]⁻ is expected to be the dominating S₂ species in aqueous solution. For Gibbs enthalpies of formation of the ions [HS_n]⁻ and of the sulfanes H₂S_n (n = 2–8) see ref. 73 and 74.

End-groups that are less reactive than hydrogen atoms have been developed taking advantage of the chemical and thermal stability of the carbon–sulfur bond. Numerous organic polysulfanes R–S_n–R with up to 13 sulfur atoms have been prepared as pure compounds and have been characterized by X-ray diffraction on single crystals; even much longer sulfur chains have been detected by HPLC techniques.^13,75 Therefore, alkylation of polysulfide anions in solution seems to be a suitable derivatization procedure. A first attempt was made by Rethmeier et al. in 1997 using monobromobimane (BmBr) as a reagent to convert inorganic sulfur anions into derivatives which were suitable for fluorescence detection after HPLC analysis.⁷⁶ Bimane (Bm) is a bicyclic diketone with a central NN bond and four methyl groups one of which has been brominated in BmBr; its main property is the intense fluorescence (excitation at 380 nm and emission at 480 nm). Unfortunately, the reaction time of the brominated derivative BmBr with nucleophiles such as sulfide, sulfite, thiosulfate and polysulfides (30 min at 25 °C) is quite high and specific polysulfides could not be identified by this method. Nevertheless, this method has been applied several times in microbiology for the quantitative trace analysis of certain sulfur compounds in bacterial cultures (Section 5.3), e.g.:

2Bm–Br + [HS]⁻ → Bm–S–Bm + 2Br⁻ + H⁺ (7a)

In a similar fashion, Takata et al. in 2003 used benzyl chloride to convert polysulfide dianions into the corresponding bis(benzyl)polysulfanes:¹⁷

2C₆H₅CH₂Cl + [S_n]²⁻ → (C₆H₅CH₂)₂S_n + 2Cl⁻ (7b)

However, later work showed that the reaction time of 1 h at 25 °C in strongly alkaline solution is much too long to prevent longer sulfur chains from disproportionation. Nevertheless, this method was applied in a subsequent publication by the same group to determine the speciation of polysulfide dianions in a lithium–sulfur battery with a reaction time of 3 h.⁷⁷

Argyropoulos et al. in 2006 used dimethyl sulfate as an alkylating agent for an aqueous solution of nominal composition Na₂S_2.58 at 25 °C. However, the reaction time of 2 h together with the absence of a buffer to keep the pH constant (despite sulfuric acid production by hydrolysis of Me₂SO₄) may be responsible for the observation that mainly Me₂S₂, Me₂S₃ and Me₂S₄ were detected by ¹H NMR spectroscopy, while the penta- and hexasulfane were present in trace concentrations only and longer-chain species Me₂S_>6 were completely absent in the derivatized polysulfide solutions.⁷⁸

The formal disproportionation of polysulfide anions in solution is usually expressed by equations such as:

[S_y]²⁻ + [S_z]²⁻ = 2[S_x]²⁻ (with y + z = 2x) (8)

This reaction proceeds in water by a series of nucleophilic attacks of shorter-chain anions (i.e., the stronger nucleophiles) on the longer chains, but the true reacting species may be protonated anions or ion pairs to reduce the Coulombic repulsion between the two anions. In the absence of elemental sulfur, reduction of the pH value from ca. 12 to ca. 9 shifts the equilibrium in aqueous polysulfide solutions to larger dianions which can be explained as follows:

[S_x]²⁻ + [HS]⁻ + [OH]⁻ = [S_y]²⁻ + [S_z]²⁻ + H₂O (x + 1 = y + z) (9a)

Kinetic measurements showed that this disproportionation follows first order reversible reaction dynamics and needs about 10 seconds at ambient conditions to be completed.^79a Therefore, it is impossible to use direct chromatographic or electrophoretic separations for determination of polysulfide dianions, and derivatization reactions must be completed in less than 10 s. In a similar fashion, the nucleophilic degradation of S₈ by aqueous hydrogensulfide anions proceeds initially according to eqn (9b):^79b

S₈ + [HS]⁻ + [OH]⁻ = [S₉]²⁻ + H₂O (9b)

In a series of important publications Lev, Kamyshny et al. described in 2004 and the following years a reliable derivatization protocol reducing the reaction time of the alkylating agent to less than 2 s at room temperature. First, methyl iodide was used and it was shown that a polysulfide solution obtained by reduction of elemental sulfur with hydrazine sulfate in aqueous NaOH reacted with MeI to give a mixture of oligosulfanes Me₂S_n with n = 1–11, with the di-, tri- and tetrasulfanes as the major species.⁸⁰ This result indicated once more that aqueous polysulfide solutions also contain dianions well beyond hexasulfide. The composition of the mixture and the thermal stability of single members in solution were investigated by HPLC. However, the reaction time of the methylation step in a methanol–water mixture containing a phosphate buffer at room temperature was 30 min. A much shorter alkylation time of just a few seconds was finally achieved using methyl triflate (trifluoromethyl sulfonate) in a single-phase alkylation reaction at 25 °C:⁷³

[S_n]²⁻ + 2CF₃SO₃CH₃ → Me₂S_n + 2[CF₃SO₃]⁻ (10)

Reversed-phase HPLC was then used to separate and determine the dimethyl polysulfanes (Fig. 9).

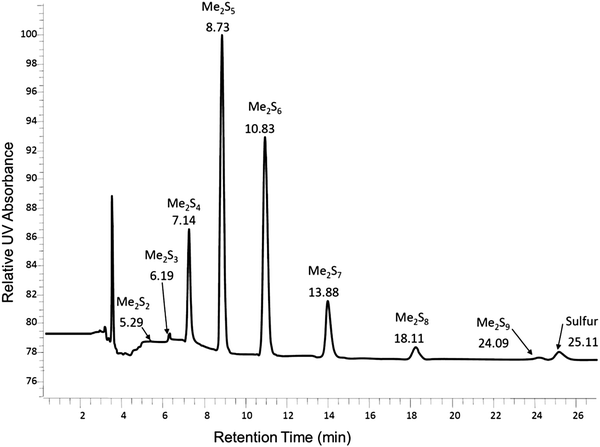Fig. 9 Chromatogram of the dimethyl polysulfane mixture obtained by derivatization of aqueous K₂S₅ by methyl triflate in a phosphate buffer at 25 °C (figure courtesy of A. Kamyshny, Jr).⁷³

This sophisticated technique together with isotopic dilution experiments allowed the following facts to be established:⁷³

1. When an aqueous solution of Na₂S₄ with natural abundance of isotopes and a solution of Na₂³⁴S₄ were mixed the isotopic exchange between the various anions was ca. 70% complete within 8 s.

2. When solid K₂S₅ was dissolved in water using a phosphate buffer the anions detected after derivatization with CF₃SO₃CH₃ were (in the order of decreasing concentrations): [S₅]²⁻ ≫ [S₆]²⁻ > [S₄]²⁻ ≫ [S₇]²⁻ > [S₃]²⁻ > [S₈]²⁻ > [S₂]²⁻.

3. In aqueous polysulfide solutions saturated with elemental sulfur (S₈) the ratio of the activities of any two polysulfide species is constant at equilibrium and invariant to pH change, i.e. the distribution of the polysulfide dianions remains constant regardless of the overall concentration.

4. In unsaturated (dilute) polysulfide solutions decreasing pH values favour larger chain-lengths until sulfur precipitation occurs at pH < 7. S₈ is thought to be ejected from either [S₉]²⁻ or [HS₉]⁻ by protonation and elimination of [HS]⁻ or H₂S (or from longer polysulfide chains).

The polysulfide derivatization by methyl triflate has later been modified to analyze polysulfides at low concentrations as in environmental samples.^79,81 In addition, it was shown in 2006 that oxidation of aqueous hydrogen sulfide by H₂O₂ produces initially all polysulfide dianions from [S₃]²⁻ to [S₈]²⁻ before sulfate ions are formed eventually.⁸¹

When aqueous polysulfide solutions are heated, slow disproportionation of the “zero-valent” sulfur atoms (S⁰) within the chains and formation of thiosulfate are observed; the same holds for the disproportionation of elemental sulfur suspended in alkaline solutions:¹²

1/2S₈ (or 4S⁰) + 4[OH]⁻ → 2[HS]⁻ + [S₂O₃]²⁻ + H₂O (11)

This reaction had to be taken into account when the Gibbs free energies, reaction enthalpies and entropies of formation for polysulfide dianions were calculated by Kamyshny et al. using analytical data for the following reaction (obtained by the derivatization method) as well as its temperature dependency:⁷⁴

[HS]⁻(aq.) + (n − 1)/8S₈(s.) → [S_n]²⁻(aq.) + H⁺(aq.) (12)

In Table 2 the thermodynamic results for room temperature are summarized [using 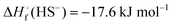]. The equilibrium constants (pK values) for the reactions in eqn (12) are: 11.5, 10.4, 9.7, 9.5, 9.7, 10.2 and 10.8 for n = 2 to 8.⁷³

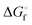Table 2 Gibbs energies and enthalpies 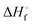of formation (in kJ mol⁻¹) as well as entropies S° (in J mol⁻¹ K⁻¹) of aqueous polysulfide dianions [S_n]²⁻ with n = 2–8 derived from the analysis of the reaction products of solid elemental sulfur (S₈) with aqueous hydrogen sulfide according to eqn (12) (adapted from ref. 74)

Parameter^a	n = 2	n = 3	n = 4	n = 5	n = 6	n = 7	n = 8
a Slightly different 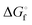values have been published by Kamyshny et al. in 2004.^73 b Extrapolated value.
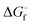
	77.4 ± 1.3	71.1 ± 0.7	67.1 ± 0.1	66.0 ± 0.1	67.4 ± 0.1	70.7 ± 0.3	74.9 ± 0.5
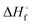
	13.0^b	6.6 ± 0.1	9.0 ± 0.1	9.6 ± 0.1	13.3 ± 0.1	16.5 ± 0.1	23.8 ± 0.2
S°	−22^b	9 ± 4	63 ± 1	100 ± 2	139 ± 1	171 ± 4	213 ± 8

---

From the data in Table 2 it follows that aqueous [S₅]²⁻ is thermodynamically favoured over other chain lengths and that the enthalpy change by consecutive addition of one sulfur atom at a time to a polysulfide chain gradually increases with the length of the sulfur chain. Thus, the disulfide to trisulfide transition is slightly exothermic, but since the reaction enthalpy is gradually increasing the conversion of pentasulfide to hexasulfide is already endothermic; the same holds for the higher polysulfides. While at low values of n the main driving force for further addition of a sulfur atom to the polysulfide chain is the exothermicity of the reaction, at high values of n the entropy gain becomes a more important factor in overcoming the endothermic nature of the reaction. This entropy increase results from the increasing number of rotational isomers as the chain-length grows due to the almost free rotation about the SS bonds and the many possible conformations of the larger anions; the torsional angle at each SS axis can be either positive or negative. The average length of the polysulfide chains in an equilibrium mixture increases with temperature, since species with n > 5 increase in concentration at the expense of the shorter chains.⁷⁴

Zheng et al. used the fast derivatization of polysulfides by methyl triflate in 2016 to identify the anions obtained by electrochemical reduction of S₈ in a Li–S battery.⁸² It was convincingly shown that in situ derivatization within the electrochemical cell gives results different from those of ex situ derivatizations as used by previous researchers. The details will be discussed in Section 5.1.3.

3.5 EPR spectra of polysulfide radical anions

Species with an unpaired electron give rise to a strong signal in the electron paramagnetic resonance (EPR) spectrum. Consequently, EPR spectroscopy is a valuable diagnostic technique for the detection of polysulfide radical anions [S_n]˙⁻ (n = 2, 3 or 4) either in solution or in the solid state. As discussed in earlier reviews,^6,8 the radical anions [S_n]˙⁻ (n = 2, 3) have been identified by EPR spectroscopy in ultramarine pigments. The trisulfide radical anion [S₃]˙⁻ predominates in ultramarine blue, while [S₂]˙⁻ is also present in ultramarine green and it is the primary component in ultramarine yellow. There is controversy over the identity of the chromophore in ultramarine red as either the neutral S₄ allotrope or the radical anion [S₄]˙⁻ (vide infra).

Ultramarines are aluminosilicate sodalite minerals Na₈[Al₆Si₆O₂₄]Cl₂ with a zeolitic architecture. The cavities in this framework incorporate Na⁺ cations and Cl⁻ anions some of which may be replaced by [S_n]˙⁻ radical anions. Early work attributed distinct EPR signals to two different trisulfide radical anions [S₃]˙⁻. The most common one was an isotropic signal with g = 2.029, while other reports associated [S₃]˙⁻ with a rhombic g tensor with values of 2.005, 2.036 and 2.046. In order to explain this discrepancy, Goldfarb et al. carried out high-field EPR and ENDOR (electron nuclear double resonance) measurements on three blue pigments that were obtained by calcination of sodalite samples prepared from aluminum sulfate and [Me₄N][OH] at high temperatures.^83a On the basis of the spectroscopic results together with DFT calculations, two different [S₃]˙⁻ radicals, both of which have an open C_2v structure, were identified. The ENDOR spectra showed that the number and location of ²³Na⁺ cations around these species are different. A third [S₃]˙⁻ radical with an isotropic g value was also detected in some samples.^83a Subsequently, Goslar et al. described combined EPR and electron spin echo studies of the structure and dynamics of [S₃]˙⁻ in ultramarines and determined g values of 2.016, 2.0355 and 2.0505 in the temperature range 4.2–50 K.^83b Above 300 K re-positioning of [S₃]˙⁻ between 12 possible orientations in the sodalite cage with a very low energy barrier results in a single line with an average g value of 2.028.^83b In 2011 Raulin and co-workers provided the first unambiguous EPR identification of [S₂]˙⁻ by using continuous wave and field-sweep echo detected EPR.^83c The highly anisotropic g values were determined to be 2.69(6), 2.03(4) and 1.86(4).^83c In 2018 Rejmak performed all-electron DFT calculations of [S₃]˙⁻ and [S₂]˙⁻ in ultramarine pigments with periodic structure optimization and showed that different orientations of [S₃]˙⁻ within a sodalite cage have little effect on the calculated g tensor components, which were in excellent agreement with experimental values.^83d This author also found that embedded [S₂]˙⁻ ions are more sensitive to the local environment than [S₃]˙⁻. Unfortunately, reliable values of the g tensor for [S₂]˙⁻ could not be obtained.^83d

EPR spectra of solutions of lithium polysulfides Li₂S_n in DMF show a strong signal for [S₃]˙⁻ radical anions when n < 6. For higher sulfur contents (n > 6) an additional EPR resonance attributed to [S₄]˙⁻ is observed.⁵¹ The concentration of this radical anion is very low and the equilibrium constant for the dissociation [S₈]²⁻ ↔ 2[S₄]˙⁻ was estimated to be about 10⁻⁹ M. The [S₄]˙⁻ radical anion has been considered for the identity of the chromophore in ultramarine red, but this assignment has been controversial (Section 3.2). In 2016 spectroscopic investigations of an ultramarine that was prepared by encapsulation of the red chromophore inside a microporous zeolitic imidazolate framework with Na₂S₄ as the sulfur source were reported.⁸⁴ The lack of an EPR signal for the red solid product indicated the absence of any radical anions. However, the red solid exhibited a broad visible absorption band at ca. 525 nm (cf. ≈ 530 nm for ultramarine red), which was attributed to a neutral cis-S₄ chain. This assignment is supported by time-dependent DFT calculations at different levels of theory, which yielded values in the range 542–564 nm for this isomer compared to 562–604 nm for the radical anion [S₄]˙⁻ (Section 3.2).⁷¹

During the past 4–5 years EPR spectroscopy has been employed to address the role of polysulfide radical anions in the redox chemistry that occurs in lithium–sulfur batteries as well as the use of the transient species [S₃]˙⁻ as a reagent in organic syntheses. Details of these applications are discussed in Sections 5.1 and 5.2, respectively.

3.6 Lithium and sodium NMR spectra of inorganic polysulfides

The limited natural abundance and quadrupole moment of ³³S (I = 3/2, 0.76%) combined with the low symmetry of the sulfur centers render ³³S NMR spectra uninformative for the characterization of polysulfide anions. On the other hand, both ⁷Li (I = 3/2, 92.6%) and ²³Na (I = 3/2, 100%) have the potential to provide chemical shift data for the identification of individual alkali-metal polysulfides as long as the cations and anions are in contact. In this context several in situ⁷Li NMR studies have been carried out on the formation of lithium polysulfides during the discharge of lithium–sulfur batteries.^85–88 In 2013 Nazar and co-workers reported the ⁷Li NMR spectra of solid lithium polysulfides prepared by the reduction of appropriate amounts of elemental sulfur with Li[Et₃BH] in THF.⁸⁵ However, with the exception of Li₂S and Li₂S₆, which showed isotropic NMR shifts of 2.3 and 1.0 ppm, respectively, the other polysulfides with nominal compositions Li₂S_n (n = 2, 4, 8) were found to be phase mixtures. In their 2017 study of the lithium–sulfur redox process Wang and co-workers were able to track the formation and evolution of lithium polysulfides by ⁷Li NMR spectroscopy and showed that it followed a four-step sequence (Section 5.1.3); however, ⁷Li chemical shifts for individual polysulfides could not be obtained.⁸⁸

By contrast, in 2016 Mali and co-workers employed solid-state ²³Na NMR spectra, supported by X-ray diffraction patterns and ab initio computational predictions, to determine the ²³Na chemical shifts of the different sodium crystallographic sites in the series Na₂S_n (n = 1–5) and, hence, provide a quantitative estimate of the composition of samples of sodium polysulfides.¹⁸ The unit cells of known crystalline sodium polysulfides are shown in Fig. 10a and their ²³Na magic angle spinning (MAS) NMR spectra are depicted in Fig. 10b, which reveals that the different crystalline sites in Na₂S_n (n = 2, 4, 5) can be resolved. The capability of ²³Na MAS NMR spectroscopy is demonstrated impressively by the spectrum of the Na₂S₃ sample, which clearly shows that this material is a mixture of almost equal amounts of β-Na₂S₂ and Na₂S₄.¹⁸

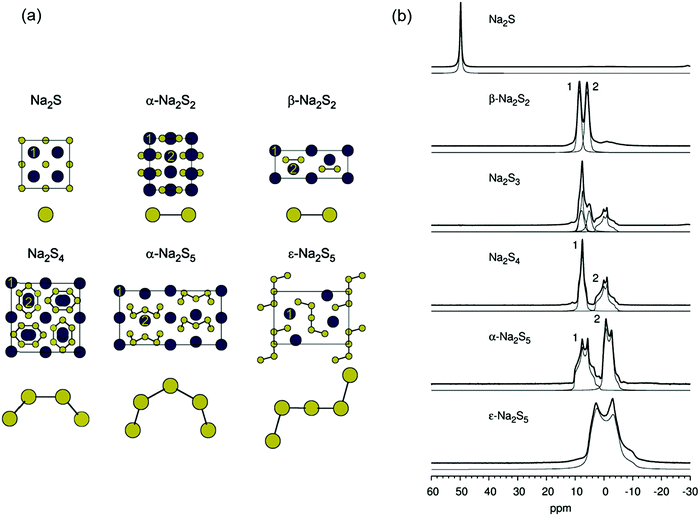Fig. 10 (a) Unit cells and (b) ²³Na MAS NMR spectra of crystalline sodium polysulfides (blue circles = Na, yellow circles = S; crystallographically inequivalent Na sites are labeled 1 and 2. Reproduced from ref. 18 with permission from Wiley. Copyright 2016.

3.7 X-ray absorption (XAS) and photoelectron spectra (XPS)

X-ray absorption spectroscopy (XAS) involves the determination of the energy of core electrons that are ejected when a sample absorbs X-rays. This technique can be applied to powders, liquids, solutions, polymeric materials or surfaces. XANES spectra are obtained by using synchrotron radiation with an energy of ca. 2500 eV. An X-ray absorption near edge structure (XANES) spectrum arises from excitation of core electrons (1s in the case of a K edge) to high-level vacant orbitals. For sulfur compounds the energy of the absorption depends on the oxidation state, which may vary from 2− in metal sulfides to 6+ in sulfate. In the specific case of polysulfides [S_n]²⁻ different absorption lines are to be expected for the central and terminal sulfur atoms, since the negative charge resides predominantly on the latter (Section 4).⁸⁹ Polysulfide radical anions [S_n]˙⁻ (n = 2–4) may be expected to exhibit characteristic XANES spectra depending on the value of n. XANES is also well-suited to the in situ identification of sulfur species in biological samples that may contain long sulfur chains in the form of polythionates [O₃S–S_n–SO₃]²⁻ as well as cyclo-S₈ (Section 5.3).⁹⁰

Pioneering work by Fleet and co-workers on the sulfur K-edge XANES spectra of ultramarine pigments revealed a pre-peak at ca. 2468.0 eV, which was attributed to the presence of the unpaired electron in [S₃]˙⁻. The intensity of this pre-peak is directly proportional to the depth of the blue colour of the mineral.⁹¹ Subsequent studies of sulfur K-edge XANES spectra of lithium polysulfides attributed the pre-edge to significant concentrations of [S₃]˙⁻.⁹² However, this assignment has been questioned on the basis of DFT calculations, which revealed that the XAS of polysulfide dianions [S_n]²⁻ (n = 2–8) are characterized by pre-edge and main-edge features in the same energy range.^93,94 More recent studies dispute the assignment of the pre-edge feature in sulfur K-edge XAS of lithium polysulfides to [S₃]˙⁻.^95–97

In 2015, in order to provide a more solid foundation for the interpretation of XAS of lithium polysulfides, Pascal et al. conducted DFT-based simulations of the XAS of neutral sulfur allotropes and the corresponding radical anions and dianions ranging from two to eight sulfur atoms.⁹⁸ They found that the source of the pre-edge feature near 2470 eV in the sulfur K-edge XAS is primarily due to core excitations of the terminal atoms of polysulfides to σ* orbitals. They also predicted a spectral feature that is unique to the radicals in the range 0.5–1 eV below the pre-edge that arises from 1s → σ* transitions of the terminal atoms. The energy of this feature for [S₃]˙⁻ was calculated to be 2468.5 eV, but its intensity is weak and it was suggested that it may only be observed for radical mol fractions >20%.⁹⁸ This prediction was confirmed in the same year by Nazar et al. in an experimental study of dissolved lithium polysulfides in which [S₃]˙⁻ was identified by a pre-edge feature in the XAS near 2468.5 eV.⁹⁹ In a contemporaneous study of intermediates produced in a lithium–sulfur battery, Gorlin and co-workers used XANES to determine the influence of solvent on the conversion of polysulfides to Li₂S and found that this process proceeds more rapidly in a solvent with a low dielectric constant.¹⁰⁰

Further to the earlier work of Fleet et al. (vide supra),⁹¹ sulfur K-edge XANES spectra have been used to determine the presence of polysulfide radical anions in a variety of solid-state materials, including the mineral lazurite from different geographical locations, slag-based materials such as mortars or concretes, and artists’ pigments. In 2016, Schmidt Patterson, Walton and co-workers analyzed samples of lazurite from Afghanistan, Russia, Chile, the USA, Iran, Tajikistan and Myanmar by XANES spectroscopy with a view to using this technique to determine the source of this mineral.^101a In addition to a peak at 2482.5 eV attributed to sulfate, all averaged XANES spectra exhibited a peak at 2469.1 eV attributed to [S₃]˙⁻, which was more prevalent than that of [S₂]˙⁻. They also observed an envelope of peaks between 2470 and 2475 eV with a variable spectral profile. For example, samples from Chile showed two distinct peaks near 2471.7 and 2473.5 eV, whereas those from Afghanistan displayed an absorption maximum at 2472.5 eV implying a unique geological environment for the Chilean samples.

In an intriguing and somewhat related application of XANES spectroscopy carried out in 2018, samples taken during the extraction of the blue component, lazurite, from lapis lazuli employing the method used to generate a blue pigment for artists were analyzed.^101b All spectra displayed a strong absorption peak at 2483 eV for sulfate, an envelope of peaks between 2470 and 2475 eV, and a pre-peak at 2469.1 eV attributable to [S₃]˙⁻. This study elucidated the changes in composition of sulfur species that occur during the extraction process. Interestingly, an increase in the [S₃]˙⁻ content of the pigments was observed upon prolonged exposure to X-rays.^101b

Slag-based materials such as mortars and concretes are known to exhibit a blue-green colour upon hydration. Analysis of slags activated with sodium silicate or Portland cement by XANES spectroscopy revealed that, in addition to major peaks for sulfate at 2482.5 eV and thiosulfate at 2481.0 and 2471.7 eV, a pre-peak at 2469.6 eV attributed to [S₃]˙⁻ was associated with the blue colour.¹⁰² The green colour of these slags is likely due to the additional presence of yellow [S₂]˙⁻, cf. ultramarine green,⁸ but this species was not detected in the XANES study.¹⁰² The genesis of [S₃]˙⁻ can be attributed to the formation of polysulfides from sulfur(0) and sulfide (S²⁻), which were also detected in the XANES spectra. The simultaneous creation of aluminosilicates with a zeolitic structure provides a trap for the blue [S₃]˙⁻ radical anions.

X-ray photoelectron spectroscopy (XPS) also provides information about the energies of core electrons. Typically, Al K_α (1487 eV) excitation is used as the X-ray source and 2p binding energies in the region 160–172 eV have been determined for sulfur compounds. In 2015 Fantauzzi et al. utilized XPS for the identification of sulfides and polysulfides on surfaces.⁸⁹ Commercial samples of anhydrous Li₂S and Na₂S, Na₂S₄ (90–95%; <5% H₂O) and potassium polysulfide K₂S_n were analyzed by this technique and it was possible to assign the S(2p) binding energies for sulfide S²⁻ and the central and terminal S atoms in polysulfide chains. Sulfur in the terminal position is shifted by ca. 1.6 eV to lower binding energies compared to sulfur in a central position, confirming that the negative charge is mainly located at the end of polysulfide chains (Section 4).

In 2018 Cato et al. applied XPS to the determination of the ratio of polysulfide radical anions [S₃]˙⁻/[S₂]˙⁻ in ultramarines ranging in colour from deep blue to green.¹⁰³ The samples under investigation were swatches of synthetic ultramarine paints taken from the 1939 catalogue of a German manufacturer. Importantly, the same samples were also analyzed by Raman spectroscopy, which is the method of choice for determining [S₃]˙⁻/[S₂]˙⁻ ratios (Section 3.1). The sulfur 2p spectra revealed peaks in the regions 161.6–161.9, 164.3–165.2 and 168.8–169.2 eV assigned to sulfide (S²⁻), sulfite (S⁴⁺) and sulfate (S⁶⁺), respectively. In addition, peaks at 162.9 and 163.8 eV were attributed to yellow [S₂]˙⁻ and blue [S₃]˙⁻ chromophores, respectively.¹⁰³ The XPS measurements and the Raman spectra showed the same trend for the [S₃]˙⁻/[S₂]˙⁻ ratio with markedly lower values for green compared to blue samples.

In the context of the assignments above for sulfur species in ultramarines, the interpretation of the sulfur 2p XPS spectrum of synthetic ultramarine red, prepared as described in Section 3.5,⁸⁴ should be regarded as tentative except for the ubiquitous peak for sulfate, which is observed at 168.7 eV. In addition, a peak at 162.7 eV is assigned to polysulfide anions [S_n]²⁻, although the expected difference in energies for terminal and central S atoms (vide supra) is not mentioned. A third peak at 164.0 eV is attributed to a sulfur(0) species, possibly S₄.⁸⁴

In 2013 the high-resolution photoelectron spectrum using slow electron velocity-map imaging was reported for cryogenically cooled [S₃]˙⁻.¹⁰⁴ The electron affinity was found to be 2.6330(9) eV and the wavenumber of the bending mode ν₂ was 260(2) cm⁻¹, a somewhat lower value than determined for gaseous S₃ (for more details on the vibrational spectrum see Section 3.1).

4 Computational studies of polysulfide dianions and radical anions

Reliable thermodynamic data on polysulfide di- and monoanions have only become available in recent years through high-level quantum-mechanical calculations taking the special requirements for second-row elements into account. As shown by Wong in 2003, higher levels of theory than those needed to obtain the underlying geometries are required to obtain satisfactory relative energies of isomeric structures as well as reliable activation energies. MP2 is the most economical and popular method to incorporate electron correlation. To predict thermochemical data with an accuracy of ±8 kJ mol⁻¹, quantum-chemical calculations using high-level correlation methods such as QCISD(T) and CCSD(T) in conjunction with very large basis sets are required.⁶¹

For sulfur compounds without highly electronegative substituents the Hartree–Fock (HF) method reproduces the experimental geometries reasonably well. Density Functional Theory (DFT) is nowadays the most frequently used method because of its relatively low cost. However, as shown below, HF methods yield more realistic geometries and vibrational frequencies of polysulfide dianions than DFT methods such as B3LYP, B3P86 and B3PW91. Nevertheless, the relatively new DFT methods G3X and G3X(MP2) in conjunction with B3LYP/6-31+G(2df,p) optimized geometries do yield reliable energies and enthalpies. The G3X(MP2) method represents a modification of the G3(MP2) method with the addition of a g polarization function to the G3Large basis set for the second-row atoms at the HF level.⁶¹ All three features are important for the proper description of sulfur-containing species including radicals and only data obtained at this or comparably high levels of theory will be discussed in this section.

The electron affinities of all neutral sulfur molecules S_n are positive, i.e. addition of an electron with formation of a radical anion is exothermic and exergonic both in the gas phase and in polarizable media with dielectric constants of between 8 (THF) and 78 (water). However, the addition of a second electron with formation of dianions is endothermic and endergonic in the gas phase, but exothermic and exergonic in the mentioned polarizable media.⁴⁴ Therefore, the theoretical treatment of isolated anions [S_n]²⁻ with n = 5–8 is problematic since their gas phase structures do not correspond to global minima on the potential energy hypersurface. Especially density functional theory does not always reproduce the experimental geometrical and vibrational data correctly as shown by the data for [S₆]²⁻ in Tables 3 and 4.

Table 3 Bond lengths (pm) of the hexasulfide dianion (atom numbering along the sulfur chain from left to right; molecular symmetry C₂) as determined by X-ray crystallography of Cs₂S₆ (row 2) and by different quantum-chemical calculations for either the gas phase (rows 3 and 5) or a polarizable continuum of dielectric constants ε = 8 (THF) and 78 (water)

	S1–S2	S2–S3	S3–S4	S4–S5	S5–S6	Ref.
Cs2S6 (s.)	203.7	204.3	206.3	206.4	202.5	21
[S6]^2− (g.)	209.1	208.5	208.7	208.5	209.1	45
[S6]^2^− PCM	207.4	207.7	209.2	207.7	207.4	105
[S6]^2− (g.)	207.4	209.4	215.8	209.7	207.4	44
[S6]^2− (ε = 8)	207.5	208.3	213.2	208.3	207.5	44
[S6]^2− (ε = 78)	207.6	208.2	213.0	208.2	207.6	44

---

Table 4 Vibrational data for the helical hexasulfide dianion of C₂ symmetry in solid Cs₂S₆ (a: symmetric, b: asymmetric mode) as well as in the gas phase and in a polarizable continuum. Given are the wavenumbers (cm⁻¹) of the SS stretching modes recorded by Raman spectroscopy (rows 2 and 3), or predicted from assumed force constants (row 4) and by quantum chemical calculations using DFT methods in the gas phase (row 5) as well as for a polarizable continuum of dielectric constants ε = 8 (row 6), in THF (row 7) and in water (ε = 78)

Symmetry	a	b	a	b	a	Ref.
Cs2S6 (s.)	503	493	449	423	408	37
Cs2S6 (s.)	505	494	450	424	410	21
[S6]^2− (g.)	501	497	478	447	425	36
[S6]^2− (g.)	485	477	409	399	313	44
[S6]^2− (ε = 8)	488	483	427	426	354	44
[S6]^2− (in THF)	482	479	426	425	358	62
[S6]^2− (ε = 78)	486	483	430	428	360	44

---

In Table 3 the S–S bond lengths of Cs₂S₆ determined in 2015 by an X-ray crystallographic study are compared to the theoretical results obtained by different methods. Cederbaum et al. used a SCF Hartree–Fock technique with double-ζ basis set augmented with d-type polarization and s-type diffuse functions in 1998 (row 3).⁴⁵ Evidently the calculated structural data agree reasonably well with the experimental results. The same holds for the bond lengths obtained by Tossell in 2012 with the cc-pvTZ CCSD method and PCM correction (row 4; without any specification of the dielectric constant).¹⁰⁵ In contrast, the density functional calculations used later by other authors gave a too long central bond S₃–S₄ of the hexasulfide dianion (row 5) which, however, became shorter if the polarizability of the solvent was increased (rows 6 and 7).

The long central bond calculated for the hexasulfide anion by DFT methods also results in too low a wavenumber for the corresponding SS stretching mode, as shown in Table 4. This mode of a symmetry has been predicted by a normal coordinate analysis at 425 cm⁻¹ using force constants from S₈ and [NH₄]₂[S₅] (row 4), but was predicted by DFT methods in the region 310–360 cm⁻¹ (rows 5–7) while it has been observed by several authors near 409 cm⁻¹ in solid Cs₂S₆ (rows 2 and 3).

Similar predictions using DFT methods have been made for the penta-, hepta- and octasulfide dianions for which one SS stretching mode each was calculated in the region 360–380 cm⁻¹ (with ε = 8) which is silent in the Raman spectra of corresponding salts.⁴⁴ Evidently, the cations in crystalline polysulfides withdraw enough electron density from the anions that the sulfur chain is stabilized and SS bond lengths shrink to normal single-bond values compared to the theoretical gas phase values as shown in Table 3.

As mentioned before, gaseous polysulfide dianions are subject to electron autodetachment and homolytic dissociation (Coulomb explosion). Symmetrical dissociations are more favourable thermodynamically than asymmetrical ones, but the activation energies for these processes are not known with certainty, especially for condensed phases. Vijayakumar et al. estimated the activation energies for the symmetrical cleavage of the hypothetical gaseous tetra- and hexasulfide dianions producing 2[S₂]˙⁻ and 2[S₃]˙⁻, respectively.¹⁰⁶ Using the functional PBE-D3 with all-electron TZ2P basis sets the cleavage of the central bonds was found to be slightly exothermic with activation energies of 1.25 eV (tetrasulfide) and 0.25 eV (hexasulfide). However, the overall reaction energies of ca. 0.20 eV do not agree with the results obtained at higher levels of theory which predict these reactions to be much more exothermic in the gas phase (see below, Table 5).

Table 5 Standard reaction enthalpies ΔH° and Gibbs energies ΔG° for the dissociation of polysulfide dianions at 298 K and partly at 600 K (in kJ mol⁻¹), both in the gas phase and with PCM corrections for the simulation of solvent effects using ε = 8.0 and 78.0 (calculated by the modified G3X(MP2) theory). Reproduced from ref. 44 with permission from Wiley. Copyright 2013

	Reaction	Symmetry of products	gas phase	PCM (ε = 8)	PCM (ε = 78)
1	[S8]^2− → 2[S4]˙^−	C 2v	−109.1/−158.2	+72.5/+22.2 (−23.5)	+96.7/+46.6
2	[S8]^2− → [S3]˙^− + [S5]˙^−	C 2v + Cs	−93.0/−139.9	+79.7/+31.4 (−12.4)	+102.8/+54.8
3	[S7]^2− → [S3]˙^− + [S4]˙^−	C 2v + C2v	−143.8/−190.3	+54.8/+6.4 (−37.3)	+97.1/+33.3
4	[S6]^2− → 2[S3]˙^−	C 2v	−187.0/−230.7	+34.2/−11.5 (−52.4)	+64.9/+19.0
5	[S5]^2− → [S2]˙^− + [S3]˙^−	D ∞h + C2v	−175.5/−215.0	+63.1/−7.2 (−16.1)	+96.9/+ 55.6
6	[S4]^2− → 2[S2]˙^−	D ∞h	−179.2/−215.0	+86.5/+49.9 (−14.9)	+124.0/+87.2

---

At the high-level G3X(MP2) theory with geometry optimization at the B3LYP/6-31+G(2df,p) level the dissociation enthalpies and Gibbs energies for the symmetrical and asymmetrical dissociation of penta- through octasulfide show that these reactions are all strongly exothermic and exergonic in the gas phase, but with two exceptions are endothermic and endergonic in a polarizable continuum (Table 5).⁴⁴ In other words, the polarizable phase stabilizes these anions. The two exceptions are the slightly negative Gibbs free energies ΔG° for the homolytic dissociation of penta- and hexasulfide dianions in a continuum of ε = 8.0 (rows 4 and 5). This result is consistent with the observation that the trisulfide radical anion has been observed in many experiments and even in natural samples, unlike the di- and especially the tetrasulfide radical ions which have been observed more rarely. The value of 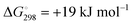for ε = 78 for the dissociation of hexasulfide ions in water is in excellent agreement with the results reported by Tossell, who obtained 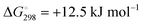in 2012 by Hartree–Fock methods.¹⁰⁵ The finding that the dissociation reactions are endergonic with ε = 78 indicates that dianions are more stabilized than the monoanions by this type of continuum.

At 600 K all dissociation reactions listed in Table 5 are predicted to be exergonic in a polarizable continuum of ε = 8 (column 5) as in high-temperature Na–S batteries (see below). Solvents such as n-butyl acetate, ethylene glycol dimethyl ether (glyme), THF, trifluoroacetic acid, o-dichlorobenzene and even pyridine show dielectric constants at 25 °C in the range of 5 to 12, and the same holds for water at the critical point of 374 °C.

In the following parts of this section structural details and thermodynamic data of the radical monoanions and the related dianions, both for the free (gaseous) species and with the PCM corrections for the two polarizable phases ordered by increasing number of sulfur atoms, are discussed.

The diatomic species [S₂]˙⁻ and [S₂]²⁻ are of D_∞h symmetry with the following calculated bond lengths: [S₂]˙⁻ 202.8 pm (gas), 202.7 pm (PCM8), 202.7 pm (PCM78); [S₂]²⁻ 218.1 pm (PCM8), 218.1 pm (PCM78).⁴⁴ The experimental S–S bond length of the anion in α-Na₂S₂ is 215 pm which is in good agreement with the PCM-corrected value of 218 pm. The disulfide dianion cannot be calculated in the gas phase due to the expected electron autodetachment.

The triatomic ions [S₃]˙⁻ and [S₃]²⁻ are of C_2v symmetry. The trisulfide radical anion has been most thoroughly studied by several theoretical methods to predict its structure, vibrational spectrum and UV-vis absorption wavelengths. The most elaborate calculation of this radical by Koch et al. using highly correlated MRCI and CCSD(T) wavefunctions together with large atomic natural orbital (ANO) basis sets confirmed the C_2v structure as the global minimum on the potential energy surface and predicted the D_3h isomer as higher in energy by ca. 170 kJ mol⁻¹.¹⁰⁷ The MRCI+Q/ANO6532 calculation yielded S–S bond lengths of 200.2 pm and an SSS bond angle of 115.1°. The computed electron affinity of S₃ of 2.10 eV is in perfect agreement with photoelectron spectroscopic results (2.09 eV).¹⁰⁷ Other methods gave similar geometrical values, for example the following bond lengths d (pm) and angles α obtained at the B3LYP/6-31+G(2df,p) level: [S₃]˙⁻ 201.8/115.8° (gas), 201.7/114.4° (PCM8), 201.7/114.1° (PCM78); [S₃]²⁻ 213.3/114.4° (gas), 211.9/111.2° (PCM78), 211.8/110.5° (PCM78). The NPA atomic charges of the terminal atoms of [S₃]˙⁻ and [S₃]²⁻ are −0.53 and −0.86 in the gas phase and −0.55 and −0.90, respectively, with both PCM8 or PCM78 correction.⁴⁴ In solid K₂S₃ the experimental geometrical parameters of the anion are d_SS = 208.3 pm and α = 105.4°,⁴⁴ and in the room temperature form of Cs₂S₃: d_SS = 212.6 pm and α = 106°.¹⁹

The unpaired electron of [S₃]˙⁻ resides in an antibonding π* orbital of b₁ symmetry (SOMO) to which all atoms contribute almost equally.¹⁰⁵ The dissociation energy as well as the equilibrium geometries and harmonic wavenumbers for six electronically excited states of [S₃]˙⁻ have been reported by Linguerri et al. in 2008 and the dissociation of [S₃]˙⁻ into S₂ and S˙⁻ was predicted to be strongly endothermic.⁵⁷

Reliable experimental information on the tetrasulfide radical anion is scarce, but several theoretical calculations on its structure, fundamental vibrational modes, UV-vis spectrum and thermodynamics have been published.^{44,60,108,109} Contradictory results have been obtained since DFT calculations on sulfur compounds without additional energy refinements sometimes yield relative energies in conflict with results obtained at a higher level of theory. As shown above, molecular structures of dianions do not always agree with well-established experimental data such as X-ray structures. At the highest theoretical level applied so far [S₄]˙⁻ forms a cis-planar chain of C_2v symmetry both in the gas phase and in a polarizable continuum of ε = 78. However, the trans-isomer of C_2h symmetry with a centre of symmetry is only slightly less stable, by in the gas phase and by +15.3/+14.0 kJ mol⁻¹ in the simulated aqueous phase (ε = 78).⁴⁴ Geometrical parameters and atomic charges are given in Fig. 11.

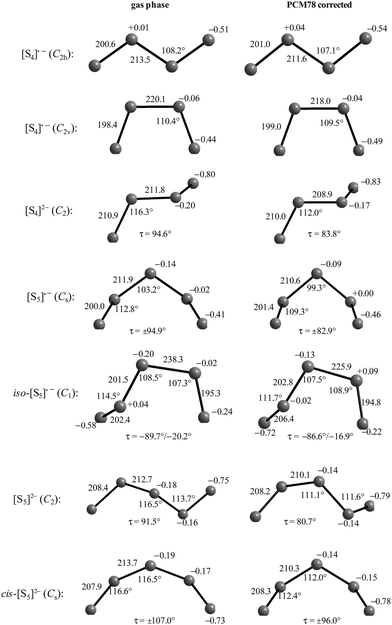Fig. 11 Calculated structures and NPA atomic charges of the more stable isomers of the anions [S_n]˙⁻ and [S_n]²⁻ (n = 4 and 5) in the gas phase (left) and in a polarizable continuum of ε = 78 (right). Bond lengths are in pm. Reproduced from ref. 44 with permission from Wiley. Copyright 2013.

The most stable tetrasulfide dianion is of C₂ symmetry as in the crystal structures of the corresponding alkali-metal salts.⁴⁴ The PCM78-corrected bond lengths (d) and bond angles (α) calculated for [S₄]²⁻ (Fig. 11) are in better agreement with the experimental data for solid α-Na₂S₄ [d = 206.1 (twice) and 207.4 pm, α = 109.8°]⁴⁰ than the calculated gas-phase geometry. An isomeric pyramidal tetrasulfide anion of C_3v symmetry (not shown) in analogy to the isovalent sulfite ion [SO₃]²⁻ is by only 22.3 kJ mol⁻¹ (gas phase), 10.3 kJ mol⁻¹ (PCM8) or 8.9 kJ mol⁻¹ (PCM78) less stable than the C₂ symmetric chain structure. At 600 K the relative Gibbs energy of this C_3v isomer has been predicted as 13.0 kJ mol⁻¹. This isomer has in fact been observed in 2018, trapped in a cage of a zeolite structure and surrounded by sodium cations which evidently stabilize this novel species (see Fig. 2).^32a

Calculated bond lengths, bond angles and torsion angles (τ) of the more stable pentaatomic polysulfide anions are given in Fig. 11. The addition of an electron to the cyclic molecules S₅ to S₈ is strongly exothermic in the gas phase and even more so in a polarizable continuum (Table 6), rows 1–4. The resulting radical anions are of either C₂ or C_s symmetry (Fig. 11).

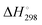Table 6 Reaction enthalpies and Gibbs energies ΔG° at 298 K (kJ mol⁻¹) for the reduction of cyclic sulfur species both in the gas phase and with PCM corrections for ε = 8.0 and 78.0, calculated by the modified G3X(MP2) theory; product symmetries in the gas phase are also given. Reproduced from ref. 44 with permission from Wiley. Copyright 2013

Entry	Reaction	Symmetry of products	gas phase	PCM8	PCM78
1	S8 + e^− → [S8]˙^−	C 2	−151.1/−162.4	−294.5/−305.2	−315.3/−326.1
2	S7 + e^− → [S7]˙^−	C s	−162.1/−171.8	−312.5/−321.4	−334.1/−342.7
3	S6 + e^− → [S6]˙^−	C 2	−151.1/−160.4	−308.7/−317.6	−330.7/−339.6
4	S5 + e^− → [S5]˙^−	C s	−177.9/−189.0	−350.6/−360.0	−375.1/−383.9
5	[S8]˙^− + e^− → [S8]^2−	C 2	+16.2/+ 8.0	−379.5/−385.1	−432.5/−38.1
6	[S7]˙^− + e^− → [S7]^2−	C 2	+39.8/+34.0	−377.2/−381.1	−432.9/−437.0
7	[S6]˙^− + e^− → [S6]^2−	C 2	+68.2/+ 62.5	−376.1/−380.2	−435.9/−439.8
8	S8 + 2e^− → [S8]^2−	C 2	−134.9/−154.4	−673.9/−690.3	−747.8/−764.2
9	S7 + 2e^− → [S7]^2−	C 2	−122.2/−137.8	−669.7/−702.5	−767.0/−779.7
10	S6 + 2e^− → [S6]^2−	C 2	−82.9/−97.9	−684.8/−697.8	−766.5/−779.4

---

The further reduction of the cyclic radical anions to the helical polysulfide dianions is endothermic in the gas phase, but strongly exothermic and exergonic in polarizable media (Table 6, rows 5–7). The first step of a hypothetical two-electron reduction of the neutral homocycles (rows 1–4) is more exothermic than the second step is endothermic (rows 5–7); therefore, the overall enthalpy change for the formation of the dianions from neutral molecules S_n is surprisingly exothermic for n > 5 (rows 8–10). However, this formal stability of the gaseous polysulfides is questionable since they are all unstable in the gas phase with respect to homolytic dissociation at one of the central bonds producing two radical monoanions (Table 5). This homolytic reaction is only endothermic and endergonic at 298 K in polarizable media; at 600 K all six dissociation reactions shown in Table 5 are exergonic in a medium of ε = 8.0 (see the data in parentheses).

Neither the neutral cyclic S₅ molecule nor the radical anion [S₅]˙⁻ have definitely been observed in solution or in the solid state. According to high-level quantum-chemical calculations their most stable isomers are both of C_s symmetry. However, S₅ is cyclic while the pentasulfide radical anion [S₅]˙⁻ differs from S₅ by the large internuclear distance of 473.5 pm (gas phase) or 392.0 pm (PCM78) between the terminal atoms of the sulfur chain (Fig. 11). Other chain-like [S₅]˙⁻ isomers of C₁ and C₂ symmetry are less stable. However, the structure of the novel species iso-[S₅]˙⁻ shown in Fig. 11 is by only 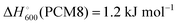above the C_s symmetric global minimum structure, despite its unusual asymmetrical geometry (Table 7, entry 3). Because of its long S–S bond of >225 pm this isomer may be considered as an adduct between the radical [S₃]˙⁻ and triplet state S₂(³Σ_g) in analogy to the adduct between [S₃]˙⁻ and O₂(³Σ_g), which will be discussed below (Section 5.3). Polysulfide species like iso-[S₅]˙⁻ may be present in high temperature polysulfide melts and fluids.⁴⁴

Table 7 Reaction enthalpies and Gibbs energies ΔG° at 298 K and – in parentheses – at 600 K (all in kJ mol⁻¹) for the isomerization of some polysulfide anions both in the gas phase and with PCM corrections for ε = 8.0 and 78.0, calculated by the modified G3X(MP2) theory. Reproduced from ref. 44 with permission from Wiley. Copyright 2013

Entry	Reaction	gas phase	PCM8	PCM78
1	[S4]˙^− (C2v)→ iso-[S4]˙^− (C2h)	+4.6/+4.2	—	+15.3/+14.0
2	[S4]^2− (C2) → [S4]^2− (C3v)	+19.5/+22.3	+7.8/+10.3 (+13.0)	+6.5/+8.9
3	[S5]˙^− (Cs)→ iso-[S5]˙^− (C1)	+4.3/+0.7	+3.5/+2.2 (+1.2)	+2.4/+1.0
4	[S5]^2− (C2) → cis-[S5]^2− (Cs)	+12.1/+11.4	+8.0/+7.6 (+7.1)	+6.1/+5.8
5	[S5]^2− (C2) → iso-[S5]^2− (C1)	+31.3/+31.9	+19.3/+20.5 (+21.9)	+18.2/+19.6
6	[S5]^2− (C2) → [S5]^2− (Td)	+101.0/+109.1	+64.5/+71.4 (+78.8)	+59.4/+66.2
7	[S6]^2− (C2) → iso1-[S6]^2− (C2v)	+39.9/+35.2	+7.7/+ 8.5 (+9.8)	+2.8/+4.2
8	[S6]^2− (C2) → iso2-[S6]^2− (C1)	+27.6/+27.0	+18.7/+19.5(+20.4)	+17.5/+18.2

---

The pentasulfide dianion is of C_s symmetry in the crystal structure of α-Na₂S₅ but of C₂ symmetry in crystalline ε-Na₂S₅, K₂S₅, Rb₂S₅ and Cs₂S₅.^18,44 Both in the gas phase and with PCM corrections the helical C₂ symmetric isomer represents the global minimum structure with torsion angles of 91.5° (gas) and 80.7° (PCM78) (Fig. 11). Since the rotational barriers of sulfur chains and the energy differences between rotational isomers are small, the C_s symmetric isomer with a relative Gibbs energy of +5.8 kJ mol⁻¹ at 25 °C (PCM78-corrected) can be expected to exist in addition to the C₂ isomer, both in pentasulfide melts and other polysulfide solutions (Table 7). The geometry of cis-[S₅]²⁻ calculated with the PCM78 correction (Fig. 11) is in much better agreement with the data of α-Na₂S₅ (d₁₂ = 206.1 and d₂₃ = 206.6 pm, α = 107.3° and 108.1°, τ = ±88.6°) than the calculated gas-phase geometry demonstrating the usefulness of the polarizable continuum model.⁴⁴

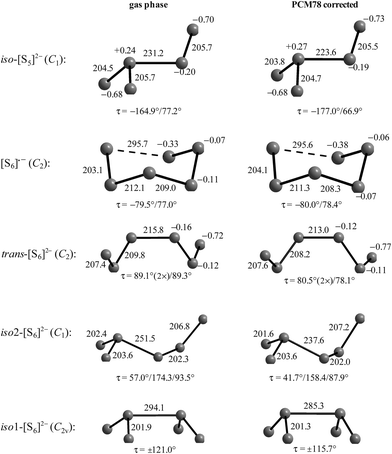Fig. 12 Calculated structures and NPA atomic charges of isomeric anions [S_n]˙⁻ and [S_n]²⁻ (n = 5 and 6) in the gas phase (left) and with PCM correction for ε = 78 (right); bond lengths in pm. Reproduced from ref. 44 with permission from Wiley. Copyright 2013.

The hexasulfide radical anion [S₆]˙⁻ is the only polysulfide monoanion, which has been prepared in pure form and structurally characterized as the salt [Ph₄P][S₆].⁹ The cyclic anion has two long bonds of 263 pm connecting two S₃ units and the average S–S bond length within the S₃ fragments is 206 pm, cf. 205 pm in S₈. Density functional calculations yielded a global minimum structure of C₂ symmetry in which the two S₃ fragments are connected by one normal (212.5 pm) and just one very long (294.3 pm) bond. However, ab initio MP2/6-31+G* computations favoured a chair conformation of C_2h symmetry. At the B3LYP/6-31+G(2df,p) level the radical is of C₂ symmetry with a conformation similar to that of the homocyclic S₆ molecule (D_3d), but again with one very long (“broken”) bond of 295.7 pm in the gas phase or 295.6 pm with the PCM78 correction, respectively.⁴⁴ All other bonds have expected lengths of between 203 and 212 pm (Fig. 12). The difference between the experimental and calculated structures may be explained by a disorder of the anions in the crystal structure. In addition, it has been shown that the observed structure is a transition state in the gas phase (at the DFT level) which is only slightly less stable than the global minimum structure of C₂ symmetry.⁹ Also, the anion-cation interaction may play a role for the relative stabilities of these conformers.

The experimental structure and vibrational spectrum of the helical dianion [S₆]²⁻ have been discussed in Section 3.1; its calculated structure is shown in Fig. 12. The branching of [S₆]²⁻ has also been studied computationally, since an isomeric hexasulfide anion [(S₂)S–S(S₂)]²⁻ (iso1-[S₆]²⁻) in analogy to the isovalent dithionite anion [S₂O₄]²⁻ has been claimed as a constituent of molten Cs₂S₆ on the basis of Raman spectra taken after quenching the melt from 300 °C to 25 °C.³⁷ At the G3X(MP2) level of theory this branched isomer is of C_2v symmetry (Fig. 12) and was found to be less stable than the helical chain, by 35.2 (gas phase) and 8.5 kJ mol⁻¹ (PCM8); at 600 K the relative Gibbs energy is 9.8 kJ mol⁻¹ (Table 7, entry 7).⁴⁴ Consequently, small concentrations of branched polysulfide anions can be expected in sulfur-rich polysulfide melts at temperatures near 300 °C (as in Na–S batteries). However, such melts contain the trisulfide radical anion which, on cooling, could recombine to the C_2v symmetric hexasulfide dianion, as discussed below; the latter may return to the helical ground-state conformation on annealing.

The hepta- and octasulfide radical anions [S₇]˙⁻ and [S₈]˙⁻ are probably the most important species in the primary reduction processes occurring at the sulfur electrodes in sulfur-based batteries. So far, both radicals have been observed only by mass spectrometry. Surprisingly, their calculated structures strongly resemble those of the related homocycles. The neutral chair-like homocycle S₇ is of C_s symmetry in the crystal structures of γ- and δ-S₇,^2a and G3X(MP2) calculations predicted the same symmetry for [S₇]˙⁻ both in the gas phase and with PCM corrections.⁴⁴ The main geometrical difference between S₇ and [S₇]˙⁻ is the large internuclear distance of 308 pm between the terminal atoms of the sulfur chain of [S₇]˙⁻ which could be considered as a “broken bond” since the van der Waals distance between sulfur atoms is 350 pm. In cyclo-S₇ the longest bond is of length 217.5 pm; all other bonds and the torsion angles of [S₇]˙⁻ are very similar to those of S₇. On further reduction of [S₇]˙⁻ the helical chain-like dianion [S₇]²⁻ is formed in which all bonds are of normal length: 206.4–212.5 pm in the gas phase and 207.2–210.6 pm with PCM78 correction (Fig. 13). The latter data are consistent with the range of bond lengths determined by X-ray crystallography of six ionic heptasulfides with large cations (196.3–209.8 pm).⁶

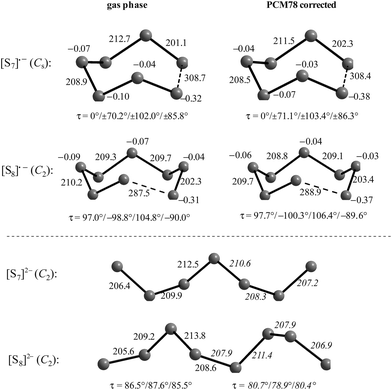Fig. 13 Calculated structures and NPA atomic charges of the anions [S_n]˙⁻ (n = 7 and 8) in the gas phase (left) as well as with PCM78 correction (right). Bond lengths in pm. For the two helical dianions [S_n]²⁻ (n = 7 and 8) shown at the bottom the data in italics are with PCM78 correction, otherwise for the gas phase. Reproduced from ref. 44 with permission from Wiley. Copyright 2013.

In orthorhombic α-S₈ the average experimental bond length is 204.6 pm (ideal symmetry D_4d). One-electron reduction of S₈ produces a radical of almost identical conformation, which is of C₂ symmetry mainly due to one very long bond of 287.5 pm (gas phase), 288.2 pm (PCM8) or 288.9 pm (PCM78). The remaining bonds of [S₈]˙⁻ vary in length between 202.3 and 210.2 pm (Fig. 13) with the typical bond-length alternation frequently observed for cumulated sulfur–sulfur bonds. In contrast, the octasulfide dianion [S₈]²⁻ is most stable as a helical chain of C₂ symmetry which has two relatively long symmetry-related bonds of 213.8 pm (gas phase), 211.5 pm (PCM8) and 211.4 pm (PCM78) at the B3LYP/6-31+G(2df,p) level (Fig. 13).⁴⁴ This feature may be an indication of the ease of the exothermic thermal dissociation into the two radical monoanions [S₃]˙⁻ and [S₅]˙⁻ (Table 5). For the dianion of the salt [Et₃NH]₂[S₈] the range of bond lengths has been determined crystallographically as 204.1–207.3 pm, which may however be influenced by hydrogen bonds to the cations; the motifs of the chiral anions in this salt are ++−++ and −−+−− (enantiomers of symmetry C₂) (see Section 2 for an explanation of the nomenclature for these motifs).^26b The thermodynamic properties of [S₇]˙⁻, [S₈]˙⁻, [S₇]²⁻ and [S₈]²⁻ will be discussed further in Section 5.1.

5 Significance and applications of polysulfides and polysulfide radical anions

5.1 Sulfur-based batteries

The reaction of alkali metals with elemental sulfur to produce polysulfides is highly exothermic, especially with a high metal-to-sulfur ratio resulting in mono- and disulfides which are characterized by large lattice energies. These reactions can be reversed by electrolysis, provided the polysulfides are either soluble or can be melted without decomposition. Enormous efforts have been undertaken in recent years to utilize such reactions for energy storage systems since lithium and sodium are environmentally friendly metals while elemental sulfur is an inexpensive by-product from refineries. Since the high-temperature solvent-free sodium–sulfur battery is the simplest device from a chemical point of view it will be discussed first followed by a critical evaluation of the rather complex polysulfide redox chemistry in room-temperature sodium–sulfur and lithium–sulfur batteries, which normally require a solvent and an additional electrolyte. The first descriptions of lithium– and sodium–sulfur secondary batteries have been published in the 1960s, and thousands of papers on these subjects have appeared since. The technical aspects of sulfur-based batteries have been outlined in detail in recent reviews.^110–112 The use of magnesium¹¹³ as well as zinc¹¹⁴ as anode materials in sulfur-based batteries has also been reported, but these devices are less well-studied and will not be discussed here. Furthermore, polysulfides play an important role in certain redox-flow batteries.¹¹⁵

5.1.1 High-temperature sodium–sulfur (Na–S) batteries. In high-temperature (HT) sodium–sulfur batteries liquid sodium forms the anode and liquid sulfur together with porous carbon the cathode. The electrodes are separated by a solid ceramic electrolyte consisting of β′′-alumina (Na[Al₁₁O₁₇] doped with MgO, TiO₂ and/or Li₂O), which is a conductor for sodium cations at high temperatures. The insulating liquid elemental sulfur is sucked into a carbon felt or a similar graphite-based porous matrix to make it electrically conducting. Since elemental sulfur is only slightly soluble in sulfur-rich Na₂S_n melts and sodium polysulfides are almost insoluble in liquid sulfur, the so-called sulfur electrode consists of the following phases: solid carbon, liquid as well as gaseous sulfur and liquid polysulfides. The battery is contained in a tubular, coated stainless-steel airtight cylinder. Metallic current collectors connect the two electrodes to the outside circuit (Fig. 14).

Fig. 14 Schematic structure of a cell of high-temperature sodium–sulfur batteries.

During discharge sodium cations are generated at the sodium electrode and migrate through the ceramic separator into the sulfur melt to compensate the charge of the polysulfide anions generated by the electrochemical reduction of sulfur. Therefore, the volume of liquid sodium decreases and the volume of the “sulfur/polysulfide electrode” increases during discharge. The formation of solid polysulfides such as high-melting Na₂S₂ must be avoided.

The energy density of the Na–S system is much higher than that of the lead–acid battery and large-scale batteries with more than 1000 single cells and weighing about 100 tons have been established in Japan, USA, China, Korea and elsewhere. The Na–S battery was the first commercialized battery system capable of megawatt-level electric power storage from solar devices and wind-powered electric generators. It has several superior features, including large capacity, high energy density, and long service life, thus enabling a high output of electric power for long periods of time (cell voltage 1.8–1.9 V). Na–S batteries may be charged at night when power demand is low and provide power at daytime to reduce peak power. Moreover, the Na–S battery system can be used as an emergency power supply during power outages and momentary drops in voltage. Disadvantages are the elevated operating temperature and the high manufacturing costs of the ceramic separator as well as corrosion and leakage problems.¹¹⁶ Therefore, the battery is restricted to stationary applications. The following discussion is mainly concerned with the polysulfide redox chemistry rather than the technology of this battery.

The underlying basic chemical reaction is the reversible formation of polysulfides from elemental sulfur by reduction with sodium metal, often simplified to the following equation:

2Na + 1/2S₈ → Na₂S₄ (13)

This reaction is strongly exothermic since the standard enthalpy of formation of crystalline Na₂S₄ at 298 K is −412 kJ mol⁻¹. The reaction can be reversed by electrolysis, and in this way electrical energy can be stored by turning it into chemical energy. It has been demonstrated that several thousand cycles of this type are possible in Na–S batteries. The whole process is carried out at temperatures of 320–350 °C to maintain the polysulfide mixture in the liquid state despite the varying composition of the melt during charging and discharging. The phase diagram of the Na/S system shows that the melting point of Na₂S₄ is 290 ± 5 °C and that other melts of compositions Na₂S_n with n = 3–5 solidify at lower temperatures. However, a discharge of the battery to melt compositions as low as Na₂S₃ is not recommended since it reduces the number of possible cycles due to precipitation of Na₂S₂ resulting from the exothermic disproportionation of the metastable Na₂S₃ to Na₂S₂ and Na₂S₄ (see below). At compositions Na₂S_>5.3 the melt consists of two liquid phases which solidify at 253 °C (Na₂S₅) and 115 °C (β-S₈), respectively.⁴⁴

At the sulfur electrode of Na–S batteries the various sulfur molecules present in liquid sulfur¹¹⁷ are expected to be reduced in a similar fashion as has been observed in solvents by cyclic voltammetry. Sulfur radical anions are likely to be the first products [eqn (14)].

S₈ + e⁻ → [S₈]˙⁻ (14)

To the best of our knowledge, the adiabatic electron affinity of S₈ is unknown but recent DFT calculations predicted a value of 1.57 eV at the G3X(MP2) level⁴⁴ and 2.02 eV at the B3PW91/aug-cc-pVDZ level of theory¹⁰⁹ for the gaseous molecule. For gaseous S₇ slightly higher values were predicted. However, anions are stabilized in molten sodium polysulfides and in polar solvents. This effect has been modeled by PCM calculations using a dielectric constant ε of 8. Under these circumstances the electron affinity of S₈ was predicted as 3.05 eV; with larger values of ε only slightly higher affinities were calculated.⁴⁴

The octasulfide radical anion [S₈]˙⁻ formed in eqn (14) is thermodynamically unstable at the operating temperatures of NaS batteries since its disproportionation to S₈ and [S₈]²⁻ has been predicted to be exergonic by at 600 K. Even the dissociation of [S₈]˙⁻ into [S₃]˙⁻ and cyclo-S₅ is exergonic by −33.4 kJ mol⁻¹ at this temperature and the same holds for a dissociation into [S₂]˙⁻ and cyclo-S₆. The octasulfide dianion [S₈]²⁻ formed from [S₈]˙⁻ by either disproportionation or by addition of another electron is also thermodynamically unstable at 600 K since its dissociation into 2[S₄]˙⁻ or [S₃]˙⁻ plus [S₅]˙⁻ is exergonic, by −23.5 kJ mol⁻¹ and −12.4 kJ mol⁻¹, respectively (Table 5).⁴⁴ Therefore, the polysulfide melt of Na–S batteries will contain a complex mixture of radical monoanions as well as dianions; sulfur radicals had in fact been detected in sodium polysulfide melts by Raman, EPR and UV-Vis spectroscopy already in the 1970s.⁶

Owing to the high concentrations of cations and anions in polysulfide melts there will also be contact ion pairs like [NaS_m]˙, [NaS_n]⁻ and, possibly, also neutral ion-triples [Na₂S_n]. Such species have been studied computationally at the G3X(MP2) level and cyclic as well as cluster-like structures with chelating polysulfide ligands have been identified as global minimum geometries. The calculated structures of [NaS_m]˙ (m = 2, 3) and [NaS_n]⁻ (n = 3–5) both for the gas phase and for a polarizable continuum with ε = 8 are shown in Fig. 15. None of the species [NaS_n]˙ and [NaS_n]⁻ adopts a conformation similar to that of the sulfur homocycle of the same number of atoms and all are of relatively low symmetry: C_2v and C_s for the smaller and C₂ or C_s for the larger ion pairs. The formation of the species [NaS₂]˙ and [NaS_n]⁻ (n = 3–6) from Na⁺ and the corresponding anions is expected to be strongly exergonic, even at 600 K and ε = 8.⁴⁴

Fig. 15 Structures and symmetries of the ion pairs [NaS_n]˙ and [NaS_n]⁻ (n = 2–5) in the gas phase (left) and with PCM8 correction using ε = 8.0 (right), calculated at the B3LYP/6-31+G(2df,p) level of theory; bond lengths are given in pm and atomic charges in electrostatic units. Reproduced from ref. 44 with permission from Wiley. Copyright 2013.

The formation of ion pairs [NaS_n]⁻ by one-electron reduction of the radicals [NaS_n]˙ is also strongly exergonic both in the gas phase and in polarizable phases. Since the absolute values of the corresponding electron affinities increase with the molecular size, electron-transfer reactions of the type

[NaS_x]⁻ + [NaS_y]˙ → [NaS_x]˙ + [NaS_y]⁻ (x < y) (15)

are exothermic and exergonic in the gas phase as well as in the polarizable phases for x < y. Most probably the reduction of [NaS_n]˙ takes place at the sulfur electrode of NAS batteries since in this way the diffusion of negatively charged species such as [S₈]˙⁻ to the equally charged electrode is avoided. The more sulfur-rich ion pairs can then be formed by sulfurization of [NaS_x]⁻ according to eqn (16):

[NaS_x]⁻ + 1/8S₈ → [NaS_x+1]⁻ (16)

Such reactions are exergonic for all x < 5, even at 600 K.⁴⁴

The Coulombic interaction between sodium cations and polysulfide dianions is very strong and the corresponding reaction energies in the gas phase are almost twice as large as for the monoanions. The Gibbs reaction energies in the polarizable phase with ε = 8 are much smaller but still negative, both at 298 and 600 K. It is interesting to note that the homolytic dissociation of [NaS₆]⁻ into [NaS₃]˙ and [S₃]˙⁻ is predicted to be endergonic by +137.8 kJ mol⁻¹ in the gas phase and by +29.8 kJ mol⁻¹ with PCM8 correction at 300 K. This result is in agreement with the detection of the large gaseous ion pairs [NaS_n]⁻ (n = 7–9) by negative ion EI mass spectrometry of aqueous sodium polysulfide solutions although these measurements took place under non-equilibrium conditions.⁴⁷ However, at 600 K the dissociation of [NaS₆]⁻ into [NaS₃]˙ and [S₃]˙⁻ is calculated to be exergonic by −14.4 kJ mol⁻¹ and charged ion pairs of the size similar to [NaS₆]⁻ are therefore predicted to be unimportant in HT Na–S batteries. In other words, polysulfide dianions larger than [S₄]²⁻ are not stabilized by ion-pair formation with Na⁺ at high temperatures.⁴⁴

In the neutral ion triples [Na₂S_n] the coordination numbers of all atoms are either 2 or 2 + 1. The bonding between the cations and the polysulfide ligands is mainly ionic as can be concluded from the NPA atomic charges on the sodium atoms, which decrease with increasing sulfur content from +0.92 in Na₂S₂ (+0.97 with PCM8 or PCM78 correction) to +0.86 in [Na₂S₈]. The coordination numbers of the cations increase with molecular size from 2 in [Na₂S_n] (n = 2–4) to 2 + 1 in [Na₂S₅] and the larger species.⁴⁴

The thermodynamically stable crystalline forms of sodium polysulfides with small unit cells have been calculated in 2016 using the crystal-structure prediction algorithm USPEX (Section 3.6). The formation energies per atom at zero pressure and temperature were found to increase linearly from penta- to monosulfide, while Na₂S₄ and ε-Na₂S₅ were predicted to be the most stable phases at 100 kbar. α-Na₂S₅ and ε-Na₂S₅ were identified as metastable at ambient temperature, transforming to Na₂S₄ and sulfur on heating.¹⁸ Solid Na₂S₃ is another metastable sodium polysulfide, and Na₂S₂ as well as Na₂S₄ also exist as several metastable phases.¹¹⁸

5.1.2 Room-temperature sodium–sulfur (Na–S) batteries. The corrosion and safety problems with HT Na–S systems, as well as their complicated heat management, have led to several investigations on room-temperature (RT) versions of the sodium–sulfur battery in analogy to lithium–sulfur batteries. The chemistry of such RT systems is more complex since a solvent is now needed for the transport of sodium ions from one electrode to the other one (usually an organic carbonate). In addition, an inert sodium salt (e.g. Na[ClO₄], Na[CF₃SO₃]) is added to increase the conductivity.

Nevertheless, there have been some demonstrations of RT sodium–sulfur batteries in the literature, most of which focus on improving the cycling stability on the sulfur cathode side.^111,119 Examples include the use of polyacrylonitrile–sulfur composites, small sulfur molecules in microporous carbon, Nafion separators, carbon interlayers, polymer electrolytes, etc. The application of sodium polysulfide catholytes and sodium sulfide cathodes on high surface area carbon supports have also been demonstrated with some success. However, the overall cycling performance of RT sodium–sulfur batteries, in terms of their specific capacity, Coulombic efficiency and cycle life, still lag behind that of lithium–sulfur batteries. The key to achieve progress is to solve the crucial problems on the sodium metal anode side, which is the major bottleneck in the performance of RT sodium–sulfur batteries. Like in the case of lithium metal, sodium metal anodes are plagued with challenges of poor reversibility, dendrite growth and non-uniform solid electrolyte interfaces on the surface during repeated plating and stripping.

While the polysulfide chemistry of RT Na–S batteries is quite analogous to the high-temperature system discussed above, the thermodynamics at 298 K is slightly different from that at 600 K as will be outlined below. In addition, there is now a competition between polysulfide ligands and the solvent molecules for access to the sodium cations since organic carbonates are well-known O-donor ligands as are the anions of Na[ClO₄] and Na[CF₃SO₃].

There has been a considerable debate in the literature whether the first step in the electroreduction of dissolved S₈ molecules is a one- or a two-electron transfer producing either octasulfide radical anions [S₈]˙⁻ or octasulfide dianions [S₈]²⁻ as primary products. In a series of remarkable studies Levillain et al. have shown by cyclic voltammetry and spectro-electrochemical experiments in the 1990s that S₈ dissolved in dimethylformamide (DMF, ε = 36.7 at 25 °C) yields two reduction waves, at −1.05 V and −1.80 V with a pre-wave at −1.30 V at 298 K versus Fc⁺/Fc. The first wave was assigned to the one-electron transfer producing [S₈]˙⁻ which subsequently disproportionates spontaneously to S₈ and [S₈]²⁻:^44,51

S₈ + e⁻ → [S₈]˙⁻ (17)

2[S₈]˙⁻ → S₈ + [S₈]²⁻ (18)

Similar observations have been made using other aprotic polar solvents. More recent G3X(MP2) calculations have in fact shown that the disproportionation of [S₈]˙⁻ by reaction (18) is exothermic and exergonic in a polarizable continuum at 298 K.⁴⁴ The octasulfide dianion formed in reaction (18) is expected to equilibrate with tetrasulfide radical anions, which may subsequently degrade the octa- to the hexasulfide dianion from which the trisulfide radical ion can be formed explaining the blue colour of such solutions in organic solvents:

[S₈]²⁻ → 2[S₄]˙⁻ (19)

[S₈]²⁻ + [S₄]˙⁻ → [S₆]²⁻ + [S₆]˙⁻ (20)

[S₆]²⁻ → 2[S₃]˙⁻ (21)

Reaction (19) may be triggered by the fact that the octasulfide dianion formed in reaction (18) will probably be vibrationally excited, since it is produced in an exothermic reaction and from a cyclic precursor by a simple electron transfer [eqn (18)]. Relaxation from the cyclic to the chain-like conformation of [S₈]²⁻ releases energy which may initiate subsequent dissociation. In fact, even direct dissociation of 2[S₈]˙⁻ into 2[S₄]˙⁻ plus S₈ has been predicted as exothermic by −12.5 kJ mol⁻¹ and decomposition of 2[S₈]˙⁻ into [S₃]˙⁻, [S₅]˙⁻ and S₈ is exothermic by −5.3 kJ mol⁻¹ at 298 K in a polarizable medium of ε = 8.⁴⁴

Reaction (21) has been predicted to be slightly exergonic in solvents of ε = 8 at 298 K.⁴⁴ The second wave at −1.80 V and the pre-wave at −1.30 V in the voltammograms have been explained by the reduction of polysulfide radical anions to the corresponding dianions, especially [S₃]˙⁻ (−1.80 V) and [S₄]˙⁻ (−1.30 V).⁵¹ However, according to G3X(MP2) calculations the homolytic dissociation of polysulfide dianions [S_n]²⁻ with n = 7 and 8 is slightly endergonic in a polarizable continuum at 298 K, although this may change under the influence of the cations with formation of ion pairs [NaS_n]⁻. The important message here is that dianions are not reducible electrochemically in solutions at 298 K, whereas monoanions are being reduced.^44,51 Other possible reaction channels so far not discussed in the literature for production of radical anions are the following dissociative reductions of [S₈]˙⁻ at the cathode producing simultaneously two radical monoanions rather than [S₈]²⁻:

[S₈]˙⁻ + e⁻ → [S₃]˙⁻ + [S₅]˙⁻ (22)

[S₈]˙⁻ + e⁻ → 2[S₄]˙⁻ (23)

These two reactions have been predicted to be strongly exothermic and exergonic in polar environments of either ε = 8 or 78 (assuming free electrons delivered by the carbon–sulfur electrode).⁴⁴ The reactions (19) through (23) explain the formation of smaller polysulfide anions rather than [S₈]²⁻ on electrochemical reduction of S₈ as has been observed by Zheng et al. in 2016 by in situ derivatization with methyl triflate.⁸² The importance of polysulfide radical anions has only recently been appreciated by the battery research community and the reactions of these radicals with polysulfide dianions seem to be almost unexplored except for information obtained from high-level quantum-chemical calculations, which will be discussed in the following sections.

After polysulfide dianions have been formed they are assumed to undergo several disproportionation as well as sulfurization reactions to produce other anionic polysulfides. However, the often-cited disproportionation reactions according to eqn (24)

2[S_x]²⁻ → [S_y]²⁻ + [S_z]²⁻ (2x = y + z) (24)

have been predicted in 2013 to be endothermic and endergonic both in the gas phase and in polarizable phases and therefore will not take place at 298 or 600 K.⁴⁴ Only the reverse reactions are likely to occur. This view is supported by the Gibbs reaction energies calculated by Assary et al. at the G4MP2-B3LYP/6-31(2df,p) level in 2014.¹²⁰ Instead two other types of reactions by which polysulfide dianions can be interconverted are predicted to be important. The first one is the nucleophilic attack of a small dianion on a larger radical monoanion with formal exchange of sulfur atoms according to eqn (25):

[S_x]²⁻ + [S_y]˙⁻ → [S_m]²⁻ + [S_n]˙⁻ (x < y; m > n; x + y = m + n) (25)

For electrostatic reasons, the attack is expected to occur at one of the almost uncharged central atoms of the radical [S_y]˙⁻ with displacement of a corresponding fragment [S_n]˙⁻. Such reactions have been predicted to be fairly strongly exothermic and exergonic in the gas phase and in polarizable phases.⁴⁴ Furthermore, a novel one-electron transfer reaction between small dianions and larger radical monoanions (without sulfur atom transfer) according to eqn (26) has been suggested in 2013 to distribute the atomic charges more evenly over all participating atoms.⁴⁴

[S_x]²⁻ + [S_y]˙⁻ → [S_x]˙⁻ + [S_y]²⁻ (x < y) (26)

Such reactions are predicted as generally exothermic and exergonic both in the gas phase and in a polarizable continuum with ε = 8 or 78 and both at 298 K and at 600 K.⁴⁴Reactions (25) and (26) allow the observed equilibria between polysulfide dianions of differing chain length to be established in solutions both at room temperature and above. Evidently, the driving force for such reactions is the reduction of the average atomic charges in the products compared to the starting materials (charge equalization).

Aqueous sulfide, hydrogensulfide and polysulfide ions are strong nucleophiles, which attack elemental sulfur at room temperature to yield mixtures of sulfur-rich polysulfides. In principle, sulfurization reactions as in eqn (27) may also occur with radical monoanions [eqn (28)].

[S_n]²⁻ + 1/8S₈ → [S_n+1]²⁻ (27)

[S_n]˙⁻ + 1/8S₈ → [S_n+1]˙⁻ (28)

As far as the radical anions are concerned, only the sulfurization of the disulfide radical ion is exergonic in the gas phase and in polarizable phases. The driving force for this reaction may again be the exceptionally high stability of [S₃]˙⁻. The corresponding sulfurization reactions of [S₃]˙⁻ and [S₄]˙⁻ are predicted to be endothermic and endergonic under all conditions investigated.⁴⁴ This result is in agreement with the finding that [S₂]˙⁻ and [S₅]˙⁻ are difficult to observe in solutions if excess elemental sulfur is present while [S₃]˙⁻ and, to a much lesser extent, [S₄]˙⁻ are almost ubiquitous radicals in inorganic sulfur chemistry.⁸

On the other hand, the sulfurization reactions of the dianions according to eqn (27) are predicted to be exothermic and exergonic for all n < 7, both in the gas phase and in a polarizable medium of ε = 8.0 at 298 K. The corresponding Gibbs reaction energies become smaller as the length of the polysulfide chain [S_n]²⁻ grows. For n = 6 and 7 the production of the hepta- and octasulfide dianions 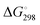is already slightly positive if a dielectric constant of 78.0 is applied.⁴⁴ This result is in perfect agreement with the speciation of anions in aqueous polysulfide solutions saturated with elemental sulfur in which the tri, tetra-, penta- and hexasulfide dianions dominate. Experimental thermodynamic data for the reactions discussed here are not available.

The thermodynamic considerations discussed in this section apply to solvated polysulfide di- and monoanions. However, ion pairs such as [NaS_n]⁻ and [NaS_n]˙ may also be components of the electrolytes in RT Na–S batteries. For the smaller ion pairs (n < 5) the calculated structures are shown in Fig. 15 and those for the larger ones are given in Fig. 16. All species are cyclic for ε = 8 and 300 K with a coordination number of 2 or, in some cases, 2 + 2 for the sodium ions.

Fig. 16 Structures and symmetries of the ion pairs [NaS_n]˙ (left) and [NaS_n]⁻ (right) for n = 6–9 in the gas phase, calculated at the B3LYP/6-31+G(2df,p) level of theory; bond lengths are given in pm and atomic charges in electrostatic units. Reproduced from ref. 44 with permission from Wiley. Copyright 2013.

The formation of ions [NaS_n]⁻ from Na⁺ and the corresponding polysulfide dianions is exothermic and exergonic for all values of n = 2–8 and at ε = 8 (Table 8).

Table 8 Reaction enthalpies and Gibbs energies ΔG° at 298 K (in kJ mol⁻¹) for the formation of the most stable sodium polysulfide ion pairs [NaS_n]˙ and [NaS_n]⁻ as well as ion triples [Na₂S_n] both in the gas phase and with PCM corrections for ε = 8.0, calculated at the modified G3X(MP2) level of theory (for more data, see ref. 44)

Entry	Reaction	gas phase	PCM8
1	Na^+ + [S2]˙^− → [NaS2]˙	−529.4/−505.3	−50.9/−30.3
2	Na^+ + [S3]˙^− → [NaS3]˙	−514.9/−485.4	−40.9/−15.3
3	Na^+ + [S4]˙^− → [NaS4]˙	−503.8/−476.5	—
4	Na^+ + [S6]˙^− → [NaS6]˙	−483.8/−457.1	—
5	Na^+ + [S7]˙^− → [NaS7]˙	−494.6/−460.5	—
6	Na^+ + [S8]˙^− → [NaS8]˙	−429.9/−404.1	—
9	[NaS2]^− + [NaS3]˙ → [NaS2]˙ + [NaS3]^−	−61.3/−62.1	−18.6/−19.2
10	Na^+ + [S2]^2− → [NaS2]^−	—	−110.0/−87.6
11	Na^+ + [S3]^2− → [NaS3]^−	−958.8/−928.4	−104.7/−77.3
12	Na^+ + [S4]^2− → [NaS4]^−	−938.9/−905.5	−103.8/−74.6
13	Na^+ + [S5]^2− → [NaS5]^−	−910.4/−873.0	−98.7/−68.1
14	Na^+ + [S6]^2− → [NaS6]^−	−888.5/−853.9	−86.7/−56.7
15	Na^+ + [NaS2]^− → [Na2S2]	−600.1/−570.7	−74.6/−48.6
16	Na^+ + [NaS3]^− → [Na2S3]	−572.9/−539.4	−65.4/−37.7

---

The question then arises whether ion-pair formation stabilizes the polysulfide dianions with respect to homolytic dissociation at one of the central S–S bonds. However, it turns out that the opposite is true. For example, the reaction in eqn (29)

[NaS₆]⁻ → [NaS₃]˙ + [S₃]˙⁻ (29)

is exothermic by −80.0 kJ mol⁻¹ and exergonic by −29.9 kJ mol⁻¹ at 300 K and ε = 8 while the dissociation of the hexasulfide dianion alone is endothermic by +34.3 kJ mol⁻¹ and exergonic by −11.5 kJ mol⁻¹ under the same conditions (Table 5); the cited enthalpy values for the ion pair dissociation have been calculated from the G3X(MP2) data in Tables 5 and 8. The structure of [NaS₆]⁻ in the gas phase does indeed exhibit a particularly long central S–S bond of 221.5 pm (Fig. 16) which shrinks to 213.2 pm for ε = 8.

One of the problems of metal–sulfur batteries working at room temperature is the decomposition of the solvent by either the bulk metal or by nucleophilic attack of the polysulfide dianions and radical anions. In addition, the self-discharge of the battery by diffusion of the polysulfide anions and radical anions to the metal anode followed by chemical reduction to shorter anions results in loss of capacity. This shuttle mechanism, shuttle effect or shuttle phenomenon will be further discussed in Section 5.1.3. The shuttle effect can best be suppressed using an ion-selective separator between the two half-cells which rejects any anions. However, such membranes are expensive. Other means are modified sulfur electrodes in which the sulfur is confined in a nanoporous carbon material either physically or chemically by additional, positively charged components to bind the sulfur anions by Coulombic forces. Numerous attempts of this type to solve the shuttle problem have been described in the literature.^111,112

Another possible solution to the shuttle problem may be the use of an organic polysulfane R₂S_n (n > 2) instead of elemental sulfur in which the strong C–S bonds would keep the terminal sulfur atoms in place with the hope that the remaining S atoms would bind on these terminal atoms on recharging the battery.¹²¹ However, the capacity of such batteries is unavoidably smaller than with just elemental sulfur since the organic matrix also needs some space; in all cases porous carbon materials are needed as a conducting additive.

A totally different approach to overcome the shuttle problem is the use of an all-solid-state sodium–sulfur battery at room temperature in which a glass ceramic based on sodium tetrathiophosphate Na₃[PS₄] serves as electrolyte. The sulfur is mixed with acetylene black as conductive additive and can be reduced to Na₂S resulting in a very high capacity, but the voltage drops from initially 2.1 V to 1.5 V since the slow migration of the sodium cations through the solid electrolyte produces a higher than predicted overpotential.¹²² Therefore, a gel-type electrolyte consisting of a polymeric isocyanurate as a sodium cation conducting material has been proposed to suppress the shuttle effect resulting in a high reversible capacity and extended cycling stability.¹²¹

However, ambient-temperature Na–S batteries still face many intrinsic obstacles. These include the poor electrical conductivity of sulfur and its large volumetric variation during cycling, the high costs for the preparation of the sulfur electrode as a composite material and of the membrane, the poor kinetics of conversion from short-chain Na polysulfides or Na₂S to long-chain polysulfides, the passivation of the anode by solid Na₂S₂, and the uncontrollable growth of Na dendrites during charging. More research is needed to overcome these problems before commercialization of RT Na–S batteries will be possible.¹²³ On the other hand, sodium is much more abundant and, therefore, cheaper than lithium the reserves of which may not be sufficient to satisfy the demand of the rapidly growing world population.

5.1.3 Lithium–sulfur (Li–S) batteries. The room-temperature (RT) lithium–sulfur battery is currently considered the most promising device for future energy storage in electrically powered vehicles instead of the lithium-ion batteries used at present. Consequently, there are enormous research efforts to develop a battery of this type to the stage where it can be commercialized. These activities are directed to improve the sulfur-containing electrode, to find solvents stable against strong nucleophiles and solvated electrons, to suppress the shuttle effect of the polysulfide anions as well as the growth of dendrites at the lithium anode, and to enhance the kinetics of the sulfur redox processes, which are still only partly understood. Almost all analytical methods known in physical and inorganic chemistry have been applied to study the varying composition of the electrolytes and electrodes of Li–S batteries during discharge and re-charge processes, and the results will be discussed below. A schematic drawing of the Li–S battery is shown in Fig. 17.

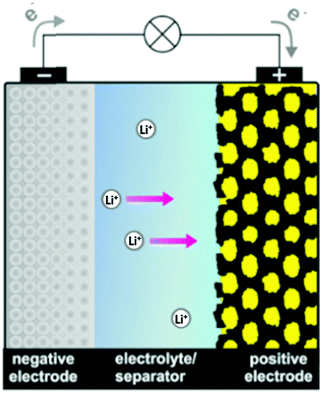Fig. 17 Schematic representation of a cell of a Li–S battery (adapted from Fig. 2 of ref. 110).

In principle the polysulfide chemistry of Li–S batteries should be analogous to that of RT Na–S batteries discussed in Section 5.1.2, although the solubilities of lithium sulfide and polysulfides are different from those of their sodium counterparts. But the strong electric field of the naked lithium cation is responsible for the fact that lithium polysulfides dissolve not only as solvated ions but also as ion pairs of the type [LiS_n]⁻, while neutral ion triples [Li₂S_n] are less likely in solvents of medium or high polarity (ε > 10). However, the presence of ion pairs will also depend on the overall salt concentration. In general, the attractive force f between two opposite ionic charges q_i at a distance d is given by Coulomb's law as f = q₁ × q₂/4πε₀ × ε × d² with ε₀ being the dielectric constant of vacuum and ε the relative dielectric constant of the medium (solution). From this equation it follows that ion-pair formation is favored by the following factors:

(a) high ionic charges (dianions are more likely to form ion pairs than radical anions of same size),

(b) small ionic radii (Li⁺ is more likely to form ion pairs than Na⁺),

(c) a small dielectric constant of the medium (THF with ε ≈ 8 favors ion pair formation more than water with ε = 78),

(d) low temperatures, since ion-pair formation is exothermic, and

(e) high ion concentrations according to the law of mass action.

Remarkably, even LiCl is not completely dissociated in aqueous solution at 25 °C as indicated by the activity coefficient γ of less than 1.0 in the wide concentration range of 0.001 < c < 2.0 mol L⁻¹ with a minimum value of γ = 0.73 at c = 0.5 mol L⁻¹.

Salts dissolve in solvents only if the combined solvation enthalpies of cations and anions are absolutely larger than the lattice enthalpy of the crystalline material. Li₂S and Li₂S₂ have high lattice enthalpies and therefore are insoluble in most solvents used in Li–S batteries. Crystal structures of lithium salts with more than two sulfur atoms are known only for solvated species and not for the binary compounds; consequently, the lattice energies of the binary species with more than two sulfur atoms are unknown (Section 2).

The reaction mechanisms for the redox processes of elemental sulfur and of polysulfides discussed even in the most recent literature are not always in agreement with the existing spectroscopic, voltammetric and thermodynamic data obtained in contemporary fundamental research. In particular, some authors still assume even-numbered polysulfide anions as the only important sulfur species in batteries while inorganic chemists have known for a long time that there is no fundamental difference between odd- and even-numbered dianions [S_n]²⁻.⁶ In Section 4 it has been shown that the aqueous pentasulfide dianion is thermodynamically favoured over ions of similar chain lengths since its Gibbs energy of formation is lower than those of other polysulfide dianions with between 2 and 8 atoms (Table 2).

The ideal overall reaction during discharge of Li–S batteries is:

16Li + S₈ → 8Li₂S (30)

On this basis the specific capacity of the Li–S battery would be as high as 1672 mA h g⁻¹ and the theoretical energy density ca. 2600 W h kg⁻¹, much higher than for lithium-ion batteries (both by volume and by weight). However, since Li₂S and even Li₂S₂ are insoluble in suitable polar solvents, these values cannot be attained in experiments.

The technical aspects of Li–S batteries^{15d,110,123–131} and the available analytical tools^15b,e,f have been reviewed previously and will not be repeated here. Instead, we present our view of the most probable pathways from elemental sulfur or sulfur-rich composites with S atoms in the oxidation state zero (S⁰) to products with sulfur atoms in the oxidation state 2− and back. To a certain extent this chemistry depends on the polarity of the solvent used since the solubility of the lithium salts is strongly influenced by the dielectric constant ε. Most frequently, ether-based solvents or solvent mixtures such as dimethoxyethane/dioxolane (DME/DOL; ε near 7) have been used. In addition, propylene, ethylene and diethylcarbonates, as well as high-ε solvents such as dimethylsulfoxide, ethylmethylsulfone, 1-methylimidazole, dimethylacetamide, dimethylformamide and tetramethylurea/dioxolane mixtures, have been investigated. For systematic studies of the influence of different solvents, see ref. 132a. Various lithium salts such as Li[N(SO₂CF₃)₂], Li[PF₆], Li[ClO₄] and Li[CF₃SO₃] have been applied to increase the conductivity of the electrolyte; thus the Li⁺ cation concentration in such batteries is quite high, which favours ion-pair formation. It should be noted that the oxo-anions of these salts as well as of Li[NO₃] also serve as potential ligands (O-donors) to Li⁺ ions.

The sulfur cathode is usually a composite of a carbon-rich (electrically conducting) material and elemental sulfur in the form of either S₈, polymeric sulfur or an organic sulfur-rich covalent polysulfane R₂S_n. Many publications deal with the suppression of the above-mentioned “shuttle effect” of polysulfide anions by designing special cathodes using carbon nanotubes, graphene, reduced graphene oxide, mesoporous carbon or hollow carbon spheres to confine or encapsulate the active material but sometimes even the carbon is replaced, e.g. by molybdenum carbide nanorods¹³³ or other transition-metal substrates.¹³⁴ Claims of encapsulation of small and highly endothermic sulfur molecules such as S₂, S₃ and S₄ have been made, but have never been substantiated by direct detection and therefore are doubtful, especially since the carbon material of Li–S batteries is more like a sponge rather than a rock-solid matrix which would be needed to trap such high-temperature molecules at room temperature. Since the carbon–sulfur electrode changes its volume periodically due to the influx of cations during discharge and their exodus during recharge, the carbon material needs to be mechanically flexible in order to allow for diffusion. A nitrogen-doped carbon sponge has also been investigated as a cathode material with the aim that lithium cations bind to the pyridinic or pyrrolic nitrogen atoms and the polysulfide ions would then interact with the immobilized Li⁺ ions to suppress the shuttle effect.¹³⁵

The anode consists of metallic lithium covered by a thin protecting layer, which helps to prevent dendrite growth and self-discharge due to polysulfide reduction (so-called solid electrolyte interface, SEI). Li[NO₃] in rather high concentrations is sometimes used to improve the morphology of this layer which needs to be an electrical insulator but a Li⁺ conductor; many other compounds have been tried for this purpose.¹³⁶ It should be noted, however, that nitrate ions are reduced both by lithium metal and by polysulfide dianions, which are strong reductants.¹³⁷ Lithium bis(oxalate)borate has also been applied to give the lithium anode a smooth and dense surface morphology needed for a high reversible capacity.¹³⁸ However, a dendrite-free Li⁰ anode has seldom been obtained under practical conditions, such as with large current densities (>1 mA cm⁻²) and high area capacity (>2 mA h cm⁻²). A working dendrite-free lithium anode could perhaps be realized through the use of novel additives.

To explain the shuttle effect, it has been demonstrated by HPLC analysis in 2016 that a solution of lithium polysulfides in dimethoxyethane (DME) being in contact with lithium metal changed its composition during several hours so that the concentrations of hexa- and heptasulfide, as well as of S₈ decreased, while the concentration of tetrasulfide ions increased. The concentration of trisulfide remained low, probably due to the low solubility of Li₂S₃, and octasulfide was practically absent in the solution investigated. This chemical reduction of the higher polysulfides by Li metal could be slowed down by addition of lithium nitrate, but could not be completely prevented since the nitrate ions were irreversibly consumed over time.¹³⁹ A separator or an ion-selective membrane may be applied between the two half-cells of a Li–S battery in order to hinder the diffusion of polysulfides to the lithium electrode.¹⁴⁰

The electrochemical reduction of S₈ and other sulfur-rich substrates in Li–S batteries proceeds via radical anions from which the polysulfide dianions may be generated by disproportionation, by recombination or by direct reduction at the cathode as shown in Scheme 3.

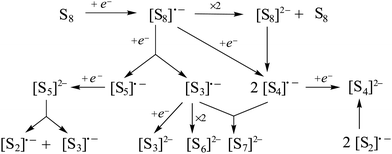Scheme 3 Most likely reactions occurring during electrochemical reduction of S₈ molecules in Li–S batteries on discharging. Most reactions are reversible, and the reversed processes may occur on recharging the battery. Reproduced from ref. 44 with permission from Wiley. Copyright 2013.

As discussed in Section 5.1.2, the polysulfide radical ion [S₈]˙⁻ is likely to be the primary product formed during discharge of a Li–S battery loaded with S₈. This highly reactive ion is predicted to disproportionate exothermically to S₈ and [S₈]²⁻, while its further electrochemical reduction most probably results in dissociation to either 2[S₄]˙⁻ or [S₃]˙⁻ + [S₅]˙⁻. These smaller radical ions can be reduced directly to the corresponding dianions or they recombine with each other to form the whole range of polysulfide ions [S_n]²⁻ (n = 3–8), which have been detected by HPLC analysis after in situ derivatization by methyl triflate CF₃SO₃CH₃ (Section 3.4); dimethyl polysulfanes Me₂S_n of medium chain-lengths had the highest concentrations, while only marginal amounts of Me₂S₂ and Me₂S₈ were detected (Fig. 9).⁸² A mixture of polysulfide dianions and radical anions with between three and seven sulfur atoms is expected to show at least 20 Raman lines in the region 390–510 cm⁻¹ due to the SS stretching vibrations (Section 3.1). In addition, some of these ions are expected to form ion pairs with the lithium cations enhancing the complexity of the vibrational spectra even more. Most of the reactions shown in Scheme 3 are exothermic in polar solvents, but their rate constants and concentration-dependence will be different. Therefore, the product distribution is expected to depend on the current density as well as on the polarity and viscosity of the solvent mixture. On the surface of the metal anode additional reactions occur including the formation of mono- and disulfide ions by chemical rather than electrochemical reduction.

For the description of the reaction mechanisms during discharge and re-charge of Li–S batteries by chemical equations the use of mass balances with fractional molecules or electrons should be avoided. Also, imaginary ions such as [S₈]⁴⁻ are unacceptable from a chemical point of view. For example, the frequently cited equation

[S₈]²⁻ → [S₆]²⁻ + 1/4S₈ (31)

does not describe the molecular mechanism of disproportionation of the octasulfide dianion, but just the mass balance. The real reaction pathway may be as follows:

[S₈]²⁻ → 2[S₄]˙⁻ (32)

[S₈]²⁻ + [S₄]˙⁻ → [S₆]²⁻ + [S₆]˙⁻ (33)

[S₄]˙⁻ + [S₆]˙⁻ → [S₁₀]²⁻ (34)

[S₁₀]²⁻ → [S₂]²⁻ + cyclo-S₈ (35)

[S₄]²⁻ + [S₈]²⁻ → 2[S₆]²⁻ (36)

The stoichiometric addition of these five equations gives the correct mass balance of eqn (31), and all but one of the five reactions have been predicted as exergonic in polar solvents.⁴⁴ However, other reaction sequences are also plausible and should be investigated computationally. Furthermore, reactions of ion pairs rather than free dianions should also be studied. In any case, the cyclic S₈ molecules are eliminated from long-chain anions which necessarily have to be composed of at least 9 sulfur atoms.

Several authors have tried to elucidate the sulfur redox reactions in Li–S batteries by in situ Raman spectroscopy^54,59,141 but, besides the radical anion [S₃]˙⁻, a convincing identification of specific polysulfide dianions has not been obtained since the composition of the solutions is too complex and the spectra of the dianions do not differ sufficiently from each other. Surprisingly, the most intense fundamental modes of free polysulfide dianions in the region 400–500 cm⁻¹ have seldom been detected and the spectra of ion pairs have usually not been considered at all. Furthermore, anions with an odd number of sulfur atoms were often neglected in the modelling of the reaction sequence. However, the disappearance and reappearance of the strong Raman signal of S₈ at 217 cm⁻¹ during discharging and re-charging has been reported by Wu et al. in 2015.⁵⁹ The assignment of a weak line at 518 cm⁻¹ to [S₄]˙⁻ in the latter work is probably in error since it does not fit the predicted fundamental modes of this ion (Section 3.1). In addition, a band at 1066 cm⁻¹ attributed by Wu et al. to the dithionite anion is most probably caused by the first overtone 2ν₁ of the trisulfide radical, calculated at ca. 1060 cm⁻¹ (Section 3.1, Table 1); this line appears simultaneously with the 534 cm⁻¹ Raman line of [S₃]˙⁻.⁵⁹

In general, in situ Raman spectroscopy may not be the best method to analyze the redox reactions in Li–S cells, since the spectra also include lines originating from solvent molecules and from the anions of the Li salts added to increase the conductivity and to protect the lithium anode. In 2015, Hannauer et al. recorded Raman spectra in situ using a helium–neon laser emitting at 632.8 nm, which fits the absorption band of the trisulfide radical anion near 600 nm. Therefore, these authors observed a strong resonance enhancement of the symmetric stretching vibration ν₁ of [S₃]˙⁻ and of the overtones 2ν₁ and 3ν₁, which together dominate the spectrum despite the probably low radical concentration in the tetraethyleneglycol dimethylether–dioxolane (1 : 1) solvent mixture. Two additional weak and rather broad signals at 369 and 429 cm⁻¹ were assigned to a polysulfide dianion mixture, although the first line does not match the experimental Raman spectrum of any polysulfide dianion. These signals occur and disappear simultaneously with the signals of [S₃]˙⁻ on discharge and re-charge of the model battery.⁵⁴ The signal at 369 cm⁻¹ may therefore arise from the LiS stretching vibrations of [LiS_n]⁻ ion pairs and the line-width indicates a superposition of two or more closely neighbouring lines. Only the 429 cm⁻¹ line indicates an SS stretching vibration of a polysulfide anion or a mixture thereof.

The disappearance of S₈ and formation of [S₃]˙⁻ during discharge of an Li–S battery has also been monitored by XANES measurements in 2015,⁴⁸ but EPR spectra had already revealed the formation of [S₃]˙⁻ in 2012.⁶⁷ Dominko et al. reported in 2018 the disappearance of S₈ during discharge and formation of long-chain polysulfides followed by short-chain polysulfides and finally formation of Li₂S and Li₂S₂ by XAS (Section 3.7).¹⁴² However, it is not clear whether the observed signals stem from free polysulfide anions or – more likely – from the ion pairs discussed above. Similar results have been reported by Patel et al., but were discussed on the basis of even-membered polysulfide ions only.⁹⁶

Prior to 2010 the active sulfur species in the redox reactions of Li–S batteries have mainly been assumed to be free polysulfide dianions together with S₈ and the radical anion [S₃]˙⁻. However, in more recent work small, undissociated molecule-like clusters [Li₂S_n] have been assumed to be the active ingredients. Polysulfide dianions are in fact stronger ligands (S-donors) than most solvents used in Li–S batteries. But lithium polysulfide solutions conduct electricity and, therefore, must contain ions. Consequently, anionic ion pairs [LiS_n]⁻ are probably the dominant species, with the lithium cations additionally coordinated by solvent molecules (or O-donor oxoanions) to obtain a coordination number of 4. The equilibrium between Li⁺ and [S_n]²⁻ and the ion pair [LiS_n]⁻ will depend on the nature of the solvent. It has in fact been reported in 2017 that the UV-vis spectra of lithium polysulfide solutions strongly depend on the nature of the solvent,^15e and in 2018 it was found that the voltammetric results are also solvent-dependent.¹³¹ Molecular dynamics (MD) calculations on molecular clusters [Li₂S₆] and [Li₂S₈] in DME or DOL did not show any dissociation of these ion pairs, but the cell dimensions (15 × 10 × 10 Å) may have been too small to allow for the polarization of the solvent continuum by the expected cations and anions.¹⁴³ This solvent polarization stabilizes polysulfide anions enormously.⁴⁴

Several authors have tried to elucidate the sulfur redox reactions in Li–S batteries by in situ⁷Li NMR spectroscopy (Section 3.6).^86–88,96 While the formation of lithium polysulfides and Li₂S during discharge and their disappearance during charging can clearly be seen in the spectra from a broad signal extending from −260 to +100 ppm, specific polysulfides could not be identified. During discharge the total area under this peak gradually increases, reaching a maximum at about 2.0 V and then gradually decreases and reaches a minimum at nearly the fully discharged state. Therefore, this peak which could be deconvoluted into four subpeaks was assigned to a mixture of Li₂S_n species. The most important result is, however, the likely in situ detection of neutral ion pairs [LiS_n]˙ by the strong influence of the unpaired electron on the chemical shift of the lithium ion. A broad signal near 200 ppm has been tentatively assigned to this type of species.⁸⁷

The structures of the ion pairs [LiS_n]⁻ (n = 4, 6) as well as of [LiS_n]˙ (n = 2, 3), each solvated by two DME molecules, have been investigated by computational methods using DFT theory and ε = 7.0 (Fig. 18).⁸⁷ However, whether these structures represent the global minimum geometries needs to be confirmed, since the polyether ligands may also function as bidentate ligands forming bis-chelate complexes of composition [(DME)LiS_n]˙ and [(DME)LiS_n]⁻. Chelate complexes are usually of higher thermodynamic stability due to the lower reaction entropy.

Fig. 18 Molecular structures of the ion pairs (a) [(DME)₂LiS_n]⁻ (n = 4 and 6) and (b) [(DME)₂LiS_n]˙ (n = 2, 3) solvated by dimethoxyethane molecules, calculated at the B3LYP/ccVQZ level using the COSMO correction for ε = 7 to simulate the solvent's influence. Reproduced from ref. 87 with permission. Copyright 2015, American Chemical Society.

The Raman spectra of the various species [S_n]˙⁻, [S_n]²⁻, [LiS_n]˙, [LiS_n]⁻ and cluster-like [Li₂S_n], possibly present in the electrolytes of Li–S batteries, will be significantly different from each other, and Li–S stretching modes are to be expected in the region 200–350 cm⁻¹.⁴⁴ But with this complexity the spectroscopic determination of single species during discharge and recharge of Li–S batteries by any spectroscopic technique will be problematic. Unfortunately, anionic ion pairs of the type [LiS_n]⁻ have not been studied systematically by high-level quantum chemical calculations taking the solvation enthalpies into account in order to predict their thermodynamic properties. However, the analogous ion pairs of type [NaS_n]⁻ (n = 2–9) have been calculated and were shown to be cyclic with the polysulfide anions functioning as bidentate ligands (Fig. 15 and 16).

The influence of different alkali-metal cations M⁺ on the redox potentials of M–S batteries and their in situ UV-vis spectra has been studied by Zou et al. in 2018.¹²¹

Attempts have been made to elucidate the thermodynamics of neutral lithium polysulfide molecules [Li₂S_n] in solution by high-level quantum-chemical calculations taking the solvation enthalpy into account.¹²⁰ However, the structures of the [Li₂S_n] clusters (n = 1–8) were calculated without coordinated solvent molecules, and some of the predicted clusters have puzzling geometries with Li–Li bonds. Experimental structures of solvate-free lithium polysulfides are unknown excepting Li₂S₂ for which a crystal structure determination is available.⁶ The reason is the very high electric field strength of the small naked Li⁺ ion resulting in strong coordinate bonds to polar solvent molecules, which function as chelating ligands. Therefore, lithium polysulfides always crystallize from solvents as solvates (Section 3.1, Fig. 6).

Finally, it should be mentioned that the decomposition of carbonate-type solvent molecules by nucleophilic attack of polysulfide dianions has been studied computationally.¹²⁰ Ether-based solvents are more resistant to the polysulfide dianions and radical anions. However, a completely different approach to the solubility and shuttle problems has been reported by two groups who used either all lithium polysulfides as insoluble solids or all Li–S species completely dissolved. In 2017, Krossing, Nazar et al.^144a replaced the conventional ether-based solvents by N,N-dimethyl trifluoromethylsulfonyl amine (DMT), which does not dissolve lithium polysulfides, and used the lithium salt of the particularly weakly coordinating anion [Al(OCHCF₃)₄]⁻ at a concentration of 0.2 M as an ion carrier to suppress the dissolution of the lithium polysulfides formed during discharge at the carbon–sulfur cathode. In this way the shuttle phenomenon could be effectively suppressed, but the poor kinetics required an operating temperature of 50 °C. On the other hand, Yang et al.^144b reported recently that all Li₂S_n salts with n = 1–8 are soluble in a eutectic 1 : 1 mixture of ε-caprolactam and acetamide (m.p. −8 °C) up to a concentration of 0.7 M due to the high dielectric constant. This mixture has therefore been used as solvent for an inexpensive, almost non-flammable electrolyte together with the conducting salts Li[N(SO₂CF₃)₂] and Li[NO₃]. This type of battery not only avoids the massive volume expansion of the carbon electrode during discharge, but also uses the full energy capacity of the lithium–sulfur system since neither Li₂S nor Li₂S₂ are precipitating. By addition of some DOL/DME to the solvent mixture the viscosity has been reduced to an acceptable level, and a high retention of the capacity during cycling is observed while growth of dendrites and shuttle effects are hardly noticeable. On the other hand, the detection of SH bonds by Raman and NMR spectroscopy indicated chemical reactions between the solvent mixture and the polysulfide dianions or radical anions. The authors stated that further studies are needed with high-mass loading of solid sulfur, the solubility of which is much lower than that of lithium sulfides.

Despite its extraordinary high specific energy, the Li–S battery in its present form (with ether-based solvent mixtures) can still not compete with the well-established lithium-ion battery for applications in the transport sector since the following inherent challenges still exist:

1. The formation of Li dendrites is a critical issue in most Li⁰-based rechargeable batteries. It leads to problems with safety, low Coulombic efficiencies, and short lifespans.

2. Solubility of active species and polysulfide (PS) shuttling: The redox shuttle phenomenon occurs as a result of the diffusion of soluble high-order PS such as Li₂S₆ formed on discharge through the separator and its reaction with the Li anode to form low-order and partially or completely insoluble lithium di- and monosulfide (Li₂S₂ and Li₂S) in each cycle. This leads to the loss of active sulfur in the cathode and thereby lowers the degree of S utilization. The gradual accumulation of insulating sulfides can also seriously impede rapid access to the Li anode, thereby resulting in a poor rate capability. Furthermore, the PS could react negatively with the electrolyte components such as solvents, salt anions etc., depending on their functionality.

3. Insulating nature: S₈ (10⁻³⁰ S cm⁻¹ at RT) and its various discharge products (Li₂S_n, mainly Li₂S (ca. 10⁻¹³ S cm⁻¹ at RT) and Li₂S₂ exhibit poor electronic and ionic conductivities, which lead to an increase in the internal resistance of the Li–S cell, and thereby to high voltage polarization. This in turn results in a reduction in the Coulombic and energy efficiencies of the Li–S cell.¹³⁶

4. The high costs of some of the lithium salts and of Nafion-type separators used in some cases are another limitation.

In order to overcome some of these problems bulk-type all-solid-state lithium–sulfur batteries without organic liquid electrolytes have been studied. Solid-state Li–S batteries are made up of negative/positive electrodes separated by a solid electrolyte resulting in a high energy density due to the compact structure. In addition, solid-state ionic electrolytes prevent polysulfide shuttling, are inert toward metallic lithium, can resist the growth of lithium dendrites, have excellent temperature stability and a wide stable electrochemical window that enables high voltage cathodes. But there are still many critical challenges to be overcome for large-scale application, including a large interfacial resistance between electrolyte and electrodes, low ionic conductivity of electrode materials, volume change of the cathode during cycling, and instability in contact with the anode.¹⁴⁵

5.2 Organic syntheses

The use of inorganic polysulfides for the synthesis of organosulfur compounds (OSCs) either in the form of an ammonium salt or generated in situ in solutions of sulfur in liquid ammonia or amines has a long history, e.g. in the Willgerodt–Kindler reaction for the conversion of alkyl aryl ketones into thioamides.⁷⁵ The formation of a blue colour when sulfur is treated with a base in water or acetone is also well-documented, although it was not until the early 1970s that this blue species was unequivocally identified as the trisulfur radical anion [S₃]˙⁻.^8,16 Solutions of elemental sulfur in combination with bases such as M₂[CO₃] (M = K, Cs), M[O^tBu] (M = Na, K), K[OH] or Na[SH] in electron-pair donor solvents are now widely used in organic synthesis.⁷⁵ Since this combination produces polysulfides and, hence, polysulfide radical anions as evidenced by a blue colour, it is surprising that more effort has not been made until very recently to target [S₃]˙⁻ as a reagent. This section will focus on advances in the last few years in the use of this radical anion in organic syntheses.

In a 2013 study related to formation of organosulfur compounds (OSCs) under geological conditions, Said-Ahmed et al. reported that the reaction of elemental sulfur with 1-octene and water at 100–130 °C in the pH range 8.0–8.5 produces OSCs and 2-octanone.^146a These authors also observed a pale blue colour (possibly [S₃]˙⁻) for the reaction solution and proposed a radical mechanism for the transformation. However, in a re-investigation two years later, Ding and Adam challenged this proposal and suggested an alternative concerted mechanism to explain the experimental results.^146b

This controversy implies that direct evidence for the involvement of polysulfide radical anions is essential to any mechanistic proposal involving the reactions of organic compounds with sulfur in the presence of a base. In that context, in 2014 Zhang and co-workers investigated the synthesis of thiophenes via the interaction of 1,3-diynes with sulfur and Na[O^tBu] (Scheme 4a).¹⁴⁷ In a separate experiment they showed that the blue solution formed upon treatment of sulfur with Na[O^tBu] in DMF at room temperature displays the characteristic EPR signal for [S₃]˙⁻ (g = 2.0292) (Section 3.5) which, they suggested, plays an essential role as an intermediate in the formation of thiophenes. These authors also demonstrated that this cheap, environmentally attractive use of elemental sulfur provides a general route to both symmetrically and unsymmetrically 2,5-disubstituted thiophenes in 56–76% yields.¹⁴⁷ Two years later Wang and co-workers described a related synthesis in which diarylannulated sulfides were constructed in high yields via sulfur–iodine exchange from the reaction of diaryliodonium salts with sulfur and Cs₂[CO₃] in DMSO at 120 °C (Scheme 4b).¹⁴⁸ The formation of [S₃]˙⁻ was also demonstrated in that study by the EPR spectrum of a blue DMSO solution of sulfur and Cs₂[CO₃] when heated to 100 °C. The same reagent has been used to prepare thiazole derivatives by reaction with a mixture of ketoxime acetates and PhNCS.¹⁴⁹

Scheme 4 (a) Na[O^tBu]/^tBuOH, DMF, 25 °C; (b) Cs₂[CO₃], DMSO, 100 °C; (c) and (d) DMF, 130 °C; (e) Cu[OAc]₂, 2,2′-dipyridyl, NaOH, NMP.

Potassium sulfide K₂S has also been used as a source of [S₃]˙⁻ for organic synthesis. Thus, Ji and co-workers obtained benzothiazine derivatives in high yields (47–96%) from reactions of K₂S with enaminones in DMF at 130 °C (Scheme 4c).¹⁴⁹ Evidence for the formation of [S₃]˙⁻ in this system was provided by the observation of a strong EPR signal, g = 2.02, for a DMF solution of K₂S at room temperature. Furthermore, the presence of the trisulfide radical anion in such solutions was confirmed by the characteristic broad visible absorption band at ca. 615 nm (Section 3.2) and the symmetric S–S–S stretching vibration at 531 cm⁻¹ in the Raman spectrum (Section 3.1). The authors proposed that “DMF activates the electron-donating agent K₂S to give [S₃]˙⁻”,^150a but evidence for this suggestion is lacking and the generation of [S₃]˙⁻ must involve either the presence or formation of polysulfides. The same group has also employed [S₃]˙⁻, generated in situ from K₂S in DMF, for the synthesis of thiophenes via [1+2+2] cycloaddition (Scheme 4d).^150b

In a further development of this synthetic strategy, Jiang and co-workers used a combination of K₂S and chloroform as an alternative to carbon disulfide for the synthesis of a library of benzothiazine-thiones from N-substituted-2-iodobenzylamines in N-methylpyrrolidone (NMP) in the presence of a Cu(II) catalyst.⁶⁴ Of particular interest is the application of this protocol to the synthesis of 2-mercaptobenzothiazole, which is manufactured on a multi-ton scale for use as an accelerator in rubber vulcanization as well as an antioxidant stabilizer and metal corrosion inhibitor for rubber and plastics (Scheme 4e). The authors established the presence of [S₃]˙⁻ in solutions of K₂S in NMP via characteristic UV-visible and EPR spectroscopic signatures (vide supra) and concluded that the radical anion plays a key role in the final thiocarbonyl formation.⁶⁴

In an investigation of the use of sulfur–amine solutions for the production of metal sulfide nanocrystals, Ozin and co-workers provided insights relevant to the application of these reagents in organic synthesis.¹⁵¹ These authors confirmed earlier observations that solutions of sulfur in octylamine form octylammonium polysulfides at low temperature and, on warming to 130 °C, generate H₂S which reacts with the amine to produce thioamides [eqn (37)]. Although the possibility of sulfur radical anions in this transformation was recognized, the specific role of [S₃]˙⁻ was not pursued. However, it was shown that thioamides exhibit more rapid kinetics than sulfur–alkylamine solutions in the synthesis of metal sulfide nanocrystals.¹⁵¹

C₇H₁₅CH₂NH₂ + [S_n]²⁻ → C₇H₁₅(C=S)NH₂ + H₂S + [S_n−2]²⁻ (37)

5.3 Biological chemistry of polysulfides

Sulfur compounds of oxidation states ranging from 2− to 6+ are abundant on Earth and are essential for life. Therefore, sulfur is the fourth most abundant element in artificial fertilizers, after N, P and K. As for other elements a natural cycle also exists for sulfur, and microorganisms play a critical role in driving sulfur cycling by sulfide oxidation to sulfate in one habitat and by reduction of the latter back to sulfide in another environment.⁷² The corresponding oxidation, reduction and disproportionation reactions include intermediate species such as polysulfides [S_n]²⁻, elemental sulfur (S⁰), thiosulfate [S₂O₃]²⁻ and polythionates [S_nO₆]²⁻.

Polysulfide anions are the key reactants in a large number of important biological and microbiological oxygen-poor systems.^46,152 They can be generated during mitochondrial oxidative catabolism,^153–155 by metalloprotein-catalyzed oxidation of sulfide^156–158 or by reaction of sulfide with NO.¹⁵⁹ However, direct oxidation of sulfide by reactive oxygen species (ROS) is relatively slow in many cases.¹⁶⁰

The mechanism of polysulfide formation by transition-metal catalyzed oxidation of monosulfide anions is well understood.¹⁶¹ Removal of an electron from [HS]⁻ ions gives hydrogen sulfide radicals which are relatively strong acids and therefore are deprotonated in water at pH values near or above 7; the product radicals then dimerize to disulfide dianions:

[HS]⁻– e⁻ → [HS]˙ (38)

[HS]˙ + H₂O → S˙⁻ + [H₃O]⁺ (39)

2S˙⁻ → [S₂]²⁻ (40)

In a similar fashion, the disulfide dianion can be oxidized catalytically to the disulfide radical ion [S₂]˙⁻, which would dimerize to the tetrasulfide dianion and so forth:

[S₂]²⁻– e⁻ → [S₂]˙⁻ (41)

2[S₂]˙⁻ → [S₄]²⁻ (42)

[S₄]²⁻– e⁻ → [S₄]˙⁻ (43)

2 [S₄]˙⁻ → [S₈]²⁻ (44)

After sufficiently long polysulfide anions have been formed, S₈ molecules (and other small sulfur rings such as S₆, S₇ and S₉) can be eliminated as discussed in Section 5.1.3. These processes occur in the industrial, catalytic conversion of H₂S to elemental sulfur, as well as in cultures of chemotrophic bacteria. The latter use the energy released upon enzymatic oxidation of sulfide by metalloproteins for their metabolism (CO₂ reduction) while, simultaneously, poisonous H₂S is transformed into less toxic elemental sulfur; the latter precipitates from the aqueous phase, often as spherical globules.¹⁶² For example, polysulfides occur as the primary reaction products of the oxidation of sulfide in purple^162,163 and green¹⁶⁴ sulfur bacteria as well as in Beggiatoa species.¹⁶⁵ Purple sulfur bacteria of the families Chromatiaceae and Ectothiorhodospiraceae preferentially use reduced sulfur compounds as electron donors during photolithoautotrophic growth. The most important difference between the two families is that Chromatiaceae produce intracellular sulfur globules when growing on either sulfide, thiosulfate, polysulfides or elemental sulfur, while the Ectothiorhodospiraceae accumulate extracellular sulfur. All phototrophic members of the Chromatiaceae use sulfide and sulfur of the oxidation state zero as photosynthetic electron donors. Polysulfide oxidation is probably ubiquitous in such systems. This does not appear surprising because polysulfides are formed as intermediates of the oxidation of sulfide to sulfur globules.¹⁶² Polysulfides are especially stable intermediates of sulfide oxidation by members of the Ectothiorhodospiraceae because these bacteria thrive under alkaline growth conditions, which are essential for longer-term stability of polysulfides.¹⁶⁶

In some sulfur bacteria the growth of a chain of sulfur atoms may begin with the cleavage of the sulfur–sulfur bond of cystine (R₂S₂) as a component of an enzyme by the nucleophilic attack of sulfide ions and may proceed stepwise by a series of oxidation and chain-cleavage reactions, possibly catalyzed by a transition metal (see below), e.g.:

R–S–S–R + [HS]⁻ → [R–S₂]⁻ + [R–S]⁻ + H⁺ (45)

[R–S₂]⁻– e⁻ → [R–S₂]˙ (46)

[R–S₂]˙ + S˙⁻ → [R–S₃]⁻ (47)

etc. until:

[R–S_n]⁻ → cyclo-S₈ + [R–S_n−8]⁻ (n > 8) (48)

The last reaction is expected to be reversible. Of course, there are alternative pathways yielding inorganic polysulfides early in the reaction sequence, e.g.:

R–S₂˙ + [HS]⁻ → [R–S]⁻ + [S₂]˙⁻ + H⁺ (49)

2[S₂]˙⁻ → [S₄]²⁻ (50)

etc.

The electrons formally released in the above reactions reduce the transition metal (usually iron) from Fe³⁺ to Fe²⁺ which is then re-oxidized to Fe³⁺ by O₂. The latter is reduced to [O₂]˙⁻ from which H₂O₂ and its anion [HO₂]⁻ are formed by disproportionation:¹⁵⁷

Fe³⁺–OH₂ + [HS]⁻ → Fe²⁺–SH + H₂O (51)

Fe²⁺–OH₂ + O₂ → Fe²⁺–O₂ + H₂O (52)

Fe²⁺–O₂ + [HS]⁻ → Fe³⁺–SH + [O₂]˙⁻ (53)

Fe³⁺–SH + O₂ → Fe²⁺−O₂ + [HS]˙ (54)

2[O₂]˙⁻ + H₂O → HO₂⁻ + [OH]⁻ + O₂ (55)

The reactive oxygen species (ROS) are then available for other oxidation reactions, e.g. thiosulfate and sulfate formation, but a direct reaction of [HS]⁻ ions with either O₂ or [O₂]˙⁻ is spin-forbidden. Therefore, Fe–SH complexes are formed at the beginning of the reaction cascade to produce polysulfide anions via [HS]˙ radicals as shown above.

Polysulfide ions in biological samples have been notoriously challenging to quantify due to their reactivity, sensitivity to sample handling and the analytical complexity associated with their measurement. Some authors tried to identify these ions during enzymatic sulfide oxidation by derivatization with bromobimane but, as described in Section 3.4, this reaction is too slow to yield reliable results. However, the appearance and disappearance of polysulfide ions has definitely been observed during bacterial oxidation of sulfide to elemental sulfur (forming “globules”), and for the further oxidation of the “globules” to sulfate after all sulfide has been depleted. The polysulfides are also essential to solubilize the water-insoluble elemental sulfur (globule degradation).^162–164

Marnocha et al. reported in 2016 that a standard polysulfide solution prepared from sulfide and S₈ yielded four peaks in the HPLC chromatogram after derivatization by monobromobimane, but the sulfur chain-lengths of the suspected Bm₂S_x species were not determined.¹⁶⁴ Recently, Nagy⁴⁶ studied the polysulfide speciation in aqueous solution using the cell-permeable alkylating agents iodoacetamide (I–CH₂–CO–NH₂) and N-ethylmaleimide [Et–N(C=O)₂C₂H₂] for the derivatization procedure, but observed that the derivatization changed the speciation of the polysulfide mixture substantially. This may be due to the amine-type nitrogen atoms in these two reagents, since amines like ammonia are well-known catalysts for the interconversion of polysulfide and polysulfane compounds by nucleophilic attack.¹³ Nevertheless, polysulfide ions have definitely been detected in biological samples, but the exact quantitative distribution needs to be demonstrated (for references, see ref. 46). The formation of chain-like sulfur compounds during enzymatic sulfide oxidation has also been demonstrated by XANES measurements, which revealed differing chain-terminating groups depending on the organism.⁹⁰

An unresolved question seems to be the reaction of polysulfide ions with molecular oxygen in microbiological samples, although the autoxidation of aqueous polysulfide yielding thiosulfate and sulfur has been studied extensively.³⁸ However, the formation of sulfur-chains via condensation of a sulfenic acid derivative of cysteine with H₂S or thiols has been discussed in 2017.¹⁶⁷ The sulfenic acids may well be reactive intermediates in the oxidative metabolism of sulfur bacteria, but solid evidence seems to be missing.

–S–OH + H–S– → –S–S– + H₂O (56)

The ubiquitous radical [S₃]˙⁻ is expected to react with molecular oxygen in a diffusion-controlled reaction with insignificant activation energy:

[S₃]˙⁻ + O₂˙˙ → [SSSOO]˙⁻ (57)

The process depicted in eqn (57) could account for the peak at m/z = 127.9057 (cf. [S₃O₂]˙⁻ calcd 127.9061) observed by Bogdándi et al. in 2018 by negative ion electrospray mass spectrometry of aqueous sodium polysulfide solutions (Section 3.3).⁴⁶ The authors assigned this peak to the almost isobaric radical ion [S₄]˙⁻ (calcd mass 127.8883). Apparently, the polysulfide solutions were not handled with exclusion of air. In addition, the formation of the protonated radical anion [HS₃O₂]˙⁻ is indicated by a peak at m/z = 128.9178 (calcd 128.9139), but this signal was not assigned by the authors. The presence of adventitious molecular oxygen in these experiments is also indicated by the observed peaks for sulfite, sulfate and thiosulfate radical ions. The proposed chain-like dioxopentasulfide or peroxotrisulfide radical ion [SSSOO]˙⁻ is expected to rearrange to the dithiosulfite radical ion [SSS(O)₂]˙⁻, which may be the precursor of the observed sulfur oxoanions.

The validity of eqn (57) can be inferred from the well-studied reaction of [PenSS]˙ radicals with molecular oxygen (Pen = penicillamine).¹⁶⁸ This reaction was monitored by following the decay kinetics of [PenSS]˙ after pulse irradiation of aqueous solutions containing 1 × 10⁻³ M PenSSSPen, 1.0 M tert-butanol and different O₂ concentrations at pH = 5.9. In the presence of molecular oxygen, the pure second-order decay kinetics of [PenSS]˙ (due to dimerization) observed in N₂-saturated solutions, changed to pseudo-first-order kinetics showing a linear decrease of the [PenSS]˙ lifetimes with increasing oxygen concentrations:

[PenSS]˙ + O₂ → [PenSSOO]˙ (58)

The latter radical was assumed to be the precursor of sulfate, the formation of which was observed during this pulse radiolysis.¹⁶⁸ Therefore, strict exclusion of molecular oxygen is required when ionic polysulfides or their anionic organic derivatives are being studied.

5.4 Geochemical transformations

Inorganic polysulfides are salient reagents in numerous geochemical processes in sediments and oxygen-poor systems.^{152,169–171} For example, both the diagenetic formation of pyrite [iron(II) disulfide] and the production of organosulfur compounds have been attributed in part to reactions of polysulfides with metal ions and unsaturated organic substrates, respectively.^172,173 Polysulfides are also the possible source of malodorous, volatile sulfur compounds such as organic polysulfanes R–S_n–R via reactions with chlorinated pollutants.^174–176 Many metals have a high affinity for polysulfide ligands and the role of polysulfide radical anions in the transport of economically important metals such as Cu, Au and Pt at elevated temperatures and pressures has been the subject of recent studies (vide infra).

Traditional studies of sulfur speciation in geological fluids have focused on dissolved sulfide and sulfate, since these anions predominate in sulfur-bearing minerals. In 2011 Pokrovski and Dubrovinsky reported the identification of the trisulfur radical anion [S₃]˙⁻ in aqueous solutions at elevated temperatures and pressures (>250 °C and 5–35 kbar) over a wide pH range by in situ Raman spectroscopy using a diamond anvil cell.^8,177 As pointed out by these authors⁵⁶ and by Manning,¹⁷⁷ this ground-breaking discovery has important implications for the nature of geochemical processes such as metal transport and sulfur-isotope fractionation. The role of [S₃]˙⁻ in these processes has subsequently been investigated extensively by both experimental and computational approaches.

In a further illustration of the capability of in situ Raman spectroscopy for the detection of [S₃]˙⁻ in sulfur-rich hydrothermal fluids, it was shown that the formation of this radical anion commences in the temperature range 200–300 °C and grows up to (at least) 500 °C and 1 kbar.⁵³ In addition, this process was found to be reversible, since the spectroscopic signature for [S₃]˙⁻ disappears on cooling and reappears on heating. The observation of [S₃]˙⁻ under these conditions suggests that this sulfur species may serve as a ligand for Cu–Au–Mo deposits. The long-held belief that H₂S and Cl⁻ ions are the ligands responsible for gold transport and precipitation in the Earth's crust has been challenged by the results of recent investigations by Pokrovski and co-workers using in situ X-ray absorption spectroscopy.¹⁷⁸ By the use of this technique, in combination with first-principles molecular dynamics, these authors established that [S₃]˙⁻ makes a major contribution to gold solubility in aqueous solutions at elevated temperatures (>250 °C) and pressures (>100 bar) and [Au(SH)S₃]⁻ was identified as the most stable complex.¹⁷⁸ Experimental results on metal complexes of polysulfide radical anions [S_n]˙⁻ (n = 2, 4) are described in Section 5.5.

Thermochemical sulfate reduction (TSR) plays a critical role in the global sulfur cycle and may affect measurements of sulfur isotope fractionation. In contrast to sulfate reduction induced by bacteria, TSR generally occurs at high temperatures (T > 150 °C), while abiogenic reduction may occur at lower temperatures in some geological environments. Based on in situ Raman spectra, in 2014 Truche and co-workers demonstrated that [S₃]˙⁻ is the dominant intermediate sulfur species involved in abiogenic sulfate reduction by H₂S in the temperature range 100–350 °C.¹⁷⁹ This finding necessitates a re-evaluation of the sulfur isotope exchange mechanisms between sulfate and sulfide in order to include the possible role of [S₃]˙⁻. Three years later Barré et al. disclosed the formation of [S₃]˙⁻ (and polysulfide dianions) above 100 °C in natural fluids from a typical buried sedimentary environment where TSR occurred; only sulfide and sulfate were observed at 25 °C.¹⁸⁰ They estimated the [S₃]˙⁻ concentration to be 0.2–3.0% of total sulfur in the temperature range 200–300 °C.

Having established the existence and potential importance of [S₃]˙⁻ in aqueous sulfur-bearing fluids at high temperatures, in 2015 Pokrovsky and Dubessy turned their attention to the quantification of the stability and abundance of this ephemeral species.¹⁸¹In situ Raman spectra were obtained on model thiosulfate, sulfide and sulfate aqueous solutions for a wide range of sulfur concentrations (0.5–10.0 wt%), acidities (pH 3–8), temperatures (200–500 °C) and pressures (15–1500 bar). They found that [S₃]˙⁻ represents up to 10% of dissolved sulfur at 300–500 °C and more than 50% at 600–700 °C in sulfur-rich fluids. The disulfur radical anion [S₂]˙⁻ was also tentatively identified at 450–500 °C via observation of a small peak at 580 ± 5 cm⁻¹ accompanied by weak overtone bands at 1160 ± 10 cm⁻¹ and 1740 ± 15 cm⁻¹.¹⁸¹

5.5 Metal complexes

The chemistry of both main-group and transition-metal complexes with polysulfido ligands [S_n]²⁻ (n = 2–9) has a long history, which has been discussed extensively in the review literature.⁴³ These homoatomic dianionic ligands usually undergo S,S′-chelation to the metal in mononuclear complexes or act as bridging ligands in dinuclear complexes. Information on metal complexes of polysulfide radical anions is relatively sparse and has mostly appeared in the last 15 years. The discussion in this section will be limited to complexes of [S_n]˙⁻ (n = 2, 3, 4) ligands in view of their novelty and relevance both to computational studies (Section 4) and metal transport in geochemical systems (Section 5.4).

Transition-metal complexes that may contain the end-on supersulfide radical anion [S₂]˙⁻ have been known for more than 45 years, e.g. [Cp(EtS)FeSSFe(SEt)Cp] and [(NH₃)₅RuSSRu(NH₃)₅]Cl₄·2H₂O.¹⁸² The nature of the bridging S₂ ligand in these dinuclear complexes depends on the assignment of oxidation states to the two metal centers and may fall between the monoanion [S₂]˙⁻ and the dianion [S₂]²⁻. For example, on the basis of structural and spectroscopic evidence, Elder and Trkula described the ruthenium complex as primarily a mixed-valent [Ru(II)/Ru(III)] species with a bridging [S₂]˙⁻ ligand accompanied by a minor contribution from the corresponding Ru(III)/Ru(III) combination bridged by a [S₂]²⁻ moiety.^182b The SS stretching vibration in this complex is 519 cm⁻¹,^182bcf. ν(SS) = 594–623 cm⁻¹ for the [S₂]˙⁻ radical anion in alkali-metal halide matrices,¹⁸³ while the S–S distance is 202.4 (1) pm, cf. d(S–S) = 199.5–202.3 pm in complexes with a central M–S–S–M unit.⁴³ In 2005 Tolman and co-workers characterized the binuclear complex [LCu(μ-S₂)CuL][OTf]₂ (L = tmeda; OTf = CF₃SO₃), which exhibited ν(SS) = 613 cm⁻¹ and d(S–S) = 195.0(1) pm, leading to the conclusion that it is a Cu(II)/Cu(II) complex with two bridging [S₂]˙⁻ ligands.¹⁸⁴

Three years later Driess and co-workers characterized an interesting nickel(II) complex of the [S₂]˙⁻ ligand, [LNi(η²-S₂)]_n with L = [CH{(CMe)(2,6-ⁱPr₂C₆H₃N)}₂]⁻, which exists as a centrosymmetric dimer (n = 2) with a four-membered rectangular S₄ ring in the solid state [d(S–S) = 194.4(2) and 277.7(2) pm].¹⁸⁵ In solution, the ¹H NMR and EPR spectra reveal the partial dissociation of this complex into the paramagnetic monomer (n = 1) (Scheme 5). DFT calculations of this monomer reveal that the HOMO is a singly occupied π* orbital (SOMO) completely located on the disulfur ligand, consistent with a complex of [S₂]˙⁻. The dimer is formed from a π*(SOMO)–π*(SOMO) interaction to give a four-center two-electron bond.¹⁸⁵ The reaction of [LNi(η²-S₂)]_n with Ph₃P produces (LNi)(μ-η²:η²–S₂), a side-on complex of the dianion [S₂]²⁻ with d(S–S) = 205.1(1) pm (Scheme 5).¹⁸⁵

Scheme 5 Monomer–dimer equilibrium for [LNi(η²-S₂)]_n and reaction with PPh₃.

Metal complexes of the trisulfur radical anion are of interest in view of the possible role of [S₃]˙⁻ in the transport of coinage (and other) metals in geological systems (Section 5.4). Based on calculated free energies, Tossell found that [S₃]˙⁻ forms complexes with Cu⁺ that are similar in stability to Cu⁺ complexes with [HS]⁻ and he predicted bidentate (S,S′) ligation of the trisulfide radical anion in the complexes [CuS₃(OH₂)] and [Cu(S₃)₂]⁻.¹⁰⁵ Similarly, Mei and co-workers reported that the ligands [S₃]˙⁻ and [HS]⁻ are of comparable strengths for Au⁺ as determined by ab initio molecular dynamics simulations.¹⁸⁶ In experimental work Pokrovski et al. have provided evidence for the formation of the stable complex [Au(SH)S₃]⁻ at elevated temperatures and pressures from the interpretation of X-ray absorption spectra (Section 5.4).¹⁷⁸ Although no molecular complexes of this important sulfur ligand have been isolated and characterized, Cummins and co-workers have described the reversible generation of [S₃]˙⁻ from a di-tin complex with bridging pentasulfido and monosulfido ligands [(μ-S₅)Sn₂(μ-S)(mBDCA-5t)]²⁻ (Scheme 6).¹⁸⁷ Solutions of this yellow polysulfido complex in DMF or DMSO are dark blue-green and exhibit the characteristic spectroscopic signatures of [S₃]˙⁻ (a strong absorption at λ_max = 617 nm in the UV-visible spectrum and a broad signal centred at g = 2.0290 in the EPR spectrum). ¹⁸⁷ The amount of [S₃]˙⁻ in DMF solution increases as (a) the concentration of the di-tin complex is diluted or (b) the temperature is increased from 20 to 85 °C. The formation of the neutral di-tin complex [(μ-S₅)Sn₂(μ-S)(mBDCA-5t)] as a result of this dissociation was proposed, but not confirmed.¹⁸⁷

Scheme 6 A polysulfido di-tin complex as a reversible source of [S₃]˙⁻.

A metal complex of the tetrasulfide radical anion [S₄]˙⁻ was first proposed in the mid-1990s by Isobe and co-workers for the tetranuclear rhodium dication [{Rh₂Cp*₂(μ-CH₂)₂}₂(μ-S₄)]²⁺.^188a The rectangular S₄ unit in this complex has two short and two long S–S distances of 197.9(1) and 270.2(1) pm, respectively. The suggested radical monoanion formulation was based on a population analysis, which gave a charge of −0.7e on the S₄ ligand.^188b In 2004 the same group structurally characterized a related tetranuclear iridium dication [{Ir₂Cp*₂(μ-CH₂)₂}₂(μ-S₄)]²⁺ with S–S bond lengths of 204.9(3) and 289.5(3) pm.^188c In the case of the iridium complex, however, the shorter S–S bonds lie parallel to the Ir–Ir bonds and the longer ones are perpendicular to the Ir₂ backbone, whereas the reverse is true in the corresponding Rh₄ complex (Fig. 19). Hofmann and co-workers have addressed this structural dichotomy for tetranuclear group 9 complexes of the rectangular [S₄]²⁻ ligand by using DFT and extended Hückel calculations.¹⁸⁹ They found that either orientation is attainable for both metals with a barrier for interconversion of ca. 46 kcal mol⁻¹ (192 kJ mol⁻¹). The viability of both orientations is attributed to a Jahn–Teller distortion from a square, which is favoured by a −2 charge. In both arrangements the [S₄]²⁻ rectangle has two S–S σ bonds and two three-electron S–S bonds.¹⁸⁹

Fig. 19 Chair-like structures of [{M₂Cp*₂(μ-CH₂)₂}₂(μ-S₄)]²⁺ with rectangular S₄ units (a) M = Rh (b) M = Ir; bond lengths are given in pm (adapted from Fig. 1 in ref. 189).

The first structurally characterized complex of [S₄]˙⁻ was reported in 2017 by Coles and co-workers as part of an investigation of the reactions of bismuth(II) radicals of the type Bi(NON^R) (NON^R = [O(SiMe₂NR)₂]²⁻).¹⁰ They found that treatment of ˙Bi(NON^Ar*) (Ar* = 2,6-[(C₆H₅)₂CH]₂-4-^tBuC₆H₂), with cyclo-S₈ gave yellow crystals of the dimer [Bi(NON^Ar*)]₂(μ-S₈) (Scheme 7). The [S₈]²⁻ ligand in this Bi(III)/Bi(III) complex is quite different from that in dinuclear coinage-metal complexes, e.g. [(S₆)Cu(μ-S₈)Cu(S₆)]⁴⁻,¹⁹⁰ or in the ion-separated salts [Ni(N-MeIm)₆]S₈^26a and [HNEt₃][S₈]^26b (Fig. 1). In the centrosymmetric bismuth complex two Bi(NON^Ar*)(S₄) monomer units with S–S bond lengths in the range 202.1(3)–211.3(3) pm are linked by weak S⋯S interactions [2.758(4)–321.3(4) pm]. Thus, the bismuth complex can be viewed as a Bi(III) complex of the elusive [S₄]˙⁻ radical anion which, according to DFT calculations, dimerizes via a π*(SOMO)–π*(SOMO) interaction similar to that described above for the Ni(II) complex of the [S₂]˙⁻ ligand [LNi(η²-S₂)].¹⁸⁵

Scheme 7 Formation of a Bi(III) complex of [S₄]˙⁻ from Bi(II) radical ˙Bi(NON^Ar*) and cyclo-S₈.

5.6 Atmospheric chemistry

In contrast to the salts of the hydrosulfide ion [HS]⁻ with organic cations, e.g. [NBu₄][HS], which are used to prepare soluble long-chain polysulfides (Section 2), ammonium hydrosulfide [NH₄][HS] is unstable at ambient temperatures with respect to the formation of H₂S and NH₃. However, condensed [NH₄][HS] is thought to be present in the cold atmospheres of planets, notably in Jovian clouds. The identity of the chromophore(s) responsible for Jupiter's Great Red Spot remains an enigma. Since Jupiter's atmosphere is subject to energetic particle bombardment, Loeffler and co-workers have investigated the effect of ≈0.9 MeV proton irradiation on [NH₄][HS] at 10–160 K by using IR and UV-visible spectroscopy to identify the products.¹⁹¹ In the IR study both natural abundance and ¹⁵N-enriched (98%) [NH₄][HS] was used, which enabled the identification of binary sulfur-nitrogen anions [NS_n]⁻ (n = 3, 4) based on the isotopic shift of SN stretching vibrations.^191c,192 In addition, the IR spectra exhibited strong bands at 566 and 491 cm⁻¹ attributed to [S₃]˙⁻and the polysulfides [S_n]²⁻/[HS_n]⁻, respectively.^191c The observation of an absorption band at 610 cm⁻¹ in the UV-visible spectrum, which is more pronounced with an increase in temperature or radiation dose, is consistent with the formation of [S₃]˙⁻ as is the change in the colour of the sample from yellow to red and then to green. These observations are reminiscent of the behaviour of solutions of sulfur in liquid ammonia, which are red at lower temperatures and green or blue at room temperature and have been shown to contain [NS₄]⁻ and [S₃]˙⁻ ions, both of which are blue species, and yellow-orange polysulfide dianions.¹⁹³

6 Summary and conclusions

The synthesis and X-ray structures of polysulfide dianions [S_n]²⁻ with alkali or alkaline earth metal cations have been studied for at least 70 years. With the exception of the recently identified branched isomer of the tetrasulfide, pyramidal [SS₃]²⁻ (C_3v), these dianions exist as chain-like species with up to 13 atoms and the negative charges concentrated on the terminal atoms. Odd- and even-membered dianions are equally important and the pentasulfide dianion is thermodynamically favoured in water. The entrapment of polysulfide radical anions [S_n]˙⁻ in a zeolitic matrix, e.g. in ultramarines, and their characterization by spectroscopic methods also has a long history. However, the importance of these simple homoatomic anionic species across a broad range of chemical, physical and biological sciences has only come to the forefront in recent years. In this review we have discussed critically the significant advances that have been made during the past ca. 15 years in the synthesis, characterization by physical and computational techniques, reactions and applications of these pervasive chalcogenide anions.

The contemporary emphasis in synthetic work is on the generation of pure, soluble salts of polysulfide dianions in order to determine their function in alkali-metal sulfur batteries and biological systems. The long-known reaction of hydrosulfide ions [HS]⁻ with cyclo-S₈ has been employed effectively for this purpose using large organic cations, e.g. tetraalkylammonium or pyrrolidinium in the case of [Me₃SiS]⁻ salts. The counter-cation has a notable influence on the stability of [HS]⁻ salts. Thus, while [NBu₄][HS] is stable under ambient conditions, the ammonium salt [NH₄][HS] must be cooled to avoid decomposition. Spectroscopic evidence (IR/Raman, UV-visible) indicates that irradiation of cold [NH₄][HS], which is present in planetary atmospheres, produces a mixture of polysulfides [S_n]²⁻, [HS_n]⁻, [S₃]˙⁻ as well as binary sulfur–nitrogen anions [S_nN]⁻ (n = 3, 4), which contribute to the chromophore of Jupiter's Great Red Spot.

The identification of individual polysulfides [S_n]²⁻ in solution is of utmost importance in the context of lithium–sulfur batteries and in biological and geological settings, but difficult owing to the existence of equilibria between different dianions as well as the partial dissociation or disproportionation to give polysulfide radical anions. In aqueous solutions, isotopic exchange between the various dianions is ca. 70% complete within 8 s. The polarity of the solvent has a strong influence on the extent of S–S homolytic dissociation of [S_n]²⁻ chains, which are thermodynamically stable in an aqueous environment at 25 °C, but dissociate in solvents of low polarity, e.g. THF, and in the gas phase. The best approach to the identification of dissolved polysulfide dianions is rapid derivatization with methyl triflate (CF₃SO₃CH₃) followed by characterization of the polysulfanes Me–S_n–Me so formed by HPLC and ¹H NMR spectra. Solid and dissolved polysulfides also undergo autoxidation to give elemental sulfur and sulfur oxo-anions such as thiosulfate and sulfate; the novel adduct [S₃O₂]²⁻, formed by reaction of [S₃]˙⁻ with triplet state O₂ and detected by mass spectrometry, is probably the primary reaction product in solution.

In the gas phase polysulfide dianions [S_n]²⁻ (n < 7) are unstable thermodynamically owing to Coulomb explosion. Consequently, the use of density functional methods to calculate vibrational modes has to be applied with caution, whereas Hartree–Fock and valence force field calculations yield reliable results. In solution, the cations of polysulfide salts are coordinated to solvent molecules or to the polysulfide dianions, depending on the donor strength. This effect is particularly important with Li⁺ ions due to their extremely high field strength resulting in ion pairs such as [Li(solvent)S_n]⁻ (n = 2–8) with cyclic or cluster-like structures, which are probably the active species in lithium–sulfur batteries. However, their thermodynamic properties under realistic conditions still need to be explored, e.g. by high-level quantum-chemical calculations. In contrast, the chemical reactions in solvent-free high-temperature Na–S batteries and their thermodynamics are well understood and dominated by polysulfide dianions and radical monoanions, as well as cyclic ion pairs [NaS_n]⁻, the thermodynamic properties of which have been investigated by high-level quantum-chemical calculations. Computational studies show that the Gibbs energy of the pyramidal isomer [SS₃]²⁻ is only ca. 13.0 kJ mol⁻¹ higher than for the [S₄]²⁻ chain suggesting that branched isomers could be present in polysulfides at high temperatures, e.g. in HT sodium–sulfur batteries.

Spectroscopic techniques, especially Raman, UV-visible and, in the case of the radical anions, EPR, are potentially useful for the identification of polysulfide species. The highly coloured radical anions [S_n]˙⁻ are readily distinguished by their distinctive strong visible absorption bands at ca. 410 nm (n = 2) and 595–620 nm (n = 3). On the other hand, the absorption maxima for the series of dianions [S_n]²⁻ (n = 2–8) lie close together and the interpretation of UV-visible spectra may be complicated by the additional presence of radical anions. Consequently, the use of a combination of spectroscopic techniques is advisable for a definitive identification of these homoatomic species. Raman spectra of solid and dissolved alkali metal polysulfides M₂S_n are characterized by SS stretching modes in the region 390–510 cm⁻¹, and bending and torsion modes occur below 300 cm⁻¹. The polysulfide radical anions [S_n]˙⁻ (n = 2,3) show characteristic Raman bands that are enhanced in the Resonance Raman spectra so that overtones can be observed. In a very recent example, Raman spectroscopy supplied the unambiguous identification of [S₃]˙⁻ in the blue mineral (lapis lazuli) recently found in a monastery in Germany in the teeth of a medieval woman, who was probably working on illuminated manuscripts. EPR spectra have been used to show that the bent trisulfide species [S₃]˙⁻ adopts different orientations within the sodalite cage of ultramarines as well as to provide a definitive characterization of the homologue [S₂]˙⁻.

The occurrence of the tetrasulfide radical anion [S₄]˙⁻ has been proposed frequently on the basis of solitary spectroscopic evidence, e.g. EPR, UV-visible or Raman spectra, but the definitive characterization of this species is still elusive. In some cases, the possibility of an alternative species, e.g. neutral S₄, the dianion [S₈]²⁻ or even the isobaric species [S₃O₂]²⁻, cannot be ruled out. A combined spectroscopic study of dilute solutions of a [S₈]²⁻ salt in electron-pair donor solvents may elucidate this conundrum. With the exception of the [PPh₄]⁺ salt of cyclo-[S₆]˙⁻, the larger polysulfide radical anions [S_n]˙⁻ (n = 5, 7, 8) have not been characterized experimentally in condensed phases. The six-membered ring in [S₆]˙⁻ incorporates two long S–S bonds (263 pm) and computational studies for [S_n]˙⁻ (n = 7, 8) predict “broken ring” structures with even longer S–S bonds. Electrochemical reduction of S₈ produces [S₈]˙⁻ as the primary product, which, however, is unstable and disproportionates to S₈ and [S₈]²⁻ and can also be further reduced with simultaneous dissociation to [S₃]˙⁻ + [S₅]˙⁻ or 2[S₄]˙⁻. These exothermic reactions are proposed to occur in room-temperature alkali metal–sulfur batteries. The main problems with these batteries are the growth of dendrites at the metal anode, the destruction of the sulfur-based cathode by massive volume changes during charging and discharging, the reaction of the solvent(s) with the sulfur species and the self-discharge owing to the shuttle effect (diffusion) of the anions and their chemical reduction by the metal. During charging of batteries, as well as during oxidation of sulfide by sulfur bacteria, S₈ is formed from long-chain polysulfide dianions by intramolecular nucleophilic attack with extrusion of the sulfur homocycle.

Ammonium polysulfides [NH₄]₂[S_n] or solutions of cyclo-S₈ in ammonia or amines have been used as reagents in organic synthesis for >100 years, e.g. for the transformation of carbonyls into thiocarbonyls. Although such solutions are known to contain the trisulfide radical anion [S₃]˙, the targeted use of this reagent for the preparation of organosulfur compounds is a recent development. In these applications [S₃]˙⁻ is generated from solutions of cyclo-S₈ with a base, e.g. Na[O^tBu], Cs₂[CO₃] or Na[SH] in electron-pair donor solvents or from K₂S in DMF, and its presence is demonstrated by UV-visible and EPR spectroscopy. Reactions of [S₃]˙⁻ generated in this way give high yields of a variety of heterocyclic organosulfur compounds, including thiophenes and the industrially important 2-mercaptobenzothiazole. The pathway for the production of [S₃]˙⁻ in solutions of K₂S in DMF has not been elucidated, but it must involve the formation of polysulfides [S_n]²⁻, presumably by autoxidation. Very recently, the combination of S₈ and NaOH followed by oxidation with H₂O₂ has been used to generate sulfur quantum dots with unique optical properties.¹⁹⁴ While this process undoubtedly involves the initial formation of polysulfide dianions [S_n]²⁻,^194a the suggestion that these are limited to the di- and octa-sulfides (n = 2, 8)^194a should be re-visited in the light of the information presented in this review.

In situ Raman spectroscopy has also been pivotal in investigations of the formation of [S₃]˙⁻ in hydrothermal fluids at elevated temperatures and pressures and the role that polysulfide radical ions [S_n]˙⁻ (n = 2, 3) play in the transport of metals such as Cu and Au. Significantly, the gold(I) species [Au(SH)S₃]⁻ has been identified by X-ray absorption spectroscopy as the most stable complex under these conditions. Complexes of the disulfide radical anion [S₂]˙⁻ with transition metals such as Cu and Ni have been structurally characterised. In addition, the first complex of the tetrasulfide radical anion [S₄]˙⁻, in the form of a dimeric Bi(III) species, was reported recently. To date, however, no metal complexes of the trisulfide radical anion [S₃]˙⁻ are known. In view of their geological significance, such complexes, e.g. with Cu or Au, represent a worthwhile challenge for inorganic chemists.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

Financial support from NSERC (Canada) is gratefully acknowledged. The authors are thankful to Mr Chris Gendy and Dr Yana Steudel for the preparation of figures and schemes. The support of Profs. A. Pfitzner and H. Hartl for providing Fig. 4 and 5, respectively, and Dr A. Kamyshny Jr for Fig. 9 is also acknowledged.

References

1. For the correct spelling of sulfur, see the editorial entitled “So long Sulphur”:, Nat. Chem., 2009, 1, 333.
2. (a) R. Steudel and B. Eckert, Top. Curr. Chem., 2003, 230, 1–79; (b) I. Krossing, in Handbook of Chalcogen Chemistry: New Perspectives in Sulfur, Selenium and Tellurium, ed. F. A. Devillanova and W.-W. du Mont, RSC Publishing, 2nd edn, 2013, vol. 1, ch. 7.1, pp. 349–381.
3. H. S. Low and R. A. Beaudet, J. Am. Chem. Soc., 1976, 98, 3849–3852.
4. I. Krossing and J. Passmore, Inorg. Chem., 2004, 43, 1000–1011.
5. J. Derendorf, C. Jenne and M. Keßler, Angew. Chem., Int. Ed., 2017, 56, 8281–8284.
6. R. Steudel, Top. Curr. Chem., 2003, 231, 127–152 , and references cited therein.
7. W. S. Sheldrick, in Handbook of Chalcogen Chemistry: New Perspectives in Sulfur, Selenium and Tellurium, ed. F. A. Devillanova and W.-W. du Mont, RSC Publishing, 2nd edn, 2013, vol. 1, ch. 9.2, pp. 514–545. This review includes polyselenides and polytellurides and emphasizes synthetic and structural aspects.
8. T. Chivers and P. J. W. Elder, Chem. Soc. Rev., 2013, 42, 5996–6005 , and references cited therein.
9. B. Neumüller, F. Schmock, R. Kirmse, A. Voigt, A. Diefenbach, F. M. Bickelhaupt and K. Dehnicke, Angew. Chem., Int. Ed., 2000, 39, 4580–4582.
10. R. J. Schwamm, M. Lein, M. P. Coles and C. M. Fitchett, J. Am. Chem. Soc., 2017, 139, 16490–16493.
11. A. K. Hearley, B. F. G. Johnson, J. S. McIndoe and D. G. Tuck, Inorg. Chim. Acta, 2002, 334, 105–112.
12. R. Steudel, Top. Curr. Chem., 2003, 231, 99–125.
13. R. Steudel, Chem. Rev., 2002, 102, 3905–3945.
14. Sulfur: Its Significance for Chemistry, for the Geo-, Bio- and Cosmosphere and Technology, ed. A. Müller and B. Krebs, Elsevier, Amsterdam, 1984.
15. For recent reviews, see (a) K. H. Wujcik, D. R. Wang, A. A. Teran, E. Nasybulin, T. A. Pascal, D. Prendergast and N. P. Balsara, in Electrochemical Engineering: From Discovery to Product, ed. R. C. Alkire, P. N. Bartlett and M. Kopev, John Wiley and Sons, 2018, vol. 10, ch. 3, pp. 41–74; (b) X. Chen, T. Hou, K. A. Persson and Q. Zhang, Mater. Today, 2019, 22, 142–158; (c) E. Zhao, K. Nie, X. Yu, Y.-S. Hu, F. Wang, J. Xiao, H. Li and X. Huang, Adv. Funct. Mater., 2018, 28, 1707543; (d) D. Zheng, G. Wang, D. Liu, J. Si, T. Ding, D. Qu, X. Yang and D. Qu, Adv. Mater. Technol., 2018, 3, 1700233; (e) G. Zhang, Z.-W. Zhang, H.-J. Peng, J.-Q. Huang and Q. Zhang, Small Methods, 2017, 1, 1700134; (f) R. Xu, J. Lu and K. Amine, Adv. Energy Mater., 2015, 5, 1500408; (g) M. Wild, L. O’Neill, T. Zhang, R. Purkayastha, G. Minton, M. Marinescu and G. J. Offer, Energy Environ. Sci., 2015, 8, 3477–3494.
16. (a) T. Chivers, Nature, 1974, 252, 32; (b) T. Chivers, in Homoatomic, Rings, Chains and Macromolecules of Main-Group Elements, ed. A. L. Rheingold, Elsevier, Amsterdam, 1977, ch. 22, pp. 499–537.
17. T. Takata, D. Saeki, Y. Makita, N. Yamada and N. Kihara, Inorg. Chem., 2003, 42, 3712–3714.
18. G. Mali, M. U. M. Patel, M. Mazaj and R. Dominko, Chem. – Eur. J., 2016, 22, 3355–3360.
19. P. Stüble, A. Berroth, F. Wortelkamp and C. Röhr, Z. Naturforsch., B: J. Chem. Sci., 2019, 74, 33–47.
20. (a) F. Dornhaus, M. Bolte, M. Wagner and H.-W. Lerner, Z. Anorg. Allg. Chem., 2007, 633, 425–428; (b) J. Getzschmann and S. Kaskel, Z. Anorg. Allg. Chem., 2014, 640, 905–906.
21. D. Friedrich, F. Pielnhofer, M. Schlosser, R. Weihrich and A. Pfitzner, Chem. – Eur. J., 2015, 21, 1811–1817 , and references cited therein.
22. Q. Zou, Z. Liang, G.-Y. Du, E. Y. Li and Y.-C. Lu, J. Am. Chem. Soc., 2018, 140, 10740–10745.
23. R. D. Rauh, F. S. Shuker, J. M. Marston and S. B. Brummer, J. Inorg. Nucl. Chem., 1977, 39, 1761–1766.
24. N. A. Cañas, D. N. Fronczek, N. Wagner, A. Latz and K. A. Friedrich, J. Phys. Chem. C, 2014, 118, 12106–12114.
25. N. Saqib, C. J. Silva, C. M. Maupin and J. M. Porter, Appl. Spectrosc., 2017, 71, 1593–1599.
26. (a) S. Dev, E. Ramli, T. B. Rauchfuss and S. R. Wilson, Inorg. Chem., 1991, 30, 2514–2519; (b) A. Schliephake, H. Fallius, H. Buchkremer-Hermanns and P. Böttcher, Z. Naturforsch., B: J. Chem. Sci., 1988, 43, 21–24.
27. T. Chivers, F. Edelmann, J. F. Richardson and K. J. Schmidt, Can. J. Chem., 1986, 64, 1509–1513.
28. G. Bieker, J. Wellmann, M. Kolek, K. Jalkanen, M. Winter and P. Bieker, Phys. Chem. Chem. Phys., 2017, 19, 11152–11162.
29. M. D. Hartle, D. J. Meininger, L. N. Zakharov, Z. J. Tonzetich and M. D. Pluth, Dalton Trans., 2015, 44, 19782–19785.
30. (a) L. H. Finger, F. Wohde, E. I. Grigoryev, A.-K. Hansmann, R. Berger, B. Roling and J. Sundermeyer, Chem. Commun., 2015, 51, 16169–16172; (b) L. H. Finger and J. Sundermeyer, Chem. – Eur. J., 2016, 22, 4218–4230; (c) L. H. Finger, B. Scheibe and J. Sundermeyer, Inorg. Chem., 2015, 54, 9568–9575.
31. T. S. Bailey, H. A. Henthorn and M. D. Pluth, Inorg. Chem., 2016, 55, 12618–12625.
32. (a) H. S. Lim, N. H. Heo and K. Seff, J. Phys. Chem. C, 2018, 122, 28133–28141; (b) the anion in the black solid formed upon melting Cs₂S₆ has been tentatively identified by vibrational spectra as [S₂S₄]²⁻, a branched isomer of the [S₆]²⁻ chain, cf. dithionite [S₂O₄]²⁻, see ref. 6.
33. H. Ohtsu, W. Choi, N. Islam, Y. Matsushita and M. Kawano, J. Am. Chem. Soc., 2013, 135, 11449–11452.
34. T. Chivers and I. Drummond, Inorg. Chem., 1972, 11, 2525–2527.
35. A. Radini, M. Tromp, A. Beach, E. Tong, C. Speller, M. McCormick, J. Dudgeon, M. J. Collins, F. Rühli, R. Kröger and C. Warinner, Sci. Adv., 2019, 5, eaau7126.
36. R. Steudel and F. Schuster, Z. Naturforsch., A: Phys. Sci., 1977, 32, 1313–1319.
37. (a) H. Ziemann and W. Bues, Z. Anorg. Allg. Chem., 1979, 455, 69–87; (b) W. Bues and H. Ziemann, Z. Anorg. Allg. Chem., 1979, 456, 54–60.
38. W. E. Kleinjan, A. de Keizer and A. J. H. Janssen, Water Res., 2005, 39, 4093–4100.
39. S. A. Khan, R. W. Hughes and P. A. Reynolds, Vib. Spectrosc., 2011, 56, 241–244.
40. R. Tegman, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1973, 29, 1463–1469.
41. K. Tatsumi, Y. Inoue, A. Nakamura, R. E. Cramer, W. VanDoorne and J. W. Gilje, Angew. Chem., Int. Ed. Engl., 1990, 29, 422–424.
42. K. Tatsumi, H. Kawaguchi, K. Inoue, K. Tani and R. E. Cramer, Inorg. Chem., 1993, 32, 4317–4323.
43. For a review, see N. Takeda, N. Tokitoh and R. Okazaki, Top. Curr. Chem., 2003, 231, 153–202.
44. R. Steudel and Y. Steudel, Chem. – Eur. J., 2013, 19, 3162–3176 and references cited therein.
45. V. Berghof, T. Sommerfeld and L. S. Cederbaum, J. Phys. Chem. A, 1998, 102, 5100–5105.
46. V. Bogdándi, T. Ida, T. R. Sutton, C. Bianco, T. Ditrói, G. Koster, H. A. Henthorn, M. Minnion, J. P. Toscano, A. van der Vliet, M. D. Pluth, M. Feelisch, J. M. Fukuto, T. Akaike and P. Nagy, Br. J. Pharmacol., 2019, 176, 646–670.
47. J. Gun, A. D. Modestov, A. Kamshny Jr., D. Ryzkov, V. Gitis, A. Goifman, O. Lev, V. Hultsch, T. Grischek and E. Worch, Microchim. Acta, 2004, 146, 229–237.
48. M. Cuisinire, C. Hart, M. Balasubramanian, A. Garsuch and L. F. Nazar, Adv. Energy Mater., 2015, 5, 140181.
49. K. H. Wujcik, D. R. Wang, A. Raghunathan, M. Drake, T. A. Pascal, D. Prendergast and N. P. Balsara, J. Phys. Chem. C, 2016, 120, 18403–18410.
50. D. P. Shoemaker, D. Y. Chung, J. F. Mitchell, T. H. Bray, L. Soderholm, P. J. Chupas and M. G. Kanatzidis, J. Am. Chem. Soc., 2012, 134, 9456–9463.
51. E. Levillain, P. Leghié, N. Gobeltz and J. P. Lelieur, New J. Chem., 1997, 21, 335–341.
52. B. Ledé, A. Demortier, N. Gobeltz-Hautecoeur, J.-P. Lelieur, E. Picqenard and C. Duhayon, J. Raman Spectrosc., 2007, 38, 1461–1468.
53. N. Jacquemet, D. Guillaume, A. Zwick and G. S. Pokrovski, Am. Mineral., 2014, 99, 1109–1118.
54. J. Hannauer, J. Scheers, J. Fullenwarth, B. Fraisse, L. Stievano and P. Johansson, ChemPhysChem, 2015, 16, 2755–2759.
55. Q. Gao, Y. Xiu, G.-D. Li and J.-S. Chen, J. Mater. Chem., 2010, 20, 3307–3312.
56. G. S. Pokrovski and L. S. Dubrovinsky, Science, 2011, 331, 1052–1054.
57. R. Linguerri, N. Komiha, J. Fabian and P. Rosmus, Z. Phys. Chem., 2008, 222, 163–176.
58. N. Gobeltz-Hautecoeur, A. Demortier, B. Lede, J. P. Lelieur and C. Duhayon, Inorg. Chem., 2002, 41, 2848–2854.
59. H.-L. Wu, L. A. Huff and A. A. Gewirth, ACS Appl. Mater. Interfaces, 2015, 7, 1709–1719.
60. J. Fabian, N. Komiha, R. Linguerri and P. Rosmus, J. Mol. Struct. THEOCHEM, 2006, 801, 63–69 , and references cited therein.
61. M. W. Wong, Top. Curr. Chem., 2003, 231, 1–29.
62. M. Hagen, P. Schiffels, M. Hammer, S. Dörfler, J. Tübke, M. J. Hoffmann, H. Althues and S. Kaskel, J. Electrochem. Soc., 2013, 160, A1205–A1214.
63. B. Eckert and R. Steudel, Top. Curr. Chem., 2003, 231, 31–98.
64. W. Tan, C. Wang and X. Jiang, Org. Chem. Front., 2018, 5, 2390–2394 , and references cited therein.
65. Q. Zou and Y.-C. Lu, J. Phys. Chem. Lett., 2016, 7, 1518–1525.
66. (a) M. U. M. Patel and R. Dominko, ChemSusChem, 2014, 7, 2167–2175; (b) M. U. M. Patel, R. Demir-Cakan, M. Morcrette, J.-M. Tarascon, M. Gaberscek and R. Dominko, ChemSusChem., 2013, 6, 1177–1181.
67. C. Barchasz, F. Molton, C. Duboc, J.-C. Lepretre, S. Patoux and F. Alloin, Anal. Chem., 2012, 84, 3973–3980.
68. Y.-C. Lu, Q. He and H. A. Gasteiger, J. Phys. Chem. C, 2014, 118, 5733–5741 , and references cited therein.
69. N. S. A. Manan, L. Aldous, Y. Alias, P. Murray, L. J. Yellowlees, M. C. Lagunas and C. Hardacre, J. Phys. Chem. B, 2011, 115, 13873–13879 , and references cited therein.
70. E. Boros, M. J. Earle, M. A. Gilea, A. Metlen, A.-V. Mudring, F. Rieger, A. J. Robertson, K. R. Seddon, A. A. Tomaszowska, L. Trusov and J. S. Vyle, Chem. Commun., 2010, 46, 716–718.
71. M. M. Cortese-Krott, G. G. C. Kuhnle, A. Dyson, B. O. Fernandez, M. Grman, J. F. DuMond, M. P. Barrow, G. McLeod, H. Nakagawa, K. Ondrias, P. Nagy, S. B. King, J. E. Saavedra, L. K. Keefer, M. Singer, M. Kelm, A. R. Butler and M. Feelisch, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, E4651–E4660.
72. R. Steudel, in Environmental Technologies to Treat Sulfur Pollution, ed. P. N. L. Lens and L. H. Pol, IWA, London, 2000, pp. 1–31.
73. A. Kamyshny Jr., A. Goifman, J. Gun, D. Rizkov and O. Lev, Environ. Sci. Technol., 2004, 38, 6633–6644.
74. A. Kamyshny Jr., J. Gun, D. Rizkov, T. Voitsekovski and O. Lev, Environ. Sci. Technol., 2007, 41, 2395–2400.
75. For a comprehensive recent review of the applications of elemental sulfur in synthetic organic chemistry, see T. B. Nguyen, Adv. Synth. Catal., 2017, 359, 1066–1130.
76. J. Rethmeier, A. Rabenstein, M. Langer and U. Fischer, J. Chromatogr. A, 1997, 760, 295–302.
77. A. Kawase, S. Shirai, Y. Yamoto, R. Arakawa and T. Takata, Phys. Chem. Chem. Phys., 2014, 16, 9344–9350.
78. I. Filipponen, A. Guerra, A. Hai, L. A. Lucia and D. S. Argyropoulos, Ind. Eng. Chem. Res., 2006, 45, 7388–7392.
79. (a) A. Kamyshny Jr., A. Goifman, D. Rizkov and O. Lev, Aquat. Geochem., 2003, 9, 291–304; (b) K. Avetisyan, T. Buchshtav and A. Kamyshny Jr., Geochim. Cosmochim. Acta, 2019, 247, 96–105.
80. D. Rizkov, O. Lev, J. Gun, B. Anisimov and I. Kuselman, Accredit. Qual. Assur., 2004, 9, 399–403.
81. A. Kamyshny Jr., I. Ekeltchik, J. Gun and O. Lev, Anal. Chem., 2006, 78, 2631–2639.
82. D. Zheng, X. Zhang, J. Wang, D. Qu and X. Yang, J. Power Sources, 2016, 301, 312–316.
83. (a) D. Arieli, D. E. W. Vaughan and D. Goldfarb, J. Am. Chem. Soc., 2004, 126, 5776–5788 , and references cited therein; (b) J. Goslar, S. Lijewski, K. Stanislaw, A. Jankowska and S. Kowalak, J. Chem. Phys., 2009, 130, 204504; (c) K. Raulin, N. Gobletz, H. Vezin, N. Touati, B. Ledé and A. Moissette, Phys. Chem. Chem. Phys., 2011, 13, 9253–9259; (d) P. Rejmak, J. Phys. Chem. C, 2018, 122, 29338–29349.
84. S. A. Basnayake, K. Tan, M. Leonard, Y. Chabal and K. J. Balkus, Microporous Mesoporous Mater., 2016, 219, 172–177.
85. M. Cuisinier, P.-E. Cabelguen, S. Evers, G. He, M. Kolbeck, A. Garsuch, T. Bolin, M. Balasubramanian and L. F. Nazar, J. Phys. Chem. Lett., 2013, 4, 3227–3232.
86. K. A. See, M. Leskes, J. M. Griffin, S. Britto, P. D. Matthews, A. Emly, A. van der Ven, D. S. Wright, A. J. Morris, C. P. Grey and R. Seshadri, J. Am. Chem. Soc., 2014, 136, 16368–16377.
87. J. Xiao, J. Z. Hu, H. Chen, M. Vijayakumar, J. Zheng, H. Pan, E. D. Walter, M. Hu, X. Deng and J. Feng, Nano Lett., 2015, 15, 3309–3316.
88. H. Wang, N. Sa, M. He, X. Liang, L. F. Nazar, M. Balusubramanian, K. G. Gallagher and B. Key, J. Phys. Chem. C, 2017, 121, 6011–6017.
89. M. Fantauzzi, B. Elsener, D. Atzei, A. Rigoldi and A. Rossi, RSC Adv., 2015, 5, 75953–75963.
90. A. Prange, R. Chauvistré, H. Modrow, J. Hormes, H. G. Trüper and C. Dahl, Microbiology, 2002, 148, 267–276.
91. (a) M. E. Fleet, X. Liu, S. L. Harmer and H. W. Nesbitt, Can. Mineral., 2005, 43, 1589–1603; (b) M. E. Fleet and X. Liu, Spectrochim. Acta, Part B, 2010, 65, 75–79.
92. (a) M. A. Lowe, J. Gao and H. D. Abruña, RSC Adv., 2014, 4, 18347–18353; (b) J. Gao, M. A. Lowe, Y. Kiya and H. D. Abruña, J. Phys. Chem. C, 2011, 115, 25132–25137.
93. M. Vijayakumar, N. Govind, E. Walter, S. D. Burton, A. Shukla, A. Devaraj, J. Xiao, J. Liu, C. Wang and A. Karim, Phys. Chem. Chem. Phys., 2014, 16, 10923–10932.
94. T. A. Pascal, K. H. Wujcik, J. J. Velasco-Velez, C.-H. Wu, A. A. Teran, M. Kapilashrami, J. Cabana, J. Guo, M. Salmeron and N. P. Balsara, J. Phys. Chem. Lett., 2014, 5, 1547–1551.
95. L. Nazar, M. Cuisinier, P.-E. Cabelguen, B. Adams, A. Garsuch and M. Balasubramanian, Energy Environ. Sci., 2014, 7, 2697–2705.
96. M. U. M. Patel, I. Arčon, G. Aquilanti, L. Stievano, G. Mali and R. Dominko, ChemPhysChem, 2014, 15, 894–904.
97. K. H. Wujcik, J. J. Velasco-Velez, C.-H. Wu, T. A. Pascal, A. A. Teran, M. A. Marcus, J. Cabana, J. Guo, D. Prendergast and M. Salmeron, J. Electrochem. Soc., 2014, 161, A1100–A1106.
98. T. A. Pascal, C. D. Pemmaraju and D. Prendergast, Phys. Chem. Chem. Phys., 2015, 17, 7743–7753.
99. M. Cuisinier, C. Hart, B. Adams, M. Balasubramanian, A. Garsuch and L. F. Nazar, Adv. Energy Mater., 2015, 5, 1401801.
100. Y. Gorlin, A. Siebel, M. Piana, T. Huthwelker, H. Jha, G. Monsch, F. Kraus, H. A. Gasteiger and M. Tromp, J. Electrochem. Soc., 2015, 162, A1146–A1155.
101. (a) A. A. Gambardella, C. M. Schmidt Patterson, S. M. Webb and M. S. Walton, Microchem. J., 2016, 125, 299–307; (b) M. Ganio, E. S. Pouyet, S. M. Webb, C. M. Schmidt Patterson and M. S. Walton, Pure Appl. Chem., 2018, 90, 463–475.
102. M. Chaouche, X. X. Gao, M. Cyr, M. Cotte and L. Frouin, J. Am. Ceram. Soc., 2017, 100, 1707–1716.
103. E. Cato, A. Rossi, N. C. Scherrer and E. S. B. Ferreira, J. Cult. Herit., 2018, 29, 30–35.
104. J. B. Kim, C. Hock, T. I. Tacovitch and D. M. Neumark, J. Phys. Chem. A, 2013, 117, 8126–8131.
105. J. A. Tossell, Geochim. Cosmochim. Acta, 2012, 95, 79–92.
106. M. Vijayakumar, N. Govind, E. Walter, S. D. Burton, A. Shukla, A. Devaraj, J. Xiao, J. Liu, C. Wang, A. Karim and S. Thevuthasan, Phys. Chem. Chem. Phys., 2014, 16, 10923–10932.
107. W. Koch, J. Natterer and C. Heinemann, J. Chem. Phys., 1995, 102, 6159–6167.
108. H. Sormova, R. Linguerri, P. Rosmus, J. Fabian and N. Komiha, Collect. Czech. Chem. Commun., 2007, 72, 83–99.
109. Y. Jin, G. Maroulis, X. Kuang, L. Ding, C. Lu, J. Wang, J. Lv, C. Zhang and M. Ju, Phys. Chem. Chem. Phys., 2015, 17, 13590–13597.
110. P. Adelhelm, P. Hartmann, C. L. Bender, M. Busche, C. Eufinger and J. Janek, Beilstein J. Nanotechnol., 2015, 6, 1016–1055.
111. Y.-X. Wang, B. Zhang, W. Lai, Y. Xu, S.-L. Chou, H.-K. Liu and S.-X. Dou, Adv. Energy Mater., 2017, 7, 1602829.
112. D. Kumar, S. K. Rajouria, S. B. Kuhar and D. K. Kanchen, Solid State Ionics, 2017, 312, 8–16.
113. Z. Zhao-Karger and M. Fichtner, MRS Commun., 2017, 7, 770–784.
114. M. M. Gross and A. Manthiram, ACS Appl. Mater. Interfaces, 2018, 10, 10612–10617.
115. (a) P. Leung, X. Li, C. P. de León, L. Berlouis, C. T. J. Lowa and F. C. Walshab, J. Power Sources, 2009, 189, 1220–1230; (b) F. Pan and Q. Wang, Molecules, 2015, 20, 20499–20517.
116. Z. Wen, Y. Hu, X. Wu, J. Han and Z. Gu, Adv. Funct. Mater., 2013, 23, 1005–1018.
117. R. Steudel, Top. Curr. Chem., 2003, 230, 81–116.
118. (a) J. Sangster and A. D. Pelton, J. Phase Equilib., 1997, 18, 89–96; (b) X. Yu and A. Manthiram, J. Phys. Chem. Lett., 2014, 5, 1943–1947; (c) Y. Wang, Y. Hao, L.-C. Xu, Z. Yang, M.-Y. Di, R. Liu and X. Li, J. Phys. Chem. C, 2019, 123, 3988–3995.
119. (a) C. W. Park, J. H. Ahn, H. S. Ryu, K. W. Kim and H. J. Ahn, Electrochem. Solid-State Lett., 2006, 9, A123–A125; (b) H. Ryu, T. Kim, K. Kim, J. H. Ahn, T. Nam, G. Wang and H. J. Ahn, J. Power Sources, 2011, 196, 5186–5190.
120. R. S. Assary, L. A. Curtiss and J. S. Moore, J. Phys. Chem. C, 2014, 118, 11545–11548 . The cyclic geometry of neutral S₃ (D_3h) obtained in this work is in conflict with the experimental acyclic structure (C_2v), and the geometry of [S₈]˙⁻ is determined to be a chain while other authors found a ring with one long bond (Section 4).
121. (a) D. Zhou, Y. Chen, B. Li, H. Fan, F. Cheng, D. Shanmukaraj, T. Rojo, M. Armand and G. Wang, Angew. Chem., Int. Ed., 2018, 57, 10168–10172; (b) P. Sang, Y. Si and Y. Fu, Chem. Commun., 2019, 55, 4857–4860; (c) H. Zhou, F. Yu, M. Wei, Y. Su, Y. Ma, D. Wang and Q. Shen, Chem. Commun., 2019, 55, 3729–3732.
122. N. Tanibata, M. Deguchi, A. Hayasi and M. Tatsumisago, Chem. Mater., 2017, 29, 5232–5238.
123. S. Choudhury, S. Wei1, Y. Ozhabes, D. Gunceler, M. J. Zachman, Z. Tu, J. H. Shin, P. Nath, A. Agrawal, L. F. Kourkoutis, T. A. Arias and L. A. Archer, Nat. Commun., 2017, 8, 898.
124. Y.-X. Yin, S. Xin, Y.-G. Guo and L.-J. Wan, Angew. Chem., Int. Ed., 2013, 52, 13186–13200.
125. Y. Yang, G. Zheng and Y. Cui, Chem. Soc. Rev., 2013, 42, 3018–3032.
126. A. Manthiram, Y. Fu and Y.-S. Su, Acc. Chem. Res., 2013, 46, 1125–1134.
127. A. Manthiram, Y. Fu, S.-H. Chung, C. Zu and Y.-S. Su, Chem. Rev., 2014, 114, 11751–11787.
128. A. Manthiram, S.-H. Chung and C. Zu, Adv. Mater., 2015, 27, 1980–2006.
129. W. Kang, N. Deng, J. Ju, Q. Li, D. Wu, X. Ma, L. Li, M. Naebe and B. Cheng, Nanoscale, 2016, 8, 16541–16588.
130. Z. W. Seh, Y. Sun, Q. Zhang and Y. Cui, Chem. Soc. Rev., 2016, 45, 5605–5634.
131. H.-J. Peng, J.-Q. Huang and Q. Zhang, Chem. Soc. Rev., 2017, 46, 5237–5288.
132. (a) Q. He, Y. Gorlin, M. U. M. Patel, H. A. Gasteiger and Y.-C. Lu, J. Electrochem. Soc., 2018, 165, A4027–A4033; (b) A. Gupta, A. Bhargav and A. Manthiram, Adv. Energy Mater., 2019, 9, 1803096; (c) Y. Jung, S. Kim, B.-S. Kim, D.-H. Han, S.-M. Park and J. Kwak, J. Electrochem. Sci. Eng., 2008, 3, 566–577.
133. Z. Wang, J. Liu, L. Sun, Y. Zhang, Q. Fu, H. Xie and H. Sun, Chem. – Eur. J., 2018, 24, 14154–14161.
134. C. Ye, Y. Jiao, H. Jin, A. D. Slattery, K. Davey, H. Wang and S.-Z. Qiao, Angew. Chem., Int. Ed., 2018, 57, 16703.
135. M. Zhen, J. Wang, X. Wang and C. Wang, Chem. – Eur. J., 2018, 24, 5860–5867 , and references cited therein.
136. M. Armand, Angew. Chem., Int. Ed., 2018, 57, 15002–15027.
137. S. S. Zhang, J. Power Sources, 2016, 322, 99–105.
138. D. Bresser, S. Passerini and B. Scrosati, Chem. Commun., 2013, 49, 10545–10562.
139. D. Zheng, X.-Q. Yang and D. Qu, ChemSusChem, 2016, 9, 2348–2350.
140. W. Lu, Z. Yuan, Y. Zhao, H. Zhang, H. Zhang and X. Li, Chem. Soc. Rev., 2017, 46, 2199–2236.
141. J.-J. Chen, R.-M. Yuan, J.-M. Feng, Q. Zhang, J.-X. Huang, G. Fu, M. S. Zheng, B. Ren and Q.-F. Dong, Chem. Mater., 2015, 27, 2048–2055.
142. R. Dominko, A. Vizintin, G. Aquilanti, L. Stievano, M. J. Helen, A. R. Munnangi, M. Fichtner and I. Arcon, J. Electrochem. Soc., 2018, 165, A5014–A5019.
143. E. P. Kamphaus and P. B. Balbuena, J. Phys. Chem. C, 2017, 121, 21105–21117.
144. (a) A. Shyamsunder, W. Beichel, P. Klose, Q. Pang, H. Scherer, A. Hoffmann, G. K. Murphy, I. Krossing and L. F. Nazar, Angew. Chem., Int. Ed., 2017, 56, 6192–6197; (b) Q. Cheng, W. Xu, S. Qin, S. Das, T. Jin, A. Li, A. C. Li, B. Qie, P. Yao, H. Zhai, C. Shi, X. Yong and Y. Yang, Angew. Chem., Int. Ed., 2019, 58, 5557–5561.
145. R. Xu, S. Zhang, X. Wang, Y. Xia, X. Xia, J. Wu, C. Gu and J. Tu, Chem. – Eur. J., 2018, 24, 6007–6018.
146. (a) W. Said-Ahmad, A. Amrani and Z. Aizenshtat, Org. Geochem., 2013, 59, 82–86; (b) K. Ding and P. Adam, Org. Geochem., 2015, 8, 133–136.
147. G. Zhang, H. Yi, C. Bian, C. Liu and A. Lei, Org. Lett., 2014, 16, 6156–6159.
148. M. Wang, Q. Fan and X. Jiang, Org. Lett., 2016, 18, 5756–5759.
149. H. Huang, Z. Qu, X. Ji and G.-J. Deng, Org. Chem. Front., 2019, 1146–1150 , and references cited therein.
150. (a) Z.-Y. Gu, J.-J. Cao, S.-Y. Wang and S.-J. Ji, Chem. Sci., 2016, 7, 4067–4072; (b) J.-H. Li, Q. Huang, S.-Y. Wang and S.-J. Ji, Org. Lett., 2018, 20, 4704–4708.
151. J. W. Thomson, K. Nagashima, P. M. Macdonald and G. A. Ozin, J. Am. Chem. Soc., 2011, 133, 5036–5041.
152. A. J. Findlay, FEMS Microbiol. Lett., 2016, 363, fnw103.
153. F. Bouillaud and F. Blachier, Antioxid. Redox Signaling, 2011, 15, 379–391.
154. C. Szabo, C. Ransy, K. Modis, M. Andriamihaja, B. Murghes, C. Coletta, G. Olah, K. Vanagi and F. Bouillaud, Br. J. Pharmacol., 2014, 171, 2099–2122.
155. T. V. Mishanina, M. Libiad and R. Banerjee, Nat. Chem. Biol., 2015, 11, 457–464.
156. Z. Palinkas, P. G. Furtmuller, A. Nagy, C. Jakopitsch, K. F. Pirker, M. Magierowski, K. Jasnos, J. L. Wallace, C. Obinger and P. Nagy, Br. J. Pharmacol., 2015, 172, 1516–1532.
157. T. Bostelaar, V. Vitvitsky, J. Kumutima, B. E. Lewis, P. K. Yadav, T. C. Brunold, M. Filipovic, N. Lehnert, T. L. Stemmler and R. Banerjee, J. Am. Chem. Soc., 2016, 138, 8476–8488.
158. K. R. Olson, Y. Gao, E. R. DeLeon, M. Arif, F. Arif, N. Arora and K. D. Straub, Redox Biol., 2017, 12, 325–339.
159. M. M. Cortese-Krott, G. G. C. Kuhnle, A. Dyson, B. O. Fernandez, M. Grman, J. F. DuMond, M. P. Barrow, G. McLeod, H. Nakagawa, K. Ondrias, P. Nagy, S. B. King, J. E. Saavedra, L. K. Keefer, M. Singer, M. Kelm, A. R. Butler and M. Feelisch, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, E4651–E4660.
160. S. Carballal, M. Trujillo, E. Cuevasanta, S. Bartesaghi, M. N. Möller, L. K. Folkes, M. A. Garcia-Bereguiain, C. Gutiérrez-Merino, P. Wardman, A. Denicola, R. Radi and B. Alvarez, Free Radical Biol. Med., 2011, 50, 196–205.
161. R. Steudel, Ind. Eng. Chem. Res., 1996, 35, 1417–1423.
162. A. Prange, H. Engelhardt, H.-G. Trüper and C. Dahl, Arch. Microbiol., 2004, 182, 165–174.
163. B. Franz, T. Gehrke, H. Lichtenberg, J. Hormes, C. Dahl and A. Prange, Microbiology, 2009, 155, 2766–2774.
164. C. L. Marnocha, A. T. Levy, D. H. Powell, T. E. Hanson and C. S. Chan, Microbiology, 2016, 162, 1125–1134.
165. J. S. Berg, A. Schwedt, A.-C. Kreutzmann, M. M. M. Kuypers and J. Milucka, Appl. Environ. Microbiol., 2014, 80, 629–636.
166. C. Dahl, in Sulfur Metabolism in Phototrophic Bacteria, ed. P. C. Hallenbeck, Modern Topics in Phototrophic Prokaryotes, Springer, Berlin, 2017, pp. 27–66.
167. V. Vitvitsky, P. K. Yadav, S. An, J. Seravalli, U.-S. Cho and R. Banerjee, J. Biol. Chem., 2017, 292, 5584–5592.
168. S. A. Everett, C. Schöneich, J. H. Stewart and K.-D. Asmus, J. Phys. Chem., 1992, 96, 306–314.
169. A. Kamyshny Jr., C. G. Borkenstein and T. G. Ferdelman, Geostand. Geoanal. Res., 2009, 33, 415–435 , and references cited therein.
170. A. Kamyshny Jr., M. Zilberbrand, I. Ekeltchik, T. Voitsekovski, J. Gun and O. Lev, Aquat. Geochem., 2008, 14, 171–192.
171. G. W. Luther, B. Glazer, S. F. Ma, R. Trouborst, B. R. Shultz, G. Drischel and C. Kraiya, Aquat. Geochem., 2003, 9, 87–110.
172. A. Amrani and Z. Aizenshtat, Org. Geochem., 2004, 35, 909–921.
173. A. Amrani, J. W. Turner, Q. Ma, Y. Tang and P. G. Hatcher, Geochim. Cosmochim. Acta, 2007, 71, 4141–4160.
174. B. Ginzburg, L. Dor, I. Chalifa, O. Hadas and O. Lev, Environ. Sci. Technol., 1999, 33, 571–579.
175. A. Heitz, R. I. Kagi and R. Alexander, Water Sci. Technol., 2000, 41, 271–278.
176. P. D. Franzmann, A. Heitz, L. R. Zappia, J. E. Wajon and K. Xanthis, Water Res., 2001, 35, 1730–1738.
177. C. E. Manning, Science, 2011, 331, 1018.
178. G. S. Pokrovski, M. A. Kokh, D. Guillaume, A. Y. Borisova, P. Gisquet, J.-L. Hazemann, E. Lahera, W. Del Net, O. Proux, D. Testemale, V. Haigis, R. Jonchiere, A. P. Seitsonen, G. Ferlat, R. Vuilleumier, A. M. Saitta, M.-C. Boiron and J. Dubessy, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 13484–13489.
179. L. Truche, E. F. Bazarkina, G. Barré, E. Thomassot, G. Berger, J. Dubessy and P. Robert, Earth Planet. Sci. Lett., 2014, 396, 190–200.
180. G. Barré, L. Truche, E. F. Bazarkina, R. Michels and J. Dubessy, Chem. Geol., 2017, 462, 1–14.
181. G. Pokrovski and J. Dubessy, Earth Planet. Sci. Lett., 2015, 411, 298–309.
182. (a) A. Terzis and R. Rivest, Inorg. Chem., 1973, 12, 2132; (b) R. C. Elder and M. Trkula, Inorg. Chem., 1977, 48, 4551–4554.
183. H. Fabian and F. Fischer, J. Raman Spectrosc., 1989, 20, 639–643.
184. J. T. York, E. C. Brown and W. B. Tolman, Angew. Chem., Int. Ed., 2005, 44, 7745–7777.
185. S. Yao, C. Milsmann, E. Bill, K. Wieghardt and M. Driess, J. Am. Chem. Soc., 2008, 130, 13536–13537.
186. Y. Mei, D. M. Sherman, W. Liu and J. Brugger, Chem. Geol., 2013, 347, 34–42.
187. J. M. Stauber, P. Müller, Y. Dai, G. Wu, D. G. Nocera and C. C. Cummins, Chem. Sci., 2016, 7, 6928–6933 (Note 15 in this paper defines the abbreviation for the cryptand ligand[mBCDA-5t]6^–).
188. (a) K. Isobe, Y. Ozawa, A. Vazquez de Miguel, T.-W. Zhu, K.-M. Zhao, T. Nishioka, T. Ogura and T. Kitigawa, Angew. Chem., Int. Ed. Engl., 1994, 33, 1882–1883; (b) A. M. Mebel, K. Morokuma and K. Isobe, Inorg. Chem., 1995, 34, 1208–1211; (c) T. Nishioka, H. Kitayama, B. K. Breedlove, K. Shiomi, I. Kinoshita and K. Isobe, Inorg. Chem., 2004, 43, 5688–5697.
189. A. Poduska, R. Hoffmann, A. Ienco and C. Mealli, Chem. – Asian J., 2009, 4, 302–313 , and references cited therein.
190. A. Müller, F.-W. Baumann, H. Bögge, M. Römer, E. Krickemeyer and K. Schmitz, Angew. Chem., Int. Ed. Engl., 1984, 23, 632–633.
191. (a) M. J. Loeffler and R. L. Hudson, Icarus, 2018, 302, 418–425; (b) M. J. Loeffler, R. L. Hudson, N. J. Chanover and A. A. Simon, Icarus, 2016, 271, 265–268; (c) M. J. Loeffler, R. L. Hudson, N. J. Chanover and A. A. Simon, Icarus, 2015, 258, 181–191.
192. T. Chivers and R. S. Laitinen, Chem. Soc. Rev., 2017, 46, 5182–5192 , and references cited therein.
193. T. Chivers and C. Lau, Inorg. Chem., 1982, 21, 453–455.
194. (a) H. Wang, Z. Wang, Y. Xiong, S. V. Kershaw, T. Li, Y. Wang, Y. Zhai and A. L. Rogach, Angew. Chem., Int. Ed., 2019 DOI:10.1002/anie.201902344; (b) L. Shen, H. Wang, S. Liu, Z. Bai, S. Zhang, X. Zhang and C. Zhang, J. Am. Chem. Soc., 2018, 140, 7878–7884.

---