Surface nanostructuring via femtosecond lasers
Abstract
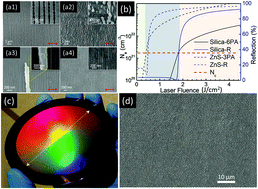
Periodical structures induced by pulsed lasers are a unique phenomenon when pulsed lasers irradiate on some material surfaces. These periodical structures with a subwavelength-scale period hold potential in integrated-optics and biomimetic micro-nanodevices for their direct shaping by laser pulses. However, the blurred nature of the laser-induced structuring hinders its further exploration in these application scopes. In this review, the plasmon-mediated structuring targeted on various materials, both organic and inorganic, will be discussed profoundly.
- This article is part of the themed collection: 2019 PCCP HOT Articles


 Please wait while we load your content...
Please wait while we load your content...