Intracluster proton transfer in protonated benzonitrile–(H₂O)_n≤6 nanoclusters: hydrated hydronium core for n ≥ 2

Abstract

Protonation and hydration of aromatic hydrocarbon molecules and their derivatives play a key role in many biological and chemical processes. The recent detection of benzonitrile (BN, cyanobenzene, C₆H₅CN) in the interstellar medium suggests the existence of its protonated form (H⁺BN) in both the gas phase and in or on ice grains. Herein, we analyze the vibrational signatures of size-selected protonated clusters composed of BN and water (W, H₂O), H⁺(BN–W_n=1–6), in the XH stretch range (X = C, N, O) with the aid of dispersion-corrected density functional theory calculations (B3LYP-D3/aug-cc-pVTZ). The size-dependent frequency shifts provide detailed insight about the site of protonation and the structure of the hydration shell. For n = 1, the proton is attached to the N atom of the CN group in BN, and W acts as a proton acceptor in an NH⋯O ionic hydrogen bond (H-bond) of a H⁺BN–W type structure with cation–dipole configuration. For n ≥ 2, the proton is transferred to the H-bonded hydration network, consistent with thermochemical arguments arising from both the relative proton affinities of BN and W_n and the solvation energies. In these proton-transferred BN–H⁺W_n structures, the excess proton is more or less localized at a H₃O⁺ hydronium core solvated by neutral W and BN ligands. At least for the considered cluster size (n ≤ 6), the BN impurity molecule is located in the first solvation shell of the H₃O⁺ ion, consistent with the larger electric dipole moment and proton affinity of BN as compared to W. However, the energy gap between these structures and surface isomers with BN solvated further away from the charge decreases with cluster size, suggesting that BN is located at the surface in large BN–H⁺W_n clusters. While for smaller clusters (n ≤ 4) the hydration network prefers branched structures at T = 0 K, in larger clusters (n ≥ 5) cyclic configurations with four- or five-membered H⁺W_n rings are most stable because they feature more H-bonds than the branched structures. Comparison with bare H⁺W_n clusters reveals the substantial effects of the perturbation by the BN impurity on the structure of the hydration network.

---

1. Introduction

Protonation and subsequent hydration of aromatic molecules are fundamental processes in chemistry and biology. For example, protonated arenes often appear as reactive intermediates (Wheland intermediates, σ complexes) in chemical reaction mechanisms.¹ Furthermore, many biomolecules including proteins occur in their protonated state at physiological pH values.^2–4 Hydration of these biomolecules is also crucial for their structure, stability, dynamics, reactivity, and function. As a result, “interfacial” or “biological” water is now considered as an integral part of these bioactive molecules.^5–9 The hydration shell also acts as a proton transport (or proton pump) medium through the formation of a hydrogen-bonded (H-bonded) hydration network.^10–12 Microhydrated aromatic cluster ions, both protonated closed-shell clusters and open-shell radical cations, isolated in the gas phase are suitable model systems to study the protonation and hydration process of arenes at the molecular level. Depending on the proton affinity (PA) and the solvation energy of the aromatic compound and the water cluster, the proton sticks to the arene or to the solvent. Because the proton affinity of water clusters, (H₂O)_n or W_n, increases substantially and monotonically with cluster size n (e.g., PA = 691 kJ mol⁻¹ for n = 1 and 908 kJ mol⁻¹ for n = 6),^13–17 the location of the excess proton may strongly depend on the cluster size. Because the PA of most aromatic molecules (A), in particular heterocyclic arenes or arenes with functional groups containing N or O atoms, is substantially higher than that of W, the monohydrated protonated cluster has the form H⁺A–W. Upon further hydration, the PA of the W_n solvent cluster increases, and intracluster proton transfer from AH⁺ to W_n may occur at a critical cluster size (n_c), leading to the proton-transferred structure, A–H⁺W_n. In case of open-shell aromatic radical cations, such proton transfer to solvent has been observed, for example, for benzene (A = phenyl) at a critical size of n_c = 4,^16,18,19 and for phenol (A = phenoxy) at n_c = 3.^20,21 For closed-shell protonated aromatic ions, examples include naphthalene (n_c = 2)²² and benzaldehyde (n_c = 3).²³ Interestingly, although benzene has a significantly larger PA than W (750 vs. 691 kJ mol⁻¹),²⁴ the most stable structure of the protonated dimer is benzene–H₃O⁺ (i.e., n_c = 1),^25,26 even though the higher-energy C₆H₇⁺–H₂O isomer has also been detected.²⁷ The latter example clearly emphasizes that, in addition to the relative PA values of A and W_n, the (sometimes substantial) difference in the solvation energies in H⁺A–W_n and A–H⁺W_n has to be taken into account as well to determine the position of the excess proton.^28,29

In this work, we apply infrared photodissociation (IRPD) spectroscopy to microhydrated clusters of protonated benzonitrile, H⁺(BN–W_n), in the size range n = 1–6, and analyse these with the aid of dispersion-corrected density functional theory (DFT) calculations. This cluster system has been chosen for the following reasons. (1) BN has been the first aromatic molecule detected recently in the taurus molecular cloud (TMC-1) by radioastronomy,³⁰ and this observation supports the long-standing hypothesis that (polycyclic) aromatic molecules are present in the interstellar medium (ISM).³¹ Because of the large abundance of H₃⁺ in the ISM,³² many molecules occur in these environments also in their protonated form.^31,33–35 To this end, laboratory spectra of protonated aromatic molecules are highly requested.^36–43 In addition to the isolated aromatic ion, also the structure and spectroscopy of microhydrated clusters^{16,18,19,22,26,44,45} are interesting in the context of their reactivity in ice grains and on ice surfaces.^22,45–48 (2) Triggered by the astronomical detection of BN, we recently characterized BN⁺–L_n clusters with nonpolar (L = Ar, n ≤ 2), quadrupolar (L = N₂, n ≤ 4), and dipolar ligands (L = H₂O, n = 1) by IRPD spectroscopy and DFT calculations.⁴⁹ As a major result, the preferred binding site changes from π-bonding for L = Ar and N₂ to bifurcated CH⋯O H-bonding for L = W, illustrating the differences in the interaction potential as a function of the polarity of the ligand. Significantly, the excess positive charge present in BN⁺–W changes the preferred binding motif from in-plane H-bonding (OH⋯N and CH⋯O) in neutral BN–W^50–54 to bifurcated CH⋯O bonding in BN⁺–W because of the dominant charge–dipole forces.⁴⁹ The current work explores the effect of protonation of BN–W_n on the preferred hydration motif. Neutral BN–W_n clusters with n = 1–3 have cyclic structures, in which the linear W_n unit connects the ortho CH proton (CH⋯O) with the CN group at the N end (OH⋯N),^52,53 and we expect a big change in geometry and binding energy upon protonation. (3) The information available about the structure, reactivity, and spectroscopy of H⁺BN and its clusters is rather limited. Substituted (or heterocyclic) arenes may protonate at the aromatic ring (carbenium ions) or the functional group (or heteroatom).^55–63 The early low-resolution electronic ultraviolet photodissociation spectrum of H⁺BN does not unravel the protonation site.^64,65 Mass spectrometric studies using isotopic labelling conclude N-protonation at the CN group,⁶⁶ with a recommended PA of 812 kJ mol⁻¹,¹³ in line with previous low-level quantum chemical calculations.⁶⁷ In our recent combined IRPD and high-level DFT study of H⁺BN–L_n clusters with L = Ar and N₂ (n ≤ 4), we confirmed for the first time with spectroscopic tools that N-protonation is strongly preferred over C-protontation.⁶⁸ Analysis of the IRPD spectra recorded in the CH and NH stretch range yields vibrational frequencies relevant for astronomical purposes and information about the acidity of the N–H and aromatic C–H bonds. The hydrophobic Ar and N₂ ligands prefer H-bonding to the acidic NH proton of H⁺BN via linear NH⋯L bonds to π-bonding at the aromatic ring, illustrating the large impact of protonation on the interaction potential. Herein, we extend these studies to H⁺(BN–W_n) clusters with n = 1–6 to probe for the first time the solvation of H⁺BN by hydrophilic protic dipolar ligands. As the recommended PA of BN (812 kJ mol⁻¹)¹³ is in the range of the PAs of small W_n clusters (PA = 691, 808, 862, 900, 904, and 908 kJ mol⁻¹ for n = 1–6),^13–17 we expect intracluster proton transfer from H⁺BN to the W_n solvent cluster at the cluster size n_c ∼ 2. Thus, larger H⁺(BN–W_n) clusters with n ≥ 2 are predicted to be of the type BN–H⁺W_n, and it is interesting to explore the effects of the BN impurity or dopant molecule on the structure, energetics, and bonding of the well-characterized bare H⁺W_n+1 clusters.^69–80 While BN has a larger electric dipole moment and PA than W, W can be better integrated in a H-bonded network because it can be involved in a larger number of strong σ-type H-bonds (up to four) than BN (only one).

2. Experimental and computational methods

2.1 Experimental methods

IRPD spectra of mass-selected H⁺(BN–W_n) clusters (n ≤ 6) are measured in a quadrupole tandem mass spectrometer coupled to an electron ionization (EI) source and an octopole ion guide.^81,82 Briefly, H⁺(BN–W_n) clusters are produced in a pulsed supersonic plasma expansion by electron/chemical ionization of BN and subsequent three-body hydration reactions in the high-pressure region of expansion. A carrier gas mixture of Ar and 5% H₂/He in a ratio 5 : 1 (10 bar) is bubbled through a reservoir containing liquid BN (Sigma-Aldrich, >99%, heated to 60 °C). To generate hydrated clusters, a few drops of water are added to the gas line just before entering the BN sample reservoir. Protonation of BN is achieved by proton transfer from H₃⁺ or H⁺W_n clusters generated by chemical ionization of H₂ and W_n. The addition of H₂ substantially increases the H⁺BN/BN⁺ ratio in the ion source, indicating that H₃⁺ is an efficient proton donor toward BN under the employed plasma conditions.⁶⁸ Clusters of the type BN–H⁺W_n may also be produced by simple three-body aggregation of H⁺W_n and BN or by bimolecular W → BN ligand exchange reactions. The desired H⁺(BN–W_n) parent clusters are filtered by the first quadrupole and irradiated in the adjacent octupole with a tuneable IR laser pulse (ν_IR) emitted from an optical parametric oscillator pumped by a nanosecond Q-switched Nd:YAG laser. The IR laser is characterized by a pulse energy of 2–5 mJ in the XH stretch range, a repetition rate of 10 Hz, and a bandwidth of 1 cm⁻¹. Calibration of ν_IR to better than 1 cm⁻¹ is achieved by a wavemeter. Resonant vibrational excitation of H⁺(BN–W_n) is followed by intracluster vibrational energy redistribution and subsequent evaporation of a single neutral W ligand. Only the loss of W is observed because its binding energy is lower than that of BN. This observation is consistent with the smaller dipole moment and PA of W as compared to BN. The resulting H⁺(BN–W_n−1) daughter ions are size-selected by the second quadrupole mass spectrometer and recorded with a Daly detector as a function of ν_IR to derive the IRPD spectrum of the parent cluster. The separation of the laser-induced dissociation signal from metastable decay is achieved by (i) triggering the ion source at twice the laser repetition rate and (ii) subtracting the fragment signals from alternating triggers. The reported IRPD yield is normalized for laser intensity variations measured with a pyroelectric detector. The widths of the peaks observed in the IRPD spectra are mainly due to unresolved rotational structure of the vibrational transitions, sequence hot bands involving inter- and low-frequency intramolecular modes, lifetime broadening, and possibly contributions from different structural isomers.

2.2 Computational methods

Quantum chemical calculations are performed for H⁺(BN–W_n) clusters and their subunits at the B3LYP-D3/aug-cc-pVTZ level to determine their structural, energetic, and vibrational properties.⁸³ The employed dispersion-corrected functional accounts well for the electrostatic, induction, and dispersion forces of the investigated clusters, and reproduces their experimental binding energies and IR spectra to satisfactory accuracy.^{45,49,68,84–91} For example, the binding energy computed for W₂ (D₀ = 1103 cm⁻¹) is in excellent agreement with the measured value (D₀ = 1105 ± 10 cm⁻¹),⁹² indicating that the H-bond interactions in the hydration networks are modeled accurately by this computational approach. All coordinates are allowed to relax during the search for stationary points, and their nature as minima or transition states are verified by harmonic frequency analysis. For energy optimization, the tight convergence criterion with ultrafine integration grid is employed. We manually generate a substantial number of conceivable starting structures, guided by the dimer potentials, experimental spectra, sequential cluster growth, and the comparison with well-known H⁺W_n structures. Throughout this paper, the lowest energy structure found is denoted “global minimum”. For the cluster sizes n = 1–4, we are confident that these structures are indeed the true global minima. For n = 5 and 6, global optimization techniques (not used here) would be required to ensure the reliable determination of the true global minima. Cartesian coordinates of all relevant structures and their energies are available in the ESI.† Harmonic intramolecular vibrational XH stretch frequencies are subjected to a linear scaling factor of 0.9586,⁶⁸ derived previously from fitting the calculated harmonic CH stretch frequencies of neutral BN to available experimental values.⁹³ Intramolecular frequencies below 2500 cm⁻¹ are scaled by 0.98, while intermolecular frequencies remain unscaled. Computed scaled IR stick spectra are convoluted with a Gaussian line profile (fwhm = 10 cm⁻¹) to facilitate convenient comparison with the experimental IRPD spectra. All relative energies (E₀) and dissociation energies (D₀) are corrected for harmonic zero-point vibrational energy. Relative free energies (G) are obtained for T = 298.15 K. If not stated otherwise, the total intermolecular dissociation energies are determined with respect to the molecular H⁺BN and W monomer fragments (also for the proton-transferred isomers of BN–H⁺W_n). Previous experience with the employed DFT level demonstrates that basis set superposition errors are less than 1%,^45,90 and thus they are not considered further here. Natural bond orbital (NBO) analysis is employed to evaluate the effects of protonation and hydration on the atomic charge distribution.⁹⁴ Second-order perturbation energies (E⁽²⁾) of the interaction between donor and acceptor NBOs involved in the H-bonds are used to quantify their relative strengths.⁹⁵ Regarding the strength of these H-bonds, noncovalent interaction (NCI) calculations are performed by evaluating the reduced gradient of the electron density ρ, s(ρ) ∼ |grad(ρ)|/ρ^4/3, as a function of ρ oriented by the sign of second eigenvalue (λ₂) of the Hessian, ρ* = ρ·sign(λ₂).^96,97 The strength of the intermolecular H-bonds is related to the absolute value of their negative ρ* values.

3. Results and discussion

Fig. 1 compares the experimental IRPD spectra of H⁺(BN–W_n) with n = 1–6 recorded between 2650 and 3850 cm⁻¹ in the single W loss channel. The positions and widths of the transitions observed (A–E) are listed in Table 1, along with the suggested vibrational and isomer assignments. Significantly, the spectra show a large variation with cluster size n, because the investigated spectral range encompasses the OH (ν_OH), NH (ν_NH), and CH (ν_CH) stretch fundamentals, which are highly sensitive to the position of the excess proton and the structure of the H-bonded solvent network. The predicted IR intensities of the ν_CH modes are, however, much weaker than those of ν_OH and ν_NH (by 2–4 orders of magnitude, I_CH < 10 km mol⁻¹ for BN and H⁺BN)⁶⁸ and thus not observed at the current experimental sensitivity (Table S1 in the ESI†). As will be shown below, the bands A–C arise from free OH stretch modes, while transitions D and E are attributed to bound OH and NH stretch vibrations, respectively. In the following, we first discuss the calculated structures of the BN, H⁺BN, and W monomers and then compare the IR spectra predicted for the lowest-energy isomers of H⁺(BN–W_n) with the measured IRPD spectra to determine the observed cluster structures. For completeness, we also include a comparison of the H⁺BN–W monohydrate with previous results obtained for H⁺BN–L with L = Ar and N₂,⁶⁸ to discuss similarities and differences of the microsolvation of H⁺BN with ligands of different polarity.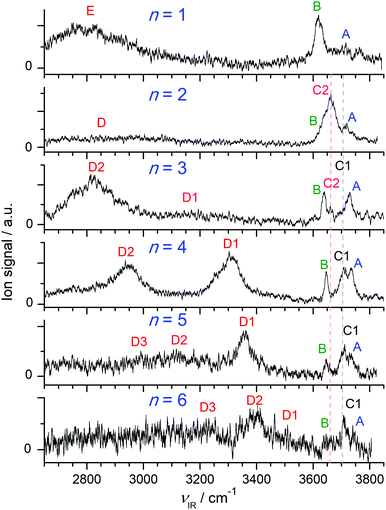

Fig. 1 IRPD spectra of H⁺(BN–W_n) with n = 1–6 recorded in the single W loss channel. The positions, widths, and vibrational and isomer assignments of the transitions observed (A–E) are listed in Table 1.

Table 1 Positions, widths (fwhm in parentheses), and suggested vibrational and isomer assignments of the transitions observed in the IRPD spectra of H⁺(BN–W_n) clusters compared to frequencies calculated at the B3LYP-D3/aug-cc-pVTZ level. All values are given in cm⁻¹. For comparison, spectral data of W are provided. For n = 5 and 6, the given isomer assignments are tentative

	Exp.^a	Mode	Calc.^b	Isomer
a The notation (b) indicates broad bands for which it is difficult to extract the widths. b Vibrational symmetry species and IR intensities (in km mol^−1) are listed in parentheses. c Ref. 102. d Ref. 68 .e The notations A, W, and D are abbreviations for ‘acceptor’, ‘water’, and ‘donor’, respectively.
W	3756^c	ν 3	3738 (63, b2)
	3657^c	ν 1	3639 (5, a1)
H^+BN^d	F 3555 ± 3	ν ^fNH	3560 (1221, a1)
H^+(BN–W)	A 3710 (b)	ν 3	3708 (173, a′′)	(A/W)^e H^+BN–W(H)
	B 3620 (34)	ν 1	3621 (84, a′)	(A/W) H^+BN–W(H)
	E 2750 (b)	ν ^bNH	2505 (5246, a′)	H^+BN–W(H)
H^+(BN–W2)	A 3719 (30)	ν 3	3714(162)	(A/W) BN–H^+W2
	C2 3657 (53)	ν f	3643 (174)	(DD/H^+W)^e BN–H^+W2
	B 3625	ν 1	3626 (64)	(A/W) BN–H^+W2
	D 2850 (b)	ν ^bOH	2760 (1844)	(DD/H^+W⋯W) BN–H^+W2
H^+(BN–W3)	A 3729 (27)	ν 3	3719 (293, a′), 3719 (1, a′′)	(A/W) BN–H^+W3(b)
	A 3729 (27)	ν 3	3718 (133)	(A/W) BN–H^+W3(l)
	C1 3694	ν f	3682 (124)	(DA/W) BN–H^+W3(l)
	C2 3660 (14)	ν f	3650 (168)	(DD/H^+W) BN–H^+W3(l)
	B 3640 (17)	ν 1	3631 (15, a′), 3630 (75, a′′)	(A/W) BN–H^+W3(b)
	B 3640 (17)	ν 1	3630 (34)	(A/W) BN–H^+W3(l)
	D1 3195 (b)	ν ^bOH	3175 (1140)	(DA/W) BN–H^+W3(l)
	D2 2815 (210)	ν ^bOH	2946 (758, a′), 2878 (2548, a′′)	(DDD/H^+W⋯W) BN–H^+W3(b)
H^+(BN–W4)	A 3733 (b)	ν 3	3728 (127), 3721 (138)	(A/W) BN–H^+W4(b)
	C1 3706 (b)	ν f	3693 (104)	(DA/W) BN–H^+W4(b)
	B 3646 (12)	ν 1	3638 (30), 3632 (42)	(A/W) BN–H^+W4(b)
	D1 3310 (113)	ν ^bOH	3265 (964)	(DA/W) BN–H^+W4(b)
	D2 2955 (115)	ν ^bOH	3002 (1278)	(DDD/H^+W⋯W) BN–H^+W4(b)
			2661 (3299)	(DDD/H^+W⋯BN) BN–H^+W4(b)
H^+(BN–W5)	A 3729	ν 3	3731 (123), 3730 (120)	(A/W) BN–H^+W5(b1)
	A 3729	ν 3	3731 (115), 3721 (133)	(A/W) BN–H^+W5(b3)
	C1 3711 (25)	ν f	3698 (110), 3695 (95)	(DA/W) BN–H^+W5(b1)
	C1 3711 (25)	ν f	3707 (97), 3695 (89)	(DA/W) BN–H^+W5(b3)
	B 3646 (14)	ν 1	3640 (27), 3639 (27)	(A/W) BN–H^+W5(b1)
	B 3646 (14)	ν 1	3639 (23), 3632 (38)	(A/W) BN–H^+W5(b3)
	D1 3357 (67)	ν ^bOH	3307 (1012), 3301 (738)	(DA/W) BN–H^+W5(b1)
	D1 3357 (67)	ν ^bOH	3374 (732)	(DA/W) BN–H^+W5(b3)
	D2 3116 (b)	ν OH (s/a)	3053 (967)/3033 (1748)	(DDD/H^+W)/(DA/W) BN–H^+W5(b3)
	D3 2990 (b)	ν ^bOH	2833 (1331)	(DDD/H^+W⋯BN) BN–H^+W5(b1)
	D3 2990 (b)	ν ^bOH	2752 (3769)	(DDD/H^+W⋯BN) BN–H^+W5(b3)
H^+(BN–W6)	A 3735	ν 3	3729 (126), 3728 (108), 3726 (101)	(A/W) BN–H^+W6(b1)
	A 3735	ν 3	3727 (123)	(A/W) BN–H^+W6(c1)
	C1 3707 (18)	ν f	3699 (104)	(DA/W) BN–H^+W6(b1)
	C1 3707 (18)	ν f	3704 (103), 3697 (98), 3692 (127), 3672 (96)	(DA/W, DAA/W) BN–H^+W6(c1)
	B 3650 (b)	ν 1	3638 (18), 3636 (24), 3635 (20)	(A/W) BN–H^+W6(b1)
	B 3650 (b)	ν 1	3637 (30)	(A/W) BN–H^+W6(c1)
	D1 3509 (b)	ν ^bOH	3439 (381)	(DA/W) BN–H^+W6(c1)
	D2 3390 (110)	ν ^bOH	3384 (1231), 3355 (413), 3340 (747)	(DDA/W) BN–H^+W6(b1)
				(DA/W) BN–H^+W6(b1)
	D2 3390 (110)	ν ^bOH	3335 (694), 3274 (1229), 3210 (1021)	(DA/W) BN–H^+W6(c1)
	D3 3220 (b)	ν ^bOH	2948 (2090), 2766 (317)	(DDD/H^+W⋯BN), (DDD/H^+W⋯W2)
				BN–H^+W6(b1)
	D3 3220 (b)	ν ^bOH (s/a)	2842 (1018)/2693 (471)	(DDD/H^+W) BN–H^+W6(c1)

---

3.1 BN, H⁺BN, and W monomers

The structural and vibrational properties of both BN and H⁺BN calculated at the B3LYP-D3/aug-cc-pVTZ level are discussed in detail in our previous reports.^49,68 Briefly, the computed structural, rotational, and vibrational data of the planar BN molecule (C_2v, ²A₁) are in good agreement with available experimental data (Table S2 in the ESI†),^{49,68,93,98,99} and the calculated dipole moment is close to the measured one (μ = 4.71 vs. 4.51 D).¹⁰⁰ Protonation of BN occurs preferentially at the terminal N atom of the CN group, leading to a planar structure with C_2v symmetry in the ¹A₁ ground electronic state.⁶⁸ Protonation at the aromatic C atoms is highly unfavourable (E₀ > 115 kJ mol⁻¹) and thus not observed (Fig. S1 in the ESI†).⁶⁸ Interestingly, N-protonation contracts both the C≡N (Δr_CN = −5.2 mÅ) and the adjacent aliphatic C–C bond (Δr_CC = −35.6 mÅ). The frequency of the most intense IR-active fundamental, ν_NH = 3560 cm⁻¹ (1221 km mol⁻¹), is close to its measured value (3555 ± 3 cm⁻¹).⁶⁸ Concerning W, the O–H bond parameters in its ¹A₁ ground state (r_OH = 0.9619 Å, ν_1/3 = 3639/3738 cm⁻¹) agree reasonably well with the experimental data (0.9578 Å, 3657/3756 cm⁻¹).^101,102 The computed ν_1/3 frequencies are systematically lower by 18 cm⁻¹, because the ν_OH modes are not accounted for in the evaluation of the single scaling factor in the XH stretch range, which however fits well the ν_CH and ν_NH frequencies of (H⁺)BN.⁶⁸ Similar to BN, the calculated dipole moment of W agrees well with the experimental value (μ = 1.847 vs. 1.855 D). In addition, the proton affinities computed for BN and W (PA = 827 and 681 kJ mol⁻¹) are close to the measured values (PA = 812 and 691 kJ mol⁻¹),¹³ indicating that the electrostatic intermolecular interactions between H⁺BN/BN and W/H⁺W are well described at this level of theory.

3.2 H⁺BN–Ar, H⁺BN–N₂, and H⁺BN–W dimers

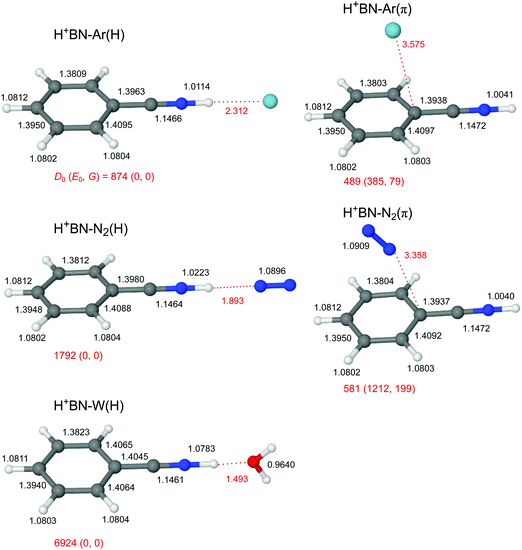
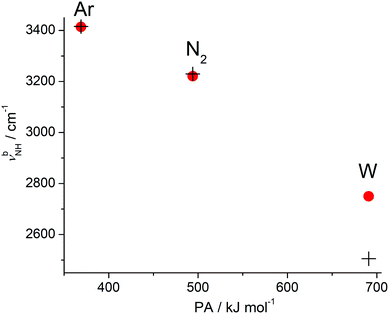
The global minimum on the H⁺(BN–L) dimer potential is for all three considered ligands L the planar H-bonded H⁺BN–L(H) structure with C_2v symmetry, in which L forms a linear NH⋯L ionic H-bond to N-protonated H⁺BN (Fig. 2). The binding energy increases as D₀ = 874 < 1792 < 6924 cm⁻¹ along the series Ar < N₂ < W, in line with their proton affinities (PA = 369.2 < 493.8 < 691 kJ mol⁻¹).¹³ The H-bond length contracts accordingly (R = 2.31 > 1.89 > 1.49 Å). The charge transfer from H⁺BN to L (Δq = 27 < 46 < 109 me, Fig. S2 in the ESI†) upon formation of the NH⋯L ionic H-bond, the corresponding NBO orbital interaction energies (E⁽²⁾ = 28.9 < 74.7 < 329.9 kJ mol⁻¹, Fig. S3 in the ESI†), and the NCI analysis (−ρ* = 0.015 < 0.029 < 0.075 a.u., Fig. S4 in the ESI†) confirm this trend. The formation of the H-bond causes an elongation of the N–H proton donor bond (Δr_NH = 7.2 < 18.1 < 74.1 mÅ), accompanied by a reduction in the NH stretch frequency (−Δν_NH = 145 < 331 < 1055 cm⁻¹) and an enhancement in its IR activity (ΔI_NH = 1325 < 2362 < 4025 km mol⁻¹, Fig. 3 and Table S3 in the ESI†). In the NH⋯L H-bonded dimers, the NH proton attacks the 2p_z lone pairs of N₂ (N atom) and H₂O (O atom), leading to a linear ionic H-bond. The anisotropy of the electrostatic charge–quadrupole (L = N₂) and charge–dipole (L = W) interaction favours such a linear approach. For H⁺BN–W(H), the partial charge transfer from H⁺BN to W elongates the O–H bonds (by 2.1 mÅ), and thus reduces the OH stretch frequencies by −Δν_1/3 = 18/30 cm⁻¹, accompanied by an intensity enhancement, in particular for ν₁ (Table 1). The barrier for internal rotation of W around its C₂ axis at the planar transition state is relatively low (V_b = 65 cm⁻¹, Fig. S5 in the ESI†), in particular in view of the low harmonic torsional frequency (τ = 58 cm⁻¹). Actually, optimization of H⁺BN–W(H) yields a structure with a tiny deviation from C_2v symmetry due to a slightly nonlinear NH⋯W bond (θ = 177.6°). The C_2v-symmetric transition state corresponds to a very small barrier (V_b = 7 cm⁻¹) for the in-plane bending motion with low imaginary frequency (128i cm⁻¹), so that the zero-point energy level lies above the barrier leading to a vibrationally-averaged ground state structure with C_2v symmetry.

Fig. 2 Optimized structures of H⁺BN–L with L = Ar, N₂, and W calculated at the B3LYP-D3/aug-cc-pVTZ level. Binding energies (D₀) and bond lengths are given in cm⁻¹ and Å, respectively. Numbers in parentheses correspond to relative energies and free energies in cm⁻¹ (E₀, G).

Fig. 3 Comparison of experimental IRPD spectra of H⁺BN–L (L = Ar, N₂, W) with linear IR absorption spectra of the most stable isomers calculated at the B3LYP-D3/aug-cc-pVTZ level. High computed IR intensities are multiplied with a factor of 0.1 to display the weak features.

In addition to the NH-bonded H⁺BN–L(H) global minima, less stable π-bonded local minima exist for L = Ar and N₂ (Fig. 2), in which the ligand is attached to the aromatic π-electron system mostly by dispersion and induction forces with D₀ = 489 and 581 cm⁻¹, respectively.⁶⁸ In these H⁺BN–L(π) isomers, the ligands have a negligible influence on the structural and vibrational properties of H⁺BN. As a result, ν_NH remains almost unshifted (Δν_NH ≤ 2 cm⁻¹) from the value in bare H⁺BN (ν_NH = 3560 cm⁻¹), with nearly unchanged IR intensities. All attempts to locate a π-bonded H⁺BN–W(π) minimum fail and converge to H-bonded isomers. On the other hand, two further nonequivalent in-plane minima exist on the H⁺BN–W potential, in which the W ligand forms a bifurcated CH⋯O H-bond to two adjacent CH protons of the aromatic ring (Fig. S6 in the ESI†). The resulting isomers, H⁺BN–W(o/m) and H⁺BN–W(p/m), are much less stable (D₀ = 2332 and 2188 cm⁻¹) than the NH-bonded global minimum (by ΔE₀ ≥ 4592 cm⁻¹ or 54.9 kJ mol⁻¹). Similar to the π-bonded H⁺BN–L(π) local minima, their IR spectra have an unperturbed free ν_NH band near 3570 cm⁻¹ (Fig. S7 in the ESI†). However, the aromatic ν_CH modes exhibit a slight intensity enhancement due to the formation of the bifurcated CH⋯O H-bond. The barriers between the CH-bonded minima are relatively low (e.g., V_b = 225 cm⁻¹ for the transition state between two equivalent H⁺BN–W(p/m) minima, Fig. S8 in the ESI†).

Because the PA of BN (812 kJ mol⁻¹) is much higher than those of any of the three ligands (by more than 120 kJ mol⁻¹), and this energy difference is much larger than any of the solvation energies, the excess proton in H⁺(BN–L) remains with BN, justifying the notation of H⁺BN–L for all ligands. All attempts to locate H₃O⁺–BN minima with either an OH⋯π or an OH⋯N H-bond fail. This is in contrast to clusters of H₃O⁺–A with A = benzene or naphthalene, for which π-bonded structures of H₃O⁺ with the aromatic ring are the global or at least local minima.^22,25,26 This difference is due to the lower PA of benzene and naphthalene (PA = 750.4 and 802.9 kJ mol⁻¹)¹³ and the lack of a dipole moment. The large dipole moment of BN along the CN axis does not favour a cation–π interaction with an OH⋯π ionic H-bond of H₃O⁺ and the aromatic π electron system of BN. At this point, we note that a peak at m/z 122 observed in very recent electron impact mass spectra of a BN/H₂O mixture has wrongly been assigned to H₃O⁺–BN (rather than H⁺BN–H₂O),¹⁰³ illustrating that mass spectrometry is not sensitive to determine the position of the excess proton in clusters.

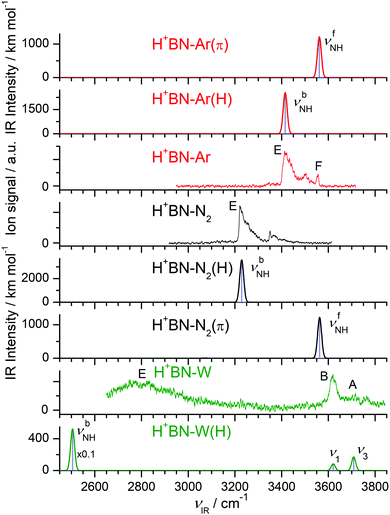
The IRPD spectra of the H⁺BN–L dimers are compared in Fig. 3 to linear IR absorption spectra computed for the most stable isomers with the NH⋯L ionic H-bond. The spectra for L = Ar and N₂ have been discussed previously⁶⁸ and are included here only for comparison with L = W. The weak and symmetric band F at 3556 cm⁻¹ in the spectrum of H⁺BN–Ar is assigned to the free ν^f_NH mode of H⁺BN–Ar(π) computed as 3561 cm⁻¹. It provides a good approximation for ν_NH of bare H⁺BN as 3555 ± 3 cm⁻¹,⁶⁸ which is taken as reference point herein to evaluate Δν_NH shifts upon cluster formation. This band is missing in the H⁺BN–L spectra with L = N₂ and W, indicating that in the observed clusters with these ligands the NH group is solvated by L. That means, only the NH-bonded global minima H⁺BN–N₂(H) and H⁺BN–W(H) are detected, and other isomers are below the detection limit (Fig. 3 and Fig. S7 in the ESI†). For L = Ar, the abundance ratio of 1 : 5 estimated for the π and NH isomers is ascribed to their small energy difference of only 400 cm⁻¹. For L = N₂ and W, the less stable π and CH isomers are much higher in energy, which explains their complete absence in the IRPD spectra. Following this isomer assignment, the intense bands E at 3414, 3221, and 2750 cm⁻¹ are readily assigned to the H-bonded ν^b_NH mode of H⁺BN–L(H) with L = Ar, N₂, and W, respectively, in good agreement with the predicted values of 3415, 3229, and 2505 cm⁻¹, respectively. These proton donor stretch bands are broader and typically exhibit a sharp rise on the red side (P branch head) and a long tail toward the blue side.^82,104,105 The latter is attributed to absorption of clusters with initial internal energy, giving rise to sequence hot bands of the type ν^b_NH + ν_x ← ν_x, where ν_x are low-frequency inter- and intramolecular modes. Cold H⁺BN–L(H) clusters with L = Ar and N₂ can be dissociated from the ground vibrational state under the employed single-photon absorption conditions, and their ν^b_NH bands display indeed such a blue-shaded contour. In contrast, the high calculated binding energy of H⁺BN–W(H), D₀ = 6924 cm⁻¹, implies that only clusters with an internal energy of more than ∼4000 cm⁻¹ can be fragmented upon single-photon IRPD. This may explain that the ν^b_NH band of these internally hot H⁺BN–W(H) clusters is substantially blue-shifted from its predicted value (+245 cm⁻¹), while those measured for L = Ar and N₂ are computed well (to within ±10 cm⁻¹). The free OH stretch modes of H⁺BN–W(H) are observed as sharper bands at ν₁ = 3620 and ν₃ = 3708 cm⁻¹, respectively, and their red shifts from the values of bare W (−Δν_1/3 = 37/46 cm⁻¹) are in accordance with the computed ones (−Δν_1/3 = 18/30 cm⁻¹). Interestingly, the observed relative intensities of ν_1/3 appear to be reversed from the predictions. This may be related to the high effective temperature of the clusters and/or the much larger width of the ν₃ band. Finally, the remaining bands in the spectra of L = Ar and N₂ at 3500 and 3351 cm⁻¹ are attributed to combination bands ν^b_NH + ν_s, where ν_s is the intermolecular stretch frequency in the ν^b_NH excited state (86 and 130 cm⁻¹). This mode is not included in harmonic calculations. It is also absent in the IRPD spectrum with L = W, for which ν_s is computed as 255 cm⁻¹ (and thus ν^b_NH + ν_s is expected near 3060 cm⁻¹). Clearly, the IRPD spectrum measured for H⁺(BN–W) lacks any signature of the free OH stretch bands of the H₃O⁺ ion expected near 3500–3550 cm⁻¹ for a H₃O⁺–BN cluster (with either an OH⋯N or OH⋯π H-bond).²⁶ Thus, we can safely exclude any detectable contributions from a H₃O⁺–BN type isomer to the H⁺(BN–W) ion population in the plasma beam, which thus is assigned completely to the H⁺BN–W(H) isomer. This experimental conclusion is in line with the failure of locating any H₃O⁺–BN minimum on the H⁺(BN–W) potential by the B3LYP-D3 calculations.

3.3 H⁺(BN–W₂)

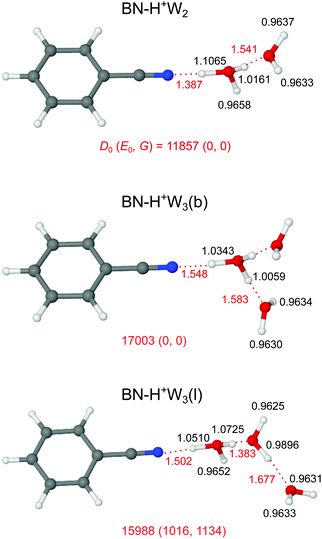
Our search on the potential energy surface of the n = 2 cluster results in three low-energy structural isomers (Fig. 4 and Fig. S9 in the ESI†), which are obtained by adding a second W ligand to the clearly most stable H⁺BN–W(H) dimer either at the W or the CH binding sites, resulting in BN–H⁺W₂, H⁺BN–W₂(o/m), and H⁺BN–W₂(m/p). The by far most stable structure is the proton-transferred BN–H⁺W₂ isomer with a total dissociation energy of D₀ = 11 857 cm⁻¹, in which the neutral W and BN ligands individually bind to a central H₃O⁺ cation core via OH⋯O and OH⋯N ionic H-bonds. This means that we observe an intracluster proton transfer from H⁺BN to the solvent cluster upon attachment of the second W ligand. This result is in accordance with the similar PA values of BN and W₂ (812 and 808 kJ mol⁻¹),^13,14 when taking into account that the solvation energy of the H₃O⁺ ion is larger than that of H⁺BN. Because this proton transfer is barrierless, we can not optimize a H⁺BN–W₂ local minimum, in which a neutral W₂ dimer binds to the NH proton of H⁺BN via an NH⋯O H-bond. The OH⋯N bond of H₃O⁺ to BN (R = 1.387 Å, D₀ = 11 955 cm⁻¹) is much stronger and shorter than the OH⋯O bond to W (R = 1.541 Å, D₀ = 4933 cm⁻¹), because both the PA and μ of BN are larger than those of W so that BN is the better proton acceptor. This result is supported by the larger charge transfer from H₃O⁺ to BN as compared to W (Δq = 199 vs. 80 me, Fig. S2 in the ESI†), the larger E⁽²⁾ energy (757.3 vs. 249.9 kJ mol⁻¹, Fig. S3 in the ESI†), and the NCI data (−ρ* = 0.111 vs. 0.066 a.u., Fig. S4 in the ESI†). As a result of the substantially stronger H-bond, the O–H donor bond in the OH⋯N bond is more elongated than that in the OH⋯O bond (by 90.4 mÅ), resulting in a much lower ν^b_OH frequency (1361 vs. 2760 cm⁻¹). The predicted free OH stretch frequencies of the W ligand (ν_1/3 = 3626/3714 cm⁻¹) are slightly blue-shifted compared to the n = 1 cluster because the OH⋯O H-bond to the W ligand in n = 2 is weaker than the NH⋯O H-bond in n = 1 (D₀ = 4933 vs. 6924 cm⁻¹), as also demonstrated by the smaller charge transfer (Δq = 80 vs. 108 me), the lower E⁽²⁾ energy (249.9 vs. 329.9 kJ mol⁻¹), and the smaller −ρ* value (0.066 vs. 0.075 a.u.). The free OH stretch frequency of the H₃O⁺ core ion occurs between ν₁ and ν₃ at ν_f = 3643 cm⁻¹ (Fig. 5). Finally, we note that the BN–H⁺W₂ structure is formally derived from the most stable symmetric H⁺W₃ isomer (H₇O₃⁺, W–H₃O⁺–W, Fig. S10 in the ESI†)⁶⁹ by simple substitution of one W ligand by BN. H₇O₃⁺ has a large total binding energy of D₀ = 19 767 cm⁻¹ (i.e., 9884 cm⁻¹ per W) and relatively short OH⋯O H-bonds (R = 1.456 Å). Hence, replacing one W ligand by BN substantially destabilizes the remaining OH⋯O H-bond to W, because of the much stronger OH⋯N H-bond to BN.

Fig. 4 Optimized structures of BN–H⁺W₂ and two isomers of BN–H⁺W₃ calculated at the B3LYP-D3/aug-cc-pVTZ level. Binding energies (D₀) and bond lengths are given in cm⁻¹ and Å, respectively. Numbers in parenthesis correspond to relative energies and free energies in cm⁻¹ (E₀, G).

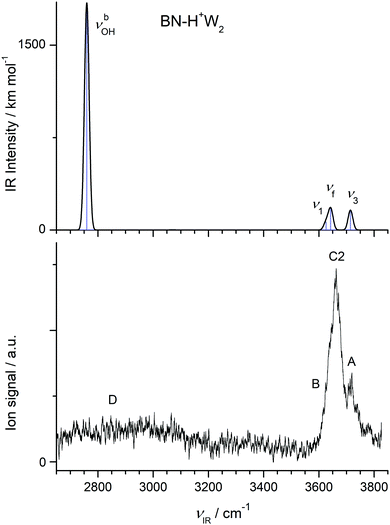Fig. 5 Comparison of experimental IRPD spectrum of H⁺(BN–W₂) with linear IR absorption spectrum of the most stable BN–H⁺W₂ isomer calculated at the B3LYP-D3/aug-cc-pVTZ level.

In the H⁺BN–W₂(o/m) and H⁺BN–W₂(m/p) isomers, the two W ligands bind separately to the H⁺BN core via NH⋯O and bifurcated CH⋯O H-bonds (Fig. S9 in the ESI†). Their total binding energies of D₀ = 8925 and 8825 cm⁻¹ are far lower than that of the proton-transferred global minimum. Moreover, because of noncooperative three-body effects involved in interior ion solvation, the total binding energy is somewhat smaller than the sum of the binding energies of the individual H-bonds in the H⁺BN–W dimer of 9256 and 9112 cm⁻¹ (corresponding to a noncooperativity in energy of 331 and 287 cm⁻¹ or 3.6 and 4.2%, respectively). Thus, the H-bonds in these H⁺BN–W₂ trimers are somewhat weaker and longer than in the corresponding H⁺BN–W dimer isomers. As a consequence, the proton remains with BN in these clusters, because the CH-bonded W ligand decreases the acidity of the NH proton. The IR spectra predicted for these isomers are more or less a superposition of the IR spectra of the respective dimers (Fig. S11 in the ESI†). Significantly, in the considered spectral range, the appearance of the IR spectra predicted for these H⁺BN–W₂ isomers of n = 2 is quite similar to the one of the H⁺BN–W(H) isomer of n = 1, with a modest blue shift of around 50 cm⁻¹ for the intense ν^b_NH band upon adding the CH-bonded W ligand.

In Fig. 5, we compare the IRPD spectrum of H⁺(BN–W₂) recorded in the W loss channel with the IR spectrum predicted for the most stable BN–H⁺W₂ dimer. The very intense ν^b_OH mode of BN–H⁺W₂ calculated at 2760 cm⁻¹ appears as broad absorption band D starting at 3200 cm⁻¹ and extending down to the edge of the scanning range at 2650 cm⁻¹, where the laser intensity becomes weak. Peak A at 3719 cm⁻¹ is assigned to ν₃ of the W ligand and is indeed blue-shifted compared to the n = 1 cluster (by 9 cm⁻¹) as predicted by the computations (6 cm⁻¹). The intense band C2 at 3657 cm⁻¹ is attributed to ν_f of the H₃O⁺ moiety predicted at 3643 cm⁻¹, which is a unique signature of the BN–H⁺W₂ isomer. The discrepancy of +14 cm⁻¹ is expected because the computed OH stretch bands of bare W are also underestimated by +18 cm⁻¹ using the employed scaling factor. The predicted ν₁ mode (3626 cm⁻¹) occurs in the red shoulder of band C2 (denoted band B), which has its onset at 3602 cm⁻¹. Although the calculated binding energy of the free W in BN–H⁺W₂ (D₀ = 4933 cm⁻¹) exceeds the photon energy, we observe IRPD into the single W loss channel from the population of internally hot clusters. However, we do not detect any fragmentation into the BN loss channel because of the substantially higher binding energy of this ligand with larger dipole moment (11 955 cm⁻¹). Interestingly, during the IRPD process of BN–H⁺W₂ the proton must transfer (back) to BN upon W loss, i.e. the overall photofragmentation reaction can be written as BN–H⁺W₂ + hν_IR → H⁺BN–W(H) + W.

The much less stable H⁺BN–W₂(o/m) and H⁺BN–W₂(m/p) isomers should be much colder than the assigned global minimum (because of the low binding energy of the CH-bonded W ligand of D₀ < 2500 cm⁻¹). Hence, they can dissociate from the ground vibrational state upon single-photon absorption. However, although the IR spectra predicted for these local minima are not in serious conflict with the measured IRPD spectrum of the n = 2 cluster (Fig. S11 in the ESI†), the large change between the IRPD spectra of n = 1 and n = 2 in Fig. 1 (in particular the disappearance of the strong band E assigned to ν^b_NH) suggests that n = 2 isomers with a single W ligand solvated at the NH group do not have significant abundance. This is in line with the roughly four times lower predicted IR intensity of ν^b_OH of the assigned BN–H⁺W₂ isomer (I_OH = 1844 km mol⁻¹) as compared to ν^b_OH of both H⁺BN–W₂ isomers (I_OH = 5597 and 5724 km mol⁻¹). Hence, we will not consider such isomers with interior H⁺BN hydration any further for the larger clusters and instead focus on structures, in which BN is attached to a H-bonded H⁺W_n cluster.

3.4 H⁺(BN–W₃)

Our computational search for H⁺(BN–W₃) structures has resulted in two low-energy isomers of the form BN–H⁺W₃, which are obtained by adding a third W ligand to the available free OH binding sites of the BN–H⁺W₂ global minimum (Fig. 4). This strategy of searching for BN–H⁺W₃ structures with the proton attached to the solvent cluster is also motivated by the much higher PA of W₃ as compared to BN (862 vs. 812 kJ mol⁻¹).^13,15 In the most stable branched BN–H⁺W₃(b) isomer with D₀ = 17 003 cm⁻¹ and C_s symmetry, the H₃O⁺ core is fully solvated by one BN and two equivalent W ligands. Similar to the corresponding n = 2 cluster, the OH⋯N H-bond to BN is still stronger (R = 1.548 Å, D₀ = 9613 cm⁻¹) than each of the two OH⋯O H-bonds to W (R = 1.583 Å, D₀ = 5146 cm⁻¹) but the difference in bond length shrinks from 154 to 35 mÅ due to the increased PA of W₃. On the other hand, the OH⋯O and OH⋯N H-bonds in the n = 3 cluster are weaker and longer than for n = 2 (by 161 and 42 mÅ) due to the noncooperative effect of interior H₃O⁺ ion solvation resulting from enhanced charge delocalization. Consequently, charge transfer to each W and BN is reduced by 12 and 76 me to 68 and 123 me, the E⁽²⁾ energies are lowered by 111.7 and 339.0 kJ mol⁻¹ to 138.2 and 418.3 kJ mol⁻¹, and the −ρ* values decrease from 0.110 and 0.066 to 0.073 and 0.059 a.u., respectively (Fig. S2–S4 in the ESI†). The intense symmetric and antisymmetric ν^b_OH modes of the H₃O⁺ ion involved in the OH⋯O H-bonds are strongly red-shifted to 2946 and 2878 cm⁻¹ (I_OH = 758 and 2548 km mol⁻¹, Fig. 6), and this red shift and IR oscillator strength are even higher for the ν^b_OH mode of the OH⋯N H-bond (ν^b_NH = 2424 cm⁻¹, I_NH = 5374 km mol⁻¹). Compared to the n = 2 case, the OH⋯N H-bond is more asymmetric for n = 3, with the excess proton sticking more strongly to W₃, as reflected in the shorter O–H bond (1.1065 vs. 1.0343 Å). In this branched isomer, the O–H bonds of the two equivalent W ligands do not participate in H-bonding and thus their coupled OH stretch modes appear as ν_1/3 bands near 3630 and 3719 cm⁻¹, i.e. slightly blue-shifted by further 5 cm⁻¹ from the corresponding n = 2 modes. The BN–H⁺W₃(b) isomer is essentially an Eigen ion (H₉O₄⁺ = H⁺W₄ = H₃O⁺–W₃, Fig. S10 in the ESI†),^69,106 in which one W ligand is replaced by BN, resulting in a slightly asymmetric solvent configuration due to the larger dipole moment of BN. Similar to the n = 2 case, also in the BN–H⁺W₃(b) structure the substitution of W by BN results in a destabilization of the remaining OH⋯O H-bonds (from 1.551 to 1.583 Å).

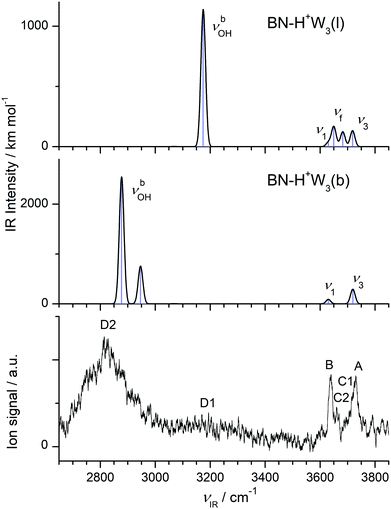Fig. 6 Comparison of experimental IRPD spectrum of H⁺(BN–W₃) with linear IR absorption spectra of the most stable BN–H⁺W₃ isomers (Fig. 4) calculated at the B3LYP-D3/aug-cc-pVTZ level.

In the BN–H⁺W₃(l) isomer with a linear H-bonded H⁺W₃ chain, the central H₃O⁺ ion is only twofold solvated by BN and a W₂ dimer. Because of the incomplete solvation of the H₃O⁺ ion, this isomer is less stable than BN–H⁺W₃(b) by ΔE₀ = 1016 cm⁻¹. In this linear isomer, the OH⋯N bond is much weaker and longer than the OH⋯O bond to W₂ (1.502 vs. 1.383 Å), because the PA of W₂ is similar to that of BN but the solvation energy of W₂ is larger than for BN. Both corresponding ν^b_OH frequencies (2268 and 2254 cm⁻¹) of the O–H proton donor bonds are below the available IR photon energy. The remaining free O–H bond of the H₃O⁺ ion is shorter than the two H-bonded ones, with a ν_f mode predicted at 3650 cm⁻¹ (Fig. 6). The remote W acts only as H-bond acceptor, whose ν₁ and ν₃ modes appear at 3630 and 3718 cm⁻¹, respectively. The remaining middle neutral W ligand participates in H-bond formation as a single donor and single acceptor (DA) with one free and one H-bonded OH stretch, ν_f = 3682 and ν^b_OH = 3175 cm⁻¹. The BN–H⁺W₃(l) isomer is essentially a twofold hydrated Zundel ion (H⁺W₂–W₂ = H₅O₂⁺–W₂),^69,70,107 in which one terminal W ligand is replaced by BN, resulting in a strongly asymmetric configuration of the Zundel ion with the excess proton localized at the W molecule next to BN, because the PA of BN is larger than the one of a single W ligand. Because of strong cooperative effects induced by the polarization of the nearby positive charge,⁸² the OH⋯O bond in the W₂ unit in BN–H⁺W₃(l) is much stronger and shorter (D₀ = 4130 cm⁻¹, R = 1.677 Å) than in bare W₂ (D₀ = 1003 cm⁻¹, R = 1.947 Å).⁸⁸

The IRPD spectrum of H⁺(BN–W₃) is compared in Fig. 6 to the IR spectra predicted for the two considered BN–H⁺W₃ isomers. The measured IRPD spectrum is dominated by the three peaks A, B, and D2 at 3729, 3640, and 2815 cm⁻¹, which can be assigned in a straightforward way to the ν₃, ν₁, and two overlapping ν^b_OH transitions of the branched BN–H⁺W₃(b) global minimum predicted at 3719, 3631/3630, and 2946/2878 cm⁻¹, respectively. Part of the signal in the blue tail of the H-bonded ν^b_OH bands near 3200 cm⁻¹ (denoted D1) may arise from bending overtones (2β_OH) of the W ligands, which are not included in the harmonic simulations (but predicted at 3197 and 3201 cm⁻¹ using 0.98 as scaling factor). While the contribution of the branched global minimum to the IRPD spectrum is obvious, the indication for the presence of the linear BN–H⁺W₃(l) local minimum is at first glance less certain. Its unique intense ν^b_OH transition predicted at 3175 cm⁻¹ may contribute to the plateau near 3200 cm⁻¹ (D1), and its ν_f mode at 3682 cm⁻¹ (band C1 at 3694 cm⁻¹) may be blended by the red wing of the ν₃ bands of the branched isomer (A). Its ν_1/3 modes overlap with those of the branched isomers (bands A and B). Band C2 observed at 3660 cm⁻¹ is considered as the clearest signature of the linear isomer arising from the free OH stretch mode of the incompletely solvated H₃O⁺ core ion. Its frequency is similar to the corresponding mode of the BN–H⁺W₂ ion both experimentally (+3 cm⁻¹) and computationally (+7 cm⁻¹), which occurs as a single isomer, thus confirming this interpretation. In conclusion, the H⁺(BN–W₃) spectrum is dominated by the branched BN–H⁺W₃(b) global minimum, while the less stable linear BN–H⁺W₃(l) local minimum has a smaller population (estimated to be ≤20% from the ratio of the integrated peak intensities of bands C2 and B and the corresponding calculated IR cross sections), consistent with the lower thermochemical stability (ΔE₀ = 1016 cm⁻¹).

3.5 H⁺(BN–W₄)

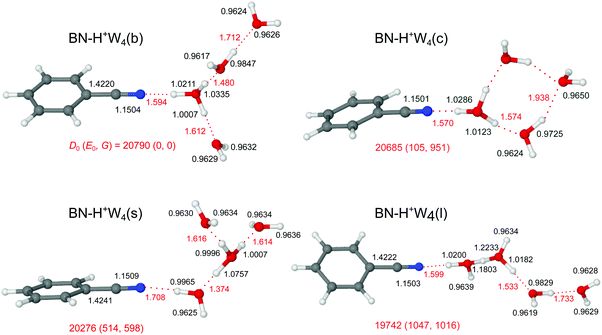
Starting from the n = 3 case, we find two related low-energy structural isomers for n = 4, namely the branched BN–H⁺W₄(b) global minimum and the linear BN–H⁺W₄(l) local minimum (Fig. 7). The BN–H⁺W₄(b) isomer has an Eigen-type structure with BN and two W ligands in the first complete solvation shell around H₃O⁺ and one W ligand in the second shell. The OH⋯O H-bond to the W₂ unit is stronger than that to W (R = 1.480 vs. 1.612 Å). The addition of W in the second shell leads to an elongation of both the OH⋯O H-bond to the single W (ΔR = 29 mÅ) and the OH⋯N H-bond to BN (ΔR = 46 mÅ), because of the noncooperative effects of interior ion solvation. On the other hand, the OH⋯O H-bond to the W₂ unit contracts (ΔR = −103 mÅ), because of the cooperative effects arising from forming the H-bonded network (and the higher PA of W₂ compared to W). As a result, W₂ drags more positive charge from H₃O⁺ ion than the single W (Δq = 105 vs. 62 me, Fig. S2 in the ESI†), and the corresponding ν^b_OH mode is more red-shifted (2431 vs. 3002 cm⁻¹). The enhanced solvation of the H₃O⁺ ion in BN–H⁺W₄(b) as compared to BN–H⁺W₃(b) weakens the OH⋯N H-bond further (R = 1.594 vs. 1.548 Å) and reduces the charge transfer to BN (from 123 to 104 me) as well as the E⁽²⁾ energy (from 418.3 to 349.1 kJ mol⁻¹) and the −ρ* value (from 0.073 to 0.065 a.u.), as documented in Fig. S2–S4 in the ESI.† Moreover, the O–H donor bond becomes shorter (by 13.2 mÅ) and its ν^b_OH mode is blue-shifted from 2424 to 2661 cm⁻¹. The two OH groups of the two remaining W ligands remain free. However, the ν₁ and ν₃ modes of W in the first solvation shell have a slightly lower frequency than those in the second shell (3632 vs. 3638 cm⁻¹, 3721 vs. 3728 cm⁻¹) due to the smaller distance from the excess charge. The remaining partially solvated W has one free ν_f mode (3693 cm⁻¹) and one red-shifted ν^b_OH mode (3265 cm⁻¹).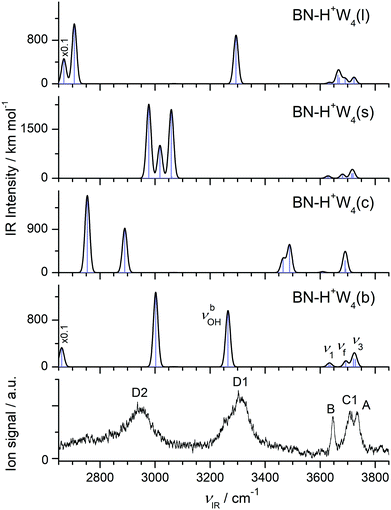

Fig. 7 Optimized structures of BN–H⁺W₄ calculated at the B3LYP-D3/aug-cc-pVTZ level. Binding energies (D₀) and bond lengths are given in cm⁻¹ and Å, respectively. Numbers in parentheses correspond to relative energies and free energies in cm⁻¹ (E₀, G).

Fig. 8 Comparison of experimental IRPD spectrum of H⁺(BN–W₄) with linear IR absorption spectra of the low-energy BN–H⁺W₄ isomers (Fig. 7) calculated at the B3LYP-D3/aug-cc-pVTZ level. High computed IR intensities are multiplied with a factor of 0.1 to display the weak features.

Unlike BN–H⁺W₃(l) with a partially solvated H₃O⁺ core, the linear BN–H⁺W₄(l) local minimum contains a twofold solvated Zundel ion (H₅O₂⁺). Partial solvation of H₅O₂⁺ with W₂ and BN makes the linear isomer substantially less stable than the branched isomer (E₀ = 1047 cm⁻¹). The ν₁ and ν₃ modes of the terminal W are predicted at 3634 and 3723 cm⁻¹, whereas ν_f of the partially solvated W and the central H₅O₂⁺ appear at 3691, 3670, and 3664 cm⁻¹ (Fig. 8). The corresponding H-bonded ν^b_OH frequencies are 3294 (to W), 2707 (to W₂), and 2669 (to BN) cm⁻¹, consistent with the O–H and OH⋯O bond lengths.

Motivated by the three lowest-energy structures identified for H⁺W₅ by IR–IR double-resonance spectroscopy,⁷⁵ denoted ring (R), branched (B), and chain (C), with relative energies of E₀ = 0, 0.6, and 11.6 kJ mol⁻¹ (0, 50, 970 cm⁻¹) using the very same B3LYP-D3/aug-cc-pVTZ level as used herein (E₀ = 100, 0, 825 cm⁻¹, Fig. S10 in the ESI†), we find two further low-energy BN–H⁺W₄ isomers by simply replacing a W unit with BN, namely a cyclic one (isomer c) and a surface one (isomer s). The linear and branched isomers of BN–H⁺W₄ discussed above are derived from the B and C isomers of H⁺W₅. The BN–H⁺W₄(s) isomer with E₀ = 514 cm⁻¹, also resulting from the B isomer of H⁺W₅, is essentially an Eigen ion solvated by BN, i.e. it differs from the branched global minimum such that BN is located in the second solvation shell of H₃O⁺, i.e. at the surface of the H⁺W₄ Eigen cluster. It is less stable than the b isomer, because BN with its higher dipole moment is further away from the positive charge. As a result, the OH⋯N H-bond of H⁺W₄ to BN is weaker and longer (1.708 vs. 1.594 Å). Clearly, both branched isomers (b and s) have very different IR spectra (Fig. 8), in particular in the H-bonded range.

The cyclic BN–H⁺W₄(c) isomer with E₀ = 105 cm⁻¹ and C_s symmetry results from the R isomer of H⁺W₅. It differs from the most stable branched isomer such that the W ligand in the second solvation shell is not forming a single H-bond to the BN–H⁺W₃ ion core but acts as a double acceptor with two weak H-bonds which close the cyclic H⁺W₄ ring in BN–H⁺W₄(c). This cyclic structure has also a very characteristic IR spectrum with two OH stretch bands of these two weak H-bonds occurring near 3500 cm⁻¹, a strong single free OH stretch band near 3690 cm⁻¹ (arising from the overlapping coupled ν_f modes of the two W molecules in the ring at 3693 and 3691 cm⁻¹), and strongly red-shifted ν^b_OH modes of the H₃O⁺ core.

The comparison of the IRPD spectrum of H⁺(BN–W₄) to the IR spectra predicted for the four considered stable BN–H⁺W₄ isomers in Fig. 8 provides a clear indication for the predominant presence of the most stable branched isomer (b). There is a good match of the intense broad peaks D1 and D2 at 3310 and 2955 cm⁻¹ with the characteristic ν^b_OH modes of BN–H⁺W₄(b) predicted at 3265 and 3002 cm⁻¹, respectively. There is a similar good match between the free OH stretch peaks observed at 3646 (B), 3733 (A), and 3706 cm⁻¹ (C1) with ν₁ (3632/3638 cm⁻¹), ν₃ (3721/3728 cm⁻¹), and ν_f (3693 cm⁻¹) of this isomer. We do not observe ν^b_OH of the OH⋯N moiety predicted at 2661 cm⁻¹, probably owing to the low laser power in that range and/or the large anharmonicity of this mode. While band D2 is a clear indicator for the presence of the branched isomer, the possible contribution of the linear isomer is less certain, because of substantial overlap of its predicted bands with those of the branched isomer within the achieved spectral resolution. This concerns particularly bands D1 (ν^b_OH), B (ν₁), A (ν₃), and C1 (ν_f of W₂ unit). However, no pronounced signal is observed in the range of the two ν_f modes of the H₅O₂⁺ unit (C2), which are the strongest modes predicted in the free OH stretch range at 3664/3670 cm⁻¹ (expected at 3682/3688 cm⁻¹ when accounting for the deficiency of the employed scaling factor) and characteristic of this isomer. In addition, the characteristic bands predicted for the cyclic isomer near 3500 and 2800 cm⁻¹ are missing (or lost in the broader background) in the IRPD spectrum indicating that this isomer does also not contribute substantially to the observed ion population. Similarly, significant population of the surface isomer can be excluded, because of the comparable intensities of the intense bands D1 and D2 in the experimental spectrum and the lack of any transition predicted for this isomer in the vicinity of band D1 near 3300 cm⁻¹. Thus, we conclude that the experimental IRPD spectrum is mostly dominated by the branched global minimum, while the population of the linear, cyclic, and surface isomers is at most minor, in line with the thermochemical data (D₀, E₀, G).

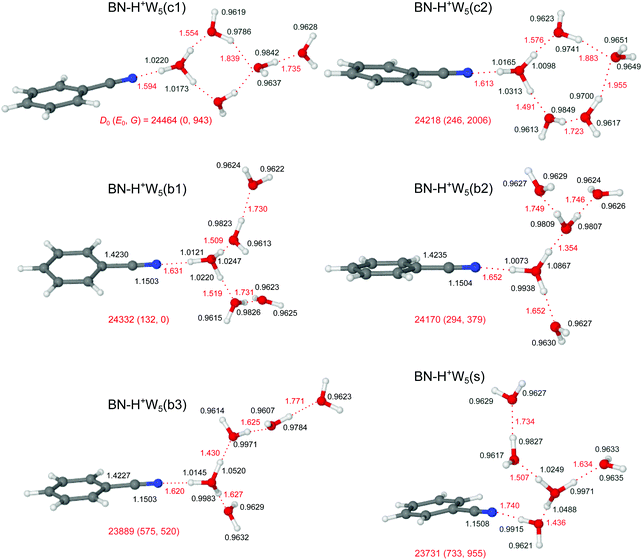
3.6 H⁺(BN–W₅)

Similar to bare H⁺W_n clusters, the number of low-energy competing isomers increases drastically with size for the H⁺(BN–W_n) clusters with n ≥ 5, because of the various possibilities for the structure of the H-bonded hydration network and the position of the BN molecule within the cluster. Because the PA of BN is much lower than that of W₅ (812 vs. 904 kJ mol⁻¹),^13,15 the excess proton is attached to the water cluster for all considered isomers, BN–H⁺W_n. Starting from the most stable structures of BN–H⁺W₄, and considering the low-energy H⁺W₆ structures with replacement of one W by BN (Fig. S10 in the ESI†),^71,74,76 our computations yield three low-energy branched structures for the n = 5 cluster, denoted b1–b3 (Fig. 9). In the b1 isomer (E₀ = 132 cm⁻¹), an H₃O⁺ core is fully solvated by BN and two W₂ dimers. It may be derived from simple addition of BN to the chain isomer (C) of H⁺W₅.⁷⁵ It is essentially an Eigen-type ion, with BN in the first shell of a fully solvated H₃O⁺ ion and two W ligands in the second shell. It may thus also be derived from the Eigen isomer of H⁺W₆ (6E) by simply replacing one W by BN in the first shell.⁷⁶ In the significantly less stable b3 isomer (E₀ = 575 cm⁻¹), the H₃O⁺ core is fully solvated by BN, W, and a linear W₃ trimer, while in the somewhat more stable related b2 isomer (E₀ = 294 cm⁻¹), the linear W₃ unit is replaced by a branched structure. Actually, the b2 isomer can also be viewed as a strongly distorted Zundel ion, which is fourfold solvated by BN and three single W ligands, and is thus derived from the Zundel isomer of H⁺W₆ (6Z) by replacing one W by BN.⁷⁶ In the three branched isomers, the H₃O⁺ (or distorted H₅O₂⁺) ion bearing the positive charge is fully solvated by neutral ligands, which optimizes the electrostatic and induction forces. Like for the n = 3 and 4 clusters, the linear isomer of n = 5 is substantially less stable than the branched isomers (E₀ = 1656 cm⁻¹), because it contains an H₃O⁺ core ion with a free O–H bond (Fig. S12 in the ESI†).

Fig. 9 Optimized structures of BN–H⁺W₅ calculated at the B3LYP-D3/aug-cc-pVTZ level. Binding energies (D₀) and bond lengths are given in cm⁻¹ and Å, respectively. Numbers in parentheses correspond to relative energies and free energies in cm⁻¹ (E₀, G).

Interestingly, n = 5 is the first cluster size, in which the branched structures are not the global minima at T = 0 K. Instead, the cyclic c1 and c2 isomers, in which BN binds to a four- or five-membered H⁺W_4/5 ring become very low in energy (E₀ = 0 and 246 cm⁻¹), because they exhibit one more H-bond than the branched isomers. Interestingly, at room temperature, still the branched b1 isomer is most stable, because it is most flexible and not as rigid as the cyclic structures. In the lowest-energy cyclic BN–H⁺W₅(c1) isomer, which is the global minimum at T = 0 K (E₀ = 0), BN binds to the H₃O⁺ ion of a cyclic H⁺W₄ unit, while the fifth W is attached at the opposite site. Because this structure is quite rigid, the entropic contribution implies a quite high free energy for this isomer (G = 943 cm⁻¹). The c1 isomer is derived from the ring isomer (R) of H⁺W₅ by simple addition of BN and exchanging BN and W such that BN is attached to H₃O⁺.⁷⁵ In the similar BN–H⁺W₅(c2) isomer, BN binds to the H₃O⁺ ion of a cyclic H⁺W₅ unit, which is also characterized by low relative energy and high free energy (E₀ = 113 cm⁻¹, G = 2006 cm⁻¹). Finally, we consider one low-energy isomer with BN located on the surface of a branched Eigen-type H⁺W₅ cluster. This BN–H⁺W₅(s) isomer is derived from simple addition of BN to the most stable branched isomer (B) of H⁺W₅ or from W → BN substitution of the 6E isomer of H⁺W₆.^75,76 It is rather high in relative energy (E₀ = 600 cm⁻¹), because BN with its high dipole moment is solvated in the second shell of the central H₃O⁺ cation, resulting in a weaker and much longer OH⋯N H-bond compared to the other isomers in Fig. 9, in which BN is located in the first solvation shell. The shape of the solvation network in the various BN–H⁺W₅ isomers and the strengths of the individual H-bonds resulting from the cooperative and noncooperative effects described for the smaller clusters (resulting from PA values for BN and the W_m fragment units) are directly reflected in the O–H bond lengths and corresponding free and bound OH stretch frequencies (and IR intensities), the resulting effects on the charge distribution, and the NBO and NCI analyses discussed in detail for the smaller clusters.

The IRPD spectrum measured for H⁺(BN–W₅) is compared in Fig. 10 to the IR spectra predicted for the six stable BN–H⁺W₅ isomers shown in Fig. 9 (b1–b3, s, c1/c2), while the comparison with the IR spectrum of the much less stable linear BN–H⁺W₅(l) isomer is available in Fig. S12 in the ESI.† At first glance, the measured IRPD spectrum is consistent with the one of the most stable branched structures (b1). Following this scenario, the bands B (3646 cm⁻¹) and A (3729 cm⁻¹) are assigned to the ν₁ (3640/3639 cm⁻¹) and ν₃ modes (3731/3730 cm⁻¹) of the free W ligands in the second shell of H₃O⁺, each acting as a single acceptor (A). Transition C1 at 3711 cm⁻¹ corresponds to the overlapping ν_f modes of the two W ligands in the first shell around H₃O⁺, which are single-donor single-acceptor molecules (DA). Peak D1 at 3357 cm⁻¹ agrees well with the ν^b_OH modes of these DA ligands in their neutral OH⋯O H-bonds predicted at 3307 and 3301 cm⁻¹. The IRPD spectrum of the n = 5 cluster shows a continuous absorption below 3300 cm⁻¹, with weak peak maxima at 2990 (D3) and 3116 (D2) cm⁻¹. Comparison with the n = 4 spectrum and the calculations indicates that the latter frequencies are consistent with ν^b_OH modes of a H₃O⁺ core with an OH⋯O bond to a single W ligand. Such a bonding situation is not apparent in the b1 isomer but in the b2 and b3 isomers. Hence, these transitions may indicate a minor population of the b2/b3 structures. The pattern observed in the free OH stretch range suggests that the b2 and b3 isomers are not the dominant species. For example, the b2 structure does not possess neutral W ligands with a single dangling OH group (DA) and thus lacks the C1 band, which is the most intense transition observed in the more reliable free OH stretch range. To this end, transition D2 can only be attributed to ν^b_OH of the b3 isomer when considering merely branched isomers. The remaining ν^b_OH transitions of the b1 isomer predicted in the considered spectral range are the two OH stretches of the H₃O⁺ core binding more strongly to BN (2833 cm⁻¹) and the two W₂ units (2637 and 2548 cm⁻¹). The latter modes are probably too low in frequency to be detected, while the former one may contribute to band D3 and the associated background. Part of the signal contributing to band D2 may also arise from bending overtones of the W ligands (2β_OH). Interestingly, the spectrum predicted for the surface isomer, BN–H⁺W₅(s), is also consistent with the measured spectrum, in particular when comparing only the peak positions of the bound and free OH stretch bands. Hence, we can not exclude a substantial contribution of this isomer to the observed ion population, although its relative energy is quite high at both T = 0 and 298 K (E₀ = 733 and G = 955 cm⁻¹). However, this isomer can be formed by simple attachment of BN to the surface of the most stable preformed H⁺W₅ cluster (or by ligand exchange with H⁺W₆), and can be kinetically trapped in this geometry behind significant isomerization barriers upon rapid cooling. This scenario is supported by the similarity of the IRPD spectra recorded for BN–H⁺W₅ and H⁺W₆ recorded at high temperature.⁷¹ Substantial contributions of the cyclic BN–H⁺W₅(c2) isomer may be excluded because the IRPD spectrum lacks any of the transitions near 3450 and 3520 cm⁻¹ characteristic for this ring-like configuration. In addition, its predicted free OH stretch spectrum with a single dominant band is inconsistent with the experimental pattern. The same arguments apply also to the most stable BN–H⁺W₅(c1) isomer, whose spectrum shows a mismatch in the pattern in both the free and bound OH stretch range. Along a similar line, the much less stable linear isomer can be excluded as a major contributor, although the overall pattern of the predicted spectrum is compatible with the measured one. Apart from its high relative energy (E₀ = 1788 cm⁻¹), its characteristic free OH stretches of the Zundel core expected between 3676 and 3700 cm⁻¹ (such as band C2 for n = 2 and 3) are not observed. Although there is good overall agreement of the experimental IRPD spectrum with the IR spectrum predicted for the most stable branched BN–H⁺W₅(b1) isomer, minor contributions of the less stable branched b2 and b3 isomers as well as the kinetically-trapped surface isomer cannot be ruled out because a similar match of their predicted IR spectra and the IRPD spectrum. As a conclusion, we prefer to assign the IRPD spectrum mostly to the b1 minimum, with possibly minor contributions of the s and b2/b3 isomers, while substantial contributions of the low-energy cyclic isomers are not evident.

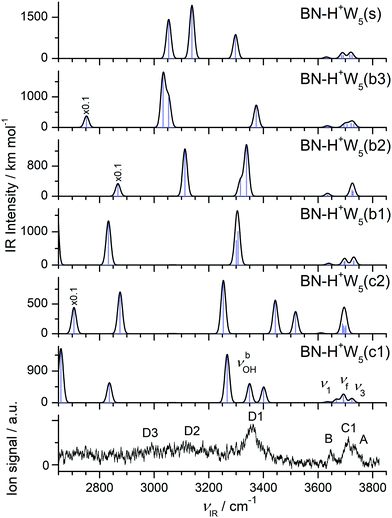Fig. 10 Comparison of experimental IRPD spectrum of H⁺(BN–W₅) with linear IR absorption spectra of the BN–H⁺W₅ isomers (Fig. 9) calculated at the B3LYP-D3/aug-cc-pVTZ level. High computed IR intensities are multiplied with a factor of 0.1 to display the weak features.

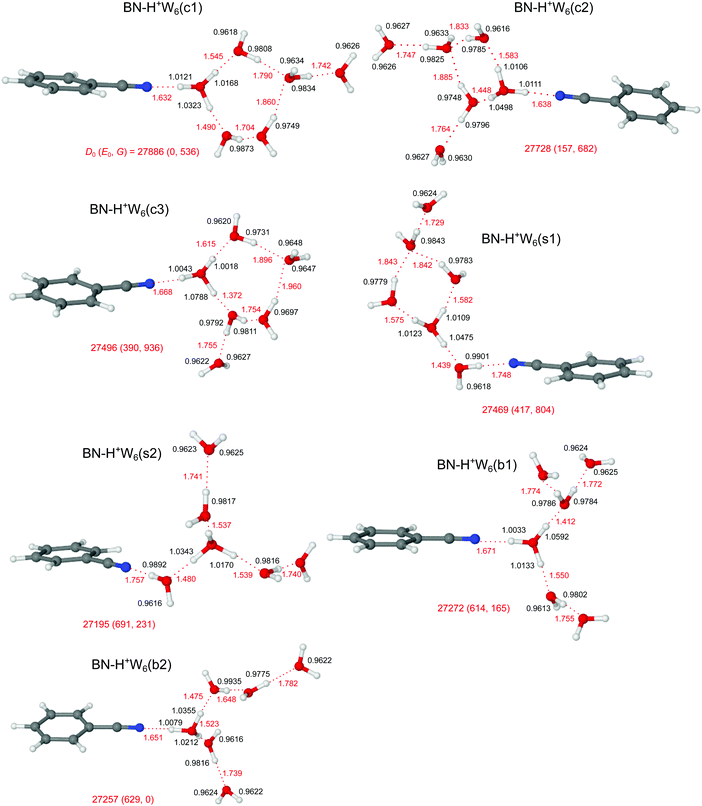
3.7 H⁺(BN–W₆)

The potential energy surface of H⁺(BN–W₆) is getting very complex, as is also illustrated by the large number of computed (≥14) and detected (4) H⁺W₇ isomers.^71,77 Starting by (i) adding one more W ligand to the lowest-energy isomers of BN–H⁺W₅ or (ii) replacing one W by BN in the most stable structures of H⁺W₇,^71,77 or (iii) adding one W to the identified two isomers of H⁺W₆,^71,74,76 we obtain for BN–H⁺W₆ the two branched (b1/b2), three cyclic (c1–c3), and two surface (s1/s2) structures, along with one linear isomer, as shown in Fig. 11 and Fig. S13 in the ESI.† Clearly, the large difference in PA of BN and W₆ of 96.5 kJ mol⁻¹ implies that the excess proton remains with the solvent network. In all considered branched and cyclic structures, the H₃O⁺ ion is fully solvated, and BN is located in the first solvation shell due to its large dipole moment. In the branched structures, H₃O⁺ is solvated by BN, W₂, and W₃ (either branched or linear, b1 and b2, E₀ = 614 and 629 cm⁻¹). The quite similar b1 and b2 isomers are essentially isoenergetic, whereby b1 is slightly more stable at T = 0 K (by 15 cm⁻¹) because the W ligands are closer to the charge. Similar to n = 5, the branched structures are not the global minima for the n = 6 clusters at T = 0 K. Instead, the four lowest-energy structures c1–c3 and s1 considered here have cyclic hydration rings, because they exhibit one more H-bond than the branched (and linear) isomers. In the c1 and c3 isomers (E₀ = 0 and 390 cm⁻¹), BN and W bind to a five-membered H⁺W₅ ring, while in the c2 (s1) isomer BN and two W (or BN–W and W) are attached to a four-membered H⁺W₄ ring (E₀ = 157 and 417 cm⁻¹). Interestingly, at room temperature, still the branched b2 isomer is most stable, because it is most flexible and not as rigid as the cyclic structures. Finally, at this cluster size, also the surface-solvated isomers become quite competitive, with E₀ = 417 and 691 cm⁻¹ for s1 and s2, because for larger clusters the advantage of the higher dipole moment of BN is partly compensated by the possibility of W to form a larger number of H-bonds (up to four) compared to BN (only one). The formation of H-bonded networks allows to better delocalize the excess charge and to benefit more from cooperative effects. Finally, the linear isomer is very high in energy (E₀ = 2220 cm⁻¹) because the H₅O₂⁺ ion is not fully solvated. However, as the number of W ligands increases, the excess proton moves further away from the BN end. While for n = 2 and 3 BN is next to the H₃O⁺ core, for n = 4–6 the excess proton is closest to the second W molecule from the BN end.

Fig. 11 Optimized structures of BN–H⁺W₆ calculated at the B3LYP-D3/aug-cc-pVTZ level. Binding energies (D₀) and bond lengths are given in cm⁻¹ and Å, respectively. Numbers in parentheses correspond to relative energies and free energies in cm⁻¹ (E₀, G).

The IRPD spectrum observed for H⁺(BN–W₆) is compared in Fig. 12 with the IR spectra predicted for the seven BN–H⁺W₆ isomers considered in Fig. 11 (c1–c3, s1/s2, b1/b2), while the comparison with the IR spectrum of the much less stable linear BN–H⁺W₆(l) isomer is presented in Fig. S13 in the ESI.† Although the IRPD spectrum exhibits a limited signal-to-noise ratio, three features A, B, and C1 are clearly discernible in the free OH stretch range at 3735 (ν₃), 3650 (ν₁), and 3707 cm⁻¹ (ν_f), whereas the bound OH stretch range shows a broad and unresolved absorption below 3600 cm⁻¹ with three maxima near 3509 (D1), 3390 (D2), and 3220 (D3) cm⁻¹ due to ν^b_OH modes. Because of the limited spectral resolution, it is difficult to infer any reliable assignment to specific considered structures, and it is likely that several of the low-energy isomers contribute to the measured spectrum. The IRPD spectrum shows some unresolved signal in the spectral range between 3450 and 3550 cm⁻¹ (D1), which is characteristic for cyclic isomers. This signal is certainly higher than in the n = 5 case, which may indicate that, similar to the bare H⁺W_n clusters,^{71–73,77,80} cyclic (and eventually cage-like) structures become more important for increasing cluster size. Quite a good match is observed between the IRPD spectrum and the IR spectra predicted for the two surface isomers in both the free and bound OH stretch ranges. This is particularly true for the s2 isomer, which is derived by simple addition of BN to the detected Eigen isomer of H⁺W₆ (6E)⁷⁶ or by simple W → BN substitution of the most stable noncyclic H⁺W₇ isomer.⁷⁷ This interpretation is supported by the similarity of the IRPD spectrum of BN–H⁺W₆ with that recorded for H⁺W₇ at elevated temperature.⁷¹ The high-energy linear isomer can be excluded for its high energy and its incompletely solvated H₅O₂⁺ core ion, which should produce a C2 band which is absent in the IRPD spectrum.

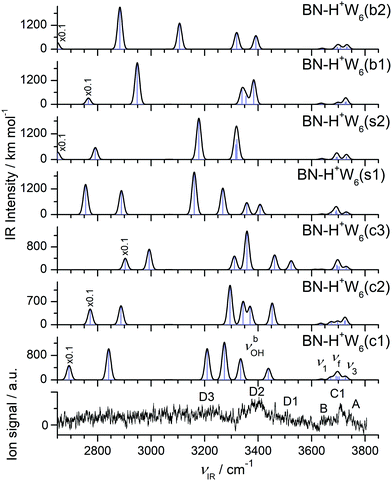Fig. 12 Comparison of experimental IRPD spectrum of H⁺(BN–W₆) with linear IR absorption spectra of the BN–H⁺W₆ isomers (Fig. 11) calculated at the B3LYP-D3/aug-cc-pVTZ level. High computed IR intensities are multiplied with a factor of 0.1 to display the weak features.

4. Further discussion

The present work combines IRPD spectroscopy of mass-selected H⁺(BN–W_n) clusters with DFT calculations to investigate the protonation and hydration processes in mixed clusters of BN and W in the size range n = 1–6. Comparison with the previously studied H⁺BN–L_n clusters with L = Ar and N₂ (n ≤ 4) reveals the differences between aprotic hydrophobic and protic hydrophilic ligands.⁶⁸ Furthermore, comparison with neutral BN–W and the BN⁺–W radical cation demonstrates the drastic impact of protonation and ionization on the intermolecular potential.⁴⁹ In case of the smaller H⁺(BN–W_n) clusters (up to n ≤ 4), the observed IRPD spectra are safely assigned to the most stable structures predicted by the calculations, while for the larger clusters several low-energy isomers may compete, and the observed structures may depend on the preparation conditions. Of particular interest is also the comparison of H⁺(BN–W_n) with bare H⁺W_n+1 clusters to unravel the effects of substituting a W ligand by the aromatic and strongly dipolar but aprotic BN molecular impurity on the structure of the hydration network. The salient results may be summarized as follows.

The cluster growth of H⁺(BN–L_n) with the protic, hydrophilic, and dipolar W ligands differs qualitatively from that with hydrophobic, aprotic, and nonpolar (L = Ar) or quadrupolar (L = N₂) ligands.⁶⁸ The L⋯L interaction between the aprotic ligands is very weak so that the H⁺BN–L_n cluster structures are dominated by the H⁺BN⋯L interaction.⁸² This drastic imbalance results in interior ion solvation, in which individual ligands L bind separately to the H⁺BN cation core without the formation of a solvent network (at least for small n). The thermodynamically favoured solvation process begins by H-bonding of L to the acidic NH proton of H⁺BN and is continued by attachment to the less favourable π and CH binding sites. While for L = Ar, the population of the π-bound local minimum in the molecular beam is estimated as 20%, the concentration of π-bound and CH-bound minima is below the detection limit for L = N₂ (and also W), because of the much larger energy gap to the H-bound global minimum. Significantly, the proton affinity of L = Ar and N₂ is much smaller than that of BN so that the excess proton in the clusters remains at BN, justifying the H⁺BN–L_n notation for all cluster sizes. In contrast, solvating H⁺BN with the protic W ligands leads to the formation of an H-bonded hydration network due to strong cooperative effects. For n = 1, W is connected as a proton acceptor to the NH proton of H⁺BN, whereas for larger clusters with n ≥ 2 exothermic intracluster proton transfer from H⁺BN to W_n occurs for the most stable isomers leading to structures of the type BN–H⁺W_n. Common to all considered H⁺BN–L dimers is that the global minimum structure of the intermolecular potential features a linear NH⋯L ionic H-bond of the neutral ligand to the acidic NH proton. The strength of this ionic H-bond increases with the PA of the ligand along the series Ar < N₂ < W, and this effect is visible in the intermolecular NH⋯L bond length (R), dissociation energy (D₀), and stretch frequency (ν_s), the complexation-induced changes in the properties of the intramolecular N–H donor bond (Δr_NH, Δν_NH, ΔI_NH), the charge transfer from H⁺BN to L (Δq), the NBO donor–acceptor orbital interaction (E⁽²⁾), and the NCI analysis (ρ*), as discussed in detail in Section 3.2. The monotonic correlation between the PA of L and the resulting computed and measured red shift in ν_NH is visualized in Fig. 13. The IRPD spectra of the H⁺BN–L dimers confirm the previous indirect mass spectrometric experimental evidence⁶⁶ that protonation of BN occurs exclusively at the N end of the CN group, in line with the computational thermochemical prediction.^67,68

Fig. 13 Observed (filled circles) and calculated (crosses, B3LYP-D3/aug-cc-pVTZ) NH stretch frequencies (ν^b_NH) of the H-bonded H⁺BN–L(H) dimers with L = Ar, N₂, W as a function of the proton affinity (PA) of the ligands.

It is instructive to compare the structure and bonding of H⁺BN–W with that of neutral BN–W^50–54 and the BN⁺–W radical cation⁴⁹ to infer the effects of protonation and ionization on the shape of the intermolecular interaction potential and resulting hydration network. Neutral BN–W has a cyclic and nearly planar structure, in which W acts both as a proton donor and a proton acceptor, thereby bridging the gap between the ortho CH proton and the CN group via CH⋯O and OH⋯N H-bonds (D₀ = 1562 cm⁻¹).^49,50 This structure becomes repulsive for the BN⁺–W radical cation, which favours a charge–dipole configuration with a bifurcated CH⋯O H-bond and a much higher binding energy (D₀ = 3191 cm⁻¹).⁴⁹ In N-protonated H⁺BN–W, which also has a charge–dipole configuration, W forms a very strong NH⋯O ionic H-bond to the newly available NH proton (D₀ = 6924 cm⁻¹).

In general, the cluster growth found in neutral BN–W_n clusters^52,53 is quite different from that of H⁺(BN–W_n). IR-UV double resonance spectra provide clear evidence for nearly planar H-bonded cyclic structures of BN–W_n with n = 1–3, in which the chain-type W_n unit closes a ring including the ortho CH and CN groups of BN by CH⋯O and OH⋯N H-bonds. These cyclic rings maximize the number of H-bonds, in which all W molecules act as single-donor single-acceptor molecules (DA), thereby maximizing the cooperative effects. Such hydration motifs are not stable for the protonated clusters, in which the H₃O⁺ core in BN–H⁺W_n with n ≥ 2 serves as double-donor or triple-donor but cannot be an H-bond acceptor. Thus, BN–H⁺W_n clusters with small n (n = 2–4) prefer branched structures with BN in the first solvation shell because the dipole moment of BN is larger than that of W. Branched structures also ensure that the protonated H₃O⁺ moiety is fully solvated (starting from n = 3), which makes them more stable than the linear structures with their incomplete hydration of H₃O⁺ (or H₅O₂⁺). The energy gap between the linear and most stable branched or cyclic structure substantially increases with n (ΔE₀ = 1016, 1047, 1788, 2220 cm⁻¹ for n = 3–6), clearly proving that linear hydration motifs are unfavourable. This is in line with results previously reported for Np⁺–W_n (Np = naphthalene) clusters using IRPD and DFT calculations.⁴⁵ This result is however in contrast to the earlier prediction of linear hydration structures for Np⁺–W_n suggested on the basis of mass spectrometry and DFT calculations, indicating that structural assignments of clusters without spectroscopy is often highly unreliable.¹⁰⁸ Interestingly, the excess proton in the linear BN–H⁺W_n(l) isomers moves away from the BN end as n increases. This observation is in line with the increasing PA of W_m subclusters as m increases. Nonetheless, the excess proton remains closer to the BN end than to the W end, because the PA of BN is larger than that of W. For larger BN–H⁺W_n clusters, cyclic structures become possible (n ≥ 4) and competitive in energy as n increases. In fact, they are the most stable structural motif at T = 0 K starting from n = 5, because the ring structures can maximize the number of H-bonds. However, at elevated temperature, the branched structures benefit from entropy because they are more flexible than cyclic rings. As a result, branched structures remain the global minima on the free energy surface for all cluster sizes investigated (n ≤ 6), although the energy gap to cyclic structures becomes smaller as n increases (ΔG = 951, 943, 536 cm⁻¹ for n = 4–6). Finally, as the cluster grows further, surface isomers, in which BN is located in the second shell of a hydrated H₃O⁺ ion, become lower in energy because BN can only act as a single acceptor in the H-bonded network (when neglecting OH⋯π bonding), while W can be involved in as many as four H-bonds (double-donor double-acceptor, DDAA). However, in the investigated size range of up to n = 6, BN is always located in the first solvation shell of H₃O⁺, although the relative energy of the most stable surface isomer tends to become smaller (E₀ = 514, 733, 417 cm⁻¹ for n = 4–6).

The PA of W_n clusters increases with size as 691, 808, 862, 900, 904, and 908 kJ mol⁻¹ for n = 1–6.^13–17 The PA of BN is reported as 812 kJ mol⁻¹,¹³ and thus the difference in PA between BN and W_n amounts to ΔPA = +121, +4, −50, −88, −92, and −96 kJ mol⁻¹. From this consideration, it is expected that the excess proton in H⁺(BN–W_n) is located at BN for n = 1 (H⁺BN–W) and at W_n for n ≥ 3 (BN–H⁺W_n), because of the large absolute values of ΔPA (≥50 kJ mol⁻¹). For n = 2, the proton is expected to be roughly equally shared between BN and W₂ (BN⋯H⁺⋯W₂) due to the similar PA values. However, first one has to keep in mind that the PA values of W_n are not accurately measured (in particular for larger n). Moreover they substantially depend on the exact geometry of both W_n and H⁺W_n and thus may be substantially modified when changing from bare H⁺W_n to the molecularly doped H⁺(BN–W_n) cluster. Second, for the correct prediction of the position of the excess proton, one has not only to consider ΔPA but also differences in the solvation energy of H⁺BN–W_n and BN–H⁺W_n. For example, protonation of benzene–H₂O leads to the formation of C₆H₆–H₃O⁺ rather than C₆H₇⁺–H₂O,^25,26 although the PA of benzene (750.4 kJ mol⁻¹) exceeds the one of H₂O by as much as 59.4 kJ mol⁻¹,¹³ indicating that solvation energy differences can be quite substantial.

In the case of H⁺(BN–W_n), the IRPD spectra and computations give a clear answer to the question of the position of the excess proton. For n = 1, the observation of the H-bonded NH stretch band is a clear indication for the H⁺BN–W structure expected from ΔPA and the DFT computations. Hence, the assignment of a BN–H₃O⁺ structure in the mass spectra in ref. 103 is clearly wrong. Indeed, our DFT calculations could not locate any BN–H₃O⁺ (local) minimum with either an OH⋯N or OH⋯π H-bond. The absence of any ν^b_NH band and appearance of the ν^b_OH band for n = 2 are clear indications for a proton-transferred BN–H⁺W₂ structure. Moreover, the excess proton is clearly closer to W₂ than to BN (1.107 vs. 1.387 Å), suggesting that the solvation energy of BN⋯H⁺W₂ is substantially higher than the one of H⁺BN⋯W₂. It is difficult to compute the latter energy because this intracluster proton transfer reaction is barrierless and no stable H⁺BN⋯W₂ minimum is obtained. Thus, the IRPD spectra and DFT calculations agree that the critical size for proton transfer to solvent in H⁺(BN–W_n) clusters is n_c = 2.

The IRPD spectra of H⁺(BN–W_n) in Fig. 1 provide some further general conclusions about the cluster growth and hydration structure after proton transfer occurs at n_c = 2. First, the appearance of the H-bonded OH⋯O bands (ν^b_OH, bands D) and the uncoupled free OH stretch bands (ν_f, bands C) for n ≥ 2 provide unequivocal evidence for the formation of the H-bonded hydration network of the H⁺W_n subunit in BN–H⁺W_n. Second, the transition C2 is an indicator of a free and uncoupled OH stretch band (ν_f) of an H₃O⁺ core, and its disappearance at n = 4 implies that in all clusters with n ≥ 4, the H₃O⁺ unit is fully solvated either by BN or W, leading to the Eigen analogue of H⁺W₄ (H₃O⁺–W₃ or H₉O₄⁺). This result is expected because of the strong electrostatic charge–dipole forces involved in hydration or solvation of a cation with dipolar ligands. Third, the pronounced appearance of the transitions C1 assigned to a free and uncoupled OH stretch band (ν_f) of a neutral W ligand at the cluster size n = 4 indicates the presence of incompletely solvated W ligands (single-donor single-acceptor, DA) in the cluster. Indeed, the computations predict such clusters to be dominant only for n ≥ 4. Fourth, all spectra exhibit the coupled free OH stretch modes ν₁ and ν₃ of W ligands not acting as a proton donor (i.e., A or AA), and indeed all computed structures possess such W molecules. Fifth, cyclic structures are becoming more prominent at larger cluster sizes, as indicated by the increasing signal in the 3500–3600 cm⁻¹ range. Finally, as the cluster size increases, all related free and bound OH stretch transitions (A–D) shift monotonically to higher frequency, indicating that the H-bonds of W become gradually weaker because of increasing delocalization (dilution) of the excess positive charge. For example, band A shifts from 3710 to 3735 cm⁻¹ (n = 1–6, ν₃), band B from 3620 to 3650 cm⁻¹ (n = 1–6, ν₁), band C2 from 3657 to 3660 cm⁻¹ (n = 2–3, ν_f of H₃O⁺), band C1 from 3694 to 3707 (n = 3–6, ν_f of W), band D1/D2 from 2850 to 3390 cm⁻¹ (n = 4–6, ν^b_OH of W⋯W), and band D2/D3 from 2815 to 3200 cm⁻¹ (n = 3–6, ν^b_OH of H₃O⁺⋯W or H₃O⁺⋯BN).

The latter spectral observations can readily be explained by the computed structures (bond distances of inter- and intramolecular bonds), intermolecular binding energies of the H-bonds, charge transfer, NBO interactions, and NCI analysis. To this end, we consider the data obtained for the most stable branched isomer found for each cluster size at T = 298 K (G = 0 for isomers b for n = 2–4, b1 for n = 5, and b2 for n = 6), because these are safely assigned to the measured IRPD spectrum at least for n = 2–4. For example, the OH⋯N H-bond of H⁺W_n to BN becomes gradually weaker as n increases from 2 to 6, as seen by the H-bond length and binding energy (R = 1.387, 1.548, 1.594, 1.631, 1.671 Å; D₀ = 11 955, 9613, 7247, 6505, 5292 cm⁻¹ for n = 2–6). This trend is also reflected in the decreasing charge transfer from H⁺W_n to BN (Δq = 199, 123, 104, 89, 81 me), E⁽²⁾ energy (757, 418, 349, 183, 169 kJ mol⁻¹), and NCI parameter (−ρ = 0.111, 0.073, 0.065, 0.059, 0.056 a.u.) as illustrated in Fig. S2–S4 in the ESI.† The weakest OH⋯O H-bonds between neutral W ligands become longer (R = 1.712, 1.731, 1.782 Å for n = 4–6). At the same time, the intramolecular free O–H bonds of terminal W ligands become shorter (0.935, 0.932, 0.9625, 0.9624, 0.9622 Å for n = 2–6), explaining the gradual blue shifts of ν₁ and ν₃.

The size-dependent proton transfer to solvent has been observed for a number of closed-shell aromatic H⁺(A–W_n) clusters, including A = benzene (PA = 750.3 kJ mol⁻¹, n_c = 1),^25,26 naphthalene (PA = 802.9 kJ mol⁻¹, n_c = 2),¹⁰⁹ BN (PA = 812 kJ mol⁻¹, n_c = 2), and benzaldehyde (PA = 834 kJ mol⁻¹, n_c = 3).²³ As can be seen, the larger the PA of A, the larger is the critical hydration size n_c. Moreover, in all these cases (except for benzene as explained above), the observed n_c value is consistent with the difference to the size-dependent PA values of W_n. The case of phenol is more complex because this substituted arene has two competing protonation sites, with largely different PA values for the ring and the substituent. While the PA for ring protonation (PA = 817.3 kJ mol⁻¹ for C_ortho/para) is much higher than for protonation at the substituent (∼740 kJ mol⁻¹ for O),¹¹⁰ hydration is strongly preferred at the OH group(s) in both cases, so that n_c is strongly dependent on the protonation site and concluded to be in the n_c = 3–4 range.⁵⁹ In these clusters, the hydration structure includes OH⋯π H-bonds between the H⁺W_n subcluster and the aromatic ring. Similar structures with OH⋯π docking to the aromatic ring are observed for benzene and naphthalene, which do not possess a polar functional group.^26,109 This behaviour is different from the BN–H⁺W_n clusters studied here, in which the strongly directional OH⋯N H-bond between H⁺W_n and the linear CN group of BN causes the hydration network to grow away from the aromatic ring. In that sense, BN behaves similar to benzaldehyde, in which also the large spacing between the polar C=O group (to which H⁺W_n is attached) and the aromatic ring prevents the formation of OH⋯π H-bonds.²³

Comparison between BN–H⁺W_n and the well-studied bare H⁺W_n clusters with the same n is interesting, because it reveals the effects of simple addition of BN to H⁺W_n. On the other hand, comparison of BN–H⁺W_n with H⁺W_n+1 unravels the effects of W → BN substitution by keeping the same number of molecules in the cluster. In this scenario, BN may be considered as a dopant or impurity molecule in the cluster. BN has several properties different from W. First, while W has four possible binding sites for H-bonding (two lone pairs of O acting as acceptor, two OH donor groups), BN offers only a single binding site for σ H-bonds (the N lone pair along the CN bond acting as acceptor). As discussed above, π H-bonding to the aromatic ring is not feasible in BN–H⁺W_n clusters in the size range studied herein and π H-bonding to the C≡N triple bond is energetically unfavourable. The lower number of binding sites of BN only comes into play for clusters with larger n, where the bulky and hydrophobic phenyl ring can not readily be involved in the formation of a solvation network for both steric reasons and the modest strength of the aromatic OH⋯π interaction. For smaller n, BN does not need to be incorporated into the hydration network to form the most stable structures. Further, when acting as a single H-bond acceptor, BN produces a much stronger OH⋯N H-bond than the OH⋯O H-bond formed by W, because BN has a much larger dipole moment and PA. This is only true as long as single W ligands are considered, because the PA of W_n with n ≥ 2 is comparable or larger than the PA of BN. Nonetheless, this difference in molecular parameters is the reason why BN is located in the first solvation shell of the H₃O⁺ core ion in the most stable BN–H⁺W_n isomers for clusters in the size range n = 2–6. Interesting aspects of introducing the BN dopant molecule into the H⁺W_n clusters include the impact on structure, including the position of BN and the excess proton in the cluster, the degree of asymmetry caused by symmetry breaking through steric factors and changes in the strength of the H-bonds, and the energy ordering of the various related isomers. The lowest-energy structures of H⁺W_n are well known,^69–80 and their geometries, binding energies, and IR spectra computed at the B3LYP-D3/aug-cc-pVTZ level are shown in Fig. S10 in the ESI.† Briefly, only a single low-energy isomer is observed for n = 1–4, namely the hydronium ion (n = 1, H₃O⁺), the Zundel ion (n = 2, H₅O₂⁺), a symmetrically twofold solvated hydronium ion (n = 3, H₇O₃⁺, W–H₃O⁺–W), and the Eigen ion (n = 4, H₉O₄⁺, H₃O⁺–W₃) which is a symmetrically threefold solvated hydronium ion with a completed first solvation shell. Starting from n = 5, more than a single isomer is observed even at low cryogenic temperature, and their geometries have been determined by elegant IR–IR double resonance experiments for n = 5–7, namely the three ring (R), branched (B), and chain (C) isomers of n = 5,⁷⁵ the two Eigen and Zundel type isomers of n = 6 (6E and 6Z),⁷⁶ and the four 7Z, 7E_C, 7E_4R, and 7E_5R isomers of n = 7.⁷⁷ Moreover, it was shown that the relative abundance of the various isomers depends on temperature and choice of tagging ligand.^71,74,75 Similar to the bare H⁺W_n clusters, we observe a dominant single isomer for H⁺(BN–W_n) clusters up to the size range of four molecules. However, there are important differences in the energetics and structures. For example, while the Zundel ion has a symmetric W–H⁺–W configuration with a shared proton, H⁺BN–W(H) has a strongly asymmetric structure, with the excess proton clearly localized at BN. The BN–H⁺W₂ structure is similar to the one of H₇O₃⁺, with a twofold solvated H₃O⁺ ion, although again BN breaks the symmetry because the H₃O⁺⋯BN H-bond is stronger than the H₃O⁺⋯W H-bond. A similar situation results from comparison between BN–H⁺W₃(b) and the H⁺W₄ Eigen ion. Interestingly, we have evidence for the minor presence of the less stable linear BN–H⁺W₃(l) isomer, while the corresponding asymmetric H⁺W₄ isomer has not been detected.⁷⁸ As a general rule, the H-bond to BN is stronger than the one to W, and as a result W → BN substitution weakens the remaining H-bonds of H₃O⁺ to W. Because the IRPD spectra of cryogenic H⁺W_n clusters with n = 5–7 have been assigned to three, two, and four isomers, we expect a similar situation for the related BN–H⁺W_n clusters with n = 4–6, because all low-energy structures identified by the DFT calculations can be derived from the low-energy H⁺W_n structures as outlined in the sections dealing with the individual cluster sizes. Interestingly, the IRPD spectra of BN–H⁺W_n are similar in appearance and trends to those recorded for H⁺W_n+1 recorded at elevated temperature for n = 4–6,⁷¹ suggesting that, at least in these clusters one W ligand is simply substituted by BN. Clearly, the achieved resolution of the corresponding IRPD spectra recorded for n = 4–6 does not allow for a detailed isomer identification. To this end, future efforts will have to employ cryogenic cooling or tagging of the clusters and/or IR–IR double resonance experiments.^74–78

5. Concluding remarks

The analysis of IRPD spectra of mass-selected H⁺(BN–W_n) clusters in the size range n = 1–6 with the aid of DFT calculations reveals detailed information about the location of the excess proton and the structure of the hydration network. The spectra of the clusters with small n (n ≤ 4) are dominated by the most stable isomers, while several isomers contribute to the spectra of the larger clusters with n = 5 and 6. The n = 1 dimer has a H⁺BN–W type structure, in which W is attached to the NH proton of N-protonated H⁺BN. H⁺(BN–W_n) clusters with n ≥ 2 have proton-transferred structures of the type BN–H⁺W_n. This intracluster proton transfer to solvent at the critical size n_c = 2 is consistent with thermochemical predictions from the relative proton affinities of BN and W_n when including effects of solvation energy. The n = 2 and 3 structures are derived from the related Eigen ions of the corresponding H⁺W_n clusters by simple W → BN substitution. The symmetry is reduced by the aromatic dopant molecule, and the H-bonds of H₃O⁺ to BN are stronger than those to W, because of the larger dipole moment and PA of BN as compared to W. In particular, BN substitution weakens the H-bonds to the remaining W ligands, as a result of noncooperative effects of interior ion solvation. In the size range n = 4–6, cyclic isomers with four- and five-membered H⁺W_n rings become energetically more stable than the branched isomers, because they feature one more H-bond. However, the more flexible branched isomers remain the global minima on the free energy surface because of entropy. Clearly, linear isomers with incompletely solvated H₃O⁺ (or H₅O₂⁺) ion cores are not favoured, and the energy gap to the most stable branched or cyclic isomers increases substantially with increasing n. In the most stable structures, BN is located in the first solvation shell of the H₃O⁺ ion, because of its larger dipole moment and PA. However, the strength of the H-bond between BN and the H⁺W_n cluster decreases with n. It is extrapolated that surface isomers will become more favourable for the larger clusters, because W can be better integrated in the hydration network than BN with its bulky hydrophobic phenyl ring. As a general trend, the excess charge becomes more delocalized as the cluster grows in size, and as a result individual H-bonds become weaker as indicated by incremental blue shifts (or reduced red shifts) in the free and bound OH stretch frequencies. The cluster growth in H⁺(BN–W_n) differs from that in H⁺BN–L_n with the hydrophobic aprotic Ar and N₂ ligands. While H⁺BN–L_n with the inert ligands L = Ar and N₂ exhibit interior ion solvation around the N-protonated H⁺BN core ion, clusters with L = W prefer the formation of an H-bonded hydration network and display intracluster proton transfer from H⁺BN to W_n for clusters larger than n_c = 2. Protonation of BN–W_n cluster has a drastic impact on both the cluster structure, the shape of the hydration network, and the interaction strength. The major astrochemical implication of this study is the prediction that H⁺BN is unstable in and on ice grains because of exothermic and barrierless proton transfer to the ice structure. Although the isomer assignment is very clear up to the size range n ≤ 4, the achieved resolution of the IRPD spectra recorded for n = 5–6 is limited and does not allow for a detailed isomer identification. To this end, future efforts will have to employ cryogenic cooling or tagging of the clusters and/or IR–IR double resonance experiments.^74–78,111

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This study was supported by Deutsche Forschungsgemeinschaft (DO 729/3-3).

References

1. F. A. Carey and R. J. Sundberg, Advanced Organic Chemistry, Plenum Press, New York, 5th edn, 2007.
2. J. P. Schermann, Spectroscopy and Modelling of Biomolecular Building Blocks, Elsevier, Amsterdam, 2008.
3. L. Stryer, Biochemistry, Freeman, New York, 4th edn, 1995.
4. G. A. Jeffrey and W. Saenger, Hydrogen Bonding in Biological Systems, Springer, Heidelberg, 1991.
5. P. Ball, Chem. Rev., 2008, 108, 74–108.
6. P. Ball, Nature, 2011, 478, 467–468.
7. S. K. Pal and A. H. Zewail, Chem. Rev., 2004, 104, 2099–2123.
8. Y. Levy and J. N. Onuchic, Annu. Rev. Biophys. Biomol. Struct., 2006, 35, 389–415.
9. B. Bagchi, Chem. Rev., 2005, 105, 3197–3219.
10. F. Garczarek and K. Gerwert, Nature, 2006, 439, 109–112.
11. C. L. Perrin and J. B. Nielson, Annu. Rev. Phys. Chem., 1997, 48, 511–544.
12. J. M. J. Swanson, C. M. Maupin, H. Chen, M. K. Petersen, J. Xu, Y. Wu and G. A. Voth, J. Phys. Chem. B, 2007, 111, 4300–4314.
13. E. P. L. Hunter and S. G. Lias, J. Phys. Chem. Ref. Data, 1998, 27, 413–656.
14. D. J. Goebbert and P. G. Wenthold, Eur. J. Mass Spectrom., 2004, 10, 837–845.
15. A. Courty, M. Mons, J. Le Calve, F. Piuzzi and I. Dimicoli, J. Phys. Chem. A, 1997, 101, 1445–1450.
16. M. Miyazaki, A. Fujii, T. Ebata and N. Mikami, Chem. Phys. Lett., 2004, 399, 412–416.
17. R. Knochenmuss, O. Cheshnovsky and S. Leutwyler, Chem. Phys. Lett., 1988, 144, 317–323.
18. N. Solcà and O. Dopfer, J. Phys. Chem. A, 2003, 107, 4046–4055.
19. M. Miyazaki, A. Fujii, T. Ebata and N. Mikami, Phys. Chem. Chem. Phys., 2003, 5, 1137–1148.
20. S. Sato and N. Mikami, J. Phys. Chem., 1996, 100, 4765–4769.
21. T. Ebata, A. Fujii and N. Mikami, Int. Rev. Phys. Chem., 1998, 17, 331–361.
22. I. Alata, M. Broquier, C. Dedonder-Lardeux, C. Jouvet, M. Kim, W. Y. Sohn, S. Kim, H. Kang, M. Schütz, A. Patzer and O. Dopfer, J. Chem. Phys., 2011, 134, 074307.
23. O. Dopfer, A. Patzer, S. Chakraborty, I. Alata, R. Omidyan, M. Broquier, C. Dedonder and C. Jouvet, J. Chem. Phys., 2014, 140, 124314.
24. S. G. Lias, J. E. Bartmess, J. F. Liebman, J. L. Holmes, R. D. Levin and W. G. Mallard, J. Phys. Chem. Ref. Data, 1984, 13, 695.
25. E. S. Kryachko and M. T. Nguyen, J. Phys. Chem. A, 2001, 105, 153–155.
26. T. C. Cheng, B. Bandyopadhyay, J. D. Mosley and M. A. Duncan, J. Am. Chem. Soc., 2012, 134, 13046–13055.
27. N. Solcà and O. Dopfer, Chem. – Eur. J., 2003, 9, 3154–3163.
28. I. Alata, C. Dedonder, M. Broquier, E. Marceca and C. Jouvet, J. Am. Chem. Soc., 2010, 132, 17483–17489.
29. D. Bing, T. Hamashima, C.-W. Tsai, A. Fujii and J.-L. Kuo, Chem. Phys., 2013, 421, 1–9.
30. B. A. McGuire, A. M. Burkhardt, S. Kalenskii, C. N. Shingledecker, A. J. Remijan, E. Herbst and M. C. McCarthy, Science, 2018, 359, 202–205.
31. A. G. G. M. Tielens, Annu. Rev. Astron. Astrophys., 2008, 46, 289–337.
32. T. Oka, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 12235–12242.
33. T. Snow, L. V. Page, Y. Keheyan and V. M. Bierbaum, Nature, 1998, 391, 259–260.
34. E. E. Etim, P. Gorai, A. Das and E. Arunan, Adv. Space Res., 2017, 60, 709–721.
35. B. A. McGuire, Astrophys. J., Suppl. Ser., 2018, 239, 17.
36. O. Dopfer, EAS Publication Series, 2011, vol. 46, pp. 103–108.
37. N. Solcà and O. Dopfer, Angew. Chem., Int. Ed., 2002, 41, 3628–3631.
38. U. J. Lorenz, N. Solca, J. Lemaire, P. Maitre and O. Dopfer, Angew. Chem., Int. Ed., 2007, 46, 6714–6716.
39. H. Knorke, J. Langer, J. Oomens and O. Dopfer, Astrophys. J., Lett., 2009, 706, L66–L70.
40. I. Alata, R. Omidyan, M. Broquier, C. Dedonder, O. Dopfer and C. Jouvet, Phys. Chem. Chem. Phys., 2010, 12, 14456–14458.
41. A. M. Ricks, G. E. Douberly and M. A. Duncan, Astrophys. J., 2009, 702, 301–306.
42. G. E. Douberly, A. M. Ricks, P. V. R. Schleyer and M. A. Duncan, J. Phys. Chem. A, 2008, 112, 4869–4874.
43. M. Tsuge, C.-Y. Tseng and Y.-P. Lee, Phys. Chem. Chem. Phys., 2018, 20, 5344–5358.
44. N. Solcà and O. Dopfer, Chem. Phys. Lett., 2001, 347, 59–64.
45. K. Chatterjee and O. Dopfer, Chem. Sci., 2018, 9, 2301–2318.
46. M. P. Bernstein, S. A. Sandford, L. J. Allamandola, J. S. Gillette, S. J. Clemett and R. N. Zare, Science, 1999, 283, 1135–1138.
47. T. Henning and F. Salama, Science, 1998, 282, 2204–2210.
48. A. M. Cook, A. Ricca, A. L. Mattioda, J. Bouwman, J. Roser, H. Linnartz, J. Bregman and L. J. Allamandola, Astrophys. J., 2015, 799, 14.
49. K. Chatterjee and O. Dopfer, J. Chem. Phys., 2018, 149, 174315.
50. R. M. Helm, H. P. Vogel, H. J. Neusser, V. Storm, D. Consalvo and H. Dreizler, Z. Naturforsch., A: Phys. Sci., 1997, 52, 655–664.
51. S. Melandri, D. Consalvo, W. Caminati and P. G. Favero, J. Chem. Phys., 1999, 111, 3874–3879.
52. S. Ishikawa, T. Ebata and N. Mikami, J. Chem. Phys., 1999, 110, 9504–9515.
53. T. Kobayashi, K. Honma, O. Kajimoto and S. Tsuchiya, J. Chem. Phys., 1987, 86, 1111–1117.
54. E. S. Kryachko and M. T. Nguyen, J. Chem. Phys., 2001, 115, 833–841.
55. N. Solcà and O. Dopfer, Chem. Phys. Lett., 2001, 342, 191–199.
56. N. Solcà and O. Dopfer, J. Am. Chem. Soc., 2003, 125, 1421–1430.
57. N. Solcà and O. Dopfer, Angew. Chem., Int. Ed., 2003, 42, 1537–1540.
58. N. Solcà and O. Dopfer, J. Chem. Phys., 2004, 121, 769–772.
59. M. Katada and A. Fujii, J. Phys. Chem. A, 2018, 122, 5822–5831.
60. F. M. Pasker, N. Solcà and O. Dopfer, J. Phys. Chem. A, 2006, 110, 12793–12804.
61. U. J. Lorenz, J. Lemaire, P. Maitre, M. E. Crestoni, S. Fornarini and O. Dopfer, Int. J. Mass Spectrom., 2007, 267, 43–53.
62. J. Klyne and O. Dopfer, J. Phys. Chem. B, 2018, 122, 10700–10713.
63. S. Chakraborty, A. Patzer and O. Dopfer, J. Chem. Phys., 2010, 133, 044307.
64. B. S. Freiser and J. L. Beauchamp, J. Am. Chem. Soc., 1977, 99, 3214–3225.
65. B. S. Freiser, R. L. Woodin and J. L. Beauchamp, J. Am. Chem. Soc., 1975, 97, 6893–6894.
66. H. Wincel, R. H. Fokkens and N. M. M. Nibbering, J. Am. Soc. Mass Spectrom., 1990, 1, 225–232.
67. M. Eckert-Maksic, M. Hodoscek, D. Kovacek, Z. B. Maksic and M. Primorac, THEOCHEM, 1997, 417, 131–143.
68. K. Chatterjee and O. Dopfer, Astrophys. J., 2018, 865, 114.
69. L. I. Yeh, M. Okumura, J. D. Myers, J. M. Price and Y. T. Lee, J. Chem. Phys., 1989, 91, 7319–7330.
70. L. I. Yeh, Y. T. Lee and J. T. Hougen, J. Mol. Spectrosc., 1994, 164, 473–488.
71. J. C. Jiang, Y. S. Wang, H. C. Chang, S. H. Lin, Y. T. Lee, G. Niedner-Schatteburg and H. C. Chang, J. Am. Chem. Soc., 2000, 122, 1398–1410.
72. M. Miyazaki, A. Fujii, T. Ebata and N. Mikami, Science, 2004, 304, 1134–1137.
73. J.-W. Shin, N. I. Hammer, E. G. Diken, M. A. Johnson, R. S. Walters, T. D. Jaeger, M. A. Duncan, R. A. Christie and K. D. Jordan, Science, 2004, 304, 1137–1140.
74. K. Mizuse and A. Fujii, Phys. Chem. Chem. Phys., 2011, 13, 7129–7135.
75. M. R. Fagiani, H. Knorke, T. Esser, N. Heine, C. Wolke, S. Gewinner, W. Schöllkopf, M.-P. Gaigeot, R. Spezia, M. A. Johnson and K. R. Asmis, Phys. Chem. Chem. Phys., 2016, 18, 26743–26754.
76. N. Heine, M. R. Fagiani, M. Rossi, T. Wende, G. Berden, V. Blum and K. R. Asmis, J. Am. Chem. Soc., 2013, 135, 8266–8273.
77. N. Heine, M. R. Fagiani and K. R. Asmis, J. Phys. Chem. Lett., 2015, 6, 2298–2304.
78. T. K. Esser, H. Knorke, K. R. Asmis, W. Schöllkopf, Q. Yu, C. Qu, J. M. Bowman and M. Kaledin, J. Phys. Chem. Lett., 2018, 9, 798–803.
79. C. T. Wolke, J. A. Fournier, L. C. Dzugan, M. R. Fagiani, T. T. Odbadrakh, H. Knorke, K. D. Jordan, A. B. McCoy, K. R. Asmis and M. A. Johnson, Science, 2016, 354, 1131–1135.
80. J. A. Fournier, C. T. Wolke, M. A. Johnson, T. T. Odbadrakh, K. D. Jordan, S. M. Kathmann and S. S. Xantheas, J. Phys. Chem. A, 2015, 119, 9425–9440.
81. O. Dopfer, Int. Rev. Phys. Chem., 2003, 22, 437–495.
82. O. Dopfer, Z. Phys. Chem., 2005, 219, 125–168.
83. M. J. Frisch, et al., GAUSSIAN09, Rev. D.1, Gaussian, Inc., Wallingford CT, 2009.
84. K. Chatterjee and O. Dopfer, Phys. Chem. Chem. Phys., 2017, 19, 32262–32271.
85. M. Schütz, Y. Matsumoto, A. Bouchet, M. Öztürk and O. Dopfer, Phys. Chem. Chem. Phys., 2017, 19, 3970–3986.
86. A. Bouchet, M. Schütz and O. Dopfer, ChemPhysChem, 2016, 17, 232–243.
87. K. Chatterjee, Y. Matsumoto and O. Dopfer, Angew. Chem., Int. Ed., 2019, 58, 3351–3355.
88. K. Chatterjee and O. Dopfer, J. Phys. Chem. A, 2019, 123, 7637–7650.
89. J. Klyne and O. Dopfer, J. Mol. Spectrosc., 2017, 337, 124–136.
90. J. Klyne, M. Miyazaki, M. Fujii and O. Dopfer, Phys. Chem. Chem. Phys., 2018, 20, 3092–3108.
91. K. Chatterjee and O. Dopfer, Phys. Chem. Chem. Phys., 2019, 21, 15157–15166.
92. B. E. Rocher-Casterline, L. C. Ch'ng, A. K. Mollner and H. Reisler, J. Chem. Phys., 2011, 134, 211101.
93. J. H. S. Green and D. J. Harrison, Spectrochim. Acta, Part A, 1976, 32, 1279–1286.
94. E. D. Glendening, J. K. Badenhoop, A. E. Reed, J. E. Carpenter, J. A. Bohmann, C. M. Morales, C. R. Landis and F. Weinhold, NBO 6.0, Wisconsin, Madison, 2013.
95. A. E. Reed, L. A. Curtiss and F. Weinhold, Chem. Rev., 1988, 88, 899–926.
96. E. R. Johnson, S. Keinan, P. Mori-Sanchez, J. Contreras-Garcia, A. J. Cohen and W. T. Yang, J. Am. Chem. Soc., 2010, 132, 6498–6506.
97. J. Contreras-Garcia, E. R. Johnson, S. Keinan, R. Chaudret, J. P. Piquemal, D. N. Beratan and W. T. Yang, J. Chem. Theory Comput., 2011, 7, 625–632.
98. J. Casado, L. Nygaard and G. O. Sørensen, J. Mol. Struct., 1971, 8, 211–224.
99. A. G. Csaszar and G. Fogarasi, Spectrochim. Acta, Part A, 1989, 45, 845–854.
100. K. Wohlfart, M. Schnell, J.-U. Grabow and J. Küpper, J. Mol. Spectrosc., 2008, 247, 119–121.
101. A. G. Csaszar, G. Czako, T. Furtenbacher, J. Tennyson, V. Szalay, S. V. Shirin, N. F. Zobov and O. L. Polyansky, J. Chem. Phys., 2005, 122, 214305.
102. G. Herzberg, Molecular Spectra and Molecular Structure. II. Infrared and Raman Spectra of Polyatomic Molecules, Krieger Publishing Company, Malabar, Florida, 1991.
103. K. A. Mason, A. C. Pearcy, A. M. Hamid and M. S. El-Shall, J. Chem. Phys., 2019, 150, 124303.
104. N. Solcà and O. Dopfer, Chem. Phys. Lett., 2000, 325, 354–359.
105. R. V. Olkhov and O. Dopfer, Chem. Phys. Lett., 1999, 314, 215–222.
106. M. Eigen, Angew. Chem., Int. Ed. Engl., 1964, 3, 1–19.
107. G. Zundel, in The Hydrogen Bond-Recent Developments in Theory and Experiments. II Structure and Spectroscopy, ed. P. Schuster, G. Zundel and C. Sandorfy, North-Holland, Amsterdam, 1976.
108. I. K. Attah, S. P. Platt, M. Meot-Ner, M. S. El-Shall, S. G. Aziz and A. O. Alyoubi, Chem. Phys. Lett., 2014, 613, 45–53.
109. I. Alata, M. Broquier, C. Dedonder, C. Jouvet and E. Marceca, Chem. Phys., 2012, 393, 25–31.
110. N. Solcà and O. Dopfer, J. Am. Chem. Soc., 2004, 126, 1716–1725.
111. C. M. Leavitt, A. B. Wolk, J. A. Fournier, M. Z. Kamrath, E. Garand, M. J. Van Stipdonk and M. A. Johnson, J. Phys. Chem. Lett., 2012, 3, 1099–1105.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c9cp05042f

---