A global CHIPR potential energy surface for ground-state C3H and exploratory dynamics studies of reaction C2 + CH → C3 + H†
Abstract
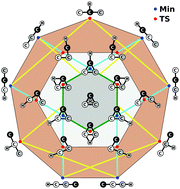
A full-dimensional global potential-energy surface (PES) is first reported for ground-state doublet C3H using the combined-hyperbolic-inverse-power-representation (CHIPR) method and accurate ab initio energies extrapolated to the complete basis set limit. The PES is based on a many-body expansion-type development where the two-body and three-body energy terms are from our previously reported analytic potentials for C2H(2A′) and C3(1A′,3A′), while the effective four-body one is calibrated using an extension of the CHIPR formalism for tetratomics. The final form is shown to accurately reproduce all known stationary structures of the PES, some of which are unreported thus far, and their interconversion pathways. Moreover, it warrants by built-in construction the appropriate permutational symmetry and describes in a physically reasonable manner all long-range features and the correct asymptotic behavior at dissociation. Exploratory quasi-classical trajectory calculations for the reaction C2 + CH → C3 + H are also performed, yielding thermalized rate coefficients for temperatures up to 4000 K.
- This article is part of the themed collection: 2019 PCCP HOT Articles


 Please wait while we load your content...
Please wait while we load your content...