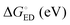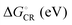Open Access Article
Open Access ArticleElectronic couplings and rates of excited state charge transfer processes at poly(thiophene-co-quinoxaline)–PC71BM interfaces: two- versus multi-state treatments†
Tuuva
Kastinen
 *a,
Demetrio Antonio
da Silva Filho
*a,
Demetrio Antonio
da Silva Filho
 b,
Lassi
Paunonen
b,
Lassi
Paunonen
 c,
Mathieu
Linares
c,
Mathieu
Linares
 def,
Luiz Antonio
Ribeiro Junior
def,
Luiz Antonio
Ribeiro Junior
 b,
Oana
Cramariuc
b,
Oana
Cramariuc
 gh and
Terttu I.
Hukka
gh and
Terttu I.
Hukka
 *a
*a
aChemistry and Advanced Materials, Faculty of Engineering and Natural Sciences, Tampere University, FI-33014 Tampere University, P. O. Box 541, Finland. E-mail: tuuva.kastinen@tuni.fi; terttu.hukka@tuni.fi
bInstitute of Physics, University of Brasília, Brasília, DF, Brazil
cMathematics, Faculty of Information Technology and Communication Sciences, Tampere University, FI-33014 Tampere University, P. O. Box 692, Finland
dLaboratory of Organic Electronics, ITN, Campus Norrköping, Linköping University, SE-581 83 Linköping, Sweden
eScientific Visualization Group, ITN, Campus Norrköping, Linköping University, SE-581 83 Linköping, Sweden
fSwedish e-Science Research Centre (SeRC), Linköping University, SE-581 83 Linköping, Sweden
gPhysics, Faculty of Engineering and Natural Sciences, Tampere University, FI-33014 Tampere University, P. O. Box 692, Finland
hCentrul IT pentru Stiinta si Tehnologie, Av. Radu Beller 25, Bucharest, Romania
First published on 1st November 2019
Abstract
Electronic coupling between adjacent molecules is one of the key parameters determining the charge transfer (CT) rates in bulk heterojunction (BHJ) polymer solar cells (PSCs). We calculate theoretically electronic couplings for exciton dissociation (ED) and charge recombination (CR) processes at local poly(thiophene-co-quinoxaline) (TQ)–PC71BM interfaces. We use eigenstate-based coupling schemes, i.e. the generalized Mulliken–Hush (GMH) and fragment charge difference (FCD) schemes, including 2 to multiple (3–11) states. Moreover, we study the effects of functionals, excited state methods, basis sets, surrounding media, and relative placements of TQ and PC71BM on the coupling values. Generally, both schemes provide consistent couplings with the global hybrid functionals, which yield more charge-localized diabatic states and constant coupling values regardless of the number of states, and so the 2-state schemes may be sufficient. The (non-tuned and optimally tuned) long-range corrected (LRC) functionals result in more notable mixing of the local components with the CT states. Employing multiple states reduces the mixing and thus improves the LRC results, although the method still affects the GMH CR couplings. As the FCD scheme is less sensitive, we recommend combining it with the multi-state treatment for polymer–fullerene systems when using the LRC functionals. Finally, we employ the 11-state FCD couplings to calculate the ED and CR rates, which are consistent with the experimental rates of the polymer–fullerene systems. Our results provide more insight into choosing a suitable eigenstate-based coupling scheme for predicting the electronic couplings and CT rates in photoactive systems.
Introduction
Polymer solar cells (PSCs), which consist of conjugated donor–acceptor (D–A) copolymers as electron donor (eD) materials, have recently reached power conversion efficiencies (PCEs) up to 12%1,2 when using a fullerene derivative, e.g. PC71BM (phenyl-C71-butyric acid methyl ester), as an electron acceptor (eA) material. In recent years, PCEs up to 13–14%3,4 have been achieved with non-fullerene materials as the eAs. These best performing PSCs make use of a bulk heterojunction (BHJ) architecture5 in the photoactive layer, where the eD is mixed with the eA, ensuring the closest contact and an efficient charge transfer (CT) between the eD and eA materials.Charge generation at the eD–eA interface is based on photoinduced electron transfer (PET), whose efficiency is determined by the following CT processes6,7 (Fig. 1a): (i) absorption of light by the eD (or the eA in some cases) leading to the formation of a locally excited state (LE, i.e. eD*–eA) and excitons (i.e. coulombically bound electron–hole pairs); (ii) diffusion of excitons to the eD–eA interface; (iii) exciton dissociation (ED) via an electron transfer from the eD* to eA and the formation of a CT state (eD+–eA−); (iv) if the charge carriers overcome the Coulomb binding energy, their separation into free carriers; and (v) migration of charges towards the electrodes. Alternatively, the CT state can decay via radiative emission or irradiative charge recombination (CR) to the ground state (GS, i.e. eD–eA), which hinders the charge generation and thus reduces the performance of the device. Thus, maximizing the ED (and charge separation) rate and minimizing the CR rate are crucial for the efficiency of a PSC.
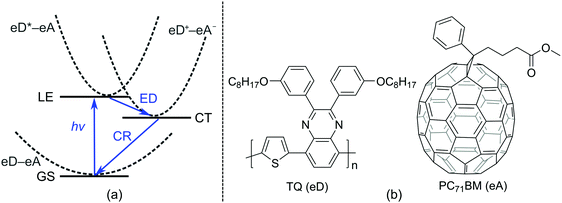 | ||
| Fig. 1 (a) Schematic energy diagram illustrating the main steps of the photophysical processes occurring in the photoactive layer of a BHJ PSC. (b) Structures of an eD (TQ) and an eA (PC71BM). | ||
Predicting the rates of the ED and CR processes gives more insight into the efficiency of the charge generation at the eD–eA interface. In the high-temperature (weak-coupling), kBT ≫ ℏω, regime, the semi-classical Marcus theory8–10 can be used to calculate the ED and CR rates:
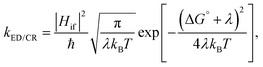 | (1) |
The electronic coupling Hif describes the strength of the interaction between the initial and final charge-localized (diabatic) states. It is defined as the off-diagonal matrix element of the electronic Hamiltonian (H): Hif = 〈ψi|H|ψf〉, where ψi and ψf are the wave functions of the initial and final diabatic states of interest.11 Thus, the value of Hif depends on the overlap of ψi and ψf and is very sensitive to the relative intermolecular position and distance of the eD and eA molecules.12,13 For this reason, an accurate estimation and prediction of the Hif values between the interacting species is a challenging subject of research in biology, chemistry, and physics.11,14
Experimentally, Hif has been evaluated from spectroscopic data by fitting them into theoretical expressions.15 Theoretically, a number of computational methods based on ab initio quantum mechanics (QM) have been proposed and applied to estimate the CT couplings.11,16,17 For calculating Hif of the CT processes involving excited states, e.g. ED and CR, different diabatization schemes have been developed. In these schemes, adiabatic states retrieved from QM calculations are transformed to diabatic states by using either the wave-function, as in the Boys localization,18 the Edmiston–Ruedenberg localization,19 and block diagonalization,20,21 or an additional operator, e.g. dipole moment (μ) in the generalized Mulliken–Hush (GMH)22,23 scheme or charge difference (Δq) in the fragment charge difference (FCD)24 scheme. In addition, more simple approaches have been developed recently, where electronic couplings are obtained either directly25 from excitation energies and oscillator strengths or by defining the quasi-diabatic states,26 which are derived from the excited electronic states of the reference structures. In this paper, we will focus on the GMH and FCD schemes that are available in the Q-Chem software,27 as they have proven to be useful and flexible for calculating electronic couplings for the excited state processes22,24,28 and they can be employed for large molecules, as well.16
Previously, a number of theoretical investigations have been reported using the two-state GMH and FCD schemes for determining Hif at local photoactive eD–eA interfaces, such as phthalocyanine–C60,29 pentacene–C60,30–32 and D–A copolymer–fullerene systems.33–39 In particular, the two-state GMH scheme has been used in several studies of D–A copolymers and fullerene derivatives.33–38 However, in these studies, mainly the electronic couplings between the GS and excited states, i.e. the CR couplings, have been taken into account,33–36 while there are fewer studies37,38 which consider the couplings between the excited states, e.g. the LE and CT states, in the case of the ED process. In the PET, all these states are relevant for describing the ED and CR processes at the copolymer–fullerene interfaces. Moreover, to the best of our knowledge the effectiveness of the FCD scheme for predicting Hif in these systems in comparison with the GMH scheme has not yet been studied, and thus further information about this is required.
Typically, two eigenstates are included in the GMH and FCD calculations to form charge-localized diabatic states. However, previous studies of the complexes consisting of small or medium sized organic molecules,28,40,41 DNA π stacks,24,42–44 donor–bridge–acceptor systems,28,45 and TiO2–dye systems46 have shown that sometimes several adiabatic states are necessary to describe the diabatic states accurately. In such instances, the corresponding multi-state GMH and FCD approaches are required.28,40 This is commonly the case, for example, when the component of the local excitation of the eD or eA is mixed with the CT state, and the two-state GMH scheme may lead to overestimated electronic coupling values.47 However, to our knowledge, there are not yet studies which take account of the multi-state effects when predicting the coupling values with either the GMH or FCD scheme for the photoactive components of the active layers in PSCs containing D–A copolymers.
Previous studies have shown48,49 that electronic couplings are sensitive to the choice of density functional theory (DFT). Global hybrid functionals with a fixed, global fraction of explicit Hartree–Fock (HF) exchange, including especially B3LYP,50,51 have been generally a popular choice in the theoretical studies of photovoltaic compounds, but they are known to tend to overdelocalize the electron density due to the many-electron self-interaction error (MSIE).52,53 However, among the global hybrids, PBE0,54–56 which is mainly based on fundamental constants rather than on fitting to empirical parameters, has been demonstrated to produce relatively accurate electron densities for a set of atomic species57 and also for larger organic molecules with two to ten heavy atoms (e.g. carbon, oxygen, nitrogen, and sulfur).58 Long-range corrected (LRC) functionals, where the exchange term in the Kohn–Sham energy functional is partitioned into short-range (SR) and long-range (LR) components by employing a splitting function (e.g. the standard error function or its extended versions59), have resulted in improved excitation energies of copolymers and copolymer–fullerene systems with respect to B3LYP.53 In LRC functionals, DFT exchange is used for the SR part to treat the SR static correlation effects, while semilocal correlation is used for the LR part together with the full (100%) HF exchange, which will ensure the correct description of the asymptotic potential.53 In particular, the LRC functional CAM-B3LYP60 has been employed to reveal the excited state properties in the previous GMH coupling and CT rate calculations of copolymer–fullerene systems.33–36 However, here we note that not all functionals based on the range separation formalism actually include the full HF exchange, CAM-B3LYP with the 65% HF exchange in the LR component being one example, which may have consequences on the predicted values.61 In LRC functionals, the amount of (de)localization error is dependent on the range-separation parameter (ω), which defines the switching between the SR and LR. As ω is system-dependent,62 using the default ω values can lead to inaccurate results, and thus to address the problem of the MSIE, optimally tuned (OT) LRC functionals have been introduced.53 Tuning of ω in the LRC functionals is known to improve the calculated excitation energies of D–A copolymers with respect to the experimental ones.63–66 Moreover, the FCD scheme has been reported to yield electronic couplings of stacked small molecules (i.e. ethylene, pyrrole, and naphthalene) closer to the experimental Mulliken–Hush values, when the OT version of the LRC Baer–Neuhauser–Livshits (BNL)67,68 functional (incorporating the full 100% HF exchange into the LR component) has been used.49
In the present work, we calculate the electronic couplings of the ED and CR processes at local polymer–fullerene interfaces with two- and multi-state GMH and FCD schemes. For our model systems of the eD–eA interfacial complexes, we have chosen to use a D–A copolymer, poly[thiophene-2,5-diyl-alt-2,3-bis-(3-octyloxyphenyl)quinoxaline-5,8-diyl]69,70 (TQ, Fig. 1b), as the eD and a fullerene derivative, PC71BM,71 as the eA. These photoactive components have been widely used in BHJ PSCs, demonstrating promising efficiencies and high open-circuit voltages,72 making them a representative model system for this study. In particular, TQ has several interesting characteristics such as being an easily synthesized copolymer with a low bandgap, whose solubility and twisting can be effectively controlled with different side chains.70,73 Recently, TQ and its fluorinated counterparts have been employed successfully as the eDs also in all-polymer solar cells.74 Furthermore, from a theoretical point of view, a small size of TQ allows using suitably long oligomers in the complex systems, while maintaining small enough systems in the computationally heavy time-dependent (TD) DFT calculations.
Our purpose is to determine how the inclusion of multiple states affects the GMH and FCD couplings of relatively large photovoltaic complexes. Additionally, we consider the performance of the aforementioned coupling schemes relative to the choice of functional, excited state method, basis set, and surrounding medium. We have selected a small series of representative functionals, namely two global hybrid functionals, B3LYP and PBE0, and two LRC functionals, (non-tuned) CAM-B3LYP and OT-BNL, which we have chosen based on the reasons presented above. As the tuning of ω in the LRC functionals is known to improve results for the polymer–fullerene systems with respect to the global hybrid and non-tuned LRC functionals (see above), we pay close attention to the performance of the tuned LRC functional with respect to the other selected functionals. Finally, we calculate the rates for the ED and CR processes at two TQ–PC71BM interface configurations, where PC71BM locates on either the D or A unit of TQ. Our findings provide insight into choosing the electronic coupling schemes for these types of eD–eA systems used in PSCs.
Computational details
Models
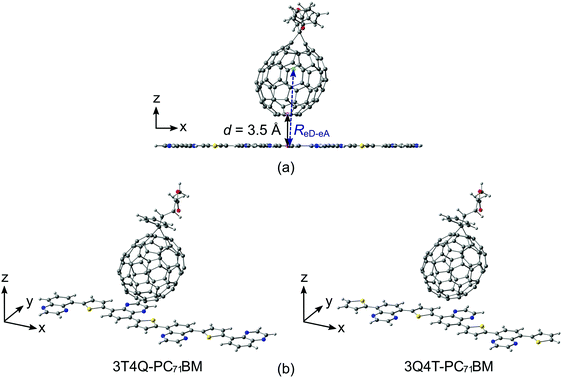
Two different series of TQ–PC71BM complexes were constructed using the separately optimized B3LYP GS geometries of the (neutral) TQ oligomers and PC71BM (the α isomer71): one, where PC71BM was on top of the middle thiophene (the D unit) of TQ, and another, where PC71BM was on top of the middle quinoxaline (the A unit) of TQ (see the ESI† for more detailed information about the models). The alkoxyphenyl side groups of the TQ oligomers (Fig. 1b) were replaced with hydrogens to reduce the computational cost and to ensure planar backbones. Because the DFT-based methods, e.g. TDDFT, set restrictions to the sizes of the eD–eA complexes, we modeled the TQ oligomers with several lengths to choose the TQ models that would best represent the polymeric limit in the electronic coupling calculations. We note that the studied complexes present only two options for the possible placements of PC71BM on TQ that can exist in real solution or thin film environments. Although the face-on configurations (i.e. PC71BM on top of TQ) can be expected to yield larger electronic couplings than the edge-on configurations (i.e. PC71BM on the side of TQ),39,75,76 there might be a relative positioning of the compounds different from the ones used here that yields the maximum electronic coupling between them. The intermolecular distance between TQ and PC71BM (d, Fig. 2a) was set at 3.5 Å, which is an average we predicted in our previous study for poly(benzodithiophene-co-quinoxaline)–PC71BM complexes with functionals including long-range and dispersion corrections.66 The same intermolecular distance has also been employed in other theoretical polymer–fullerene interface studies.34,77 The distances between the centers of mass (ReD–eA, Fig. 2a) of TQ and PC71BM are ca. 8.6 Å.Methods
We carried out the DFT and TDDFT calculations using the Q-Chem 4.2 software.27 The medium was taken into account, as specified later. The GS geometries of the isolated models of the neutral TQ oligomers and PC71BM and their radical states (cations for TQ and anions for PC71BM; only for the longest TQ oligomers, see the ESI†) were fully optimized in vacuum using DFT with the global hybrid functional B3LYP and the 6-31G** basis set. Moreover, the geometries of the lowest singlet excited (S1) of the longest TQ oligomers were optimized with TDDFT at the same level of theory. In all the geometry optimizations, the fine grid EML(75,302) with 75 Euler–Maclaurin radial grid points78 and 302 Lebedev angular grid points,79 an SCF convergence criterion of 10−9, and a cutoff for neglect of two electron integrals of 10−14 were employed. In the single point (SP) calculations of the isolated compounds related to the excited state, reorganization energy, and Gibbs free energy calculations and those of the selected complexes (Fig. 2b) related to the excited state and electronic coupling calculations, the 6-31G* basis set, the standard SG-1 grid, and the default values for the SCF convergence (10−5) and cutoff of two electron integrals (10−8) were used, unless stated otherwise. The excited state SP energy calculations of both the isolated models and the complexes were carried out for the lowest 10 singlet excited states with both the full TDDFT and TDA-DFT schemes, incorporating the Tamm–Dancoff approximation (TDA)80 in the latter. We note that sometimes ED and CR processes may involve triplet states,81 but here we have concentrated on those including only singlet states. B3LYP and the LRC functional CAM-B3LYP (with the default range-separation parameter, ω, of 0.33 Bohr−1) were used in all SP calculations. Additionally, the global hybrid functional, PBE0, and the OT version of the BNL LRC functional (OT-BNL) were used in the SP calculations of the selected TQ–PC71BM complexes (see ‘Models’ and ‘Length of the TQ oligomer and the polymeric limit’). The OT ω values (originally 0.5 Bohr−1) for the selected TQ–PC71BM complexes were determined using eqn (S1) and the tuning procedure is presented in the ESI.† We note that, in addition to the tuning of ω, incorporation of some amount of HF exchange in the SR component has been observed to improve the prediction of the optoelectronic properties of several aromatic heterocycles,82 DNA nucleobase compounds and their complexes,61 and compounds employed in organic light emitting diodes.59 The BNL functional we employ here does include only the LR HF exchange, but due to the extent of the various theoretical aspects studied here, we have chosen to concentrate only on the effect of the ω tuning in this study. Pictorial representations of the geometries and natural transition orbitals (NTOs)83 were generated using ChemCraft 1.8.84 The contributions of the electron densities of TQ and PC71BM to the NTOs were determined with the C-squared Population Analysis (C-SPA).85Furthermore, we checked the role of the basis set and surrounding medium in the electronic couplings. We employed, besides 6-31G*, also 6-31G** and 6-31+G* with TDDFT and the B3LYP functional, and 6-31G** with the PBE0, CAM-B3LYP, and OT-BNL functionals. As these calculations were too heavy for the studied complexes, we were unable to verify the effect of 6-31+G* with the LRC functionals and the effect of any larger basis sets. Nor did we consider the other types of basis sets (e.g. Dunning's) here. The influence of the medium was taken into account in the coupling and CT rate calculations by means of the conductor-like polarizable continuum model (CPCM)86,87 with a Switching/Gaussian (SWIG) implementation88 without geometry optimizations. Two different polarized media were considered: (i) a solvent with the static (εs) and dynamic (optical, εop) dielectric constants of 10.1210 and 2.4072 for 1,2-dichlorobenzene (1,2-DCB, at 293.15 K),89 respectively, and (ii) a blend, i.e. a film with εs and εop of 3.600090 and 3.2761, respectively. The εop of the blend was calculated77 by εop = n2 from the experimental refractive index (n) of the TQ–PC71BM blend (ca. 1.81 at 532 nm).91
For determining the electronic couplings, we used both the GMH22,23 and FCD24 schemes as implemented in Q-Chem 4.227 to calculate the adiabatic electronic (μadii) and transition dipole moments (μadij) (within the GMH scheme) and the charge differences (Δqadii and Δqadij, within the FCD scheme) for the GS and ten lowest singlet excited states. Among these 11 adiabatic states, the relevant states for the ED and CR processes, i.e. the GS [eD–eA], the LE state of TQ [eD*–eA], and the lowest CT state [CT1, eD+–eA−] (Fig. 1), were assigned on the basis of the μii and Δqii values and the NTOs (for more details see ‘Assignment of the states’ in the ESI†). The electronic couplings (eqn (S2)–(S11), ESI†), reorganization energies (eqn (S12)–(S18), ESI†), and Gibbs free energies (eqn (S19)–(S22), ESI†) for the ED and CR processes were calculated using the equations presented in the ESI.† The CT rates for the ED and CR processes were calculated with the Marcus theory (eqn (1)) at a temperature of 293.15 K. The 11-state FCD Hif values (eqn (S2)–(S4) in the ESI†) were used in the CT rate calculations.
Results and discussion
Length of the TQ oligomer and the polymeric limit
To select the TQ model that best represents the polymeric limit in the electronic coupling and CT rate calculations, we have studied the effect of the TQ length on the excited state properties of the isolated TQ models and the TQ–PC71BM complexes (Fig. S1, ESI†). The results apply to both the B3LYP and CAM-B3LYP functionals used in these calculations unless stated otherwise (see the ESI† for more detailed information). In general, both the T- and Q-series follow similar trends (Tables S1–S3, ESI†). The S1 energies of the isolated TQ oligomers with the corresponding lengths are almost equal (Table S1, ESI†): the singlet energies decrease only slightly, when the chain length increases, as expected.28,40,45 The placement of PC71BM, i.e. above either the central T or Q unit of the TQ oligomer, has a negligible or a very small effect on the excited state energies and oscillator strengths in the complexes of the T- and Q-series with the corresponding lengths (Tables S2 and S3, ESI†). In contrast, the energies of the main vertical excitation (Evert,main, i.e. the excitation having the largest oscillator strength) and the CT1 state decrease (the peaks red-shift), and the oscillator strengths of the peaks increase (except for the CT1 state with CAM-B3LYP), when the length, and, therefore, the contribution of the TQ oligomer, increases in the complex. In the complexes with the shortest TQs, only local excitations of PC71BM (LF) are observed and no LE or CT states are predicted (Tables S2 and S3, ESI†) within the ten lowest singlet excited states. The oligomers consisting of five units, i.e. 3T2Q and 3Q2T, are long enough for the LE and CT states to appear in the complexes, with LE being the main excitation. However, we have selected the complexes with the longest oligomers consisting of seven units, i.e. 3T4Q–PC71BM and 3Q4T–PC71BM, for the further calculations, as they have even more distinguishable LE and CT1 states with both B3LYP and CAM-B3LYP. Foremost, the B3LYP energies of the CT1 (ca. 1.6 eV) and LE states (ca. 1.9 eV) of 3T4Q–PC71BM and 3Q4T–PC71BM are closest to the experimental excited state energies (ECT = 1.4–1.5 eV92,93 and ELE = 1.97 eV taken from the absorption maximum in the experimental UV-Vis absorption spectrum of a TQ–PC71BM (3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) film93). For the aforementioned reasons, 3T4Q–PC71BM and 3Q4T–PC71BM are expected to be our best candidates for further modeling of the properties of the TQ–PC71BM complexes.
1) film93). For the aforementioned reasons, 3T4Q–PC71BM and 3Q4T–PC71BM are expected to be our best candidates for further modeling of the properties of the TQ–PC71BM complexes.
Effect of the functional on the excited state characteristics and electronic couplings
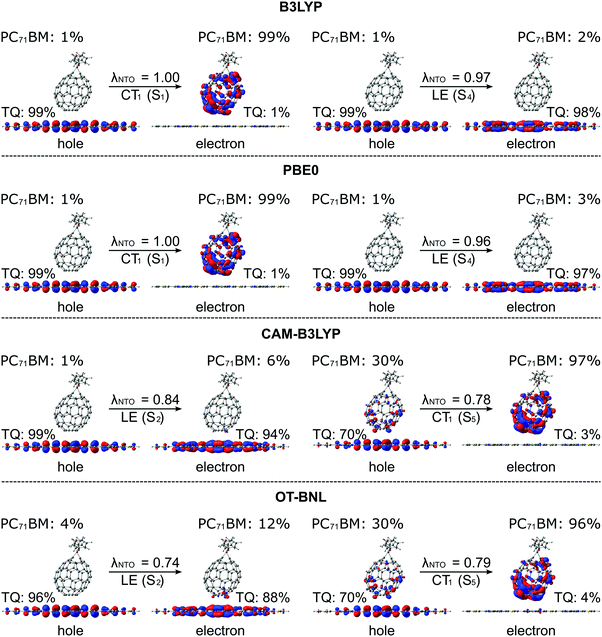
The functional has a clear effect on the excited state characteristics (i.e. excitation energies and nature of the state) of the studied complexes, 3T4Q–PC71BM and 3Q4T–PC71BM (Fig. 2b). Generally, when considering the 10 lowest adiabatic states of the complexes obtained with TDDFT (in vacuum), the excitation energies for the S1–S10 states increase in the order B3LYP (20% HF) < PBE0 (25% HF) < OT-BNL (with an OT ω of 0.17 Bohr−1, see Table S4, ESI†) < CAM-B3LYP (Table S5, ESI†). The global hybrids B3LYP and PBE0 predict the three lowest excited states as the CT states, whereas the fourth state is the intramolecular excitation of TQ, i.e. the LE state. This ordering of the CT1 and LE states, i.e. the CT1 state is lower in energy than the LE state, is consistent with the experimental results92,93 (see above). Above the CT1 and LE states in energy, the global hybrids predict local excitations of PC71BM, i.e. the LF states, and higher-energy CT states, whose nature (‘pure’ vs. partial CT) and number (between one and three) vary somewhat regarding the functional and position of PC71BM on TQ. With the LRC functionals, CAM-B3LYP and OT-BNL, the order of the CT1 and LE states is reverse, i.e. the CT1 state is higher in energy (the fifth or sixth state) than the LE state (the second excited state in the most cases), which is in contrast to the results given by the global hybrids and experiments.92,93 Additionally, the LRC functionals predict fewer CT states among the calculated 10 lowest adiabatic excited states than the global hybrids.These differences in the tendencies between the global hybrid and LRC functionals to predict the ordering of the states of polymer–fullerene complexes have been previously observed also for other systems by us66 and others.81 Moreover, Zheng et al. observed the same ordering of the CT1 and LE states also for pentacene–C60 complexes94 when using the OT LRC ωB97X-D and BNL functionals. Zheng et al. noticed that the OT values of ω are smaller when using PCM compared to those obtained in vacuum. Moreover, the energy of the CT1 state is affected by ω and decreases with decreasing ω, eventually locating at an energy lower than that of the LE state. However, in their recent paper, Kronik and Kümmel pointed out95 that including the PCM in the tuning of ω may lead to inconsistent results, as the PCM affects the total energies but not the DFT eigenvalues, resulting in the OT ω values that are notably smaller than those in vacuum. Thus, we have used the OT ω of OT-BNL obtained under vacuum also in the 1,2-DCB and blend environments explained later.
The functional has a notable effect on the nature of the adiabatic CT1 state of the studied complexes, whereas the nature of the LE state is very similar regardless of the functional. The global hybrid functionals predict almost negligible mixing of the local states with the adiabatic CT1 state, which is observed from the adiabatic Δqii values of the CT1 state (i.e. ΔqadCT1 of 1.9–2.0 in Tables 1 and 2) as they are already close to the ideal value of 2.28 This can be observed also from the NTOs of the two complexes (Fig. 3 and Fig. S2, ESI†), for which B3LYP and PBE0 predict a complete CT from TQ to PC71BM, as the hole NTO localizes totally on TQ and the electron NTO on PC71BM. Similarly, the adiabatic Δμii values of the CT1 state (i.e. ΔμadCT1 in Table 1) are rather large (29.9–31.4 D), although not close to the ideal dipole moments (41.1 D for 3T4Q–PC71BM and 41.3 D for 3Q4T–PC71BM, see the ESI†). The LRC functionals predict a partial CT character for the CT1 state (ΔμadCT1 of 11.3–16.6 D and ΔqadCT1 of 0.7–1.1, Tables 1 and 2), i.e. mixing of the local LF states with the CT state. When considering the corresponding NTOs, it can be seen that the hole NTO of the CT1 state localizes on both TQ and PC71BM and the electron NTO on PC71BM. In this case, 3T4Q–PC71BM has somewhat larger mixing of a LF component with the CT state and thus a smaller amount of CT compared to 3Q4T–PC71BM. For the LE state, the global hybrid and LRC functionals predict small adiabatic Δqii (i.e. ΔqadLE of 0.0–0.1 in Tables 1 and 2) and Δμii values (i.e. ΔμadLE of 0.1–1.7 D in Tables 1 and 2). The NTOs of the LE state of both complexes have the same shapes with all four functionals, i.e. both the hole and electron NTOs are delocalized along the TQ backbone, although the global hybrids yield slightly more delocalized descriptions compared to the LRC functionals. Additionally, OT-BNL predicts a small amount of CT mixed with the LE state. These differences between the global hybrid and (non-tuned and OT) LRC functionals in predicting the nature of the adiabatic states of polymer–fullerene complexes have been previously observed also by us66 and others.81
| Scheme | GMH | FCD | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Functional | N | ΔμadCT1 | ΔμdiabCT1 | ΔμadLE | ΔμdiabLE | ΔqadCT1 | ΔqdiabCT1 | ΔqadLE | ΔqdiabLE |
| a Relative to the GS. b Values calculated in vacuum. c Number of the states. | |||||||||
| B3LYP | 2 | 31.0 | 31.0 | 1.1 | 0.6 | 1.9 | 1.9 | 0.1 | 0.1 |
| 3 | 31.6 | 0.5 | 2.0 | 0.1 | |||||
| 4 | 31.4 | 0.5 | 2.0 | 0.1 | |||||
| 11 | 31.2 | 0.3 | 2.0 | 0.0 | |||||
| PBE0 | 2 | 29.9 | 30.0 | 1.4 | 0.7 | 1.9 | 1.9 | 0.1 | 0.1 |
| 3 | 30.6 | 0.7 | 2.0 | 0.1 | |||||
| 4 | 30.5 | 0.7 | 2.0 | 0.1 | |||||
| 11 | 30.2 | 0.2 | 2.0 | 0.0 | |||||
| CAM-B3LYP | 2 | 12.5 | 12.5 | 1.3 | 1.1 | 0.7 | 0.7 | 0.1 | 0.0 |
| 3 | 13.6 | 0.2 | 0.8 | 0.0 | |||||
| 4 | 19.4 | 0.1 | 1.5 | 0.0 | |||||
| 11 | 26.6 | 0.6 | 1.9 | 0.0 | |||||
| OT-BNL | 2 | 11.3 | 11.4 | 1.7 | 2.1 | 0.7 | 0.7 | 0.2 | 0.0 |
| 3 | 13.5 | 0.4 | 0.8 | 0.0 | |||||
| 4 | 20.1 | 0.5 | 1.6 | 0.0 | |||||
| 11 | 24.5 | 0.3 | 1.8 | 0.0 | |||||
| Scheme | GMH | FCD | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Functional | N | ΔμadCT1 | ΔμdiabCT1 | ΔμadLE | ΔμdiabLE | ΔqadCT1 | ΔqdiabCT1 | ΔqadLE | ΔqdiabLE |
| a Relative to the GS. b Values calculated in vacuum. c Number of states. | |||||||||
| B3LYP | 2 | 31.4 | 31.4 | 0.2 | 0.0 | 2.0 | 2.0 | 0.0 | 0.0 |
| 3 | 31.6 | 0.0 | 2.0 | 0.0 | |||||
| 4 | 31.6 | 0.0 | 2.0 | 0.0 | |||||
| 11 | 31.4 | 0.1 | 2.0 | 0.0 | |||||
| PBE0 | 2 | 30.5 | 30.5 | 0.1 | 0.2 | 2.0 | 2.0 | 0.0 | 0.0 |
| 3 | 30.7 | 0.1 | 2.0 | 0.0 | |||||
| 4 | 30.8 | 0.1 | 2.0 | 0.0 | |||||
| 11 | 30.7 | 0.3 | 2.0 | 0.0 | |||||
| CAM-B3LYP | 2 | 16.6 | 16.6 | 0.8 | 0.8 | 1.1 | 1.1 | 0.1 | 0.0 |
| 3 | 17.4 | 0.0 | 1.2 | 0.0 | |||||
| 4 | 21.8 | 0.0 | 1.6 | 0.0 | |||||
| 11 | 27.9 | 0.3 | 1.9 | 0.0 | |||||
| OT-BNL | 2 | 15.9 | 15.9 | 0.6 | 1.3 | 1.1 | 1.1 | 0.1 | 0.0 |
| 3 | 17.3 | 0.7 | 1.2 | 0.0 | |||||
| 4 | 21.6 | 0.7 | 1.7 | 0.0 | |||||
| 11 | 26.3 | 0.5 | 1.9 | 0.0 | |||||
The nature of the diabatic states of the complexes obtained with the 2–11-state GMH and FCD schemes is very similar to that of the adiabatic ones when employing the global hybrid functionals, whereas with the LRC functionals the diabatic states are more localized than the adiabatic states. With B3LYP and PBE0, the Δμdiab (GMH) and Δqdiab (FCD) values of the LE and CT1 states do not differ much from the adiabatic values (Tables 1 and 2). This is most probably because the mixing of the states is small already for the adiabatic states, as mentioned above. The ΔqdiabCT1 values predicted by the 2–11-state FCD schemes with the global hybrids mainly reach the ideal value of 2, indicating a complete CT from TQ to PC71BM. However, the ΔμdiabCT1 values calculated with the 2–11-state GMH schemes and the global hybrids are still smaller than the ideal dipole moments (41.1 D for 3T4Q–PC71BM and 41.3 D for 3Q4T–PC71BM). This might indicate that the number of states used here is not enough for generating more localized diabatic states in the GMH schemes and thus for reaching the ideal dipole moments. When employing the LRC functionals in the 2–11-state FCD schemes, the diabatization effectively removes the local components that are present in the CT1 state, yielding ΔqdiabCT1 values of 1.8–1.9, which are quite close to the ideal one. Similarly, the ΔμdiabCT1 values, predicted with the 3–11-state GMH schemes and the LRC functionals, are now clearly larger than the adiabatic ones (Tables 1 and 2), although still not reaching the ideal dipole moments either. Thus, diabatization has a larger effect on the localization of the CT1 state with the (non-tuned and OT) LRC functionals compared to the global hybrids.
In most cases, all functionals predict that the 2–11-state CR electronic couplings calculated in vacuum are larger than the corresponding ED couplings (Tables S14 and S15, ESI†). However, when PC71BM is above quinoxaline (the A unit) of TQ (3Q4T–PC71BM), the LRC functionals predict mainly the opposite, i.e. larger ED couplings than the CR couplings with both the GMH and FCD schemes (except for the 11-state GMH scheme). The global hybrid functionals yield quite similar couplings (Fig. 4 and Fig. S3, ESI†), whereas the LRC functionals predict somewhat larger values (Fig. 5 and Fig. S4, ESI†). Overall, the ED couplings predicted with B3LYP and PBE0 for 3T4Q–PC71BM and 3Q4T–PC71BM are ca. 36–47 meV and 21–31 meV, respectively, whereas the CR couplings are ca. 43–56 meV and 25–34 meV, respectively. The ED couplings calculated with CAM-B3LYP and OT-BNL for 3T4Q–PC71BM and 3Q4T–PC71BM are ca. 49–83 meV and 33–56 meV, respectively, and the CR couplings are ca. 74–142 meV and 3–92 meV, respectively. In general, the couplings increase in the order of B3LYP (20% HF) < PBE0 (25% HF) < CAM-B3LYP ≤ OT-BNL. Sini et al. also noticed that the coupling values increase with the increasing amount of HF exchange48 in their study of a tetrathiafulvalene–tetracyanoquinodimethane complex with the direct coupling method.13 Even though we have not calculated the amounts of effective HF exchange48 in CAM-B3LYP and OT-BNL for our complexes, as this would require a larger set of functionals with the known amounts of HF exchange, we expect that the electronic coupling value increases with the increasing amount of effective HF exchange in the functional.
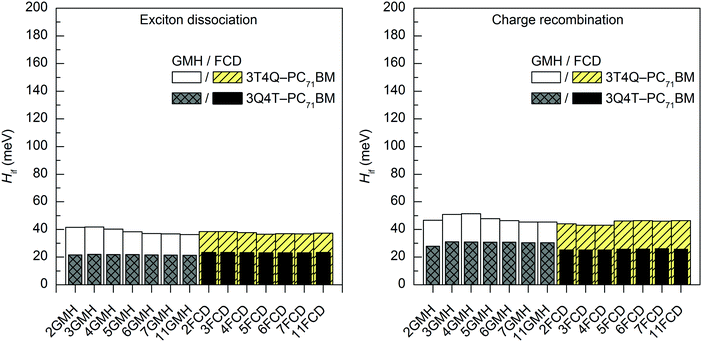 | ||
| Fig. 4 Electronic coupling values of the studied TQ–PC71BM complexes calculated with TDDFT at the B3LYP/6-31G* level of theory using the GMH and FCD schemes with different numbers of states (2–11). | ||
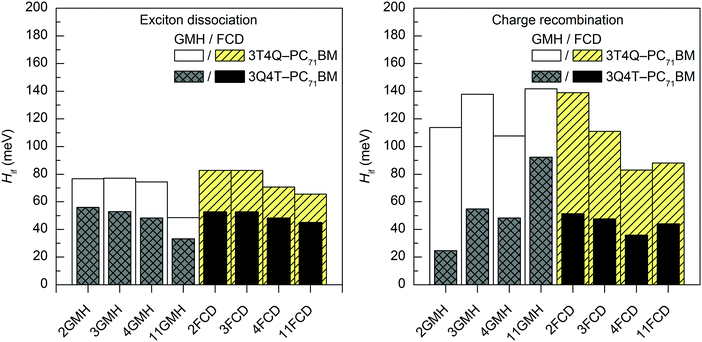 | ||
| Fig. 5 Electronic coupling values of the studied TQ–PC71BM complexes calculated with TDDFT at the OT-BNL/6-31G* level of theory using the GMH and FCD schemes with different numbers of states (2–11). | ||
To summarize, the functional has a notable effect on the excited state characteristics, i.e. the vertical excitation energies and nature of the adiabatic and diabatic states, and therefore the electronic couplings. With the global hybrid functionals, both the adiabatic and diabatic CT1 states have a similar, localized nature, i.e. a complete CT from TQ to PC71BM. With the LRC functionals, local components mixed with the adiabatic CT1 state are effectively removed by diabatization, especially with the FCD scheme. The couplings are larger with the LRC functionals than with the global hybrids.
Effect of the number of states on the electronic coupling values
The evolutions of the ED and CR electronic couplings of the selected complexes (in vacuum) with different numbers of states indicate that the functional has a clear effect on the relationship between the coupling and the number of states (Fig. 4 and Fig. S3, ESI,† for the global hybrids, and Fig. 5 and Fig. S4, ESI,† for the LRC functionals). The corresponding numerical values are given in Tables S14 and S15, ESI.† With the global hybrid functionals, the number of states does not seem to have a very strong effect on the coupling values, as increasing the number of states decreases both the ED and CR couplings only slightly (by 0–5 meV) and they are rather constant with both the GMH and FCD schemes. This is most probably because the global hybrids predict small or negligible mixing of the adiabatic states for the studied TQ–PC71BM complexes (see ‘Effect of the functional on the excited state characteristics and electronic couplings’ above), and the diabatization does not change the nature of the states much even with the increased number of states. This can be observed from the ΔμdiabCT1 and ΔqdiabCT1 values (Tables 1 and 2), as they remain rather unchanged with an increasing number of states and are already close or equal to the ideal ones of 41.1 D and 41.3 D (for 3T4Q–PC71BM and 3Q4T–PC71BM, respectively) and of 2, respectively. Additionally, the GMH and FCD schemes yield quite similar coupling values when using the global hybrids, indicating that both schemes yield similar diabatic states.28 Thus, with the global hybrids, the 2-state schemes seem to be sufficient for calculating the electronic couplings.With the LRC-functionals (Fig. 5 and Fig. S4, ESI†), the electronic couplings of the studied complexes change more significantly with the number of states compared to the global hybrids. The GMH and FCD ED couplings predicted with the LRC functionals decrease with the increasing number of states, although in some cases the 3-state results are slightly higher than the 2-state results (Tables S14 and S15, ESI†). The 2–4-state GMH ED couplings are rather similar, whereas the 11-state values are notably smaller. With the FCD scheme, the ED couplings decrease in a more constant way. The GMH and FCD CR couplings oscillate somewhat with the increasing number of states. The GMH scheme predicts larger CR couplings with 11 states than with 2–4 states, whereas the FCD CR couplings mainly decrease when the number of states increases. Here, the tuning of ω does not seem to have a strong effect on the overall trends in the couplings, as both CAM-B3LYP and OT-BNL predict similar changes.
The number of states used here is restricted by the size of the systems and the computational time limit and therefore we are not able to judge whether the electronic couplings obtained with the LRC functionals have converged to certain values28 already with 11 states or whether more states would improve the results. However, both the ΔμdiabCT1 and ΔqdiabCT1 values increase with the increasing number of states (Tables 1 and 2). Moreover, even though the 11-state ΔμdiabCT1 values do not reach the ideal dipole moments of 41.1 D and 41.3 D (for 3T4Q–PC71BM and 3Q4T–PC71BM, respectively), they have improved compared to the 2–4-state values. Furthermore, the ΔqdiabCT1 values are almost equal to the ideal value of 2. Thus, the 11-state GMH and FCD schemes can be expected to yield better descriptions of the diabatic states and the couplings than the 2–4 states, and for that reason, we have employed the 11-state GMH and FCD schemes in the further electronic coupling calculations.
Effect of the TD method on the excited state characteristics and the electronic couplings
Generally, the TD method does not seem to have any effect on the vertical excitation energies of the studied TQ–PC71BM complexes, as both TDDFT and TDA yield almost identical values (in vacuum, Tables S5 and S6, ESI†). Next to equal excitation energies with both TD methods have also been observed for both small molecules80 and large interfacial complexes (pentacene–C6094 and copolymer–fullerene96) in previous studies. However, here we observe that the number of CT states and the ordering of the states are in some cases slightly different with TDDFT and TDA, especially with the LRC functionals, which seem to have an effect on the GMH electronic couplings (see below).The nature of the adiabatic LE and CT1 states does not change significantly with the TD method when employed together with the global hybrid functionals, as TDDFT and TDA yield similar Δμadii and Δqadii values in most cases (Tables 1 and 2 and Table S13, ESI†). With the LRC functionals, TDA yields slightly larger (0.2–0.5) ΔqadCT1 values and somewhat larger (2.8–4.5) ΔμadCT1 values than TDDFT; that is, the mixing of the LF component with the adiabatic CT1 state is not as strong with TDA as with TDDFT. However, diabatization of the adiabatic states with the 11-state GMH and FCD schemes results mostly in similar Δμdiab and Δqdiab values with both TDDFT and TDA for diabatic LE and CT1 states.
Both TD methods yield very similar 11-state electronic couplings with the global hybrid functionals, with the difference between them being only 0–4 meV (Fig. 6 and 7 and Tables S14–S16, ESI†). In addition, the 11-state FCD couplings calculated with the LRC functionals are only moderately different (by 0–12 meV) when using either TDDFT or TDA. However, the 11-state GMH couplings obtained with TDDFT and TDA and the LRC functionals differ more, namely by 2–49 meV, with TDA predicting larger couplings in most cases. The largest differences between the two TD methods are in the GMH CR couplings, which is most probably due to the differences in the Δμad values other than those of the CT1 and LE states. The tuning of ω does not seem to have a clear effect, as overall both the non-tuned CAM-B3LYP and OT-BNL functionals predict the same trends. Overall, TDA predicts the same trends as TDDFT: mostly larger CR couplings than the ED couplings (and vice versa for some 11-state FCD results for 3Q4T–PC71BM with the LRC functionals), larger ED and CR couplings for 3T4Q–PC71BM than for 3Q4T–PC71BM, and larger ED and CR couplings with the LRC functionals than with the global hybrids.
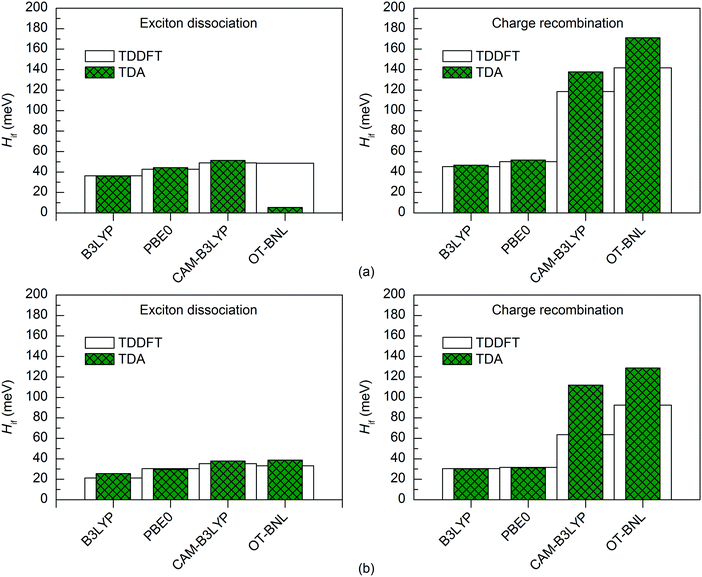 | ||
| Fig. 6 Electronic couplings of (a) 3T4Q–PC71BM and (b) 3Q4T–PC71BM calculated with the 11-state GMH scheme using TDDFT and TDA with different functionals and the 6-31G* basis set. | ||
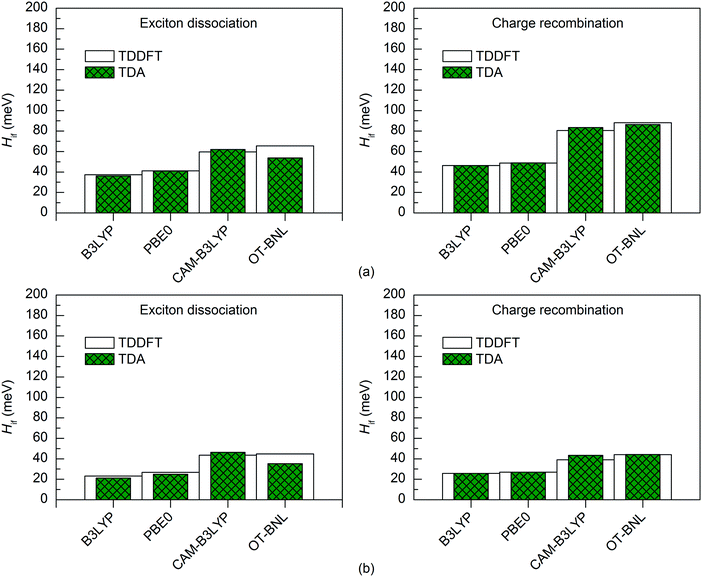 | ||
| Fig. 7 Electronic couplings of (a) 3T4Q–PC71BM and (b) 3Q4T–PC71BM calculated with the 11-state FCD scheme using TDDFT and TDA with different functionals and the 6-31G* basis set. | ||
To conclude, for the studied TQ–PC71BM complexes, TDA yields consistent results with TDDFT when using the global hybrids. Thus, as TDA is computationally less costly,97 it is a good alternative to TDDFT when combined with the global hybrids. However, when using the LRC functionals, these two TD methods might end up with rather different GMH electronic couplings. Thus, when using TDA together with the LRC functionals, the FCD scheme seems to be a more reliable choice, as the Δq values are generally not affected as much by the choice of TD method as the Δμ values.
Effect of the basis set
The basis set has a minimal effect on the exited state energies of the studied complexes: the vertical excitation energies are almost the same with both the 6-31G* (Table S5, ESI†) and 6-31G** (Table S7, ESI†) basis sets. With B3LYP, the 6-31+G* basis set yields only slightly (0.0–0.2 eV, Table S8, ESI†) smaller excitation energies for 3T4Q–PC71BM than the two smaller basis sets. As this calculation was computationally already very demanding, we did not carry out the calculation for 3Q4T–PC71BM at the same level of theory.The basis set does not affect the nature of the adiabatic CT1 and LE states much and their Δμadii and Δqadii values calculated with the 11-state GMH and FCD schemes are mostly the same with 6-31G* (Tables 1 and 2) and 6-31G** (Table S12, ESI†). The only exception is ΔμadCT1 of 3Q4T–PC71BM calculated with CAM-B3LYP, which is 0.7 D smaller with 6-31G** (15.9 D) than with 6-31G* (16.6 D), indicating a larger amount of the local component in the CT1 state. The 6-31+G* basis set yields smaller ΔqadCT1 of 1.6 with B3LYP than 6-31G* or 6-31G** (1.9 for both basis sets, see Tables 1 and 2 and Table S12, ESI†). The diabatic CT1 and LE states determined with the 11-state GMH and FCD schemes have almost the same Δμdiab and Δqdiab values with both 6-31G* (Tables 1 and 2) and 6-31G** (Table S12, ESI†), which indicates that both basis sets yield similar descriptions of these states. Interestingly, the ΔqdiabCT1 value predicted with 6-31+G* and B3LYP does not change from the adiabatic value of 1.6 (Table S12, ESI†), indicating that in this case the diabatization does not remove the mixing of the local states with the CT1 state.
The basis set has only a small effect on the 11-state electronic couplings when using the global hybrid functionals: the couplings calculated with the 6-31G* and 6-31G** basis sets (Fig. 8 and 9 and Tables S14, S15, S17, and S18, ESI†) differ by 0–5 meV. This is consistent with the study of Voityuk and Rösch,24 in which they have presented their FCD scheme and observed that inclusion of polarization functions on hydrogen does not influence the 2-state GMH and FCD couplings of the small DNA fragments, when using HF. Here, moreover, the couplings predicted with the 6-31+G* basis set and B3LYP for 3T4Q–PC71BM are only 1–2 meV larger than with 6-31G* and 6-31G** (Fig. 9 and Table S17, ESI†). This is also in line with the study of Voityuk and Rösch,24 where the polarization functions on hydrogen and diffusion functions (on all atoms) (6-31G* vs. 6-31+G*) have been reported to have only a small (5%) effect on the couplings. Here, the smaller ΔqdiabCT1 value obtained with 6-31+G* (see above) does not affect the couplings, which may be due to the compensation of other states included in the calculations. With the LRC functionals, the differences in the 11-state ED couplings predicted with two basis sets together with both the GMH and FCD schemes are also rather small, i.e. 0–9 meV. However, the 11-state GMH CR couplings predicted by the LRC functionals differ more, as the 6-31G** basis set yields somewhat larger (19–47 meV) couplings than 6-31G*. Generally, the 6-31G** basis set yields larger couplings in all cases, except for some PBE0 and OT-BNL values of 3Q4T–PC71BM. Thus, the size of the basis set can have an effect on the dipole moments and the GMH couplings when using the LRC functionals as opposite to the global hybrids. Similar to the results obtained with different numbers of states and different TD methods, the tuning of ω does not have a notable effect on the results and both CAM-B3LYP and OT-BNL predict the same trends.
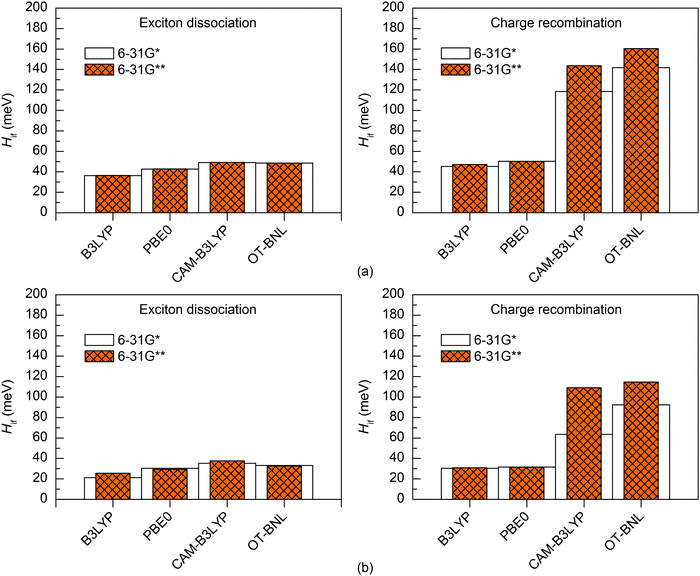 | ||
| Fig. 8 Electronic couplings of (a) 3T4Q–PC71BM and (b) 3Q4T–PC71BM calculated with the 11-state GMH scheme using TDDFT with different functionals and basis sets. | ||
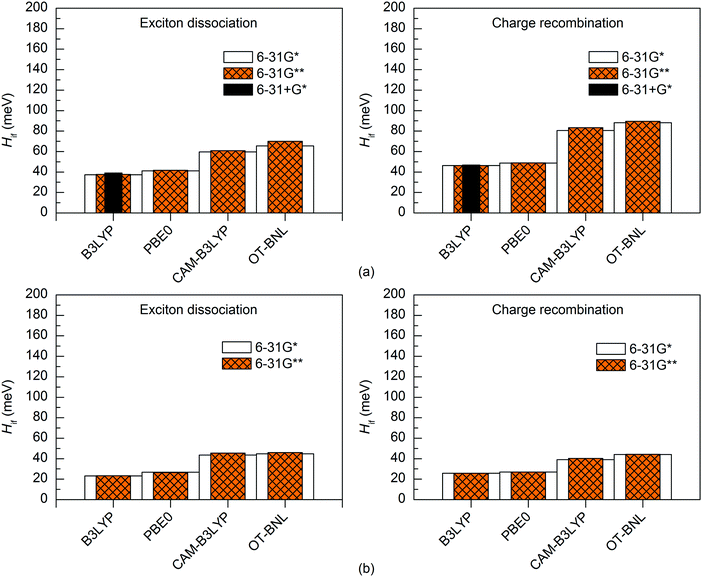 | ||
| Fig. 9 Electronic couplings of (a) 3T4Q–PC71BM and (b) 3Q4T–PC71BM calculated with the 11-state FCD scheme using TDDFT with different functionals and basis sets. | ||
Effect of the surrounding medium
The excitation energies of the selected complexes are practically the same in different environments differing only by 0.0–0.1 eV (Tables S5, S9, and S10, ESI†). Thus, the polarity of the medium does not affect the adiabatic energies of the LE and CT1 states in most cases. However, with the LRC functionals, the order of the excited states is somewhat different in 1,2-DCB and the blend from that under vacuum and the CT1 state is at a higher energy (the sixth or seventh state). Zheng et al. also observed slightly higher CT1 state energies for the pentacene–C60 complex with the OT ωB97X-D functional when using PCM compared to vacuum.94The nature of the adiabatic CT1 and LE states are generally quite similar in different media (Table S11, ESI†). However, in some cases the portion of the LF component in the CT1 state increases slightly in 1,2-DCB and the blend than under vacuum; namely, all functionals predict somewhat smaller ΔμadCT1 and the LRC functionals yield smaller ΔqadCT1. For the LE state, the ΔμadLE and ΔqadLE values are mainly the same or smaller in 1,2-DCB and the blend than under vacuum, but for 3T4Q–PC71BM the global hybrids predict larger values in 1,2-DCB and the blend. When comparing the diabatic states of the studied complexes obtained with the 11-state electronic coupling schemes in different media, the nature of LE states remains unchanged, and the ΔμdiabLE and ΔqdiabLE values are close to zero in all the media. Moreover, the nature of the CT1 state remains mainly unaffected by the medium polarity, although the ΔμdiabCT1 values of both complexes and the ΔqdiabCT1 values of 3T4Q–PC71BM are slightly smaller in 1,2-DCB and the blend than under vacuum. This indicates that, while the diabatic states are quite similar in the different media, the diabatization does not completely remove the local component present in the adiabatic CT1 state in 1,2-DCB and the blend and thus the amount of CT is slightly reduced compared to that under vacuum.
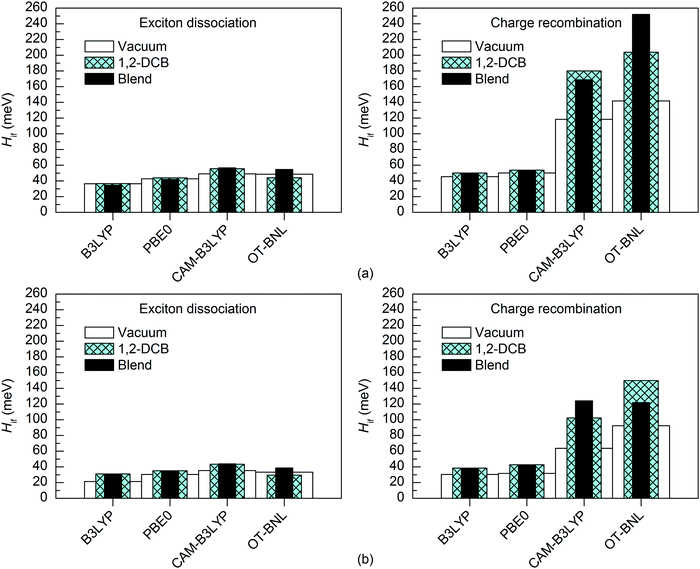
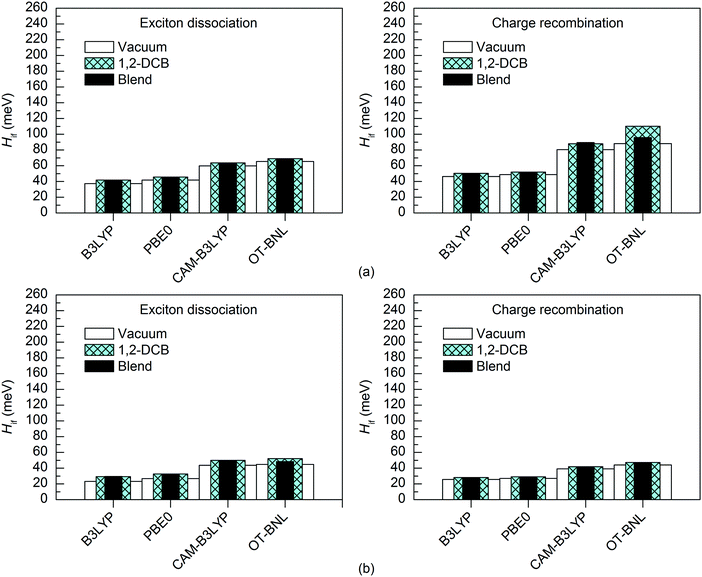
The surrounding medium has only a small effect on the 11-state electronic couplings (Fig. 10 and 11 and Tables S14, S15, S19, and S20, ESI†) of the complexes when using the global hybrid functionals. Moreover, the GMH and FCD results are very similar. The couplings increase only slightly (by ca. 0–11 meV) in the order of vacuum < blend < 1,2-DCB, i.e. with the increasing polarity of the medium (εs of 3.6 for the TQ–PC71BM blend and 10.1210 for 1,2-DCB) in most cases. A similar trend has been observed by Lemaur et al. with the GMH couplings of a phthalocyanine–perylene bisimide (Pc–PTCDI) complex.6 With the LRC functionals, the effect of the environment on the 11-state couplings is generally also moderate (0–22 meV), but the GMH CR couplings differ more significantly, especially for 3T4Q–PC71BM (by ca. 11–110 meV). In this case, the GMH CR couplings predicted with OT-BNL seem to be most affected by the choice of medium. Overall, the electronic couplings calculated in the different media with the LRC functionals do not follow any clear trend, although the couplings are in most cases smaller under vacuum than in 1,2-DCB or the blend. In addition, similar to that under vacuum, the 11-state FCD couplings differ somewhat from the GMH couplings in 1,2-DCB or the blend.
Effect of the placement of PC71BM on TQ
The placement of PC71BM on TQ (Fig. 2b) has no effect on the vertical excitation energies and they are practically the same for both 3T4Q–PC71BM and 3Q4T–PC71BM (Tables S5–S7, S9, and S10, ESI†) regardless of the calculation method or surrounding medium. We have also observed negligible changes in the excitation energies for poly(benzodithiophene-co-quinoxaline)–fullerene complexes, when the orientation of PC71BM is altered.66 As the adiabatic and diabatic ΔμCT1 and ΔqCT1 values are somewhat larger for 3Q4T–PC71BM (Tables 1 and 2 and Tables S11–S13, ESI†), it has smaller mixing of the local LF component to the CT1 state compared to 3T4Q–PC71BM, indicating more efficient CT from TQ to PC71BM.In contrast to the vertical excitation energies, the electronic couplings are clearly affected by the placement of PC71BM, as can be expected based on the previous studies of the local eD–eA interfaces of photoactive materials.30,31,75,76,98 The ED couplings of 3T4Q–PC71BM and 3Q4T–PC71BM are 36–83 meV and 21–52 meV, respectively, whereas the CR couplings are 45–252 meV and 25–150 meV, respectively (Tables S14–S20, ESI†). Thus, the ED and CR couplings are ca. 4–30 meV and 12–132 meV stronger, respectively, when PC71BM is located on the thiophene donor unit of TQ (3T4Q–PC71BM) than when PC71BM is on the quinoxaline acceptor unit of TQ (3Q4T–PC71BM). Based on the coupling values, we anticipate faster ED and CR rates for 3T4Q–PC71BM than for 3Q4T–PC71BM, which is also observed from the calculated CT rates of the complexes in 1,2-DCB (see ‘Calculating charge transfer rates in 1,2-DCB and the blend’ below). For 3T4Q–PC71BM, the CR couplings are larger than the ED couplings, in all cases. For 3Q4T–PC71BM, the opposite, i.e. larger ED couplings than the CR couplings, is predicted when using the 11-state FCD scheme (and 2–4-state GMH and FCD schemes in some cases) in conjunction with the LRC functionals.
A similar effect of the relative placement on the ED and CR electronic couplings was observed by Wang et al. when examining 1473 complexes of polybenzo[1,2-b:4,5-b′]dithiophene–thieno[3,4-c]pyrrole-4,6-dione and PC61BM extracted from the molecular dynamics simulations.99 They predicted larger ED and CR coupling values when PC61BM was closer to the D unit than the A unit of the copolymer, although they employed a different coupling scheme (fragment orbital approach) and functional (ωB97X-D). In their later study of a benzothiadiazole-quaterthiophene-based copolymer with PC71BM, Wang et al. also observed39 larger CR couplings with the 2-state FCD and the OT ωB97X-D functional when PC71BM was on top of the D unit than on top of the A unit of the copolymer. Furthermore, Wang et al. also predicted larger couplings for the CR process than for the ED process.99 Likewise, similar results have been obtained for the PTB7-Th–PC71BM complex with the 2-state GMH37 and for the α-sexithienyl–C60 complex98 with a diabatic-state approach.75,100 However, no clear conclusion can be drawn merely from the above findings, as opposite results have been observed, as well.76,98
The differences between the electronic couplings of the two complexes are quite similar despite the calculation method (i.e. coupling scheme, functional, number of states, basis set, and surrounding medium), especially with the global hybrid functionals (ca. 4–28 meV). However, the LRC functionals predict more notable differences (7–132 meV) between the electronic couplings of 3T4Q–PC71BM and 3Q4T–PC71BM, especially for the CR couplings (33–132 meV).
Effect of the coupling scheme on the electronic couplings
The choice of coupling scheme has either a small or a significant effect on the coupling values of the two complexes depending on the calculation method (i.e. functional, basis set, and surrounding medium) used. With the global hybrids, the 2–11-state GMH and FCD electronic couplings are quite similar despite the basis set or surrounding medium and the GMH values are only slightly (0–17 meV) larger in most cases. Moreover, both schemes predict mainly larger CR couplings compared to the ED couplings when using the global hybrids (Tables S14 and S15, ESI†), except for some FCD values of 3Q4T–PC71BM calculated with PBE0 (Table S15, ESI†). With the LRC functionals, the differences (0–157 meV) between the GMH and FCD couplings are more significant compared to the global hybrids, especially in the case of the CR values. Moreover, large differences between the GMH and FCD couplings are predicted with the 6-31G** basis set (60–71 meV, in vacuum) and with the 6-31G* basis set in the 1,2-DCB or blend (61–156 meV) media. Both schemes predict larger CR couplings than ED couplings for 3T4Q–PC71BM in all cases and for 3Q4T–PC71BM in some cases (Tables S14 and S15, ESI†). For 3Q4T–PC71BM, the 2–11-state FCD and 2–4-state GMH schemes in conjunction with the LRC functionals predict mainly larger ED couplings than the CR couplings.Thus, the GMH scheme and more precisely the Δμ values employed in the GMH scheme seem to be more sensitive to the choice of functional, basis set, and surrounding medium than the FCD scheme. These findings complement the earlier studies, which have pointed out that the Δq values in the FCD scheme are less sensitive to the mixing of the local excited and CT states, while the Δμ values in the GMH scheme are more affected by the mixing of the states.16,45 The GMH electronic couplings have been observed to improve when employing a solvent model (e.g. the image charge approximation, ICA), as it can lower the energy of the CT1 state and thus decouple it from the undesired high-lying local excitations.16,47 However, this is not always the case, as can be seen from our results above, where the CT1 state energies and the couplings increase somewhat in 1,2-DCB compared to vacuum. Lee et al. also observed relatively larger GMH couplings for a series of heptacyclo[6.6.0.0.2,60.3,1301.4,1105,9.010,14]-tetradecane-linked D–A molecules than the FCD values with and without the ICA solvent model, when the couplings should be small due to symmetry.45 Increasing the number of states has also resulted in improved GMH and FCD couplings.28 As stated above, in this study, both coupling schemes yield very similar values despite the number of states when using the global hybrid functionals (Fig. 4 and 5 and Fig. S3 and S4, ESI†). However, with the LRC functionals, the number of states affects the couplings more, especially the CR values. With the GMH scheme, the CR values oscillate with the increasing number of states, whereas with the FCD scheme, they decrease. Overall, the FCD scheme seems to produce couplings that are more constant and, when combined with the multi-state treatment, may be more suitable than GMH for calculating the couplings for the polymer–fullerene systems. Thus, we will employ the 11-state FCD couplings for calculating the ED and CR rates.
Calculating charge transfer rates in 1,2-DCB and the blend
Finally, we have estimated the CT rates for the ED and CR processes at the two TQ–PC71BM interfaces modelled by complexes using the 11-state FCD electronic couplings. The couplings and other parameters required for calculating the rates in both 1,2-DCB and the blend are listed in Tables 3 and 4, respectively. Generally, the inner reorganization energies (λi) of both complexes are smaller for the ED process than for the CR process. This can be attributed to the larger geometric changes (Fig. S5, ESI†) taking place in TQ during CR, i.e. when going from the cation geometry to that of the neutral GS (eD+ → eD), than during ED, i.e. when going from the S1 geometry to that of the cation (eD* → eD+). In other words, the geometries of the cation and the S1 states of TQ are closer to each other than those of the cation and GS. The contributions of the geometric changes of PC71BM to λi are the same during the ED and CR, i.e. when going from the GS to the radical anion and vice versa, respectively. The polarity of the medium has only a minimal effect on the λi values, which are basically the same in 1,2-DCB and the blend. The global hybrids yield somewhat smaller λi values than the LRC functionals in the increasing order of B3LYP < PBE0 < OT-BNL < CAM-B3LYP. The position of PC71BM on TQ does not affect λi much and the values are almost the same for the two complexes, λi of 3Q4T–PC71BM being slightly larger than that of 3T4Q–PC71BM, indicating slightly larger geometric changes for 3Q4T. As the accurate prediction of the outer reorganization energy (λs) is a rather challenging task and it is highly affected by the uncertainty of the calculated parameters,7,77 we have chosen to keep it as an adjusted parameter in the range of 0.10–0.75 eV. The selection of this range is based on the values of λs (0.11–0.50 eV) used in the previous theoretical studies of other copolymer–fullerene systems.33,38,77,81 We have also considered the λs values of 0.5–0.75 eV, because in some cases the CR rates start to compete with the ED rates in this region (see below). This region is also in line with the experimental λ of 0.22–0.8 eV101–103 obtained for the blends of different copolymers and fullerene derivatives.| Functional | Complex | H if,ED (meV) | H if,CR (meV) | λ i,ED (eV) | λ i,CR (eV) | ΔGED (eV) | ΔGCR (eV) | ΔECoul,ED (eV) | ΔECoul,CR (eV) |
|---|---|---|---|---|---|---|---|---|---|
| a Electronic couplings obtained with the 11-state FCD scheme. | |||||||||
| B3LYP | 3T4Q–PC71BM | 41.9 | 50.3 | 0.1298 | 0.2039 | −0.1373 | −1.6166 | −0.1373 | 0.1376 |
| 3Q4T–PC71BM | 29.2 | 28.0 | 0.1308 | 0.2058 | −0.1501 | −1.5981 | −0.1374 | 0.1372 | |
| PBE0 | 3T4Q–PC71BM | 48.8 | 52.0 | 0.1377 | 0.2180 | −0.2673 | −1.5951 | −0.1370 | 0.1372 |
| 3Q4T–PC71BM | 32.5 | 29.0 | 0.1386 | 0.2198 | −0.2788 | −1.5773 | −0.1371 | 0.1368 | |
| CAM-B3LYP | 3T4Q–PC71BM | 63.5 | 87.9 | 0.1882 | 0.3014 | −0.3179 | −1.9903 | −0.1421 | 0.1422 |
| 3Q4T–PC71BM | 49.9 | 41.7 | 0.1890 | 0.3035 | −0.3139 | −1.9927 | −0.1421 | 0.1419 | |
| OT-BNL | 3T4Q–PC71BM | 68.9 | 110.2 | 0.1728 | 0.2643 | −0.2438 | −1.7420 | −0.1413 | 0.1415 |
| 3Q4T–PC71BM | 52.2 | 47.1 | 0.1737 | 0.2660 | −0.2479 | −1.7322 | −0.1419 | 0.1416 | |
| Functional | Complex | H if,ED (meV) | H if,CR (meV) | λ i,ED (eV) | λ i,CR (eV) | ΔECoul,ED (eV) | ΔECoul,CR (eV) | ||
|---|---|---|---|---|---|---|---|---|---|
| a Electronic couplings obtained with the 11-state FCD scheme. | |||||||||
| B3LYP | 3T4Q–PC71BM | 41.8 | 50.2 | 0.1423 | 0.2160 | 0.0274 | −1.7451 | −0.3778 | 0.3786 |
| 3Q4T–PC71BM | 29.4 | 27.7 | 0.1434 | 0.2181 | −0.0813 | −1.6443 | −0.4755 | 0.4618 | |
| PBE0 | 3T4Q–PC71BM | 45.5 | 51.9 | 0.1509 | 0.2309 | −0.1006 | −1.7250 | −0.3770 | 0.3776 |
| 3Q4T–PC71BM | 32.6 | 28.9 | 0.1519 | 0.2329 | −0.2202 | −1.6540 | −0.4871 | 0.4322 | |
| CAM-B3LYP | 3T4Q–PC71BM | 63.1 | 89.5 | 0.2067 | 0.3215 | −0.1539 | −2.1203 | −0.3903 | 0.3907 |
| 3Q4T–PC71BM | 49.4 | 41.6 | 0.2077 | 0.3232 | −0.2423 | −2.0818 | −0.4856 | 0.4333 | |
| OT-BNL | 3T4Q–PC71BM | 69.1 | 95.8 | 0.1871 | 0.2798 | −0.0803 | −1.8723 | −0.3884 | 0.3889 |
| 3Q4T–PC71BM | 48.3 | 47.3 | 0.1881 | 0.2814 | −0.2109 | −1.8090 | −0.5179 | 0.4447 | |
All the functionals predict spontaneous ED and CR processes (ΔG° < 0) for the studied complexes, in other words, favorable processes in both media (Tables 3 and 4). Only the ED process of 3T4Q–PC71BM predicted by B3LYP in the blend is not spontaneous. The experimental estimation for 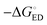 of the TQ–PC71BM blend is 0.1–0.3 eV, which is obtained104 as the difference between the optical bandgap of TQ (1.6–1.7 eV70,93) and the CT state energy (1.4–1.5 eV92,93). Thus, the calculated
of the TQ–PC71BM blend is 0.1–0.3 eV, which is obtained104 as the difference between the optical bandgap of TQ (1.6–1.7 eV70,93) and the CT state energy (1.4–1.5 eV92,93). Thus, the calculated 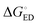 values are consistent with the experimental ones. For the selected range of λs (0.10–0.75 eV), all the functionals predict that ED occurs in the Marcus normal region
values are consistent with the experimental ones. For the selected range of λs (0.10–0.75 eV), all the functionals predict that ED occurs in the Marcus normal region 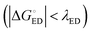 in the blend. In 1,2-DCB, B3LYP and OT-BNL predict that ED takes place in the normal region for the selected range of λs, whereas PBE0 and CAM-B3LYP predict that ED occurs in the normal region when λs ≥ 0.14. The CR process occurs in the inverted region of Marcus
in the blend. In 1,2-DCB, B3LYP and OT-BNL predict that ED takes place in the normal region for the selected range of λs, whereas PBE0 and CAM-B3LYP predict that ED occurs in the normal region when λs ≥ 0.14. The CR process occurs in the inverted region of Marcus 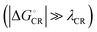 in all cases, which leads to slower CR rates than ED rates (see below).9 The ED and CR processes of another photovoltaic system, Pc–PTCDI,6 have also been observed to occur in the Marcus normal and inverted regions, respectively. The sum of ΔGED and ΔGCR is almost constant, regardless of the medium, and increases in the order of B3LYP (ca. 1.7–1.8 eV) < PBE0 (1.8–1.9 eV) < OT-BNL (2.0 eV) < CAM-B3LYP (2.3 eV). The constant sum indicates that the polarity of the medium does not have a significant effect on the separation between the GS and LE states.6 As the other energies, except that of eD* (the optimized S1 geometry of TQ), are canceled out from the sums of ΔGED and ΔGCR, the energies of eD* are consistent with the energies of the LE state (Tables S9 and S10, ESI,† S4 for the global hybrids and S2 for the LRC functionals). When the polarity, εs, increases (from 3.6 of the TQ–PC71BM blend to 10.1210 of 1,2-DCB),
in all cases, which leads to slower CR rates than ED rates (see below).9 The ED and CR processes of another photovoltaic system, Pc–PTCDI,6 have also been observed to occur in the Marcus normal and inverted regions, respectively. The sum of ΔGED and ΔGCR is almost constant, regardless of the medium, and increases in the order of B3LYP (ca. 1.7–1.8 eV) < PBE0 (1.8–1.9 eV) < OT-BNL (2.0 eV) < CAM-B3LYP (2.3 eV). The constant sum indicates that the polarity of the medium does not have a significant effect on the separation between the GS and LE states.6 As the other energies, except that of eD* (the optimized S1 geometry of TQ), are canceled out from the sums of ΔGED and ΔGCR, the energies of eD* are consistent with the energies of the LE state (Tables S9 and S10, ESI,† S4 for the global hybrids and S2 for the LRC functionals). When the polarity, εs, increases (from 3.6 of the TQ–PC71BM blend to 10.1210 of 1,2-DCB), 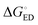 and ΔECoul,CR decrease, i.e. become more negative, whereas
and ΔECoul,CR decrease, i.e. become more negative, whereas 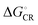 and ΔECoul,ED increase. Lemaur et al. observed6 the same dependence of ΔG° and ΔECoul on the polarity of the medium for the modeled Pc–PTCDI complex.
and ΔECoul,ED increase. Lemaur et al. observed6 the same dependence of ΔG° and ΔECoul on the polarity of the medium for the modeled Pc–PTCDI complex.
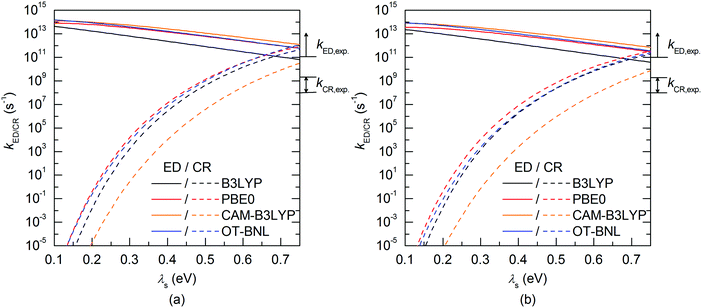
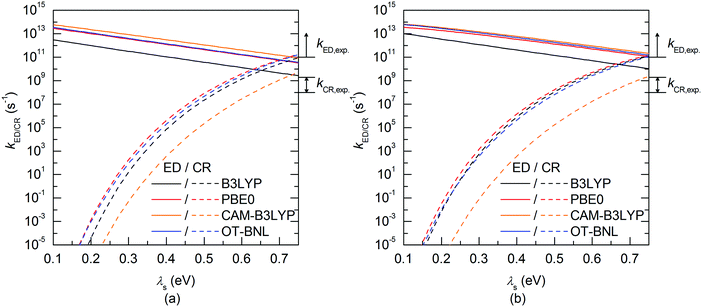
The evolutions of the ED and CR rates of the studied complexes as functions of λs are illustrated in Fig. 12 and 13 for the 1,2-DCB and blend environments, respectively. Generally, the ED process occurs more rapidly than CR, although B3LYP, PBE0, and OT-BNL predict competing CR rates with larger λs (>ca. 0.66 eV). The ED rates are slightly faster in 1,2-DCB (1010–1013 s−1) than in the blend (109–1013 s−1), decreasing with increasing λs. Similarly, the CR rates are faster in 1,2-DCB (10−14–1012 s−1) than in the blend (10−16–1011 s−1), increasing with increasing λs. The LRC functionals predict higher ED rates compared to the global hybrids in the increasing order of B3LYP < PBE0 < OT-BNL < CAM-B3LYP. The magnitude of the ED rate predicted with B3LYP differs from those predicted with the other functionals. In the case of the CR rates, there is no clear trend between the global hybrid and LRC functionals, as the CR rates increase mainly in the order of CAM-B3LYP < B3LYP < OT-BNL < PBE0. Here, the magnitude of the CAM-B3LYP CR rate is different from that given by the other functionals. The ED and CR rates in the blend are mainly larger, when PC71BM is on top of the A unit of TQ (3Q4T–PC71BM) than when it is on top of the D unit (3T4Q–PC71BM) (except for some CR rates predicted by PBE0 with λs > 0.65 eV and CAM-B3LYP with λs > 0.4 eV). In 1,2-DCB, 3T4Q–PC71BM has larger ED and CR rates than 3Q4T–PC71BM. In 1,2-DCB, both complexes have relatively similar λi and ΔG° values (Table 3), in which case the electronic coupling determines the rate differences between the two complexes. However, in the blend (Table 4), the ΔG° values of the two complexes differ to such an extent that ΔG° becomes the determining factor for the rates.
The value of λs determines, especially in the case of the CR rates, whether the ED and CR rates are in the ranges of the experimental ED (>1011)105 for TQ–PC61BM and CR rates (ca. 108–109) for different copolymer–fullerene blends. The numerical values of the CT rates at λs of 0.56 eV (Table 5), i.e. at the average of λs (ca. 0.42–0.63 eV in 1,2-DCB and 0.49–0.69 eV in the blend), for which the ED and CR rates are calculated with different functionals and in different environments are within the experimental rates. Moreover, our choices regarding the calculation methods, e.g. using the vacuum OT ω value in the 1,2-DCB and blend calculations or using the B3LYP geometries in all calculations, can induce some uncertainties in the calculated rates and rate parameters. However, as we have kept these computational settings consistent in all the calculations, we expect their relative effect to be the same. To conclude, all the functionals yield mostly ED and CR rates that are consistent with the experimental ones with larger λs values (see above), while smaller λs values lead to vanishingly small CR rates.
| Functional | Complex | λ ED (eV) | k ED (s−1) | λ CR (eV) | k CR (s−1) |
|---|---|---|---|---|---|
| a Sum of λi (values in Table 2) and λs of 0.53 eV. b Taken as the average of the λs values for which the calculated ED and CR rates are within the experimental ones (see text). | |||||
| B3LYP | 3T4Q–PC71BM | 0.6898 (0.7023) | 4.5 × 1011 (1.9 × 1010) | 0.7639 (0.7760) | 4.0 × 109 (3.0 × 108) |
| 3Q4T–PC71BM | 0.6908 (0.7034) | 2.6 × 1011 (7.5 × 1010) | 0.7658 (0.7781) | 2.0 × 109 (1.1 × 109) | |
| PBE0 | 3T4Q–PC71BM | 0.6977 (0.7109) | 3.5 × 1012 (2.3 × 1011) | 0.7780 (0.7909) | 1.1 × 1010 (9.3 × 108) |
| 3Q4T–PC71BM | 0.6986 (0.7119) | 1.8 × 1012 (7.4 × 1011) | 0.7798 (0.7929) | 5.0 × 109 (1.5 × 109) | |
| CAM-B3LYP | 3T4Q–PC71BM | 0.7482 (0.7667) | 6.8 × 1012 (6.0 × 1011) | 0.8614 (0.8815) | 6.2 × 107 (4.8 × 106) |
| 3Q4T–PC71BM | 0.7490 (0.7677) | 4.0 × 1012 (1.3 × 1012) | 0.8635 (0.8832) | 1.4 × 107 (3.2 × 106) | |
| OT-BNL | 3T4Q–PC71BM | 0.7328 (0.7471) | 3.7 × 1012 (2.6 × 1011) | 0.8243 (0.8398) | 9.2 × 109 (5.9 × 108) |
| 3Q4T–PC71BM | 0.7337 (0.7481) | 2.2 × 1012 (1.0 × 1012) | 0.8260 (0.8414) | 2.2 × 109 (6.8 × 108) | |
Conclusions
We have determined the electronic couplings of the ED and CR processes at the local interfaces of solar cell materials TQ and PC71BM theoretically using the two- and multi-state GMH and FCD coupling schemes. The results show that the choice of functional has the most significant effect on the excited state characteristics and the coupling values, especially with the GMH scheme. Mainly, the global hybrid functionals predict a more localized adiabatic CT1 state, i.e. almost a complete CT from TQ to PC71BM, whereas the LRC functionals predict a small component of the intramolecular excitation of PC71BM mixed with the CT1 state. When comparing the two- and multi-state couplings, the number of states does not have a very strong effect on the coupling values with the global hybrid functionals, and the GMH and FCD couplings are quite similar. Thus, with the global hybrid functionals, the 2-state schemes seem to be sufficient for calculating the couplings of the studied system. However, with the non-tuned and OT LRC functionals, the multi-state coupling schemes yield a more localized description of the CT1 state and thus improve couplings with respect to the two-state values. Furthermore, with the LRC functionals, the FCD scheme yields a more localized CT1 state and constant couplings while being less sensitive to the choice of calculation method compared to the GMH scheme. Thus, the FCD scheme combined with the multi-state treatment is recommended for calculating the couplings when using the LRC functionals.The electronic couplings are clearly affected by the position of PC71BM and stronger couplings are observed when PC71BM is on the donor unit of TQ than when PC71BM is on the acceptor unit of TQ. In most cases, the CR couplings of the studied TQ–PC71BM complexes are larger than the corresponding ED couplings. However, for the complex, where PC71BM is on top of the acceptor unit of TQ, the LRC functionals predict mainly larger ED couplings. Overall, the calculated ED rates are in the range of the experimental values. However, the calculated CR values are consistent with the experimental rates only with certain values of the external reorganization energy. Nevertheless, the ED process is generally predicted to occur more rapidly than the CR process in the TQ–PC71BM complexes, which is in agreement with the previous experimental results that the particular system functions efficiently in the PSCs. The slower CR rates are the consequence of the increasingly negative values of the Gibbs free energy relative to reorganization energies due to which the CR process occurs in the Marcus inverted region. We note that our study did not consider dispersion corrections, which are important for describing weak dispersion interaction in the eD–eA interface configurations, especially when determining the intermolecular distances.66 The effect of the dispersion on the multi-state electronic couplings will be the subject of future work by our group.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
Computing resources provided by the CSC-IT Center for Science Ltd, administrated by the Finnish Ministry of Education, are acknowledged. Financing of this research by the Academy of Finland (Decision No. 251823), the Graduate School of Tampere University of Technology (TUT), the Finnish Cultural Foundation, and the Faculty of Engineering and Natural Sciences of Tampere University is greatly acknowledged by TIH and TK. ML thanks the National Supercomputer Centre (NSC), Sweden, for computing time, and the Swedish e-Science Research Center (SeRC) for financial support. The Academy of Finland (Decision No. 298182 and 310489) is acknowledged by LP for the financial support.References
- J. Zhao, Y. Li, G. Yang, K. Jiang, H. Lin, H. Ade, W. Ma and H. Yan, Nat. Energy, 2016, 1, 15027 CrossRef CAS.
- Y. Jin, Z. Chen, M. Xiao, J. Peng, B. Fan, L. Ying, G. Zhang, X.-F. Jiang, Q. Yin, Z. Liang, F. Huang and Y. Cao, Adv. Energy Mater., 2017, 7, 1700944 CrossRef.
- W. Zhao, S. Li, H. Yao, S. Zhang, Y. Zhang, B. Yang and J. Hou, J. Am. Chem. Soc., 2017, 139, 7148–7151 CrossRef CAS PubMed.
- S. Li, L. Ye, W. Zhao, H. Yan, B. Yang, D. Liu, W. Li, H. Ade and J. Hou, J. Am. Chem. Soc., 2018, 140, 7159–7167 CrossRef CAS PubMed.
- G. Yu, J. Gao, J. C. Hummelen, F. Wudl and A. J. Heeger, Science, 1995, 270, 1789–1791 CrossRef CAS.
- V. Lemaur, M. Steel, D. Beljonne, J.-L. Brédas and J. Cornil, J. Am. Chem. Soc., 2005, 127, 6077–6086 CrossRef CAS PubMed.
- P. Song, Y. Li, F. Ma, T. Pullerits and M. Sun, Chem. Rec., 2016, 16, 734–753 CrossRef CAS PubMed.
- R. A. Marcus, J. Chem. Phys., 1956, 24, 966–978 CrossRef CAS.
- R. A. Marcus and N. Sutin, Biochim. Biophys. Acta, Rev. Bioenerg., 1985, 811, 265–322 CrossRef CAS.
- R. A. Marcus, Rev. Mod. Phys., 1993, 65, 599–610 CrossRef CAS.
- M. D. Newton, Chem. Rev., 1991, 91, 767–792 CrossRef CAS.
- J. L. Brédas, J. P. Calbert, D. A. da Silva Filho and J. Cornil, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 5804–5809 CrossRef PubMed.
- E. F. Valeev, V. Coropceanu, D. A. da Silva Filho, S. Salman and J.-L. Brédas, J. Am. Chem. Soc., 2006, 128, 9882–9886 CrossRef CAS PubMed.
- V. Coropceanu, J. Cornil, D. A. da Silva Filho, Y. Olivier, R. Silbey and J.-L. Brédas, Chem. Rev., 2007, 107, 926–952 CrossRef CAS PubMed.
- M. Bixon, J. Jortner and J. W. Verhoeven, J. Am. Chem. Soc., 1994, 116, 7349–7355 CrossRef CAS.
- C.-P. Hsu, Acc. Chem. Res., 2009, 42, 509–518 CrossRef CAS PubMed.
- Y. Zhao and W. Liang, Chem. Soc. Rev., 2012, 41, 1075–1087 RSC.
- J. M. Foster and S. F. Boys, Rev. Mod. Phys., 1960, 32, 300–302 CrossRef CAS.
- C. Edmiston and K. Ruedenberg, Rev. Mod. Phys., 1963, 35, 457–465 CrossRef CAS.
- T. Pacher, L. S. Cederbaum and H. Köppel, J. Chem. Phys., 1988, 89, 7367–7381 CrossRef CAS.
- Y. Mo, J. Gao and S. D. Peyerimhoff, J. Chem. Phys., 2000, 112, 5530–5538 CrossRef CAS.
- R. J. Cave and M. D. Newton, Chem. Phys. Lett., 1996, 249, 15–19 CrossRef CAS.
- R. J. Cave and M. D. Newton, J. Chem. Phys., 1997, 106, 9213–9226 CrossRef CAS.
- A. A. Voityuk and N. Rösch, J. Chem. Phys., 2002, 117, 5607–5616 CrossRef CAS.
- L. Blancafort and A. A. Voityuk, Phys. Chem. Chem. Phys., 2017, 19, 31007–31010 RSC.
- A. A. Voityuk, J. Phys. Chem. A, 2017, 121, 5414–5419 CrossRef CAS PubMed.
- Y. Shao, Z. Gan, E. Epifanovsky, A. T. B. Gilbert, M. Wormit, J. Kussmann, A. W. Lange, A. Behn, J. Deng, X. Feng, D. Ghosh, M. Goldey, P. R. Horn, L. D. Jacobson, I. Kaliman, R. Z. Khaliullin, T. Kuś, A. Landau, J. Liu, E. I. Proynov, Y. M. Rhee, R. M. Richard, M. A. Rohrdanz, R. P. Steele, E. J. Sundstrom, H. L. Woodcock III, P. M. Zimmerman, D. Zuev, B. Albrecht, E. Alguire, B. Austin, G. J. O. Beran, Y. A. Bernard, E. Berquist, K. Brandhorst, K. B. Bravaya, S. T. Brown, D. Casanova, C.-M. Chang, Y. Chen, S. H. Chien, K. D. Closser, D. L. Crittenden, M. Diedenhofen, R. A. DiStasio, H. Do, A. D. Dutoi, R. G. Edgar, S. Fatehi, L. Fusti-Molnar, A. Ghysels, A. Golubeva-Zadorozhnaya, J. Gomes, M. W. D. Hanson-Heine, P. H. P. Harbach, A. W. Hauser, E. G. Hohenstein, Z. C. Holden, T.-C. Jagau, H. Ji, B. Kaduk, K. Khistyaev, J. Kim, J. Kim, R. A. King, P. Klunzinger, D. Kosenkov, T. Kowalczyk, C. M. Krauter, K. U. Lao, A. D. Laurent, K. V. Lawler, S. V. Levchenko, C. Y. Lin, F. Liu, E. Livshits, R. C. Lochan, A. Luenser, P. Manohar, S. F. Manzer, S.-P. Mao, N. Mardirossian, A. V. Marenich, S. A. Maurer, N. J. Mayhall, E. Neuscamman, C. M. Oana, R. Olivares-Amaya, D. P. O’Neill, J. A. Parkhill, T. M. Perrine, R. Peverati, A. Prociuk, D. R. Rehn, E. Rosta, N. J. Russ, S. M. Sharada, S. Sharma, D. W. Small, A. Sodt, T. Stein, D. Stück, Y.-C. Su, A. J. W. Thom, T. Tsuchimochi, V. Vanovschi, L. Vogt, O. Vydrov, T. Wang, M. A. Watson, J. Wenzel, A. White, C. F. Williams, J. Yang, S. Yeganeh, S. R. Yost, Z.-Q. You, I. Y. Zhang, X. Zhang, Y. Zhao, B. R. Brooks, G. K. L. Chan, D. M. Chipman, C. J. Cramer, W. A. Goddard, M. S. Gordon, W. J. Hehre, A. Klamt, H. F. Schaefer, M. W. Schmidt, C. D. Sherrill, D. G. Truhlar, A. Warshel, X. Xu, A. Aspuru-Guzik, R. Baer, A. T. Bell, N. A. Besley, J.-D. Chai, A. Dreuw, B. D. Dunietz, T. R. Furlani, S. R. Gwaltney, C.-P. Hsu, Y. Jung, J. Kong, D. S. Lambrecht, W. Liang, C. Ochsenfeld, V. A. Rassolov, L. V. Slipchenko, J. E. Subotnik, T. Van Voorhis, J. M. Herbert, A. I. Krylov, P. M. W. Gill and M. Head-Gordon, Mol. Phys., 2015, 113, 184–215 CrossRef CAS.
- C.-H. Yang and C.-P. Hsu, J. Chem. Phys., 2013, 139, 154104 CrossRef PubMed.
- M. H. Lee, B. D. Dunietz and E. Geva, J. Phys. Chem. Lett., 2014, 5, 3810–3816 CrossRef PubMed.
- B.-C. Lin, B. T. Koo, P. Clancy and C.-P. Hsu, J. Phys. Chem. C, 2014, 118, 23605–23613 CrossRef CAS.
- X.-K. Chen, M. K. Ravva, H. Li, S. M. Ryno and J.-L. Brédas, Adv. Energy Mater., 2016, 6, 1601325 CrossRef.
- Z. Zheng, N. R. Tummala, Y.-T. Fu, V. Coropceanu and J.-L. Brédas, ACS Appl. Mater. Interfaces, 2017, 9, 18095–18102 CrossRef CAS PubMed.
- Y. Li, T. Pullerits, M. Zhao and M. Sun, J. Phys. Chem. C, 2011, 115, 21865–21873 CrossRef CAS.
- S.-B. Li, Y.-A. Duan, Y. Geng, H.-B. Li, J.-Z. Zhang, H.-L. Xu, M. Zhang and Z.-M. Su, Phys. Chem. Chem. Phys., 2014, 16, 25799–25808 RSC.
- Y. Li, D. Qi, P. Song and F. Ma, Materials, 2015, 8, 42–56 CrossRef CAS PubMed.
- Y. Li, Y. Feng and M. Sun, Sci. Rep., 2015, 5, 13970 CrossRef PubMed.
- D. Qian, Z. Zheng, H. Yao, W. Tress, T. R. Hopper, S. Chen, S. Li, J. Liu, S. Chen, J. Zhang, X.-K. Liu, B. Gao, L. Ouyang, Y. Jin, G. Pozina, I. A. Buyanova, W. M. Chen, O. Inganäs, V. Coropceanu, J.-L. Bredas, H. Yan, J. Hou, F. Zhang, A. A. Bakulin and F. Gao, Nat. Mater., 2018, 17, 703–709 CrossRef CAS PubMed.
- P. Song, Q. Zhou, Y. Li, F. Ma and M. Sun, Phys. Chem. Chem. Phys., 2017, 19, 16105–16112 RSC.
- T. Wang, X.-K. Chen, A. Ashokan, Z. Zheng, M. K. Ravva and J.-L. Brédas, Adv. Funct. Mater., 2018, 28, 1705868 CrossRef.
- M. Rust, J. Lappe and R. J. Cave, J. Phys. Chem. A, 2002, 106, 3930–3940 CrossRef CAS.
- C. Lambert, S. Amthor and J. Schelter, J. Phys. Chem. A, 2004, 108, 6474–6486 CrossRef CAS.
- A. A. Voityuk, J. Chem. Phys., 2006, 124, 064505 CrossRef PubMed.
- C. Butchosa, S. Simon, L. Blancafort and A. Voityuk, J. Phys. Chem. B, 2012, 116, 7815–7820 CrossRef CAS PubMed.
- A. A. Voityuk, J. Phys. Chem. C, 2013, 117, 2670–2675 CrossRef CAS.
- S.-J. Lee, H.-C. Chen, Z.-Q. You, K.-L. Liu, T. J. Chow, I.-C. Chen and C.-P. Hsu, Mol. Phys., 2010, 108, 2775–2789 CrossRef CAS.
- H.-H. Chou, C.-H. Yang, J. T. Lin and C.-P. Hsu, J. Phys. Chem. C, 2017, 121, 983–992 CrossRef CAS.
- H.-C. Chen and C.-P. Hsu, J. Phys. Chem. A, 2005, 109, 11989–11995 CrossRef CAS PubMed.
- G. Sini, J. S. Sears and J.-L. Bredas, J. Chem. Theory Comput., 2011, 7, 602–609 CrossRef CAS PubMed.
- Z.-Q. You, Y.-C. Hung and C.-P. Hsu, J. Phys. Chem. B, 2015, 119, 7480–7490 CrossRef CAS PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS PubMed.
- P. Mori-Sánchez, A. J. Cohen and W. Yang, J. Chem. Phys., 2006, 125, 201102 CrossRef PubMed.
- T. Körzdörfer and J.-L. Brédas, Acc. Chem. Res., 2014, 47, 3284–3291 CrossRef PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396 CrossRef CAS.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS.
- M. G. Medvedev, I. S. Bushmarinov, J. Sun, J. P. Perdew and K. A. Lyssenko, Science, 2017, 355, 49–52 CrossRef CAS PubMed.
- P. Bleiziffer, K. Schaller and S. Riniker, J. Chem. Inf. Model., 2018, 58, 579–590 CrossRef CAS PubMed.
- M. Alipour and Z. Safari, J. Phys. Chem. C, 2019, 123, 746–761 CrossRef CAS.
- T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57 CrossRef CAS.
- A. E. Raeber and B. M. Wong, J. Chem. Theory Comput., 2015, 11, 2199–2209 CrossRef CAS PubMed.
- T. Körzdörfer, J. S. Sears, C. Sutton and J.-L. Brédas, J. Chem. Phys., 2011, 135, 204107 CrossRef PubMed.
- L. Pandey, C. Doiron, J. S. Sears and J.-L. Brédas, Phys. Chem. Chem. Phys., 2012, 14, 14243–14248 RSC.
- I. T. Lima, C. Risko, S. G. Aziz, D. A. da Silva Filho and J.-L. Brédas, J. Mater. Chem. C, 2014, 2, 8873–8879 RSC.
- M. Niskanen and T. I. Hukka, Phys. Chem. Chem. Phys., 2014, 16, 13294–13305 RSC.
- T. Kastinen, M. Niskanen, C. Risko, O. Cramariuc and T. I. Hukka, Phys. Chem. Chem. Phys., 2016, 18, 27654–27670 RSC.
- R. Baer and D. Neuhauser, Phys. Rev. Lett., 2005, 94, 043002 CrossRef PubMed.
- E. Livshits and R. Baer, Phys. Chem. Chem. Phys., 2007, 9, 2932–2941 RSC.
- T. Yamamoto, Z. Zhou, T. Kanbara, M. Shimura, K. Kizu, T. Maruyama, Y. Nakamura, T. Fukuda, B.-L. Lee, N. Ooba, S. Tomaru, T. Kurihara, T. Kaino, K. Kubota and S. Sasaki, J. Am. Chem. Soc., 1996, 118, 10389–10399 CrossRef CAS.
- E. Wang, L. Hou, Z. Wang, S. Hellström, F. Zhang, O. Inganäs and M. R. Andersson, Adv. Mater., 2010, 22, 5240–5244 CrossRef CAS PubMed.
- M. M. Wienk, J. M. Kroon, W. J. H. Verhees, J. Knol, J. C. Hummelen, P. A. van Hal and R. A. J. Janssen, Angew. Chem., Int. Ed., 2003, 42, 3371–3375 Search PubMed.
- Y. Kim, H. R. Yeom, J. Y. Kim and C. Yang, Energy Environ. Sci., 2013, 6, 1909 RSC.
- E. Wang, J. Bergqvist, K. Vandewal, Z. Ma, L. Hou, A. Lundin, S. Himmelberger, A. Salleo, C. Müller, O. Inganäs, F. Zhang and M. R. Andersson, Adv. Energy Mater., 2013, 3, 806–814 CrossRef CAS.
- S. Chen, Y. An, G. K. Dutta, Y. Kim, Z.-G. Zhang, Y. Li and C. Yang, Adv. Funct. Mater., 2017, 27, 1603564 CrossRef.
- Y. Yi, V. Coropceanu and J.-L. Brédas, J. Am. Chem. Soc., 2009, 131, 15777–15783 CrossRef CAS PubMed.
- L. Pandey, PhD thesis, Georgia Institute of Technology, 2013.
- T. Liu and A. Troisi, J. Phys. Chem. C, 2011, 115, 2406–2415 CrossRef CAS.
- C. W. Murray, N. C. Handy and G. J. Laming, Mol. Phys., 1993, 78, 997–1014 CrossRef CAS.
- V. I. Lebedev and D. N. Laikov, Dokl. Math., 1999, 59, 477–481 Search PubMed.
- S. Hirata and M. Head-Gordon, Chem. Phys. Lett., 1999, 314, 291–299 CrossRef CAS.
- C. Leng, H. Qin, Y. Si and Y. Zhao, J. Phys. Chem. C, 2014, 118, 1843–1855 CrossRef CAS.
- D. A. Egger, S. Weissman, S. Refaely-Abramson, S. Sharifzadeh, M. Dauth, R. Baer, S. Kümmel, J. B. Neaton, E. Zojer and L. Kronik, J. Chem. Theory Comput., 2014, 10, 1934–1952 CrossRef CAS PubMed.
- R. L. Martin, J. Chem. Phys., 2003, 118, 4775–4777 CrossRef CAS.
- G. A. Zhurko, Chemcraft – graphical program for visualization of quantum chemistry computations, Ivanovo, Russia, 2005, https://chemcraftprog.com Search PubMed.
- P. Ros and G. C. A. Schuit, Theor. Chim. Acta, 1966, 4, 1–12 CrossRef CAS.
- V. Barone and M. Cossi, J. Phys. Chem. A, 1998, 102, 1995–2001 CrossRef CAS.
- M. Cossi, N. Rega, G. Scalmani and V. Barone, J. Comput. Chem., 2003, 24, 669–681 CrossRef CAS PubMed.
- A. W. Lange and J. M. Herbert, J. Chem. Phys., 2010, 133, 244111 CrossRef PubMed.
- Physical Constants of Organic Compounds, in CRC Handbook of Chemistry and Physics, ed. J. R. Rumble, CRC Press/Taylor & Francis, Boca Raton, FL, 99th edn, 2018 Search PubMed.
- A. Melianas, F. Etzold, T. J. Savenije, F. Laquai, O. Inganäs and M. Kemerink, Nat. Commun., 2015, 6, 8778 CrossRef CAS PubMed.
- M. Campoy-Quiles, C. Müller, M. Garriga, E. Wang, O. Inganäs and M. I. Alonso, Thin Solid Films, 2014, 571, 371–376 CrossRef CAS.
- D. H. K. Murthy, A. Melianas, Z. Tang, G. Juška, K. Arlauskas, F. Zhang, L. D. A. Siebbeles, O. Inganäs and T. J. Savenije, Adv. Funct. Mater., 2013, 23, 4262–4268 CrossRef CAS.
- A. A. Bakulin, Y. Xia, H. J. Bakker, O. Inganäs and F. Gao, J. Phys. Chem. C, 2016, 120, 4219–4226 CrossRef CAS.
- Z. Zheng, J.-L. Brédas and V. Coropceanu, J. Phys. Chem. Lett., 2016, 7, 2616–2621 CrossRef CAS PubMed.
- L. Kronik and S. Kümmel, Adv. Mater., 2018, 30, 1706560 CrossRef PubMed.
- G. Boschetto, M. Krompiec and C. K. Skylaris, J. Phys. Chem. C, 2018, 122, 17024–17034 CrossRef CAS.
- A. Dreuw and M. Head-Gordon, Chem. Rev., 2005, 105, 4009–4037 CrossRef CAS PubMed.
- Y. Yi, V. Coropceanu and J.-L. Brédas, J. Mater. Chem., 2011, 21, 1479–1486 RSC.
- T. Wang, M. K. Ravva and J.-L. Brédas, Adv. Funct. Mater., 2016, 26, 5913–5921 CrossRef CAS.
- T. Kawatsu, V. Coropceanu, A. Ye and J.-L. Brédas, J. Phys. Chem. C, 2008, 112, 3429–3433 CrossRef CAS.
- S. Albrecht, K. Vandewal, J. R. Tumbleston, F. S. U. Fischer, J. D. Douglas, J. M. J. Fréchet, S. Ludwigs, H. Ade, A. Salleo and D. Neher, Adv. Mater., 2014, 26, 2533–2539 CrossRef CAS PubMed.
- D. C. Coffey, B. W. Larson, A. W. Hains, J. B. Whitaker, N. Kopidakis, O. V. Boltalina, S. H. Strauss and G. Rumbles, J. Phys. Chem. C, 2012, 116, 8916–8923 CrossRef CAS.
- A. J. Ward, A. Ruseckas, M. M. Kareem, B. Ebenhoch, L. A. Serrano, M. Al-Eid, B. Fitzpatrick, V. M. Rotello, G. Cooke and I. D. W. Samuel, Adv. Mater., 2015, 27, 2496–2500 CrossRef CAS PubMed.
- J. Bergqvist, C. Lindqvist, O. Bäcke, Z. Ma, Z. Tang, W. Tress, S. Gustafsson, E. Wang, E. Olsson, M. R. Andersson, O. Inganäs and C. Müller, J. Mater. Chem. A, 2014, 2, 6146–6152 RSC.
- D. A. Vithanage, E. Wang, Z. Wang, F. Ma, O. Inganäs, M. R. Andersson, A. Yartsev, V. Sundström and T. Pascher, Adv. Energy Mater., 2014, 4, 1301706 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: Additional information regarding the TQ–PC71BM models and the methods; the excited state properties of the isolated TQ and PC71BM models and the corresponding complexes investigated with B3LYP and CAM-B3LYP; the OT ω for the isolated TQ and PC71BM models and the 3T4Q–PC71BM/3Q4T–PC71BM complexes; vertical excitation energies, and adiabatic and diabatic Δμ and Δq values for the CT1 and LE states; NTOs of 3T4Q–PC71BM, and electronic couplings of 3T4Q–PC71BM and 3Q4T–PC71BM; and bond length alternations of 3T4Q and 3Q4T. See DOI: 10.1039/c9cp04837e |
| This journal is © the Owner Societies 2019 |