Falloff curves and mechanism of thermal decomposition of CF3I in shock waves†
Received
28th August 2019
, Accepted 7th October 2019
First published on 9th October 2019
Abstract
The falloff curves of the unimolecular dissociation CF3I (+Ar) → CF3 + I (+Ar) are modelled by combining quantum-chemical characterizations of the potential energy surface for the reaction, standard unimolecular rate theory, and experimental information on the average energy transferred per collision between excited CF3I and Ar. The (essentially) parameter-free theoretical modelling gives results in satisfactory agreement with data deduced from earlier shock wave experiments employing a variety of reactant concentrations (between a few ppm and a few percent in the bath gas Ar). New experiments recording absorption–time signals of CF3I, I2, CF2 and (possibly) IF at 450–500 and 200–300 nm are reported. By analysing the decomposition mechanism, besides the unimolecular dissociation of CF3I, these provide insight into the influence of secondary reactions on the experimental observations.
I. Introduction
The thermal decomposition of CF3I has attracted considerable interest for a number of reasons. On the one hand, it has served as a source of CF3 radicals in shock waves.1–3 On the other hand, with its weak C–I bond in the presence of strong C–F bonds, it represents a prototype of a unimolecular dissociation reaction of simple bond-fission character.4–15 Furthermore, its secondary reactions are related to processes of importance in chemical lasers and laser-induced isotope separation.16,17 The role of secondary reactions, in flow system studies of CF3I dissociation up to about 800 K, remained unclear for quite some while. Only shock wave experiments, using iodine atom resonance absorption spectroscopy (ARAS) and employing very low reactant CF3I concentrations,13,15 directly led to the rate constant of the unimolecular reaction. Although some modelling of this rate constant in its falloff range had been made in earlier work, only with the ARAS results such modelling could be put on a safe basis.15 Nevertheless, the theoretical approach to the falloff curves left something to be desired. First, it was based on only simplified versions of Rice–Ramsperger–Kassel–Marcus (RRKM) theory. This approach in the present work is extended by accounting for the finer details of the potential energy surface along the reaction coordinate. Second and more seriously, the average energy 〈ΔE〉 transferred per collision between the bath gas M and excited CF3I (or the equivalent collision efficiency βc) was only treated as a fit parameter. It was overlooked that 〈ΔE〉 (for the bath gas M = Ar) had been measured directly in IR-multiphoton excitation experiments.18–21 With the background of the mentioned experimental and theoretical studies, it appeared attractive to us to investigate the reaction again and in greater detail. We model the rate constant in terms of loose-activated complex unimolecular rate theory, determining the required molecular parameters by quantum-chemical calculations. After introducing the experimental 〈ΔE〉, falloff curves are constructed and expressed in the form recommended in ref. 22 and 23. The influence of uncertainties in the C–I bond energy is also investigated. Finally, a comparison with the ARAS shock wave results is made.
Having established reliable falloff curves, new shock wave experiments were performed using alternatives to the ARAS detection method. While the ARAS experiments used reactant concentrations as low as 1–4 ppm of CF3I in Ar15 (or in Kr13), the present work employs mixtures with 100–1500 ppm (mostly about 500 ppm). The present experiments were able to monitor CF3I concentrations with considerably reduced reactant concentrations in comparison to earlier shock tube work (employing reactant concentrations of 0.5–5%6,9,14). Within the present range of reactant concentrations, the onset of secondary reactions can be monitored. Insight into the complex thermal decomposition mechanism is obtained with the help of absorption spectroscopy in the ranges 200–300 and 450–500 nm. On the basis of the detailed reaction mechanism (being probably still incomplete), the previous high-concentration shock wave experiments could also be reinterpreted. Finally, the identification of species with so far unknown high-temperature absorption coefficients was facilitated by quantum-chemical calculations of oscillator strengths.
II. Modelling of dissociation rate constants
Our modelling of rate constants for the unimolecular dissociation of the C–I bond in CF3I, first, focussed on the properties of the minimum-energy path (MEP) potential V(r) of the reaction and the change of transitional mode quanta ν(r) along the MEP reaction coordinate r. V(r) and ν(r) were derived by quantum-chemical calculations. A 6-311G(d) basis set for I atoms as tabulated in ref. 24 and 25 and a 6-311+G(3df) basis set for C and F atoms were employed. With these basis sets optimized structures and vibrational frequencies were calculated at the M06-2X level (for details of our approach, see e.g.ref. 26–30; more details are given in the ESI†). V(r) (computed at the CCSD(T)//M06-2X level) could be approximated using a Morse function (with the Morse parameters β ≈ 1.45 Å−1, re ≈ 2.16 Å, and De = 225.9 kJ mol−1). The transitional mode quanta ν(r) were found to decay exponentially along the MEP (with decay parameters α ≈ 0.59 and 0.61 Å−1, such that the ratio α/β is not far from the “standard value” α/β ≈ 0.531). The calculation of the rotational contributions requires the determination of centrifugal maxima along the MEP. This was done with the r-dependence of the rotational constant of CF3I (being approximated using (B + C)/2 ≈ 0.0505 cm−1/[1 + 0.551(r − 2.16 Å) + 0.138(r − 2.16 Å)2]). Graphical representations of V(r), ν(r), and (B + C)/2 for the CF3–I bond are given in Fig. S1–S3 of the ESI.†
The pseudo-first order rate constant k1 of the unimolecular dissociation CF3I → CF3 + I is expressed in its usual form k1/k1,∞ = [x/(1 + x)]F(x), with x = k1,0/k1,∞ (the limiting low-pressure rate constant k1,0 being proportional to the bath gas concentration [M] = Ar, while the limiting high-pressure rate constant k1,∞ is independent of [M]; F(x) denotes a suitable “broadening factor”, see below).
With the information obtained and using the statistical adiabatic channel model (in its classical trajectory version, SACM/CT, from ref. 32), limiting high-pressure rate constants
| | k1,∞ = 5.9 × 1015(T/1000 K)−2.2exp(−28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 930 K/T) s−1 930 K/T) s−1 | (1) |
were derived (for a value of the reaction enthalpy at 0 K of
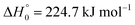 33
33). Using 〈Δ
E〉/
hc ≈ −100 cm
−1 independent of temperature, such as that determined experimentally for M = Ar in
ref. 21, and employing the formalism of
ref. 34, limiting low-pressure rate constants
| | k1,0 = [Ar]5.4 × 1021(T/1000 K)−10.5exp(−31![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 360 K/T)cm3 mol−1 s−1 360 K/T)cm3 mol−1 s−1 | (2) |
were calculated (the given value of 〈Δ
E〉 between 750 and 2000 K corresponds to the collision efficiency
βc ≈ 0.076(1000 K/
T)
1.2, see the ESI
†). The construction of falloff curves following ref.
22 and 23, furthermore, requires information on center broadening factors of the falloff curves
Fcent =
F(
x = 1).
34 These were derived with the method proposed in
ref. 23 and 35 (leading to
Fcent = 0.20, 0.16, 0.14, and 0.14 at
T/K = 750, 1000, 1500, and 2000, respectively).
Fig. 1 shows the corresponding falloff curves for selected temperatures. The latter were chosen to be 950, 1050, and 1200 K, in order to compare with the modelling from
ref. 15 (which used variational RRKM theory for
k1,∞, while
k1,0 was derived following ref.
34 with an assumed
βc ≈ 100 K/
T and
Fcent = 0.188).
Fig. 1 shows that the limiting values of the present falloff curves differ considerably from those of
ref. 15. The figure also includes experimental ARAS results from
ref. 15 (the measured points were corrected for slight temperature “mismatch” using the modelled temperature dependence of the rate constants at the given [Ar]). The agreement between the ARAS data and the modelled falloff curves appears quite satisfactory. While the differences in the modelled
k1,∞ are only small, larger discrepancies are observed in the modelled limiting low-pressure rate constants
k1,0. This could be due to differences in several input factors (see the basic formalism from
ref. 34). The most probable reason seems to us to be that centrifugal barriers were accounted for in the present work (on the basis of Fig. S3 of the ESI
†), while this was not done or done differently in
ref. 15. This reduces the rotational factors
Frot in
k1,0. A further analysis of the difference does not appear warranted at this stage.
 |
| | Fig. 1 Falloff curves for the unimolecular dissociation CF3I → CF3 + I (full lines: modelling from this work (see Section III), dashed lines: modelling from ref. 15; experimental results from this work: ● (1200 K), ■ (1050 K); from ref. 15: ○ (1200 K), □ (1050 K), Δ (950 K); from ref. 8: × (1200 K, reevaluated); influence of secondary reactions in the present work and in ref. 8 accounted for: see Section III). | |
We also inspected the influence of uncertainties in the reaction enthalpy. Increasing 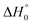 by 4 kJ mol−1 decreases k1 (at [Ar] = (5 × 10−5–1.5 × 10−4) mol cm−3) by a factor of 1.5–2 (decreasing
by 4 kJ mol−1 decreases k1 (at [Ar] = (5 × 10−5–1.5 × 10−4) mol cm−3) by a factor of 1.5–2 (decreasing  by 4 kJ mol−1 increases k1 by the same factor). Measurements and modelled (unadjusted) falloff curves, therefore, agree better than this uncertainty and confirm the validity of the thermochemistry used in the literature.33,36,37 Nevertheless, the finer details of the shape of the falloff curves should also be noted. In particular, different approaches of k1 toward the limiting low- and high-pressure rate constants (k1,0 and k1,∞, resp.) are to be accounted for when the more recent falloff expressions from ref. 22 and 23 are used instead of the older forms from ref. 34. The modelling of the falloff curves and their comparison with the ARAS results from ref. 15 in the foregoing section has been described in detail, because it forms the basis for an analysis of the decomposition mechanism under conditions of higher reactant concentrations. This analysis will be made after new experiments are described in the following section.
by 4 kJ mol−1 increases k1 by the same factor). Measurements and modelled (unadjusted) falloff curves, therefore, agree better than this uncertainty and confirm the validity of the thermochemistry used in the literature.33,36,37 Nevertheless, the finer details of the shape of the falloff curves should also be noted. In particular, different approaches of k1 toward the limiting low- and high-pressure rate constants (k1,0 and k1,∞, resp.) are to be accounted for when the more recent falloff expressions from ref. 22 and 23 are used instead of the older forms from ref. 34. The modelling of the falloff curves and their comparison with the ARAS results from ref. 15 in the foregoing section has been described in detail, because it forms the basis for an analysis of the decomposition mechanism under conditions of higher reactant concentrations. This analysis will be made after new experiments are described in the following section.
III. Experimental CF3I absorption signals
Experiments in the present work were performed in incident and in reflected shock waves in the bath gas Ar. The progress of reaction was followed by recording absorption–time profiles at selected wavelengths in the ranges 200–300 nm and 450–500 nm. Details of our experimental technique have been described before and need not be repeated here (see, e.g., ref. 27–30 and 38–40). Our experiments used reaction mixtures prepared in large mixing vessels before being introduced into a shock tube. Mixtures of CF3I (99% purity, from Sigma-Aldrich) and Ar (99.9999% purity, from Air Liquide) with reactant concentrations between about 100 and 1500 ppm of CF3I in Ar (mostly about 500 ppm) were employed. The chosen concentrations are of importance for the analysis of the dissociation mechanism, see below.
In the first part of our experiments we followed the progress of reaction by monitoring the concentration of the decomposing CF3I, recording absorption signals near the absorption maximum at 271 nm.6 Two examples of the recorded absorption–time profiles are shown in Fig. 2 and 3. The absorption increases abruptly at the arrival of the incident shock, marked by the first Schlieren peak. The second Schlieren peak indicates the arrival of the reflected shock. The second absorption rise then is followed by the decay of the CF3I absorption due to reaction. The evaluation of the signals requires careful reconstruction of the room temperature absorption level before the arrival of the incident shock. One also has to reconstruct the absorption level directly behind the reflected shock in order to separate the absorption step and Schlieren peak. These operations could be done with the help of the temperature-dependent absorption coefficients of CF3I determined in ref. 6 and 41. Finally, the zero-absorption line also had to be reconstructed. A temperature of 622 K behind the incident shock in Fig. 2 is too low to produce substantial dissociation of CF3I before the arrival of the reflected shock. At a temperature of 1030 K behind the reflected shock, however, the dissociation of CF3I sets in. It is important to note that the dissociation is not complete within the observation time of about 1.3 ms. This is of relevance when the reaction mechanism is considered in more detail, see below. It is also important to note that the disappearance of CF3I in Fig. 2 and 3 considerably slows with increasing reaction time and does not reach the zero-absorption line.
 |
| | Fig. 2 Absorption–time profile of decomposing CF3I, recorded at 271 nm (532 ppm of CF3I in Ar, T = 1031 K, [Ar] = 1.56 × 10−4 mol cm−3). | |
 |
| | Fig. 3 As Fig. 2, but at higher temperatures (536 ppm of CF3I in Ar, T = 1219 K, [Ar] = 1.27 × 10−4 mol cm−3). | |
The initial rate of CF3I disappearance was represented by a first-order rate law,
| | | [CF3I] ≈ [CF3I]t=0exp(−kt) | (3) |
with an apparent rate constant
k. Experimental values of
k were derived from reflected shocks (for [Ar] larger than 10
−4 mol cm
−3) and from incident shocks (for [Ar] in the range of (2–4) × 10
−5 mol cm
−3). In spite of the similarity of the recorded signals shown in
Fig. 2 and 3 to the signal reported in
ref. 8 (for 20 times larger [CF
3I]
t=0), it is by no means clear that the apparent initial rate constant
k corresponds to the rate constant
k1 for the unimolecular dissociation of CF
3I. This interpretation requires further analysis of the decomposition mechanism given below.
The thermal decomposition of CF3I traditionally has been discussed in terms of the reactions summarized in Table 1. For the high-temperature conditions of the present work, a number of aspects are important to note. First, the reverse reactions of all reactions have to be included (this was done here with equilibrium constants from the tabulations in ref. 33). Second, information on the two primary secondary reactions of I (reaction (R2)) and CF3 (reaction (R4)) with CF3I is needed. As this is available only for low temperatures,12,42–44 the corresponding rate constants k2 and k4 here were treated as uncertain parameters and their influence was investigated. k3 was taken unchanged from ref. 45 and k5 from ref. 39. Simulating the kinetics of the reactions given in Table 1 leads to concentration–time profiles of CF3I such as those shown in Fig. 4. The plot of [CF3I]/[CF3I]t=0 as a function of k1t well reproduces the experimentally observed slowing of the CF3I decomposition rate with time t. It is essential not to increase the fitted rate constant k1 beyond the given value because this would strongly reduce the overall yield of the reaction (a decrease of k−1 on the other hand would have no influence). An increase of k2 by a factor of 10 reduces the calculated half-life of CF3I by only 4% while an increase of k4 by a factor of 10 has an even smaller effect. The concentration–time profiles of CF3I thus are unsuitable for fitting k2 and k4. Extracting k1 from the CF3I profiles, however, required accounting for the slowing of the decomposition. As the [CF3I]/[CF3I]t=0 profile as a function of k1t hardly varies with temperature (see Fig. 4), the profile shown in Fig. 4 could be used for extracting k1 from the initial rate constant k of eqn (3) or, better, from a fit of the complete measured CF3I profile to the kinetics simulation. The resulting k1 values are summarized in Table 2. Selected values are included in Fig. 1 and compared with the ARAS data from ref. 15 and the modelled falloff curves. All data are consistent with each other. Increasing the reactant concentration from the 532 ppm of Fig. 2 and 3 to the 2% in ref. 8 has a noticeable effect: it increases the CF3I half-life by a factor of 1.6. The correspondingly reevaluated value is included in Fig. 1; it agrees well with the other results shown (the agreement with the data from ref. 6 is less satisfactory, because full CF3I profiles were not reported in ref. 6).
Table 1 Mechanism of the thermal decomposition of CF3I (notes: (a) k1 = 4.0 × 1012exp(−22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 790 K/T) s−1 modelled with
790 K/T) s−1 modelled with  for [Ar] ≈ 1.5× 10−4 mol cm−3 over the range 1000–1050 K; (b) reverse reaction: equilibrium constant from ref. 33; (c) k2 = 7.6 × 1012exp(−9500 K/T) cm3 mol−1 s−1 for 400–900 K, from ref. 42–44; (d) k3 = [Ar]8.8 × 1013exp(−14
for [Ar] ≈ 1.5× 10−4 mol cm−3 over the range 1000–1050 K; (b) reverse reaction: equilibrium constant from ref. 33; (c) k2 = 7.6 × 1012exp(−9500 K/T) cm3 mol−1 s−1 for 400–900 K, from ref. 42–44; (d) k3 = [Ar]8.8 × 1013exp(−14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 950 K/T) s−1 for 1080–1570 K and [Ar] = (0.3–1) × 10−6 mol cm−3, from ref. 45 and 46; (e) k4 ≤ 1.2 × 108 cm3 mol−1 s−1 for 300 K, from ref. 16; (f) k−5 ≤ 1.2 × 1013 cm3 mol−1 s−1 for 1200 K and [Ar] = 10−4 mol cm−3 from ref. 47–49)
950 K/T) s−1 for 1080–1570 K and [Ar] = (0.3–1) × 10−6 mol cm−3, from ref. 45 and 46; (e) k4 ≤ 1.2 × 108 cm3 mol−1 s−1 for 300 K, from ref. 16; (f) k−5 ≤ 1.2 × 1013 cm3 mol−1 s−1 for 1200 K and [Ar] = 10−4 mol cm−3 from ref. 47–49)
| Number |
Reaction |
Notes |
| R1 |
CF3I → CF3 + I |
a, b |
| R2 |
I + CF3I → I2 + CF3 |
c, b |
| R3 |
I2 + Ar → 2I + Ar |
d, b |
| R4 |
CF3 + CF3I → C2F6 + I |
e, b |
| R5 |
CF3 + CF3 → C2F6 |
f, b |
 |
| | Fig. 4 Kinetics simulation of CF3I concentration–time profiles (c = [CF3I], c0 = [CF3I]t=0, full lines: simulation with reactions of Table 1 for 500 ppm of CF3I in Ar, dashed line: for 2% of CF3I in Ar; *: profile without secondary reactions, k1 = rate constant for unimolecular dissociation of CF3I, t = time, see Section III). | |
Table 2 Experimental rate constants k1 for the unimolecular dissociation CF3I → CF3 + I (present work, evaluated with the reaction mechanism of Section III)
|
T/K |
[Ar]/mol cm−3 |
k
1/s−1 |
| 1005 |
3.2 × 10−5 |
5.5 × 102 |
| 1031 |
1.6 × 10−4 |
6.0 × 102 |
| 1045 |
6.5 × 10−5 |
1.3 × 103 |
| 1076 |
5.8 × 10−5 |
4.5 × 103 |
| 1130 |
5.7 × 10−5 |
6.5 × 103 |
| 1152 |
2.5 × 10−5 |
5.6 × 103 |
| 1160 |
1.4 × 10−4 |
1.3 × 104 |
| 1195 |
9.0 × 10−5 |
7.8 × 103 |
| 1219 |
1.3 × 10−4 |
2.5 × 104 |
| 1220 |
1.3 × 10−4 |
2.0 × 104 |
Although the measured CF3I absorption–time profiles of the present work appear consistent with the modelling of k1, additional measurements of I2 signals as described in the following section raise questions, suggesting that further reactions need to be considered. At this moment it appears uncertain whether they have an influence on kinetics simulations of CF3I profiles such as those shown in Fig. 4. Because the agreement of experimental and modelled k1 values in Fig. 1 looks satisfactory, one is tempted to assume that this is not the case.
IV. Experimental I2 absorption signals
The simulation of the CF3I profiles described in Section III indicated that conclusions on the rate constants k2 and k4 of reactions (R2) and (R4) could be drawn only to a limited extent, while the CF3I profiles independent of uncertainties in the mechanism led to k1. In order to learn more about k2 and k4, profiles of intermediate reaction species should be measured. Information on CF3-profiles would be difficult to obtain, because the absorption coefficient of this intermediate in the investigated spectral range (at wavelengths larger than 200 nm) is only a small value.50 We have, furthermore, extended the measurements of absorption coefficients of CF2 to wavelengths near 200 nm (CF2 prepared by the thermal decomposition CHF3 → CF2 + HF,38 see also ref. 27 and 51). We found that CF2 (from reactions not included in Table 1) or the strong absorber CF (which forms at considerably higher temperatures in the thermal decomposition of CF240) would not contribute to absorption signals of the present work. In contrast to this, I2 should be detectable, either in the intense Cordes bands near 200 nm or in the visible range 450–500 nm. Fig. 5 and 6 show examples for 200 and 487 nm under similar experimental conditions. While the I2 absorption coefficients at 487 nm are observed under shock wave conditions,45,46 they are observed near 200 nm only at near room temperature.51–54Fig. 5 and 6 show the absorption signals from I2, one then could calibrate the high temperature absorption coefficients of I2 near 200 nm against those from 450 to 500 nm. However, this procedure faces the following problem. Fig. 7 shows an absorption signal at 487 nm for conditions close to those of Fig. 2. The kinetics simulation predicts a profile such as that included in Fig. 7. This considerably differs from the observations. Furthermore, absorption signals at the wavelengths of Fig. 5–7 were still observable at temperatures in the range of 1300–1600 K where I2 should have disappeared by thermal decomposition (at even higher temperatures these signals finally disappeared). Apparently besides I2 an additional species must have contributed to the signals shown in Fig. 5–7 and it has similar spectral properties to I2, but is thermally more stable. Quantum-chemical calculations of oscillator strengths (for IF, I2, CF, CFI, CF2I, CF3I, and CF2, see the ESI†) indicated that this can only be IF. This species is thermally more stable than I2 (dissociation enthalpy  for IF instead of 148.8 kJ mol−1 for I233). Its calculated oscillator strength is even larger than that of I2 in the range of the visible spectrum (see the ESI†). Unfortunately, so far only information from the emission spectra of IF at 450–650 nm is available (see, e.g.ref. 55 and 56), but this looks consistent with the present identification of the additional species. IF might be formed in the reactionfollowed by reactions consuming CF2 and the dissociation of IF. An alternative could be a second, high energy, dissociation channel of CF3I leading to CF2 + IF. A problem might be seen in the endothermicity of reaction (R6), with
for IF instead of 148.8 kJ mol−1 for I233). Its calculated oscillator strength is even larger than that of I2 in the range of the visible spectrum (see the ESI†). Unfortunately, so far only information from the emission spectra of IF at 450–650 nm is available (see, e.g.ref. 55 and 56), but this looks consistent with the present identification of the additional species. IF might be formed in the reactionfollowed by reactions consuming CF2 and the dissociation of IF. An alternative could be a second, high energy, dissociation channel of CF3I leading to CF2 + IF. A problem might be seen in the endothermicity of reaction (R6), with  .33 However, this appears not to be too relevant for the high temperatures of the present work. Nevertheless, our identification of an additional absorber in Fig. 5–7 remains uncertain, such that more work is required here.
.33 However, this appears not to be too relevant for the high temperatures of the present work. Nevertheless, our identification of an additional absorber in Fig. 5–7 remains uncertain, such that more work is required here.
 |
| | Fig. 5 Absorption signal recorded at 487 nm during the thermal decomposition of CF3I (1485 ppm of CF3I in Ar, T = 1197 K, [Ar] = 1.25 × 10−4 mol cm−3, see Section IV). | |
 |
| | Fig. 6 Absorption signal recorded at 200 nm during the thermal decomposition of CF3I (529 ppm of CF3I in Ar, T = 1188 K, [Ar] = 1.31 × 10−4 mol cm−3, see Section IV). | |
 |
| | Fig. 7 Absorption signal recorded at 487 nm during the thermal decomposition of CF3I in comparison to the simulated I2 profile (1485 ppm of CF3I in Ar, T = 1048 K, [Ar] = 1.49 × 10−4 mol cm−3, t = 1 ms corresponds to t = 1.441/k1 from Section III). | |
V. Conclusions
After analysis of the decomposition mechanism of CF3I, the recorded absorption–time profiles of CF3I of the present work lead to rate constants for the unimolecular dissociation of CF3I. Within the experimental uncertainty of the C–I bond energy, experiments with various reactant concentrations and different detection methods are in agreement with the theoretically modelled rate constants. The latter confirm that all experiments correspond to the central part of the falloff curves of the unimolecular dissociation. Implementing experimental information on collisional energy transfer of vibrationally highly excited CF3I18–21, the modelling then is essentially free from adjustable parameters. In this respect, the present work goes beyond the usual modelling of other unimolecular reaction rate constants.
The present work also provides evidence for the intermediate formation of a species with larger thermal stability than I2 but having similar spectral features. Tentatively this species is identified to be IF. The importance of various secondary reactions of the decomposition was discussed, but for definite conclusions we need to wait for a confirmation of the identity of IF. The comparison of the present theoretical modelling of falloff curves for CF3I dissociation with that from ref. 15 showed major differences in the extrapolated limiting low-pressure rate constants. Our detailed analysis such as that described in the ESI† proposes that this is due to the exclusion of centrifugal barriers in ref. 15.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
Discussions of this work with K. Hintzer and A. Thaler, technical help by A. I. Maergoiz, and financial support from the Deutsche Forschungsgemeinschaft (Project TR 69/21-1) are gratefully acknowledged.
References
- A. P. Modica and S. J. Sillers, Experimental and Theoretical Kinetics of High-Temperature Fluorocarbon Chemistry, J. Chem. Phys., 1968, 48, 3283–3289 CrossRef CAS.
- N. K. Srinivasan, M.-C. Su, J. V. Michael, A. W. Jasper, S. J. Klippenstein and L. B. Harding, Thermal Decomposition of CF3 and the Reaction of CF2 + OH → CF2O + H, J. Phys. Chem. A, 2008, 112, 31–37 CrossRef CAS PubMed.
- C. J. Cobos, A. E. Croce, K. Luther and J. Troe, Shock Wave Study of the Thermal Decomposition of CF3 and CF2 Radicals, J. Phys. Chem. A, 2010, 114, 4755–4761 CrossRef CAS PubMed.
- O. B. Danilov, V. V. Elagin, V. Y. Zalesskii and I. L. Yachnev, Thermal Dissociation of Trifluoroiodomethane, Kinet. Katal., 1975, 16, 302–305 CAS.
- V. Yu. Zalesskii, A. M. Kokushkin and I. L. Yachnev, Pyrolysis of Perfluoroalkyliodide Vapor in UV Irradiation, Sov. Phys. Tech. Phys., 1977, 22, 1273–1276 Search PubMed.
- L. Brouwer and J. Troe, Shock Wave Study of the UV Spectrum of CF3I, Chem. Phys. Lett., 1981, 82, 1–4 CrossRef CAS.
- G. A. Skorobogatov, Rate Constant of Thermal Dissociation of Gaseous Trifluoromethyl Iodide, Kinet. Katal., 1982, 23, 18–21 CAS.
- K. Saito, Y. Yoneda, H. Tahara, S. Kidoguchi and I. Murakami, The Thermal Decomposition of CF3I in Ar, Bull. Chem. Soc. Jpn., 1984, 57, 2661–2662 CrossRef CAS.
- I. S. Zaslonko, Y. I. Mukossev, G. A. Skorobogatov and S. V. Slinkin, Parameters of the Thermal Dissociation of Gaseous CF3I, Kinet. Katal., 1986, 27, 734–739 CAS.
- V. Y. Zalesskii, Determination of the Rate Constant for Thermal Dissociation of Molecules by the Shock-Tube Method, Kinet. Katal., 1988, 29, 528–535 CAS.
- I. S. Zaslonko, Y. K. Mukoseev, G. A. Skorobogatov and V. K. Khripun, Measurement of the Rate Constant for the Thermal Dissociation of Gaseous CF3I in a Shock Tube, Kinet. Katal., 1989, 31, 1046–1052 Search PubMed.
- G. A. Skorobogatov, B. P. Dymov and V. K. Khripun, Determination of Rate Constants and Equilibrium Constants of RI = R + I and I + RI = I2 + R for R = CF3, C2F5, or CF4F9, Kinet. Katal., 1991, 32, 252–259 CAS.
- S. S. Kumaran, M.-C. Su, K. P. Lim and J. V. Michael, Thermal Decomposition of CF3I using I-Atom Absorption, Chem. Phys. Lett., 1995, 243, 59–63 CrossRef CAS.
- J. H. Kiefer and R. Sathyanarayana, Vibrational Relaxation and Dissociation in the Perfluoromethyl Halides, CF3Cl, CF3Br, and CF3I, Int. J. Chem. Kinet., 1997, 29, 705–716 CrossRef CAS.
- N. S. Bystrov, A. V. Emelianov, A. V. Eremin and P. I. Yatsenko, Direct Measurements of Rate Coefficients for Thermal Decomposition of CF3I using Shock-Tube ARAS technique, J. Phys. D: Appl. Phys., 2018, 51, 1–8 CrossRef.
- T. I. Andreeva, S. V. Kuznetsova, A. I. Maslov, I. I. Sobel’man and V. N. Sorokin, Investigation of Reactions of Excited Iodine Atoms by Means of a Photodissociation Laser, Khim. Vys. Energ., 1972, 6, 418–424 CAS.
- C. N. Plum and P. L. Houston, Improved Isotope Separation in Laser Dissociation of Trifluoromethyl Halides: Scavenging of CF3 with HI, Appl. Phys., 1981, 24, 143–146 CAS.
- B. Abel, B. Herzog, H. Hippler and J. Troe, Infrared Multiphoton Excitation of CF3I. I. Transient Ultraviolet Absorption Study of After-Pulse Dissociation and Excited State Populations, J. Chem. Phys., 1989, 91, 890–899 CrossRef CAS.
- B. Abel, B. Herzog, H. Hippler and J. Troe, Infrared Multiphoton Excitation of CF3I. II. Collisional Energy Transfer of Vibrationally Highly Excited CF3I, J. Chem. Phys., 1989, 91, 900–905 CrossRef CAS.
- B. Abel, H. Hippler and J. Troe, Infrared Multiphoton Excitation Dynamics of CF3I.
I. Populations and Dissociation Rates of Highly Excited Rovibrational States, J. Chem. Phys., 1992, 96, 8863–8870 CrossRef CAS.
- B. Abel, H. Hippler and J. Troe, Infrared Multiphoton Excitation Dynamics of CF3I. II. Collisional Effects on Vibrational and Rotational State Populations, J. Chem. Phys., 1992, 96, 8872–8876 CrossRef CAS.
- J. Troe and V. G. Ushakov, Revisiting Falloff Curves of Thermal Unimolecular Reactions, J. Chem. Phys., 2011, 135, 054304 CrossRef CAS PubMed.
- J. Troe and V. G. Ushakov, Representation of “Broad” Falloff Curves for Dissociation and Recombination Reactions, Z. Phys. Chem., 2014, 228, 1–10 CAS.
- D. Feller, The Role of Databases in Support of Computational Chemistry Calculations, J. Comput. Chem., 1996, 17, 1571–1586 CrossRef CAS.
- K. L. Schuchardt, B. T. Didier, T. Elsethagen, L. Sun, V. Gurumoorthi, J. Chase, J. Li and T. L. Windus, Basis Set Exchange: A Community Database for Computational Sciences, J. Chem. Inf. Model., 2007, 47, 1045–1052 CrossRef CAS PubMed.
-
M. J. Frisch, et al., Gaussian 09, Revision A.02-SMP, Gaussian Inc., Wallingford, CT, 2009 Search PubMed.
- C. J. Cobos, A. E. Croce, K. Luther, L. Sölter, E. Tellbach and J. Troe, Experimental and Modeling Study of the Reaction C2F4 (+M) ↔ CF2 + CF2 (+M), J. Phys. Chem. A, 2013, 117, 11420–11429 CrossRef CAS PubMed.
- C. J. Cobos, L. Sölter, E. Tellbach and J. Troe, Shock Wave Study of the Thermal Dissociations of C3F6 and c-C3F6. I. Dissociation of Hexafluoropropene, J. Phys. Chem. A, 2014, 118, 4880–4888 CrossRef CAS PubMed.
- C. J. Cobos, K. Hintzer, A. Thaler, L. Sölter, E. Tellbach and J. Troe, Shock Wave and Theoretical Modelling of the Dissociation of CH2F2. I. Primary Processes, J. Phys. Chem. A, 2017, 121, 7813–7819 CrossRef CAS PubMed.
- C. J. Cobos, G. Knight, L. Sölter, E. Tellbach and J. Troe, Kinetic and Spectroscopic Studies of the Reaction of CF2 with H2 in Shock Waves, J. Phys. Chem. A, 2017, 121, 7827–7834 CrossRef CAS PubMed.
- C. J. Cobos and J. Troe, Theory of Thermal Unimolecular Reactions at High Pressures. II. Analysis of Experimental Results, J. Chem. Phys., 1985, 83, 1010–1015 CrossRef CAS.
- A. I. Maergoiz, E. E. Nikitin, J. Troe and V. G. Ushakov, Classical Trajectory and Statistical Adiabatic Channel Study of the Dynamics of Capture and Unimolecular Bond Fission. V. Valence Interactions between Linear Rotors, J. Chem. Phys., 1998, 108, 9987–9998 CrossRef CAS.
- M. W. Chase, NIST-JANAF Thermochemical Tables, 4th edition, J. Phys. Chem. Ref. Data, Monogr., 1998, 9, 1–1951 Search PubMed.
- J. Troe, Predictive Possibilities of Unimolecular Rate Theory, J. Phys. Chem., 1979, 83, 114–126 CrossRef CAS.
- J. Troe, Theory of Thermal Unimolecular Reactions in the Falloff Range. I. Strong Collision Rate Constants, Ber. Bunsen-Ges., 1983, 87, 161–169 CrossRef CAS.
-
J. B. Burkholder, J. P. D. Abbatt, R. E. Huie, M. J. Kurylo, D. M. Wilmouth, S. P. Sander, J. R. Barker, C. E. Kolb, V. L. Orkin and P. H. Wine, Chemical Kinetics and Photochemical Data for Use in Atmospheric Studies Evaluation Number 18, JPL Publication 15-10, Jet Propulsion Laboratory, Pasadena, 2015.
-
E. Goos, A. Burcat and B. Rusic, Extended Third Millenium Ideal Gas and Condensed Phase Thermochemical Database for Combustion with Updates from Active Thermochemical Tables. http://burcat.technion.ac.il/div, September 2005, January 2015.
- C. J. Cobos, A. E. Croce, K. Luther and J. Troe, Experimental and Modelling Study of the Unimolecular Thermal Decomposition of CHF3, Z. Phys. Chem., 2011, 225, 1019–1028 CrossRef CAS.
- G. Knight, L. Sölter, E. Tellbach and J. Troe, Shock Wave and Modeling Study of the Reaction CF4 (+M) ↔ CF3 + F (+M), Phys. Chem. Chem. Phys., 2016, 18, 17592–17596 RSC.
- C. J. Cobos, G. Knight, L. Sölter, E. Tellbach and J. Troe, Experimental and Modeling Study of the Multichannel Thermal Decomposition of CH3F and CH2F, Phys. Chem. Chem. Phys., 2018, 20, 2627–2636 RSC.
- B. Abel, L. Brouwer, B. Herzog, H. Hippler and J. Troe, Direct Measurement of Near-Threshold Rate Constants for Unimolecular Dissociation of CF3I after IR Multiphoton Excitation, Chem. Phys. Lett., 1986, 127, 541–546 CrossRef CAS.
- S. L. Dobychin, V. I. Mashendzhinov, V. I. Mishin, V. N. Semenov and V. S. Shpak, Kinetics of Thermal Decomposition of Perfluoroalkyl Iodides and D(R-I) Binding Energy, R – CF3, C2F5, n-C3F7, iso-C3F7, n-C4F9, tert-C4F9, Dokl. Akad. Nauk SSSR, 1990, 312, 1166–1168 CAS.
- G. S. Laurence, Thermal and Photochemical Exchange of Iodine with Trifluoro-methyl Iodide, Trans. Faraday Soc., 1967, 63, 1155–1165 RSC.
- J. C. Amphlet and E. Whittle, Reactions of Trifluoromethyl Radicals with Iodine and Hydrogen Iodide, Trans. Faraday Soc., 1967, 63, 2695–2701 RSC.
- D. Britton, N. Davidson and G. Schott, Shock Waves in Chemical Kinetics. The Rate of Dissociation of Molecular Iodine, Discuss. Faraday Soc., 1954, 17, 58–68 RSC.
- D. Britton, N. Davidson, W. Gehman and G. Schott, Shock Waves in Chemical Kinetics: Further Studies on the Rate of Dissociation of Molecular Iodine, J. Chem. Phys., 1956, 25, 804–809 CrossRef CAS.
- C. J. Cobos, A. E. Croce, K. Luther and J. Troe, Temperature and Pressure Dependence of the Reaction 2 CF3 (+M) ↔ C2F6 (+M), J. Phys. Chem. A, 2010, 114, 4748–4754 CrossRef CAS PubMed.
- G. A. Skorobogatov, V. K. Khripun and A. G. Rebrova, Isochoric Isothermal Pyrolysis of Trifluoroiodomethane: CF3° Recombination Kinetics, Kinet. Catal., 2008, 49, 466–473 CrossRef CAS.
- G. A. Skorobogatov, A. G. Rebrova and V. K. Khripun, Rate Constant of the Recombination CF3° Radicals in a Gas (He, Ar, N2, or CF3I), Kinet. Catal., 2010, 51, 485–491 CrossRef CAS.
- K. Glänzer, M. Maier and J. Troe, Shock-Wave Study of the High-Temperature UV Absorption and the Recombination of CF3 Radicals, J. Phys. Chem., 1980, 84, 1681–1686 CrossRef.
- A. P. Modica, Electronic Oscillator Strength of CF3, J. Phys. Chem., 1968, 72, 4594–4598 CrossRef CAS.
- P. Sulzer and K. Wieland, Intensitätsverteilung eines kontinuierlichen Absorptionsspektrums in Abhängigkeit von Temperatur und Wellenzahl, Helv. Phys. Acta, 1951, 25, 653–676 Search PubMed.
- J. A. Myer and J. A. R. Samson, Absorption Cross Section and Photoionization Yield of I2 between 1050 and 2200 Å, J. Chem. Phys., 1970, 52, 716–718 CrossRef CAS.
- A. Saiz-Lopez, R. W. Saunders, D. M. Joseph, S. H. Ashworth and J. M. C. Plane, Absolute Absorption Cross-Section and Photolysis Rate of I2, Atmos. Chem. Phys., 2004, 4, 1443–1450 CrossRef CAS.
- L. G. Piper, W. J. Marinelli, W. T. Rawlins and B. D. Green, The Excitation of IF (B
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3Π0+) by N2 (A
3Π0+) by N2 (A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3Σu+), J. Chem. Phys., 1985, 83, 5602–5609 CrossRef CAS.
3Σu+), J. Chem. Phys., 1985, 83, 5602–5609 CrossRef CAS.
- W. J. Marinelli and L. G. Piper, Franck-Condon Factors and Absolute Transition Probabilities for the IF (B3Π0+X1Σ+) Transition, J. Quant. Spectrosc. Radiat. Transfer, 1985, 34, 321–330 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: (1) Modelling of rate constants and (2) modelling of spectral properties. See DOI: 10.1039/c9cp04771a |
|
| This journal is © the Owner Societies 2019 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *bc
*bc
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 930 K/T) s−1
930 K/T) s−1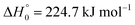 33). Using 〈ΔE〉/hc ≈ −100 cm−1 independent of temperature, such as that determined experimentally for M = Ar in ref. 21, and employing the formalism of ref. 34, limiting low-pressure rate constants
33). Using 〈ΔE〉/hc ≈ −100 cm−1 independent of temperature, such as that determined experimentally for M = Ar in ref. 21, and employing the formalism of ref. 34, limiting low-pressure rate constants![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 360 K/T)cm3 mol−1 s−1
360 K/T)cm3 mol−1 s−1
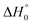 by 4 kJ mol−1 decreases k1 (at [Ar] = (5 × 10−5–1.5 × 10−4) mol cm−3) by a factor of 1.5–2 (decreasing
by 4 kJ mol−1 decreases k1 (at [Ar] = (5 × 10−5–1.5 × 10−4) mol cm−3) by a factor of 1.5–2 (decreasing  by 4 kJ mol−1 increases k1 by the same factor). Measurements and modelled (unadjusted) falloff curves, therefore, agree better than this uncertainty and confirm the validity of the thermochemistry used in the literature.33,36,37 Nevertheless, the finer details of the shape of the falloff curves should also be noted. In particular, different approaches of k1 toward the limiting low- and high-pressure rate constants (k1,0 and k1,∞, resp.) are to be accounted for when the more recent falloff expressions from ref. 22 and 23 are used instead of the older forms from ref. 34. The modelling of the falloff curves and their comparison with the ARAS results from ref. 15 in the foregoing section has been described in detail, because it forms the basis for an analysis of the decomposition mechanism under conditions of higher reactant concentrations. This analysis will be made after new experiments are described in the following section.
by 4 kJ mol−1 increases k1 by the same factor). Measurements and modelled (unadjusted) falloff curves, therefore, agree better than this uncertainty and confirm the validity of the thermochemistry used in the literature.33,36,37 Nevertheless, the finer details of the shape of the falloff curves should also be noted. In particular, different approaches of k1 toward the limiting low- and high-pressure rate constants (k1,0 and k1,∞, resp.) are to be accounted for when the more recent falloff expressions from ref. 22 and 23 are used instead of the older forms from ref. 34. The modelling of the falloff curves and their comparison with the ARAS results from ref. 15 in the foregoing section has been described in detail, because it forms the basis for an analysis of the decomposition mechanism under conditions of higher reactant concentrations. This analysis will be made after new experiments are described in the following section.

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 790 K/T) s−1 modelled with
790 K/T) s−1 modelled with  for [Ar] ≈ 1.5× 10−4 mol cm−3 over the range 1000–1050 K; (b) reverse reaction: equilibrium constant from ref. 33; (c) k2 = 7.6 × 1012exp(−9500 K/T) cm3 mol−1 s−1 for 400–900 K, from ref. 42–44; (d) k3 = [Ar]8.8 × 1013exp(−14
for [Ar] ≈ 1.5× 10−4 mol cm−3 over the range 1000–1050 K; (b) reverse reaction: equilibrium constant from ref. 33; (c) k2 = 7.6 × 1012exp(−9500 K/T) cm3 mol−1 s−1 for 400–900 K, from ref. 42–44; (d) k3 = [Ar]8.8 × 1013exp(−14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 950 K/T) s−1 for 1080–1570 K and [Ar] = (0.3–1) × 10−6 mol cm−3, from ref. 45 and 46; (e) k4 ≤ 1.2 × 108 cm3 mol−1 s−1 for 300 K, from ref. 16; (f) k−5 ≤ 1.2 × 1013 cm3 mol−1 s−1 for 1200 K and [Ar] = 10−4 mol cm−3 from ref. 47–49)
950 K/T) s−1 for 1080–1570 K and [Ar] = (0.3–1) × 10−6 mol cm−3, from ref. 45 and 46; (e) k4 ≤ 1.2 × 108 cm3 mol−1 s−1 for 300 K, from ref. 16; (f) k−5 ≤ 1.2 × 1013 cm3 mol−1 s−1 for 1200 K and [Ar] = 10−4 mol cm−3 from ref. 47–49)

 for IF instead of 148.8 kJ mol−1 for I233). Its calculated oscillator strength is even larger than that of I2 in the range of the visible spectrum (see the ESI†). Unfortunately, so far only information from the emission spectra of IF at 450–650 nm is available (see, e.g.ref. 55 and 56), but this looks consistent with the present identification of the additional species. IF might be formed in the reaction
for IF instead of 148.8 kJ mol−1 for I233). Its calculated oscillator strength is even larger than that of I2 in the range of the visible spectrum (see the ESI†). Unfortunately, so far only information from the emission spectra of IF at 450–650 nm is available (see, e.g.ref. 55 and 56), but this looks consistent with the present identification of the additional species. IF might be formed in the reaction .33 However, this appears not to be too relevant for the high temperatures of the present work. Nevertheless, our identification of an additional absorber in Fig. 5–7 remains uncertain, such that more work is required here.
.33 However, this appears not to be too relevant for the high temperatures of the present work. Nevertheless, our identification of an additional absorber in Fig. 5–7 remains uncertain, such that more work is required here.


![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3Π0+) by N2 (A
3Π0+) by N2 (A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3Σu+), J. Chem. Phys., 1985, 83, 5602–5609 CrossRef CAS.
3Σu+), J. Chem. Phys., 1985, 83, 5602–5609 CrossRef CAS.
