Stabilization of aqueous graphene dispersions utilizing a biocompatible dispersant: a molecular dynamics study

Abstract

Flavin mononucleotide sodium (FMNS) was recently reported as a highly efficient dispersant for the exfoliation of defect-free, few-layer, stabilized aqueous graphene dispersions. Most importantly, FMNS is innocuous and eco-friendly and can facilitate biomedical applications of graphene. Complementing those experimental studies, the influence of FMNS molecules on the aggregation behavior of graphene flakes in solution is investigated via all-atom molecular dynamics simulations. The stabilizing role of FMNS is demonstrated by the potential of mean force calculations for pairs of graphene flakes covered by FMNS molecules. These results indicate that the optimal amount ratio between FMNS molecules and carbon atoms in monolayer graphene is about 0.026 leading to a surface coverage of 0.34 FMNS molecules per nm² on the graphene flakes. Overall the simulations support the high efficiency of FMNS as a surfactant compared to other surfactants.

---

1. Introduction

Graphene, a two-dimensional carbon-based nanomaterial with only one atom-layer thickness, has attracted extensive attention due to its extraordinary physical and chemical properties.^1,2 Moreover, it has shown great potential for biomedical applications, especially for drug delivery, biosensing and tissue engineering.^3–6

One of the big challenges remains producing high-quality pristine graphene. Numerous bottom-up and top-down approaches have been developed, including micromechanical cleavage,⁷ chemical vapor deposition (CVD),⁸ epitaxial growth on SiC substrates,⁹ electrochemical approaches,¹⁰ and the chemical reduction of graphene oxide.¹¹ Among those approaches, the liquid-phase exfoliation of graphene from graphite, assisted by dispersants, has gained prominence recently.^12,13 This method can provide stabilized graphene in aqueous solution with high yield and good quality, which can advance the bio-medical applications of graphene.^14,15 In this context, various dispersants have been investigated, including ionic dispersants (such as sodium cholate (SC),¹⁶ sodium deoxycholate (SDC),¹⁷ sodium dodecylsulfate (SDS),¹⁸ cetyltrimethylammonium bromide (CTAB),¹⁹ sodium dodecylbenzene sulfonate (SDBS)²⁰), non-ionic/polymeric dispersants (such as Tween 80, Triton X-100 and polyvinylpyrrolidone^21,22), as well as larger biomolecules (including proteins/peptides,²³ nucleotides/DNA²⁴).

Due to the important role of the dispersants for liquid-phase exfoliation, numerous theoretical studies have focused on the aggregation behavior and the energetic barrier between graphene flakes in the presence of dispersants.^25–31 Typically, classical molecular dynamics (MD) simulations were performed to gain detailed information on the influence of the dispersants. For example, the aggregational tendencies of graphene nanoribbons with hydrogen terminated edges were compared with polyethylene glycol and n-alkoxy chains substituted along the edge of graphene.²⁵ The self-assembly of SDBS on graphene flakes and the effect of surface coverage on the aggregated structures was studied.²⁸ In particular with respect to the interaction between covered graphene flakes, it was observed that an enhanced repulsive potential of mean force (PMF) can be obtained by increasing the SDS surface coverage or by introducing the electrolyte CaCl₂.²⁶ More generally, the interfacial interaction for graphene exfoliation in different organic solvent media²⁷ and the electrostatic interactions of graphene stabilized in SC dispersant aqueous solution^29,31 were studied.

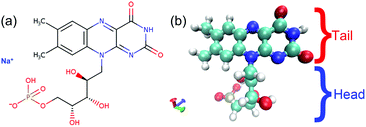
For biological applications, however, most of the abovementioned dispersants are not biodegradable or biocompatible.^32–34 Very recently, S. Villar-Rodil et al. reported an innocuous and readily available derivative of vitamin B₂,³⁵ flavin mononucleotide sodium (FMNS, C₁₇H₂₀N₄NaO₉P), shown in Fig. 1, as a highly efficient biocompatible dispersant for the exfoliation and production of stable aqueous dispersions of defect-free, few-layer graphene flakes. The attained graphene concentration in aqueous solution was up to 50 mg mL⁻¹ using a relatively low amount of FMNS compared with abovementioned dispersants, and the processed graphene films presented excellent electrical conductivity.³⁵ This benign and readily available biocompatible dispersant outperformed the other biomolecules in the preparation of stabilized graphene in aqueous solution, and showed great potential for bio-medical applications.^36–40 To the best of our knowledge, the role of the FMNS dispersant for the stabilization of graphene flakes have not been fully understood until now.

Fig. 1 (a) Chemical structure of FMNS. (b) Ball-and-stick model representation of FMNS. The isoalloxazine ring group is defined as the FMNS tail, while both the ribitol group and phosphate group are defined as the FMNS head. Color code: nitrogen (blue), oxygen (red), carbon (cyan), hydrogen (white) and phosphorous (tan).

In this work, we theoretically study the role of the FMNS molecules for the stabilization of graphene flakes in dispersions. Using classical all-atom MD simulations, the aggregation morphology of FMNS on monolayer graphene flakes is investigated. Moreover, the interaction between graphene flakes covered by FMNS is quantified by the PMF, which is also utilized to explain the graphene stabilization mechanism assisted by the FMNS molecules. Finally, the relationship between the surface coverage of monolayer graphene by FMNS molecules and the amount of FMNS in solution is studied to find the optimal FMNS concentration which stabilizes the monolayer graphene flakes.

The structure of this article is as follows: Firstly, the morphology of FMNS on a monolayer graphene flake is calculated via all-atom molecular dynamics simulations. The radial distribution function (RDF) and the density distribution of FMNS molecules, as well as their orientations are discussed. Then the PMF of pairs of parallel graphene flakes is calculated. Finally, according to the PMF results, the relationship between FMNS surface coverage on monolayer graphene flake and FMNS concentration is discussed.

2. Simulation methods

The simulation work was divided into two parts: the simulation of FMNS morphology on monolayer graphene flakes, and the calculation of the PMF of pairs of graphene flakes coated with FMNS. All calculations were performed with GROMACS 5.1.2.^41–44 Water molecules and FMNS molecules were modelled adopting the SPC/E model⁴⁵ and the OPLS-AA force field,⁴⁶ respectively. The OPLS-AA force field has been used for systems involving graphene and other surfactants before.^29,31 The molecular topology of FMNS was obtained from the LigParGen server by submitting the PDB file of the FMNS (Na⁺ excluded).^47,48 Force field calculations were performed using 1.14 × CM1A method for charged molecules.⁴⁹ Bond lengths in the FMNS were constrained applying the parallel version of the LINCS algorithm while the bond lengths and angles in water molecule were constrained applying the SETTLE algorithm.⁵⁰ A monolayer graphene flake (size 4 nm × 4 nm, containing 680 carbon atoms) was selected as a representative monolayer graphene system. The position and orientation of the flakes were constrained during the simulation, wherein all carbon atoms were treated as uncharged Lennard-Jones (LJ) spheres using LJ parameters from the literature.⁵¹ van der Waals attraction and hard-core steric repulsion were treated with a cut-off distance of 1.0 nm.^52,53 Long-range electrostatic interactions were treated utilizing the particle mesh Ewald (PME) approach.^54,55 The simulation was conducted under the NPT ensemble (the number of atoms, pressure of 1 bar, temperature of 300 K, are constant) to mimic the experimental conditions. The velocity-rescaled Berendsen thermostat was applied to maintain a constant temperature⁵⁶ and the Berendsen barostat was applied to maintain a constant pressure in the system,⁴⁵ respectively. Periodic boundary conditions were applied in all three directions. The timestep during the whole simulation was 2 fs and the trajectory was saved every 2000 steps.

For the FMNS morphology on the single layer graphene flake, three cases with different amount of the FMNS molecules were studied, wherein the graphene flake size was the same. The simulation box size of the cases containing 8 FMNS and 18 FMNS was 9 nm × 9 nm × 9 nm while the box size of the case containing 36 FMNS was 12 nm × 12 nm × 12 nm. For detailed information on the simulation parameters refer to Table S1 in the ESI.† The FMNS molecules were aligned parallel to the graphene flake in each box to obtain the initial configuration for each case.^57–59

For the calculation of the PMF of pairs of graphene flakes coated by FMNS, the final configurations of the morphology simulations which had the largest FMNS surface coverage were employed as the starting configuration. A larger simulation box of size 12 nm × 12 nm × 12 nm was created, and the same configuration of the graphene flake with adsorbed molecules at the distance of 3 nm away from the original one was replicated. Subsequently, the water molecules and sodium counter ions were introduced into this box.

In order to obtain a series of configurations with different distances d between the centers of mass (COM) of the graphene flakes, steered MD was used.^60,61 In detail, we fixed one graphene flake, in x/y/z direction and the other graphene flake, only in y/z direction. A harmonic potential with a force constant k = 600 000 kJ mol⁻¹ nm⁻² was applied to the COM of the second flake, which pulled it close to the first flake by setting a velocity of 0.005 nm ps⁻¹. The pulling time was based on the distance d between the graphene flake at the beginning. Due to the very slow pulling rate, the FMNS molecules adsorbed on the surface of the graphene flakes could freely reorganize on the graphene flake surface.⁶² In this case, we obtain a series of configurations with different COM distances in an “evolutionary manner”.⁵⁷ The constraint pulling was employed to calculate the interaction force between graphene flakes along the x axis.⁴³ The PMF was then calculated by numerically integrating the constraint pulling force using the trapezoidal rule at different distances, as descripted in a previous publication.³⁰

3. Results and discussions

3.1. Morphology

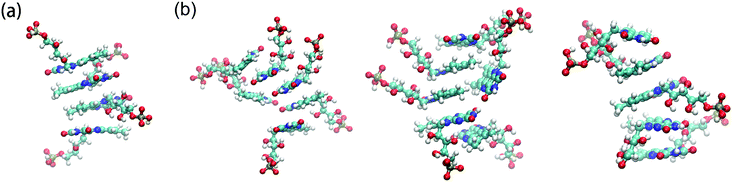
To investigate the morphology of FMNS on the surface of the graphene flakes, three different cases are studied with 8, 18 and 36 FMNS molecules, respectively. The solvent accessible surface areas (SASAs) of the flavin mononucleotide ions and graphene as a function of time was calculated to verify that all the simulations have reached equilibrium.^63,64 From the SASA results (see Fig. S1 in the ESI†), it can be seen that the systems have reached equilibrium after about 80 ns simulation time. Correspondingly, the morphology analysis is extracted from the last 20 ns of each trajectory.

The representative morphology results are shown in Fig. 2. For the case with 8 FMNS molecules, as shown in Fig. 2(a), it is found that all FMNS molecules aggregate on the surface of the graphene flake. The tail groups of FMNS are adsorbed to the graphene surface parallelly while the head groups extend toward the water. This feature is similar to the behavior of FMNS on a single wall carbon nanotube (SWCNT) surface.⁶² For the case with 18 FMNS molecules, as shown in Fig. 2(b), most of the FMNS molecules aggregate on the graphene surface. The orientation behavior of the tail and the head groups are the same as in the case with 8 FMNS. However, we observe the formation of several clusters of FMNS molecules. For the case with 36 FMNS molecules, as shown in Fig. 2(c), only a small portion of the FMNS molecules are observed to stick to the surface of the graphene flake parallelly while most of the FMNS molecules favor to stay in the solvent in the form of clusters. This finding provides further evidence that FMNS molecules possess a tendency to form dimer structures at high concentrations, which agrees well with the experimental results.^65,66

Fig. 2 Post-equilibrated representative morphology snapshots of FMNS molecules and the graphene flake (yellow) in three different cases: side views of cases containing (a) 8, (b) 18 and (c) 36 FMNS molecules. Sodium counterions are shown in green and water molecules are not shown for clarity.

As shown in Fig. 3, the unabsorbed FMNS molecules tend to form sandwich-like clusters which is favored by π–π interactions. This behavior is different from other dispersants which tend to form a mono-dispersant layer at low concentrations and hemicylindrical micelles or micelles at high concentrations.^67–69 Meanwhile, we note that the negatively charged FMNS head groups favor to keep away from each other due to the electrostatic repulsion.

Fig. 3 FMNS cluster formation in different cases: (a) representative FMNS cluster in case of 18 FMNS, (b) representative FMNS clusters in case of 36 FMNS in the simulation box.

In order to characterize the space distribution of the head and tail groups around the flakes, their radial distribution functions relative to the COM of the graphene flake are shown in Fig. 4. From the peak positions shown in Fig. 4(a)–(c), it can be seen that the tail groups prefer to approach to the graphene surface while the head groups prefer to keep away from graphene, corroborating the morphology observation in Fig. 2. Among these cases, the tail group in case of 8 FMNS molecules shows the strongest peak at around 0.41 nm while the tail group in case of 36 FMNS molecules shows the weakest peak at around 0.44 nm. The first peak position for the tail group has a shift away from graphene with increasing amount of FMNS molecules. Besides, the second peaks for the tail group appear due to the FMNS cluster formation except in the case of 8 FMNS. In case of 18 FMNS, the first peak and the second peak for the tail group are found at 0.42 nm and 0.72 nm, respectively. In case of 36 FMNS, the second peak is found at around 5.80 nm. The head groups in these cases show similar behavior as the tail groups. The sodium counterions were mostly close to the head groups because of the electrostatic attraction.

Fig. 4 RDF of tail and head groups as function of the relative distance to the COM of the graphene flake in different cases: (a) 8 FMNS molecules (b) 18 FMNS molecules and (c) 36 FMNS molecules.

Further, the density distributions of different groups in the three cases are investigated to characterize the different distributions along x axis, as shown in Fig. 5(a)–(c). For the case of 8 FMNS molecules, shown in Fig. 5(a), there are two strong peaks in the density distribution profile of both the tail groups and the head groups, which are very close to the COM position of the graphene flake (x = 0). The right peaks of both groups are higher than the left peaks, which is consistent with the morphology observation in Fig. 2(a): three molecules on the left side and five molecules on the right side. Furthermore, the peak position of the tail groups is closer than the peak position of the head groups to the graphene flake, which can be explained by the hydrophilic behavior of the phosphate group in the head of FMNS which prefer to stay in the solvent while the hydrophobic nature of the isoalloxazine group in the tail of FMNS which tends to stick to the graphene surface. For the density distribution profile of the sodium counterions, there are two main peaks observed close to the positions of the head groups due to the electrostatic interaction.

Fig. 5 Density distribution of the different groups along x coordinate in different cases: (a) 8 FMNS molecules, (b) 18 FMNS molecules and (c) 36 FMNS molecules. The Graphene flake is fixed at position x = 4.5 nm in case of 8 and 18 FMNS molecules, and at x = 6.0 nm in case of 36 FMNS molecules. (d) Tail group orientation distribution in the three different cases, the inset shows that the orientation angle θ.

In the case of 18 FMNS, shown in Fig. 5(b), additionally to the two main peaks close to the COM of the graphene flake (x = 0 nm), one more peak is found near x = 3.2 nm, which is the result of the small FMNS cluster formation. This corroborates the morphology shown in Fig. 2(b). From Fig. 5(c), in addition to the peaks located near the COM of the graphene flake (x = 0) in the profiles of both groups, several peaks can be identified away from the COM of the graphene flake (x = −2 nm and x = 4 nm). These originate from the FMNS-cluster formation as seen in Fig. 2(c). To quantify the precise orientation of the tail groups relative to the graphene flake, we use the angle θ as illustrated in Fig. 5(d). We define a tail vector connecting two nitrogen atoms in the tail group and the angle θ is the angle between the tail vector and the positive direction of the x axis, as schemed in the inset in Fig. 5(d). For the cases of 8 FMNS and 18 FMNS molecules, the orientation angle θ is mainly concentrated around 90°, which means that the tail groups of the FMNS molecules aggregated on the graphene flake favor to stay parallel to the surface. However, for the case of 36 FMNS molecules, most of them form small clusters and are distributed uniformly in the box. Only for the molecules aggregated on the surface of graphene flake, the orientation angle is θ = 90°.

3.2. Potential of mean force

The PMF is used to characterize the interaction between two graphene flakes in the presence of an aqueous medium and FMNS molecules. A positive PMF implies an effective repulsion while a negative PMF indicates an effective attraction of the flakes.⁶² The PMF results for the cases considered in this study are presented in Fig. 6. The three profiles in Fig. 6(a) are obtained for high FMNS surface coverage, low surface coverage, and no surface coverage, respectively. Here, we used the final configuration of the case of 18 FMNS as the starting configuration for high surface coverage, for which there are 11 FMNS molecules adsorbed on the surface of each flake. All the FMNS molecules whose tail groups are located within 7 nm from the graphene flake are defined as adsorbed molecules. For low surface coverage we decreased the number of adsorbed FMNS molecules to 6 molecules on each flake as the starting configuration. This corresponds to surface coverages of 0.34 molecules per nm² and 0.19 molecules per nm², respectively. The PMF of the pairs of bare graphene flakes without FMNS was done for comparison. The PMF has been set to zero at the large COM distance between pairs of graphene flakes (d = 3.0 nm).

Fig. 6 (a) The profiles of PMFs of pairs of graphene flakes coated by or without FMNS molecules. Inset shows the distance d between a pair of parallel graphene flakes. (b) The zoom of the dashed box in the (a), seven critical positions are labelled on the profile.

As one can see from Fig. 6(a), the PMF of bare graphene flakes displays a pronounced minimum at the distance of d = 0.35 nm which corresponds to the typical interlayer distance in graphite. From 0.35 nm to 3.0 nm, the PMF is negative, which indicates an attractive interaction between two bare graphene flakes in solution. The well depth of the PMF at the minimum is −2268 kJ mol⁻¹. Considering the area of graphene flake, the PMF per unit area is −142 kJ mol⁻¹ nm⁻², which is in good agreement with the previously reported PMF per unit area of −153 kJ mol⁻¹ nm⁻².⁷⁰

For the case of low surface coverage, the PMF shows attractive behavior from d = 0.45 nm to d = 1.10 nm, and it shows repulsive behavior from d = 1.10 nm to d = 3.0 nm. It reaches its highest energy barrier of +33 kJ mol⁻¹ at d = 1.25 nm. For high surface coverage, one sees that the adsorbed FMNS molecules cause relatively strong repulsion already at d = 0.7 nm, which can hinder the aggregation of graphene flakes efficiently. The highest repulsive energy of +705 kJ mol⁻¹ appears at d = 0.68 nm (the shortest distance with reliably calculated PMF).³¹ The first local maximum energy barrier appears at d = 1.18 nm and the PMF energy barrier reaches up to 164 kJ mol⁻¹. The PMF energy barrier per area is 10.25 kJ mol⁻¹ nm⁻².

To evaluate the influence of FMNS on the dispersion and stabilization of the exfoliated graphene flakes, we compare the calculated surface coverage of graphene flakes by different conventional dispersants at roughly the same PMF energy barrier, as shown in Table S3 (ESI†). To achieve the PMF energy barrier of around 10 kJ mol⁻¹ nm⁻², the surface coverage of graphene flake by FMNS is 0.34 molecules per nm² as shown above, while the surface coverage of graphene flake by SDBS is 0.58 molecules per nm²,²⁸ and the surface coverage of graphene flake by SC is 0.49 molecules per nm²,³¹ respectively. Those theoretical results provide evidence that FMNS is performing better than the other commonly used dispersants with respect to the dispersion and stabilization of exfoliated graphene flakes. This result is consistent well with the reported experimental work which showed that FMNS is an extremely efficient dispersant for the preparation of dispersions of few-layer aqueous graphene flakes.^35,36,71

Fig. 6(b) is a zoom into the dashed frame in Fig. 6(a) with seven critical points marked on the profile. On the PMF profile of graphene flakes with high surface coverage (red line), positions II, IV, VI denote local energy wells while positions III and V correspond to local energy barriers. On the PMF profile of graphene flakes with low surface coverage, positions III and V indicate energy barrier positions while position VI is a local energy well. The density distribution of the FMNS molecules in the case of high surface coverage corresponding to the 6 critical positions are plotted in Fig. 7, and the inset images are the representative snapshots. With decreasing distance d between flakes from position VI to position I, the density distribution peak of the FMNS molecules between the two graphene flakes decrease from two broad peaks to one sharp peak. For the distance with a local high energy barrier, including positions III and V, we find that the head groups of the FMNS between the two flakes try to aggregate tightly and form one strong density peak, just like a fastened zipper with two head group chains. However, for the distances of local energy wells, including positions II, IV and VI, we find the head groups of the FMNS between the two flakes kept well and so two separate peaks show on the density profile, just like an unfastened zipper with two head groups chains. This agrees well with previously reported results.^26,28 This can also be seen on the corresponding morphology image. In order to further verify this behavior, we plot the density map for the FMNS molecules between the two graphene flakes to see the overlap of the molecules, as shown in Fig. 7. We find the maximum density values for the positions of the energy barriers are higher than those at the positions with the next energy wells. The maximum values of the density are given in Table S2 in the ESI.†⁶² At the same time, we also plot the density distribution of the FMNS in the cases of low surface coverage as well as the density map of the FMNS, as shown in Fig. 8. Although position I shows a low negative PMF, there is one density peak found in Fig. 8(i), because FMNS molecules between two graphene flakes are much more mobile and some can even can escape the volume between two graphene flakes.

Fig. 7 (left panel) Density distribution of FMNS molecules along x coordinate in case of 11 FMNS molecules on each graphene flake. The red lines marked the position of the graphene flakes. The inset images show corresponding morphologies. The color code is the same as in Fig. 1, water molecules are not shown for clarity. (right panel) The 2D density map of the FMNS molecules existed in the confined volume between a pair of parallel graphene flakes with 11 FMNS molecules on each flake for the critical positions I to VI. The maximum value of density for each image can be found in Table S2 in the ESI.†

Fig. 8 (left panel) Density distribution of FMNS molecules along x coordinate in case of 6 FMNS molecules on each graphene flake. (right panel) The density map of the FMNS molecules located in the confined volume between a pair of parallel graphene flakes with 6 FMNS molecules on each flake for the critical positions I, III, IV and VI. The maximum value of density for each image can be found in Table S2 in the ESI.†

3.3. Surface coverage and optimal dispersant concentration

From the morphology results shown in Fig. 3, we already concluded that when we increase the amount of FMNS molecules, some of them aggregate to form clusters. Thus, not all molecules in the solution will be adsorbed on the flake. The final surface coverage of a single flake with FMNS molecules is shown in Fig. 9. Here, the surface coverage is defined as the total number of adsorbed FMNS molecule per area of the graphene flake. In the three cases considered before, the total available surface area for FMNS adsorption is the area of both sides of the graphene flake, i.e. 32 nm². Adsorbed molecules on the graphene flake are supposed to keep graphene flakes away from each other in an aqueous medium via electrostatic repulsion and stabilize graphene dispersions. From the results shown in Fig. 9, we can see an unusual trend different from the expected results: with the number of FMNS molecules in the solution increasing, the surface coverage of graphene increases first and then decrease again, this can be attributed to the cluster formation in case of a sufficiently high concentration of FMNS molecules, as already shown in Fig. 2(c). Experimentally, D. Frąckowiak and collaborators have previously reported that the FMNS molecules tend to form dimers in an aqueous media, and a large fraction of FMNS molecules participate in forming dimeric structures as the FMNS concentrations increase.⁶⁵ Our simulation results are consistent with this experimentally observed behavior.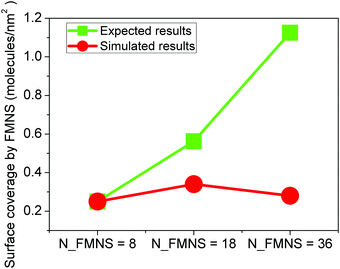

Fig. 9 Surface coverage of graphene flakes by FMNS molecules in three different cases with N = 8, 18 and 36 molecules in the simulation box.

The formation of FMNS dimers and larger clusters prohibits adsorption of FMNS molecules on the graphene flake surface.³⁵ Consequently, a lower surface coverage of FMNS molecules on the graphene flake is obtained. As shown in Fig. 6, a higher surface coverage implies a stronger repulsion of flakes to avoid aggregation. In case of lower surface coverage, the repulsion is lower and the graphene flakes tend to aggregate more easily. This observation might explain the origin of the observed relationship between the concentration of FMNS and the stabilization of graphene dispersions in a recent experimental work.³⁵ Our simulation results indicate that the optimal amount ratio between FMNS molecules and carbon atoms in monolayer graphene is 0.026 shown in the case of N_FMNS = 18 and achieve the highest surface coverage of graphene flake by FMNS (0.34 molecules per nm²).

4. Conclusions

In this work, the morphology of FMNS molecules on graphene flakes has been investigated using all-atom MD simulations. It was found that the tail group of the FMNS molecules prefers to stick to the graphene flake while the head group prefers to extend toward the solvent, consistent with their hydrophobic and hydrophilic nature, respectively.

The calculation of the PMF of a pair of graphene flakes covered with adsorbed FMNS molecules has been carried out to evaluate influence of FMNS on the dispersion and stabilization of graphene flakes. To achieve approximately the same PMF energy barrier of 10 kJ mol⁻¹ nm⁻², the surface coverage of graphene flakes by FMNS molecules is 44% lower than by SC molecules, and 71% lower than by SDBS molecules, respectively, which illustrates the superior dispersion and stabilizing performance for exfoliated graphene flake dispersion. At a high surface coverage, graphene flakes repel each other which leads to the stabilization of graphene dispersions, and at lower coverage graphene flakes can agglomerate easily.

The formation of FMNS clusters can suppress the adsorption of FMNS molecules on the graphene surface in the case of high concentration of FMNS and reduce the surface coverage of graphene flake. From our simulations we determine the optimal amount ratio between FMNS molecules and carbon atoms in monolayer graphene to be 0.026 which yields the highest surface coverage of the graphene flakes by FMNS (0.34 molecules per nm²). These simulation results provide a basis for the understanding of graphene exfoliation assisted by FMNS-like dispersant and paves a path to design highly efficient and biocompatible dispersants for liquid phase exfoliation of defect-free, few layers graphene.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Shirong Huang thanks H. Yang for his instructional help on simulations. Shirong Huang also thanks Y. Liu and J. Wang for useful discussions of results. The authors acknowledge the funding support from the China Scholarship Council (CSC) and the support from EU H2020-MSCA-RISE-2016 project CARBO IMmap (no. 734381) and by the German Federal Ministry of Education and Research (grant No. 031B0298). We also acknowledge the computational resources provided by the Centre of Information Services and High-Performance Computing (ZIH) of Dresden University of Technology.

References

1. Y. W. Zhu, S. Murali, W. W. Cai, X. S. Li, J. W. Suk, J. R. Potts and R. S. Ruoff, Adv. Mater., 2010, 22, 3906–3924.
2. K. H. Liao, Y. S. Lin, C. W. Macosko and C. L. Haynes, ACS Appl. Mater. Interfaces, 2011, 3, 2607–2615.
3. T. Kuila, S. Bose, P. Khanra, A. K. Mishra, N. H. Kim and J. H. Lee, Biosens. Bioelectron., 2011, 26, 4637–4648.
4. G. Reina, J. M. Gonzalez-Dominguez, A. Criado, E. Vazquez, A. Bianco and M. Prato, Chem. Soc. Rev., 2017, 46, 4400–4416.
5. Y. Yang, A. M. Asiri, Z. Tang, D. Du and Y. Lin, Mater. Today, 2013, 16, 365–373.
6. V. Georgakilas, J. N. Tiwari, K. C. Kemp, J. A. Perman, A. B. Bourlinos, K. S. Kim and R. Zboril, Chem. Rev., 2016, 116, 5464–5519.
7. K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666–669.
8. R. Munoz and C. Gomez-Aleixandre, Chem. Vap. Deposition, 2013, 19, 297–322.
9. X. S. Wu, Two-Dimensional Carbon: Fundamental Properties, Synthesis, Characterization, and Applications, 2014, pp. 35–66.
10. S. Yang, M. R. Lohe, K. Mullen and X. Feng, Adv. Mater., 2016, 28, 6213–6221.
11. W. F. Chen, L. F. Yan and P. R. Bangal, J. Phys. Chem. C, 2010, 114, 19885–19890.
12. J. S. Y. Chia, M. T. T. Tan, P. S. Khiew, J. K. Chin and C. W. Siong, Sci. Adv. Mater., 2016, 8, 1177–1186.
13. A. Ciesielski and P. Samori, Adv. Mater., 2016, 28, 6030–6051.
14. H. Zhao, R. H. Ding, X. Zhao, Y. W. Li, L. L. Qu, H. Pei, L. Yildirimer, Z. W. Wu and W. X. Zhang, Drug Discovery Today, 2017, 22, 1302–1317.
15. S. Goenka, V. Sant and S. Sant, J. Controlled Release, 2014, 173, 75–88.
16. A. A. Green and M. C. Hersam, Nano Lett., 2009, 9, 4031–4036.
17. T. Hasan, F. Torrisi, Z. Sun, D. Popa, V. Nicolosi, G. Privitera, F. Bonaccorso and A. C. Ferrari, Phys. Status Solidi B, 2010, 247, 2953–2957.
18. Z. Y. Sun, J. Masa, Z. M. Liu, W. Schuhmann and M. Muhler, Chem. – Eur. J., 2012, 18, 6972–6978.
19. A. Zamiranvari, E. Solati and D. Dorranian, Opt. Laser Technol., 2017, 97, 209–218.
20. M. Lotya, Y. Hernandez, P. J. King, R. J. Smith, V. Nicolosi, L. S. Karlsson, F. M. Blighe, S. De, Z. M. Wang, I. T. McGovern, G. S. Duesberg and J. N. Coleman, J. Am. Chem. Soc., 2009, 131, 3611–3620.
21. L. Guardia, J. I. Paredes, R. Rozada, S. Villar-Rodil, A. Martinez-Alonso and J. M. D. Tascon, RSC Adv., 2014, 4, 14115–14127.
22. H. Yang, V. Bezugly, J. Kunstmann, A. Filoramo and G. Cuniberti, ACS Nano, 2015, 9, 9012–9019.
23. P. Laaksonen, M. Kainlauri, T. Laaksonen, A. Shchepetov, H. Jiang, J. Ahopelto and M. B. Linder, Angew. Chem., Int. Ed., 2010, 49, 4946–4949.
24. A. J. Patil, J. L. Vickery, T. B. Scott and S. Mann, Adv. Mater., 2009, 21, 3159–3164.
25. J. D. Saathoff and P. Clancy, Carbon, 2017, 115, 154–161.
26. B. Wu and X. N. Yang, J. Phys. Chem. C, 2013, 117, 23216–23223.
27. C. Fu and X. Yang, Carbon, 2013, 55, 350–360.
28. H. Y. Sun and X. N. Yang, Colloids Surf., A, 2014, 462, 82–89.
29. S. Lin, C. J. Shih, V. Sresht, A. Govind Rajan, M. S. Strano and D. Blankschtein, Adv. Colloid Interface Sci., 2017, 244, 36–53.
30. A. Hardy, J. Dix, C. D. Williams, F. R. Siperstein, P. Carbone and H. Bock, ACS Nano, 2018, 12, 1043–1049.
31. S. Lin, C. J. Shih, M. S. Strano and D. Blankschtein, J. Am. Chem. Soc., 2011, 133, 12810–12823.
32. M. A. Lewis, Ecotoxicol. Environ. Saf., 1990, 20, 123–140.
33. S. Rebello, A. K. Asok, S. Mundayoor and M. S. Jisha, Environ. Chem. Lett., 2014, 12, 275–287.
34. L. Dong, K. L. Joseph, C. M. Witkowski and M. M. Craig, Nanotechnology, 2008, 19.
35. M. Ayan-Varela, J. I. Paredes, L. Guardia, S. Villar-Rodil, J. M. Munuera, M. Diaz-Gonzalez, C. Fernandez-Sanchez, A. Martinez-Alonso and J. M. Tascon, ACS Appl. Mater. Interfaces, 2015, 7, 10293–10307.
36. T. Yang, H. Chen, Z. Qiu, R. Yu, S. Luo, W. Li and K. Jiao, ACS Appl. Mater. Interfaces, 2018, 10, 4540–4547.
37. W. Yoon, Y. Lee, H. Jang, M. Jang, J. S. Kim, H. S. Lee, S. Im, D. W. Boo, J. Park and S. Y. Ju, Carbon, 2015, 81, 629–638.
38. M. Ayán-Varela, R. Ruiz-Rosas, S. Villar-Rodil, J. I. Paredes, D. Cazorla-Amorós, E. Morallón, A. Martínez-Alonso and J. M. D. Tascón, Electrochim. Acta, 2017, 231, 386–395.
39. A. Abellán-Llobregat, M. Ayán-Varela, L. Vidal, J. I. Paredes, S. Villar-Rodil, A. Canals and E. Morallón, J. Electroanal. Chem., 2016, 783, 41–48.
40. S. Y. Ju, J. Doll, I. Sharma and F. Papadimitrakopoulos, Nat. Nanotechnol., 2008, 3, 356–362.
41. B. Hess, Abstr. Pap. Am. Chem. Soc., 2009, 237.
42. M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, SoftwareX, 2015, 1–2, 19–25.
43. D. v. d. S. M. J. Abraham, E. Lindahl, B. Hess and the GROMACS development team, http://www.gromacs.org, 2018.
44. D. Van der Spoel, E. Lindahl, B. Hess, G. Groenhof, A. E. Mark and H. J. C. Berendsen, J. Comput. Chem., 2005, 26, 1701–1718.
45. H. J. C. Berendsen, J. P. M. Postma, W. F. Vangunsteren, A. Dinola and J. R. Haak, J. Chem. Phys., 1984, 81, 3684–3690.
46. W. L. Jorgensen, D. S. Maxwell and J. TiradoRives, J. Am. Chem. Soc., 1996, 118, 11225–11236.
47. W. L. Jorgensen and J. Tirado-Rives, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 6665–6670.
48. L. S. Dodda, I. Cabeza de Vaca, J. Tirado-Rives and W. L. Jorgensen, Nucleic Acids Res., 2017, 45, W331–W336.
49. L. S. Dodda, J. Z. Vilseck, J. Tirado-Rives and W. L. Jorgensen, J. Phys. Chem. B, 2017, 121, 3864–3870.
50. S. Miyamoto and P. A. Kollman, J. Comput. Chem., 1992, 13, 952–962.
51. A. Cheng and W. A. Steele, J. Chem. Phys., 1990, 92, 3858–3866.
52. N. R. Tummala and A. Striolo, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 80, 021408.
53. N. R. Tummala, B. P. Grady and A. Striolo, Phys. Chem. Chem. Phys., 2010, 12, 13137–13143.
54. T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089–10092.
55. U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, J. Chem. Phys., 1995, 103, 8577–8593.
56. G. Bussi, D. Donadio and M. Parrinello, J. Chem. Phys., 2007, 126.
57. Z. Xu, X. Yang and Z. Yang, Nano Lett., 2010, 10, 985–991.
58. J. Wallace and M. Sansom, Chem. Phys. Lipids, 2007, 149, S89.
59. M. Sammalkorpi, A. Z. Panagiotopoulos and M. Haataja, J. Phys. Chem. B, 2008, 112, 2915–2921.
60. J. A. Lemkul and D. R. Bevan, J. Phys. Chem. B, 2010, 114, 1652–1660.
61. S. Izrailev, S. Stepaniants, B. Isralewitz, D. Kosztin, H. Lu, F. Molnar, W. Wriggers and K. Schulten, Steered Molecular Dynamics, Berlin, Heidelberg, 1999.
62. N. R. Tummala, B. H. Morrow, D. E. Resasco and A. Striolo, ACS Nano, 2010, 4, 7193–7204.
63. B. C. Stephenson, A. Goldsipe, K. J. Beers and D. Blankschtein, J. Phys. Chem. B, 2007, 111, 1025–1044.
64. F. Eisenhaber, P. Lijnzaad, P. Argos, C. Sander and M. Scharf, J. Comput. Chem., 1995, 16, 273–284.
65. J. Łukasiewicz, H. Grajek and D. Frąckowiak, Dyes Pigm., 2007, 73, 377–382.
66. H. Grajek, I. Gryczynski, P. Bojarski, Z. Gryczynski, S. Bharill and L. Kulak, Chem. Phys. Lett., 2007, 439, 151–156.
67. Z. Király, G. H. Findenegg and Á. Mastalir, J. Phys. Chem. B, 2003, 107, 12492–12496.
68. S. Manne, J. P. Cleveland, H. E. Gaub, G. D. Stucky and P. K. Hansma, Langmuir, 1994, 10, 4409–4413.
69. H. Kawasaki, K. Ban and H. Maeda, J. Phys. Chem. B, 2004, 108, 16746–16752.
70. J. H. Park and N. R. Aluru, Surf. Sci., 2011, 605, 1616–1620.
71. R. J. Smith, M. Lotya and J. N. Coleman, New J. Phys., 2010, 12, 125008.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c9cp04742e

---