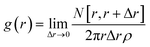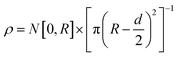A hybrid camphor–camphene wax material for studies on self-propelled motion

Abstract

A new material that combines the self-propelling properties of camphor with the malleability of camphene is reported. It has wax-like mechanical properties at room temperature and can be formed into required shapes. The speed of the self-propelled objects and the trajectory depend on the shape and camphor–camphene weight ratio.

---

Self-propelled motion represents an interesting manifestation of behaviour that can appear in a system far from thermal equilibrium.¹ Studies on self-propelled chemical objects have become popular in recent years because the observed motion results from conversion of chemical energy to kinetic energy in a way that looks similar to that of living organisms.^2,3 The complex evolution of self-propelled objects on a water surface has been investigated in many studies. The key element enabling such behaviour is a continuous flow of molecules that modify the surface tension.⁴ A classic example of a self-propelled object is a piece of camphor.^5,6 Camphor molecules dissolve poorly in water (1 g in 800 ml at 25 °C⁷). The majority of molecules dissipate from the source forming a surface layer. Under typical experimental conditions, this layer is unstable, because camphor molecules continuously evaporate. The water surface tension is a decreasing function of the camphor surface concentration and drops below 50 mN m⁻¹.⁸ As a consequence, the force acting on a camphor piece is directed toward the proximal region with the lowest camphor surface concentration.^9–11 Such a physical mechanism also describes the behaviour of other substances exhibiting similar surface activity.

The problem of a relationship between the geometrical shape, the symmetry of self-propelled objects and the character of their motion has attracted significant research attention.^3,12 For non-radially symmetric camphor particles the motion can be very complex and combines translation with rotation.^13–15 However, it is not easy to make camphor pieces of defined shape at room temperature, at which experiments are usually performed. Purified camphor is granular in form and a few techniques are available to transform the camphor grains into shaped objects. The most popular technique is performed by pressing camphor granules together in a pill maker. This technique is mainly used to make small camphor disks.¹⁶ More complex shapes can be cut-out of an inert porous support material (paper membrane,¹⁷ agar gel^18,19) and saturated with a camphor solution (in methanol for example¹⁷). However, such objects contain smaller amounts of camphor than pills and the longevity of experiments with these objects is of the order of minutes.¹⁵ Experiments performed with pills of pure camphor show a longer time window of self-motion.²⁰ Both abovementioned techniques generate objects with highly inhomogeneous distribution of camphor. The inhomogeneity of pills results from the structure of camphor grains and vacant spaces that randomly appear when a pill maker is filled with camphor, before pressure is applied or to the structure of the porous material. To obviate these problems, we describe a new wax-like material, exhibiting surface activity. It is obtained by producing a homogenous mixture of camphor and camphene in liquid form and then cooling the mixture to room temperature forming an easily shapable waxy material.

First, we compared self-motion of pills made of pure camphor or pure camphene on the water surface. Camphene exhibits similar surface activity to camphor. It is insoluble in water⁷ and forms an unstable, evaporating layer that decreases the surface tension by more than 10 mN m^−1 21 depending on the surface concentration of camphene molecules. Despite similar physical properties, camphene is not a popular material to make self-propelled objects as we have found just a single report on this subject.²¹ At room temperature camphene is a sticky, waxy solid which is very malleable. Due to low melting temperature, shapes made of pure camphene exhibit low mechanical stability compared to those made of pure camphor. Thus, pure camphene is a suboptimal material for the production of arbitrarily shaped self-propelled objects.

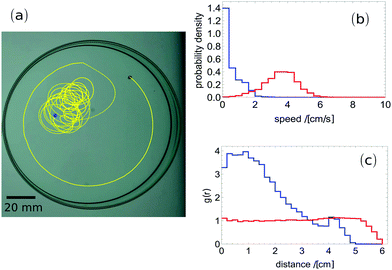
In order to make a quantitative comparison between self-propelled behaviour of camphor and camphene, we observed the motion of pills (0.4 cm diameter and 0.1 cm high) made of the respective materials. We used commercially available camphor ((1R)-(+)-camphor, 98% purity, CAS: 464-49-3, Sigma-Aldrich) and camphene (95% purity, CAS: 79-92-5, Sigma Aldrich). These experiments as well as those demonstrating properties of camphor–camphene mixtures, reported below, were performed at 23 ± 1 °C in a glass Petri dish with a diameter of 12 cm, containing 50 ml water purified using a Millipore ELIX5 system. The Petri dish was illuminated from below while recording from above using a mounted digital camera (NEX VG20EH, SONY). We placed a black marker on the top of a pill to trace its position on consecutive frames of the movie and extract the trajectory. The resulting movies were divided into frames at the rate of 25 per second using the ffmpeg program. Next the positions of a tracer were digitalized, edited and analysed using the ImageJ and Mathematica software.

The character of motion can be qualitatively described via the probability distribution of the observed speeds and the distribution of locations on the Petri dish. Having in mind the symmetry, we characterize the distribution of observed locations through the radial distribution function of pill locations g(r) at the distance, r, between the centre of the Petri dish and the pill centre. The function is defined as:

where N[r₁,r₂] is a function of two distances r₁, r₂. It describes the number of frames where the pill centre is observed at the distances q(r₁ ≤ q ≤ r₂) from the centre of the Petri dish. The symbol ρ, defined below, is the average surface numerical density of positions observed on all recorded frames:
Here R is the radius of the Petri dish and d is the diameter of the pill. The (R − d/2) factor takes into account the decrease in available locations due to the hard pill size. The function g(r) measures how much the distribution of actual locations of the pill differs from the uniform distribution on the available surface.

The results for pure camphor and for pure camphene are shown in Fig. 1. Both g(r) and the probability density of speed summarize results of a few independent experiments. The results for camphor were averaged over 3 experiments. In each experiment the observation time was longer than 1 hour (90 000 frames) and the total number of analysed frames was 310 000. For pure camphene the presented result covers 5 experiments and the total number of frames was almost 600 000. Although both camphor and camphene pills are self-propelled, the quantitative character of motion is different. For camphor, the pill distribution on the water surface is uniform. On the other hand, the camphene pill hardly penetrates the area 1 cm away from the dish edge. For a camphor pill, the probability distribution of observed speeds is Gaussian with a maximum at 4 cm s⁻¹ and the mean is equal to 3.6 cm s⁻¹. For a camphene pill the probability distribution of speeds has a Poissonian character and the average speed is 0.6 cm s⁻¹. A similar characteristic of camphene pill motion (Poissonian character of velocity, avoiding close proximity to the edge of Petri dish) was reported in ref. 21. Quantitative differences between both results can be attributed to the larger Petri dish diameter in our setup.

Fig. 1 Typical motion of camphor and camphene pills. (a) A fragment of a typical trajectory of self-propelled camphene pill (0.4 cm diameter, 0.1 cm high) on the water surface in a Petri dish (12 cm diameter). The grey dot with a black marker shows the initial position of a camphene pill. The illustrated fragment terminates at the blue dot. (b) The probability distribution of observed speeds (cm s⁻¹). (c) The radial distribution function of pill positions at a given distance (in cm) from the dish centre. The blue and red curves show results for camphene and for camphor respectively.

It may be expected that for a mixture of camphor and camphene the properties of motion should depend on the mass ratio. We introduce a variable, w, that defines the camphor mass ratio of the mixture:

The blue and red curves in Fig. 1b and c correspond to w = 0% and w = 100% respectively. Samples at different ratios of camphor and camphene, w, were prepared by adding appropriate amounts to a 50 ml beaker containing a magnetic stir bar and covered with a larger beaker in order to prevent excessive evaporation during heating. The sample was then placed on a hot plate set to 140 °C while stirring until all the camphor crystals appear to be dissolved in the molten camphene (depending on ratio it takes between 20 and 40 minutes). Liquid camphene acts as a solvent for camphor making it possible to have a liquid solution of camphor at lower temperatures. The camphor–camphene mixture is a sticky, waxy solid after it is cooled down to 23 ± 1 °C. It does not stick to rubbers such as nitrile, silicone or latex. The hardness of the wax increases with the amount of camphor. Pills of this material can be pressed out using a pill maker. Flat pieces of camphor–camphene mixture can be formed and cut to the required shape.

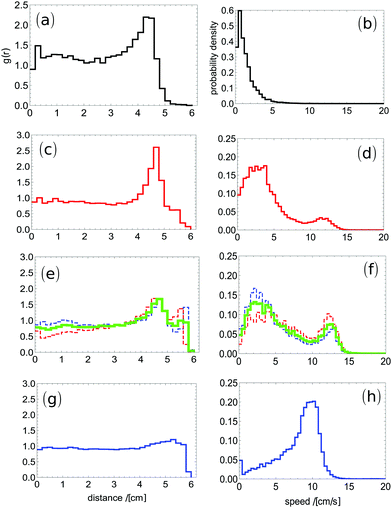
The results characterizing typical motion of pills made of camphor–camphene mixtures at different compositions are presented in Fig. 2. Here each presented result was obtained from averaging over 2 independent experiments that were more than 1 hour long (over 200 000 frames). We observed a good agreement between results of individual experiments (cf.Fig. 2e and f). As expected from the results shown in Fig. 1c, the values of g(r) for distances close to the disk radius (6 cm) increase with w, which means that more of the dish surface becomes available to the pill. The dependence of the probability distribution of observed speeds is more interesting: the Poissonian character of speeds is observed for w = 16.7%, however the mean speed is much higher (1.4 cm s⁻¹) than for pure camphene. For moderate concentrations of camphor (w = 33% and 37%) the distribution becomes bimodal and contains a low speed maximum at 2 cm s⁻¹ and a high-speed maximum at 12 cm s⁻¹. This result seems surprising. On the basis of Fig. 1b one could expect a bimodal distribution of speeds, but with the second maximum about 4 cm s⁻¹. We observe that camphor and camphene synergistically interact and pills made of the hybrid material can move much faster than those prepared using pure components. For yet larger concentrations of camphor (w = 50%) there is only a single maximum of speed distribution, but it is located around 10 cm s⁻¹, that is almost 3 times more than the maximum of the speed distribution for pure camphor. This increase in speed could be explained as follows. For pure substances the propulsion results from fluctuations in concentrations of active molecules on different sides of a self-propelled object. In the case of a mixture these fluctuations can be increased by fluctuations in the composition of active molecules and the overall effect increases. As supported in Fig. 2, we claim that the properties of the hybrid material can be tailored on demand by the camphor–camphene ratio.

Fig. 2 Analysis of motion of pills made from camphor and camphene mixtures with varying w. The radial distribution of pill positions as a function of distance from the dish centre (a, c, e and g) and the probability distribution of observed speeds (b, d, f and h) for a few selected weight ratios: (a and b) w = 16.7%, (c and d) w = 33%, (e and f) w = 37%, (g and h) w = 50%. The red and blue dashed lines in (e and f) represent results of two individual experiments that contributed to the average shown by the green curve.

We believe that the obtained material is homogeneous. Molecules of camphor and camphene are similar and thus we do not expect that the system decomposes into camphor- and camphene-rich phases. When in liquid form, the mixtures are well stirred before solidification and the liquid looks homogeneous. If essential nonhomogeneities appear during solidification then results of different experiments should differ. The results of individual experiments contributing to Fig. 2 show good reproducibility (cf.Fig. 2e and f). This implies that the microscopic variations if existent have a minor influence on the time evolution of studied objects.

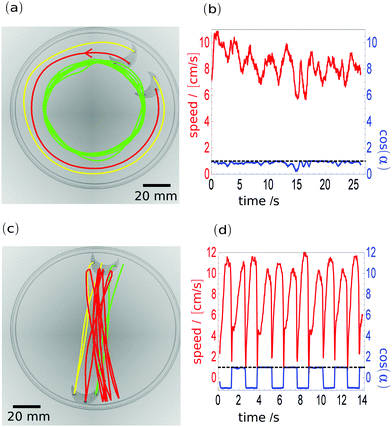
In order to demonstrate the usefulness of the hybrid material for studies on self-motion of objects with different shapes, we performed experiments with a crescent (2 × 1.5 cm size) made of material of w = 50%. We analysed the speed of the marker located at the crescent centre and the angle between the direction of velocity and the bisector of the angle defined by the markers. The crescent motion was observed for almost 40 minutes. The trajectory is complex and combines translation with rotation during the crescent time evolution (see the movie Graphical-Abstract.avi in the ESI†). However, a few characteristic metastable modes of motion can be identified. Two examples of them are illustrated in Fig. 3a and c. Fig. 3a shows crescent rotation along the edge of the Petri dish. To make Fig. 3a transparent we plotted a trajectory of 25 seconds for the tracking mark located closest to the centre of the dish (the green line) to indicate the stability of the rotational mode. The trajectories of the two other markers (the crescent centre – the red line and of the marker closest to the dish edge – the yellow line) are shown for a 2.5 second period, which is less than the time of a single rotation, to illustrate that the crescent orientation with respect to the dish edge does not change. The trajectories of all three markers are superimposed over two snapshots of the crescent position separated by 2.5 seconds. The direction of motion is marked by the arrow on the red trajectory. The red line in Fig. 3b illustrates the speed of the central mark on the crescent as a function of time. The speed fluctuated around 8 cm s⁻¹ but did not change significantly. The blue curve represents the cosine of the angle between the velocity and the bisector of the angle formed by all three markers. If the value of cosine is close to 1 it means that the crescent moves towards its concave site. If the value is −1, the motion is toward the convex site. As seen for most of the considered time intervals the cosine of the angle defined above was close to 1, which indicates that the trajectory along the dish edge with the velocity directed towards the crescent's concave site is a metastable mode of its motion. Another type of metastable motion is illustrated in Fig. 3c. The crescent moved from one edge of the dish to the other without rotation. The trajectory of the central marker (the red line) is shown for the period of 17 seconds. The trajectories of side markers (green and yellow) are indicated for one cycle only. The analysis of motion is presented in Fig. 3d. The blue and red curves represent the same quantities as in Fig. 3b. The angle between the velocity and the bisector of the angle, defined by the markers, switches between 0 and π at each approach to the dish edge. This indicates that the motion is correlated with the crescent geometry: it can be directed towards the convex or concave sides of the crescent. Again, the red line illustrates the speed of the central mark as a function of time. The speed gradually increased after the crescent stopped and then it remained stable and finally rapidly decreased when the crescent got into contact with the opposite wall of the dish. The velocity profiles as functions of time are similar for both the direction of motion towards the concave and convex sites. Small, regular differences, like the difference in speed profile before the stop seem to be related to the friction that the moving crescent experiences while moving in different directions.

Fig. 3 Two examples of metastable modes observed during self-motion of a crescent-shaped object made of the hybrid material characterized by w = 50%. (a) The rotation along the dish: 25-second-long trajectory of the marker close to the dish centre is drawn using the green line, the trajectories of the other markers are shown for 2.5 seconds only. The direction of motion is indicated by the arrow on the red line. (c) The oscillating motion: 2 snapshots separated by 1.2 seconds are superimposed and the 23-second-long trajectory of the central marker is illustrated using the red line. The trajectories of side markers (green and yellow) are indicated for one period only. Subfigures (b and d) show the speed of the central marker in cm s⁻¹ (the red curve) and the cosine of the angle α between the velocity and the bisector of the angle defined by the markers (the blue curve). The line representing f(x) = 1 is shown using a dashed line.

Summarizing, we have described a novel plastic material that can be utilized for studies on self-propelled motion on a water surface. It has a homogeneous structure and thus we can expect more uniform dissipation of the surface-active molecules than for objects formed using other methods. This should result in a higher repeatability of experimental results. We have also found that by changing the camphor/camphene ratio, w, one can control the character of motion. The material can be easily formed to any nontrivial shape, as seen in Fig. 3. This feature is especially important for studies on the relationships between the object geometry and the character of motion, as illustrated for the self-propelled crescent. The material does not lose its surface activity after melting, so it could be applied in moulds or with 3D-printers to generate self-moving objects of highly controlled and diverse shapes.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This publication is part of a project that has received funding from the European Union's Horizon 2020 (H2020-EU.1.3.4.) research and innovation program under the Marie Skłodowska-Curie Actions (MSCA-COFUND ID 711859) and from the Polish Ministry of Science and Higher Education for the implementation of an international co-financed project.

Notes and references

1. Self-organized Motion: Physicochemical Design based on Nonlinear Dynamics, ed. S. Nakata, V. Pimienta, I. Lagzi, H. Kitahata and N. J. Suematsu E, Royal Society of Chemistry, Cambridge, 2019.
2. Y. T. Maeda, J. Inose, M. Y. Matsuo, S. Iwaya and M. Sano, PLoS One, 2008, 3, e3734.
3. D. Shao, W.-J. Rappel and H. Levine, Phys. Rev. Lett., 2010, 105, 108104.
4. S. Nakata, M. Nagayama, H. Kitahata, N. J. Suematsu and T. Hasegawa, Phys. Chem. Chem. Phys., 2015, 17, 10326–10338.
5. C. Tomlinson, Proc. R. Soc. London, 1862, 11, 575–577.
6. L. Rayleigh, Proc. R. Soc. London, 1890, 47, 364–367.
7. M. J. O’Neil, The Merck Index: An Encyclopedia of Chemicals, Drugs, and Biologicals, Royal Society of Chemistry, Cambridge, 15th edn, 2013.
8. Y. Karasawa, S. Oshima, T. Nomoto, T. Toyota and M. Fujinami, Chem. Lett., 2014, 43, 1002–1004.
9. S. Nakata, Y. Iguchi, S. Ose, M. Kuboyama, T. Ishii and K. Yoshikawa, Langmuir, 1997, 13, 4454–4458.
10. Y. Hayashima, M. Nagayama and S. Nakata, J. Phys. Chem. B, 2001, 105, 5353–5357.
11. S. Soh, K. J. M. Bishop and B. A. Grzybowski, J. Phys. Chem. B, 2008, 112, 10848–10853.
12. N. Yoshinaga, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 89, 012913.
13. H. Kitahata, K. Iida and M. Nagayama, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 87, 010901.
14. K. Iida, H. Kitahata and M. Nagayama, Phys. D, 2014, 272, 39–50.
15. S. I. Ei, H. Kitahata, Y. Koyano and M. Nagayama, Phys. D, 2018, 366, 10–26.
16. N. J. Suematsu, Y. Ikura, M. Nagayama, H. Kitahata, N. Kawagishi, M. Murakami and S. Nakata, J. Phys. Chem. C, 2010, 114, 9876–9882.
17. Y. S. Ikura, E. Heisler, A. Awazu, H. Nishimori and S. Nakata, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 012911.
18. M. Hayakawa, H. Onoe, K. Nagai and M. Takinoue, Micromachines, 2016, 7, 229.
19. B. Nanzai and T. Ban, Physical Chemistry of Energy Conversion in Self-propelled Droplets Induced by Dewetting Effect, pp. 139–166 in the ref. 1.
20. Y. Koyano, M. Gryciuk, P. Skrobanska, M. Malecki, Y. Sumino, H. Kitahata and J. Gorecki, Phys. Rev. E, 2017, 96, 012609.
21. S. Nakata, Y. Doi and Y. Hayashima, J. Phys. Chem. B, 2002, 106, 11681–11684.

---

Footnote

† Electronic supplementary information (ESI) available: [Graphical-Abstract.avi] Time evolution of a system illustrated as the Graphical Abstract (avi). [Crescent-rotation.avi] Time evolution of a system illustrated in Fig. S3a (avi). [Crescent-oscillation.avi] Time evolution of a system illustrated in Fig. S3c (avi). See DOI: 10.1039/c9cp04722k

---