Absorption spectra at the iodine 3d ionisation threshold following the CH_xI⁺ (x = 0–3) cation sequence

Abstract

Yields of atomic iodine I^q+ (q ≥ 2) fragments resulting from photoexcitation and photoionisation of the target cations CH_xI⁺ (x = 0–3) have been measured in the photon-energy range 610 eV to 670 eV, which comprises the threshold for iodine 3d ionisation. The measured ion-yield spectra show two strong and broad resonance features due to the excitation of the 3d_3/2,5/2 electrons into εf states similar to atomic iodine. In the 3d pre-edge range, electrons are excited into molecular orbitals consisting of iodine, carbon, and hydrogen atomic orbitals. These transitions have been identified by comparison with literature data and by simulations using time-dependent density functional theory (TDDFT) with the KMLYP functional. The ion-yield spectrum for CH₃I⁺ resembles the spectrum of IH⁺ [Klumpp et al., Phys. Rev. A, 2018, 97, 033401] because the highest occupied molecular orbitals (HOMO) of the H and CH₃ fragments both contain a single vacancy, only. For the molecular cations with higher number of vacancies in the valence molecular orbitals CH_xI⁺ (x = 0–2), a stronger hybridisation of the molecular orbitals occurs between the organic fragment and the iodine resulting in a change of bonding from a single σ bond in CH₃I⁺ to a triple bond including two π orbitals in CI⁺. This is reflected in the resonance energies of the observed absorption lines below the iodine 3d excitation threshold.

---

Introduction

Inner-shell absorption spectroscopy utilising soft X-rays is an ideal tool to probe the chemical environment of a specific element within a molecule. The power of inner-shell excitation was proven by Siegbahn and co-workers in photoelectron spectroscopy studies of the famous ESCA molecule ethyl trifluoroacetate (see e.g. the recent review by Martensson et al.¹) which show a chemical shift of the binding energy of carbon 1s electrons depending on the chemical environments established by the different ligands.

In general, to understand the influence of each ligand on a molecule, one approach is to vary the number of the ligands (e.g. by removing them) and to determine the changes in the spectrum. However, these newly formed molecules are often not stable. Here, ionic targets offer a way to prepare various (ionic) molecular species in an ion beam that are not accessible by other methods. The different molecular ions can easily be separated by their mass-to-charge ratio and, thus, purified target beams of molecular fragments (radicals) can be provided for experiments. We have chosen the molecular target ion sequence CH_xI⁺ (x = 0–3) as a model system to study, in a combined experimental and theoretical effort, the dependence of the molecular electronic and geometric structure on the number x of hydrogen atoms bound to the central carbon atom. Previously, we examined the electronic structure of the IH⁺ cation.² The nature of most of the observed resonances was dominated by the iodine atom. However, for one observed resonance (peak E in Fig. 6b) the final molecular orbital was identified to result from hybridisation of the atomic iodine 5p and the hydrogen 1s orbital to form a (5pπ) σ* state. By exchanging the bonding partner of the iodine atom from hydrogen in IH⁺ to carbon in CH_xI⁺ the explicit changes of the electronic structure of the different molecules are studied in the present project.

Neutral iodomethane is intensively studied because it can easily be excited either by electrons,³ by high-power lasers of 193 nm,^4–8 266 nm,^9–11 or even longer wavelengths,^12–18 dissociating the molecule.^8,19,20 Photons of these different wavelengths, produced by the Sun,^21–24 can dissociate CH₃I from natural sources^25–27 in Earth's atmosphere forming atomic iodine (ions) which act as catalysts for ozone depletion.^28–30 Unravelling the dissociation and excitation mechanisms of the iodomethane molecule is important to understand its role in the chemistry of Earth's atmosphere.^31,32

Studies of iodomethane in the soft X-ray regime are limited. Olney et al.³³ provide an overview of the work done until 1997. More recent publications in which the valence structure of iodomethane is studied discuss the use of photoelectron spectroscopy with photons in the energy range of up to 30 eV.^34–38 The iodine 4d resonance was studied by absorption³⁹ and photoelectron spectroscopy,^40–43 by electron excitation techniques,^33,44 and is exploited to study charge transfer dynamics using the pump–probe technique with short X-ray pulses produced by free-electron lasers (FELs),^45–50 or a combination of optical and XUV pulses from higher harmonic generation (HHG) sources.^11,51,52

Inner-shell excitation studies of iodomethane including the carbon 1s⁵³ or the iodine 3d resonance^54,55 have been scarce, but a comprehensive study examining the iodine 3d threshold in neutral CH₃I was published recently,⁵⁶ showing photo- and Auger electron spectra in the energy regions of the 3d, 4s, and 4p thresholds.

Experiment

The experiments were carried out at the ion beamline facility PIPE at P04, PETRA III, DESY, using accelerated beams of CH_xI⁺ (x = 0–3) molecular ions. Details of the set-up and operation of PIPE^57–59 and of the photon beamline P04⁶⁰ have been discussed previously. The ion preparation and the beamline parameters for the soft X-ray photons delivered by P04 are chosen as described in the context of the IH⁺ experiment.²

For the production of the target molecular cations, liquid CH₃I was evaporated under vacuum conditions. The vapour was leaked into a 10 GHz-ECR⁶¹ ion source via an electronically controlled needle valve keeping the gas pressure within the ion source in the order of 1 × 10⁻⁴ hPa. Fig. 1 shows the mass spectrum of CH_xI⁺ (x = 0–3) molecular cations measured behind the mass analysing dipole magnet. The resolving power for the ion preparation is sufficient to distinguish each single molecular ion of the sequence without overlapping mass lines. Still, some mixing of molecular ions can occur because of different stable isotopes of the constituent elements. Iodine has only one isotope, but carbon has two. ¹³C has an abundance of 1%⁶² and its presence in the experiment is visible at the mass line marked with ¹³CH₃I⁺. The mass lines of CH_xI⁺ (x = 1–3) can be mixed with ions containing the ¹³C isotope and one hydrogen atom less, but because of the low abundance of ¹³C, we consider these contributions to be negligible.

Fig. 1 Mass spectrum of the sequence of CH_xI⁺ (x = 0–3) molecular cations showing the mass peaks to be well separated by our mass-to-charge analysing spectrometer. The red solid line is a fit with 5 Gaussian functions determining the mass resolution of the mass spectrometer with the given entrance- and exit-slit widths to be m/Δm ≈ 710.

To obtain absorption spectra of the CH_xI⁺ (x = 0–3) molecular cations, the merged-beams technique was used.^57,63,64 The 6 keV, mass-to-charge selected ion beam from the ECR source was overlaid with the photon beam from the P04 beamline in the approximately 1.5 m long merged beam section of PIPE. To reduce the background from collisions of the chosen molecular ion with residual gas, the background pressure in the merged-beam interaction region of the photons and the ions was kept below 2 × 10⁻¹⁰ mbar.

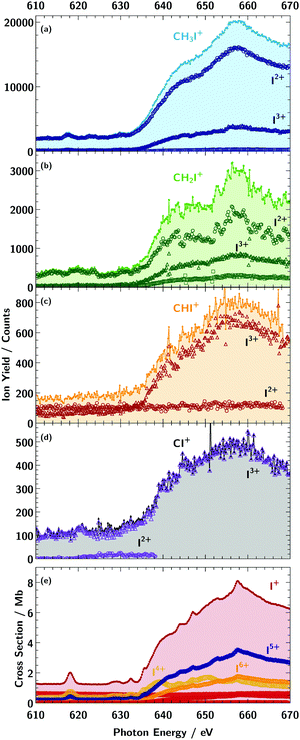
As a measure for the absorption of photons by the target ions, the atomic fragment-ion channels I^q+ (q = 2–4) were individually recorded as functions of the photon energy (Fig. 2). The maximum count rate in the different ion spectra scales roughly with the available ion current of the target ion for the direct I 3d photoionisation. Because of the low ion current for CI⁺ and CHI⁺ target ions, only the fragment channels up to q = 3 were recorded.

Fig. 2 To obtain the ion yield spectra of the different molecular cations CH_xI⁺ (x = 0–3; panels d–a), the different atomic fragment channels I^q+ (q = 2–4/dots, triangles, squares) were measured. Note: for x = 0,1 only q = 2, 3 have been measured. For atomic iodine I⁺ more fragment channels I^q+ (q = 2–8) can be observed (panel e). The prominent fragment channels here are I⁴⁺ (light orange squares), I⁵⁺ (blue stars) and I⁶⁺ (dark orange hexagons). All other fragment channels of I^q+ are depicted in light red. The upper curve in each panel is the sum of the fragment channels.

The ion fragment channels were separated by means of mass spectrometry by a second dipole magnet and were detected by a channeltron detector capable of counting single ions.^57,65 The recorded spectra were normalised to the flux of target ions, measured with a Faraday-cup behind the interaction region inside the fragment-separating dipole magnet, and to the photon flux measured with a calibrated photodiode. Both quantities were recorded in parallel to the ionic fragment counting.

To disperse the soft X-rays of beamline P04, a 400 lines per mm grating was chosen in order to achieve a photon flux of 2 × 10¹⁴ photons per s. The exit slit of the P04 monochromator was set to 1500 μm resulting in a bandwidth of the photons of about 1 eV.

Theoretical methods

To model the observed absorption spectra, the molecular geometry, the electronic structure and the transition probabilities were calculated using density functional theory (DFT) with the KMLYP functional in the ADF-2017 software suite.^66–68 The total charge for all molecules was set equal to 1+. Relativistic effects were taken into account via the non-collinear spin–orbit approximation, which gives a more accurate prediction of the electron energies for heavy elements than the collinear approach.⁶⁹ The electron transition energies and oscillator strengths were calculated within the Tamm–Dancoff approximation for the time-dependent DFT (TDDFT)^70,71 including the self-consistent calculation of spin–orbit effects. For the TDDFT calculations, no symmetry constraints were used to restrict the wavefunction, while the assignment of the transitions was performed afterwards in terms of non-relativistic symmetric molecular orbitals. The absolute energy values of the calculated spectra were shifted by 0.6 eV using peak A (Fig. 6) in the experimental absorption spectrum of I⁺ as a reference. This shift is explained by the uncertainty of theoretical DFT calculations for calculating absolute values of the core level energies.⁷² In general, for deeper core states this error increases. However, the relative chemical energy shifts are more precise within the same computational approach due to cancelling of uncertainties for different spectra originated from the same core level. In our work we have applied a rigid shift of 0.6 eV for all spectra to align them with the experimental data, while relative shifts between calculated spectra for different species were not adjusted. The calculated resonances were convoluted with a 1.0 eV (FWHM) Gaussian matching the experimentally observed width. To describe higher-energy states, the largest available quadruple-zeta basis set with four polarisation functions (QZ4P) was additionally extended with diffuse iodine p-orbitals.^2,68

Experimental results

For the cations CH_xI⁺ (x = 0–3), different ion fragment channels I^q+ up to q = 4 were observed depicted in Fig. 2, which were summed up to obtain the spectra shown in Fig. 3b. For x = 2, 3 the fragment charge states q = 2–4 and for CHI⁺ and CI⁺ the fragment channels q = 2, 3 were measured, as for these two fragments the q = 4 channel was to weak.

Fig. 3 Ion-yield curves for the primary atomic target ion I⁺ (red dots, panel a) and the primary molecular ion sequence CH_xI⁺ (panel b, light blue dots: x = 3, green squares: x = 2, orange diamonds: x = 1, and black triangles: x = 0) summed over all measured fragment channels I^q+; q = 2–8 for I⁺, q = 2–4 for x = (2, 3) and q = 2, 3 for x = (0,1). For a better comparison the spectra of the molecular ions were plotted in panel (b) on individual axes with an arbitrary offset and are scaled by a factor shown in the graph. The numbers on the y-axis indicate the yield for each individual curve. The assignment of the observed absorption resonances of I⁺ is taken from our previous publication.² For the molecular target ions, the broad 3d → εf features of I⁺ are visible as well. Below the 3d threshold comparatively weak resonance features can be observed for the molecular target ions in the vicinity of the grey dashed line.

For the IH⁺ cation we assumed that the hydrogen is ejected as H⁺ after photoionisation.² As can be seen in the partial ion-yield absorption spectra in Fig. 2, the dominating fragment channels for the atomic iodine are q = 4–6, especially I⁵⁺ (panel e in Fig. 2). For the larger molecular cations CH₃I⁺ and CH₂I⁺, the dominating fragment channel is I²⁺, while for the smaller cations CHI⁺ and IC⁺ the dominating fragment channel is I³⁺. This indicates, the more constituents a molecule has, especially hydrogen, the more charge can be carried away by its fragments after the charge has been transferred to them.⁷³ This results in a reversal of the I²⁺/I³⁺ fragment ratio from CI⁺ to CH₃I⁺. In the following the sum of the partial ion yields will be discussed which are referred to as absorption spectra. Fig. 3 compares the measured absorption spectra of CH_xI⁺ (x = 0–3) with the spectroscopic features associated with photoproduction of a 3d vacancy in the atomic I⁺ ion.²

Charged carbon, hydrogen or CH_k⁺ fragments were not observed. The reason is the large kinetic energy release of these light fragments which they acquire during the fragmentation process. With a typical charge q = 3 of the iodine fragment, a singly charged H⁺ or C⁺ fragment with a mean C–I or H–I bond length of around 2 Å, the kinetic energy release is approximately 21 eV. This results in a large transverse momentum change of the light fragments, which largely inhibits their detection. The effect reduces also the transmission of the iodine fragments. This transmission must be known for the derivation of absolute cross sections from the measured particle counts rates. In principle, an estimate for the transmission can be derived from detailed ion-optical calculations. However, such simulations are beyond the scope of the present work.

Calculations

To make a line assignment and to understand the contribution of the atomic orbitals to the absorption lines, we performed calculations based on density functional theory. Table 1 shows equilibrium bond length values and Mulliken charges on iodine for the different molecular ion species. The Mulliken charge decreases along with the number x of hydrogen atoms in the series of CH_xI⁺ (x = 0–3) upon filling the anti-bonding orbitals. Similarly, the bond length C–I is larger for CH₃I⁺ compared to CHI⁺ and CH₂I⁺.

Table 1 Ground-state geometry and Mulliken charge for the different molecular ion species CH_xI⁺ (x = 0–3) and IH⁺. The binding energy for the bent configuration of the CHI⁺ molecule ion has been determined to be energetically more favourable by 0.06 eV than the linear one

Molecular ion	I–X bond length in Angstrom (X = H or C)	Mulliken charge on I	Molecular symmetry group
IH^+	1.63	0.89	C ∞v
CI^+	1.88	1.00	C ∞v
CHI^+ linear (180°)	1.85	0.98	C ∞v
CHI^+ bent (152°)	1.85	0.94	C s
CH2I^+	2.01	0.91	C 2v
CH3I^+	2.10	0.81	C 3v

---

The relaxed geometries reported in Table 1 were used further for TDDFT simulations. The TDDFT approach does not account for all many body interactions in the iodine 5d–nf transitions which result in rich multiplet structures. However, we have recently shown² its applicability to iodine 5d–np transitions. The spectra depicted as solid lines in Fig. 7a–d show the results of the calculations in comparison with the experimentally data. Table 2 lists the final-state configurations of the observed absorption lines according to the theoretical model.

Table 2 Final-state configurations of the observed absorption lines labelled A–E in Fig. 6 and 7 of the molecular cations IH⁺ and CH_xI⁺ (x = 0–3) according to the calculations (details see text). In case of a strong mixing of different levels forming one orbital, the percentage is given in front of the configuration. Only leading atomic orbitals with a coefficient larger than 10% involved in the hybridisation (given in parenthesis in descending order of their percentage) are given for the different configurations. Due to the extended diffuse basis set QZ4P used for the calculations (see text), the p-orbitals with large principal quantum numbers n are described by linear combinations of basis atomic functions. Therefore, the assignment of higher lying np-states (n ≥ 7) in terms of 7p, 8p, etc., levels can be ambiguous. Orbitals marked with SO_c are partner spin–orbit levels, with c denoting the label of the partner, respectively. The terms labelled with E₁/E₂/E₃ for the linear geometry of CHI⁺ are split due to exchange interaction

Line label	Molecular cation
	IH^+ (C∞v)	CH3I^+ (C3v)	CH2I^+ (C2v)
A	π (I 5px, 5py)/SOB	E (I 5px, 5py)/SOB	B1 (C 2px/I 5px)/SOD
B	78%: π (I 5px, 5py)/SOA	E (I 5px, 5py)/SOA	52%: B2 (I 6py/C 3py/H 2s, 1s)
	22%: π (I 6dxz, 6dyz/I 6px, 6py/H 2px, 2py)		48%: A1 (C 2pz/I 6pz/H 2s/I 6s)
C	72%: π (I 6px, 6py/I 6dxz, 6dyz)	60%: A1 (I 6pz/H 2s)	56%: A1 (C 3pz/I 6pz/H 2pz)
	17%: π (I 6dxz, 6dyz/I 6px, 6py/H 2px, 2py)	40%: E (I 6px, 6py/H 2s)	44%: B2 (I 6py/C 2py/H 1s)
	11%: σ (I 6pz)
D	53%: σ (H 2s/H 2pz/I 6dz^2)	51%: E (I 5dxz/H 2pz/I 7px/I 5dx^2−y^2/H 1s)	73%: B1 (C 2px/I 5px)/SOA
	30%: σ (I 6pz/I 7pz)	40%: E (C 3px/I 5dxz/H 2s/H 2px)	27%: B2 (I 7py/I 5dxy)
	17%: σ (I 7Px, 7py)	9%: A1 (I 6pz)
E	σ (H 1s/I 5pz, 6dz^2)	A1 (I 5pz/C 2pz/I 3dz^2)	A1 (I 5pz/C 2pz/I 5dz^2)

---

Line label	Molecular cation
	CHI^+		CI^+ (C∞v)
	Linear (C∞v)	Bent (Cs)
A	π (C 2px, 2py/I 5px, 5py)	A′′ (C 2py/I 5py)	π (C 2px, 2py/I 5px, 5py)
B	62%: σ (I 6pz/H 2pz)	56%: A′ (I 6pz/H 2pz)	π (I 6px, 6py)
	38%: π (I 6px, 6py)	44%: A′′ (I 6py)
C	80%: π (C 3px, 3py/I 6px, 6py)	43%: A′′ (C 3py/I 5dyz/I 6py)	57%: σ (I 6pz)
	10%: π (I 6px, 6py/I 6dxz, 6dyz/C 3px, 3py)	31%: A′ (I 6px, 6pz)	33%: π (I 6dxz, 6dyz/C 6px, 6py/C 3px, 3py)
	10%: π (C 3px, 3py/I 6dxz, 6dyz/I 6px, 6py/H 2px, 2py)	26%: A′ (I 6dxz/C 3px/I 6px)	10%: π (I 7px, 7py/I 6dxz, 6dyz/C 3px, 3py)
D	46%: π (I 7px, 7py)	31%: A′′ (C 3py/I 5dyz/I 7py)	59%: σ (C 3pz/I 7pz)
	31%: σ (I 7pz)	22%: A′ (C 3px/I 7pz)	41%: σ (I 6pz)
	11%: π (C 3px, 3py/I 6dxz, 6dyz/I 7px, 7py/H 2px, 2py)	19%: A′ (I 7px)
	6%: σ (I 7pz)	17%: A′′ (C 3py/I 5dyz/I 7py)
	6%: π (C 3px, 3py/I 7px, 7py)	10%: A′ (I 7pz)
E			σ (I 5pz/I 6dz^2/C 2pz)
E1	π (C 2px, 2py/I 5px, 5py)	56%: A′′ (C 2py/I 5py)
		44%: A′ (C 2px/I 5px)
E2/E3	σ (I 5pz, 6dz2/C 2s)	A′ (I 5pz, 6dx^2−z^2/C 2s)

---

The three-dimensional visualisation of the valence molecular orbitals for the molecular cation IH⁺ and for the cationic sequence CH_xI⁺ (x = 0–3) are shown in Fig. 4.

Fig. 4 Orbital pictures of the cation IH⁺ and the cation sequence CH_xI⁺ (x = 0–3). From bottom to top the inner-shell orbitals with s-type symmetry of iodine and the organic constituents are depicted. The HOMO–LUMO orbitals are shown between the dashed lines and above the unoccupied orbitals responsible for the transitions B–E. While the final orbital for transition A is the iodine 5p_x,y oriented perpendicularly to the I–H or C–I bond, the axial 5p_z orbital hybridised with the organic fragment level is responsible for transition E. The detailed line assignments are given in Table 2. For details refer to text.

Fig. 5 shows the molecular orbitals of the neutral constituents H, CH, CH₂ and CH₃ which form the molecular orbitals after their hybridisation with the iodine 5p states. In terms of electronic configuration, H and CH₃ are very similar. As depicted in Fig. 5, both constituents miss one electron to complete their valence shell. The single bond of IH⁺ is formed by the hybridisation of the valence iodine 5p orbital and the hydrogen 1s orbital.² Though, CH₃ offers a π-type unoccupied orbital oriented along the CI bond which results in its low hybridisation with iodine 5p_x and 5p_y orbitals, oriented perpendicularly to the CI bond. In contrast, the empty carbon 2p_z orbital of C, CH, and CH₂ is suitable for hybridisation. The CI⁺ molecular ion, like neutral CO, exhibits a triple bond. The valence carbon 2p and the iodine 5p orbitals form three bonding and three anti-bonding orbitals. Two of them of π-type, directed perpendicularly to the CI bond, are degenerate.

Fig. 5 Orbital pictures of the neutral atomic I, H, and C and molecular CH, CH₂, and CH₃ fragments which are the building blocks forming the molecular (cation) sequence CH_xI (x = 0–3).

Discussion

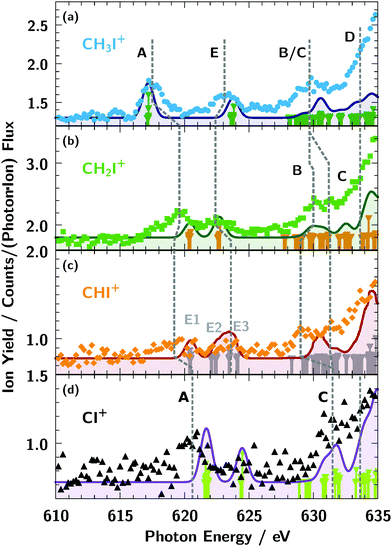
The ionisation thresholds for the 3d_5/2 and 3d_3/2 levels are located at 619.3 eV and 630.8 eV, respectively, for neutral atomic iodine.⁷⁴ In the molecular ion spectra shown in Fig. 3b, the broad iodine 3d_5/2,3/2 → εf lines are visible above 630 eV, similar to the atomic iodine ion from Fig. 3a. As indicated by the red dashed lines in Fig. 3b, the spin–orbit splitting of the εf lines is apparently larger for the molecular cation sequence and the molecular εf appear to be broader compared to the atomic ones. Further, the position of the εf lines on the energy scale are comparatively stable, slightly shifting to lower photon energies for smaller numbers of hydrogen x in the cation ion sequence CH_xI⁺. This observed small energy shift of the molecular εf lines relative to the I⁺ resonances at 647 eV and 658 eV can rather be explained by an increase of line broadening with respect to the atomic iodine ion I⁺ lines than by an increase of spin–orbit splitting of the molecular lines.

More distinct spectroscopic features can be seen below the iodine 3d ionisation threshold (Fig. 6 and 7). Obviously, the resonance structure of the cations CH_xI⁺ (x = 0–3) changes with the number of hydrogen atoms in the molecules. This can be easily understood in terms of occupation of molecular orbitals for the different CH_x fragments as we show in Fig. 5. A qualitative assignment of the resonances in CH₃I⁺ can be performed by comparison with the absorption spectra² of I⁺ and IH⁺ as shown in Fig. 6.

Fig. 6 Assignment of the resonances of CH₃I⁺ observed below the 3d ionisation threshold: (A) 3d_5/2 → 2e⁴, (B) 3d_3/2 → 2e⁴ or 3d_5/2 → 6p, (E) 3d_5/2 → 4a₁. The assignment follows the results of previous investigations.^2,11,33,75 For details see text.

Neutral CH₃I is of C_3v symmetry. Its electronic ground state can be expressed as:^11,33,75

K_IK_CL_IM_IN_I(1a₁)²(2a₁)²(1e)⁴(3a₁)²(2e)^{4 1}A₁. (1)

Accordingly, the ground state of the molecular ion CH₃I⁺ has an electron configuration:^76–79

K_IK_CL_IM_IN_I(1a₁)²(2a₁)²(1e)⁴(3a₁)²(2e)^{3 2}E_3/2,1/2 (2)

with a separation of ΔE_SO ≈ 0.6 eV of the spin–orbit split term ²E_j. The 2e orbital is attributed to a localised 5p level in the iodine of the CH₃I⁺ molecule. Attar et al.¹¹ reported a transition from iodine 4d into a molecular orbital (4a₁) which is attributed to a localised, anti-bonding σ* state of the C–I bond. With this information, the observed CH₃I⁺ resonances below the iodine 3d ionisation threshold can be assigned to (Fig. 6) (A) 3d_5/2 → 2e⁴, (B) 3d_3/2 → 2e⁴, which is the 3d_j spin–orbit partner of A, and (E) 3d_5/2 → 4a₁. The theoretical calculations discussed above predict even more lines with a rich fine structure. Nonetheless, our achieved resolving power in the experiment is not good enough to separate the components of the multiplet and all lines are strongly broadened by approximately 1 eV due to the 3d core-hole lifetime. E.g., the line C is assigned³³ to the transition 3d_5/2 → 6p, but it may contain the spin–orbit–split counterpart of line (A) 3d_3/2 → 2e⁴ which is not resolved. The (D) 7p line in IH⁺ is not observed in CH₃I⁺. Forbes et al.⁵⁶ came to a similar assignment for neutral CH₃I, recently. However, they did not observe the 3d_5/2,3/2 → 2e⁴ line pair since the 2e orbital is fully occupied in the neutral molecule.

Summarising the resonance structures below the iodine 3d ionisation threshold in Fig. 7, the CH_xI⁺ (x = 1–3) ions all show quite different behaviour in terms of line position and number of them in Table 3. However, theoretical analysis in Fig. 4 and Table 2 reveals that lines of the same origin are shifted compared relative to one another due the varying number of hydrogen atoms in the molecular ions.

Table 3 Chemical shifts observed for the absorption lines of the target cation sequence CH_xI⁺ (x = 0–3). Line E of CH₃I⁺ is shifted by (2.85 ± 0.3) eV with respect to the 3d_5/2 → 4a₁ transition at 620.35 eV in neutral CH₃I.⁵⁶ In the top row of the table, the chemical shift for CH₃I⁺ is given with respect to the cation IH⁺ (Fig. 6). For any other molecular cation in the sequence CH_xI⁺ (x = 0–2), the value of the chemical shift is given in respect to the CH₃I⁺ cation. The values are obtained by a single Gauss fit of an absorption line taking into account the iodine 3d ionisation threshold with a sigmoidal function as discussed in ref. 2. Due to the low resolving power of the exciting photons the spin–orbit split of the final states could not be fit successfully

Molecular		Line label (see text, Fig. 6 and 7); all values of the chemical shift are in eV
Reference	Target cation	A	B	C	D	E
IH^+	CH3I^+	0.3 ± 0.2	1.0 ± 0.2			0.9 ± 0.2
CH3I^+	CH2I^+	2.1 ± 0.2	0.3 ± 0.2	1.5 ± 0.2		0.7 ± 0.2
	CHI^+	1.7 ± 0.2	0.7 ± 0.2	1.6 ± 0.2	(0.7 ± 0.4)	0.5 ± 0.2
	CI^+	(1.8 ± 0.2)				2.5 ± 0.2

---

Further, the lines B and C can be resolved separately for CH₂I⁺ and CHI⁺, only. Some indication for line D can be observed in CHI⁺, but as in IH⁺, it is overshadowed by the rising edge of the 3d threshold.

The changes in the resonance structure for CI⁺ can be explained with its different electronic ground state configuration which has the same valence electronic structure as the neutral CO molecule:^80,81

(1σ)²(2σ)²(3σ)²(4σ)²(1π)⁴(5σ)^{2 1}Σ⁺. (3)

The CO molecule is bound by a characteristic triple bond attributed to the (1π) and (5σ) orbitals. In the ground state, these valence orbitals are filled. The lowest unoccupied molecular orbital is related to the anti-bonding (2π*) orbitals and contributes to line A in the CI⁺ spectrum, which is shifted with respect to the CH_xI⁺ spectra (x = 1–3) due to the stronger interaction of the iodine with the single carbon atom (Fig. 7d).⁸² Any further resonances near the iodine 3d ionisation threshold could not be resolved because of the low signal-to-noise ratio.

The bonding nature of the iodine in IH⁺ and CH₃I⁺ can be compared to the similar isoelectronic configuration of the CH₃ and H counterparts. Resonance A in the molecular cations IH⁺ and CH₃I⁺ can be described by an almost pure atomic iodine 5p orbital. Weak hybridisation for the first transition in IH⁺ and CH₃I⁺ compared to other molecules is evident also from Fig. 4. Peak A in CHI, CH₂I and CI corresponds to the transition into the anti-bonding π orbital which is described by an iodine 5p hybridised with the 2p orbital of carbon, oriented perpendicularly to the CI bond. The latter is blocked for the CH₃ constituent due to presence of three hydrogen atoms.

Resonance E in all molecules is related to the anti-bonding Σ bond between the iodine 5p_z and the π orbital of the ligand directed along the C–I (or I–H) bond. The only exception is the feature marked E1 in the CHI⁺ spectrum in Fig. 7c which arises from the opposite-spin counterpart of the feature A shifted by exchange interaction. Resonance B in the molecules IH⁺ and CH₃I⁺ is the spin–orbit counterpart of resonance A. However in CI⁺, CHI⁺, and CH₂I⁺ resonance A is shifted to higher energies and its spin–orbit counterpart overlaps with higher-energy continuum transitions. Therefore resonance B in CI⁺, CHI⁺, and CH₂I⁺ was assigned to the iodine 6p orbital directed perpendicularly to the C–I bond. Resonance C for IH⁺, CI⁺, and CHI⁺, and resonance D in CH₂I⁺ and CH₃I⁺ is related to the hybridised iodine 6p and 6d orbitals. The higher-lying resonances belong to the iodine 7p orbital of the np Rydberg series which is hardly observed in our spectrum and masked by the onset of the iodine 3d excitation threshold.

Fig. 7 Assignment and chemical shift of the resonances of the cations CH_xI⁺ (x = 0–3) below the iodine 3d ionisation threshold. For details see text. The dashed lines in the spectra of CHI⁺ and CI⁺ are to guide the eye to identify the respective resonances. The solid lines are the results for accompanying TDDFT calculations with a 1 eV resolution. The bars are plotted to give the line positions of the calculated resonances.

Conclusions

To unravel the influence of ligands on the electronic structure of a molecule we studied the sequence of CH_xI⁺ (x = 0–3) cations as a model system. The absorption resonances observed below the iodine 3d ionisation threshold show a strong dependence on the number of hydrogen atoms x. The observed lines for CH₃I⁺ and CI⁺ were assigned to electronic states known from the literature. According to (TD)DFT calculations, the resonances observed for CH₃I⁺ and IH⁺ shown in Fig. 6 have similar origins due to the similar nature of the hydrogen and CH₃ ligands. The evolution of the energy position and splitting of the resonances in the pre-edge spectra in CH_xI⁺ series is explained by a change of occupation of first molecular antibonding orbitals and value of hybridisation mainly between iodine and fragment orbitals of π-type. The two main pre-edge resonances can be well described by a molecular orbital composed of single atomic orbitals, whereas the higher lying resonances in the pre-edge are influenced by stronger hybridisation between several delocalised atomic orbitals, e.g. p and d types for iodine. Finally sharp resonances on the main edge originate from the multiplet structure of d–εf transitions.

As demonstrated in this work, inner-shell spectroscopy is a powerful tool to reveal the electronic structure of molecules within a different chemical environment. In combination with an ion beam in a merged beam geometry it allows to study molecular ions not accessible by other methods and unveil their electronic structure.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This research was carried out at the synchrotron light source PETRA III at DESY, a member of the Helmholtz Association (HGF). We would like to thank L. Glaser, G. Hartmann, F. Scholz, J. Seltmann, and J. Viefhaus for assistance in using beamline P04. The construction of PIPE and this work were funded by the German ministry for education and research (BMBF) under contracts 05KS7RG1, 05KS7GU2, 05KS7KE1, 05KS7RF2, 05K10RG1, 05K10GUB, 05K10KEA, and 05K10RF2 within the “Verbundforschung” funding scheme. KM and MM acknowledge funding by the Deutsche Forschungsgemeinschaft (DFG) via SFB925/A3. AM acknowledges support by the Deutsche Forschungsgemeinschaft via grant Mu-1068/22. AAG acknowledges the financial support from the President's Grant of Russian Federation for young scientists MK-2730.2019.2. SB and KS are thankful for funding from the Initiative and Networking Fund of the Helmholtz Association and acknowledge financial support by the Deutsche Forschungsgemeinschaft (DFG) through Sonderforschungsbereich SFB755 Nanoscale Photonic Imaging. SK acknowledges the funding of the EUCALL project within the European Union's Horizon 2020 research and innovation programme under the grant agreement No. 654220.

Notes and references

1. N. Mårtensson, E. Sokolowski and S. Svensson, J. Electron Spectrosc. Relat. Phenom., 2014, 193, 27.
2. S. Klumpp, A. A. Guda, K. Schubert, K. Mertens, J. Hellhund, A. Müller, S. Schippers, S. Bari and M. Martins, Phys. Rev. A, 2018, 97, 033401.
3. H. Kato, H. Masui, M. Hoshino, H. Cho, O. Ingólfsson, M. J. Brunger, P. Limão-Vieira and H. Tanaka, J. Chem. Phys., 2010, 133, 054304.
4. C. Fotakis, M. Martin, K. Lawley and R. Donovan, Chem. Phys. Lett., 1979, 67, 1.
5. G. V. Veen, T. Baller and A. D. Vries, Chem. Phys., 1985, 97, 179.
6. R. E. Continetti, B. A. Balko and Y. T. Lee, J. Chem. Phys., 1988, 89, 3383.
7. A. Gilchrist, G. Hancock, R. Peverall, G. Richmond, G. A. D. Ritchie and S. Taylor, J. Phys. Chem. A, 2008, 112, 4531.
8. H. Xu and S. T. Pratt, J. Chem. Phys., 2013, 139, 214310.
9. D. W. Chandler, J. W. Thoman, M. H. Janssen and D. H. Parker, Chem. Phys. Lett., 1989, 156, 151.
10. R. O. Loo, H. P. Haerri, G. E. Hall and P. L. Houston, J. Chem. Phys., 1989, 90, 4222.
11. A. R. Attar, A. Bhattacherjee and S. R. Leone, J. Phys. Chem. Lett., 2015, 6, 5072.
12. C. Kosmidis, S. Kaziannis, P. Siozos, A. Lyras, L. Robson, K. Ledingham, P. McKenna and D. Jaroszynski, Int. J. Mass Spectrom., 2006, 248, 1.
13. H. Liu, Z. Yang, Z. Gao and Z. Tang, J. Chem. Phys., 2007, 126, 044316.
14. Y. Wang, S. Zhang, Z. Wei and B. Zhang, J. Phys. Chem. A, 2008, 112, 3846.
15. G. Gitzinger, M. E. Corrales, V. Loriot, R. de Nalda and L. Bañares, J. Chem. Phys., 2012, 136, 074303.
16. G. Gitzinger, V. Loriot, L. Bañares and R. de Nalda, J. Mod. Opt., 2014, 61, 864.
17. S. G. Walt, N. Bhargava Ram, A. von Conta, O. I. Tolstikhin, L. B. Madsen, F. Jensen and H. J. Wörner, J. Phys. Chem. A, 2015, 119, 11772.
18. Y. Wang, Y. Song, W. Liu, Y. Liu, L. Duo, L. Jiang and Y. Yang, Chem. Phys. Lett., 2015, 633, 126.
19. R. de Nalda, J. Durá, A. García-Vela, J. G. Izquierdo, J. González-Vázquez and L. Bañares, J. Chem. Phys., 2008, 128, 244309.
20. M. E. Corrales, G. Gitzinger, J. González-Vázquez, V. Loriot, R. de Nalda and L. Bañares, J. Phys. Chem. A, 2012, 116, 2669.
21. G. Rottman, Space Sci. Rev., 2006, 125, 39.
22. S. K. Solanki, N. A. Krivova and J. D. Haigh, Annu. Rev. Astron. Astrophys., 2013, 51, 311.
23. K. L. Yeo, N. A. Krivova and S. K. Solanki, Space Sci. Rev., 2014, 186, 137.
24. K. L. Yeo, W. T. Ball, N. A. Krivova, S. K. Solanki, Y. C. Unruh and J. Morrill, J. Geophys. Res.: Space Phys., 2015, 120, 6055.
25. L. J. Carpenter, Chem. Rev., 2003, 103, 4953.
26. R. von Glasow, Nature, 2008, 453, 1195.
27. I. Stemmler, M. Rothe, I. Hense and H. Hepach, Biogeosciences, 2013, 10, 4211.
28. S. Solomon, R. R. Garcia and A. R. Ravishankara, J. Geophys. Res.: Atmos., 1994, 99, 20491.
29. R. Vogt, R. Sander, R. von Glasow and P. J. Crutzen, J. Atmos. Chem., 1999, 32, 375.
30. R. Teiwes, J. Elm, K. Handrup, E. P. Jensen, M. Bilde and H. B. Pedersen, Phys. Chem. Chem. Phys., 2018, 20, 28606.
31. A. Saiz-Lopez, J. M. C. Plane, A. R. Baker, L. J. Carpenter, R. von Glasow, J. C. Gómez Martín, G. McFiggans and R. W. Saunders, Chem. Rev., 2012, 112, 1773.
32. C. D. O'Dowd, J. L. Jimenez, R. Bahreini, R. C. Flagan, J. H. Seinfeld, K. Hameri, L. Pirjola, M. Kulmala, S. G. Jennings and T. Hoffmann, Nature, 2002, 417, 632.
33. T. N. Olney, G. Cooper and C. Brion, Chem. Phys., 1998, 232, 211.
34. S. Eden, P. Limao-Vieira, S. Hoffmann and N. Mason, Chem. Phys., 2007, 331, 232.
35. R. D. Molloy, A. Danielsson, L. Karlsson and J. H. Eland, Chem. Phys., 2007, 335, 49.
36. R. Locht, B. Leyh, H. Jochims and H. Baumgärtel, Chem. Phys., 2009, 365, 109.
37. R. Locht, D. Dehareng, K. Hottmann, H. W. Jochims, H. Baumgärtel and B. Leyh, J. Phys. B: At., Mol. Opt. Phys., 2010, 43, 105101.
38. D. Holland, I. Powis, G. Öhrwall, L. Karlsson and W. von Niessen, Chem. Phys., 2006, 326, 535.
39. G. O'Sullivan, J. Phys. B: At. Mol. Phys., 1982, 15, L327.
40. D. W. Lindle, P. H. Kobrin, C. M. Truesdale, T. A. Ferrett, P. A. Heimann, H. G. Kerkhoff, U. Becker and D. A. Shirley, Phys. Rev. A: At., Mol., Opt. Phys., 1984, 30, 239.
41. P. Morin and I. Nenner, Phys. Scr., 1987, 1987, 171.
42. J. N. Cutler, G. M. Bancroft and K. H. Tan, J. Chem. Phys., 1992, 97, 7932.
43. M. Pernpointner, J. P. Zobel, E. Fasshauer and A. N. Sil, Chem. Phys., 2012, 407, 39.
44. S. Hayakawa, T. Tsujinaka and A. Fujihara, J. Chem. Phys., 2012, 137, 184308.
45. K. Mertens, N. Gerken, S. Klumpp, M. Braune and M. Martins, J. Mod. Opt., 2015, 63, 383.
46. B. Erk, R. Boll, S. Trippel, D. Anielski, L. Foucar, B. Rudek, S. W. Epp, R. Coffee, S. Carron, S. Schorb, K. R. Ferguson, M. Swiggers, J. D. Bozek, M. Simon, T. Marchenko, J. Küpper, I. Schlichting, J. Ullrich, C. Bostedt, D. Rolles and A. Rudenko, Science, 2014, 345, 288.
47. K. Motomura, E. Kukk, H. Fukuzawa, S. ichi Wada, K. Nagaya, S. Ohmura, S. Mondal, T. Tachibana, Y. Ito, R. Koga, T. Sakai, K. Matsunami, A. Rudenko, C. Nicolas, X.-J. Liu, C. Miron, Y. Zhang, Y. Jiang, J. Chen, M. Anand, D. E. Kim, K. Tono, M. Yabashi, M. Yao and K. Ueda, J. Phys. Chem. Lett., 2015, 6, 2944.
48. R. Boll, B. Erk, R. Coffee, S. Trippel, T. Kierspel, C. Bomme, J. D. Bozek, M. Burkett, S. Carron, K. R. Ferguson, L. Foucar, J. Küpper, T. Marchenko, C. Miron, M. Patanen, T. Osipov, S. Schorb, M. Simon, M. Swiggers, S. Techert, K. Ueda, C. Bostedt, D. Rolles and A. Rudenko, Struct. Dyn., 2016, 3, 043207.
49. K. Nagaya, K. Motomura, E. Kukk, Y. Takahashi, K. Yamazaki, S. Ohmura, H. Fukuzawa, S. Wada, S. Mondal, T. Tachibana, Y. Ito, R. Koga, T. Sakai, K. Matsunami, K. Nakamura, M. Kanno, A. Rudenko, C. Nicolas, X.-J. Liu, C. Miron, Y. Zhang, Y. Jiang, J. Chen, M. Anand, D. E. Kim, K. Tono, M. Yabashi, M. Yao, H. Kono and K. Ueda, Faraday Discuss., 2016, 194, 537.
50. A. Rudenko, L. Inhester, K. Hanasaki, X. Li, S. J. Robatjazi, B. Erk, R. Boll, K. Toyota, Y. Hao, O. Vendrell, C. Bomme, E. Savelyev, B. Rudek, L. Foucar, S. H. Southworth, C. S. Lehmann, B. Kraessig, T. Marchenko, M. Simon, K. Ueda, K. R. Ferguson, M. Bucher, T. Gorkhover, S. Carron, R. Alonso-Mori, J. E. Koglin, J. Correa, G. J. Williams, S. Boutet, L. Young, C. Bostedt, S.-K. Son, R. Santra and D. Rolles, Nature, 2017, 546, 129.
51. A. Bhattacherjee, A. R. Attar and S. R. Leone, J. Chem. Phys., 2016, 144, 124311.
52. L. Drescher, M. C. E. Galbraith, G. Reitsma, J. Dura, N. Zhavoronkov, S. Patchkovskii, M. J. J. Vrakking and J. Mikosch, J. Chem. Phys., 2016, 145, 011101.
53. A. Hitchcock and C. Brion, J. Electron Spectrosc. Relat. Phenom., 1979, 17, 139.
54. A. Hitchcock and C. Brion, J. Electron Spectrosc. Relat. Phenom., 1978, 13, 193.
55. D. Kovaček, K. Kovačević, D. Korenić and Z. B. Maksić, THEOCHEM, 1994, 304, 163.
56. R. Forbes, A. De Fanis, C. Bomme, D. Rolles, S. T. Pratt, I. Powis, N. A. Besley, M. Simon, S. Nandi, A. R. Milosavljević, C. Nicolas, J. D. Bozek, J. G. Underwood and D. M. P. Holland, J. Chem. Phys., 2018, 149, 144302.
57. S. Schippers, S. Ricz, T. Buhr, A. B. Jr, J. Hellhund, K. Holste, K. Huber, H.-J. Schäfer, D. Schury, S. Klumpp, K. Mertens, M. Martins, R. Flesch, G. Ulrich, E. Rühl, T. Jahnke, J. Lower, D. Metz, L. P. H. Schmidt, M. Schöffler, J. B. Williams, L. Glaser, F. Scholz, J. Seltmann, J. Viefhaus, A. Dorn, A. Wolf, J. Ullrich and A. Müller, J. Phys. B: At., Mol. Opt. Phys., 2014, 47, 115602.
58. A. Müller, D. Bernhardt, A. Borovik Jr., T. Buhr, J. Hellhund, K. Holste, A. Kilcoyne, S. Klumpp, M. Martins, S. Ricz, J. Seltmann, J. Viefhaus and S. Schippers, Astrophys. J., 2017, 836, 166.
59. S. Schippers, T. Buhr, A. Borovik Jr., K. Holste, A. Perry-Sassmannshausen, K. Mertens, S. Reinwardt, M. Martins, S. Klumpp, K. Schubert, S. Bari, R. Beerwerth, S. Fritzsche, S. Ricz, J. Hellhund and A. Müller, X-Ray Spectrom., 2019 DOI:10.1002/xrs.3035.
60. J. Viefhaus, F. Scholz, S. Deinert, L. Glaser, M. Ilchen, J. Seltmann, P. Walter and F. Siewert, Nucl. Instrum. Methods Phys. Res., Sect. A, 2013, 710, 151.
61. R. Trassl, P. Hathiramani, F. Broetz, J. B. Greenwood, R. W. McCullough, M. Schlapp and E. Salzborn, Phys. Scr., 1997, 1997, 380.
62. M. Berglund and M. Wieser, Pure Appl. Chem., 2011, 83, 397.
63. S. Schippers, A. L. D. Kilcoyne, R. A. Phaneuf and A. Müller, Contemp. Phys., 2016, 57, 215–229.
64. H. Kjeldsen, J. Phys. B: At., Mol. Opt. Phys., 2006, 39, R325.
65. K. Rinn, A. Müller, H. Eichenauer and E. Salzborn, Rev. Sci. Instrum., 1982, 53, 829.
66. C. Fonseca Guerra, G. J. Snijders, G. te Velde and J. E. Baerends, Theor. Chem. Acc., 1998, 99, 391.
67. G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. Fonseca Guerra, S. J. A. van Gisbergen, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931.
68. E. Van Lenthe and E. J. Baerends, J. Comput. Chem., 2003, 24, 1142.
69. C. Van Wüllen, J. Comput. Chem., 2002, 23, 779–785.
70. S. van Gisbergen, J. Snijders and E. Baerends, Comput. Phys. Commun., 1999, 118, 119.
71. S. Hirata and M. Head-Gordon, Chem. Phys. Lett., 1999, 314, 291.
72. F. Vines, C. Sousa and F. Illas, Phys. Chem. Chem. Phys., 2018, 20, 8403–8410.
73. M. Hollstein, K. Mertens, S. Klumpp, N. Gerken, S. Palutke, I. Baev, G. Brenner, S. Dziarzhytski, M. Meyer, W. Wurth, D. Pfannkuche and M. Martins, New J. Phys., 2019, 21, 033017.
74. J. A. Bearden and A. F. Burr, Rev. Mod. Phys., 1967, 39, 125–142.
75. R. S. Mulliken, Phys. Rev., 1935, 47, 413.
76. J. L. Ragle, I. A. Stenhouse, D. C. Frost and C. A. McDowell, J. Chem. Phys., 1970, 53, 178.
77. M. Tadjeddine, G. Bouchoux, L. Malegat, J. Durup, C. Pernot and J. Weiner, Chem. Phys., 1982, 69, 229.
78. M. Tadjeddine, J. Flament and C. Teichteil, Chem. Phys., 1987, 118, 45.
79. K. Walter, R. Weinkauf, U. Boesl and E. W. Schlag, J. Chem. Phys., 1988, 89, 1914.
80. H. Brion and C. Moser, J. Chem. Phys., 1960, 32, 1194.
81. Y. A. Teterin and S. G. Gagarin, Russ. Chem. Rev., 1996, 65, 825.
82. R. K. Nesbet, J. Chem. Phys., 1965, 43, 4403.

---

Footnote

† These authors contributed equally to this work.

---