Rationalization of photo-detachment spectra of the indenyl anion (C9H7−) from the perspective of vibronic coupling theory†
Received
19th August 2019
, Accepted 16th September 2019
First published on 16th September 2019
Abstract
The nuclear dynamics of the low-lying first four electronic states of the prototypical indenyl radical is investigated based on first principles calculations to rationalize the experimental vibronic structure of the radical. The study is performed following both time-dependent and time-independent quantum-chemistry approaches using a model diabatic Hamiltonian. The construction of model Hamiltonians is based on the fits of the adiabatic energies calculated from the electronic structure method. The analyses of the static and dynamics results of the present study corroborate the experimental findings regarding the shape of the spectrum, vibrational progressions and the lifetime of the excited state. Finally, the present theoretical investigations suggest that the electronic non-adiabatic effect is extremely important for a detailed study of the vibronic structure and the electronic relaxation mechanism of the low-lying electronic states of the indenyl radical.
I. Introduction
Polycyclic aromatic hydrocarbons (PAHs), which form soot on aggregation,1–3 are major pollutants hazardous to human health and also to the ecosystem. They are formed due to incomplete combustion of fossil fuels. Although PAHs have a huge adverse effect on the environment, these compounds have attracted a great deal of interest in the timely research following their presence in the interstellar medium (ISM)4–6 and their link to prebiotic evolution in the early universe as it is known that PAHs form amino acids by reacting with the mixture of ammonia and ice in the exotic conditions of the ISM.7,8 The identification of particular PAHs in the circumstellar envelopes of carbon rich asymptotic giant branch (AGB) stars is still questionable,9 but it is believed that PAHs are carriers of the various unidentified and mysterious diffuse interstellar bands (DIBs) in infra-red and visible wavelengths.10–17 In general, the study of molecular evolution of PAHs is exclusively focused on possible expansion of the cyclo-C6 ring(s) in the parent benzene moiety in a linear18–27 and compact28–34 fashion. Naphthalene and phenanthrene are the simplest prototypical examples of linear and compact PAHs formed due to cyclo-C6 ring extension of benzene. On the other hand, the cyclo-C5 ring also plays a pivotal role in the formation of PAHs. For example, the well established DIBs corresponding to 9577 and 9632 Å were observed due to the presence of cationic fullerenes in the ISM35–40 and it is also well known that the compact PAHs and cyclo-C5 ring participated in the formation of fullerenes.41 The simplest prototypical example of this category of PAHs is indene, which is composed of fused one cyclo-C6 ring and one cyclo-C5 ring. The presence of this molecule or its cationic, anionic or dehydrogenated forms in the circumstellar space is still unidentified, but the results obtained from different spectroscopic and pyrolytic techniques applied on different carbonaceous chondrites that originated either from the solar system or from the ISM indicate the presence of indene and its isomers in those chondrites.42,43
The formation of closed-shell indene (C9H8) and its dehydrogenated radical [indenyl (C9H7˙)] species has been predicted from the addition of acetylene to fulvenallene,44 cyclopentadienyl radical,45 and benzyl radical.46 Along with these, the addition of propargyl to benzyne47 and the oxidation of the naphthyl radical followed by decomposition48–50 also suggest the possible mechanism of formation of indenyl. Indenyl is also found as a product during the flow of acetylene over nano-sized silicate particles.51 The present discussion indicates that a wealth of literature is available regarding the thermochemistry and kinetics of indenyl formation, while the physical characteristics of indenyl based on spectroscopic techniques are largely missing from the literature. The ESR characterization of indenyl was performed by abstracting a hydrogen atom from indene with a t-butoxy radical.52 Fischer and co-workers studied threshold photoionization spectroscopy to characterize the indenyl radical53 and the radical was prepared by jet flash pyrolysis. A strong peak corresponding to the first band of the indenyl radical was observed at 7.53 eV and it was obtained due to the major contribution from C–H bending and ring breathing vibrations. On the other hand, the ab initio theoretical calculations by the same group indicate negligible change in the geometry of the ground state of the indenyl cation upon first ionization from the reference indenyl radical. A less prominent peak around 8.35 eV was found and it was attributed to the first excited state (3B2) of the indenyl cation. Another study of emission and excitation spectra of the 1-indenyl radical is reported by Izumida et al.,54 and it was found that these spectra are overlapping with each other.
The gas phase vibronic characteristics of the ground and excited electronic states of neutral indenyl are rarely available in the literature. However, Römmer et al.55 measured the electron photo-detachment spectra of indenyl and fluorenyl anions in the quest of determination of the electron affinities of the corresponding radicals and the bond dissociation energies of the corresponding neutrals. In the context of rare information on vibrational frequencies and energetics of the excited states of the neutral radicals, a recent photo-detachment spectroscopic study by Neumark and coworkers3 on the deprotonated anion of indene and fluorene sheds light upon electron affinities, state energies and the vibrational structures of the ground and first excited electronic states of neutral indenyl and fluorenyl radicals. Instead of conventional photo-detachment spectroscopy (provides a resolution of 80–100 cm−1), this group has used slow electron velocity-map imaging (SEVI) combined with cryogenic cooling of the anions (indenyl and fluorenyl) to get vibronically resolved spectra (resolution within 4 cm−1) of the neutral radicals. This study reveals numerous vibrational excitations of the ground state of the neutral radicals. Large vibrational excitations of the indenyl ground state occur from non-totally symmetric vibrational modes, whereas the vibrational excitations of the fluorenyl ground state are mainly dominated by totally symmetric vibrational modes. These observations were also verified using density functional theory (DFT) and Franck–Condon (FC) spectrum simulations generated using the ezSpectrum program56 by the same group. The comparison between the theoretical results and experimental observations unveils that the experimental fluorenyl spectrum can be simulated by standard FC simulations (which means that the peaks obtained in the photo-detachment spectrum of the fluorenyl anion follow adiabatic dynamics), whereas the disagreement between the same for indenyl insisted them to speculate that the intensity gain in the ground state spectrum of the indenyl radical appears to be due to vibronic coupling between ground and excited states of the indenyl radical. A strong non-adiabatic coupling and an ultrafast non-adiabatic electronic population decay of the excited state were also speculated by observing the broad linewidth of the indenyl spectrum in relation with the calculated [CAS(9,9) and CASSCF/6-31+G*] low-lying conical intersections (CIs). Similar type of observations were found for the first two electronic states of (![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) and Ã) the naphthalene cation, anthracene cation and pyrrolyl. The observation of the first two cations was nicely explained by Mahapatra and co-workers8,57 by implementing multi-mode-vibronic-coupling (MMVC) theory on those cations and it was established that the spectroscopy of those cations is highly influenced by the ultrafast non-adiabatic electronic population transfer between à and
and Ã) the naphthalene cation, anthracene cation and pyrrolyl. The observation of the first two cations was nicely explained by Mahapatra and co-workers8,57 by implementing multi-mode-vibronic-coupling (MMVC) theory on those cations and it was established that the spectroscopy of those cations is highly influenced by the ultrafast non-adiabatic electronic population transfer between à and ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) states in the presence of low-lying CIs between them. Similarly the featureless broad excited state of the photo-detachment band of the pyrrolide anion58 was theoretically attributed to the presence of quasi-degeneracy between the excited state (2B1) saddle point and the CIs between the excited and ground (2A2) states59 of pyrrolyl. It was shown by Yarkony and Zhu59 that the inclusion of non-adiabatic coupling into the spectrum simulation significantly improved the comparison between the simulated and experimental58 photo-detachment spectrum of the pyrrolide anion than the comparison of the experimental spectrum with the theoretical spectrum obtained from adiabatic simulation.
states in the presence of low-lying CIs between them. Similarly the featureless broad excited state of the photo-detachment band of the pyrrolide anion58 was theoretically attributed to the presence of quasi-degeneracy between the excited state (2B1) saddle point and the CIs between the excited and ground (2A2) states59 of pyrrolyl. It was shown by Yarkony and Zhu59 that the inclusion of non-adiabatic coupling into the spectrum simulation significantly improved the comparison between the simulated and experimental58 photo-detachment spectrum of the pyrrolide anion than the comparison of the experimental spectrum with the theoretical spectrum obtained from adiabatic simulation.
We have taken this opportunity to explore the adiabatic and non-adiabatic dynamics of the first four electronic states of the indenyl radical to fulfil the experimental3 demands for the investigation of the role of CIs in the dynamics and spectroscopy of indenyl. In this regard, the present theoretical calculations also unveil additional information on the photo-physical process involved with the possible explanations of the experimental findings.3 The present study is based on the calculations of adiabatic potential curves of the first four low-lying electronic states of the indenyl radical along the dimensionless recti-linear normal coordinates of the vibrational modes using the ab initio electronic structure method. Later, a suitable vibronic Hamiltonian is constructed in a diabatic electronic basis following the quality of fits of the evaluated adiabatic energies along normal vibrational modes (normal modes are selected using standard vibronic symmetry selection rules60) using higher-order Taylor series expansion. The possible vibronic couplings between different electronic states are also calculated following the MMVC approach.60–69 Later, the positions of the CIs between different electronic states and the nuclear dynamics are studied using the evaluated vibronic coupling parameters in order to understand and complement some of the experimental results.3 The dynamics observables reported in the present study are calculated both from the simulations of the eigenvalue spectrum and from the results of the analyses of the time-dependent behaviour of the electronic states. The nuclear dynamics investigated in the present study following both time-dependent and time-independent quantum-chemistry approaches suggest that the electronic non-adiabatic effect is extremely important for a detailed study of the vibronic structure and the electronic relaxation mechanism of the low-lying electronic states of the indenyl radical.
II. Computational and theoretical methodology
A. Computational details
Geometry optimization of the reference electronic ground state of the indenyl anion was performed employing the Moller–Plesset perturbation (MP2) level of theory with Dunning's polarized valence triple-zeta basis set (cc-pVTZ)70 using the Gaussian 09 programs module.71 The corresponding optimized parameters of the reference equilibrium geometries are given in Table 1. Subsequent vibrational analysis of these optimized structures was also performed at the same level of theory and the harmonic vibrational frequencies of the a1 and b2 symmetric vibrational modes of the reference state and neutral ground state of the indenyl radical are given in Table 2. The full list of frequencies is given in Table S1 in the ESI.† We also performed geometry optimizations and subsequent frequency calculations of the reference, and the ground and first excited states of the indenyl radical employing density functional theory (DFT) and time-dependent version of DFT (TDDFT) using the cc-pVTZ basis set to fulfil the requirement of Franck–Condon (FC) photo-detachment spectrum simulations as implemented in Gaussian 09.71 All these calculations indicate that the optimized structures of the reference, and the ground and first excited state of the indenyl radical belong to C2v point group symmetry. A schematic representation of these optimized structures with atom number is presented in Fig. 1, to make easier the comparison of geometry parameters between the ground state equilibrium structure of the indenyl anion (reference) and the indenyl radical given in Table 1.
Table 1 Equilibrium ground state geometry parameters of the indenyl anion and indenyl radical. The available literature data of the same are also given here. The atom numbering of the structure is shown in Fig. 1
| Theory |
| Geometry |
Anion |
Neutral |
| MP2-ccpVTZ |
B3LYP/6-311+G*![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 3 |
MP2-ccpVTZ |
B3LYP/6-311+G*![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 3 |
| C1–C2 |
1.462 |
1.462 |
1.420 |
1.428 |
| C2–C3 |
1.407 |
1.389 |
1.391 |
1.388 |
| C3–C4 |
1.389 |
1.389 |
1.396 |
1.406 |
| C4–C5 |
1.415 |
1.418 |
1.400 |
1.393 |
| C2–C9 |
1.413 |
1.419 |
1.450 |
1.452 |
| C8–C9 |
1.410 |
1.410 |
1.386 |
1.401 |
| C3–H10 |
1.087 |
1.091 |
1.082 |
1.086 |
| C4–H11 |
1.085 |
1.089 |
1.081 |
1.085 |
| C8–H15 |
1.084 |
1.088 |
1.077 |
1.082 |
| C9–H16 |
1.082 |
1.086 |
1.080 |
1.083 |
| C1C2C3 |
119.0 |
119.0 |
120.5 |
120.3 |
| C2C3C4 |
120.3 |
120.4 |
118.5 |
118.9 |
| C3C4C5 |
120.6 |
120.6 |
120.9 |
120.8 |
| C7C8C9 |
110.2 |
110.2 |
109.0 |
109.0 |
| C8C9C2 |
107.4 |
107.4 |
108.6 |
108.4 |
| C9C2C1 |
107.4 |
107.4 |
106.8 |
107.1 |
| C8C9H16 |
126.3 |
126.3 |
126.0 |
126.0 |
| C2C3H10 |
119.9 |
119.9 |
121.0 |
121.0 |
| C3C4H11 |
119.9 |
119.8 |
119.6 |
119.6 |
Table 2 Harmonic frequencies [in cm−1 (eV)] of the a1 and b2 symmetric vibrational modes of ground state equilibrium structures of the indenyl anion and indenyl radical. The data of this table are obtained from the MP2/cc-pVTZ level of theory. The full list of harmonic frequencies of the vibrational modes of the same is given in Table S1 in the ESI
| Vibrational mode (symmetry) |
Anion frequency (ωi) |
Neutral frequency (ωi) |
|
ν
1(a1) |
545 (0.0676) |
541.90 |
|
ν
2(a1) |
744 (0.0923) |
752.78 |
|
ν
3(a1) |
859 (0.1065) |
888.08 |
|
ν
4(a1) |
1017 (0.1261) |
1035.16 |
|
ν
5(a1) |
1053 (0.1305) |
1119.42 |
|
ν
6(a1) |
1146 (0.1421) |
1173.27 |
|
ν
7(a1) |
1287 (0.1596) |
1277.01 |
|
ν
8(a1) |
1374 (0.1703) |
1464.00 |
|
ν
9(a1) |
1448 (0.1795) |
1512.84 |
|
ν
10(a1) |
1559 (0.1932) |
1572.97 |
|
ν
11(a1) |
1594 (0.1976) |
1635.07 |
|
ν
12(a1) |
3143 (0.3897) |
3209.68 |
|
ν
13(a1) |
3175 (0.3937) |
3233.74 |
|
ν
14(a1) |
3187 (0.3951) |
3256.70 |
|
ν
15(a1) |
3219 (0.3991) |
3285.35 |
|
|
|
ν
16(b2) |
382 (0.0474) |
381.43 |
|
ν
17(b2) |
588 (0.0728) |
632.30 |
|
ν
18(b2) |
881 (0.1092) |
894.77 |
|
ν
19(b2) |
1042 (0.1292) |
1062.20 |
|
ν
20(b2) |
1115 (0.1383) |
1153.63 |
|
ν
21(b2) |
1194 (0.1481) |
1207.54 |
|
ν
22(b2) |
1238 (0.1535) |
1267.15 |
|
ν
23(b2) |
1359 (0.1684) |
1387.12 |
|
ν
24(b2) |
1462 (0.1813) |
1427.56 |
|
ν
25(b2) |
1504 (0.1865) |
1521.23 |
|
ν
26(b2) |
1643 (0.2037) |
3087.16 |
|
ν
27(b2) |
3138 (0.3891) |
3207.36 |
|
ν
28(b2) |
3166 (0.3926) |
3222.32 |
|
ν
29(b2) |
3209 (0.3979) |
3279.79 |
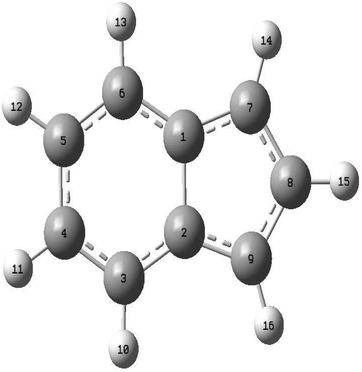 |
| | Fig. 1 Schematic representation of the energy minimized structure of the indenyl anion and indenyl radical. Atom numberings are given in this figure for easier understanding of the comparison of equilibrium geometry parameters of the indenyl anion and indenyl radical given in Table 1. | |
The vertical detachment energies (VDEs) at the reference geometry were calculated with the complete active space self consistent field (CASSCF), multi-reference configuration interactions (MRCI), second-order multi-state complete active space perturbation theory (MS-CASPT2) and outer valence Green's function (OVGF) level of theories with the same basis set of Dunning and the results obtained from these calculations were compared with available experimental and theoretical findings, and the data are given in Table 3. The calculations at the CASSCF, MRCI and MS-CASPT2 level of theories were performed with MOLPRO program modules,72 while the calculations at the OVGF level of theory were performed with Gaussian 09 program modules.71 The VDE calculations with different sets of active spaces, like (10,11), (10,12), (12,10), (12,11), (12,12), (14,10), (14,11), (14,11), and (14,13), were performed employing the CASSCF level of theory to choose the best possible computationally feasible active space for MRCI and MS-CASPT2 calculations. We found that the VDE calculations using the CASSCF, MRCI and MS-CASPT2 levels of theory with (10,11) active space, which is composed of five valence occupied molecular orbitals (MOs) and six virtual MOs with ten electrons, provide the best comparison with the available experimental value (cf.Table 3). On the other hand, the comparison between different theoretical data of the present calculations in Table 3 indicates that the OVGF method is the most suitable among the employed theories to calculate the VDE at reference geometry. Thus we chose the OVGF level of theory to calculate the single point VDEs for the rest of our calculations. It was also found that OVGF is quite a convenient electronic structure method to study the dynamical properties of PAHs.8,27,33,57,73
Table 3 Vertical detachment energies (in eV) of first four electronic states of the indenyl radical obtained from different levels of theory. The available literature values are also given in the table. CASPT2 calculations are performed with level shift values of 0.10, 0.15, 0.20, 0.25 and 0.30. The values obtained from a level shift of 0.30 are presented here
| State |
This work |
Kim et al.3 |
| CASSCF (10,11) |
MRCI (10,11) |
MS-CASPT2 (10,11) |
OVGF |
Experiment |
Theory EOM-IP-CCSD |
![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2 2A2 |
1.14 |
1.56 |
1.57 |
1.66 |
1.80 |
1.58 |
| Ã2B1 |
2.17 |
2.54 |
2.51 |
2.58 |
|
2.55 |
![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 2A2 2A2 |
4.33 |
4.69 |
4.62 |
4.49 |
|
|
![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) 2B1 2B1 |
5.39 |
5.74 |
5.50 |
5.74 |
|
|
The anionic reference structure was distorted along the dimensionless normal coordinate and single point VDEs were calculated at each distorted geometry. The mass-weighted normal displacement coordinates of the vibrational modes are calculated from the eigenvectors of the GF-matrix.74 These are then transformed to the dimensionless form, Q, by multiplying with 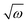 (in a.u.). The VDEs of the first four highest occupied MOs [HOMOs] were calculated at the distorted geometry of Qi (i = 1–29) = ±0.10, ±0.25, ±0.50, ±0.75, ±1.00, ±1.50,…,±5.00, along each normal coordinate. The ab initio adiabatic VDEs obtained from these calculations were then fit with the adiabatic form of the diabatic Hamiltonian of eqn (4) to estimate the Hamiltonian parameters. The linear intra-state (κ) and inter-state (λ) Hamiltonian parameters were also calculated numerically following the first-order differential equation of κ or λ = (dV/dQ)Q=0, where V is the adiabatic electronic potential or the difference of adiabatic electronic potentials of two electronic states, and the results are compared with the above analytical values of the same. The results of the analytic fits and the corresponding numerical values are given in Tables 4–6.
(in a.u.). The VDEs of the first four highest occupied MOs [HOMOs] were calculated at the distorted geometry of Qi (i = 1–29) = ±0.10, ±0.25, ±0.50, ±0.75, ±1.00, ±1.50,…,±5.00, along each normal coordinate. The ab initio adiabatic VDEs obtained from these calculations were then fit with the adiabatic form of the diabatic Hamiltonian of eqn (4) to estimate the Hamiltonian parameters. The linear intra-state (κ) and inter-state (λ) Hamiltonian parameters were also calculated numerically following the first-order differential equation of κ or λ = (dV/dQ)Q=0, where V is the adiabatic electronic potential or the difference of adiabatic electronic potentials of two electronic states, and the results are compared with the above analytical values of the same. The results of the analytic fits and the corresponding numerical values are given in Tables 4–6.
Table 4 Linear and quadratic intra-state coupling parameters (in eV) of totally symmetric vibrational modes in the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2, Ã2B1,
2A2, Ã2B1, ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 2A2 and
2A2 and ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) 2B1 electronic states of the indenyl radical. The excitation strength of these couplings is given in parentheses. The higher-order coupling parameters of the same are given in Table S2 in the ESI
2B1 electronic states of the indenyl radical. The excitation strength of these couplings is given in parentheses. The higher-order coupling parameters of the same are given in Table S2 in the ESI
| Mode |
κ((κ2)/2ω2) |
γ
|
κ((κ2)/2ω2) |
γ
|
|
|
![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2 2A2 |
Ã2B1 |
|
ν
1
|
−0.0032 (0.0011) |
−0.0004 |
−0.0693 (0.5267) |
−0.0013 |
|
ν
2
|
0.0047 (0.0013) |
−0.0019 |
0.0220 (0.0284) |
0.0019 |
|
ν
3
|
0.0658 (0.1909) |
−0.0023 |
−0.0583 (0.1502) |
0.0019 |
|
ν
4
|
−0.0111 (0.0039) |
0.0020 |
0.0167 (0.0088) |
0.0029 |
|
ν
5
|
0.0349 (0.0358) |
0.0022 |
−0.0543 (0.0868) |
0.0059 |
|
ν
6
|
−0.0416 (0.0428) |
0.0081 |
0.0543 (0.0729) |
0.0088 |
|
ν
7
|
0.0523 (0.0536) |
−0.0024 |
−0.0101 (0.0020) |
0.0021 |
|
ν
8
|
0.0399 (0.02756) |
−0.0104 |
−0.0583 (0.0587) |
0.0126 |
|
ν
9
|
0.0226 (0.0079) |
0.0046 |
−0.0514 (0.0410) |
0.0002 |
|
ν
10
|
−0.0894 (0.1071) |
−0.001 |
0.1018 (0.1388) |
0.0011 |
|
ν
11
|
0.1696 (0.3683) |
−0.0208 |
−0.1654 (0.3503) |
0.0212 |
|
ν
12
|
−0.0104 (0.0003) |
0.0054 |
−0.0216 (0.0015) |
0.0060 |
|
ν
13
|
−0.0151 (0.0007) |
0.0068 |
−0.0040 (0.00005) |
0.0074 |
|
ν
14
|
−0.0202 (0.0013) |
0.0041 |
−0.0251 (0.0020) |
0.0043 |
|
ν
15
|
0.0276 (0.0024) |
0.0053 |
0.0321 (0.0032) |
0.0049 |
|
|
|
|
![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 2A2 2A2 |
![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) 2B1 2B1 |
|
ν
1
|
0.0775 (0.6574) |
−0.0016 |
−0.0256 (0.0718) |
−0.0006 |
|
ν
2
|
0.0193 (0.0219) |
−0.0012 |
0.0312 (0.0572) |
0.0009 |
|
ν
3
|
−0.0063 (0.0018) |
0.0021 |
−0.0110 (0.0053) |
0.0016 |
|
ν
4
|
0.0137 (0.0059) |
0.0007 |
0.0945 (0.2809) |
−0.0005 |
|
ν
5
|
−0.0036 (0.0004) |
0.0045 |
−0.0638 (0.1198) |
0.0070 |
|
ν
6
|
−0.0447 (0.0495) |
0.0086 |
0.0113 (0.0032) |
0.0099 |
|
ν
7
|
−0.0471 (0.0437) |
0.0156 |
0.0424 (0.0354) |
−0.0133 |
|
ν
8
|
0.0638 (0.0701) |
0.0186 |
−0.0263 (0.0119) |
0.0077 |
|
ν
9
|
0.0270 (0.0113) |
0.0071 |
−0.1075 (0.1794) |
0.0069 |
|
ν
10
|
−0.1357 (0.2466) |
0.0096 |
0.0086 (0.0009) |
0.0197 |
|
ν
11
|
−0.0300 (0.0115) |
0.0273 |
0.0788 (0.0795) |
0.0140 |
|
ν
12
|
−0.0110 (0.0004) |
0.0052 |
−0.0145 (0.0007) |
0.0053 |
|
ν
13
|
−0.0080 (0.0002) |
0.0065 |
−0.0126 (0.0005) |
0.0064 |
|
ν
14
|
−0.0303 (0.0029) |
0.0035 |
−0.0380 (0.0046) |
0.0038 |
|
ν
15
|
0.0257 (0.0020) |
0.0037 |
0.0491 (0.0075) |
0.0044 |
Table 5 The quadratic intra-state coupling parameters (in eV) of b2 symmetric vibrational modes in the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2, Ã2B1,
2A2, Ã2B1, ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 2A2 and
2A2 and ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) 2B1 electronic states of the indenyl radical
2B1 electronic states of the indenyl radical
| Vibrational modes |
![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2 2A2 |
Ã2B1 |
![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 2A2 2A2 |
![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) 2B1 2B1 |
|
ν
16
|
0.0000 |
0.0021 |
−0.0030 |
−0.0024 |
|
ν
17
|
−0.0046 |
0.0047 |
−0.0010 |
0.0006 |
|
ν
18
|
0.0009 |
0.0013 |
0.0006 |
0.0000 |
|
ν
19
|
0.0032 |
0.0160 |
0.0056 |
0.0108 |
|
ν
20
|
−0.0035 |
0.0148 |
−0.0035 |
0.0124 |
|
ν
21
|
0.0060 |
0.0059 |
0.0030 |
0.0107 |
|
ν
22
|
−0.0026 |
0.0081 |
0.0102 |
0.0064 |
|
ν
23
|
−0.0037 |
0.0140 |
0.0053 |
0.0073 |
|
ν
24
|
−0.0363 |
0.0464 |
−0.0115 |
0.0289 |
|
ν
25
|
−0.0153 |
0.0276 |
−0.0112 |
0.0215 |
|
ν
26
|
−0.0125 |
0.0105 |
0.0175 |
0.0093 |
|
ν
27
|
0.0060 |
0.0066 |
0.0059 |
0.0060 |
|
ν
28
|
0.0057 |
0.0055 |
0.0055 |
0.0052 |
|
ν
29
|
0.0065 |
0.0056 |
0.0045 |
0.0054 |
Table 6 The linear inter-state coupling parameter (in eV) between the electronic states of the indenyl radical. The excitation strength (λi2/2ωi2) of these couplings is given in parentheses
| Coupled states |
Vib. mode (symmetry) |
λ((λ2)/2ω2) |
Coupled states |
Vib. mode (symmetry) |
λ((λ2)/2ω2) |
![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) –Ã –Ã |
ν
16(b2) |
0.0223 (0.1115) |
![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) – –![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) |
ν
16(b2) |
0.0496 (0.5487) |
|
ν
17(b2) |
0.0473 (0.2110) |
ν
17(b2) |
0.0726 (0.4978) |
|
ν
18(b2) |
0.0093 (0.0037) |
ν
18(b2) |
0.0322 (0.0437) |
|
ν
19(b2) |
0.0561 (0.0942) |
ν
19(b2) |
0.0883 (0.2339) |
|
ν
20(b2) |
0.0671 (0.1177) |
ν
20(b2) |
0.1250 (0.4092) |
|
ν
21(b2) |
— |
ν
21(b2) |
0.0697 (0.1108) |
|
ν
22(b2) |
0.0502 (0.0535) |
ν
22(b2) |
0.0935 (0.1856) |
|
ν
23(b2) |
0.0654 (0.0753) |
ν
23(b2) |
0.1011 (0.1801) |
|
ν
24(b2) |
0.1381 (0.2902) |
ν
24(b2) |
0.0977 (0.1452) |
|
ν
25(b2) |
0.0984 (0.1392) |
ν
25(b2) |
0.1672 (0.4019) |
|
ν
26(b2) |
0.0835 (0.0841) |
ν
26(b2) |
0.2457 (0.7277) |
|
ν
27(b2) |
0.0116 (0.0004) |
ν
27(b2) |
0.0047 (0.0001) |
|
ν
28(b2) |
— |
ν
28(b2) |
0.0239 (0.0018) |
|
ν
29(b2) |
— |
ν
29(b2) |
0.03234 (0.0033) |
|
|
Ö![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) |
ν
16(b2) |
0.0492 (0.5382) |
![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) – –![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) |
ν
16(b2) |
0.0132 (0.0391) |
|
ν
17(b2) |
0.0518 (0.2530) |
ν
17(b2) |
0.0225 (0.0478) |
|
ν
18(b2) |
0.0190 (0.0152) |
ν
18(b2) |
0.0141 (0.0084) |
|
ν
19(b2) |
0.0694 (0.1445) |
ν
19(b2) |
0.0410 (0.0504) |
|
ν
20(b2) |
0.0907 (0.2153) |
ν
20(b2) |
0.0720 (0.1358) |
|
ν
21(b2) |
0.0370 (0.0313) |
ν
21(b2) |
0.0499 (0.0568) |
|
ν
22(b2) |
0.0298 (0.0189) |
ν
22(b2) |
0.0340 (0.0245) |
|
ν
23(b2) |
0.0634 (0.0708) |
ν
23(b2) |
0.0225 (0.0089) |
|
ν
24(b2) |
0.1358 (0.2809) |
ν
24(b2) |
0.1133 (0.1955) |
|
ν
25(b2) |
0.1167 (0.1959) |
ν
25(b2) |
0.0891 (0.1142) |
|
ν
26(b2) |
0.0616 (0.0457) |
ν
26(b2) |
0.1354 (0.2210) |
|
ν
27(b2) |
0.0183 (0.0011) |
ν
27(b2) |
0.0054 (0.0001) |
|
ν
28(b2) |
0.0054 (0.0001) |
ν
28(b2) |
0.0108 (0.0004) |
|
ν
29(b2) |
0.0229 (0.0016) |
ν
29(b2) |
0.0175 (0.0009) |
B. Construction of the molecular Hamiltonian
The present study deals with the nuclear dynamics of the first four low-lying electronic states of the indenyl radical. The indenyl anion belongs to the C2v point group in its ground state (11A1) energy minimized structure. This structure was treated as the reference in the present study for the single point energy calculations and also for construction of the molecular Hamiltonian. The symmetry and term of the first four low-lying electronic states of the indenyl radical are ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2, Ã2B1,
2A2, Ã2B1, ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 2A2 and
2A2 and ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) 2B1, respectively. The energy order of these states was determined from the increasing vertical detachment energy (VDE) from the ground state minimum of the indenyl anion. The forty-two normal vibrational modes of the indenyl anion were decomposed in the following irreducible representation:
2B1, respectively. The energy order of these states was determined from the increasing vertical detachment energy (VDE) from the ground state minimum of the indenyl anion. The forty-two normal vibrational modes of the indenyl anion were decomposed in the following irreducible representation:| | | Γ = 15a1 ⊕ 7b1 ⊕ 14b2 ⊕ 6a1. | (1) |
The molecular Hamiltonian for the present calculations was constructed in a diabatic electronic representation as described by Köppel et al.60 and the potential corresponding to each Hamiltonian element was expanded in a Taylor's series along the recti-linear dimensionless normal coordinate at the Franck–Condon (FC) geometry following the quality of fits (correlation coefficient) between the calculated ab intio energy points and the adiabatic form of the diabatic Hamiltonian. The molecular Hamiltonian, rather the vibronic Hamiltonian, can be written in the following form:| |  | (2) |
where  ,
, 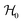 and
and 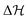 represent the overall molecular Hamiltonian, the Hamiltonian of the reference configuration (unperturbed) and the Hamiltonian corresponding to electron detachment, respectively. 1 stands for a unit matrix, whose dimension is dependent upon the number of considered electronic states. Thus it is a 4 × 4 unit matrix in the present study. Within the harmonic approximation the unperturbed Hamiltonian can be written as
represent the overall molecular Hamiltonian, the Hamiltonian of the reference configuration (unperturbed) and the Hamiltonian corresponding to electron detachment, respectively. 1 stands for a unit matrix, whose dimension is dependent upon the number of considered electronic states. Thus it is a 4 × 4 unit matrix in the present study. Within the harmonic approximation the unperturbed Hamiltonian can be written as| | 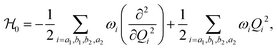 | (3) |
where ω and Q represent the frequency of the normal mode and the corresponding normal coordinate at the reference geometry. The non-vanishing elements of the detachment Hamiltonian (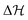 ) of eqn (2) were determined using standard vibronic selection rules as described in ref. 60, 62, 66, 69, 75, 76 and these can be written as
) of eqn (2) were determined using standard vibronic selection rules as described in ref. 60, 62, 66, 69, 75, 76 and these can be written as| | 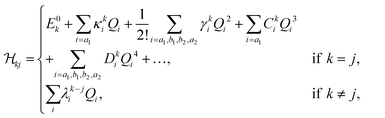 | (4) |
where k and j are electronic state indices and i indicates the vibrational mode. The VDE is represented by E0k, whereas the first-order intra-state and inter-state coupling following the linear vibronic coupling (LVC) scheme are represented by κki and λk−ji, respectively. The diagonal elements of the matrix were expanded in higher-order Taylor's series. γki, Cki and Dki represent quadratic, third-order and fourth-order intra-state coupling parameters following the quadratic vibronic coupling (QVC) and higher-order vibronic coupling scheme. The constructed largest model Hamiltonian consists of four coupled electronic states and eighteen vibrational modes in the present study. Several reduced dimensional Hamiltonians were also constructed in the quest of acquiring useful information on the nuclear dynamics.
C. Quantum dynamics calculations
The quantum dynamics calculations of the present study were performed within the multi-configuration time-dependent Hartree (MCTDH) framework77–81 as implemented in the Heidelberg MCTDH package82 using both time-dependent (TD) and time-independent (TI) formalisms. The TD Schrödinger equation was solved by expressing the wave function as a sum of products of single particle functions (SPFs) {φ(k)jk} in MCTDH formalism.83,84 The representation of SPFs is as follows:| | 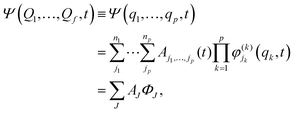 | (5) |
where Ψ(Q1,…,Qf,t) represents the wave function in f degrees of freedom and Ψ(q1,…,qp,t) is the wave function in p combined modes (MCTDH particles) and the value of p < f. Later, Ψ(q1,…,qp,t) is expanded as the product of time-dependent MCTDH coefficients (AJ ≡ Aj1,…,jp) and orthonormal TD SPFs. The quantity, ΦJ, in the third line of eqn (5) represents the product of SPFs, termed as the Hartree product. The TD SPFs are again expanded in TI primitive basis functions. The Hermite discrete variable representation (DVR) was employed for the construction of the primitive basis in the present calculations. The number of SPFs (nk) was chosen in a way that it is always less than the number of primitive functions (Nx) for each MCTDH particle and it also maintains an appropriate balance between two limiting cases of time-dependent-Hartree (TDH) and standard method [i.e. propagating wavepacket (WP) on the primitive basis] of wavepacket propagation. In this way an appropriate correlation between the interacting particles is introduced in our calculations.
The equation of motion of MCTDH was derived by using the Dirac–Frenkel variational principle85,86 based on the nuclear wave function given in eqn (5). This gives the following MCTDH working equations:
| | 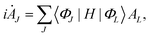 | (6) |
| | i![[small phi (variant), Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a4.gif) (k) = (1 − P(k))−1(ρ(k))−1〈H〉(k)φ(k), (k) = (1 − P(k))−1(ρ(k))−1〈H〉(k)φ(k), | (7) |
where the vector notation of the MCTDH coefficient and SPFs are previously defined and
ρ(k) and 〈
H〉
(k) represent the one-particle density matrix and the matrix of mean-field operators, respectively. The MCTDH projector is defined by
P(k), and it ensures that SPFs stay orthonormal during the propagation. The MCTDH coefficient (
A vector) and SPFs (
φ vector) were propagated under the constant mean-field (CMF) integration scheme. We have chosen by default the most efficient short iterative Lancozs (SIL) and Bulirsch–Stoer (BS) integrators for
A and
φ vectors, respectively, with variable step sizes. An initial WP pertinent to the reference ground state of the indenyl anion was vertically promoted to the four low-lying electronic states of the indenyl radical and then it was propagated up to 200 fs in the coupled
![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2
2A
2–Ã
2B
1–
![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 2
2A
2–
![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) 2
2B
1 electronic states of the indenyl radical. The autocorrelation functions [
C(
t) = 〈
Ψ(0)|
Ψ(
t)〉] of the WP were recorded in time during the propagation. Later, the autocorrelation functions obtained from individual calculations were combined with equal weighted. The obtained autocorrelation function was damped with an exponential function
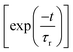
and Fourier transformed to get an energy value spectrum.
The TI part of the present nuclear dynamics was solved by diagonalising the Hermitian Hamiltonian presented in eqn (2) using the Lanczos algorithm63–65 as implemented in the MCTDH program module82 and representing the Hamiltonian of eqn (2) in the direct product harmonic oscillator (HO) basis of the reference state. The stick line spectrum obtained from these calculations was convoluted with a Gaussian type of function to get the spectrum envelope.
The eigenenergies and the WP densities of the first fifty eigenstates were calculated using the improved relaxation method87,88 in block form.89 The WP was propagated in negative imaginary time in the block-improved relaxation method to obtain information on the ground vibronic state and the A-vector was determined by diagonalization instead of relaxation. The applied CMF integration scheme is slightly different in this approach as compared to propagation. Instead of the standard variant of the CMF step size control, CMF/varphi, where the CMF step size is controlled only by SPFs, is used in block-improved relaxation calculations as the A-vector changes discontinuously. The determination of the A-vector is performed by using the Davidson diagonalizer.
III. Results and discussion
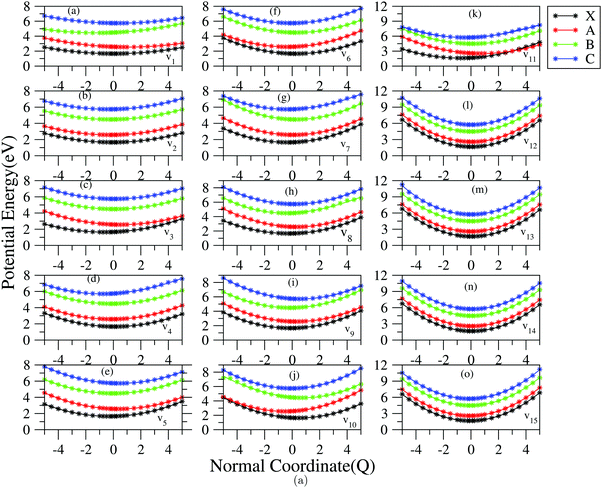
A. Adiabatic potential energy curves
In order to study the nuclear dynamics in detail, first we examine the nature of topography of adiabatic potential energy curves (PECs) along the totally symmetric vibrational mode. The PECs are generated by diagonalizing the electronic matrix Hamiltonian of eqn (4) and using the Hamiltonian parameters of Tables 3 and 4 with the addition of the harmonic potential of the reference state (cf.eqn (3)). The PECs of the first four electronic states (![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2, Ã2B1,
2A2, Ã2B1, ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 2A2 and
2A2 and ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) 2B1) of the indenyl radical are shown in Fig. 2. In this figure, the points represent the energy obtained from the ab initio quantum chemistry method and the solid lines represent the potential obtained from the constructed model vibronic Hamiltonian. The superposition of the ab initio energy points and solid lines indicates the quality of the fits performed in the present study. The fittings of the ab initio energy points indicate that a higher-order expansion of the Taylor's series is needed for a few vibrational modes (cf. Table S2 in the ESI†). Overall, the PECs of Fig. 2 indicate that
2B1) of the indenyl radical are shown in Fig. 2. In this figure, the points represent the energy obtained from the ab initio quantum chemistry method and the solid lines represent the potential obtained from the constructed model vibronic Hamiltonian. The superposition of the ab initio energy points and solid lines indicates the quality of the fits performed in the present study. The fittings of the ab initio energy points indicate that a higher-order expansion of the Taylor's series is needed for a few vibrational modes (cf. Table S2 in the ESI†). Overall, the PECs of Fig. 2 indicate that ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 2A2 and
2A2 and ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) 2B1 states are well separated from each other as well as from the first two electronic states (
2B1 states are well separated from each other as well as from the first two electronic states (![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2 and Ã2B1) of the indenyl radical in the Franck–Condon region, while the energy difference between the former two states and the Ã2B1 state is reduced towards positive or negative values along some normal coordinates. On the other hand, several intersections and energy proximities are found between
2A2 and Ã2B1) of the indenyl radical in the Franck–Condon region, while the energy difference between the former two states and the Ã2B1 state is reduced towards positive or negative values along some normal coordinates. On the other hand, several intersections and energy proximities are found between ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2 and Ã2B1 states (cf.Fig. 2).
2A2 and Ã2B1 states (cf.Fig. 2).
 |
| | Fig. 2 Adiabatic potential energy curves of ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2, Ã2B1, 2A2, Ã2B1, ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 2A2 and 2A2 and ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) 2B1 electronic states of the indenyl radical along dimensionless normal coordinates of totally symmetric modes. The ab initio energies represented by points and solid lines are generated from the adopted vibronic coupling model. The superposition of ab initio points and solid lines indicates the quality of fits performed in the present study and the indication of normal vibrational modes is given in the right-hand bottom corner of each panel. 2B1 electronic states of the indenyl radical along dimensionless normal coordinates of totally symmetric modes. The ab initio energies represented by points and solid lines are generated from the adopted vibronic coupling model. The superposition of ab initio points and solid lines indicates the quality of fits performed in the present study and the indication of normal vibrational modes is given in the right-hand bottom corner of each panel. | |
The data presented in Table 4 indicate the existence of moderate to low intra-state couplings in the first four electronic states of the indenyl radical. The strength (excitation strength) of the intra-state coupling is estimated by calculating the Huang–Rhys parameter, which is defined as 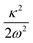 . The positional and directional shift of the energy minimum of an electronic state with respect to its reference electronic configuration can be measured from this parameter. The amount of shift of the minimum of an electronic state increases with the increment of the value of this parameter in an opposite direction of the sign of κ. For example, ν11 possesses the strongest Condon activity in
. The positional and directional shift of the energy minimum of an electronic state with respect to its reference electronic configuration can be measured from this parameter. The amount of shift of the minimum of an electronic state increases with the increment of the value of this parameter in an opposite direction of the sign of κ. For example, ν11 possesses the strongest Condon activity in ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2 state; as a result, the largest shift of the energy minimum of the ground state of the indenyl radical is found along this normal mode in the negative direction (cf. panel k of Fig. 2). Similarly, the largest shift of the energy minima of Ã2B1,
2A2 state; as a result, the largest shift of the energy minimum of the ground state of the indenyl radical is found along this normal mode in the negative direction (cf. panel k of Fig. 2). Similarly, the largest shift of the energy minima of Ã2B1, ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 2A2 and
2A2 and ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) 2B1 states can be found along ν1 (cf. panel a of Fig. 2), ν1 (cf. panel a of Fig. 2) and ν4 (cf. panel d of Fig. 2), respectively. A similar analysis indicates that a considerable shift of energy minima of
2B1 states can be found along ν1 (cf. panel a of Fig. 2), ν1 (cf. panel a of Fig. 2) and ν4 (cf. panel d of Fig. 2), respectively. A similar analysis indicates that a considerable shift of energy minima of ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2 and Ã2B1 states is observed along ν10 and ν11 vibrational modes and later these states also intersect (cf. panels j and k of Fig. 2) along these normal coordinates. On the other hand, PECs along the other vibrational modes indicate energetic proximity between these states.
2A2 and Ã2B1 states is observed along ν10 and ν11 vibrational modes and later these states also intersect (cf. panels j and k of Fig. 2) along these normal coordinates. On the other hand, PECs along the other vibrational modes indicate energetic proximity between these states.
Analysing the PECs of ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2 and Ã2B1 states in panels a, c, d, e, f, g, h, i, j and k of Fig. 2, we also calculated the energetic locations of different conical intersections (CIs) in the multi-dimensional space within the quadratic vibronic coupling model and employing the Lagrange constrained minimization scheme as implemented in the Mathematica programs module.90 The energetic locations of the state's minima and CIs between the states are presented in the diagonal and off-diagonal entries of Table 7, respectively. It can be seen from this table that the minimum of Ã2B1 state is just ∼0.087 eV below with respect to
2A2 and Ã2B1 states in panels a, c, d, e, f, g, h, i, j and k of Fig. 2, we also calculated the energetic locations of different conical intersections (CIs) in the multi-dimensional space within the quadratic vibronic coupling model and employing the Lagrange constrained minimization scheme as implemented in the Mathematica programs module.90 The energetic locations of the state's minima and CIs between the states are presented in the diagonal and off-diagonal entries of Table 7, respectively. It can be seen from this table that the minimum of Ã2B1 state is just ∼0.087 eV below with respect to ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2–Ã2B1 CI. This value is quite consistent with the value (0.056 eV) obtained from ab initio state-average CAS(9,9)SCF with 6-31+G* basis set calculation of ref. 3. On the other hand, the minimum of
2A2–Ã2B1 CI. This value is quite consistent with the value (0.056 eV) obtained from ab initio state-average CAS(9,9)SCF with 6-31+G* basis set calculation of ref. 3. On the other hand, the minimum of ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2 state is energetically quite low (∼0.97 eV) from the
2A2 state is energetically quite low (∼0.97 eV) from the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2–Ã2B1 CI. Therefore, it can be speculated that low vibronic levels of
2A2–Ã2B1 CI. Therefore, it can be speculated that low vibronic levels of ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2 state cannot be perturbed in the presence of
2A2 state cannot be perturbed in the presence of ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2–Ã2B1 CI, while the same for Ã2B1 are very likely to be perturbed in the presence of
2A2–Ã2B1 CI, while the same for Ã2B1 are very likely to be perturbed in the presence of ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2–Ã2B1 CI. The present topic would be discussed later in detail in relation with the Poisson spectrum and coupled state nuclear dynamics.
2A2–Ã2B1 CI. The present topic would be discussed later in detail in relation with the Poisson spectrum and coupled state nuclear dynamics.
Table 7 Estimated energy (in eV) of the equilibrium minimum (diagonal ones) of electronic states and minimum of CIs (off diagonal ones) between different electronic states of the indenyl radical
|
|
![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2 2A2 |
Ã2B1 |
![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 2A2 2A2 |
![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) 2B1 2B1 |
![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2 2A2 |
1.5096 |
2.4802 |
17.8842 |
22.9303 |
| Ã2B1 |
|
2.3924 |
5.8926 |
11.6279 |
![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 2A2 2A2 |
|
|
4.3648 |
6.1661 |
![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) 2B1 2B1 |
|
|
|
5.6192 |
B. Influence of conical intersections and electronic non-adiabatic effects on the nuclear dynamics of the first four electronic states of the indenyl radical
The comparatively higher energetic location of the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2–Ã2B1 CI with respect to the minimum of
2A2–Ã2B1 CI with respect to the minimum of ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2 state indicates that the lower vibronic levels of the
2A2 state indicates that the lower vibronic levels of the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2 state of the indenyl radical cannot be perturbed in the presence of
2A2 state of the indenyl radical cannot be perturbed in the presence of ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2–Ã2B1 CI. Therefore, it would be worthwhile to examine the nature of the vibronic energy levels of the ground electronic state of the indenyl radical by studying the nuclear dynamics in uncoupled state formalism first and later examining the impact of electronic non-adiabatic effects in conjunction with CIs following coupled state formalism.
2A2–Ã2B1 CI. Therefore, it would be worthwhile to examine the nature of the vibronic energy levels of the ground electronic state of the indenyl radical by studying the nuclear dynamics in uncoupled state formalism first and later examining the impact of electronic non-adiabatic effects in conjunction with CIs following coupled state formalism.
1. Nuclear dynamics of the uncoupled ground state of indenyl radical.
Two different approaches are considered to simulate the ground uncoupled vibronic structure of the indenyl radical in the present study. In the first approach, we simulated the Franck–Condon (FC) spectrum of the ground state (![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2) of the indenyl radical following the pre-screening scheme91,92 of the FC simulation as implemented in the Gaussian 09 program module.71 In the second approach we have used the formalism of the Poisson distribution spectrum in the uncoupled potential energy surface (λ = 0) as defined in ref. 93 and 94. We performed the optimization of the ground state energy minima geometries and the corresponding normal mode analysis of the initial (anionic indenyl) and final (indenyl radical) states following the requirement of necessary inputs for FC spectrum simulations.91,92 These calculations were performed employing both MP2 and DFT (B3LYP) level of theories using the cc-pVTZ and 6-311+G* basis set, respectively, and geometry parameters of the energy minima of both indenyl anion and indenyl radical are given in Table 1, while the corresponding frequencies of a1 and b2 symmetric vibrational modes calculated from the MP2 level of theory are given in Table 2. It is found from these calculations that both ground states of the anion and indenyl radical belong to C2v point group symmetry. The result obtained from FC simulations using anion and radical geometries of the MP2 level of theory is presented in panel b of Fig. 3, while the same using the DFT level of theory is presented in panel b of Fig. S1 in the ESI.† Both results obtained from FC simulations are then compared with the available overview SEVI spectra of the indenyl anion digitized from ref. 3 and given in panel a of Fig. 3 and panel a of Fig. S1 in the ESI.† We also simulated the FC spectrum of the first excited state (Ã2B1) of indenyl using the time-dependent version of DFT and shown in panel b of Fig. S1 in the ESI.† Both the simulated FC spectra are shifted to the experimental onset (∼14
2A2) of the indenyl radical following the pre-screening scheme91,92 of the FC simulation as implemented in the Gaussian 09 program module.71 In the second approach we have used the formalism of the Poisson distribution spectrum in the uncoupled potential energy surface (λ = 0) as defined in ref. 93 and 94. We performed the optimization of the ground state energy minima geometries and the corresponding normal mode analysis of the initial (anionic indenyl) and final (indenyl radical) states following the requirement of necessary inputs for FC spectrum simulations.91,92 These calculations were performed employing both MP2 and DFT (B3LYP) level of theories using the cc-pVTZ and 6-311+G* basis set, respectively, and geometry parameters of the energy minima of both indenyl anion and indenyl radical are given in Table 1, while the corresponding frequencies of a1 and b2 symmetric vibrational modes calculated from the MP2 level of theory are given in Table 2. It is found from these calculations that both ground states of the anion and indenyl radical belong to C2v point group symmetry. The result obtained from FC simulations using anion and radical geometries of the MP2 level of theory is presented in panel b of Fig. 3, while the same using the DFT level of theory is presented in panel b of Fig. S1 in the ESI.† Both results obtained from FC simulations are then compared with the available overview SEVI spectra of the indenyl anion digitized from ref. 3 and given in panel a of Fig. 3 and panel a of Fig. S1 in the ESI.† We also simulated the FC spectrum of the first excited state (Ã2B1) of indenyl using the time-dependent version of DFT and shown in panel b of Fig. S1 in the ESI.† Both the simulated FC spectra are shifted to the experimental onset (∼14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 cm−1) in order to compare with the experimental findings3 and it can be seen from panel b of Fig. 3 and panel b of Fig. S1 in the ESI† that both FC simulations nicely reproduce the experimental overview SEVI scan of the ground state of the indenyl anion. This comparison indicates that a minute change in the geometry occurs in the neutral ground state of indenyl radical upon photo-detachment from ground state anionic indenyl. This fact is also well supported from the geometry parameters of these states given in Table 1. The largest change of the C–C bond is ∼0.04 Å, C–H bond is ∼0.01 Å, C–C–C angle is ∼2 degree and C–C–H angle is ∼1 degree upon photo-detachment of anionic indenyl (data are presented following MP2 calculations). Therefore it is found that the FC spectrum of the indenyl radical is dominated by a single peak at 0–0 transition contributed from the excitation of fundamental vibrational levels, where the FC integral possesses the highest value [as indicated by the square of the transition dipole moment integral (TDMI), the value is ∼0.4]. The overall contribution from the fundamental vibrational progressions in the FC spectrum is found to be ∼40%, while the vibrational progressions of the first overtones of the ν2–ν10 (excluding ν4) vibrational modes and combination excitations between ν3, ν5 and ν8 vibrational modes contribute ∼40% and ∼16%, respectively, in the overall ground state FC spectrum of the indenyl radical.
500 cm−1) in order to compare with the experimental findings3 and it can be seen from panel b of Fig. 3 and panel b of Fig. S1 in the ESI† that both FC simulations nicely reproduce the experimental overview SEVI scan of the ground state of the indenyl anion. This comparison indicates that a minute change in the geometry occurs in the neutral ground state of indenyl radical upon photo-detachment from ground state anionic indenyl. This fact is also well supported from the geometry parameters of these states given in Table 1. The largest change of the C–C bond is ∼0.04 Å, C–H bond is ∼0.01 Å, C–C–C angle is ∼2 degree and C–C–H angle is ∼1 degree upon photo-detachment of anionic indenyl (data are presented following MP2 calculations). Therefore it is found that the FC spectrum of the indenyl radical is dominated by a single peak at 0–0 transition contributed from the excitation of fundamental vibrational levels, where the FC integral possesses the highest value [as indicated by the square of the transition dipole moment integral (TDMI), the value is ∼0.4]. The overall contribution from the fundamental vibrational progressions in the FC spectrum is found to be ∼40%, while the vibrational progressions of the first overtones of the ν2–ν10 (excluding ν4) vibrational modes and combination excitations between ν3, ν5 and ν8 vibrational modes contribute ∼40% and ∼16%, respectively, in the overall ground state FC spectrum of the indenyl radical.
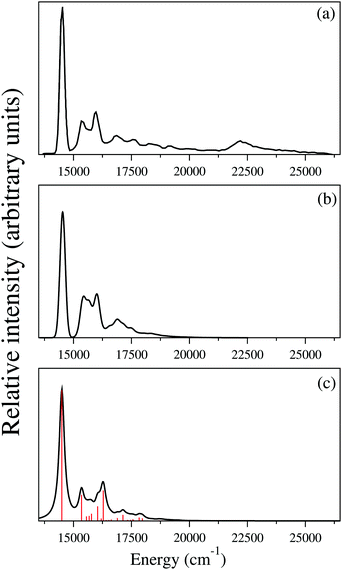 |
| | Fig. 3 Comparison of the spectrum obtained from Franck–Condon simulations (panel b) and the uncoupled absorption spectrum obtained from vibronic coupling theory (panel c) with the experimental observation of overview of SEVI spectra of the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2 state of the indenyl radical (digitized from ref. 3 and shown in panel a) is shown in this figure. 2A2 state of the indenyl radical (digitized from ref. 3 and shown in panel a) is shown in this figure. | |
It would be worthwhile to check the individual contribution of the totally symmetric (a1) vibrational mode in the Poisson intensity distribution before the discussion of the cumulative effect of the considered a1 symmetric vibrational modes in the ground state uncoupled spectrum of the indenyl radical. According to Poisson distribution,93,94 the sum of the normalised intensities of an individual vibrational mode is 1 and the intensities would be distributed over the fundamental and overtones of the individual vibrational mode depending upon its excitation strength (Huang–Rhys parameter). A wide spectrum would be observed upon high excitation of a vibrational mode, while the intensity concentrates mainly in the vibrational quantum level 0, upon low excitation of a vibrational mode. Following this we also plot the intensity distribution along the vibrational quantum number of the vibrational modes possessing the highest values (first three in decreasing order) of excitation strength in the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2 state of the indenyl radical (cf.Table 4) in panels a, b and c of Fig. 4, while the same with the lowest excitation strength (last three in increasing order) is shown in panels d, e and f in the same figure. It is seen from these figures that the maximum intensity is concentrated in the vibrational quantum level 0 for all considered vibrational modes, which is consistent with the estimated low excitation strength of these vibrational modes (cf.Table 4). As a result we find the highest intensity in the 0–0 peak of the ground state photo-detachment band of the indenyl anion (see panel c in Fig. 3) due to the cumulative contribution of all totally symmetric vibrational modes excited at the vibronic quantum level 0. In contrast to the above a very little contribution from the first overtones of the relatively strong (in terms of excitation strength) vibrational modes, ν11 and ν3, is found (cf. panels a and b in Fig. 4). Therefore, the intensity of the overall uncoupled ground state spectrum of the indenyl radical (cf. panel c in Fig. 3) is drastically reduced after excitation at the 0–0 level. The same characteristic of the recorded SEVI ground state spectrum of the indenyl anion was found in ref. 3 and it was attributed to the p-wave photo-detachment phenomena of dramatically diminished intensity after the intense 0–0 band.
2A2 state of the indenyl radical (cf.Table 4) in panels a, b and c of Fig. 4, while the same with the lowest excitation strength (last three in increasing order) is shown in panels d, e and f in the same figure. It is seen from these figures that the maximum intensity is concentrated in the vibrational quantum level 0 for all considered vibrational modes, which is consistent with the estimated low excitation strength of these vibrational modes (cf.Table 4). As a result we find the highest intensity in the 0–0 peak of the ground state photo-detachment band of the indenyl anion (see panel c in Fig. 3) due to the cumulative contribution of all totally symmetric vibrational modes excited at the vibronic quantum level 0. In contrast to the above a very little contribution from the first overtones of the relatively strong (in terms of excitation strength) vibrational modes, ν11 and ν3, is found (cf. panels a and b in Fig. 4). Therefore, the intensity of the overall uncoupled ground state spectrum of the indenyl radical (cf. panel c in Fig. 3) is drastically reduced after excitation at the 0–0 level. The same characteristic of the recorded SEVI ground state spectrum of the indenyl anion was found in ref. 3 and it was attributed to the p-wave photo-detachment phenomena of dramatically diminished intensity after the intense 0–0 band.
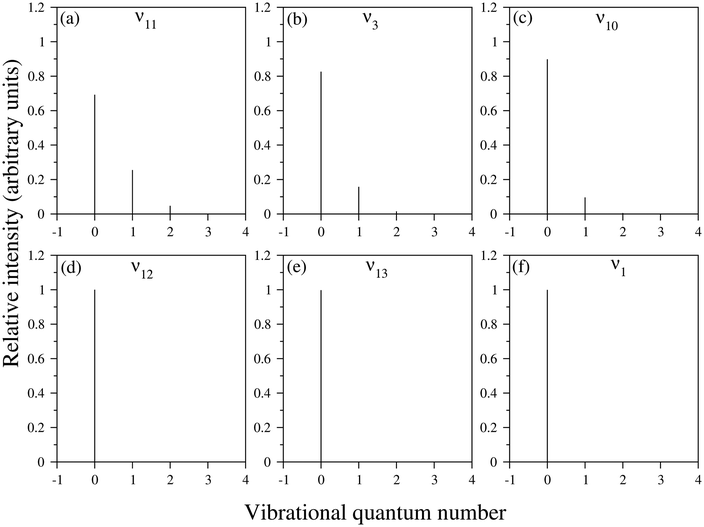 |
| | Fig. 4 The pattern of Poisson intensity distribution in the vibrational quantum levels of the totally symmetric vibrational modes of the indenyl radical in the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2 state is shown in this figure. The intensity distribution of vibrational modes which possess the highest values (first three in decreasing order) of excitation strength is presented in panels a–c and the same with low excitation strength (last three in increasing order) is presented in panels d–f. The excitation strength of the vibrational modes indicated in each panel can be found in Table 4. 2A2 state is shown in this figure. The intensity distribution of vibrational modes which possess the highest values (first three in decreasing order) of excitation strength is presented in panels a–c and the same with low excitation strength (last three in increasing order) is presented in panels d–f. The excitation strength of the vibrational modes indicated in each panel can be found in Table 4. | |
The composite Poisson spectrum of the ground state of indenyl is generated considering harmonic oscillator (HO) functions for vibrational modes, ν1, ν3, ν5, ν6, ν7, ν10 and ν11, up to 8, 10, 6, 6, 6, 8 and 10, respectively, and employing 8000 Lanczos iterations. The choice of HO basis is made following the excitation strength of the vibrational modes given in Table 4. The result of the present calculation is shown in panel c of Fig. 3 and compared with the result obtained from FC simulations (see panel b of Fig. 3) and also with available experimental SEVI recording3 (see panel a of Fig. 3). Both the envelope of the FC simulation and that of the Poisson spectrum are obtained using the Gaussian convolution function with a full width at half maximum (FWHM) of 135 cm−1. As discussed above, both the theoretical spectra (FC and Poisson spectra) are in good agreement with the experimental envelope.3 The present discussion is mainly devoted to assigning the stick vibronic lines of panel c of Fig. 3 by employing the block-improved relaxation method95–97 as implemented in the MCTDH program module.82 The vibrational energy level assignments are performed by examining the corresponding wavepacket (WP) density plots and following the same procedure as previously demonstrated by Sarkar et al.98–101 The WP density plots of some selected vibrational energy levels of the uncoupled ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2 state of the indenyl radical are presented in Fig. 5. The assignments of the vibronic energy levels are mainly performed by identifying the fundamental vibrational progressions first. Later, based on the fundamental progressions, vibrational progressions of overtones and combination peaks are assigned. For example, the WP density plot of panel a in Fig. 5 shows a nodal plane along the Q1 normal coordinate at ∼544 cm−1 from the onset of the spectrum. This means that the energy line corresponds to the excitation of the first overtone of vibrational mode ν1 and the energy gap of the vibronic line from the 0–0 line is 544 cm−1 which matches with the fundamental frequency of the vibrational mode ν1. Therefore, the present vibronic line is assigned for fundamental vibrational progression of ν1. Similarly, the vibronic lines at ∼850 cm−1, ∼1179 cm−1, ∼1277 cm−1 and ∼1545 cm−1 are assigned for the fundamentals of ν3, ν6, ν7 and ν10, respectively, and their corresponding WP density plots are shown in panels b, c, d and e, respectively, in Fig. 5. Assignments of the first overtone of ν3 and combination peaks between (ν6 and ν1), (ν6 and ν3) and (ν10 and ν3), at ∼1699 cm−1, 1722 cm−1, 2028 cm−1 and 2395 cm−1, respectively, are performed following two nodal planes along Q3 and a simultaneous nodal plane along two normal coordinates. The WP density plots of the above mentioned vibronic energy lines are shown in panels f, g, h and i, respectively in Fig. 5. In an identical manner, we also perform the possible assignments of other vibrational energy levels in the uncoupled
2A2 state of the indenyl radical are presented in Fig. 5. The assignments of the vibronic energy levels are mainly performed by identifying the fundamental vibrational progressions first. Later, based on the fundamental progressions, vibrational progressions of overtones and combination peaks are assigned. For example, the WP density plot of panel a in Fig. 5 shows a nodal plane along the Q1 normal coordinate at ∼544 cm−1 from the onset of the spectrum. This means that the energy line corresponds to the excitation of the first overtone of vibrational mode ν1 and the energy gap of the vibronic line from the 0–0 line is 544 cm−1 which matches with the fundamental frequency of the vibrational mode ν1. Therefore, the present vibronic line is assigned for fundamental vibrational progression of ν1. Similarly, the vibronic lines at ∼850 cm−1, ∼1179 cm−1, ∼1277 cm−1 and ∼1545 cm−1 are assigned for the fundamentals of ν3, ν6, ν7 and ν10, respectively, and their corresponding WP density plots are shown in panels b, c, d and e, respectively, in Fig. 5. Assignments of the first overtone of ν3 and combination peaks between (ν6 and ν1), (ν6 and ν3) and (ν10 and ν3), at ∼1699 cm−1, 1722 cm−1, 2028 cm−1 and 2395 cm−1, respectively, are performed following two nodal planes along Q3 and a simultaneous nodal plane along two normal coordinates. The WP density plots of the above mentioned vibronic energy lines are shown in panels f, g, h and i, respectively in Fig. 5. In an identical manner, we also perform the possible assignments of other vibrational energy levels in the uncoupled ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2 state of the indenyl radical and the results are tabulated in Table 8. Analysing the data given in Table 8, we also assign four experimental3 peak positions (peaks D, J, Q and X, see Table I in ref. 3). The peaks D, J, Q and X of the experimental SEVI spectrum of the ground state of the indenyl anion3 are assigned to the fundamentals of ν1 (544 cm−1), ν3 (850 cm−1), ν6 (1179 cm−1) and ν10 (1545 cm−1), respectively. The maximum deviation of these peaks from the experimental one is ∼9 cm−1, corresponding to ν10. Although the present composite Poisson spectrum (cf. panel c of Fig. 3) nicely reproduces the overall structure of the ground state SEVI spectrum of indenyl,3 the experimental peak positions are not properly located by the present calculations and the intensity of the Poisson spectrum of the
2A2 state of the indenyl radical and the results are tabulated in Table 8. Analysing the data given in Table 8, we also assign four experimental3 peak positions (peaks D, J, Q and X, see Table I in ref. 3). The peaks D, J, Q and X of the experimental SEVI spectrum of the ground state of the indenyl anion3 are assigned to the fundamentals of ν1 (544 cm−1), ν3 (850 cm−1), ν6 (1179 cm−1) and ν10 (1545 cm−1), respectively. The maximum deviation of these peaks from the experimental one is ∼9 cm−1, corresponding to ν10. Although the present composite Poisson spectrum (cf. panel c of Fig. 3) nicely reproduces the overall structure of the ground state SEVI spectrum of indenyl,3 the experimental peak positions are not properly located by the present calculations and the intensity of the Poisson spectrum of the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2 state is diminished at ∼18
2A2 state is diminished at ∼18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 750 cm−1, which is in contrast to the experimental observations.3 This indicates an indirect agreement with the experimental speculation of excitations of non-totally symmetric vibrational modes and the influence of electronic non-adiabatic effects from the excited states on the ground state SEVI spectrum of the indenyl anion.3 Therefore it would be worthwhile now to examine the role of non-totally symmetric vibrational modes in the coupled state dynamics in relation with electronic non-adiabatic effects in addition to the totally symmetric vibrational modes, which are involved in the energetic modulation between the coupled states. The next section is mainly devoted to this endeavour to understand the experimental speculation more rigorously by performing nuclear dynamics of the coupled
750 cm−1, which is in contrast to the experimental observations.3 This indicates an indirect agreement with the experimental speculation of excitations of non-totally symmetric vibrational modes and the influence of electronic non-adiabatic effects from the excited states on the ground state SEVI spectrum of the indenyl anion.3 Therefore it would be worthwhile now to examine the role of non-totally symmetric vibrational modes in the coupled state dynamics in relation with electronic non-adiabatic effects in addition to the totally symmetric vibrational modes, which are involved in the energetic modulation between the coupled states. The next section is mainly devoted to this endeavour to understand the experimental speculation more rigorously by performing nuclear dynamics of the coupled ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2–Ã2B1 states.
2A2–Ã2B1 states.
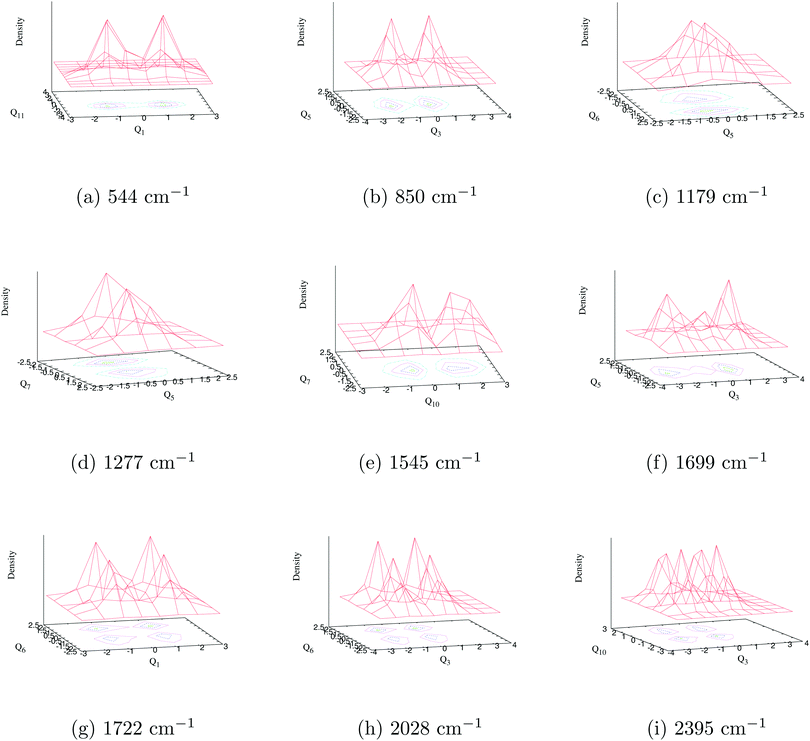 |
| | Fig. 5 The wave packet density plots of the vibronic energy levels in the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2 state of the indenyl radical are shown in this figure. The results are obtained from uncoupled vibronic dynamics of 2A2 state of the indenyl radical are shown in this figure. The results are obtained from uncoupled vibronic dynamics of ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2 state. The fundamental vibrational progression along ν1, ν3, ν6, ν7 and ν10 vibrational modes is shown in panels a, b, c, d and e, respectively, observing one nodal plane along the normal coordinate of the respective vibrational mode. The first overtone along the ν3 vibrational mode is shown in panel f, observing two nodal planes along that mode. The combination vibrational progression along (ν6, ν1), (ν6, ν3) and (ν10, ν3) vibrational modes is shown in panels g, h and i, respectively, observing one nodal plane along each vibrational mode of the combination pairs. 2A2 state. The fundamental vibrational progression along ν1, ν3, ν6, ν7 and ν10 vibrational modes is shown in panels a, b, c, d and e, respectively, observing one nodal plane along the normal coordinate of the respective vibrational mode. The first overtone along the ν3 vibrational mode is shown in panel f, observing two nodal planes along that mode. The combination vibrational progression along (ν6, ν1), (ν6, ν3) and (ν10, ν3) vibrational modes is shown in panels g, h and i, respectively, observing one nodal plane along each vibrational mode of the combination pairs. | |
Table 8 Assignment of vibronic energy levels (in cm−1) of totally symmetric vibrational modes of ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2 electronic state of the indenyl radical. The results are obtained from uncoupled vibronic dynamics of the
2A2 electronic state of the indenyl radical. The results are obtained from uncoupled vibronic dynamics of the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2 state
2A2 state
| No. |
Vibronic energy level |
Assignment |
No. |
Vibronic energy level |
Assignment |
| 1 |
0 |
0 |
21 |
2395 |
ν
10 + ν3 |
| 2 |
544 |
ν
1
|
22 |
2480 |
ν
7 + ν6 |
| 3 |
850 |
ν
3
|
23 |
2549 |
2ν7 |
| 4 |
1179 |
ν
6
|
24 |
2572 |
ν
11 + ν5 |
| 5 |
1277 |
ν
7
|
25 |
2632 |
ν
10 + 2ν1 |
| 6 |
1393 |
ν
3 + ν1 |
26 |
2636 |
ν
10 + 2ν1 |
| 7 |
1545 |
ν
10
|
27 |
2671 |
2ν5 + ν1 |
| 8 |
1631 |
ν
5 + ν1 |
28 |
2718 |
ν
10 + ν6 |
| 9 |
1699 |
2ν3 |
29 |
2786 |
ν
11 + ν7 |
| 10 |
1722 |
ν
6 + ν1 |
30 |
2810 |
ν
10 + ν7 |
| 11 |
1821 |
ν
7 + ν1 |
31 |
2874 |
ν
6 + 2ν3 |
| 12 |
1937 |
ν
3 + 2ν1 |
32 |
2908 |
2ν6 + ν1 |
| 13 |
2028 |
ν
6 + ν3 |
33 |
2938 |
2ν5 + ν3 |
| 14 |
2089 |
ν
10 + ν1 |
34 |
2977 |
ν
7 + 2ν3 |
| 15 |
2127 |
ν
7 + ν3; 2ν5 |
35 |
3024 |
2ν11 |
| 16 |
2174 |
ν
5 + 2ν1 |
36 |
3064 |
2ν10 |
| 17 |
2243 |
ν
6 + ν5; 2ν3 + ν1 |
37 |
3090 |
2ν7 + ν1 |
| 18 |
2266 |
ν
6 + 2ν1 |
38 |
3116 |
2ν2 |
| 19 |
2330 |
ν
7 + ν5; 2ν5 |
39 |
3176 |
2ν6 + ν3 |
| 20 |
2365 |
ν
7 + 2ν1 |
40 |
3245 |
ν
10 + 2ν3 |
2. Impact of non-adiabaticity on the nuclear dynamics of the ![[X with combining tilde]](https://www.rsc.org/images/entities/b_char_0058_0303.gif) 2A2–Ã2B1 coupled potential energy surfaces.
The existence of less than an eV vertical energy gap between Ã2B1 and
2A2–Ã2B1 coupled potential energy surfaces.
The existence of less than an eV vertical energy gap between Ã2B1 and ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2 states (cf.Table 3) and the moderate inter-state coupling between them (cf.Table 6) encouraged us to examine the plausible vibronic coupling between these states in the coupled-state framework. In this study we include five totally symmetric vibrational modes (ν1, ν3, ν6, ν10 and ν11) and six coupling vibrational modes (ν16, ν17, ν19, ν20, ν24 and ν25) of b2 symmetry (A2 ⊗ B1 ⊃ b2) to perform the nuclear dynamics of the
2A2 states (cf.Table 3) and the moderate inter-state coupling between them (cf.Table 6) encouraged us to examine the plausible vibronic coupling between these states in the coupled-state framework. In this study we include five totally symmetric vibrational modes (ν1, ν3, ν6, ν10 and ν11) and six coupling vibrational modes (ν16, ν17, ν19, ν20, ν24 and ν25) of b2 symmetry (A2 ⊗ B1 ⊃ b2) to perform the nuclear dynamics of the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2–Ã2B1 coupled potential energy surfaces (PESs). Selection of totally symmetric modes is performed following the above discussions in relation with Poisson spectrum simulation, while the coupling vibrational modes are selected considering their excitation strength given in Table 6. We choose less values of HO basis for totally symmetric modes as compared to the selected HO basis for the simulation of the spectrum of panel c of Fig. 3 by re-examining the results of Fig. 4. Finally, the HO basis for the coupling and totally symmetric vibrational modes is chosen by comparing the strength of inter-state and intra-state coupling, respectively. This helps us to perform computationally demanding matrix diagonalization (in a time-independent framework) calculations within our computational limit. The composite vibronic spectra of the
2A2–Ã2B1 coupled potential energy surfaces (PESs). Selection of totally symmetric modes is performed following the above discussions in relation with Poisson spectrum simulation, while the coupling vibrational modes are selected considering their excitation strength given in Table 6. We choose less values of HO basis for totally symmetric modes as compared to the selected HO basis for the simulation of the spectrum of panel c of Fig. 3 by re-examining the results of Fig. 4. Finally, the HO basis for the coupling and totally symmetric vibrational modes is chosen by comparing the strength of inter-state and intra-state coupling, respectively. This helps us to perform computationally demanding matrix diagonalization (in a time-independent framework) calculations within our computational limit. The composite vibronic spectra of the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2–Ã2B1 coupled states of the indenyl radical are generated considering HO functions for vibrational modes, ν1, ν3, ν6, ν10, ν11, ν16, ν17, ν19, ν20, ν24 and ν25, up to 4, 6, 4, 7, 7, 5, 6, 4, 5, 7 and 5, respectively, and employing 12
2A2–Ã2B1 coupled states of the indenyl radical are generated considering HO functions for vibrational modes, ν1, ν3, ν6, ν10, ν11, ν16, ν17, ν19, ν20, ν24 and ν25, up to 4, 6, 4, 7, 7, 5, 6, 4, 5, 7 and 5, respectively, and employing 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Lanczos iterations. The results of these calculations are shown in Fig. 6 (black spectra) and compared with the plotted digitized experimental spectra of ref. 3 (blue spectra). The vibronic energy lines obtained from
000 Lanczos iterations. The results of these calculations are shown in Fig. 6 (black spectra) and compared with the plotted digitized experimental spectra of ref. 3 (blue spectra). The vibronic energy lines obtained from ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2 and Ã2B1 states are represented by red and maroon stick lines in the same figure. The envelope of the theoretical coupled state spectra is obtained by convoluting the vibronic stick lines with a Gaussian type of function using 135 cm−1 FWHM. The maximum peak of the theoretical band of the
2A2 and Ã2B1 states are represented by red and maroon stick lines in the same figure. The envelope of the theoretical coupled state spectra is obtained by convoluting the vibronic stick lines with a Gaussian type of function using 135 cm−1 FWHM. The maximum peak of the theoretical band of the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2 state is shifted at ∼14
2A2 state is shifted at ∼14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 cm−1, while the maximum peak of the Ã2B1 state is shifted at ∼22
500 cm−1, while the maximum peak of the Ã2B1 state is shifted at ∼22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 cm−1 when comparing the theoretical results with the experimental findings of ref. 3. The quality of superposition (in relation with the spectral band shape of both states) of the theoretical and experimental spectra in Fig. 6 indicates the necessity of considering vibronic coupling between
200 cm−1 when comparing the theoretical results with the experimental findings of ref. 3. The quality of superposition (in relation with the spectral band shape of both states) of the theoretical and experimental spectra in Fig. 6 indicates the necessity of considering vibronic coupling between ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2 and Ã2B1 states in theoretical calculations. A more detailed discussion of the present fact is presented in the next paragraph.
2A2 and Ã2B1 states in theoretical calculations. A more detailed discussion of the present fact is presented in the next paragraph.
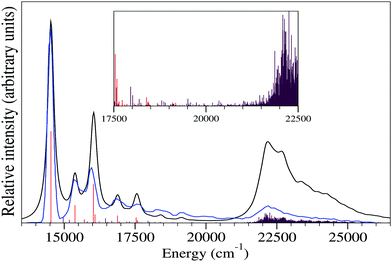 |
| | Fig. 6 The comparison between the experimental SEVI spectra3 and spectra obtained from coupled ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2–Ã2B1 state dynamics following the time-independent approach is shown in this figure. The blue envelope corresponds to experimental observations (digitized from ref. 3) and the black envelope is obtained from the present theoretical calculations. The vibronic energy lines obtained from the present time-independent calculations are indicated by red (for 2A2–Ã2B1 state dynamics following the time-independent approach is shown in this figure. The blue envelope corresponds to experimental observations (digitized from ref. 3) and the black envelope is obtained from the present theoretical calculations. The vibronic energy lines obtained from the present time-independent calculations are indicated by red (for ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2 state) and maroon (for Ã2B1 state) stick lines. The magnified view of these stick lines is presented in the inset of the figure to show the impact of non-adiabaticity between these electronic states in the energy range of ∼17 2A2 state) and maroon (for Ã2B1 state) stick lines. The magnified view of these stick lines is presented in the inset of the figure to show the impact of non-adiabaticity between these electronic states in the energy range of ∼17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 cm−1 to ∼22 500 cm−1 to ∼22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 cm−1. 500 cm−1. | |
The minimum of ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2 state is energetically well below with respect to
2A2 state is energetically well below with respect to ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2–Ã2B1 CI, while the minimum of Ã2B1 is quasi-degenerate (within ∼0.1 eV) with respect to
2A2–Ã2B1 CI, while the minimum of Ã2B1 is quasi-degenerate (within ∼0.1 eV) with respect to ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2–Ã2B1 CI. This means that the low vibrational energy levels of the
2A2–Ã2B1 CI. This means that the low vibrational energy levels of the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2 state would not be affected upon non-adiabaticity in the presence of Ã2B1 state, while the vibrational levels of Ã2B1 state would be affected and the nuclear dynamics would proceed in a non-adiabatic manner in the
2A2 state would not be affected upon non-adiabaticity in the presence of Ã2B1 state, while the vibrational levels of Ã2B1 state would be affected and the nuclear dynamics would proceed in a non-adiabatic manner in the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2–Ã2B1 coupled surfaces. This can be justified by comparing the results of the uncoupled
2A2–Ã2B1 coupled surfaces. This can be justified by comparing the results of the uncoupled ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2 state spectrum shown in panel c of Fig. 3 and the coupled
2A2 state spectrum shown in panel c of Fig. 3 and the coupled ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2 state spectrum shown in Fig. 6. The overall shape of these two figures is similar up to ∼16
2A2 state spectrum shown in Fig. 6. The overall shape of these two figures is similar up to ∼16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 250 cm−1, which is quite below with respect to
250 cm−1, which is quite below with respect to ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2–Ã2B1 CI (∼20
2A2–Ã2B1 CI (∼20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1). After that the relative intensity of the two peaks around 17
000 cm−1). After that the relative intensity of the two peaks around 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 cm−1 is increased in the case of the coupled state spectrum (cf.Fig. 6) as compared to the observed relative intensity of the same peaks in the uncoupled spectrum (cf. panel c of Fig. 3). While in the uncoupled spectrum, the relative intensity diminished around ∼18
500 cm−1 is increased in the case of the coupled state spectrum (cf.Fig. 6) as compared to the observed relative intensity of the same peaks in the uncoupled spectrum (cf. panel c of Fig. 3). While in the uncoupled spectrum, the relative intensity diminished around ∼18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 750 cm−1 (well below with respect to
750 cm−1 (well below with respect to ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2–Ã2B1 CI), the same in the coupled state spectrum shows quite reasonable relative intensity comparable with the experimental one (see black and blue lines in Fig. 6) in the energy range of ∼17
2A2–Ã2B1 CI), the same in the coupled state spectrum shows quite reasonable relative intensity comparable with the experimental one (see black and blue lines in Fig. 6) in the energy range of ∼17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 cm−1 to ∼21
500 cm−1 to ∼21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1. This indicates that the increase of relative intensity in the ∼17
000 cm−1. This indicates that the increase of relative intensity in the ∼17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 cm−1 to ∼21
500 cm−1 to ∼21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 range occurs due to the vibrational levels of Ã2B1 states, situated near to the
000 cm−1 range occurs due to the vibrational levels of Ã2B1 states, situated near to the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2–Ã2B1 CI and the nuclear dynamics proceed in this energy region in a non-adiabatic manner. We have shown an enlarged view of the stick lines obtained from
2A2–Ã2B1 CI and the nuclear dynamics proceed in this energy region in a non-adiabatic manner. We have shown an enlarged view of the stick lines obtained from ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2–Ã2B1 coupled state nuclear dynamics calculations in the inset of Fig. 6. It can be seen from this inset that additional vibrational excitations compared to the uncoupled state spectrum (cf. panel c Fig. 3) in the ∼17
2A2–Ã2B1 coupled state nuclear dynamics calculations in the inset of Fig. 6. It can be seen from this inset that additional vibrational excitations compared to the uncoupled state spectrum (cf. panel c Fig. 3) in the ∼17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 cm−1 to ∼21
500 cm−1 to ∼21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 range are observed mainly from the Ã2B1 state (maroon stick lines) and also a few lines corresponding to
000 cm−1 range are observed mainly from the Ã2B1 state (maroon stick lines) and also a few lines corresponding to ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2 state (red stick lines) are found in this energy range. Therefore, the present discussion indicates that the generation of the photo-detachment band of the indenyl anion occurs due to the vibronic interaction between
2A2 state (red stick lines) are found in this energy range. Therefore, the present discussion indicates that the generation of the photo-detachment band of the indenyl anion occurs due to the vibronic interaction between ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2 and Ã2B1 states through the involvement of totally symmetric (a1) and b2 symmetric coupling vibrational modes. Hence, both totally symmetric and b2 symmetric vibrational modes take part in the vibrational progressions of the ground state photo-detachment band of the indenyl anion, which is discussed in detail in relation with the assignment of vibrational levels in the next paragraph.
2A2 and Ã2B1 states through the involvement of totally symmetric (a1) and b2 symmetric coupling vibrational modes. Hence, both totally symmetric and b2 symmetric vibrational modes take part in the vibrational progressions of the ground state photo-detachment band of the indenyl anion, which is discussed in detail in relation with the assignment of vibrational levels in the next paragraph.
The assignment of vibronic energy levels in the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2 state is performed by analyzing the results of nuclear dynamics of the
2A2 state is performed by analyzing the results of nuclear dynamics of the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2–Ã2B1 coupled states and by examining the WP packet density plots in a similar fashion as described in the previous section. The most probable assignments of vibronic energy lines are presented in Table 9 and the WP density plots of some of these assignments are shown in Fig. 7. The comparison of data presented in Tables 8 and 9 indicates a minute change of the energetic locations of the fundamental vibrational progressions of the totally symmetric vibrational modes. For example, the fundamental vibrational progression of ν1 is found at ∼544 cm−1 (cf.Table 8) in the uncoupled spectrum, while the same is found in the coupled state spectrum at ∼543 cm−1 (cf.Table 9). The maximum energetic locational shift of the fundamental totally symmetric vibrational progression between uncoupled and coupled spectrum is ∼9 cm−1, which corresponds to the ν6 vibrational mode. As a result combination excitations between totally symmetric modes in the coupled state spectrum are also found at similar energy locations as found in the uncoupled spectrum [e.g. the energetic location of ν3 + ν1]. On the other hand, several vibrational excitations from the b2 symmetric vibrational modes are also found in the coupled state spectrum. These vibrational modes participated in the formation of combination peaks between them and also with totally symmetric modes. This means that the overall structure of the ground state photo-detachment band of the indenyl anion is constructed from the vibrational motion of the totally symmetric modes, while the bandwidth and the proper shape of the band are generated due to vibrational motion of the non-totally symmetric modes (b2) around the vibrational motion of totally symmetric modes (tuning activity). We have assigned the vibronic energy levels up to ∼1670 cm−1 (well below with respect to
2A2–Ã2B1 coupled states and by examining the WP packet density plots in a similar fashion as described in the previous section. The most probable assignments of vibronic energy lines are presented in Table 9 and the WP density plots of some of these assignments are shown in Fig. 7. The comparison of data presented in Tables 8 and 9 indicates a minute change of the energetic locations of the fundamental vibrational progressions of the totally symmetric vibrational modes. For example, the fundamental vibrational progression of ν1 is found at ∼544 cm−1 (cf.Table 8) in the uncoupled spectrum, while the same is found in the coupled state spectrum at ∼543 cm−1 (cf.Table 9). The maximum energetic locational shift of the fundamental totally symmetric vibrational progression between uncoupled and coupled spectrum is ∼9 cm−1, which corresponds to the ν6 vibrational mode. As a result combination excitations between totally symmetric modes in the coupled state spectrum are also found at similar energy locations as found in the uncoupled spectrum [e.g. the energetic location of ν3 + ν1]. On the other hand, several vibrational excitations from the b2 symmetric vibrational modes are also found in the coupled state spectrum. These vibrational modes participated in the formation of combination peaks between them and also with totally symmetric modes. This means that the overall structure of the ground state photo-detachment band of the indenyl anion is constructed from the vibrational motion of the totally symmetric modes, while the bandwidth and the proper shape of the band are generated due to vibrational motion of the non-totally symmetric modes (b2) around the vibrational motion of totally symmetric modes (tuning activity). We have assigned the vibronic energy levels up to ∼1670 cm−1 (well below with respect to ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2–Ã2B1 CI) from the onset of the
2A2–Ã2B1 CI) from the onset of the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2 state spectrum and possible assignments are compared with the experimental SEVI peak positions3 of indenyl anion (within 20 cm−1 of the experimental peaks) in Table 9. Our theoretical data indicate that vibrational transitions up to ∼850 cm−1 are mainly dominated by fundamental vibrational progressions (i.e. Δν = 1), which is in good agreement with the experimental findings.3 Our findings are also in agreement with the experimental observation3 of fundamental vibrational progressions of non-totally symmetric modes in the considered energy range. We also confirm that these non-totally symmetric modes (b2) would be combined with themselves and also with totally symmetric modes. Additional assignments of the experimental peaks3 as compared to the data given in Table 8 (peaks D, J, Q and X of Table I in ref. 3) are performed in Table 9. The peaks E, M, P, U and W of the experimental SEVI spectrum3 are assigned to the fundamentals of ν17 (549 cm−1), combination of ν17 and ν16 (930 cm−1), combination of ν17 and ν1 (1093 cm−1), combination of ν3 and ν1 (1392 cm−1) and combination of ν16 and 2ν1 (1474 cm−1), respectively.
2A2 state spectrum and possible assignments are compared with the experimental SEVI peak positions3 of indenyl anion (within 20 cm−1 of the experimental peaks) in Table 9. Our theoretical data indicate that vibrational transitions up to ∼850 cm−1 are mainly dominated by fundamental vibrational progressions (i.e. Δν = 1), which is in good agreement with the experimental findings.3 Our findings are also in agreement with the experimental observation3 of fundamental vibrational progressions of non-totally symmetric modes in the considered energy range. We also confirm that these non-totally symmetric modes (b2) would be combined with themselves and also with totally symmetric modes. Additional assignments of the experimental peaks3 as compared to the data given in Table 8 (peaks D, J, Q and X of Table I in ref. 3) are performed in Table 9. The peaks E, M, P, U and W of the experimental SEVI spectrum3 are assigned to the fundamentals of ν17 (549 cm−1), combination of ν17 and ν16 (930 cm−1), combination of ν17 and ν1 (1093 cm−1), combination of ν3 and ν1 (1392 cm−1) and combination of ν16 and 2ν1 (1474 cm−1), respectively.
Table 9 The vibronic energy levels (in cm−1) of ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2 state obtained from
2A2 state obtained from ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2–Ã2B1 coupled state calculations. The vibronic energy levels are assigned and compared with the experimental findings of ref. 3. The indication of experimental peaks and the corresponding energetic locations of the experimental peaks from the origins of the experimental spectrum are also given in the table
2A2–Ã2B1 coupled state calculations. The vibronic energy levels are assigned and compared with the experimental findings of ref. 3. The indication of experimental peaks and the corresponding energetic locations of the experimental peaks from the origins of the experimental spectrum are also given in the table
| No. |
Vibronic energy level |
Assignment |
Kim et al.3 |
| 1 |
0.0 |
0 |
0.0 |
| 2 |
381 |
ν
16
|
|
| 3 |
543 |
ν
1
|
545 (D) |
| 4 |
549 |
ν
17
|
567 (E) |
| 5 |
849 |
ν
3
|
848 (J) |
| 6 |
924 |
ν
16 + ν1 |
|
| 7 |
930 |
ν
17 + ν16 |
929 (M) |
| 8 |
1093 |
ν
17 + ν1 |
1073 (P) |
| 9 |
1099 |
2ν17 |
|
| 10 |
1119 |
ν
20
|
|
| 11 |
1188 |
ν
6
|
1186 (Q) |
| 12 |
1230 |
ν
16 + ν3 |
|
| 13 |
1392 |
ν
3 + ν1 |
1379 (U) |
| 14 |
1399 |
ν
17 + ν3 |
|
| 15 |
1474 |
ν
16 + 2ν1 |
1461 (W) |
| 16 |
1478 |
2ν17 + ν16 |
|
| 17 |
1500 |
ν
11
|
|
| 18 |
1552 |
ν
10
|
1554 (X) |
| 19 |
1569 |
ν
16 + ν6 |
|
| 20 |
1663 |
ν
20 + ν1 |
|
 |
| | Fig. 7 The wave packet density plots of the vibronic energy levels in the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2 state of the indenyl radical. The results are obtained from the 2A2 state of the indenyl radical. The results are obtained from the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2–Ã2B1 coupled state dynamics. The fundamental vibrational progression along ν16, ν17, ν3, ν20, ν11 and ν10 vibrational modes is shown in panels a, b, c, e, h and i, respectively, observing one nodal plane along the respective vibrational mode. The combination vibrational progression along (ν17, ν16), (ν16, ν3) and (ν17, ν3) vibrational modes is shown in panels d, f and g, respectively, observing one nodal plane along each vibrational mode of the combination pairs. 2A2–Ã2B1 coupled state dynamics. The fundamental vibrational progression along ν16, ν17, ν3, ν20, ν11 and ν10 vibrational modes is shown in panels a, b, c, e, h and i, respectively, observing one nodal plane along the respective vibrational mode. The combination vibrational progression along (ν17, ν16), (ν16, ν3) and (ν17, ν3) vibrational modes is shown in panels d, f and g, respectively, observing one nodal plane along each vibrational mode of the combination pairs. | |
It can be seen from previous discussions that the stick line density is increased upon introduction of inter-state coupling between ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2 and Ã2B1 states of the indenyl radical. As a result spectral broadening is observed for both the photo-detachment bands of the indenyl anion. It is also well established that the vibrational energy levels of Ã2B1 state near
2A2 and Ã2B1 states of the indenyl radical. As a result spectral broadening is observed for both the photo-detachment bands of the indenyl anion. It is also well established that the vibrational energy levels of Ã2B1 state near ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2–Ã2B1 CI should be perturbed. Thus it is expected that a very fast non-radiative decay of electronic population of Ã2B1 state would be observed, which would increase the line-broadening of the photo-detachment spectra of the indenyl anion, like photoelectron spectra of naphthalene and anthracene.8 Hence, following the demand of the present circumstances, we also performed time-dependent WP propagation calculations on the
2A2–Ã2B1 CI should be perturbed. Thus it is expected that a very fast non-radiative decay of electronic population of Ã2B1 state would be observed, which would increase the line-broadening of the photo-detachment spectra of the indenyl anion, like photoelectron spectra of naphthalene and anthracene.8 Hence, following the demand of the present circumstances, we also performed time-dependent WP propagation calculations on the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2–Ã2B1 coupled PESs to rationalize the experimental speculation3 about the lifetime of the first excited state. The WP propagation in the
2A2–Ã2B1 coupled PESs to rationalize the experimental speculation3 about the lifetime of the first excited state. The WP propagation in the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2–Ã2B1 coupled state formalism is performed with fourteen vibrational modes including seven (ν1, ν3, ν5, ν6, ν7, ν10 and ν11) totally symmetric modes and seven coupling (ν16, ν17, ν19, ν20, ν24, ν25 and ν26) modes by employing the MCTDH82 program module. The numerical details of the present calculations are given in Table S3 in the ESI.† The spectra obtained from these calculations are shown in panel a of Fig. 8 and also compared with the experimental recording3 in the same panel. The time-autocorrelation function recorded during WP propagation is damped with an exponential function,
2A2–Ã2B1 coupled state formalism is performed with fourteen vibrational modes including seven (ν1, ν3, ν5, ν6, ν7, ν10 and ν11) totally symmetric modes and seven coupling (ν16, ν17, ν19, ν20, ν24, ν25 and ν26) modes by employing the MCTDH82 program module. The numerical details of the present calculations are given in Table S3 in the ESI.† The spectra obtained from these calculations are shown in panel a of Fig. 8 and also compared with the experimental recording3 in the same panel. The time-autocorrelation function recorded during WP propagation is damped with an exponential function, 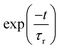 [where τr = 40 fs for
[where τr = 40 fs for ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2 state and τr = 20 fs for Ã2B1 state], and later we performed Fourier transformation of the autocorrelation function to generate the spectral envelope with a shift of the 0–0 line about ∼0.69 eV for
2A2 state and τr = 20 fs for Ã2B1 state], and later we performed Fourier transformation of the autocorrelation function to generate the spectral envelope with a shift of the 0–0 line about ∼0.69 eV for ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2 state and about ∼0.73 eV for Ã2B1 state. The overall band shape of the theoretical spectra obtained from these calculations (see panel a of Fig. 8) is well in accordance with the experimental spectra.3 The diabatic electronic population transfer between the
2A2 state and about ∼0.73 eV for Ã2B1 state. The overall band shape of the theoretical spectra obtained from these calculations (see panel a of Fig. 8) is well in accordance with the experimental spectra.3 The diabatic electronic population transfer between the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2 and Ã2B1 states during the WP propagation (up to 200 fs), while the initial WP is prepared in Ã2B1 state, is shown in panel b of Fig. 8. It can be seen from panel b of Fig. 8 that 50% of Ã2B1 state population transfers to the
2A2 and Ã2B1 states during the WP propagation (up to 200 fs), while the initial WP is prepared in Ã2B1 state, is shown in panel b of Fig. 8. It can be seen from panel b of Fig. 8 that 50% of Ã2B1 state population transfers to the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2 state within ∼40 fs and later a gradual growth of electronic population of
2A2 state within ∼40 fs and later a gradual growth of electronic population of ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2 state and a gradual decay of electronic population of Ã2B1 state is observed. The fit with a monoexponential function of the decay curve of the Ã2B1 state indicates the lifetime of Ã2B1 state to be about ∼87 fs. Hence, it can be attributed that the large spectral broadening of the photo-detachment band of Ã2B1 state compared to that of
2A2 state and a gradual decay of electronic population of Ã2B1 state is observed. The fit with a monoexponential function of the decay curve of the Ã2B1 state indicates the lifetime of Ã2B1 state to be about ∼87 fs. Hence, it can be attributed that the large spectral broadening of the photo-detachment band of Ã2B1 state compared to that of ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2 state occurs due to the immediate (within 40 fs) transfer of electronic population from Ã2B1 to
2A2 state occurs due to the immediate (within 40 fs) transfer of electronic population from Ã2B1 to ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2 state. The present theoretical results within the
2A2 state. The present theoretical results within the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2–Ã2B1 coupled state formalism agree with the experimental3 attribution of very fast non-radiative decay to the
2A2–Ã2B1 coupled state formalism agree with the experimental3 attribution of very fast non-radiative decay to the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2 state of the indenyl radical in the presence of low-lying
2A2 state of the indenyl radical in the presence of low-lying ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2–Ã2B1 CI, but they cannot circumvent the experimental prediction of the lifetime of Ã2B1 state of 7 fs estimated from the peak width. Therefore it would be worthwhile to check the electronic non-adiabatic effects of the other two relatively close lying excited states (
2A2–Ã2B1 CI, but they cannot circumvent the experimental prediction of the lifetime of Ã2B1 state of 7 fs estimated from the peak width. Therefore it would be worthwhile to check the electronic non-adiabatic effects of the other two relatively close lying excited states (![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 2A2 and
2A2 and ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) 2B1) of the indenyl radical on the nuclear dynamics of the Ã2B1 state in the
2B1) of the indenyl radical on the nuclear dynamics of the Ã2B1 state in the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2–Ã2B1–
2A2–Ã2B1–![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 2A2–
2A2–![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) 2B1 coupled state formalism. The results of these four coupled state calculations are discussed in the next section.
2B1 coupled state formalism. The results of these four coupled state calculations are discussed in the next section.
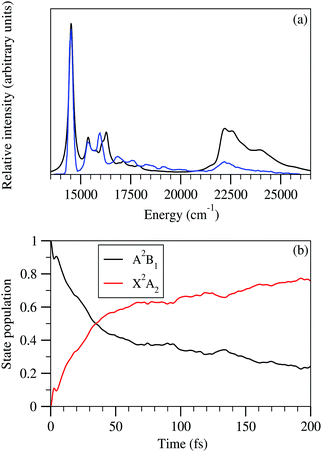 |
| | Fig. 8 The comparison between the experimental SEVI spectra3 and spectra obtained from coupled ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2–Ã2B1 state dynamics following the time-dependent approach is shown in panel (a). The blue envelope corresponds to experimental observations (digitized from ref. 3) and the black envelope is obtained from the present theoretical calculations. The electronic population transfer from Ã2B1 state to 2A2–Ã2B1 state dynamics following the time-dependent approach is shown in panel (a). The blue envelope corresponds to experimental observations (digitized from ref. 3) and the black envelope is obtained from the present theoretical calculations. The electronic population transfer from Ã2B1 state to ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2 state of the indenyl radical is shown in panel (b), when the initial WP is prepared in Ã2B1 state. 2A2 state of the indenyl radical is shown in panel (b), when the initial WP is prepared in Ã2B1 state. | |
3. Influence of ![[B with combining tilde]](https://www.rsc.org/images/entities/b_char_0042_0303.gif) 2A2 and
2A2 and ![[C with combining tilde]](https://www.rsc.org/images/entities/b_char_0043_0303.gif) 2B1 states on the internal conversion of Ã2B1 state.
In order to perform the
2B1 states on the internal conversion of Ã2B1 state.
In order to perform the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2–Ã2B1–
2A2–Ã2B1–![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 2A2–
2A2–![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) 2B1 coupled state nuclear dynamics, we have included the contribution of four extra vibrational modes (three totally symmetric modes, ν4, ν8 and ν9, and one coupling mode, ν21) as compared to our previous WP propagation in the
2B1 coupled state nuclear dynamics, we have included the contribution of four extra vibrational modes (three totally symmetric modes, ν4, ν8 and ν9, and one coupling mode, ν21) as compared to our previous WP propagation in the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2–Ã2B1 coupled PESs following their excitation strength in
2A2–Ã2B1 coupled PESs following their excitation strength in ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 2A2 and
2A2 and ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) 2B1 state (cf.Tables 4–6). The results of the present calculations are shown in Fig. 9. The envelope of the spectra obtained from these calculations is shown in panel a, and the transfer of diabatic electronic population between these states while the initial WP is prepared in the Ã2B1 state is shown in panel b of Fig. 9. The numerical details of the present calculations are given in Table S3 in the ESI.† Following the consistency of the previous two coupled state calculations, the time-autocorrelation function recorded during WP propagation is damped with an exponential function,
2B1 state (cf.Tables 4–6). The results of the present calculations are shown in Fig. 9. The envelope of the spectra obtained from these calculations is shown in panel a, and the transfer of diabatic electronic population between these states while the initial WP is prepared in the Ã2B1 state is shown in panel b of Fig. 9. The numerical details of the present calculations are given in Table S3 in the ESI.† Following the consistency of the previous two coupled state calculations, the time-autocorrelation function recorded during WP propagation is damped with an exponential function, 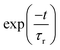 [where τr = 40 fs for
[where τr = 40 fs for ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2 state and τr = 20 fs for Ã2B1,
2A2 state and τr = 20 fs for Ã2B1, ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 2A2 and
2A2 and ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) 2B1 states], and later we performed Fourier transformation of the autocorrelation function to generate the spectral envelope. The electronic population analysis of panel b of Fig. 9 indicates a relatively quick decay of electronic population of Ã2B1 state to the
2B1 states], and later we performed Fourier transformation of the autocorrelation function to generate the spectral envelope. The electronic population analysis of panel b of Fig. 9 indicates a relatively quick decay of electronic population of Ã2B1 state to the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2 state as compared to the same presented in panel b of Fig. 8. It can be seen from this figure that more than 50% of electronic population of Ã2B1 state transfers to
2A2 state as compared to the same presented in panel b of Fig. 8. It can be seen from this figure that more than 50% of electronic population of Ã2B1 state transfers to ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2 state within ∼18 fs (40 fs in the
2A2 state within ∼18 fs (40 fs in the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2–Ã2B1 coupled state formalism), while the fit with a monoexponential function of the decay curve of the Ã2B1 state indicates the lifetime of Ã2B1 state to be about ∼39 fs. This fact can be attributed to the involvement of more electronic states and vibrational modes in the dynamics, where the increment of totally symmetric vibrational modes is involved in the fine-tuning of PESs and, as a consequence, the modulation of non-adiabatic coupling through b2 symmetric vibrational modes becomes more prominent. It can be seen from Table 3 that the Ã2B1 state is vertically ∼1.91 and ∼3.16 eV separated from the
2A2–Ã2B1 coupled state formalism), while the fit with a monoexponential function of the decay curve of the Ã2B1 state indicates the lifetime of Ã2B1 state to be about ∼39 fs. This fact can be attributed to the involvement of more electronic states and vibrational modes in the dynamics, where the increment of totally symmetric vibrational modes is involved in the fine-tuning of PESs and, as a consequence, the modulation of non-adiabatic coupling through b2 symmetric vibrational modes becomes more prominent. It can be seen from Table 3 that the Ã2B1 state is vertically ∼1.91 and ∼3.16 eV separated from the ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 2A2 and
2A2 and ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) 2B1 states, respectively. This energy gap between Ã2B1 and
2B1 states, respectively. This energy gap between Ã2B1 and ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 2A2 states is diminished slowly towards the negative values of ν1, ν3, ν5, ν8, ν9 and ν11 normal coordinates, respectively, while the same is observed towards positive values of ν6 and ν10 normal coordinates (cf. panels a, c, e, h, i, k, f, and j, respectively, in Fig. 2). This cumulative tuning through the above mentioned totally symmetric vibrational modes causes the observed non-adibaticity between the Ã2B1 and
2A2 states is diminished slowly towards the negative values of ν1, ν3, ν5, ν8, ν9 and ν11 normal coordinates, respectively, while the same is observed towards positive values of ν6 and ν10 normal coordinates (cf. panels a, c, e, h, i, k, f, and j, respectively, in Fig. 2). This cumulative tuning through the above mentioned totally symmetric vibrational modes causes the observed non-adibaticity between the Ã2B1 and ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 2A2 states (cf.Table 6). On the other hand, the PECs presented in the different panels of Fig. 2 indicate well energy separation between
2A2 states (cf.Table 6). On the other hand, the PECs presented in the different panels of Fig. 2 indicate well energy separation between ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2 and
2A2 and ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) 2B1 states both vertically and along the normal coordinates. Hence, the non-adiabaticity between these states through inter-state coupling is less effective as these couplings are determined from less sensitive repulsive PECs.60 In the present coupled state calculations, the contribution from
2B1 states both vertically and along the normal coordinates. Hence, the non-adiabaticity between these states through inter-state coupling is less effective as these couplings are determined from less sensitive repulsive PECs.60 In the present coupled state calculations, the contribution from ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2–
2A2–![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 2A2 and Ã2B1–
2A2 and Ã2B1–![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) 2B1 inter-state couplings (out of scope due to the adopted electronic structure methods in the present study) and some important coupling modes like, ν22, ν23, etc. is missing. Hence, it is expected that the consideration of the above mentioned points might rectify the present calculations and can provide better agreement with experiment.3
2B1 inter-state couplings (out of scope due to the adopted electronic structure methods in the present study) and some important coupling modes like, ν22, ν23, etc. is missing. Hence, it is expected that the consideration of the above mentioned points might rectify the present calculations and can provide better agreement with experiment.3
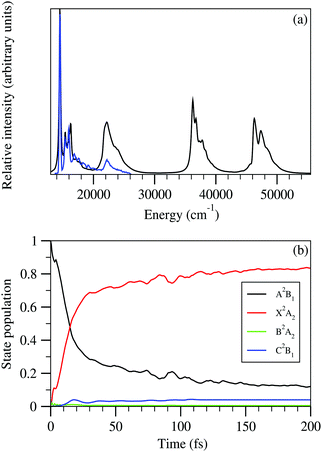 |
| | Fig. 9 The comparison between the experimental SEVI spectra3 and spectra obtained from coupled ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2–Ã2B1– 2A2–Ã2B1–![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 2A2– 2A2–![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) 2B1 state dynamics following the time-dependent approach is shown in panel (a). The blue envelope corresponds to experimental observations (digitized from ref. 3) and the black envelope is obtained from the present theoretical calculations. The electronic population transfer from Ã2B1 state to 2B1 state dynamics following the time-dependent approach is shown in panel (a). The blue envelope corresponds to experimental observations (digitized from ref. 3) and the black envelope is obtained from the present theoretical calculations. The electronic population transfer from Ã2B1 state to ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2, 2A2, ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 2A2 and 2A2 and ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) 2B1 states of the indenyl radical is shown in panel (b), when the initial WP is prepared in Ã2B1 state. 2B1 states of the indenyl radical is shown in panel (b), when the initial WP is prepared in Ã2B1 state. | |
IV. Summary
The present theoretical study is undertaken to understand and rationalize the formation of the photo-detachment band of the indenyl anion. For this purpose several molecular Hamiltonians are constructed in terms of number of vibrational modes and electronic states in a diabatic electronic basis following standard vibronic coupling theory. Later, based on these vibronic Hamiltonians several nuclear dynamics studies are performed following time-independent and time-dependent quantum chemistry approaches. The results of these calculations are then compared with the available experimental findings. The present study is performed in a systematic manner to find detailed physics behind the formation of the photo-detachment band of the indenyl anion employing both adiabatic (FC simulation and Poisson spectrum simulation) and non-adiabatic (coupled state dynamics) nuclear dynamics. The results of FC simulation and Poisson spectrum of ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2 state of the indenyl radical provide reasonably good comparison with the experimentally observed first photo-detachment band of the indenyl anion up to ∼17
2A2 state of the indenyl radical provide reasonably good comparison with the experimentally observed first photo-detachment band of the indenyl anion up to ∼17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 cm−1 from the onset of the first experimental band (well below with respect to
500 cm−1 from the onset of the first experimental band (well below with respect to ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2–Ã2B1 CI). The D, J, Q and X peaks of the experimental SEVI spectrum are nicely assigned in this energy range based on the WP density plots of the vibrational energy levels of the composite Poisson spectrum. While the intensity of the Poisson spectrum is diminished around ∼18
2A2–Ã2B1 CI). The D, J, Q and X peaks of the experimental SEVI spectrum are nicely assigned in this energy range based on the WP density plots of the vibrational energy levels of the composite Poisson spectrum. While the intensity of the Poisson spectrum is diminished around ∼18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 750 cm−1, the same reappeared in the nuclear dynamics of the
750 cm−1, the same reappeared in the nuclear dynamics of the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2–Ã2B1 coupled PESs. The appearance of a comparable intensity with the experimental spectrum employing
2A2–Ã2B1 coupled PESs. The appearance of a comparable intensity with the experimental spectrum employing ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2–Ã2B1 coupled state dynamics in the energy range of ∼17
2A2–Ã2B1 coupled state dynamics in the energy range of ∼17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 cm−1 to ∼21
500 cm−1 to ∼21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 is attributed to vibrational motions of the Ã2B1 state near the
000 cm−1 is attributed to vibrational motions of the Ã2B1 state near the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2–Ã2B1 CI. This indicates the importance of electronic non-adiabatic effects between the
2A2–Ã2B1 CI. This indicates the importance of electronic non-adiabatic effects between the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2 and the Ã2B1 states of the indenyl radical in the ground state photo-detachment band of the indenyl anion. We have also assigned five experimental peaks, E, M, P, U and W, in addition to the previous four peaks comparing the results of
2A2 and the Ã2B1 states of the indenyl radical in the ground state photo-detachment band of the indenyl anion. We have also assigned five experimental peaks, E, M, P, U and W, in addition to the previous four peaks comparing the results of ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2–Ã2B1 coupled state dynamics with available SEVI recording. We also performed the time-dependent nuclear dynamics study in the
2A2–Ã2B1 coupled state dynamics with available SEVI recording. We also performed the time-dependent nuclear dynamics study in the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2–Ã2B1 coupled state formalism in the quest of obtaining excited state lifetime as well as the population flow between electronic states of indenyl radical. The results of these calculations indicate that ∼50% of electronic population of Ã2B1 state transfers to
2A2–Ã2B1 coupled state formalism in the quest of obtaining excited state lifetime as well as the population flow between electronic states of indenyl radical. The results of these calculations indicate that ∼50% of electronic population of Ã2B1 state transfers to ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2 state within ∼40 fs and the lifetime of Ã2B1 state is ∼87 fs, which is quite high compared to the experimentally estimated lifetime of Ã2B1 state. In order to rationalize the present fact we also performed the time-dependent nuclear dynamics study in the
2A2 state within ∼40 fs and the lifetime of Ã2B1 state is ∼87 fs, which is quite high compared to the experimentally estimated lifetime of Ã2B1 state. In order to rationalize the present fact we also performed the time-dependent nuclear dynamics study in the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2–Ã2B1–
2A2–Ã2B1–![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 2A2–
2A2–![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) 2B1 coupled state formalism. The results of these studies indicate that more than 50% of electronic population of the Ã2B1 state transfers to the
2B1 coupled state formalism. The results of these studies indicate that more than 50% of electronic population of the Ã2B1 state transfers to the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2 state within ∼18 fs and the lifetime of Ã2B1 state is ∼39 fs. The improvement of the lifetime of the Ã2B1 state in comparison with the experiment in the four coupled state formalism indicates that the involvement of more vibrational modes (which is out of scope for the present calculation) might rectify the present calculations and can provide better agreement with experiment.
2A2 state within ∼18 fs and the lifetime of Ã2B1 state is ∼39 fs. The improvement of the lifetime of the Ã2B1 state in comparison with the experiment in the four coupled state formalism indicates that the involvement of more vibrational modes (which is out of scope for the present calculation) might rectify the present calculations and can provide better agreement with experiment.
Conflicts of interest
The authors declare no conflict of interest.
Acknowledgements
We thank the Department of Science and Technology, New Delhi, for the financial support (through grant no. DST/INSPIRE/04/2015/000094). We also thank Miss. Daradi Baishya, School of Chemistry, University of Hyderabad, India, for fruitful discussions in many occasions.
References
- U.S. EPA (Environmental Protection Agency). Provisional Guidance for Quantitative Risk Assessment of Polycyclic Aromatic Hydrocarbons; Environmental Criteria and Assessment Office, Office of Health and Environmental Assessment: Cincinnati, OH, 1993.
- A. M. Mebel, A. Landera and R. I. Kaiser, J. Phys. Chem. A, 2017, 121, 901–926 CrossRef CAS PubMed.
- J. B. Kim, M. L. Weichman, T. I. Yacovitch, C. Shih and D. M. Neumark, J. Chem. Phys., 2013, 139, 104301 CrossRef PubMed.
- E. Dwek, R. Arendt, D. Fixsen, T. Sodroski, N. Odegard, J. Weiland, W. Reach, M. Hauser, T. Kelsall and S. Moseley, Astrophys. J., 1997, 475, 565–579 CrossRef CAS.
- P. Ehrenfreund and S. B. Charnley, Annu. Rev. Astron. Astrophys., 2000, 38, 427–483 CrossRef CAS.
- P. Ehrenfreund and M. A. Sephton, Faraday Discuss., 2006, 133, 277–288 RSC.
- F. Salama,
et al.
, Astrophys. J., 1999, 526, 265–273 CrossRef CAS.
- S. Ghanta, V. S. Reddy and S. Mahapatra, Phys. Chem. Chem. Phys., 2011, 13, 14531–14541 RSC.
- A. G. G. M. Tielens, Rev. Mod. Phys., 2013, 85, 1021–1081 CrossRef CAS.
- F. E. Salama, E. L. O. Bakes, L. J. Allamandola and A. G. G. M. Tielens, Astrophys. J., 1996, 458, 621–636 CrossRef CAS.
- T. P. Snow, Spectrochim. Acta, Part A, 2001, 57, 615–626 CrossRef CAS.
-
B. T. Draine, Interstellar Dust Grains, 2003, arXiv preprint astro-ph/0304489.
-
A. G. Tielens, The Physics and Chemistry of the Interstellar Medium, Cambridge University Press, Cambridge, UK, 2005 Search PubMed.
- T. P. Snow and B. J. McCall, Annu. Rev. Astron. Astrophys., 2006, 44, 367 CrossRef CAS.
- W. Duley, Faraday Discuss., 2006, 133, 415–425 RSC.
- A. G. G. M. Tielens, Annu. Rev. Astron. Astrophys., 2008, 46, 289–337 CrossRef CAS.
- A. M. Ricks, G. E. Douberly and M. A. Duncan, Astrophys. J., 2009, 702, 301–306 CrossRef CAS.
- R. Boschi, E. Clar and W. Schmidt, J. Chem. Phys., 1974, 60, 4406–4418 CrossRef CAS.
- W. Schmidt, J. Chem. Phys., 1977, 66, 828–845 CrossRef CAS.
- O. Parisel, G. Berthier and Y. Ellinger, Astron. Astrophys., 1992, 266, L1–L4 CAS.
- F. Salama, Origins Life Evol. Biospheres, 1998, 28, 349–364 CrossRef CAS.
- M. S. Deleuze, A. B. Trofimov and L. S. Cederbaum, J. Chem. Phys., 2001, 115, 5859–5882 CrossRef CAS.
- M. S. Deleuze, J. Chem. Phys., 2002, 116, 7012–7026 CrossRef CAS.
- E. S. Kadantsev, M. J. Stott and A. Rubio, J. Chem. Phys., 2006, 124, 134901 CrossRef PubMed.
- G. Malloci, G. Mulas and C. Joblin, Astron. Astrophys., 2004, 426, 105–117 CrossRef CAS.
- R. Mondal, C. Tönshoff, D. Khon, D. C. Neckers and H. F. Bettinger, J. Am. Chem. Soc., 2009, 131, 14281–14289 CrossRef CAS PubMed.
- S. N. Reddy and S. Mahapatra, J. Phys. Chem. A, 2013, 117, 8737–8749 CrossRef CAS PubMed.
- F. Salama and L. J. Allamandola, Nature, 1992, 358, 42–43 CrossRef CAS PubMed.
- P. Bréchignac and T. Pino, Astron. Astrophys., 1999, 343, L49–L52 Search PubMed.
- P. Bréchignac, T. Pino and N. Boudin, Spectrochim. Acta, Part A, 2001, 57, 745–756 CrossRef.
- L. Biennier, F. Salama, L. J. Allamandola and J. J. Scherer, J. Chem. Phys., 2003, 118, 7863–7872 CrossRef CAS.
- L. Biennier, F. Salama, M. Gupta and A. O'Keefe, Chem. Phys. Lett., 2004, 387, 287–294 CrossRef CAS.
- X. Tan and F. Salama, Chem. Phys. Lett., 2006, 422, 518–521 CrossRef CAS.
- S. N. Reddy and S. Mahapatra, J. Phys. Chem. B, 2015, 119, 11391–11402 CrossRef CAS PubMed.
- B. H. Foing and P. Ehrenfreund, Nature, 1994, 369, 296–298 CrossRef CAS.
- T. P. Snow and B. J. McCall, Annu. Rev. Astron. Astrophys., 2006, 44, 367 CrossRef CAS.
- E. K. Campbell, M. Holz, D. Gerlich and J. P. Maier, Nature, 2015, 523, 322–323 CrossRef CAS PubMed.
- G. A. H. Walker, D. Bohlender, J. P. Maier and E. K. Campbell, Astrophys. J., Lett., 2015, 812, L8 CrossRef.
- E. K. Campbell, M. Holz, J. P. Maier, D. Gerlich, G. A. H. Walker and D. Bohlender, Astrophys. J., 2016, 822, 17 CrossRef.
- J. Soler, R. Sarkar and M. Boggio-Pasqua, J. Phys. Chem. A, 2019, 123, 1824–1829 CrossRef CAS PubMed.
- M. Frenlach and L. B. Ebert, J. Phys. Chem., 1988, 92, 561 CrossRef.
- L. Remusat, S. Derenne, F. Robert and H. Knicker, Geochim. Cosmochim. Acta, 2005, 69, 3919 CrossRef CAS.
- N. Chalyavi, V. Dryza, J. A. Sanelli and E. J. Bieske, J. Chem. Phys., 2013, 138, 224307 CrossRef PubMed.
- G. D. Silva and J. W. Bozzelli, J. Phys. Chem. A, 2009, 113, 8971–8978 CrossRef PubMed.
- S. Fascella, C. Cavallotti, R. Rota and S. Carrá, J. Phys. Chem. A, 2005, 109, 7546–7557 CrossRef CAS PubMed.
- S. Granata, T. Faravelli, E. Ranzi, N. Olten and S. Senkan, Combust. Flame, 2002, 131, 273–284 CrossRef CAS.
- L. Vereecken and J. Peeters, Phys. Chem. Chem. Phys., 2003, 5, 2807–2817 RSC.
- A. Matsugi and A. Miyoshi, Phys. Chem. Chem. Phys., 2012, 14, 9722–9728 RSC.
- N. M. Marinov, M. J. Castaldi, C. F. Melius and W. Tsang, Combust. Sci. Technol., 1997, 128, 295 CrossRef CAS.
- C.-W. Zhou, V. V. Kislov and A. M. Mebel, J. Phys. Chem. A, 2012, 116, 1571–1585 CrossRef CAS PubMed.
- M. Tian, B. S. Liu, M. Hammonds, N. Wang, P. J. Sarre and A. S. C. Cheung, Phys. Chem. Chem. Phys., 2012, 14, 6603–6610 RSC.
- A. Atto, A. Hudson, R. A. Jackson and N. P. C. Simmons, Chem. Phys. Lett., 1975, 33, 477–478 CrossRef CAS.
- P. Hemberger, M. Steinbauer, M. Schneider, I. Fischer, M. Johnson, A. Bodi and T. Gerber, J. Phys. Chem. A, 2010, 114, 4698–4703 CrossRef CAS.
- T. Izumida, K. Inoue, S. Noda and H. Yoshida, Bull. Chem. Soc. Jpn., 1981, 54, 2517–2518 CrossRef CAS.
- B. Römer, G. A. Janaway and J. I. Brauman, J. Am. Chem. Soc., 1997, 119, 2249 CrossRef.
-
V. A. Mozhayskiy and A. I. Krylov, Computer program ezSpectrum, see http://iopenshell.usc.edu/downloads.
- S. Ghanta, V. S. Reddy and S. Mahapatra, Phys. Chem. Chem. Phys., 2011, 13, 14523–14530 RSC.
- A. J. Gianola, T. Ichino, R. L. Hoenigman, S. Kato, V. M. Bierbaum and W. C. Lineberger, J. Phys. Chem. A, 2004, 108, 10326 CrossRef CAS.
- X. L. Zhu and D. R. Yarkony, J. Phys. Chem. C, 2010, 114, 5312 CrossRef CAS.
-
H. Köppel, W. Domcke and L. S. Cederbaum, in Advances in Chemical Physics, ed. I. Prigogine and S. A. Rice, John Wiley and Sons, Inc., Hoboken, NJ, 2007, vol. 57 Search PubMed.
- H. Köppel, L. S. Cederbaum and W. Domcke, Chem. Phys., 1982, 69, 175 CrossRef.
- L. S. Cederbaum, W. Domcke and H. Köppel, Chem. Phys. Lett., 1978, 33, 319 CAS.
- C. Lanczos, J. Res. Natl. Bur. Stand., 1950, 45, 255–282 CrossRef.
-
J. Cullum and R. Willoughby, Lanczos Algorithms for Large Symmetric Eigenvalue Problems, Birkhäuser, Boston, 1985, vol. I and II Search PubMed.
-
W. Domcke and H. Köppel, Encyclopedia of Computational Chemistry, ed. P. v. R. Schleyer, Wiley, New York, 1998, p. 3166 Search PubMed.
-
Conical Intersections: Electronic Structure, Dynamics and Spectroscopy, ed. W. Domcke, D. R. Yarkony and H. Köppel, World Scientific, Singapore, 2004 Search PubMed.
- S. Mahapatra, Int. Rev. Phys. Chem., 2004, 23, 483–512 Search PubMed.
-
M. Baer, Beyond Born-Oppenheimer: Electronic Non-adiabatic coupling Terms and Conical Intersections, Wiley, New York, 2006 Search PubMed.
- S. Mahapatra, Acc. Chem. Res., 2009, 42, 1004–1015 CrossRef CAS PubMed.
- T. H. Dunning, Jr, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef.
-
M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision B.01, Gaussian, Inc., Wallingford, CT, 2010 Search PubMed.
-
H.-J. Werner, P. J. Knowles, G. Knizia and F. R. Manby, et al., Molpro, version 2012.1, a package of ab initio programs, 2012, see http://www.molpro.net.
- V. S. Reddy, S. Ghanta and S. Mahapatra, Phys. Rev. Lett., 2010, 104, 111102 CrossRef.
-
E. B. Wilson, Jr, J. C. Decius and P. C. Cross, Molecular Vibrations, McGraw-Hill, New York, 1995 Search PubMed.
- W. Domcke, H. Köppel and L. S. Cederbaum, Mol. Phys., 1981, 43, 851 CrossRef CAS.
- H. Köppel, L. S. Cederbaum and W. Domcke, Chem. Phys., 1982, 69, 175 CrossRef.
- H.-D. Meyer, U. Manthe and L. S. Cederbaum, Chem. Phys. Lett., 1990, 165, 73 CrossRef CAS.
- U. Manthe, H.-D. Meyer and L. S. Cederbaum, J. Chem. Phys., 1992, 97, 3199 CrossRef CAS.
- M. H. Beck and H.-D. Meyer, J. Phys. D: At., Mol. Cluster, 1997, 42, 113 CAS.
- M. H. Beck, A. Jäckle, G. A. Worth and H.-D. Meyer, Phys. Rep., 2000, 324, 1 CrossRef CAS.
- H.-D. Meyer and G. A. Worth, Theor. Chem. Acc., 2003, 109, 251 Search PubMed.
-
G. A. Worth, M. H. Beck, A. Jäckle and H.-D. Meyer, The mctdh package, Version 8.4, 2007, University of Heidelberg, Heidelberg, Germany. See: http://mctdh.uni-hd.de.
- H.-D. Meyer and J. Phys, Conf. Ser., 2005, 4, 66 Search PubMed.
- L. J. Doriol, F. Gatti, C. Lung and H.-D. Meyer, J. Chem. Phys., 2008, 129, 224109 CrossRef PubMed.
- P. A. M. Dirac, Proc. Cambridge Philos. Soc., 1930, 26, 376 CrossRef CAS.
-
J. Frenkel, Wave Mechanics, Clarendon, Oxford, 1934 Search PubMed.
- R. Kosloff and H. Tai-Ezer, Chem. Phys. Lett., 1986, 127, 223 CrossRef CAS.
- H.-D. Meyer, F. Le Quéré, C. Léonard and F. Gatti, Chem. Phys., 2006, 329, 179 CrossRef CAS.
- L. J. Doriol, F. Gatti, C. Iung and H.-D. Meyer, J. Chem. Phys., 2008, 129, 224109 CrossRef PubMed.
- Mathematica 8.0; Wolfram Research Inc, System Modeler, Version 3.0, Champaign, IL, 2012.
- F. Santoro, R. Improta, A. Lami, J. Blonio and V. Barone, J. Chem. Phys., 2007, 126, 084509 CrossRef PubMed.
- F. Santoro, A. Lami, R. Improta, J. Blonio and V. Barone, J. Chem. Phys., 2008, 128, 224311 CrossRef PubMed.
- L. S. Cederbaum and W. Domcke, Chem. Phys., 1977, 36, 205 CAS.
- L. S. Cederbaum, W. Domcke and H. Köppel, Chem. Phys. Lett., 1978, 33, 319 CAS.
- R. Kosloff and H. Tai-Ezer, Chem. Phys. Lett., 1986, 127, 223 CrossRef CAS.
- H.-D. Meyer, F. Le Quéré, C. Léonard and F. Gatti, Chem. Phys., 2006, 329, 179–192 CrossRef CAS.
- L. J. Doriol, F. Gatti, C. Iung and H.-D. Meyer, J. Chem. Phys., 2008, 129, 224109 CrossRef PubMed.
- R. Sarkar and S. Mahapatra, J. Phys. Chem. A, 2016, 120, 3504–3517 CrossRef CAS PubMed.
- R. Sarkar and S. Mahapatra, J. Chem. Phys., 2017, 147, 194305 CrossRef PubMed.
- R. Sarkar, S. R. Reddy, S. Mahapatra and H. Köppel, Chem. Phys., 2017, 482, 39–51 CrossRef CAS.
- R. Sarkar, D. Baishya and S. Mahapatra, Chem. Phys., 2018, 515, 679–691 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9cp04594e |
| ‡ Present address: Department of Physics and Astronomy, University College London, London, WC1E 6BT, UK. |
|
| This journal is © the Owner Societies 2019 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *b
*b
![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) and Ã) the naphthalene cation, anthracene cation and pyrrolyl. The observation of the first two cations was nicely explained by Mahapatra and co-workers8,57 by implementing multi-mode-vibronic-coupling (MMVC) theory on those cations and it was established that the spectroscopy of those cations is highly influenced by the ultrafast non-adiabatic electronic population transfer between à and
and Ã) the naphthalene cation, anthracene cation and pyrrolyl. The observation of the first two cations was nicely explained by Mahapatra and co-workers8,57 by implementing multi-mode-vibronic-coupling (MMVC) theory on those cations and it was established that the spectroscopy of those cations is highly influenced by the ultrafast non-adiabatic electronic population transfer between à and ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) states in the presence of low-lying CIs between them. Similarly the featureless broad excited state of the photo-detachment band of the pyrrolide anion58 was theoretically attributed to the presence of quasi-degeneracy between the excited state (2B1) saddle point and the CIs between the excited and ground (2A2) states59 of pyrrolyl. It was shown by Yarkony and Zhu59 that the inclusion of non-adiabatic coupling into the spectrum simulation significantly improved the comparison between the simulated and experimental58 photo-detachment spectrum of the pyrrolide anion than the comparison of the experimental spectrum with the theoretical spectrum obtained from adiabatic simulation.
states in the presence of low-lying CIs between them. Similarly the featureless broad excited state of the photo-detachment band of the pyrrolide anion58 was theoretically attributed to the presence of quasi-degeneracy between the excited state (2B1) saddle point and the CIs between the excited and ground (2A2) states59 of pyrrolyl. It was shown by Yarkony and Zhu59 that the inclusion of non-adiabatic coupling into the spectrum simulation significantly improved the comparison between the simulated and experimental58 photo-detachment spectrum of the pyrrolide anion than the comparison of the experimental spectrum with the theoretical spectrum obtained from adiabatic simulation.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3
3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3
3
![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2
2A2![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 2A2
2A2![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) 2B1
2B1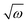 (in a.u.). The VDEs of the first four highest occupied MOs [HOMOs] were calculated at the distorted geometry of Qi (i = 1–29) = ±0.10, ±0.25, ±0.50, ±0.75, ±1.00, ±1.50,…,±5.00, along each normal coordinate. The ab initio adiabatic VDEs obtained from these calculations were then fit with the adiabatic form of the diabatic Hamiltonian of eqn (4) to estimate the Hamiltonian parameters. The linear intra-state (κ) and inter-state (λ) Hamiltonian parameters were also calculated numerically following the first-order differential equation of κ or λ = (dV/dQ)Q=0, where V is the adiabatic electronic potential or the difference of adiabatic electronic potentials of two electronic states, and the results are compared with the above analytical values of the same. The results of the analytic fits and the corresponding numerical values are given in Tables 4–6.
(in a.u.). The VDEs of the first four highest occupied MOs [HOMOs] were calculated at the distorted geometry of Qi (i = 1–29) = ±0.10, ±0.25, ±0.50, ±0.75, ±1.00, ±1.50,…,±5.00, along each normal coordinate. The ab initio adiabatic VDEs obtained from these calculations were then fit with the adiabatic form of the diabatic Hamiltonian of eqn (4) to estimate the Hamiltonian parameters. The linear intra-state (κ) and inter-state (λ) Hamiltonian parameters were also calculated numerically following the first-order differential equation of κ or λ = (dV/dQ)Q=0, where V is the adiabatic electronic potential or the difference of adiabatic electronic potentials of two electronic states, and the results are compared with the above analytical values of the same. The results of the analytic fits and the corresponding numerical values are given in Tables 4–6.![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2, Ã2B1,
2A2, Ã2B1, ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 2A2 and
2A2 and ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) 2B1 electronic states of the indenyl radical. The excitation strength of these couplings is given in parentheses. The higher-order coupling parameters of the same are given in Table S2 in the ESI
2B1 electronic states of the indenyl radical. The excitation strength of these couplings is given in parentheses. The higher-order coupling parameters of the same are given in Table S2 in the ESI
![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2
2A2![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 2A2
2A2![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) 2B1
2B1![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2, Ã2B1,
2A2, Ã2B1, ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 2A2 and
2A2 and ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) 2B1 electronic states of the indenyl radical
2B1 electronic states of the indenyl radical
![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2
2A2![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 2A2
2A2![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) 2B1
2B1![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) –Ã
–Ã![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) –
–![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif)
![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif)
![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) –
–![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif)
![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2, Ã2B1,
2A2, Ã2B1, ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 2A2 and
2A2 and ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) 2B1, respectively. The energy order of these states was determined from the increasing vertical detachment energy (VDE) from the ground state minimum of the indenyl anion. The forty-two normal vibrational modes of the indenyl anion were decomposed in the following irreducible representation:
2B1, respectively. The energy order of these states was determined from the increasing vertical detachment energy (VDE) from the ground state minimum of the indenyl anion. The forty-two normal vibrational modes of the indenyl anion were decomposed in the following irreducible representation: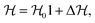
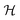 ,
, 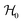 and
and 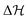 represent the overall molecular Hamiltonian, the Hamiltonian of the reference configuration (unperturbed) and the Hamiltonian corresponding to electron detachment, respectively. 1 stands for a unit matrix, whose dimension is dependent upon the number of considered electronic states. Thus it is a 4 × 4 unit matrix in the present study. Within the harmonic approximation the unperturbed Hamiltonian can be written as
represent the overall molecular Hamiltonian, the Hamiltonian of the reference configuration (unperturbed) and the Hamiltonian corresponding to electron detachment, respectively. 1 stands for a unit matrix, whose dimension is dependent upon the number of considered electronic states. Thus it is a 4 × 4 unit matrix in the present study. Within the harmonic approximation the unperturbed Hamiltonian can be written as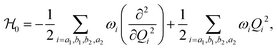
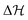 ) of eqn (2) were determined using standard vibronic selection rules as described in ref. 60, 62, 66, 69, 75, 76 and these can be written as
) of eqn (2) were determined using standard vibronic selection rules as described in ref. 60, 62, 66, 69, 75, 76 and these can be written as
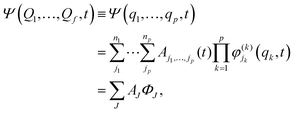
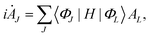
![[small phi (variant), Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a4.gif) (k) = (1 − P(k))−1(ρ(k))−1〈H〉(k)φ(k),
(k) = (1 − P(k))−1(ρ(k))−1〈H〉(k)φ(k),![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2–Ã2B1–
2A2–Ã2B1–![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 2A2–
2A2–![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) 2B1 electronic states of the indenyl radical. The autocorrelation functions [C(t) = 〈Ψ(0)|Ψ(t)〉] of the WP were recorded in time during the propagation. Later, the autocorrelation functions obtained from individual calculations were combined with equal weighted. The obtained autocorrelation function was damped with an exponential function
2B1 electronic states of the indenyl radical. The autocorrelation functions [C(t) = 〈Ψ(0)|Ψ(t)〉] of the WP were recorded in time during the propagation. Later, the autocorrelation functions obtained from individual calculations were combined with equal weighted. The obtained autocorrelation function was damped with an exponential function 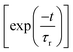 and Fourier transformed to get an energy value spectrum.
and Fourier transformed to get an energy value spectrum.
![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2, Ã2B1,
2A2, Ã2B1, ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 2A2 and
2A2 and ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) 2B1) of the indenyl radical are shown in Fig. 2. In this figure, the points represent the energy obtained from the ab initio quantum chemistry method and the solid lines represent the potential obtained from the constructed model vibronic Hamiltonian. The superposition of the ab initio energy points and solid lines indicates the quality of the fits performed in the present study. The fittings of the ab initio energy points indicate that a higher-order expansion of the Taylor's series is needed for a few vibrational modes (cf. Table S2 in the ESI†). Overall, the PECs of Fig. 2 indicate that
2B1) of the indenyl radical are shown in Fig. 2. In this figure, the points represent the energy obtained from the ab initio quantum chemistry method and the solid lines represent the potential obtained from the constructed model vibronic Hamiltonian. The superposition of the ab initio energy points and solid lines indicates the quality of the fits performed in the present study. The fittings of the ab initio energy points indicate that a higher-order expansion of the Taylor's series is needed for a few vibrational modes (cf. Table S2 in the ESI†). Overall, the PECs of Fig. 2 indicate that ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 2A2 and
2A2 and ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) 2B1 states are well separated from each other as well as from the first two electronic states (
2B1 states are well separated from each other as well as from the first two electronic states (![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2 and Ã2B1) of the indenyl radical in the Franck–Condon region, while the energy difference between the former two states and the Ã2B1 state is reduced towards positive or negative values along some normal coordinates. On the other hand, several intersections and energy proximities are found between
2A2 and Ã2B1) of the indenyl radical in the Franck–Condon region, while the energy difference between the former two states and the Ã2B1 state is reduced towards positive or negative values along some normal coordinates. On the other hand, several intersections and energy proximities are found between ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2 and Ã2B1 states (cf.Fig. 2).
2A2 and Ã2B1 states (cf.Fig. 2).
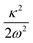 . The positional and directional shift of the energy minimum of an electronic state with respect to its reference electronic configuration can be measured from this parameter. The amount of shift of the minimum of an electronic state increases with the increment of the value of this parameter in an opposite direction of the sign of κ. For example, ν11 possesses the strongest Condon activity in
. The positional and directional shift of the energy minimum of an electronic state with respect to its reference electronic configuration can be measured from this parameter. The amount of shift of the minimum of an electronic state increases with the increment of the value of this parameter in an opposite direction of the sign of κ. For example, ν11 possesses the strongest Condon activity in ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2 state; as a result, the largest shift of the energy minimum of the ground state of the indenyl radical is found along this normal mode in the negative direction (cf. panel k of Fig. 2). Similarly, the largest shift of the energy minima of Ã2B1,
2A2 state; as a result, the largest shift of the energy minimum of the ground state of the indenyl radical is found along this normal mode in the negative direction (cf. panel k of Fig. 2). Similarly, the largest shift of the energy minima of Ã2B1, ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 2A2 and
2A2 and ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) 2B1 states can be found along ν1 (cf. panel a of Fig. 2), ν1 (cf. panel a of Fig. 2) and ν4 (cf. panel d of Fig. 2), respectively. A similar analysis indicates that a considerable shift of energy minima of
2B1 states can be found along ν1 (cf. panel a of Fig. 2), ν1 (cf. panel a of Fig. 2) and ν4 (cf. panel d of Fig. 2), respectively. A similar analysis indicates that a considerable shift of energy minima of ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2 and Ã2B1 states is observed along ν10 and ν11 vibrational modes and later these states also intersect (cf. panels j and k of Fig. 2) along these normal coordinates. On the other hand, PECs along the other vibrational modes indicate energetic proximity between these states.
2A2 and Ã2B1 states is observed along ν10 and ν11 vibrational modes and later these states also intersect (cf. panels j and k of Fig. 2) along these normal coordinates. On the other hand, PECs along the other vibrational modes indicate energetic proximity between these states.![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2 and Ã2B1 states in panels a, c, d, e, f, g, h, i, j and k of Fig. 2, we also calculated the energetic locations of different conical intersections (CIs) in the multi-dimensional space within the quadratic vibronic coupling model and employing the Lagrange constrained minimization scheme as implemented in the Mathematica programs module.90 The energetic locations of the state's minima and CIs between the states are presented in the diagonal and off-diagonal entries of Table 7, respectively. It can be seen from this table that the minimum of Ã2B1 state is just ∼0.087 eV below with respect to
2A2 and Ã2B1 states in panels a, c, d, e, f, g, h, i, j and k of Fig. 2, we also calculated the energetic locations of different conical intersections (CIs) in the multi-dimensional space within the quadratic vibronic coupling model and employing the Lagrange constrained minimization scheme as implemented in the Mathematica programs module.90 The energetic locations of the state's minima and CIs between the states are presented in the diagonal and off-diagonal entries of Table 7, respectively. It can be seen from this table that the minimum of Ã2B1 state is just ∼0.087 eV below with respect to ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2–Ã2B1 CI. This value is quite consistent with the value (0.056 eV) obtained from ab initio state-average CAS(9,9)SCF with 6-31+G* basis set calculation of ref. 3. On the other hand, the minimum of
2A2–Ã2B1 CI. This value is quite consistent with the value (0.056 eV) obtained from ab initio state-average CAS(9,9)SCF with 6-31+G* basis set calculation of ref. 3. On the other hand, the minimum of ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2 state is energetically quite low (∼0.97 eV) from the
2A2 state is energetically quite low (∼0.97 eV) from the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2–Ã2B1 CI. Therefore, it can be speculated that low vibronic levels of
2A2–Ã2B1 CI. Therefore, it can be speculated that low vibronic levels of ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2 state cannot be perturbed in the presence of
2A2 state cannot be perturbed in the presence of ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2–Ã2B1 CI, while the same for Ã2B1 are very likely to be perturbed in the presence of
2A2–Ã2B1 CI, while the same for Ã2B1 are very likely to be perturbed in the presence of ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2–Ã2B1 CI. The present topic would be discussed later in detail in relation with the Poisson spectrum and coupled state nuclear dynamics.
2A2–Ã2B1 CI. The present topic would be discussed later in detail in relation with the Poisson spectrum and coupled state nuclear dynamics.![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2
2A2![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 2A2
2A2![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) 2B1
2B1![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2
2A2![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 2A2
2A2![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) 2B1
2B1![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2–Ã2B1 CI with respect to the minimum of
2A2–Ã2B1 CI with respect to the minimum of ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2 state indicates that the lower vibronic levels of the
2A2 state indicates that the lower vibronic levels of the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2 state of the indenyl radical cannot be perturbed in the presence of
2A2 state of the indenyl radical cannot be perturbed in the presence of ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2–Ã2B1 CI. Therefore, it would be worthwhile to examine the nature of the vibronic energy levels of the ground electronic state of the indenyl radical by studying the nuclear dynamics in uncoupled state formalism first and later examining the impact of electronic non-adiabatic effects in conjunction with CIs following coupled state formalism.
2A2–Ã2B1 CI. Therefore, it would be worthwhile to examine the nature of the vibronic energy levels of the ground electronic state of the indenyl radical by studying the nuclear dynamics in uncoupled state formalism first and later examining the impact of electronic non-adiabatic effects in conjunction with CIs following coupled state formalism.
![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2) of the indenyl radical following the pre-screening scheme91,92 of the FC simulation as implemented in the Gaussian 09 program module.71 In the second approach we have used the formalism of the Poisson distribution spectrum in the uncoupled potential energy surface (λ = 0) as defined in ref. 93 and 94. We performed the optimization of the ground state energy minima geometries and the corresponding normal mode analysis of the initial (anionic indenyl) and final (indenyl radical) states following the requirement of necessary inputs for FC spectrum simulations.91,92 These calculations were performed employing both MP2 and DFT (B3LYP) level of theories using the cc-pVTZ and 6-311+G* basis set, respectively, and geometry parameters of the energy minima of both indenyl anion and indenyl radical are given in Table 1, while the corresponding frequencies of a1 and b2 symmetric vibrational modes calculated from the MP2 level of theory are given in Table 2. It is found from these calculations that both ground states of the anion and indenyl radical belong to C2v point group symmetry. The result obtained from FC simulations using anion and radical geometries of the MP2 level of theory is presented in panel b of Fig. 3, while the same using the DFT level of theory is presented in panel b of Fig. S1 in the ESI.† Both results obtained from FC simulations are then compared with the available overview SEVI spectra of the indenyl anion digitized from ref. 3 and given in panel a of Fig. 3 and panel a of Fig. S1 in the ESI.† We also simulated the FC spectrum of the first excited state (Ã2B1) of indenyl using the time-dependent version of DFT and shown in panel b of Fig. S1 in the ESI.† Both the simulated FC spectra are shifted to the experimental onset (∼14
2A2) of the indenyl radical following the pre-screening scheme91,92 of the FC simulation as implemented in the Gaussian 09 program module.71 In the second approach we have used the formalism of the Poisson distribution spectrum in the uncoupled potential energy surface (λ = 0) as defined in ref. 93 and 94. We performed the optimization of the ground state energy minima geometries and the corresponding normal mode analysis of the initial (anionic indenyl) and final (indenyl radical) states following the requirement of necessary inputs for FC spectrum simulations.91,92 These calculations were performed employing both MP2 and DFT (B3LYP) level of theories using the cc-pVTZ and 6-311+G* basis set, respectively, and geometry parameters of the energy minima of both indenyl anion and indenyl radical are given in Table 1, while the corresponding frequencies of a1 and b2 symmetric vibrational modes calculated from the MP2 level of theory are given in Table 2. It is found from these calculations that both ground states of the anion and indenyl radical belong to C2v point group symmetry. The result obtained from FC simulations using anion and radical geometries of the MP2 level of theory is presented in panel b of Fig. 3, while the same using the DFT level of theory is presented in panel b of Fig. S1 in the ESI.† Both results obtained from FC simulations are then compared with the available overview SEVI spectra of the indenyl anion digitized from ref. 3 and given in panel a of Fig. 3 and panel a of Fig. S1 in the ESI.† We also simulated the FC spectrum of the first excited state (Ã2B1) of indenyl using the time-dependent version of DFT and shown in panel b of Fig. S1 in the ESI.† Both the simulated FC spectra are shifted to the experimental onset (∼14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 cm−1) in order to compare with the experimental findings3 and it can be seen from panel b of Fig. 3 and panel b of Fig. S1 in the ESI† that both FC simulations nicely reproduce the experimental overview SEVI scan of the ground state of the indenyl anion. This comparison indicates that a minute change in the geometry occurs in the neutral ground state of indenyl radical upon photo-detachment from ground state anionic indenyl. This fact is also well supported from the geometry parameters of these states given in Table 1. The largest change of the C–C bond is ∼0.04 Å, C–H bond is ∼0.01 Å, C–C–C angle is ∼2 degree and C–C–H angle is ∼1 degree upon photo-detachment of anionic indenyl (data are presented following MP2 calculations). Therefore it is found that the FC spectrum of the indenyl radical is dominated by a single peak at 0–0 transition contributed from the excitation of fundamental vibrational levels, where the FC integral possesses the highest value [as indicated by the square of the transition dipole moment integral (TDMI), the value is ∼0.4]. The overall contribution from the fundamental vibrational progressions in the FC spectrum is found to be ∼40%, while the vibrational progressions of the first overtones of the ν2–ν10 (excluding ν4) vibrational modes and combination excitations between ν3, ν5 and ν8 vibrational modes contribute ∼40% and ∼16%, respectively, in the overall ground state FC spectrum of the indenyl radical.
500 cm−1) in order to compare with the experimental findings3 and it can be seen from panel b of Fig. 3 and panel b of Fig. S1 in the ESI† that both FC simulations nicely reproduce the experimental overview SEVI scan of the ground state of the indenyl anion. This comparison indicates that a minute change in the geometry occurs in the neutral ground state of indenyl radical upon photo-detachment from ground state anionic indenyl. This fact is also well supported from the geometry parameters of these states given in Table 1. The largest change of the C–C bond is ∼0.04 Å, C–H bond is ∼0.01 Å, C–C–C angle is ∼2 degree and C–C–H angle is ∼1 degree upon photo-detachment of anionic indenyl (data are presented following MP2 calculations). Therefore it is found that the FC spectrum of the indenyl radical is dominated by a single peak at 0–0 transition contributed from the excitation of fundamental vibrational levels, where the FC integral possesses the highest value [as indicated by the square of the transition dipole moment integral (TDMI), the value is ∼0.4]. The overall contribution from the fundamental vibrational progressions in the FC spectrum is found to be ∼40%, while the vibrational progressions of the first overtones of the ν2–ν10 (excluding ν4) vibrational modes and combination excitations between ν3, ν5 and ν8 vibrational modes contribute ∼40% and ∼16%, respectively, in the overall ground state FC spectrum of the indenyl radical.

![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2 state of the indenyl radical (digitized from ref. 3 and shown in panel a) is shown in this figure.
2A2 state of the indenyl radical (digitized from ref. 3 and shown in panel a) is shown in this figure.![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2 state of the indenyl radical (cf.Table 4) in panels a, b and c of Fig. 4, while the same with the lowest excitation strength (last three in increasing order) is shown in panels d, e and f in the same figure. It is seen from these figures that the maximum intensity is concentrated in the vibrational quantum level 0 for all considered vibrational modes, which is consistent with the estimated low excitation strength of these vibrational modes (cf.Table 4). As a result we find the highest intensity in the 0–0 peak of the ground state photo-detachment band of the indenyl anion (see panel c in Fig. 3) due to the cumulative contribution of all totally symmetric vibrational modes excited at the vibronic quantum level 0. In contrast to the above a very little contribution from the first overtones of the relatively strong (in terms of excitation strength) vibrational modes, ν11 and ν3, is found (cf. panels a and b in Fig. 4). Therefore, the intensity of the overall uncoupled ground state spectrum of the indenyl radical (cf. panel c in Fig. 3) is drastically reduced after excitation at the 0–0 level. The same characteristic of the recorded SEVI ground state spectrum of the indenyl anion was found in ref. 3 and it was attributed to the p-wave photo-detachment phenomena of dramatically diminished intensity after the intense 0–0 band.
2A2 state of the indenyl radical (cf.Table 4) in panels a, b and c of Fig. 4, while the same with the lowest excitation strength (last three in increasing order) is shown in panels d, e and f in the same figure. It is seen from these figures that the maximum intensity is concentrated in the vibrational quantum level 0 for all considered vibrational modes, which is consistent with the estimated low excitation strength of these vibrational modes (cf.Table 4). As a result we find the highest intensity in the 0–0 peak of the ground state photo-detachment band of the indenyl anion (see panel c in Fig. 3) due to the cumulative contribution of all totally symmetric vibrational modes excited at the vibronic quantum level 0. In contrast to the above a very little contribution from the first overtones of the relatively strong (in terms of excitation strength) vibrational modes, ν11 and ν3, is found (cf. panels a and b in Fig. 4). Therefore, the intensity of the overall uncoupled ground state spectrum of the indenyl radical (cf. panel c in Fig. 3) is drastically reduced after excitation at the 0–0 level. The same characteristic of the recorded SEVI ground state spectrum of the indenyl anion was found in ref. 3 and it was attributed to the p-wave photo-detachment phenomena of dramatically diminished intensity after the intense 0–0 band.
![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2 state is shown in this figure. The intensity distribution of vibrational modes which possess the highest values (first three in decreasing order) of excitation strength is presented in panels a–c and the same with low excitation strength (last three in increasing order) is presented in panels d–f. The excitation strength of the vibrational modes indicated in each panel can be found in Table 4.
2A2 state is shown in this figure. The intensity distribution of vibrational modes which possess the highest values (first three in decreasing order) of excitation strength is presented in panels a–c and the same with low excitation strength (last three in increasing order) is presented in panels d–f. The excitation strength of the vibrational modes indicated in each panel can be found in Table 4.![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2 state of the indenyl radical are presented in Fig. 5. The assignments of the vibronic energy levels are mainly performed by identifying the fundamental vibrational progressions first. Later, based on the fundamental progressions, vibrational progressions of overtones and combination peaks are assigned. For example, the WP density plot of panel a in Fig. 5 shows a nodal plane along the Q1 normal coordinate at ∼544 cm−1 from the onset of the spectrum. This means that the energy line corresponds to the excitation of the first overtone of vibrational mode ν1 and the energy gap of the vibronic line from the 0–0 line is 544 cm−1 which matches with the fundamental frequency of the vibrational mode ν1. Therefore, the present vibronic line is assigned for fundamental vibrational progression of ν1. Similarly, the vibronic lines at ∼850 cm−1, ∼1179 cm−1, ∼1277 cm−1 and ∼1545 cm−1 are assigned for the fundamentals of ν3, ν6, ν7 and ν10, respectively, and their corresponding WP density plots are shown in panels b, c, d and e, respectively, in Fig. 5. Assignments of the first overtone of ν3 and combination peaks between (ν6 and ν1), (ν6 and ν3) and (ν10 and ν3), at ∼1699 cm−1, 1722 cm−1, 2028 cm−1 and 2395 cm−1, respectively, are performed following two nodal planes along Q3 and a simultaneous nodal plane along two normal coordinates. The WP density plots of the above mentioned vibronic energy lines are shown in panels f, g, h and i, respectively in Fig. 5. In an identical manner, we also perform the possible assignments of other vibrational energy levels in the uncoupled
2A2 state of the indenyl radical are presented in Fig. 5. The assignments of the vibronic energy levels are mainly performed by identifying the fundamental vibrational progressions first. Later, based on the fundamental progressions, vibrational progressions of overtones and combination peaks are assigned. For example, the WP density plot of panel a in Fig. 5 shows a nodal plane along the Q1 normal coordinate at ∼544 cm−1 from the onset of the spectrum. This means that the energy line corresponds to the excitation of the first overtone of vibrational mode ν1 and the energy gap of the vibronic line from the 0–0 line is 544 cm−1 which matches with the fundamental frequency of the vibrational mode ν1. Therefore, the present vibronic line is assigned for fundamental vibrational progression of ν1. Similarly, the vibronic lines at ∼850 cm−1, ∼1179 cm−1, ∼1277 cm−1 and ∼1545 cm−1 are assigned for the fundamentals of ν3, ν6, ν7 and ν10, respectively, and their corresponding WP density plots are shown in panels b, c, d and e, respectively, in Fig. 5. Assignments of the first overtone of ν3 and combination peaks between (ν6 and ν1), (ν6 and ν3) and (ν10 and ν3), at ∼1699 cm−1, 1722 cm−1, 2028 cm−1 and 2395 cm−1, respectively, are performed following two nodal planes along Q3 and a simultaneous nodal plane along two normal coordinates. The WP density plots of the above mentioned vibronic energy lines are shown in panels f, g, h and i, respectively in Fig. 5. In an identical manner, we also perform the possible assignments of other vibrational energy levels in the uncoupled ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2 state of the indenyl radical and the results are tabulated in Table 8. Analysing the data given in Table 8, we also assign four experimental3 peak positions (peaks D, J, Q and X, see Table I in ref. 3). The peaks D, J, Q and X of the experimental SEVI spectrum of the ground state of the indenyl anion3 are assigned to the fundamentals of ν1 (544 cm−1), ν3 (850 cm−1), ν6 (1179 cm−1) and ν10 (1545 cm−1), respectively. The maximum deviation of these peaks from the experimental one is ∼9 cm−1, corresponding to ν10. Although the present composite Poisson spectrum (cf. panel c of Fig. 3) nicely reproduces the overall structure of the ground state SEVI spectrum of indenyl,3 the experimental peak positions are not properly located by the present calculations and the intensity of the Poisson spectrum of the
2A2 state of the indenyl radical and the results are tabulated in Table 8. Analysing the data given in Table 8, we also assign four experimental3 peak positions (peaks D, J, Q and X, see Table I in ref. 3). The peaks D, J, Q and X of the experimental SEVI spectrum of the ground state of the indenyl anion3 are assigned to the fundamentals of ν1 (544 cm−1), ν3 (850 cm−1), ν6 (1179 cm−1) and ν10 (1545 cm−1), respectively. The maximum deviation of these peaks from the experimental one is ∼9 cm−1, corresponding to ν10. Although the present composite Poisson spectrum (cf. panel c of Fig. 3) nicely reproduces the overall structure of the ground state SEVI spectrum of indenyl,3 the experimental peak positions are not properly located by the present calculations and the intensity of the Poisson spectrum of the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2 state is diminished at ∼18
2A2 state is diminished at ∼18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 750 cm−1, which is in contrast to the experimental observations.3 This indicates an indirect agreement with the experimental speculation of excitations of non-totally symmetric vibrational modes and the influence of electronic non-adiabatic effects from the excited states on the ground state SEVI spectrum of the indenyl anion.3 Therefore it would be worthwhile now to examine the role of non-totally symmetric vibrational modes in the coupled state dynamics in relation with electronic non-adiabatic effects in addition to the totally symmetric vibrational modes, which are involved in the energetic modulation between the coupled states. The next section is mainly devoted to this endeavour to understand the experimental speculation more rigorously by performing nuclear dynamics of the coupled
750 cm−1, which is in contrast to the experimental observations.3 This indicates an indirect agreement with the experimental speculation of excitations of non-totally symmetric vibrational modes and the influence of electronic non-adiabatic effects from the excited states on the ground state SEVI spectrum of the indenyl anion.3 Therefore it would be worthwhile now to examine the role of non-totally symmetric vibrational modes in the coupled state dynamics in relation with electronic non-adiabatic effects in addition to the totally symmetric vibrational modes, which are involved in the energetic modulation between the coupled states. The next section is mainly devoted to this endeavour to understand the experimental speculation more rigorously by performing nuclear dynamics of the coupled ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2–Ã2B1 states.
2A2–Ã2B1 states.![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2 electronic state of the indenyl radical. The results are obtained from uncoupled vibronic dynamics of the
2A2 electronic state of the indenyl radical. The results are obtained from uncoupled vibronic dynamics of the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2 state
2A2 state
![[X with combining tilde]](https://www.rsc.org/images/entities/b_char_0058_0303.gif) 2A2–Ã2B1 coupled potential energy surfaces.
The existence of less than an eV vertical energy gap between Ã2B1 and
2A2–Ã2B1 coupled potential energy surfaces.
The existence of less than an eV vertical energy gap between Ã2B1 and ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2 states (cf.Table 3) and the moderate inter-state coupling between them (cf.Table 6) encouraged us to examine the plausible vibronic coupling between these states in the coupled-state framework. In this study we include five totally symmetric vibrational modes (ν1, ν3, ν6, ν10 and ν11) and six coupling vibrational modes (ν16, ν17, ν19, ν20, ν24 and ν25) of b2 symmetry (A2 ⊗ B1 ⊃ b2) to perform the nuclear dynamics of the
2A2 states (cf.Table 3) and the moderate inter-state coupling between them (cf.Table 6) encouraged us to examine the plausible vibronic coupling between these states in the coupled-state framework. In this study we include five totally symmetric vibrational modes (ν1, ν3, ν6, ν10 and ν11) and six coupling vibrational modes (ν16, ν17, ν19, ν20, ν24 and ν25) of b2 symmetry (A2 ⊗ B1 ⊃ b2) to perform the nuclear dynamics of the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2–Ã2B1 coupled potential energy surfaces (PESs). Selection of totally symmetric modes is performed following the above discussions in relation with Poisson spectrum simulation, while the coupling vibrational modes are selected considering their excitation strength given in Table 6. We choose less values of HO basis for totally symmetric modes as compared to the selected HO basis for the simulation of the spectrum of panel c of Fig. 3 by re-examining the results of Fig. 4. Finally, the HO basis for the coupling and totally symmetric vibrational modes is chosen by comparing the strength of inter-state and intra-state coupling, respectively. This helps us to perform computationally demanding matrix diagonalization (in a time-independent framework) calculations within our computational limit. The composite vibronic spectra of the
2A2–Ã2B1 coupled potential energy surfaces (PESs). Selection of totally symmetric modes is performed following the above discussions in relation with Poisson spectrum simulation, while the coupling vibrational modes are selected considering their excitation strength given in Table 6. We choose less values of HO basis for totally symmetric modes as compared to the selected HO basis for the simulation of the spectrum of panel c of Fig. 3 by re-examining the results of Fig. 4. Finally, the HO basis for the coupling and totally symmetric vibrational modes is chosen by comparing the strength of inter-state and intra-state coupling, respectively. This helps us to perform computationally demanding matrix diagonalization (in a time-independent framework) calculations within our computational limit. The composite vibronic spectra of the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2–Ã2B1 coupled states of the indenyl radical are generated considering HO functions for vibrational modes, ν1, ν3, ν6, ν10, ν11, ν16, ν17, ν19, ν20, ν24 and ν25, up to 4, 6, 4, 7, 7, 5, 6, 4, 5, 7 and 5, respectively, and employing 12
2A2–Ã2B1 coupled states of the indenyl radical are generated considering HO functions for vibrational modes, ν1, ν3, ν6, ν10, ν11, ν16, ν17, ν19, ν20, ν24 and ν25, up to 4, 6, 4, 7, 7, 5, 6, 4, 5, 7 and 5, respectively, and employing 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Lanczos iterations. The results of these calculations are shown in Fig. 6 (black spectra) and compared with the plotted digitized experimental spectra of ref. 3 (blue spectra). The vibronic energy lines obtained from
000 Lanczos iterations. The results of these calculations are shown in Fig. 6 (black spectra) and compared with the plotted digitized experimental spectra of ref. 3 (blue spectra). The vibronic energy lines obtained from ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2 and Ã2B1 states are represented by red and maroon stick lines in the same figure. The envelope of the theoretical coupled state spectra is obtained by convoluting the vibronic stick lines with a Gaussian type of function using 135 cm−1 FWHM. The maximum peak of the theoretical band of the
2A2 and Ã2B1 states are represented by red and maroon stick lines in the same figure. The envelope of the theoretical coupled state spectra is obtained by convoluting the vibronic stick lines with a Gaussian type of function using 135 cm−1 FWHM. The maximum peak of the theoretical band of the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2 state is shifted at ∼14
2A2 state is shifted at ∼14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 cm−1, while the maximum peak of the Ã2B1 state is shifted at ∼22
500 cm−1, while the maximum peak of the Ã2B1 state is shifted at ∼22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 cm−1 when comparing the theoretical results with the experimental findings of ref. 3. The quality of superposition (in relation with the spectral band shape of both states) of the theoretical and experimental spectra in Fig. 6 indicates the necessity of considering vibronic coupling between
200 cm−1 when comparing the theoretical results with the experimental findings of ref. 3. The quality of superposition (in relation with the spectral band shape of both states) of the theoretical and experimental spectra in Fig. 6 indicates the necessity of considering vibronic coupling between ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2 and Ã2B1 states in theoretical calculations. A more detailed discussion of the present fact is presented in the next paragraph.
2A2 and Ã2B1 states in theoretical calculations. A more detailed discussion of the present fact is presented in the next paragraph.

![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2–Ã2B1 state dynamics following the time-independent approach is shown in this figure. The blue envelope corresponds to experimental observations (digitized from ref. 3) and the black envelope is obtained from the present theoretical calculations. The vibronic energy lines obtained from the present time-independent calculations are indicated by red (for
2A2–Ã2B1 state dynamics following the time-independent approach is shown in this figure. The blue envelope corresponds to experimental observations (digitized from ref. 3) and the black envelope is obtained from the present theoretical calculations. The vibronic energy lines obtained from the present time-independent calculations are indicated by red (for ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2 state) and maroon (for Ã2B1 state) stick lines. The magnified view of these stick lines is presented in the inset of the figure to show the impact of non-adiabaticity between these electronic states in the energy range of ∼17
2A2 state) and maroon (for Ã2B1 state) stick lines. The magnified view of these stick lines is presented in the inset of the figure to show the impact of non-adiabaticity between these electronic states in the energy range of ∼17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 cm−1 to ∼22
500 cm−1 to ∼22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 cm−1.
500 cm−1.![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2 state is energetically well below with respect to
2A2 state is energetically well below with respect to ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2–Ã2B1 CI, while the minimum of Ã2B1 is quasi-degenerate (within ∼0.1 eV) with respect to
2A2–Ã2B1 CI, while the minimum of Ã2B1 is quasi-degenerate (within ∼0.1 eV) with respect to ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2–Ã2B1 CI. This means that the low vibrational energy levels of the
2A2–Ã2B1 CI. This means that the low vibrational energy levels of the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2 state would not be affected upon non-adiabaticity in the presence of Ã2B1 state, while the vibrational levels of Ã2B1 state would be affected and the nuclear dynamics would proceed in a non-adiabatic manner in the
2A2 state would not be affected upon non-adiabaticity in the presence of Ã2B1 state, while the vibrational levels of Ã2B1 state would be affected and the nuclear dynamics would proceed in a non-adiabatic manner in the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2–Ã2B1 coupled surfaces. This can be justified by comparing the results of the uncoupled
2A2–Ã2B1 coupled surfaces. This can be justified by comparing the results of the uncoupled ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2 state spectrum shown in panel c of Fig. 3 and the coupled
2A2 state spectrum shown in panel c of Fig. 3 and the coupled ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2 state spectrum shown in Fig. 6. The overall shape of these two figures is similar up to ∼16
2A2 state spectrum shown in Fig. 6. The overall shape of these two figures is similar up to ∼16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 250 cm−1, which is quite below with respect to
250 cm−1, which is quite below with respect to ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2–Ã2B1 CI (∼20
2A2–Ã2B1 CI (∼20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1). After that the relative intensity of the two peaks around 17
000 cm−1). After that the relative intensity of the two peaks around 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 cm−1 is increased in the case of the coupled state spectrum (cf.Fig. 6) as compared to the observed relative intensity of the same peaks in the uncoupled spectrum (cf. panel c of Fig. 3). While in the uncoupled spectrum, the relative intensity diminished around ∼18
500 cm−1 is increased in the case of the coupled state spectrum (cf.Fig. 6) as compared to the observed relative intensity of the same peaks in the uncoupled spectrum (cf. panel c of Fig. 3). While in the uncoupled spectrum, the relative intensity diminished around ∼18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 750 cm−1 (well below with respect to
750 cm−1 (well below with respect to ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2–Ã2B1 CI), the same in the coupled state spectrum shows quite reasonable relative intensity comparable with the experimental one (see black and blue lines in Fig. 6) in the energy range of ∼17
2A2–Ã2B1 CI), the same in the coupled state spectrum shows quite reasonable relative intensity comparable with the experimental one (see black and blue lines in Fig. 6) in the energy range of ∼17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 cm−1 to ∼21
500 cm−1 to ∼21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1. This indicates that the increase of relative intensity in the ∼17
000 cm−1. This indicates that the increase of relative intensity in the ∼17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 cm−1 to ∼21
500 cm−1 to ∼21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 range occurs due to the vibrational levels of Ã2B1 states, situated near to the
000 cm−1 range occurs due to the vibrational levels of Ã2B1 states, situated near to the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2–Ã2B1 CI and the nuclear dynamics proceed in this energy region in a non-adiabatic manner. We have shown an enlarged view of the stick lines obtained from
2A2–Ã2B1 CI and the nuclear dynamics proceed in this energy region in a non-adiabatic manner. We have shown an enlarged view of the stick lines obtained from ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2–Ã2B1 coupled state nuclear dynamics calculations in the inset of Fig. 6. It can be seen from this inset that additional vibrational excitations compared to the uncoupled state spectrum (cf. panel c Fig. 3) in the ∼17
2A2–Ã2B1 coupled state nuclear dynamics calculations in the inset of Fig. 6. It can be seen from this inset that additional vibrational excitations compared to the uncoupled state spectrum (cf. panel c Fig. 3) in the ∼17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 cm−1 to ∼21
500 cm−1 to ∼21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 range are observed mainly from the Ã2B1 state (maroon stick lines) and also a few lines corresponding to
000 cm−1 range are observed mainly from the Ã2B1 state (maroon stick lines) and also a few lines corresponding to ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2 state (red stick lines) are found in this energy range. Therefore, the present discussion indicates that the generation of the photo-detachment band of the indenyl anion occurs due to the vibronic interaction between
2A2 state (red stick lines) are found in this energy range. Therefore, the present discussion indicates that the generation of the photo-detachment band of the indenyl anion occurs due to the vibronic interaction between ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2 and Ã2B1 states through the involvement of totally symmetric (a1) and b2 symmetric coupling vibrational modes. Hence, both totally symmetric and b2 symmetric vibrational modes take part in the vibrational progressions of the ground state photo-detachment band of the indenyl anion, which is discussed in detail in relation with the assignment of vibrational levels in the next paragraph.
2A2 and Ã2B1 states through the involvement of totally symmetric (a1) and b2 symmetric coupling vibrational modes. Hence, both totally symmetric and b2 symmetric vibrational modes take part in the vibrational progressions of the ground state photo-detachment band of the indenyl anion, which is discussed in detail in relation with the assignment of vibrational levels in the next paragraph.![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2 state is performed by analyzing the results of nuclear dynamics of the
2A2 state is performed by analyzing the results of nuclear dynamics of the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2–Ã2B1 coupled states and by examining the WP packet density plots in a similar fashion as described in the previous section. The most probable assignments of vibronic energy lines are presented in Table 9 and the WP density plots of some of these assignments are shown in Fig. 7. The comparison of data presented in Tables 8 and 9 indicates a minute change of the energetic locations of the fundamental vibrational progressions of the totally symmetric vibrational modes. For example, the fundamental vibrational progression of ν1 is found at ∼544 cm−1 (cf.Table 8) in the uncoupled spectrum, while the same is found in the coupled state spectrum at ∼543 cm−1 (cf.Table 9). The maximum energetic locational shift of the fundamental totally symmetric vibrational progression between uncoupled and coupled spectrum is ∼9 cm−1, which corresponds to the ν6 vibrational mode. As a result combination excitations between totally symmetric modes in the coupled state spectrum are also found at similar energy locations as found in the uncoupled spectrum [e.g. the energetic location of ν3 + ν1]. On the other hand, several vibrational excitations from the b2 symmetric vibrational modes are also found in the coupled state spectrum. These vibrational modes participated in the formation of combination peaks between them and also with totally symmetric modes. This means that the overall structure of the ground state photo-detachment band of the indenyl anion is constructed from the vibrational motion of the totally symmetric modes, while the bandwidth and the proper shape of the band are generated due to vibrational motion of the non-totally symmetric modes (b2) around the vibrational motion of totally symmetric modes (tuning activity). We have assigned the vibronic energy levels up to ∼1670 cm−1 (well below with respect to
2A2–Ã2B1 coupled states and by examining the WP packet density plots in a similar fashion as described in the previous section. The most probable assignments of vibronic energy lines are presented in Table 9 and the WP density plots of some of these assignments are shown in Fig. 7. The comparison of data presented in Tables 8 and 9 indicates a minute change of the energetic locations of the fundamental vibrational progressions of the totally symmetric vibrational modes. For example, the fundamental vibrational progression of ν1 is found at ∼544 cm−1 (cf.Table 8) in the uncoupled spectrum, while the same is found in the coupled state spectrum at ∼543 cm−1 (cf.Table 9). The maximum energetic locational shift of the fundamental totally symmetric vibrational progression between uncoupled and coupled spectrum is ∼9 cm−1, which corresponds to the ν6 vibrational mode. As a result combination excitations between totally symmetric modes in the coupled state spectrum are also found at similar energy locations as found in the uncoupled spectrum [e.g. the energetic location of ν3 + ν1]. On the other hand, several vibrational excitations from the b2 symmetric vibrational modes are also found in the coupled state spectrum. These vibrational modes participated in the formation of combination peaks between them and also with totally symmetric modes. This means that the overall structure of the ground state photo-detachment band of the indenyl anion is constructed from the vibrational motion of the totally symmetric modes, while the bandwidth and the proper shape of the band are generated due to vibrational motion of the non-totally symmetric modes (b2) around the vibrational motion of totally symmetric modes (tuning activity). We have assigned the vibronic energy levels up to ∼1670 cm−1 (well below with respect to ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2–Ã2B1 CI) from the onset of the
2A2–Ã2B1 CI) from the onset of the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2 state spectrum and possible assignments are compared with the experimental SEVI peak positions3 of indenyl anion (within 20 cm−1 of the experimental peaks) in Table 9. Our theoretical data indicate that vibrational transitions up to ∼850 cm−1 are mainly dominated by fundamental vibrational progressions (i.e. Δν = 1), which is in good agreement with the experimental findings.3 Our findings are also in agreement with the experimental observation3 of fundamental vibrational progressions of non-totally symmetric modes in the considered energy range. We also confirm that these non-totally symmetric modes (b2) would be combined with themselves and also with totally symmetric modes. Additional assignments of the experimental peaks3 as compared to the data given in Table 8 (peaks D, J, Q and X of Table I in ref. 3) are performed in Table 9. The peaks E, M, P, U and W of the experimental SEVI spectrum3 are assigned to the fundamentals of ν17 (549 cm−1), combination of ν17 and ν16 (930 cm−1), combination of ν17 and ν1 (1093 cm−1), combination of ν3 and ν1 (1392 cm−1) and combination of ν16 and 2ν1 (1474 cm−1), respectively.
2A2 state spectrum and possible assignments are compared with the experimental SEVI peak positions3 of indenyl anion (within 20 cm−1 of the experimental peaks) in Table 9. Our theoretical data indicate that vibrational transitions up to ∼850 cm−1 are mainly dominated by fundamental vibrational progressions (i.e. Δν = 1), which is in good agreement with the experimental findings.3 Our findings are also in agreement with the experimental observation3 of fundamental vibrational progressions of non-totally symmetric modes in the considered energy range. We also confirm that these non-totally symmetric modes (b2) would be combined with themselves and also with totally symmetric modes. Additional assignments of the experimental peaks3 as compared to the data given in Table 8 (peaks D, J, Q and X of Table I in ref. 3) are performed in Table 9. The peaks E, M, P, U and W of the experimental SEVI spectrum3 are assigned to the fundamentals of ν17 (549 cm−1), combination of ν17 and ν16 (930 cm−1), combination of ν17 and ν1 (1093 cm−1), combination of ν3 and ν1 (1392 cm−1) and combination of ν16 and 2ν1 (1474 cm−1), respectively.![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2 state obtained from
2A2 state obtained from ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2–Ã2B1 coupled state calculations. The vibronic energy levels are assigned and compared with the experimental findings of ref. 3. The indication of experimental peaks and the corresponding energetic locations of the experimental peaks from the origins of the experimental spectrum are also given in the table
2A2–Ã2B1 coupled state calculations. The vibronic energy levels are assigned and compared with the experimental findings of ref. 3. The indication of experimental peaks and the corresponding energetic locations of the experimental peaks from the origins of the experimental spectrum are also given in the table
![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2 and Ã2B1 states of the indenyl radical. As a result spectral broadening is observed for both the photo-detachment bands of the indenyl anion. It is also well established that the vibrational energy levels of Ã2B1 state near
2A2 and Ã2B1 states of the indenyl radical. As a result spectral broadening is observed for both the photo-detachment bands of the indenyl anion. It is also well established that the vibrational energy levels of Ã2B1 state near ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2–Ã2B1 CI should be perturbed. Thus it is expected that a very fast non-radiative decay of electronic population of Ã2B1 state would be observed, which would increase the line-broadening of the photo-detachment spectra of the indenyl anion, like photoelectron spectra of naphthalene and anthracene.8 Hence, following the demand of the present circumstances, we also performed time-dependent WP propagation calculations on the
2A2–Ã2B1 CI should be perturbed. Thus it is expected that a very fast non-radiative decay of electronic population of Ã2B1 state would be observed, which would increase the line-broadening of the photo-detachment spectra of the indenyl anion, like photoelectron spectra of naphthalene and anthracene.8 Hence, following the demand of the present circumstances, we also performed time-dependent WP propagation calculations on the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2–Ã2B1 coupled PESs to rationalize the experimental speculation3 about the lifetime of the first excited state. The WP propagation in the
2A2–Ã2B1 coupled PESs to rationalize the experimental speculation3 about the lifetime of the first excited state. The WP propagation in the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2–Ã2B1 coupled state formalism is performed with fourteen vibrational modes including seven (ν1, ν3, ν5, ν6, ν7, ν10 and ν11) totally symmetric modes and seven coupling (ν16, ν17, ν19, ν20, ν24, ν25 and ν26) modes by employing the MCTDH82 program module. The numerical details of the present calculations are given in Table S3 in the ESI.† The spectra obtained from these calculations are shown in panel a of Fig. 8 and also compared with the experimental recording3 in the same panel. The time-autocorrelation function recorded during WP propagation is damped with an exponential function,
2A2–Ã2B1 coupled state formalism is performed with fourteen vibrational modes including seven (ν1, ν3, ν5, ν6, ν7, ν10 and ν11) totally symmetric modes and seven coupling (ν16, ν17, ν19, ν20, ν24, ν25 and ν26) modes by employing the MCTDH82 program module. The numerical details of the present calculations are given in Table S3 in the ESI.† The spectra obtained from these calculations are shown in panel a of Fig. 8 and also compared with the experimental recording3 in the same panel. The time-autocorrelation function recorded during WP propagation is damped with an exponential function, 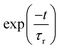 [where τr = 40 fs for
[where τr = 40 fs for ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2 state and τr = 20 fs for Ã2B1 state], and later we performed Fourier transformation of the autocorrelation function to generate the spectral envelope with a shift of the 0–0 line about ∼0.69 eV for
2A2 state and τr = 20 fs for Ã2B1 state], and later we performed Fourier transformation of the autocorrelation function to generate the spectral envelope with a shift of the 0–0 line about ∼0.69 eV for ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2 state and about ∼0.73 eV for Ã2B1 state. The overall band shape of the theoretical spectra obtained from these calculations (see panel a of Fig. 8) is well in accordance with the experimental spectra.3 The diabatic electronic population transfer between the
2A2 state and about ∼0.73 eV for Ã2B1 state. The overall band shape of the theoretical spectra obtained from these calculations (see panel a of Fig. 8) is well in accordance with the experimental spectra.3 The diabatic electronic population transfer between the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2 and Ã2B1 states during the WP propagation (up to 200 fs), while the initial WP is prepared in Ã2B1 state, is shown in panel b of Fig. 8. It can be seen from panel b of Fig. 8 that 50% of Ã2B1 state population transfers to the
2A2 and Ã2B1 states during the WP propagation (up to 200 fs), while the initial WP is prepared in Ã2B1 state, is shown in panel b of Fig. 8. It can be seen from panel b of Fig. 8 that 50% of Ã2B1 state population transfers to the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2 state within ∼40 fs and later a gradual growth of electronic population of
2A2 state within ∼40 fs and later a gradual growth of electronic population of ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2 state and a gradual decay of electronic population of Ã2B1 state is observed. The fit with a monoexponential function of the decay curve of the Ã2B1 state indicates the lifetime of Ã2B1 state to be about ∼87 fs. Hence, it can be attributed that the large spectral broadening of the photo-detachment band of Ã2B1 state compared to that of
2A2 state and a gradual decay of electronic population of Ã2B1 state is observed. The fit with a monoexponential function of the decay curve of the Ã2B1 state indicates the lifetime of Ã2B1 state to be about ∼87 fs. Hence, it can be attributed that the large spectral broadening of the photo-detachment band of Ã2B1 state compared to that of ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2 state occurs due to the immediate (within 40 fs) transfer of electronic population from Ã2B1 to
2A2 state occurs due to the immediate (within 40 fs) transfer of electronic population from Ã2B1 to ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2 state. The present theoretical results within the
2A2 state. The present theoretical results within the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2–Ã2B1 coupled state formalism agree with the experimental3 attribution of very fast non-radiative decay to the
2A2–Ã2B1 coupled state formalism agree with the experimental3 attribution of very fast non-radiative decay to the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2 state of the indenyl radical in the presence of low-lying
2A2 state of the indenyl radical in the presence of low-lying ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2–Ã2B1 CI, but they cannot circumvent the experimental prediction of the lifetime of Ã2B1 state of 7 fs estimated from the peak width. Therefore it would be worthwhile to check the electronic non-adiabatic effects of the other two relatively close lying excited states (
2A2–Ã2B1 CI, but they cannot circumvent the experimental prediction of the lifetime of Ã2B1 state of 7 fs estimated from the peak width. Therefore it would be worthwhile to check the electronic non-adiabatic effects of the other two relatively close lying excited states (![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 2A2 and
2A2 and ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) 2B1) of the indenyl radical on the nuclear dynamics of the Ã2B1 state in the
2B1) of the indenyl radical on the nuclear dynamics of the Ã2B1 state in the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2–Ã2B1–
2A2–Ã2B1–![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 2A2–
2A2–![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) 2B1 coupled state formalism. The results of these four coupled state calculations are discussed in the next section.
2B1 coupled state formalism. The results of these four coupled state calculations are discussed in the next section.
![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2–Ã2B1 state dynamics following the time-dependent approach is shown in panel (a). The blue envelope corresponds to experimental observations (digitized from ref. 3) and the black envelope is obtained from the present theoretical calculations. The electronic population transfer from Ã2B1 state to
2A2–Ã2B1 state dynamics following the time-dependent approach is shown in panel (a). The blue envelope corresponds to experimental observations (digitized from ref. 3) and the black envelope is obtained from the present theoretical calculations. The electronic population transfer from Ã2B1 state to ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2 state of the indenyl radical is shown in panel (b), when the initial WP is prepared in Ã2B1 state.
2A2 state of the indenyl radical is shown in panel (b), when the initial WP is prepared in Ã2B1 state.![[B with combining tilde]](https://www.rsc.org/images/entities/b_char_0042_0303.gif) 2A2 and
2A2 and ![[C with combining tilde]](https://www.rsc.org/images/entities/b_char_0043_0303.gif) 2B1 states on the internal conversion of Ã2B1 state.
In order to perform the
2B1 states on the internal conversion of Ã2B1 state.
In order to perform the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2–Ã2B1–
2A2–Ã2B1–![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 2A2–
2A2–![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) 2B1 coupled state nuclear dynamics, we have included the contribution of four extra vibrational modes (three totally symmetric modes, ν4, ν8 and ν9, and one coupling mode, ν21) as compared to our previous WP propagation in the
2B1 coupled state nuclear dynamics, we have included the contribution of four extra vibrational modes (three totally symmetric modes, ν4, ν8 and ν9, and one coupling mode, ν21) as compared to our previous WP propagation in the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2–Ã2B1 coupled PESs following their excitation strength in
2A2–Ã2B1 coupled PESs following their excitation strength in ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 2A2 and
2A2 and ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) 2B1 state (cf.Tables 4–6). The results of the present calculations are shown in Fig. 9. The envelope of the spectra obtained from these calculations is shown in panel a, and the transfer of diabatic electronic population between these states while the initial WP is prepared in the Ã2B1 state is shown in panel b of Fig. 9. The numerical details of the present calculations are given in Table S3 in the ESI.† Following the consistency of the previous two coupled state calculations, the time-autocorrelation function recorded during WP propagation is damped with an exponential function,
2B1 state (cf.Tables 4–6). The results of the present calculations are shown in Fig. 9. The envelope of the spectra obtained from these calculations is shown in panel a, and the transfer of diabatic electronic population between these states while the initial WP is prepared in the Ã2B1 state is shown in panel b of Fig. 9. The numerical details of the present calculations are given in Table S3 in the ESI.† Following the consistency of the previous two coupled state calculations, the time-autocorrelation function recorded during WP propagation is damped with an exponential function, 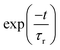 [where τr = 40 fs for
[where τr = 40 fs for ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2 state and τr = 20 fs for Ã2B1,
2A2 state and τr = 20 fs for Ã2B1, ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 2A2 and
2A2 and ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) 2B1 states], and later we performed Fourier transformation of the autocorrelation function to generate the spectral envelope. The electronic population analysis of panel b of Fig. 9 indicates a relatively quick decay of electronic population of Ã2B1 state to the
2B1 states], and later we performed Fourier transformation of the autocorrelation function to generate the spectral envelope. The electronic population analysis of panel b of Fig. 9 indicates a relatively quick decay of electronic population of Ã2B1 state to the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2 state as compared to the same presented in panel b of Fig. 8. It can be seen from this figure that more than 50% of electronic population of Ã2B1 state transfers to
2A2 state as compared to the same presented in panel b of Fig. 8. It can be seen from this figure that more than 50% of electronic population of Ã2B1 state transfers to ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2 state within ∼18 fs (40 fs in the
2A2 state within ∼18 fs (40 fs in the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2–Ã2B1 coupled state formalism), while the fit with a monoexponential function of the decay curve of the Ã2B1 state indicates the lifetime of Ã2B1 state to be about ∼39 fs. This fact can be attributed to the involvement of more electronic states and vibrational modes in the dynamics, where the increment of totally symmetric vibrational modes is involved in the fine-tuning of PESs and, as a consequence, the modulation of non-adiabatic coupling through b2 symmetric vibrational modes becomes more prominent. It can be seen from Table 3 that the Ã2B1 state is vertically ∼1.91 and ∼3.16 eV separated from the
2A2–Ã2B1 coupled state formalism), while the fit with a monoexponential function of the decay curve of the Ã2B1 state indicates the lifetime of Ã2B1 state to be about ∼39 fs. This fact can be attributed to the involvement of more electronic states and vibrational modes in the dynamics, where the increment of totally symmetric vibrational modes is involved in the fine-tuning of PESs and, as a consequence, the modulation of non-adiabatic coupling through b2 symmetric vibrational modes becomes more prominent. It can be seen from Table 3 that the Ã2B1 state is vertically ∼1.91 and ∼3.16 eV separated from the ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 2A2 and
2A2 and ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) 2B1 states, respectively. This energy gap between Ã2B1 and
2B1 states, respectively. This energy gap between Ã2B1 and ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 2A2 states is diminished slowly towards the negative values of ν1, ν3, ν5, ν8, ν9 and ν11 normal coordinates, respectively, while the same is observed towards positive values of ν6 and ν10 normal coordinates (cf. panels a, c, e, h, i, k, f, and j, respectively, in Fig. 2). This cumulative tuning through the above mentioned totally symmetric vibrational modes causes the observed non-adibaticity between the Ã2B1 and
2A2 states is diminished slowly towards the negative values of ν1, ν3, ν5, ν8, ν9 and ν11 normal coordinates, respectively, while the same is observed towards positive values of ν6 and ν10 normal coordinates (cf. panels a, c, e, h, i, k, f, and j, respectively, in Fig. 2). This cumulative tuning through the above mentioned totally symmetric vibrational modes causes the observed non-adibaticity between the Ã2B1 and ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 2A2 states (cf.Table 6). On the other hand, the PECs presented in the different panels of Fig. 2 indicate well energy separation between
2A2 states (cf.Table 6). On the other hand, the PECs presented in the different panels of Fig. 2 indicate well energy separation between ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2 and
2A2 and ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) 2B1 states both vertically and along the normal coordinates. Hence, the non-adiabaticity between these states through inter-state coupling is less effective as these couplings are determined from less sensitive repulsive PECs.60 In the present coupled state calculations, the contribution from
2B1 states both vertically and along the normal coordinates. Hence, the non-adiabaticity between these states through inter-state coupling is less effective as these couplings are determined from less sensitive repulsive PECs.60 In the present coupled state calculations, the contribution from ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2–
2A2–![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 2A2 and Ã2B1–
2A2 and Ã2B1–![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) 2B1 inter-state couplings (out of scope due to the adopted electronic structure methods in the present study) and some important coupling modes like, ν22, ν23, etc. is missing. Hence, it is expected that the consideration of the above mentioned points might rectify the present calculations and can provide better agreement with experiment.3
2B1 inter-state couplings (out of scope due to the adopted electronic structure methods in the present study) and some important coupling modes like, ν22, ν23, etc. is missing. Hence, it is expected that the consideration of the above mentioned points might rectify the present calculations and can provide better agreement with experiment.3

![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2–Ã2B1–
2A2–Ã2B1–![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 2A2–
2A2–![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) 2B1 state dynamics following the time-dependent approach is shown in panel (a). The blue envelope corresponds to experimental observations (digitized from ref. 3) and the black envelope is obtained from the present theoretical calculations. The electronic population transfer from Ã2B1 state to
2B1 state dynamics following the time-dependent approach is shown in panel (a). The blue envelope corresponds to experimental observations (digitized from ref. 3) and the black envelope is obtained from the present theoretical calculations. The electronic population transfer from Ã2B1 state to ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2,
2A2, ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 2A2 and
2A2 and ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) 2B1 states of the indenyl radical is shown in panel (b), when the initial WP is prepared in Ã2B1 state.
2B1 states of the indenyl radical is shown in panel (b), when the initial WP is prepared in Ã2B1 state.![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2 state of the indenyl radical provide reasonably good comparison with the experimentally observed first photo-detachment band of the indenyl anion up to ∼17
2A2 state of the indenyl radical provide reasonably good comparison with the experimentally observed first photo-detachment band of the indenyl anion up to ∼17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 cm−1 from the onset of the first experimental band (well below with respect to
500 cm−1 from the onset of the first experimental band (well below with respect to ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2–Ã2B1 CI). The D, J, Q and X peaks of the experimental SEVI spectrum are nicely assigned in this energy range based on the WP density plots of the vibrational energy levels of the composite Poisson spectrum. While the intensity of the Poisson spectrum is diminished around ∼18
2A2–Ã2B1 CI). The D, J, Q and X peaks of the experimental SEVI spectrum are nicely assigned in this energy range based on the WP density plots of the vibrational energy levels of the composite Poisson spectrum. While the intensity of the Poisson spectrum is diminished around ∼18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 750 cm−1, the same reappeared in the nuclear dynamics of the
750 cm−1, the same reappeared in the nuclear dynamics of the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2–Ã2B1 coupled PESs. The appearance of a comparable intensity with the experimental spectrum employing
2A2–Ã2B1 coupled PESs. The appearance of a comparable intensity with the experimental spectrum employing ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2–Ã2B1 coupled state dynamics in the energy range of ∼17
2A2–Ã2B1 coupled state dynamics in the energy range of ∼17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 cm−1 to ∼21
500 cm−1 to ∼21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 is attributed to vibrational motions of the Ã2B1 state near the
000 cm−1 is attributed to vibrational motions of the Ã2B1 state near the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2–Ã2B1 CI. This indicates the importance of electronic non-adiabatic effects between the
2A2–Ã2B1 CI. This indicates the importance of electronic non-adiabatic effects between the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2 and the Ã2B1 states of the indenyl radical in the ground state photo-detachment band of the indenyl anion. We have also assigned five experimental peaks, E, M, P, U and W, in addition to the previous four peaks comparing the results of
2A2 and the Ã2B1 states of the indenyl radical in the ground state photo-detachment band of the indenyl anion. We have also assigned five experimental peaks, E, M, P, U and W, in addition to the previous four peaks comparing the results of ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2–Ã2B1 coupled state dynamics with available SEVI recording. We also performed the time-dependent nuclear dynamics study in the
2A2–Ã2B1 coupled state dynamics with available SEVI recording. We also performed the time-dependent nuclear dynamics study in the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2–Ã2B1 coupled state formalism in the quest of obtaining excited state lifetime as well as the population flow between electronic states of indenyl radical. The results of these calculations indicate that ∼50% of electronic population of Ã2B1 state transfers to
2A2–Ã2B1 coupled state formalism in the quest of obtaining excited state lifetime as well as the population flow between electronic states of indenyl radical. The results of these calculations indicate that ∼50% of electronic population of Ã2B1 state transfers to ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2 state within ∼40 fs and the lifetime of Ã2B1 state is ∼87 fs, which is quite high compared to the experimentally estimated lifetime of Ã2B1 state. In order to rationalize the present fact we also performed the time-dependent nuclear dynamics study in the
2A2 state within ∼40 fs and the lifetime of Ã2B1 state is ∼87 fs, which is quite high compared to the experimentally estimated lifetime of Ã2B1 state. In order to rationalize the present fact we also performed the time-dependent nuclear dynamics study in the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2–Ã2B1–
2A2–Ã2B1–![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 2A2–
2A2–![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) 2B1 coupled state formalism. The results of these studies indicate that more than 50% of electronic population of the Ã2B1 state transfers to the
2B1 coupled state formalism. The results of these studies indicate that more than 50% of electronic population of the Ã2B1 state transfers to the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A2 state within ∼18 fs and the lifetime of Ã2B1 state is ∼39 fs. The improvement of the lifetime of the Ã2B1 state in comparison with the experiment in the four coupled state formalism indicates that the involvement of more vibrational modes (which is out of scope for the present calculation) might rectify the present calculations and can provide better agreement with experiment.
2A2 state within ∼18 fs and the lifetime of Ã2B1 state is ∼39 fs. The improvement of the lifetime of the Ã2B1 state in comparison with the experiment in the four coupled state formalism indicates that the involvement of more vibrational modes (which is out of scope for the present calculation) might rectify the present calculations and can provide better agreement with experiment.



