The ionization energy of the vinyl radical: a Mexican standoff with a happy ending

Abstract

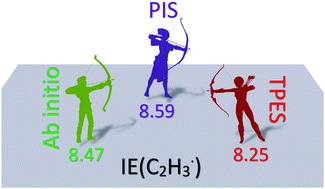
The Active Thermochemical Tables (ATcT) yield 8.477 ± 0.007 eV as the ionization energy of the vinyl radical, which agrees with wave function theory results. The photoionization spectrum yielded 8.59 ± 0.03 eV, while the photoelectron spectrum yielded 8.25 ± 0.05 eV for the adiabatic ionization energy. In order to reconcile these contradictory measurements, we produced the vinyl radical by flash pyrolysis of divinyl sulfone, and recorded its photoionization (PI) and threshold photoelectron (TPE) spectrum in the 8.10–10.45 eV photon energy range at the Swiss Light Source for the first time using double imaging photoelectron photoion coincidence (i²PEPICO) spectroscopy. In contrast to the photoelectron spectrum, the ground state TPES band exhibits a weak vibrational structure that correlates with strong peaks in the photoionization spectrum and is assigned to transitions to autoionizing Rydberg states converging to the ³A′′ cation state. While, at 8.462 eV, our calculations of the acetylene proton affinity confirm the vinyl adiabatic ionization energy from the ATcT, our experimental data agree with the literature photoelectron and photoionization spectra. The discrepancy is explained by negligible Franck–Condon factors for the origin transition from the bent Y-shaped neutral minimum to the bridge-shaped ionic minimum. We propose that the photoionization signal can instead be assigned in its entirety to three transitions: (i) straight Y-shaped C₂H₃^‡ → bridged C₂H₃⁺, (ii) straight Y-shaped C₂H₃^‡ → straight Y-shaped C₂H₃⁺ and (iii) bent Y-shaped C₂H₃ → straight Y-shaped C₂H₃⁺, tentatively assigned to the observed photoionization onsets at 8.25, 8.43, and 8.60 eV, respectively.