Dependency of f states in fluorite-type XO2 (X = Ce, Th, U) on the stability and electronic state of doped transition metals
Abstract
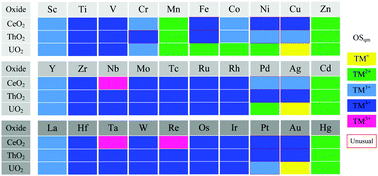
Fluorite-type XO2 (X = Ce, Th, U) have versatile technological and industrial applications, and the behavior of impurities in the oxides is one of the engaging topics for their application. However, the fundamental behaviors of impurities are still lacking. Herein, we conduct a systematic first-principles DFT+U screening to find the trends of transition metal (TM) behaviors in the three dioxides in terms of energetics and electronic states, with a particular focus on the dependency of f electronic states of the hosts. In order to overcome the long-standing bottleneck of determining the true oxidation state of multivalent TMs, Ce and U, a more rigorous method based on counting orbital occupation numbers of f and d orbitals is performed for clarification. The calculated incorporation energies and formation energies of TMs show that the relative stability of TMs in the three XO2 exhibits similar trends, indicative of the dominant roles played by the host oxides with the same crystal structure and very close lattice parameters. On the other hand, the quantitative differences in the stability and electronic state of doped TMs could be mainly attributed to the differences in the electronic structure of host XO2. The 5f electrons in UO2 are more delocalized than 4f in CeO2, suppressing the formation of high oxidation states of TMs in the former. For ThO2 with the negligible f electrons associated with monovalent Th4+, the doped TMs tend to adopt the oxidation states close to TM4+, achieving the electronically matched states. The appearance of a few unusual oxidation states of TMs sheds light on the flexible delocalization–localization mutual transition of f or d valence electrons.
- This article is part of the themed collection: 2019 PCCP HOT Articles


 Please wait while we load your content...
Please wait while we load your content...