Ultranarrow heterojunctions of armchair-graphene nanoribbons as resonant-tunnelling devices†
Abstract
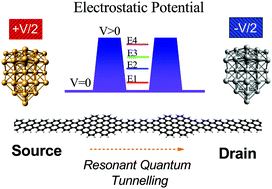
A systematic investigation is performed on the electronic transport properties of armchair-graphene nanoribbon (AGNR) heterojunctions using spin-polarized density functional theory calculations in combination with the non-equilibrium Green's function formalism. 9-AGNR and 5-AGNR structures are used to form a single-well configuration by sandwiching a 5-AGNR between two 9-AGNRs. At the same time, these 9-AGNRs are matched at the left and right to electrodes, 9 and 5 being the number of carbon dimers as width. This heterojunction mimics an electronic device with two potential barriers (9-AGNR) and one quantum well (5-AGNR) where quasi-bound states are confined. First, we study the ground state properties, and then we calculate the electron transport properties of this device as a function of the well width. We show the presence of electronic tunnelling resonances between the barriers by delocalized electron density inside the well's structure. This is corroborated by transmission curves, localized densities of states (LDOS), current-vs.-bias voltage results, and the trend of the resonances as a function of the well width. This work shows that carbon AGNRs may be used as resonant-tunnelling devices for applications in nanoelectronics.
- This article is part of the themed collections: Celebrating recent chemical science in Mexico and 2019 PCCP HOT Articles


 Please wait while we load your content...
Please wait while we load your content...