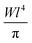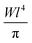Open Access Article
Open Access ArticleNeutron spin echo monitoring of segmental-like diffusion of water confined in the cores of carbon nanotubes
Alexandra
Parmentier
 a,
Marco
Maccarini
a,
Marco
Maccarini
 *b,
Alessio
De Francesco
c,
Luisa
Scaccia
d,
Giovanna
Rogati
e,
Orsolya
Czakkel
f and
Francesco
De Luca
e
*b,
Alessio
De Francesco
c,
Luisa
Scaccia
d,
Giovanna
Rogati
e,
Orsolya
Czakkel
f and
Francesco
De Luca
e
aINFN – Division of Roma Tor Vergata, 00133 Rome, Italy
bUniversitè Grenoble Alpes, Lab. TIMC/IMAG CNRS UMR 5525, La Tronche, 38700, France. E-mail: marco.maccarini@univ-grenoble-alpes.fr
cConsiglio Nazionale delle Ricerche, Istituto Officina dei Materiali, Operative Group in Grenoble (OGG), c/o Institut Laue Langevin, Grenoble, France
dUniversity of Macerata, Dept. of Economics and Law, 62100 Macerata, Italy
eSapienza University of Rome, Dept. of Physics, Rome, 00185, Italy
fInstitut Laue-Langevin, CS 20156, 38042 Grenoble cedex 9, France
First published on 11th September 2019
Abstract
Following the stream of increasing scientific interest in condensed-matter systems under ultra-hydrophobic confinement, the present work reports the first incoherent neutron spin echo assessment of the dynamics of water axially confined inside single-wall carbon nanotubes of diameter d ∼ 1.4 nm. At the time scale of nanoseconds, two water populations are retrieved, whose relative proportion matches the one expected for a concentric shell + chain arrangement with cylindrical symmetry. The time dependence of the mean square displacement related to the external component is found to be subdiffusive, with peculiar resemblance to segmental diffusion typical of entangled polymeric systems.
1 Introduction
Confinement in porous media is a tòpos or leitmotif of condensed-matter physics. In particular, confinement of water in nanometric cavities – especially in cylindrical nanopores – represents a topic of general interest, since low-dimensional water is a prototypical non-bulk system that is widespread in nature1–3 and synthetic structures of technological importance.4,5 In this context, carbon nanotubes (CNTs), which are peculiar allotropes of carbon characterized in terms of diameter and (n,m) chiral indices,6 have become popular in the field of nanofluidics as effective geometries to study small-molecule polar liquids under quasi-1D ultra-hydrophobic confinement,7–9 especially in their single-wall carbon nanotube (SWCNT) declination.Indeed, experimental and theoretical effort has been spent in the description of the structure of nanotube water as a function of SWCNT diameter,10–13 and a variety of experimental techniques, from X-ray diffraction (XRD)14 and inelastic neutron scattering (INS)9,10 to nuclear magnetic resonance (NMR),15 have been exploited to explore this type of system.
Pioneered by Mezei in the early 1970s16,17 along the same lines as the Hahn-echo method implemented in NMR, neutron spin echo (NSE) spectroscopy – with its special feature of making resolution almost independent of beam monochromatization – allows the accessible time domain to be expanded by several orders of magnitude when compared to other INS techniques, thus enabling the experimenter to probe slow processes with characteristic times of up to hundreds of ns and above. As a result, the NSE approach has developed into a versatile tool for the investigation of most diverse phenomena – from magnetism to glass formers, across superconductors, as well as a large set of biological systems18 – with a significant return, in recent years, from soft matter under confinement.19–21
In this paper, we report the first NSE analysis of water confined in the cores of long SWCNTs at the ns time scale, with particular focus on the dependence of the mean square displacement (MSD) on time. At such a scale, a peculiar subdiffusive behavior is retrieved, with an unexpected resemblance to reptation mechanisms that are typical of massive polymeric systems.
2 Materials and methods
2.1 Sample preparation
The commercial SWCNT powder (by Carbon Solutions, Inc.) used for our NSE measurements consisted of high-quality, non-functionalized, open-ended (10,10) tubes with an average diameter of (1.4 ± 0.1) nm and a longitudinal-size distribution spanning the (0.5–3.0) μm range.According to sample data sheets, the original as-Prepared (AP) material was synthesized by arc discharge with the aid of a Ni/Y catalyzer.22 The purification process included an annealing step at high temperature (∼350 °C) in open air in order to remove carbonaceous impurities via pyrolysis, followed by an acid chemical washing that melted the metal caps placed at tube ends, as confirmed by thermogravimetric analysis.
The resulting CNT high carbonaceous purity (>90%) and narrow variation in diameter were assessed by the producer by transmission electron microscopy and Raman spectroscopy, as recommended by NIST protocols.23
The reference dry sample was obtained by desiccation of the purified powder in an oven at 45 °C for 3 hours (final CNT mass: 0.1808 ± 0.0002 g), and then sealed in an aluminum sample holder using an indium gasket.
The hydrated sample was prepared starting from an analogous desiccated sample (CNT mass: 0.1887 ± 0.0002 g), which was then exposed for 2 hours to saturated vapor from a distilled and de-ionized water bath at about 120 °C in an enclosed environment at a pressure of about 2 atm. Any excess water was removed by subsequent evaporation at 45 °C until an optimal H2O/SWCNT mass ratio of about 12% – desirable in order to get rid of any adsorbed water on the outside of the tubes10 – was reached (final sample mass: 0.2125 ± 0.0002 g → water content: 0.0238 ± 0.0004 g).
Also the hydrated sample was eventually placed in a sealed Al can.
2.2 Experimental setup
NSE measurements were performed with the aid of the IN11 spectrometer located at Institut Laue–Langevin (ILL) in Grenoble, France.The spectrometer was exploited in the IN11C configuration, i.e.:
• 30° wide-angle detector (centered at 50°)
• Incoming neutron wavelength of 5.5 Å
• Time window: 5 ps–1.3 ns
• Q-range: (0.7–1.2) Å−1
NSE spectra of the hydrated sample were taken at 300, 270, 240, 210, 180, 150, 120, 90, 60, 30, and 10 K. An additional spectrum was taken at 2 K to serve as the resolution function.
The dry sample was scanned at 300 and 180 K in order to check the absence of dynamics even at high temperature.
The sample holder was a slab accommodating a 3 mm-thick layer of SWCNT powder. The choice of a thin-sample geometry was made in order to minimize any multiple-scattering contribution.
3 Basic theory
3.1 NSE experiment
The typical output of a NSE experiment is the neutron polarization, that is, the real part of the complex intermediate scattering function (ISF),17,18I(Q,t).The ISF can be, in turn, represented as the configurational Fourier transform (FT) of the van Hove correlation function
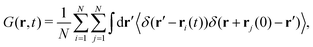 | (1) |
According to the definition of G, the ISF gives information about correlations between density fluctuations in the wave-vector domain. In addition, just like G, the ISF can be split into a one-particle and a collective contribution, of which the former gives life to the incoherent part of the scattering.24
The dynamic structure factor, S(Q,ω) – which returns the frequency spectrum of correlations between density fluctuations, and can be related to the double-differential scattering cross section – is the FT of the ISF towards the frequency domain. That is, the real part of the normalized ISF, acting as a diffusional time decay, can be written as:
 | (2) |
Normalization is usually performed with respect to a resolution function recovered from a measurement on a perfectly elastic scatterer: in our experiment, resolution was assessed by measuring a sample spectrum at 2 K, since scattering at such a low temperature can be safely considered to be elastic within the experimental time window reported in Section 2.2, with the advantage of preserving sample size and geometry.
Apart from carbon and aluminum, which are basically coherent scatterers whose relaxation time scales are outside NSE sensitivity, a quick inspection of bound scattering cross sections suggests that σ1H is mainly incoherent and dominant in comparison to cross sections of any element in the system by at least one order of magnitude. Nevertheless, in order to be sure of safely observing self-dynamics (from protons), constant monitoring of coherent-to-incoherent intensity ratio was performed, as reported in Fig. 1 for two representative temperatures.
 | ||
| Fig. 1 Coherent and incoherent contributions to signal intensity as a function of Q at 300 K and 180 K. | ||
Actually, contrary to coherent spin-echo scattering, which is completely non-spin–flip (i.e., the neutron spin state does not change before and after scattering), the 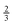 -probability of spin–flip occurring in incoherent scattering from hydrogen18 causes the net polarization to be reduced down to
-probability of spin–flip occurring in incoherent scattering from hydrogen18 causes the net polarization to be reduced down to 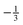 of its nominal value, which produces a reduced echo-signal on an additional background. This explains the common use of NSE to probe coherent dynamics. Nevertheless, as of late, NSE has been upgraded to being a successful tool for investigating incoherent phenomena,25–27 which has paved the way for studies such as the one presented in this paper.
of its nominal value, which produces a reduced echo-signal on an additional background. This explains the common use of NSE to probe coherent dynamics. Nevertheless, as of late, NSE has been upgraded to being a successful tool for investigating incoherent phenomena,25–27 which has paved the way for studies such as the one presented in this paper.
In addition, one has to consider that spin–flip causes residual multiple scattering to be efficiently suppressed, because double-scattering events only account for 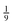 of the original polarization, and higher-order events further reduce the contribution to the echo amplitude.28
of the original polarization, and higher-order events further reduce the contribution to the echo amplitude.28
In order to improve counting statistics, all 41 components of the wide-angle detector unit have been included in binning, so as to boost signal intensity to the detriment of Q-resolution. Accordingly, at a first approximation, Q-dependency has been neglected, and an average Q-value of 0.96 Å−1 has been considered at all temperatures. This choice can be justified by virtue of signal trends in Q shown in Fig. 1, the isotropic spread of incoherent scattering over a 4π solid angle,18 and quasi-elastic neutron scattering (QENS) results on this same system reported elsewhere.9
3.2 Anomalous transport in quasi-1D confining media
Molecular transport is usually characterized via the propagator P(r,t), which is a probability density function whose 2nd moment returns the particle MSD, 〈r2〉. In those cases when the particle trajectories are pure random walks (no time or spatial correlations between elementary walk steps, i.e., no waiting-time distribution and no directional anisotropy) and the particle displacements are non-restricted on the experimental time scale, P(r,t) is a Gaussian function and the MSD scales linearly with time. Hence, any “anomalous” tranport can be classified looking at the exponent k of the MSD t-dependence| 〈r2〉 ∼ tk, | (3) |
The origin of possible anomalies is 2-fold: (1) either a time-dependent diffusion coefficient D(t) can make the MSD anomalous in spite of the Gaussianity of the propagator, as in single-file (SF) diffusion through straight, narrow cylindrical pores (〈r2〉 = 2D(t)t in 1D); or (2) the propagator is actually non-Gaussian, due to geometric restrictions that generate “traps” in which diffusing particles get temporarily slowed down.29
SF diffusion can occur in 1D or quasi-1D geometries where the moving molecules are not allowed to pass each other. At times shorter than the one needed by the system to reach equilibrium, the MSD is subdiffusive with a typical trend
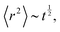 | (4) |
This is due to a time-dependent diffusion coefficient D(t), in the presence of a truly Gaussian propagator that solves Fick's second equation, as beautifully assessed by NMR pulsed-gradient spin-echo measurements on zeolites in the 1990s.30
The SF arrangement has been shown31 to belong to the same universality class of Rouse chains involved in polymeric segment displacement under topological constraints due to de Gennes’ reptation mechanism.32,33 Nonetheless, in this case, the prerequisite of the Gaussianity is no longer valid.25,29
The reptation model owes its name to the dominating polymeric motion being a reptile-like slithering along the chain profile, with lateral restrictions defined as “entanglement”, and modeled by a tube parallel to the chain with diameter d. According to its predictions:34
• For short times, smaller than a crossover
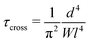 | (5) |
 the so-called elementary Rouse rate, which sets the microscopic time scale at which monomers relax, and ζ0 the friction coefficient per “bead”, if one represents the chain as a sequence of beads and springs), free Rouse motion is expected:
the so-called elementary Rouse rate, which sets the microscopic time scale at which monomers relax, and ζ0 the friction coefficient per “bead”, if one represents the chain as a sequence of beads and springs), free Rouse motion is expected: | (6) |
• For τcross < t < τR, with τR being the Rouse time (i.e., the longest time in the relaxation spectrum), the MSD takes the form:
 | (7) |
• For τR < t < τd, with τd being the disengagement time after which the chain has completed its exit from the tube, the dynamic regime is termed pure reptation and corresponds to the onset of tube renewal, with
 | (8) |
• For t > τd, the chain has left its original tube and segmental diffusion becomes negligible, the MSD becoming proportional to t again:
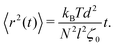 | (9) |
In the first three regimes, the motion is subdiffusive, but unlike SF, the anomaly is of purely topological nature.29
4 Experimental results
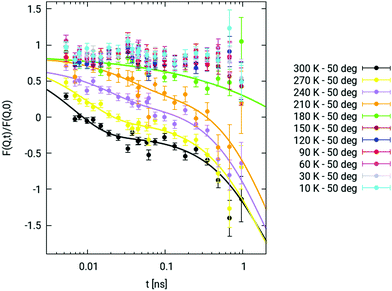
The best curve fit to any dataset at temperatures >180 K is a double exponential function (DEF) of the form | (10) |
| T [K] | A 1 | τ 1 [ns] | A 2 | τ 2 [ns] |
|---|---|---|---|---|
| 300 | 2.17 ± 0.02 | 1.8 ± 0.3 | 1.0 ± 0.2 | 0.007 ± 0.001 |
| 270 | 2.38 ± 0.03 | 1.6 ± 0.2 | 0.8 ± 0.2 | 0.009 ± 0.002 |
| 240 | 2.64 ± 0.06 | 1.8 ± 0.3 | 0.5 ± 0.1 | 0.02 ± 0.01 |
| 210 | 2.8 ± 0.1 | 2.2 ± 0.7 | 0.4 ± 0.1 | 0.03 ± 0.02 |
At the four highest temperatures, DEF fits return a slow relaxation time τ1 of the order of a nanosecond, and a fast τ2 of the order of tens of picoseconds. The corresponding component proportion A1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A2 ranges from 68%
A2 ranges from 68%![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 32% at 300 K to 88%
32% at 300 K to 88%![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 12% at 210 K.
12% at 210 K.
At 180 K, the response of the system suddenly changes. The DEF-fit procedure breaks down, with τ1 increasing towards values of a couple of orders of magnitude larger than a nanosecond. At such a temperature, the NSE decay has been fitted by a stretched exponential function (SEF) of the form:
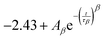 | (11) |
Due to the ability of the SEF to span many orders of magnitude, τβ and β parameters are strongly correlated. For this reason, the mean relaxation time
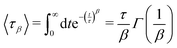 | (12) |
Yet, SEF fits in which all the three parameters, Aβ, 〈τβ〉, and β, float are hardly manageable. Consequently, one has to rely on a set of assumptions.
Indeed, recent simulations on analogous systems13,37,38 suggest that setting β = 0.4 may be a reasonable choice. Once β is fixed, a first fit round can be performed to recover first-approximation values for Aβ and 〈τβ〉. Fit results for Aβ converge to an average value of 3.3 (with errors of the order of a few % at any T), which can be used as a further fixed parameter to get a refined estimation of 〈τβ〉. Resulting errors on 〈τβ=0.4〉 are large (63 ± 25 ns). This depends on the available experimental time window (order of a nanosecond) being narrow compared to the system's relaxation times at very low temperatures, which prevents us from identifying scatterer populations with well-defined, very long characteristic times apart from large distributions marked by real heterogeneity.
In Fig. 2, DEF and SEF fits for 180 K ≤ T ≤ 300 K are reported, superimposed onto experimental NSE points at all investigated temperatures.
The limited experimental window, as well as data quality at any temperature, makes it advisable to further carry out data analysis from a different point of view, applying a Bayesian approach along with the traditional frequentist scenario with the purpose of reducing any source of arbitrariness to the minimum, especially in the choice of the number of relaxation times.
“Thinking Bayesian” can be thought of as a modern and flexible implementation of the Ockham's razor principle,39–42 which, making use of Bayes’ theorem, counteracts any possible overparametrization, while preserving a broad class of fit models.43 The RJ/MCMC-based Bayesian code exploited here is extensively described in the literature.42,44
All temperatures between 180 K and 300 K have been tested against the following model:
 | (13) |
The fact that, in a Bayesian perspective, n can be considered as a parameter allows the number of channels to be chosen on a probabilistic basis with automatic penalization of model complexity, which is not the case for a traditional least-squares fit.
As representative examples, we report here the obtained scenarios at 300 K and 180 K.
Provided that a sufficiently large number of simulation sweeps is performed (always >300![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 in our case, with a burning threshold42 of 10
000 in our case, with a burning threshold42 of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000), and in spite of no τj–βj interdependence included in eqn (13), the Bayesian approach returns the posterior probability for the number n of decay channels, as reported in Table 2.
000), and in spite of no τj–βj interdependence included in eqn (13), the Bayesian approach returns the posterior probability for the number n of decay channels, as reported in Table 2.
| T [K] | β | n = 1 | n = 2 | n = 3 | n = 4 | n = 5 |
|---|---|---|---|---|---|---|
| 300 | 1 | 0.1% | 48.0% | 37.5% | 11.8% | 2.6% |
| 180 | 0.3 ± 0.1 | 53.7% | 33.1% | 10.5% | 2.3% | 0.4% |
Although the experimental window is limited, the Bayesian algorithm selects n = 2 and n = 1 as the most probable number of channels at T = 300 K and T = 180 K, respectively. Correspondingly, Table 3 reports Bayesian parameter estimates, which, with the only exception of the characteristic time at 180 K, were obtained taking into account modal values instead of common averages, and peak half widths at half maximum (HWHM), instead of variances, as associated uncertainties. This choice can be justified taking a quick look at the shape of posterior distributions (an example is given in Fig. 3 for relaxation times), which are strictly unimodal, and markedly peaked and asymmetrical at high temperature.
| T [K] | β | n | A 1 | τ 1 [ns] | A 2 | τ 2 [ns] |
|---|---|---|---|---|---|---|
| 300 | 1 | 2 | 2.2 ± 0.4 | 1.7 ± 0.5 | 1.0 ± 0.3 | 0.007 ± 0.003 |
| T [K] | β | n | A | τ |
|---|---|---|---|---|
| 180 | 0.3 ± 0.1 | 1 | 3.3 ± 0.1 | 250 ± 141 |
It becomes clear that the fit results included in Table 3 are fairly consistent with their frequentist homologues, that is, our cross-checking is positive. Moreover, the Bayesian approach returned additional information about the posterior distributions of the number of channels, as well as of any other parameter of the model. The posterior distribution of the characteristic decay time at T ≤ 180 K, for example, clearly shows that related data are poorly informative, as clearly seen from Fig. 3.
Under the Gaussian approximation, the ISF takes the form25
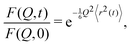 | (14) |
Fig. 4 shows the MSDs retrieved from our experimental NSE data at the average Q-value of 0.96 Å−1.
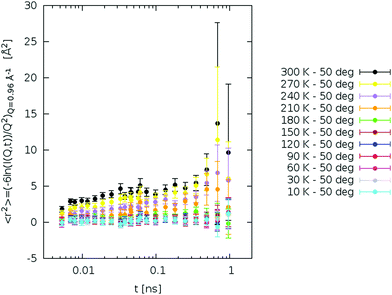 | ||
Fig. 4 MSDs retrieved from NSE data according to eqn (14). All NSE decays have been vertically shifted by the same amount prior to switching to  , and then normalized to data taken at 10 K. , and then normalized to data taken at 10 K. | ||
Let us now focus on MSD data above 180 K.
As shown in Fig. 5, a dynamic changeover can be spotted around t ∼ 0.04 ns for the slow water component. At the highest two temperatures, the time range over which the fast component is still non-negligible is removed.
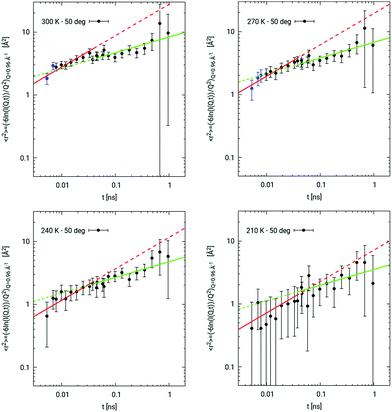 | ||
Fig. 5 Dynamic changeover appearing around t ∼ 0.04 ns at all temperatures above 180 K. In each plot, the asymptotic 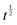 -trend is represented by the red curve, while its -trend is represented by the red curve, while its 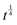 -counterpart lies along the green curve. At T = 300 K and T = 270 K, experimental points in blue are not included in the -counterpart lies along the green curve. At T = 300 K and T = 270 K, experimental points in blue are not included in the 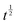 -fit in order to get rid of the non-negligible contribution from the fast water component still surviving at t ≤ τ2; at T = 240 K and T = 210 K, the entire dataset is included, since, even at the earliest time, this contribution never exceeds 10% of the total, taking into account the addend -fit in order to get rid of the non-negligible contribution from the fast water component still surviving at t ≤ τ2; at T = 240 K and T = 210 K, the entire dataset is included, since, even at the earliest time, this contribution never exceeds 10% of the total, taking into account the addend  in eqn (10). in eqn (10). | ||
5 Data interpretation
The ensemble of NSE data presented in Section 4 clearly suggests the existence, at T > 180 K, of two strictly confined populations, which are axially entrapped in the cores of long SWCNTs with average diameter d = (1.4 ± 0.1) nm. As assessed by MD computations concerning the stability of finite-size water clusters inside SWCNTs with diameters above or below a crossover transversal size of 1.4–1.6 nm,45 water encapsulation in thin tubes proves stable on cooling thanks to the persistence of the meniscus at values typical of wetting, with no chance of water evaporation and condensation into ice Ih outside the tubes since the external saturated vapor pressure, Pext, always remains smaller than that of bulk ice, PIh. Taking into account the sample preparation protocol originally developed in a previous report,10 these findings are consistent with a shell + chain scenario, which has been experimentally established at very low temperatures,9,10 but makes its appearance at room temperature as well – in both (10,10) hydrophobic and hydrophilic pores – according to recent MD simulations.12,13 With this in mind, we decided to assign A1 and A2 populations to interfacial and central water, respectively. Indeed, in approaching the 180 K crossover, the component ratio becomes closer and closer to the 8
component ratio becomes closer and closer to the 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio characterizing the ideal octagonal arrangement of a solidified outer shell and a “liquid” inner chain in a transversal section of any filled CNT at very low T (Fig. 6). The crossover temperature is completely consistent with temperatures at which a sharp drop in translational self-diffusion coefficient – though in the absence of complete freezing – is found by MD simulations on water embedded in nanoporous carbon.13
1 ratio characterizing the ideal octagonal arrangement of a solidified outer shell and a “liquid” inner chain in a transversal section of any filled CNT at very low T (Fig. 6). The crossover temperature is completely consistent with temperatures at which a sharp drop in translational self-diffusion coefficient – though in the absence of complete freezing – is found by MD simulations on water embedded in nanoporous carbon.13
When retrieving MSDs from NSE decays at T > 180 K under the Gaussian approximation, the A1 slow component (corresponding to the “water-sleeve” contribution to relaxation) is subdiffusive, undergoing a 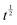 -to-
-to-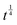 dynamic slowing down at t ∼ 0.04 ns, consistent with eqn (5) for τcross if one sets the average CNT-diameter of 1.4 nm as d. This somehow resembles a deviation of the outer shell from a Rouse-like dynamics (regime I) as established by eqn (6), followed by the onset of a regime mimicking a local reptation (regime II) as established by eqn (7), due to the impact from radial constraints (nanotube diameter). A corroboration to this scenario could be found in MD simulations on TIP4P/2005 water confined in (10,10) hydrophobic tubes recovering a double-layer arrangement in which the two components move as a global structure due to the repulsive nature of the water–wall interaction;46 as well as in experimental dielectric measurements, which deduce large-scale molecular clustering and coordinated motion of nanotube water inside 1.4 nm CNTs from unusually high values of the Kirkwood factor g.8 As reported in Table 4, this interpretation is also suggested by the estimated parameter
dynamic slowing down at t ∼ 0.04 ns, consistent with eqn (5) for τcross if one sets the average CNT-diameter of 1.4 nm as d. This somehow resembles a deviation of the outer shell from a Rouse-like dynamics (regime I) as established by eqn (6), followed by the onset of a regime mimicking a local reptation (regime II) as established by eqn (7), due to the impact from radial constraints (nanotube diameter). A corroboration to this scenario could be found in MD simulations on TIP4P/2005 water confined in (10,10) hydrophobic tubes recovering a double-layer arrangement in which the two components move as a global structure due to the repulsive nature of the water–wall interaction;46 as well as in experimental dielectric measurements, which deduce large-scale molecular clustering and coordinated motion of nanotube water inside 1.4 nm CNTs from unusually high values of the Kirkwood factor g.8 As reported in Table 4, this interpretation is also suggested by the estimated parameter 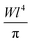 , which scales quasi-linearly with temperature in regime I like common homopolymers,34 but suddenly goes “flat” in regime II, in some sort of a saturation phenomenon.
, which scales quasi-linearly with temperature in regime I like common homopolymers,34 but suddenly goes “flat” in regime II, in some sort of a saturation phenomenon.
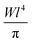 from asymptotic fits of MSD data shown in Fig. 5, entering the average CNT-diameter as d
from asymptotic fits of MSD data shown in Fig. 5, entering the average CNT-diameter as d
No safe considerations can be recovered from NSE data below 180 K, since the experimental window is too narrow with respect to the relaxation time scale at such temperatures. Yet, the outburst of τ1 at very low temperature is not incompatible with the scenario reported in the literature9,10 after the formation of the external ice shell.
6 Conclusions
In performing the first experimental incoherent NSE investigation of water dynamics in quasi-1D hydrophobic nanoconfinement (d ∼ 1.4 nm) at the ns time scale, we have collected evidence of a peculiar diffusional behavior of the outer sleeve, which unexpectedly seems to fit the theoretical framework originally developed to describe the segmental dynamics of linear polymers in a matrix.Indeed, while water molecules belonging to the central chain are plausibly subject to an axial potential for symmetry reasons, those included in the external shell experience transverse interactions in a similar way as that occurring in Edward's tube for topologically entangled rigid rods.47 This seemingly causes the diffusional dynamics to be much more influenced by wall– than bead–bead interactions, thus imitating a reptation-like time dependence.
Additional NSE experiments on H2O- and D2O-hydrated SWCNT samples, spanning a large range of nanometric diameters (0.7–2 nm) over a large range of temperatures, would be desirable in order to better characterize the impact of tube diameter on water arrangement and transport, as well as to assess whether coherent dynamics is able to confirm the reptation-like scenario envisaged for the incoherent counterpart.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank the Institut Laue Langevin for the allocation of beam time (DOI:10.5291/ILL-DATA.6.07.17) and the Partnership for Soft Condensed Matter for the use of the laboratories.Notes and references
- P. Agre, Proc. Am. Thorac. Soc., 2006, 3, 5–13 CrossRef CAS PubMed.
- J. K. Carson, V. Gonzalez-Quinones, D. V. Murphy, C. Hinz, J. A. Shaw and D. B. Gleeson, Appl. Environ. Microbiol., 2010, 76, 3936–3942 CrossRef CAS PubMed.
- J. Sam-Marcus, E. Enaworu, O. J. Rotimi and I. Seteyeobot, J. Pet. Explor. Prod. Technol., 2018, 8, 1009–1015 CrossRef CAS.
- S. F. Liu, S. Lin and T. M. Swager, ACS Sens., 2016, 1, 354–357 CrossRef CAS PubMed.
- R. Das, M. Eaqub Ali, S. B. A. Hamid, S. Ramakrishna and Z. Z. Chowdhury, Desalination, 2014, 336, 97–109 CrossRef CAS.
- S. Reich, C. Thompson and J. Maultzsch, Carbon Nanotubes: Basic Concepts and Physical Properties, Wiley-VCH, Berlin, 2004 Search PubMed.
- S. Cambré, B. Schoeters, S. Luyckx, E. Goovaerts and W. Wenseleers, Phys. Rev. Lett., 2010, 104, 207401 CrossRef PubMed.
- C. Cametti, F. De Luca and A. Parmentier, J. Chem. Phys., 2012, 137, 094908 CrossRef CAS PubMed.
- G. Briganti, G. Rogati, A. Parmentier, M. Maccarini and F. De Luca, Sci. Rep., 2017, 7, 45021 CrossRef CAS PubMed.
- A. I. Kolesnikov, J.-M. Zanotti, C.-K. Loong, P. Thiyagarajan, A. P. Moravsky, R. O. Loutfy and C. J. Burnham, Phys. Rev. Lett., 2004, 93, 035503 CrossRef PubMed.
- J. Hassan, G. Diamantopoulos, L. Gkoura, M. Karagianni, S. Alhassan, S. V. Kumar, M. S. Katsiotis, T. Karagiannis, M. Fardis, N. Panopoulos, H. J. Kim, M. Beazi-Katsioti and G. Papavassiliou, J. Phys. Chem. C, 2018, 122, 10600–10606 CrossRef CAS.
- A. Alexiadis and S. Kassinos, Mol. Simul., 2008, 34, 671–678 CrossRef CAS.
- Y. He, K.-I. Nomura, R. K. Kalia, A. Nakano and P. Vashishta, Phys. Rev. Mater., 2018, 2, 115605 CrossRef CAS.
- Y. Maniwa, H. Kataura, M. Abe, S. Suzuki, Y. Achiba, H. Kira and K. Matsuda, J. Phys. Soc. Jpn., 2002, 71, 2863–2866 CrossRef CAS.
- A. Das, S. Jayanthi, H. S. Deepak, K. V. Ramanathan, A. Kumar, C. Dasgupta and A. K. Sood, ACS Nano, 2010, 4, 1687–1695 CrossRef CAS PubMed.
- F. Mezei, Z. Physik, 1972, 255, 146–160 CrossRef CAS.
- Neutron Spin-Echo, ed. F. Mezei, Springer-Verlag, Heidelberg, 1980, vol. 128 Search PubMed.
- F. Mezei, C. Pappas and T. Gutberlet, Neutron Spin Echo Spectroscopy; Basics, Trends and Applications, Springer-Verlag, New York, 2003 Search PubMed.
- K. Lagrené, J.-M. Zanotti, M. Daoud, B. Farago and P. Judeinstein, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81, 060801(R) CrossRef PubMed.
- M. Krutyeva, S. Pasini, M. Monkenbusch, J. Allgaier, J. Maiz, C. Mijangos, B. Hartmann-Azanza, M. Steinhart, N. Jalarvo and D. Richter, J. Chem. Phys., 2017, 146, 203306 CrossRef CAS PubMed.
- O. Holderer, P. Zolnierczuk, S. Pasini, L. Stingaciu and M. Monkenbusch, Phys. B, 2019, 562, 9–12 CrossRef CAS.
- M. E. Itkis, D. E. Perea, S. Niyogi, S. M. Rickard, M. A. Hamon, H. Hu, B. Zhao and R. C. Haddon, Nano Lett., 2003, 3, 309–314 CrossRef CAS.
- Measurement Issues in Single Wall Carbon Nanotubes, ed. S. Freimanet al., NIST, 2008, vol. 960.19 Search PubMed.
- L. van Hove, Phys. Rev., 1954, 95, 249 CrossRef CAS.
- A. Wischnevski, M. Monkenbusch, L. Willner, D. Richter and G. Káli, Phys. Rev. Lett., 2003, 90, 058302 CrossRef PubMed.
- E. Mamontov, A. Faraone, E. W. Hagaman, K. S. Han and E. Fratini, J. Phys. Chem. B, 2010, 114, 16737–16743 CrossRef CAS PubMed.
- M. Karlsson, P. Fouquet, I. Ahmed and M. Maccarini, J. Phys. Chem. C, 2010, 114, 3292–3296 CrossRef CAS.
- R. M. Moon, T. Riste and W. C. Koehler, Phys. Rev., 1969, 181, 920–931 CrossRef CAS.
- R. Kimmich, Chem. Phys., 2002, 284, 253–285 CrossRef CAS.
- K. Hahn, J. Kaerger and V. Kukla, Phys. Rev. Lett., 1996, 76, 2762 CrossRef CAS PubMed.
- L. Lizana, T. Ambjoernsson, A. Taloni, E. Barkai and M. A. Lomholt, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81, 051118 CrossRef PubMed.
- P. G. de Gennes, J. Chem. Phys., 1971, 55, 572 CrossRef.
- M. Doi and S. F. Edwards, J. Chem. Soc., Faraday Trans. 2, 1978, 1789–1801 RSC.
- D. Richter, M. Monkenbusch, A. Arbe and J. Colmenero, Neutron Spin Echo in Polymer Systems, Springer-Verlag, Berlin Heidelberg, 2005, vol. 174 Search PubMed.
- D. Noferini, M. M. Koza, P. Fouquet, G. J. Nilsen, M. C. Kemei, S. M. H. Rahman, M. Maccarini, S. Eriksson and M. Karlsson, J. Phys. Chem. C, 2016, 120, 13963–13969 CrossRef CAS.
- J. Wuttke and W. Petry, J. Chem. Phys., 1996, 105, 5177–5182 CrossRef CAS.
- L. Liu, A. Faraone, C.-Y. Mou, C.-W. Yen and S.-H. Chen, J. Phys.: Condens. Matter, 2004, 16, S5403–S5436 CrossRef CAS.
- P. Gallo, M. Rovere and S.-H. Chen, J. Phys. Chem. Lett., 2010, 1, 729–733 CrossRef CAS.
- J. O. Berger and W. H. Jefferys, J. It. Statist. Soc., 1992, 1, 17–32 CrossRef.
- W. H. Jefferys and J. O. Berger, Am. Sci., 1992, 80, 64–72 Search PubMed.
- Information Theory, Inference and Learning Algorithms, ed. D. J. C. MacKay, Cambridge University Press, Cambridge, 2003 Search PubMed.
- A. De Francesco, E. Guarini, U. Bafile, F. Formisano and L. Scaccia, Phys. Rev. E, 2016, 94, 023305 CrossRef CAS PubMed.
- G. D’Agostini, Rep. Prog. Phys., 2003, 66, 1383 CrossRef.
- A. De Francesco, L. Scaccia, R. Bruce Lennox, E. Guarini, U. Bafile, P. Falus and M. Maccarini, Phys. Rev. E, 2019, 99, 052504 CrossRef CAS PubMed.
- H. Kyakuno, M. Fukasawa, R. Ichimura, K. Matsuda, Y. Nakai, Y. Miyata, T. Saito and Y. Maniwa, J. Chem. Phys., 2016, 145, 064514 CrossRef.
- M. H. Koehler, J. R. Bordin, L. B. da Silva and M. C. Barbosa, Phys. Chem. Chem. Phys., 2017, 19, 12921–12927 RSC.
- D. M. Sussman and K. S. Schweizer, Phys. Rev. Lett., 2011, 107, 078102 CrossRef PubMed.
| This journal is © the Owner Societies 2019 |