The influence of silica surface groups on the Li-ion conductivity of LiBH₄/SiO₂ nanocomposites

Abstract

Lithium borohydride is a promising lithium ion conductor for all-solid-state batteries. However, the compound only exhibits high ionic conductivity at elevated temperatures, typically above 110 °C. It was shown that the addition of oxides such as silica or alumina increases the room temperature ionic conductivity by 3 orders of magnitude. The origin of this remarkable effect is not yet well understood. Here, we investigate the influence of oxide surface groups on the ionic conductivity of LiBH₄/SiO₂ nanocomposites. We systematically varied the density and nature of the surface groups of mesoporous silica by heat treatment at different temperatures, or surface functionalization, and subsequently prepared LiBH₄/SiO₂ nanocomposites by melt infiltration. The ionic conductivity is strongly influenced by the heat treatment temperature, hence the density of the free surface silanol groups. Replacing some of the silanol groups with hydrophobic surface groups resulted in an order of magnitude reduction of the room temperature ionic conductivity, suggesting that their presence is crucial to obtain high ionic conductivity in the nanocomposites. This systematic study and insight provide a basis for further exploration of the impact of surface groups, and for the rational design of novel solid-state nanocomposite electrolytes via interface engineering.

---

Introduction

Solid-state lithium ion conductors are crucial to realize all-solid-state rechargeable batteries.^1–5 This next generation batteries promises to be safer than current Li-ion batteries due to the replacement of the organic liquid based electrolytes with solid electrolytes. The flammability and volatility of the organic compounds in the liquid electrolytes are major concerns in battery safety. In current Li-ion batteries, graphite is the typical anode and the cathode is composed of relatively heavy and expensive transition metal oxide materials such as LiCoO₂. The use of high energy density electrode materials such as Li metal as the anode and sulfur as the cathode could lead to new battery types with energy densities up to 10 times higher than the current Li-ion batteries.^6–10 However, the reactivity of metallic Li with liquid/organic-based electrolytes, and the dissolution and shuttling of lithium-sulfide intermediates in these electrolytes, prevent them from being used for this new type of batteries. On the other hand, most solid-state lithium ion conductors should prevent the sulfur shuttle. This has led to a significant interest in solid-state ionic conductors.

Lithium-containing complex hydrides such as LiBH₄, LiNH₂ and Li₂B₁₂H₁₂ have emerged about a decade ago as a new class of promising solid-state electrolytes.^11–13 For example, LiBH₄ exhibits high Li-ion conductivities (up to 10⁻³ S cm⁻¹ around 115 °C) and good electrochemical stability. Unfortunately, these high ionic conductivities only occur if LiBH₄ has a hexagonal lattice structure, hence, above the structural phase transition (orthorhombic to hexagonal) occurring around 110 °C.¹¹ The Li-ion conduction is related to the formation of Frenkel-pair defects (Li⁺ vacancies combined with interstitial Li sites) with movement coupled to the rotation of the neighboring BH₄ units (the so called “paddle wheel mechanism”).^14–19 The increased number of Li⁺ vacancies and faster rotation of the BH₄ in the high temperature (hexagonal) phase gives rise to high ionic conductivities above 110 °C.

Partial ionic substitution, mostly with lithium halides, has been shown to improve the room temperature ionic conductivity of LiBH₄, via the stabilization of the high temperature polymorph to lower temperatures, from about 10⁻⁸ S cm⁻¹ to about 10⁻⁵ S cm⁻¹.^13,20–23 In addition, Takano et al. showed that partial hydration of LiBH₄ led to about 2 orders of magnitude increase in the room temperature ion conductivity.²⁴ However, the approaches mentioned above also lead to a reduction of the electrochemical and/or thermal stability of the compounds.^13,25,26

It was recently demonstrated that composites of LiBH₄ and metal oxides such as Al₂O₃ or SiO₂ exhibit high ionic conductivities at room temperature.^27,28 For example, confinement of LiBH₄ in a mesoporous silica (MCM-41) via melt infiltration²⁹ led to about three orders of magnitude increase in its room temperature conductivity (∼10⁻⁴ S cm⁻¹), while maintaining the good electrochemical stability.^27,28 A similar increase in conductivity was reported for LiBH₄/SiO₂ and LiBH₄/Al₂O₃ composites prepared by mechanical milling.^30–32

Nanoconfinement of LiBH₄ was originally motivated by the idea that it could stabilize the high temperature (conductive) phase.³³ However, the high room temperature ionic conductivity was also observed in nanocomposites in which the structural phase transition took place well above room temperature. Reaction between LiBH₄ and silica to form stable lithium silicates and boron is thermodynamically favourable under melt-infiltration conditions. However, this reaction is supressed by applying hydrogen pressure during melt infiltration.²⁹ Lithium silicates are known to exhibit low ionic conductivities at room temperature,³⁴ hence the formation of highly conductive lithium silicates is unlikely to explain the observed increase in the conductivity. Also NMR and neutron scattering proved the presence of intact, highly mobile Li⁺ and BH₄⁻ units for LiBH₄ nanoconfined in silica and carbon scaffolds^35–38 as well as in LiBH₄/SiO₂ composites prepared by ball milling.³⁹ It is currently believed that the increased ionic conductivity is related to interface effects, such as the presence of a space charge layer and/or (partial) reaction at the LiBH₄/metal oxide interface causing a different LiBH₄ structure or stoichiometry.^{30–32,39–43}

The space-charge effect is the accumulation or depletion of mobile charge carriers near an interface between two materials with different Fermi levels, due to a local electric field.^42,44–46 This effect is held responsible for the high ionic conductivity of binary mixtures of inorganic ion conductors such as AgX or LiX (X = F, Cl, Br, I) and non-conducting materials such as metal oxides and ceramics.^43,45–50 Space charge effects are reported to lead to a remarkable increase in the proton conductivity of solid acids, such as CsHSO₄, when mixed with metal oxides.^51–53 As far as we are aware, the impact of space charge effects on the ionic conductivity of complex hydrides/metal oxide composites has not yet been proven.^30–32

Another effect that could play a role is reaction between LiBH₄ and the metal oxide surface. Although it has been shown that reaction to form stable silicates is kinetically limited by the presence of hydrogen during the synthesis of LiBH₄/SiO₂ nanocomposites, reaction is expected to be particularly favourable with reactive surface groups, such as hydroxyl groups. This could lead to the formation of highly defective LiBH₄ at the LiBH₄/oxide interface, thereby increasing the number of mobile Li ions.

Although it is not known what exactly causes the interface effect, it is clear that the LiBH₄ near the pore walls of a nanoscaffold material is clearly different from macrocrystalline LiBH₄. Evidence comes from nuclear magnetic resonance (NMR),^35,36,38,39 quasi-elastic neutron scattering (QENS)^36,37,39,54 and differential scanning calorimetry (DSC) measurements³³ on LiBH₄/C and LiBH₄/SiO₂ nanocomposites. These studies revealed that the LiBH₄ closer to carbon surface (carbon pore walls) exhibits higher Li⁺ and BH₄⁻ mobility than those at the centre of the pores and does not show a structural phase transition. Similarly, Blanchard et al. reported that only a fraction (∼10%) of the LiBH₄ in LiBH₄/SiO₂ nanocomposites (those at close proximity to the silica surface) exhibits very high Li-ion mobilities, whereas the rest of the LiBH₄ have bulk-like ion mobility.³⁹ Recently, Choi et al. used a continuum percolation model to explain that the Li-ion conductivity at the LiBH₄/Al₂O₃ interface was about 105 times higher than for macrocrystalline LiBH₄ due to a lowered activation barrier for Li⁺ mobility.³² They reported the presence of B–O bonds in the ball milled LiBH₄/Al₂O₃ composites, which was attributed to a chemical reaction between LiBH₄ and Al₂O₃ at the interface due to the high energy ball milling.

It thus appears that interfacial effects are crucial to induce high ionic conductivity in LiBH₄/metal oxide nanocomposites at room temperature. An appealing approach to study the origin of interfacial effects is to alter the surface chemistry of the scaffold through surface functionalization or modification without changing any of the other parameters in the system. In this work, we present a detailed study of the effects of surface properties of mesoporous silica on the Li-ion conductivity of LiBH₄ subsequently confined by melt infiltration in this silica matrix. The nature and concentration of the silica surface groups were varied and had a strong influence on the ionic conductivity of the LiBH₄/SiO₂ nanocomposites.

Experimental

Silica scaffolds

Mesoporous silica (SBA-15) was used as the scaffold for the preparation of LiBH₄/silica composites. SBA-15 has long, hexagonally ordered mesopores with well-defined and tuneable pore diameters (5–15 nm), which are connected by micropores.^55,56 Three batches of SBA-15 were synthesized following the procedure by Zhao et al.⁵⁵ A mixture of poly(ethylene glycol)-block-poly(propylene glycol)-block-poly(ethylene glycol) (P123), hydrochloric acid and water was stirred at 35 °C until fully dissolved. Tetraethyl orthosilicate (TEOS) was added dropwise and the mixture was stirred at 40 °C for 24 h. The molar ratios were 0.015 : 5.2 : 129 : 1 for the P123 : HCl : H₂O : TEOS respectively. The mixture was heated to 80 (SiO₂-1) or 100 °C (SiO₂-2 and SiO₂-3) in a closed polypropylene bottle for 48 h, after which the solid precipitate was washed with water. The product was dried at 60 °C in air for at least 24 h, then at 120 °C for 8 h and subsequently calcined in air by increasing the temperature to 550 °C with a ramp of 1.2 °C min⁻¹ and kept at this temperature for 6 h. This procedure produced rod-shaped silica particles with a length of a few micrometres and a diameter of about 0.5 μm with the main mesopores running along the length of the particles (Fig. S1, ESI†).

The structural properties of the three batches of SBA-15 scaffolds were determined using N₂-physisorption. N₂-Physisorption isotherms were obtained at −196 °C on a Micromeritics TriStar Surface Area and Porosity Analyzer to determine the BET surface area and constant,⁵⁷ BJH pore size distribution,⁵⁸ total volume of pores at p/p₀ = 0.997 and t-plot micropore volume using the Harkins–Jura reference isotherm.⁵⁹ Fig. S2 (ESI†) gives an overview of the N₂ physisorption isotherms and pore size distributions of the three batches of SBA-15. Table S1 (ESI†) summarizes the pore volumes and pore sizes for the three batches of SBA-15, named SiO₂-1, SiO₂-2 and SiO₂-3. SiO₂-1 had a pore diameter of approximately 7 nm and a pore volume of 0.82 cm³ g⁻¹, while SiO₂-2 and SiO₂-3 had a larger pore diameter of 8.2 and 8.5 nm and a total pore volume of 0.99 and 0.91 cm³ g⁻¹ respectively.

An important parameter in this research are the different treatments applied to the silica scaffolds before preparation of the nanocomposites via melt infiltration of LiBH₄. The series SiO₂-1 was only used to measure the infrared spectra presented in Fig. 1. Series SiO₂-2 was used for the majority of the results presented, with focus on the influence of silica pre-treatment on the conductivity of the nanocomposites presented in this paper. Series SiO₂-3 was used to assess the reproducibility of the results, these latter measurements being performed in a different laboratory.

Fig. 1 Infrared spectra of LiBH₄ at 25 °C and 150 °C, mesoporous SiO₂-1 (SBA-15), and LiBH₄/SiO₂ nanocomposites SiO₂-1-300-50 and SiO₂-1-300-75 with 50 and 75% filling of the SiO₂ pores. The figure shows the effect of heating and nanoconfinement on the vibrational properties of LiBH₄.

A fraction of the SiO₂-2, was dried under a dynamic vacuum (approximately 1 mbar) at room temperature overnight, other fractions of SiO₂-2 and SiO₂-3 were dried in a glass reactor at 100 to 700 °C for 6 h under a flow of 30–40 mL min⁻¹ N₂ and a ramp of 5 °C min⁻¹. In addition, surface functionalization was performed on part of the SiO₂-3 batch by silylation with chlorotrimethylsilane. This was performed following the procedure of Sun et al.⁶⁰ For this, 1.5 g of SiO₂-2 was dried at 150 °C under vacuum for 24 h and suspended in dry toluene. 2 g of chlorotrimethylsilane was added dropwise to the suspension and refluxed at 80 °C for 15 h in N₂ atmosphere. The suspension was filtered, and solid product washed with ethanol. The silica was then dried at 120 °C and stored in an argon-atmosphere glovebox with H₂O and O₂ levels typically <1 ppm.

The silica surface group density and nature were characterized using thermogravimetric analysis (TGA) and diffuse reflectance infrared Fourier transform (DRIFT) spectroscopy. TGA measurements were performed on a PerkinElmer Pyris 1 TGA apparatus coupled to a Pfeiffer Omnistar quadrupole mass spectrometer. The samples were placed in sealed aluminium cups (in the glove box) and pierced shortly before the measurement to allow for gas exchange. During measurements the samples were under inert atmosphere (10 mL min⁻¹ argon flow). SBA-15 that was previously dried for 6 hrs at a certain temperature (room temperature, 100, 200, 300, 400 and 500 °C) was heated from room temperature to 550 °C at 5 °C min⁻¹ and kept at 550 °C for 30 minutes, while registering the mass loss, to measure which amount of silanol groups was left after these different heat pre-treatments. The mass loss was fully ascribed to the formation of water formed by condensation (and hence disappearance) of silanol groups. After cooling down to room temperature, the heating run was repeated to obtain a reference curve that was used to correct for buoyancy effects.

DRIFT spectra were measured on a Bruker tensor 37 or PerkinElmer Frontier FT-IR spectrometer in a closed, argon-filled, Harrick Praying Mantis reaction chamber at room temperature. Background spectra (without sample) were acquired before the measurements and subtracted from the measured spectra of the sample.

Preparation of the nanocomposites

Preparation of the nanocomposites was achieved by melt-infiltration as described earlier.²⁹ The appropriate amount of either SiO₂-1, SiO₂-2 or SiO₂-3 was mixed with LiBH₄ (Sigma Aldrich, 95% pure), and the mixtures were transferred to borosilicate glass vials and placed in a stainless steel autoclave. The added amount of LiBH₄ corresponded to 50, 75, 100, 115 or 130% of the silica pore volume depending on the characterization or measurement required. This corresponded to LiBH₄ weight loadings between 21 and 46%. Approximately 50 bar H₂ gas was added and the autoclave was heated to 300 °C using a ramp of 3 °C min⁻¹ and allowed to stay at this temperature for 30 min, at a final hydrogen pressure of about 100 bar. After cooling down, the hydrogen was evacuated. The samples were stored in the argon-filled glove box. An overview of all nanocomposite samples that are discussed in this paper is given in Table S2 (ESI†). Sample names included the name of the silica scaffold that was used, its pretreatment, and the amount of LiBH₄ that was added expressed as vol% with respect to the SiO₂ pore volume. For instance, SiO₂-2-600-130 means that the nanocomposite was based on the second batch of SBA-15 scaffold, was pre-treated at 600 °C before the melt infiltration with an amount of LiBH₄ corresponding to 130% of the SiO₂ pore volume (hence in this case 46 wt% LiBH₄).

Spectroscopic investigation of the nanocomposites

Temperature dependent FTIR experiments were performed with a Biorad Excalibur Instrument equipped with a Specac Golden Gate heatable ATR set-up. Powdered samples were pressed between diamond crystal and bridge clamped sapphire anvil to ensure optimum optical contact of the powder. Samples were loaded on the ATR setup in N₂ atmosphere. The spectral resolution was set to 1 cm⁻¹. These measurements were performed with the sample set based on SiO₂-1 (7 nm pores, 744 m² g⁻¹, pore volume 0.82 cm³ g⁻¹) which was dried at 300 °C prior to preparation of the nanocomposites by melt infiltration.

Conductivity measurements

Pellets for impedance measurements were prepared by placing about 100–200 mg of the nanocomposite between two Li foils in a 13 mm evaluable pellet die set and pressing with 0.75 ton cm⁻². The final texture and density that are achieved influence the conductivity and are determined by parameters such as the pressure and time that it is applied and the mechanical properties of the sample. Pressing about 100–200 mg of nanocomposite gave a sample thickness of about 1.5–3.0 mm (excluding the lithium foils). Using the mass and dimensions of the pellets, the void fraction can be estimated, which varied between 30–37%, with nominally an amount of LiBH₄ added corresponding to 130% of the silica pore volume (for the samples based on SiO₂-2 of the silica) or 115% (for nanocomposites based on SiO₂-3 silica).

Electrochemical Impedance Spectroscopy was performed both at the Technical University of Denmark in Denmark (“DTU”) and at Utrecht University in the Netherlands (“UU”). At DTU the measurements were performed on the SiO₂-3 based series using either a Princeton Applied Research Parstat 2273 or a Gamry Reference600 potentiostat. Measurement were performed in a custom-made measurement cell in a Büchi B-585 glass oven placed in an argon glovebox. A lithium foil (0.38 mm thick and 12 mm in diameter) was firmly placed on top of two stainless steel rods (for standard 13 mm pellet dies). Thereafter, about 200 mg of the nanocomposite was placed in between the two stainless rods in a pellet die. This was done in such a way that the sample was in contact with the two Li foils. Then, the sample was pressed using a pressure of 0.75 ton cm⁻² (1 ton) for about 1 minute. A 1.0 V rms modulated AC potential with frequencies from 1 MHz to 10 Hz was used for the EIS measurements. The samples were heated at 5 °C min⁻¹ to the desired temperature (from 30 to 130 °C in steps of 10 °C) and allowed to dwell for ∼45 minutes at this temperature (for equilibration) before measurement. The sequence was repeated during cooling, and good agreement was found between the data measured on heating and cooling. Next to the samples from the SiO₂-3 series, also a few samples from the SiO₂-2-series were measured at DTU to check reproducibility of the measurements.

At UU the measurements were performed on the SiO₂-2 based series using a Princeton Applied Research Parstat 2273. The measurements were performed in a similar way as those at DTU; in a custom-made measurement cell in a Büchi B-585 glass oven that contained a sample with the thermocouple placed next to the sample, which was placed in an argon glovebox. A lithium foil (0.38 mm thick and 12 mm in diameter) was firmly placed on top of two stainless steel rods (for standard 13 mm pellet dies). Between 100 and 200 mg of the nanocomposite was placed between the two stainless rods in a pellet die. This was done in such a way that the sample was in contact with the Li foil. After that, the sample was pressed using a pressure of 0.75 ton cm⁻² (1 ton). A 20 mV rms modulated AC potential with frequencies from 1 MHz to 1 Hz was used for the EIS measurements. The samples were heated at 5 °C min⁻¹ to the desired temperature (30–130 °C) and allowed to dwell for ∼45 minutes at this temperature (for equilibration) before measurement. During cooling no measurement points were taken, hence for the measurements at UU the conductivity values mentioned are those measured upon heating only.

A single, slightly depressed semicircle was observed in all cases in the Nyquist plots. The data were fitted using an equivalent circuit consisting of a resistance and a constant phase element. The intersection of the fitted semicircle with the Z′ axis was assumed to represent the electrolyte resistance R only, and this value was used to calculate the conductivity σ of the nanocomposites using the known thickness t and geometric surface area A of these samples, excluding the lithium foil, via σ = t/(AR).

Analysis of the degree of pore filling with LiBH₄

The efficiency of the melt-infiltration was determined quantitatively based on physisorption, and differential scanning calorimetry (DSC) measurements, based on a procedure described in literature.³⁰ This series of experiments was based on the SBA-15 batch SiO₂-2, and the amount of LiBH₄ used corresponded to the pore volume of the SiO₂, i.e., an expected pore filling of 100%. Physisorption was performed as described earlier. To estimate the degree of pore filling, the total pore volume of the nanocomposite per gram of SiO₂ was subtracted from that of the pure SBA-15 prior to the melt infiltration of LiBH₄.

DSC measurements were performed in a Mettler Toledo high pressure differential scanning calorimeter (HP DSC1). About 2 to 20 mg of the nanocomposites was placed in a pierced 40 μL aluminum pan. This was done in an argon filled atmosphere glovebox but minor exposure to air might have occurred during transfer of the sample to the equipment. The measurements were performed under 2 bar Ar at a constant flow of 10 mL min⁻¹ and the data were recorded while heating and (or cooling) the sample between 30 °C and 150 °C at a heating rate of 5 °C min⁻¹. Each measurement was repeated 2–3 times to check for reproducibility. The thermograms were processed with STARe software and the enthalpy for the structural phase transition of LiBH₄ was determined from the integral of the phase transition peak. The confined fraction of LiBH₄ was determined by comparing the experimental enthalpy of the phase transition of the bulk (macrocrystalline) LiBH₄ to those of the nanocomposites measured under the same conditions. The amount of confined phase is the total amount of LiBH₄ in the sample minus the amount of macrocrystalline, hence extraporous LiBH₄. When the extraporous LiBH₄ peak was not observed, all the LiBH₄ was assumed to be confined. The error of the measured enthalpy was in the range of 6–8% as determined earlier.²⁸

Results and discussion

Vibrational spectroscopy of LiBH₄/SiO₂ nanocomposites

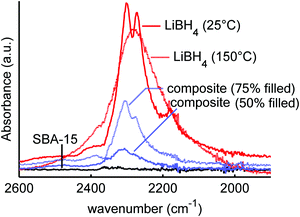
A suitable technique to study the (interaction between) LiBH₄ and SiO₂ is vibrational spectroscopy, such as infrared or Raman spectroscopy. Fig. 1 shows the infrared spectra of macrocrystalline LiBH₄ at 25 and 150 °C, and those of LiBH₄/SiO₂ nanocomposites SiO₂-1-300-50 and SiO₂-1-300-75 containing an amount of LiBH₄ corresponding to 50 or 75% (theoretical) filling of the silica pores. As a reference SiO₂-1-300 is included as well, although SiO₂ does not absorb radiation in this spectral region. The spectrum of LiBH₄ at 25 °C (the orthorhombic phase) shows a strong absorption around 2300 cm⁻¹, which is assigned to the B–H stretching vibrations of the BH₄⁻ unit. For the isolated BH₄⁻ unit this is a triple degenerate peak, but splitting and shoulders are observed due to the Fermi resonances.^61–63 The spectrum of LiBH₄ at 150 °C (hexagonal phase) shows a single broad peak due to the much higher mobility of the BH₄⁻ above the phase transition temperature. Also, the bending modes around 1100 cm⁻¹ show sharp features, characteristic for the orthorhombic LiBH₄ phase at 25 °C and a much broadened, featureless peak at 150 °C.

The spectra of a LiBH₄/SiO₂ nanocomposite with 75% pore filling (corresponding to 32 wt% LiBH₄) contains characteristic spectral features of LiBH₄ in the low temperature phase. It is interesting to note that the bands for the composite are slightly shifted to higher frequencies (about 4 cm⁻¹) with respect to pure LiBH₄, suggesting a compression by about 0.3–0.5 GPa in the composite, considering the reported pressure dependence of Raman bands for LiBH₄.⁶⁴ This low temperature LiBH₄ feature is superimposed on a broader peak that corresponds to the high temperature phase of LiBH₄. However, for the nanocomposite with 50% filling of the silica pores (21 wt% LiBH₄), only a nearly featureless asymmetric peak is observed. Interestingly, this peak differs from both the high and low temperature phase of LiBH₄ suggesting that the structure of the nanoconfined LiBH₄ is different from either of these two phases. Note that at 50% pore filling, almost all the LiBH₄ is confined in the pores, hence bulk-like behaviour is not expected. This result is in line with previous XRD, DSC, NMR and neutron scattering studies indicating the presence of non-crystalline LiBH₄ phase in the nanopores, although the nature and exact properties of this phase are not yet well understood.^{33,35–37,39,54}

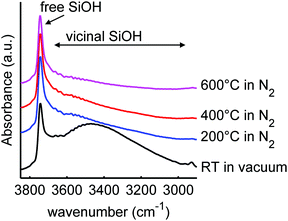
It is also interesting to investigate the effect of LiBH₄ infiltration on the silica scaffold, focussing on the possible surface or interface reactions. It has been shown before that complete reaction of the LiBH₄ and SiO₂ does not occur under our melt infiltration conditions.²⁹ The infrared region between 2900 and 3850 cm⁻¹ contains the vibrational peaks of the silanol groups. Fig. 2 shows the infrared spectra of SiO₂-3-120 (dried at 120 °C), LiBH₄, a physical mixture of the two (40 wt% LiBH₄) and the corresponding nanocomposite SiO₂-3-120-115 after melt-infiltration. For the SiO₂, a broad band between 3000–3700 cm⁻¹ is observed, which represents the hydrogen bound (vicinal) silanol groups and physisorbed water. The sharp absorption peak around 3744 cm⁻¹ is ascribed to “free” silanol groups, which means OH groups bound to a single silicon atom. This category comprises both the isolated silanol groups (a single OH group attached to a silicon atom that is connected via oxygen bonds to three other silicon atoms in SiO₂ structure) and geminal silanol groups (where two OH groups are connected to the same Si atom). In the LiBH₄ spectrum the only vibrations visible are attributed to surface contamination, most likely adsorbed water bound to BH₄⁻ units, or a LiBH₄ hydrate phase. Similar vibrations are observed for instance for NaBH₄·2H₂O.⁶⁵ Note that due to the penetration depth of DRIFT it can be very sensitive to weak absorptions, so the amount of hydrates can still be small compared to the amount of LiBH₄ present.

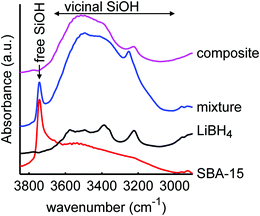Fig. 2 Diffuse reflectance infrared spectra of mesoporous SiO₂-3-120 (dried at 120 °C), LiBH₄, a physical mixture of both (40 wt% LiBH₄) and a spectrum of the corresponding composite after melt infiltration (SiO₂-3-120-115), showing the O–H stretching spectral region of SiO₂. The spectrum of SiO₂ consists of a narrow peak due to isolated and germinal silanol groups (3744 cm⁻¹) and a broad peak due to vicinal silanol groups (3000–3700 cm⁻¹). The peaks in the spectrum of LiBH₄ are attributed to impurities.⁶⁶ After melt-infiltration, the peak of free silanol groups is absent. An offset in absorbance was applied for clarity.

The spectrum of the physical mixture of 40 wt% LiBH₄/SiO₂ shows that the silanol groups, especially the isolated ones, are still present but the peaks observed in the pure LiBH₄ overlap with the broad peak of the vicinal silanol groups, hence not clearly visible. The significant change observed (in the band region corresponding to the vicinal silanol groups) after physically mixing with the LiBH₄ suggests that the mixing process (using mortar and pestle) might have induced some changes in the silica. This might also be explained by the change in total transmittance and reflectance due to the presence of the LiBH₄. Interestingly, after melt infiltration the vibration corresponding to isolated and geminal silanol groups (3744 cm⁻¹) is no longer visible in the spectrum. This suggests that they have been removed by a reaction with the molten LiBH₄ or the formation of new hydrogen bonds with this silanol groups, for instance, LiB₄O₇ or other oxidized lithium boron species. Note that the intensity of the “free” and “bound” OH vibrations is not easily relatable to their concentration, as the extinction coefficient of bound OH is larger.

Varying the silanol concentration

We heated SiO₂-2 to different temperatures in order to vary the ratio and concentration of the various types of silanol groups. The surface area of the mesoporous SiO₂ remained 730-750 m² g⁻¹, the meso- and micropore volumes 0.8 and 0.1 mL g⁻¹ respectively for the series based on SiO₂-2, and also the pore size did not change upon heat treatment (Table S3, ESI†). This is in good agreement with earlier reports that the porous structure of SBA-15 is stable in air at least up to 700 °C.^67–69 However, it is interesting to note that the BET constant, which is a direct measure for the strength of the interaction between N₂ and the SiO₂ surface, steadily decreased upon higher temperature treatment, from 173 for 100 °C drying to 129 for heat treatment at 600 °C (see Table S2, ESI†). This is a strong indication that the interaction strength of nitrogen on the surface and hence the SiO₂ surface was influenced by the heat treatment.⁷⁰ A similar series of heat treatment was applied to SiO₂-3.

Fig. 3 shows the infrared spectra of SBA-15 SiO₂-2 heated to various temperatures. In these spectra, the vibrations of the free (3744 cm⁻¹) and vicinal (3700–3000 cm⁻¹) silanol surface groups can be distinguished by their different stretching frequencies and peak width. The broad band due to vicinal silanol groups (3700–3000 cm⁻¹) (which also comprises the signal of physisorbed water on these groups) decreases drastically after drying at 200 °C. This means that at this temperature most of the physisorbed water is removed, and some of the vicinal silanol groups have condensed to form Si–O–Si bonds. Further heating to 600 °C gradually removed the remaining silanol groups vibrating in this frequency range. In contrast, the peak of the isolated and geminal silanol groups at 3744 cm⁻¹ hardly changes. The isolated silanol groups, of limited mobility, are too far apart from each other to react, while the geminal silanol groups, bound to the same silicon atom, are too close and in unfavourable position to react. Hence the fact that these groups stay largely present and intact is in line with observations in literature, where condensation of these silanol groups occurs only at temperatures well above 600 °C.^69,71,72

Fig. 3 Diffuse reflectance infrared spectra of sample SiO₂-2, before and after heating to the stated temperatures for 6 h in N₂ flow (or vacuum for the RT drying). The peaks correspond to isolated and geminal SiO–H stretching at 3744 cm⁻¹ and vicinal SiO–H stretching and physisorbed water at 3700–3000 cm⁻¹. An offset in absorbance was applied for clarity.

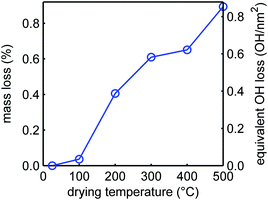
Thermogravimetric analysis allows quantification of the mass loss upon heating, which can be fully ascribed to the loss of water that is either physisorbed on the silica or from condensation of the silanols.⁷¹ In Fig. 4, the mass loss of the silica samples is plotted as a function of temperature. There is a rather steep mass loss between 100 and 200 °C, which is in good agreement with the IR experimental results showing a large loss of the vicinal silanol groups in this temperature range (Fig. 3), and also with literature which reported that condensation of these groups occurs quite readily.^68,69,71,72 For every two silanol groups that condensate, one molecule of water is released. We cannot exclude that a small amount of physisorbed water was still present after drying under vacuum for 12 h at room temperature, but if we neglect this, the mass loss can be converted into a change in silanol density (right axis in Fig. 3). Upon further heating, the mass loss is very gradual and limited, but above 400 °C the mass loss becomes more pronounced again. A density of 3.2 silanol groups per nm² is reported for a fully hydroxylated SBA-15 surface.⁷³ Hence only a quarter of the silanol surface groups, predominantly vicinal silanol groups, are removed by heating up to 500 °C. This also implies that it is not simply the heat treatment during melt infiltration (at 300 °C) that explain the disappearance of the free silanol groups (Fig. 2), but that this must rather be due to reaction or interaction with the LiBH₄ or oxidized species formed.

Fig. 4 Relative mass losses of SiO₂-2 SBA-15 upon drying for 6 h in nitrogen flow at the denoted temperatures, relative to silica dried under vacuum at room temperature. The corresponding decrease in silanol density is shown on the right axis.

Influence of scaffold heat treatment on nanocomposite conductivity

Fig. 5 shows the ionic conductivity of LiBH₄ infiltrated in SiO₂-2 dried at different temperatures and measured at UU. The conductivity ranged between 10⁻⁶ and 10⁻⁵ S cm⁻¹ at 30 °C, and clearly depended on the heat treatment of the SiO₂ prior to melt infiltration. A Nyquist plot of a representative EIS measurement at 30 °C for the sample treated at 300 °C (inset of Fig. 5) shows a single semicircle, suggesting a single process to be responsible for the conductivity. This is in accordance with an earlier report on LiBH₄/SiO₂ nanocomposites which indicates they are pure cation (Li⁺) conductor, with very high transference number (0.96).^27,28 Fig. S3 (ESI†) shows that the overall shape of the semicircle is also similar to that of bulk LiBH₄. The characteristic frequency (at which the imaginary component of the impedance reaches a maximum) is 62 kHz in this case, corresponding to a characteristic time for this conduction process in the order of 10⁻⁵ s. Below 110 °C, the impedance results can be fitted by straight lines in the Arrhenius plots. The apparent activation energies of the lithium ion motion are 0.56–0.62 eV (Table S4, ESI†), close to the value found for the high temperature phase of bulk LiBH₄ (0.53–0.56 eV)^11,19 or for LiBH₄ under high pressure.⁷⁴ Above 110 °C, the conductivity is slightly higher than expected from Arrhenius behaviour only. We attribute this to crystalline LiBH₄ outside the nanopores (as we added 130% of the silica pore volume) which becomes highly conductive above 110 °C.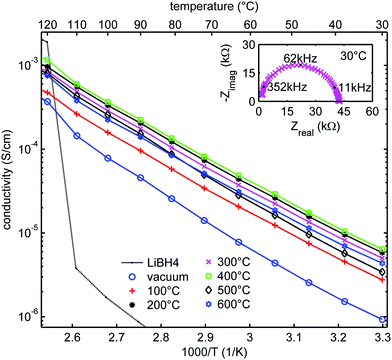

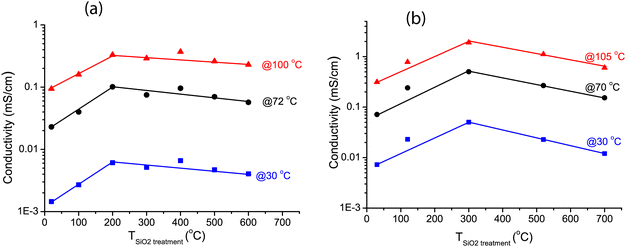
Fig. 5 Arrhenius plots of the ionic conductivity measured at UU as function of temperature for LiBH₄/SiO₂-2-130 nanocomposites (SBA-15 SiO₂-2 heat-treated at various temperatures in N₂ or at room temperature under vacuum after which a nanocomposite with LiBH₄ corresponding to 130% of the pore volume of the SiO₂ was prepared). Activation energies and pre-exponential factors were obtained from linear fits of the data points up to 100 °C (see Table S4, ESI†). Solid lines show the linear fits up to 110 °C, from which the conductivity of bulk LiBH₄ is shown as a reference. The inset shows the Nyquist plot of the impedance measurement at 30 °C for SiO₂-2-300-130, with a pellet thickness of 2.83 mm, corresponding to a conductivity of 5 × 10⁻⁶ S cm⁻¹.

Fig. 6a shows the conductivities of the LiBH₄/SiO₂-2-X-130 nanocomposites at 30, 72 and 100 °C (derived from the data in Fig. 5) as a function of the drying temperature of the SiO₂ matrix measured at UU. In all cases, the conductivity increased steeply if the SiO₂ pre-treatment temperature was raised from room temperature (vacuum drying) to 200 °C in a N₂ flow. The conductivity reached a maximum at 200–400 °C, and then decreased slightly with further increasing the pre-treatment temperature of the SiO₂ matrix. This trend is the same for all the conductivities measured between 30 and 100 °C, hence, it does not depend on the measurement temperature.

Fig. 6 Conductivities at 30, 70/72, 100 and 105 °C of LiBH₄/SiO₂ nanocomposites as function of the pretreatment temperature of the SiO₂ scaffold. For reproducibility two different SiO₂ were used. (a) series SiO₂-2-X-130 (b) series SiO₂-3-X-115. Also, the conductivities were measured in two different laboratories, at Utrecht University (a) and at the Technical University of Denmark (b). Lines were added to guide the eye.

The validity of this result was verified by testing another series of nanocomposites based on another series of SiO₂ scaffolds (SiO₂-3-X-115), measured at DTU. Arrhenius plots of the ionic conductivity and an overview of the activation energies and pre-exponential factors derived from it are given in Fig. S4 and Table S5 (ESI†). Overall the conductivities were higher than for the SiO₂-2 series. This was reflected in somewhat lower activation energies, ranging from 0.47 to 0.51 eV. Identical samples from the same batch showed up to a factor 2 difference in conductivity between measurements in the two different set-ups (at UU and DTU respectively) (Fig. S5, ESI†), explaining part of the difference. Other causes could be differences in the properties of the SiO₂ scaffolds and/or the fact that the volume fraction of LiBH₄ is different. These factors are the topic of present studies. However, while the absolute values differed, these two series show the same trend: that the drying temperature of the silica (prior to melt infiltration) has a clear impact on the ionic conductivity of LiBH₄/SiO₂ nanocomposites. Considering Fig. 6a and b, it can be inferred that the optimum drying temperature for the SiO₂ is between 200 and 400 °C.

Correlating these conductivity results to the earlier characterization with IR and TGA, we attribute the initial increase in the conductivity (as the drying temperature was increased from room temperature to 200–300 °C) to the removal of physisorbed water and some vicinal silanol groups. Careful inspection of the IR spectra in the 1500–2000 cm⁻¹ region (Fig. S6, ESI†) shows that indeed at 100 °C and under vacuum, some physisorbed water was still present. The water or reactive vicinal silanol groups probably react readily with LiBH₄. In this case LiBO₂, which has a very low ionic conductivity at room temperature,⁷⁵ is expected to form at the interface between the two compounds.^76,77 This explains the lower conductivities for these samples.

The conductivity was maximum around 200–400 °C, when all the physisorbed and most hydrogen-bound silanol groups were removed. A further increase in the SiO₂ treatment temperature led to a slight but significant decrease in the conductivity at all temperatures within 30–105 °C (below the phase transition temperature). From IR and TGA results we know that after heat treatment at 200 to 600 °C, free silanol groups were mainly present, and that, although a slight decrease in the density of the silanol groups was observed, the majority of the free groups remained present up to at least 600 °C. Note that the conductivities are still about three orders of magnitude higher than that of macrocrystalline LiBH₄. This means that the contact with these free silanol groups must have a great beneficial effect on the ionic conductivity.

From these results we can confirm a correlation between the density of free silanol groups and the ionic conductivity of the nanocomposites. A slight decrease in the free silanol group density coincides with a decrease in the conductivity of the samples. Mind that the conductivity of the nanocomposites based on SBA-15-type SiO₂ is generally lower than those based on MCM-41 as used in our previous study.²⁸ The origin of the difference is not yet clear but related to the differences in pore size and geometry (1D pores in MCM-41 versus interconnecting micropores in SBA-15), pore corrugations and the specific surface areas. We expect MCM-41 to exhibit similar effect as the SBA-15 upon drying, but SBA-15 is used here because of their larger pore sizes compared to MCM-41. This makes it possible for surface modification (via silylation) with less risk of blocking pores by the substituting groups, which would make it difficult to maintain a conducting pathway through the pores. Thus, SBA-15 is more suitable for varying the surface reactivity through surface functionalization, which will be discussed in a subsequent section.

Influence of heat treatment on the melt infiltration efficiency

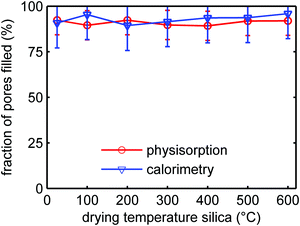
It is known that SiO₂ becomes less hydrophilic upon heating, due to the condensation of the silanol groups to form siloxane (bridged Si–O–Si) groups at the surface. From N₂-physisorption measurements (Table S3, ESI†) we observed that indeed the interaction strength with the SiO₂ surface in our series of samples decreased with increasing heat treatment. This could affect the wetting and consequently the filling of the SiO₂ pores with LiBH₄ during melt-infiltration. The ionic conductivity of the nanocomposites depends on the degree of pore filling.²⁸ Therefore, it is important to verify whether the effect of SiO₂ heat pre-treatment influences the efficiency of the LiBH₄ melt infiltration. We investigated the influence of the drying treatment on melt infiltration efficiency using two techniques. DSC was used to quantify the amount of remaining microcrystalline LiBH₄ after melt-infiltration, while with N₂-physisorption we quantified the SiO₂ pore volume loss during infiltration (for details see Experimental section and Fig. S7 and S8 in the ESI†).

Fig. 7 shows for the series SiO₂-2-X-100 the volume fractions of the silica pores that were filled by LiBH₄ after melt-infiltration. The SiO₂ had undergone different heat pre-treatments, and the amount of LiBH₄ used for these experiments corresponds to a theoretical pore filling of 100% (same volume as the total pore volume of the silica). It can be seen that ∼90% of the pores was filled with LiBH₄, irrespective of the treatment temperature of the SBA-15 within the temperature range studied. The results from physisorption and calorimetry are in excellent agreement. The fact that the pore filling is slightly lower than 100% might be due to compositional heterogeneities in the sample causing reduced contact between SiO₂ and LiBH₄ during melt infiltration. Also, it is likely that the density of non-crystalline, confined LiBH₄ is somewhat lower than that of macrocrystalline LiBH₄. In any case the results clearly show that the infiltration efficiency of LiBH₄ in the pores of SBA-15 is not significantly affected by the heat pre-treatment of the SiO₂, at least up to 600 °C. We can therefore conclude that the observed trend in conductivity as a function of SiO₂ pre-treatment temperature is not due to a reduction in the melt infiltration efficiency or the amount of LiBH₄ confined in the SiO₂ pores.

Fig. 7 Volume fraction of the pores of SiO₂-2-X-100 filled with LiBH₄ after melt infiltration as function of the treatment temperature of the SBA-15 prior to melt infiltration, derived from differential scanning calorimetry and N₂-physisorption. An amount of LiBH₄ corresponding to 100% of the silica pore volume was used for these experiments.

Importance of the free silanol groups for ionic conductivity

The results discussed until now point to a strong beneficial influence on the conductivity due to free silanol groups on the SiO₂ surface present prior to melt infiltration with LiBH₄. To verify whether it is really the chemical nature of these groups that makes the difference, an SBA-15 silica (SiO₂-3) was prepared wherein most of the silanol groups were replaced with trimethylsilyl (–Si(CH₃)₃) groups, a procedure known as silylation, lowering the surface energy of the silica. Diffuse reflectance infrared spectroscopy (Fig. S9, ESI†) confirmed that the silyl groups were successfully attached to the silica surface after silylation, with small amounts of silanol groups still remaining on the surface, in agreement with literature.⁶⁰

Table 1 lists the structural parameters of the pristine and modified SiO₂-3 scaffolds, the volume fraction of pore filling as well as the conductivity at 30 °C. As expected, the pore diameter slightly decreased upon silylation (an effect that would be more severe for silica materials such as MCM-41 which have smaller pores), and there was a modest decrease in specific surface area. Also, the degree of pore filling was lower for the silylated than for the unmodified SiO₂. These changes in physical properties could influence the Li-ion conduction. For instance it has been shown by Choi et al.^30,32 that the conductivity of nanocomposites roughly scales with the specific interface area of the scaffold material, which is about 20% lower due to silylation. Also, the degree of pore filling is expected to influence the ionic conductivity, but the impact is expected to be modest in this case. A 20% decrease in pore filling is not expected to break the interconnectivity in this 3D nanocomposite system. Also, if we assume that the conductivity is proportional to the density of the surface groups, hence the silica surface area, the 20% decrease in surface area after sylilation will lead to about 20% decrease in ionic conductivity at most. Table 1 also gives the conductivities (at 30 °C) of the nanocomposites with regular and silylated SBA-15. The conductivity of the nanocomposites was an order of magnitude lower if the isolated silanol groups were replaced by trimethylsilyl surface groups. This difference is much larger than what can reasonably be expected based on structural differences. This further implies that the presence of a high density of free silanol groups in the SiO₂ scaffold before melt infiltration is indeed crucial to obtain highly conductive LiBH₄/SiO₂ nanocomposites.

Table 1 Effect of silylation of SBA-15 on the pore diameter and surface area of the silica, the infiltration efficiency of LiBH₄ into this silica (via calorimetry), and the conductivity of the resulting nanocomposite at 30 °C. Mind that LiBH₄ loadings corresponding 115% of the total pore volumes were used

SBA-15				Nanocomposite
Functionalization	Pore diameter (nm)	Surface area (m^2 g^−1)	C BET	Pore filling (%)	Conductivity (S cm^−1)
None	8.5	741	122	90	3.5 × 10^−5
Trimethylsilyl	7.6	581	73	72	0.3 × 10^−5

---

Conclusions

We have studied the influence of SiO₂ surface groups on the ionic conductivity of LiBH₄ nanoconfined in mesoporous SiO₂. Infrared spectroscopy revealed that the free silanol groups disappeared after confinement of LiBH₄ in the SiO₂ nanopores, and that the nature of the LiBH₄ was changed by the nanoconfinement. A strong correlation was observed between the ionic conductivity of the nanocomposites and the nature and density of the surface groups of the SiO₂ scaffolds before melt infiltration. The conductivity increased if the SiO₂ was dried at temperatures of at least 200–300 °C prior to infiltration of LiBH₄. This was ascribed to the necessity to remove physisorbed water and reactive vicinal silanol groups, which lead to the formation of non-conductive phases near the LiBH₄/SiO₂ interface. On the other hand, SiO₂ pre-treatment at higher temperatures (above 400 °C) led to a gradual decrease in conductivity, concomitant with a decrease in the free silanol density on the SiO₂ scaffold surface. Replacing silanol groups by trimethylsilyl groups further strengthens the conclusion that the silanol groups play a key role in inducing high conductivities in these LiBH₄/SiO₂ composites. Hence, our work demonstrates that the chemical nature of the electrolyte/scaffold interface, and hence pre-treatment of the metal oxide before forming nanocomposites, is crucial for the lithium ion conductivity of the nanocomposites. This finding is likely applicable to other solid-state electrolytes based on nanocomposites of lithium/sodium containing complex hydrides and metal oxides.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors would like to thank Jan Willem de Rijk and Marjan Versluijs-Helder for their technical support. Peter Bramwell, Suzanne Verkleij and Pasi Paalanen are acknowledged for the nitrogen physisorption measurements, and Hans Meeldijk for the electron microscopy. This research was funded by NWO ECHO grant 712.015.005. PN has received funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation programme (ERC-2014-CoG No 648991). HH and MS received funding from the Swiss National Science Foundation (project 200021-169033).

References

1. A. Manthiram, X. Yu and S. Wang, Nat. Rev. Mater., 2017, 2, 16103.
2. J. C. Bachman, S. Muy, A. Grimaud, H.-H. Chang, N. Pour, S. F. Lux, O. Paschos, F. Maglia, S. Lupart, P. Lamp, L. Giordano and Y. Shao-Horn, Chem. Rev., 2015, 116, 140–162.
3. Y. Wang, W. D. Richards, S. P. Ong, L. J. Miara, J. C. Kim, Y. Mo and G. Ceder, Nat. Mater., 2015, 14, 1026–1031.
4. N. Kamaya, K. Homma, Y. Yamakawa, M. Hirayama, R. Kanno, M. Yonemura, T. Kamiyama, Y. Kato, S. Hama, K. Kawamoto and A. Mitsui, Nat. Mater., 2011, 10, 682.
5. J. Janek and W. G. Zeier, Nat. Energy, 2016, 1, 16141.
6. P. G. Bruce, S. A. Freunberger, L. J. Hardwick and J.-M. Tarascon, Nat. Mater., 2012, 11, 19–29.
7. P. Adelhelm, P. Hartmann, C. L. Bender, M. Busche, C. Eufinger and J. Janek, Beilstein J. Nanotechnol., 2015, 6, 1016–1055.
8. J. B. Goodenough and K.-S. Park, J. Am. Chem. Soc., 2013, 135, 1167–1176.
9. N. S. Choi, Z. Chen, S. A. Freunberger, X. Ji, Y. K. Sun, K. Amine, G. Yushin, L. F. Nazar, J. Cho and P. G. Bruce, Angew. Chem., Int. Ed., 2012, 51, 9994–10024.
10. G. Girishkumar, B. McCloskey, A. C. Luntz, S. Swanson and W. Wilcke, J. Phys. Chem. Lett., 2010, 1, 2193–2203.
11. M. Matsuo, Y. Nakamori, S.-i. Orimo, H. Maekawa and H. Takamura, Appl. Phys. Lett., 2007, 91, 224103.
12. P. E. de Jongh, D. Blanchard, M. Matsuo, T. J. Udovic and S. Orimo, Appl. Phys. A: Mater. Sci. Process., 2016, 122, 251.
13. A. Unemoto, M. Matsuo and S.-I. Orimo, Adv. Funct. Mater., 2014, 24, 2267–2279.
14. M. Jansen, Angew. Chem., Int. Ed. Engl., 1991, 30, 1547–1558.
15. W. Van Gool, Fast Ion Transport in Solids: Solid State Batteries and Devices, Elsevier Science Publishing Co. Inc., U.S., 1973, ISBN-10: 0720402239, ISBN-13: 9780720402230.
16. T. Ikeshoji, E. Tsuchida, T. Morishita, K. Ikeda, M. Matsuo, Y. Kawazoe and S.-I. Orimo, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 144301.
17. J. S. G. Myrdal, D. Blanchard, D. Sveinbjörnsson and T. Vegge, J. Phys. Chem. C, 2013, 117, 9084–9091.
18. P. C. Aeberhard, S. R. Williams, D. J. Evans, K. Refson and W. I. F. David, Phys. Rev. Lett., 2012, 108, 095901.
19. V. Epp and M. Wilkening, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 020301.
20. R. Miyazaki, T. Karahashi, N. Kumatani, Y. Noda, M. Ando, H. Takamura, M. Matsuo, S.-I. Orimo and H. Maekawa, Solid State Ionics, 2011, 192, 143–147.
21. M. Matsuo and S. i. Orimo, Adv. Energy Mater., 2011, 1, 161–172.
22. M. Matsuo, H. Takamura, H. Maekawa, H.-W. Li and S.-I. Orimo, Appl. Phys. Lett., 2009, 94, 084103.
23. M. B. Ley, D. B. Ravnsbæk, Y. Filinchuk, Y.-S. Lee, R. Janot, Y. W. Cho, J. Skibsted and T. R. Jensen, Chem. Mater., 2012, 24, 1654–1663.
24. A. Takano, I. Oikawa, A. Kamegawa and H. Takamura, Solid State Ionics, 2016, 285, 47–50.
25. D. Sveinbjörnsson, J. S. G. Myrdal, D. Blanchard, J. J. Bentzen, T. Hirata, M. B. Mogensen, P. Norby, S.-I. Orimo and T. Vegge, J. Phys. Chem. C, 2013, 117, 3249–3257.
26. D. Sveinbjörnsson, A. S. Christiansen, R. Viskinde, P. Norby and T. Vegge, J. Electrochem. Soc., 2014, 161, A1432–A1439.
27. S. Das, P. Ngene, P. Norby, T. Vegge, P. E. De Jongh and D. Blanchard, J. Electrochem. Soc., 2016, 163, A2029–A2034.
28. D. Blanchard, A. Nale, D. Sveinbjörnsson, T. M. Eggenhuisen, M. H. W. Verkuijlen, S. Suwarno, T. Vegge, A. P. M. Kentgens and P. E. de Jongh, Adv. Funct. Mater., 2015, 25, 184–192.
29. P. Ngene, P. Adelhelm, A. M. Beale, K. P. de Jong and P. E. de Jongh, J. Phys. Chem. C, 2010, 114, 6163–6168.
30. Y. S. Choi, Y.-S. Lee, K. H. Oh and Y. W. Cho, Phys. Chem. Chem. Phys., 2016, 18, 22540–22547.
31. Y.-S. Lee and Y. W. Cho, J. Phys. Chem. C, 2017, 121, 17773–17779.
32. Y. S. Choi, Y.-S. Lee, D.-J. Choi, K. H. Chae, K. H. Oh and Y. W. Cho, J. Phys. Chem. C, 2017, 121, 26209–26215.
33. S. Suwarno, P. Ngene, A. Nale, T. M. Eggenhuisen, M. Oschatz, J. P. Embs, A. Remhof and P. E. de Jongh, J. Phys. Chem. C, 2017, 121, 4197–4205.
34. S. Chatterjee, R. Maiti, S. K. Saha and D. Chakravorty, J. Phys. Chem. C, 2015, 120, 431–436.
35. M. H. W. Verkuijlen, P. Ngene, D. W. de Kort, C. Barre, A. Nale, E. R. van Eck, P. J. M. van Bentum, P. E. de Jongh and A. P. M. Kentgens, J. Phys. Chem. C, 2012, 116, 22169–22178.
36. N. Verdal, T. J. Udovic, J. J. Rush, X. Liu, E. H. Majzoub, J. J. Vajo and A. F. Gross, J. Phys. Chem. C, 2013, 117, 17983–17995.
37. A. Remhof, P. Mauron, A. Züttel, J. P. Embs, Z. Łodziana, A. J. Ramirez-Cuesta, P. Ngene and P. de Jongh, J. Phys. Chem. C, 2013, 117, 3789–3798.
38. D. T. Shane, R. L. Corey, C. McIntosh, L. H. Rayhel, R. C. Bowman Jr, J. J. Vajo, A. F. Gross and M. S. Conradi, J. Phys. Chem. C, 2010, 114, 4008–4014.
39. J. Lefevr, L. Cervini, J. M. Griffin and D. Blanchard, J. Phys. Chem. C, 2018, 122, 15264–15275.
40. S.-J. Hwang, H.-S. Lee, M. To, Y.-S. Lee, Y. W. Cho, H. Choi and C. Kim, J. Alloys Compd., 2015, 645, S316–S319.
41. J. Popovic, G. Hasegawa, I. Moudrakovski and J. Maier, J. Mater. Chem. A, 2016, 4, 7135–7140.
42. J. Maier, J. Phys. Chem. Solids, 1985, 46, 309–320.
43. C. Liang, J. Electrochem. Soc., 1973, 120, 1289–1292.
44. A. Tschöpe, Solid State Ionics, 2001, 139, 267–280.
45. N. Sata, K. Eberman, K. Eberl and J. Maier, Nature, 2000, 408, 946.
46. J. Maier, Prog. Solid State Chem., 1995, 23, 171–263.
47. K. Shahi and J. B. Wagner Jr, Solid State Ionics, 1981, 3–4, 295–299.
48. O. Nakamura and J. B. Goodenough, Solid State Ionics, 1982, 7, 119–123.
49. P. M. Skarstad, D. R. Merritt and B. B. Owens, Solid State Ionics, 1981, 3–4, 277–281.
50. G. Ardel, D. Golodnitsky, E. Peled, Y. Wang, W. Gang, S. Bajue and S. Greenbaum, Solid State Ionics, 1998, 113–115, 477–485.
51. C. R. I. Chisholm, R. B. Merle, D. A. Boysen and S. M. Haile, Chem. Mater., 2002, 14, 3889–3893.
52. L. A. Haverkate, W. K. Chan and F. M. Mulder, Adv. Funct. Mater., 2010, 20, 4107–4116.
53. V. G. Ponomareva, N. F. Uvarov, G. V. Lavrova and E. F. Hairetdinov, Solid State Ionics, 1996, 90, 161–166.
54. X. Liu, D. Peaslee, C. Z. Jost, T. F. Baumann and E. H. Majzoub, Chem. Mater., 2011, 23, 1331–1336.
55. D. Zhao, J. Feng, Q. Huo, N. Melosh, G. H. Fredrickson, B. F. Chmelka and G. D. Stucky, Science, 1998, 279, 548–552.
56. M. Imperor-Clerc, P. Davidson and A. Davidson, J. Am. Chem. Soc., 2000, 122, 11925–11933.
57. S. Brunauer, P. H. Emmett and E. Teller, J. Am. Chem. Soc., 1938, 60, 309–319.
58. E. P. Barrett, L. G. Joyner and P. P. Halenda, J. Am. Chem. Soc., 1951, 73, 373–380.
59. W. D. Harkins and G. Jura, J. Chem. Phys., 1943, 11, 430.
60. J. Sun, D. Ma, H. Zhang, X. Liu, X. Han, X. Bao, G. Weinberg, N. Pfänder and D. Su, J. Am. Chem. Soc., 2006, 128, 15756–15764.
61. S. Gomes, H. Hagemann and K. Yvon, J. Alloys Compd., 2002, 346, 206–210.
62. K. B. Harvey and N. R. McQuaker, Can. J. Chem., 1971, 49, 3282–3286.
63. P. Carbonnière and H. Hagemann, J. Phys. Chem. A, 2006, 110, 9927–9933.
64. A. V. Talyzin, O. Andersson, B. Sundqvist, A. Kurnosov and L. Dubrovinsky, J. Solid State Chem., 2007, 180, 510–517.
65. Y. Filinchuk and H. Hagemann, Eur. J. Inorg. Chem., 2008, 3127–3133.
66. V. D’Anna, A. Spyratou, M. Sharma and H. Hagemann, Spectrochim. Acta, Part A, 2014, 128, 902–906.
67. A. Galarneau, H. Cambon, F. Di Renzo and F. Fajula, Langmuir, 2001, 17, 8328–8335.
68. J. B. Lowe and R. T. Baker, J. Nanomater., 2014, 137.
69. T. da Silveira, C. Awano, D. Donatti, F. de Vicente and D. Vollet, Microporous Mesoporous Mater., 2014, 190, 227–233.
70. B. V. V. S. P. Kumar, K. V. Rao, T. Soumya, S. J. George and M. Eswaramoorthy, J. Am. Chem. Soc., 2013, 135, 10902–10905.
71. L. Zhuravlev, Colloids Surf., A, 2000, 173, 1–38.
72. J.-P. Gallas, J.-M. Goupil, A. Vimont, J.-C. Lavalley, B. Gil, J.-P. Gilson and O. Miserque, Langmuir, 2009, 25, 5825–5834.
73. M. Ide, M. El-Roz, E. De Canck, A. Vicente, T. Planckaert, T. Bogaerts, I. Van Driessche, F. Lynen, V. Van Speybroeck, F. Thybault-Starzyk and P. Van Der Voort, Phys. Chem. Chem. Phys., 2013, 15, 642–650.
74. H. Takamura, Y. Kuronuma, H. Maekawa, M. Matsuo and S. Orimo, Solid State Ionics, 2011, 192, 118–121.
75. N. S. Saetova, A. A. Raskovalov, B. D. Antonov, T. V. Yaroslavtseva, O. G. Reznitskikh and N. I. Kadyrova, J. Non-Cryst. Solids, 2016, 443, 75–81.
76. Y. Kojima, Y. Kawai, M. Kimbara, H. Nakanishi and S. Matsumoto, Int. J. Hydrogen Energy, 2004, 29, 1213–1217.
77. Z. Xiong, L. Cao, J. Wang and J. Mao, J. Alloys Compd., 2017, 698, 495–500.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c9cp04235k

‡ Both authors contributed equally to the manuscript.

---