Superconductivity in an organometallic compound†
Abstract
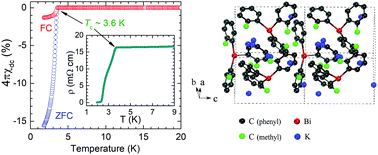
Organometallic compounds constitute a very large group of substances that contain at least one metal-to-carbon bond in which the carbon is part of an organic group. They have played a major role in the development of the science of chemistry. These compounds are used to a large extent as catalysts (substances that increase the rate of reactions without themselves being consumed) and as intermediates in the laboratory and in industry. Recently, novel quantum phenomena such as topological insulators and superconductors were also suggested in these materials. However, there has been no report on the experimental exploration of the topological state. Evidence for superconductivity from the zero-resistivity state in any organometallic compound has not been achieved yet, though much effort has been made. Here we report the experimental realization of superconductivity with a critical temperature of 3.6 K in a potassium-doped organometallic compound, i.e. tri-o-tolylbismuthine, with evidence of both the Meissner effect and the zero-resistivity state through dc and ac magnetic susceptibility measurements. The obtained superconducting parameters classify this compound as a type-II superconductor. The benzene ring is identified to be the essential superconducting unit in such a phenyl organometallic compound. The superconducting phase and its composition are determined by combined studies of X-ray diffraction and theoretical calculations as well as Raman spectroscopy measurements. These findings enrich the applications of organometallic compounds in superconductivity and add a new electron-acceptor family of organic superconductors. This work also points to a large pool for finding superconductors from organometallic compounds.
- This article is part of the themed collection: 2019 PCCP HOT Articles


 Please wait while we load your content...
Please wait while we load your content...