 Open Access Article
Open Access ArticleCalculation of vibrationally resolved absorption spectra of acenes and pyrene†
Isaac
Benkyi
a,
Enrico
Tapavicza
 b,
Heike
Fliegl
b,
Heike
Fliegl
 c and
Dage
Sundholm
c and
Dage
Sundholm
 *a
*a
aUniversity of Helsinki, Department of Chemistry, Faculty of Science, P.O. Box 55 (A.I. Virtanens plats 1), FIN-00014, Finland. E-mail: dage.sundholm@helsinki.fi
bCalifornia State University, Long Beach, Department of Chemistry and Biochemistry, 1250 Bellflower Blvd, Long Beach, CA 90840, USA
cKarlsruhe Institute of Technology (KIT), Institute of Nanotechnology, Hermann-von-Helmholtz-Platz 1, 76344 Eggenstein-Leopoldshafen, Germany
First published on 11th September 2019
Abstract
The absorption spectra of naphthalene, anthracene, pentacene and pyrene in the ultraviolet-visible (UV-Vis) range have been simulated by using an efficient real-time generating function method that combines calculated adiabatic electronic excitation energies with vibrational energies of the excited states. The vertical electronic excitation energies have been calculated at the density functional theory level using the PBE0 functional and at the second-order approximate coupled-cluster level (CC2). The absorption spectra have been calculated at the PBE0 level for the studied molecules and at the CC2 level for naphthalene. The transition probabilities between vibrationally resolved states were calculated by using the real-time generating function method employing the full Duschinsky formalism. The absorption spectrum for naphthalene calculated at the PBE0 and CC2 levels agrees well with the experimental one after the simulated spectra have been blue-shifted by 0.48 eV and 0.12 eV at the PBE0 and CC2 level, respectively. The absorption spectra for anthracene, pentacene and pyrene simulated at the PBE0 level agree well with the experimental ones when they are shifted by 0.49 eV, 0.57 eV and 0.46 eV, respectively. The strongest transitions of the main vibrational bands have been assigned.
1 Introduction
Measuring electronic absorption spectra in the ultraviolet-visible (UV-Vis) region is a standard approach for obtaining information about the electronic structure of molecules. The common procedure for simulating the UV-Vis spectra is to perform calculations of the few lowest vertical electronic excitation energies and the corresponding oscillator strengths using the molecular structure optimized for the ground state. Such calculations yield spectra consisting of sharp infinitely narrow peaks rendering comparisons with experimental spectra difficult, because the experimental spectra consist of broad bands, which sometimes have additional peaks originating from the coupling between electronic and vibrational degrees of freedom.1–4 When comparing calculated and measured UV-Vis spectra, the calculated peaks of the vertical transitions are generally broadened by using empirical Gaussian or Lorentzian functions with a fixed width leading to a spectrum that reminds of the recorded one, even though the obtained band broadening lacks physical information. Additional peaks that appear in the spectrum due to couplings between electronic transitions and the molecular vibrations cannot be obtained using that approach.The band broadening observed in experimental spectra can also be related to fluctuations in the molecular structure, which can be taken into account by considering contributions from different conformers to absorption spectra. This is typically achieved by performing molecular dynamics (MD) simulations, which are combined with calculations of vertical excitation energies and oscillator strengths for a set of structural snapshots along MD trajectories. The final absorption spectrum is then obtained by averaging over a large number of spectra after the individual peaks have been broadened using Gaussian or Lorentzian functions.5–8 This approach is particularly successful if the overall absorption spectrum of a compound is caused by different conformers present in the ground state.9–11 However, this procedure is computationally demanding and important effects arising from the quantum nature of the nuclei are not taken into account implying that peaks of pure vibrational origin are missing.4
A physically more appealing alternative for modeling the band broadening is to take vibronic effects into account by explicitly calculating the coupling between vibrational motion and electronic transitions.2–4,12–22 Since the molecular structure of the excited state differs from the molecular structure of the ground-state, the absorption intensity depends on Franck–Condon factors,23 which are according to the Franck–Condon principle in the first approximation proportional to the square of the overlap of the vibrational wave functions of the ground and excited electronic states. Since the molecular structures of the two states are different, the normal coordinates of the vibrational modes are also different leading to the Duschinsky effect.4,24–27 The Franck–Condon approximation might not be accurate enough when considering dipole forbidden or very weakly allowed transitions that become allowed due to vibronic coupling. The Renner–Herzberg–Teller effect, which considers that the electronic transition dipole moment depends on the nuclear coordinates,28–32 might lead to an enhancement of the intensity of such transitions as compared to the ones calculated in the Franck–Condon approximation.14,15,27,32,33 Duschinsky mixing of normal coordinates of the initial and final states has to be considered also when modeling the Renner–Herzberg–Teller effect.34
Zero-point corrected adiabatic excitation energies can be obtained by optimizing the molecular structures of the ground and excited states and correcting the transition energy for vibrational effects by adding the difference between the zero-point vibrational energies of the ground and excited state to the adiabatic excitation energy.35–37 The intensity of the 0–0 transition can be obtained by multiplying the oscillator strength of the vertical transition with Franck–Condon factors.17,18,20,38–40 Transitions from the zero-point vibrational state of the electronic ground state to higher vibrational states of the excited state can be obtained by adding vibrational energies and taking the corresponding Franck–Condon factors into account. Transitions from vibrationally excited states of the electronic ground state can often be omitted when comparing with experimental spectra, because excited high-energy vibrational states are not occupied at ambient temperatures.
A thorough treatment of vibrational effects is computationally demanding making it necessary to find an acceptable compromise between accuracy and computational costs.3,27 Based on the developments by Mebel et al.25 and Etinski et al.,19 Tapavicza et al.4 showed that the full Duschinsky rotation can be considered. The Renner–Herzberg–Teller effect may on the other hand be neglected for strong bands. The computationally efficient approach by Tapavicza et al. requires information of optimized ground and excited state structures as well as their harmonic frequencies as input data. The approach does not take temperature effects into account, but it allows Duschinsky mixing of all vibrational modes.4
In this work, we apply the approach developed by Tapavicza et al.4 to naphthalene, anthracene, pentacene and pyrene, which have complicated absorption spectra even though only one electronic transition contributes to the absorption band. The aim is to simulate the absorption spectra in the Franck–Condon approximation and to assign the vibrational bands in the UV-Vis range of the experimental absorption spectra by using the full Duschinsky formalism.
The computational methods used for optimizing the molecular structures of the ground and excited states, the methods for calculating electronic excitation energies, and the methods used for simulating the absorption spectra are presented in Section 2. The assignment of the spectra are discussed in Section 3 and summarized in Section 4.
2 Computational methods
2.1 Ground state structures
The molecular structure of the ground state of naphthalene, anthracene, pentacene, and pyrene were optimized at the density functional theory (DFT) level of theory using the PBE0 hybrid functional and the def2-TZVP basis set.41,42 The molecules were assumed to belong to the D2h point group. The molecules were placed in the x,y plane with the longer molecular axis in the x direction. Grimme's D3 dispersion correction was used for considering van der Waals interactions.43 Calculations of the vibrational energies using the AOFORCE module of Turbomole showed that the optimized structures are minima on the potential energy surface.44 The electronic structure calculations were performed using Turbomole versions 7.0–7.3.45–47 The optimized molecular structures are shown in Fig. 1 and the Cartesian coordinates are given in the ESI.† The molecular structure of naphthalene was also optimized at the second-order Møller–Plesset perturbation theory (MP2)48 level using the Karlsruhe triple-ζ basis sets augmented with double sets of polarization functions (def2-TZVPP).42 The vibrational frequencies calculated numerically using the NUMFORCE program of Turbomole showed that the MP2 structure is a minimum on the potential energy surface. | ||
| Fig. 1 The molecular structures of the studied molecules. The figure has been made with VMD.49 | ||
2.2 Molecular structures of excited states
The molecular structure of the two lowest excited states of naphthalene, anthracene, and pentacene, and pyrene were optimized at the time-dependent DFT (TDDFT) level using the PBE0 functional. The vibrational frequencies calculated numerically using NUMFORCE showed that the excited state structures are minima on the potential energy surface. The TDDFT calculations were performed with the ESCF and EGRAD modules of Turbomole.50,51The molecular structures of the two lowest excited singlet states of naphthalene optimized at the second-order approximate coupled-cluster (CC2) level using the Karlsruhe def2-TZVPP basis sets42 were taken from ref. 35, where the vibrational frequencies of the two excited states were also reported. The molecular structures of the excited states of naphthalene optimized at the CC2 level belong to the D2h point group, whereas at the PBE0 level the molecular structures of the excited states belong to the C2h point group.
2.3 Calculation of vertical excitation energies
The vertical excitation energies were calculated for the optimized ground-state structures at the time-dependent DFT (TDDFT) level using the PBE0 and Becke's half-and-half (BHLYP) functionals combined with the def2-TZVP basis sets.41,42,52–55 The CC2 and the algebraic diagrammatic construction to second-order (ADC(2)) methods were also used for calculating vertical excitation energies.56,57 The resolution of the identity approximation was used for speeding up the CC2 and ADC(2) calculations.58–60 The excitation energies calculated for the studied molecules at the ADC(2) and CC2 levels agree well with deviations of at most 0.03 eV. The 0–0 transition energy of the 1B3u state of naphthalene calculated at the CC2 level is 0.16 eV larger than the experimental value, whereas the corresponding energy for the 1B2u state is 0.03 eV smaller than the experimental value.35,61Comparison of the excitation energies calculated at the PBE0 and CC2 levels shows that the 1B3u excitation energies agree within 0.1 eV, whereas the corresponding excitation energies at the BHLYP level are 0.2 eV larger than the ones calculated at the PBE0 level. The 1B2u excitation energies calculated at the PBE0 level are about 0.4 eV smaller than obtained at the CC2 level, whereas the excitation energies calculated at the BHLYP level are 0.08–0.20 eV smaller than the CC2 energies. The excitation energies are systematically shifted to higher energies when increasing the amount of Hartree–Fock exchange from 25% to 50% in the functional. The 1B3u and 1B2u states for naphthalene are obtained in the wrong order at the PBE0 and BHLYP levels. The excitation energies of the 2B2u and 2B3u states are much higher in energy and are not relevant in the rest of this study. The calculated excitation energies are summarized in Tables 1 and 2.
| Molecule | State/method→ | PBE0 | BHLYP |
|---|---|---|---|
| Naphthalene | 1B3u | 4.58 (0.000) | 4.76 (0.000) |
| 2B3u | 6.06 (1.286) | 6.26 (1.403) | |
| 1B2u | 4.49 (0.060) | 4.69 (0.070) | |
| 2B2u | 6.25 (0.193) | 6.42 (0.254) | |
| Anthracene | 1B3u | 3.96 (0.000) | 4.15 (0.000) |
| 2B3u | 5.31 (2.029) | 5.53 (2.216) | |
| 1B2u | 3.30 (0.056) | 3.54 (0.078) | |
| 2B2u | 5.43 (0.000) | 5.89 (0.000) | |
| Pentacene | 1B3u | 3.30 (0.004) | 3.48 (0.006) |
| 2B3u | 4.37 (3.465) | 4.62 (3.849) | |
| 1B2u | 1.95 (0.040) | 2.18 (0.064) | |
| 2B2u | 4.16 (0.000) | 4.69 (0.026) | |
| Pyrene | 1B3u | 3.85 (0.000) | 4.07 (0.000) |
| 2B3u | 4.71 (0.277) | 5.11 (0.403) | |
| 1B2u | 3.78 (0.272) | 3.99 (0.314) | |
| 2B2u | 5.51 (0.809) | 5.72 (0.998) | |
| Molecule | State/method→ | ADC(2) | CC2 |
|---|---|---|---|
| Naphthalene | 1B3u | 4.50 (0.000) | 4.49 (0.000) |
| 2B3u | 6.20 (1.626) | 6.22 (1.443) | |
| 1B2u | 4.87 (0.094) | 4.89 (0.082) | |
| 2B2u | 6.48 (0.286) | 6.50 (0.250) | |
| Anthracene | 1B3u | 3.92 (0.000) | 3.92 (0.000) |
| 2B3u | 5.42 (2.549) | 5.45 (2.272) | |
| 1B2u | 3.69 (0.092) | 3.70 (0.077) | |
| 2B2u | 5.66 (0.000) | 5.63 (0.000) | |
| Pentacene | 1B3u | 3.29 (0.001) | 3.29 (0.003) |
| 2B3u | 4.48 (4.366) | 4.51 (3.918) | |
| 1B2u | 2.33 (0.074) | 2.34 (0.057) | |
| 2B2u | 4.51 (0.001) | 4.48 (0.001) | |
| Pyrene | 1B3u | 3.79 (0.001) | 3.78 (0.001) |
| 2B3u | 4.89 (0.408) | 4.87 (0.341) | |
| 1B2u | 4.05 (0.415) | 4.07 (0.368) | |
| 2B2u | 5.65 (1.175) | 5.67 (1.050) | |
We have studied the absorption spectra of the 1B2u states, which are lowest excited states of anthracene and pentacene and the second excited state of naphthalene and pyrene. The lowest excited singlet state of naphthalene and pyrene and the second lowest excited singlet state of anthracene and pentacene have very small oscillator strengths. We have focused on the absorption spectra originating from the 1B2u state, because the absorption intensity of the lowest B3u state is weak at the Franck–Condon level and it may be significantly enhanced by the Renner–Herzberg–Teller effect, which is not accounted for in this work.62–64
2.4 Calculations of absorption spectra
In the Franck–Condon approximation, the absorption cross section for a transition from the lowest vibrational state of the initial electronic state i to a vibrational level of the final electronic state f is given by15,25,65 | (1) |
The vibrational wave functions of the ground and excited electronic states are given by
 | (2) |
 | (3) |
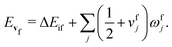 | (4) |
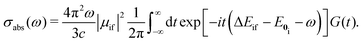 | (5) |
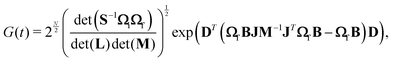 | (6) |
The time integral in eqn (5) is integrated by using the trapezoid rule. The generating function G(t) has to be constructed for at least 24 ps in order to obtain a spectrum with a resolution of 1.4 cm−1, which is enough for the present purpose. The generating function is damped by an exponentially decaying function exp(−it/τ), where τ is a lifetime parameter. In the calculations we used two different lifetime parameters for each molecule. In one calculation, the lifetime was adjusted in order to obtain spectral lines with widths similar to the ones in the experimental spectrum. In a second calculation, longer lifetimes were used, leading to narrow absorption peaks that allow a detailed assignment of the vibronic peaks. The construction of G(t) and the Fourier transformation are the most time-consuming steps of the calculation of the spectrum. However, optimizing the molecular structures and calculating harmonic vibrational frequencies are though the main computational bottlenecks. The method described in this section has been implemented in the RADLESS code.4
3 Calculated and experimental spectra
3.1 Simulation of the naphthalene spectrum at the PBE0 level
The vertical excitation energy of the first excited state of naphthalene is 4.49 eV (4.69 eV) at the DFT level using the PBE0 (BHLYP) functional. The results obtained with BHLYP functional are given in parenthesis. The first transition has an oscillator strength of 0.060 (0.070). The lowest singlet excited state belongs to the B2u irreducible representation of the D2h point group. At the DFT level, the second excited state is a B3u state with a vertical excitation energy of 4.58 eV (4.76 eV) that has a very small oscillator strength of 2.65 × 10−6 (2.45 × 10−7). Experimentally, the weak B3u state is the first excited singlet state and the B2u state is the second one.61,67,68The vibrational contributions to the absorption spectrum of naphthalene calculated at the PBE0 level using the RADLESS code4 are compared with the experimental spectrum in Fig. 2. The calculated 0–0 transition energy of 3.97 eV is 0.48 eV smaller than the experimental 0–0 energy of 4.45 eV for the B2u state, which is experimentally the second excited state. The calculated spectrum in Fig. 2 has therefore been shifted by 0.48 eV in order to obtain the same energy for the 0–0 transition in the experimental and simulated spectra. Qualitatively the same vibrational bands are obtained in the calculated and simulated spectra. The blue lines in Fig. 2 show the exact positions of the calculated transition energies when vibrational coupling is taken into account, whereas the red curve is obtained by introducing the same bandwidth as in the experimental spectrum. The second and higher vibrational bands in the calculated spectrum are slightly blue shifted, because vibrational energies are often slightly overestimated in the harmonic approximation. Scaling factors for ground state vibrational frequencies have previously been parameterized for different approximations to the exchange–correlation functional in order to obtain better agreement with experimental infrared (IR) absorption spectra.70 A better agreement between simulated and measured absorption spectra can also be obtained by introducing a scaling factor of 0.90 for the vibrational frequencies calculated at the PBE0 level. The scaled absorption spectrum of naphthalene is shown in the ESI.†
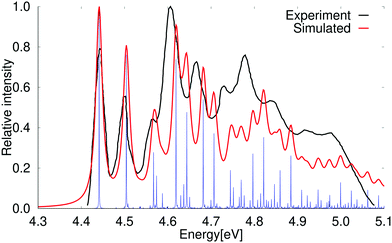 | ||
| Fig. 2 Comparison of the experimental and simulated absorption spectra of naphthalene calculated at the PBE0 level. The simulated spectrum is obtained using the electronic excitation energy and the vibrational coupling of the 1B2u excited state. The 0–0 transition energy of the simulated spectrum has been shifted by 0.48 eV to fit the 0–0 peak in the experimental spectrum. The experimental spectrum is taken from ref. 69. The red spectrum has been computed with lifetime (τ) of 72.6 fs; in the blue spectrum τ was set to 2420 fs. | ||
The strongest vibrational bands have been assigned by comparing the energy shifts with the energy of the vibrational modes of the electronic excited state that belong to the total symmetric irreducible representation (Ag) of the D2h and C2h point groups. Calculations of the vibrational contributions to the vibrational bands show that the first peak is due to the vibrational coupling with only one mode (15Ag), whereas many vibrational modes contribute to the higher vibrational bands. The vibrational bands originate mainly from the coupling with the bond stretching and skewing modes in the molecular plane as illustrated for pyrene in ref. 64. The vibrational bands in the absorption spectrum are assigned in Table 3. The numbering denotes the order of the vibrational modes as given in the ESI,† whereas 15Ag is the first vibrational mode belonging to the Ag irreducible representation.
| Energy (in eV) | Shift (in cm−1) | Rel. intensity | Assignment |
|---|---|---|---|
| 4.443 | 0 | 1.000 | 0–0 |
| 4.506 | 507 | 0.748 | 15Ag |
| 4.568 | 1014 | 0.258 | 15Ag + 15Ag |
| 4.575 | 1071 | 0.165 | 31Ag |
| 4.620 | 1433 | 0.723 | 40Ag |
| 4.645 | 1634 | 0.475 | 46Ag |
| 4.683 | 1940 | 0.512 | 15Ag + 40Ag |
| 4.708 | 2142 | 0.343 | 31Ag + 31Ag |
| 4.771 | 2648 | 0.223 | 15Ag + 15Ag + 46Ag |
| 4.823 | 3067 | 0.302 | 40Ag + 46Ag |
| 4.848 | 3268 | 0.158 | 46Ag + 46Ag |
| 4.861 | 3373 | 0.213 | 15Ag + 40Ag + 40Ag |
| 4.886 | 3574 | 0.304 | 15Ag + 40Ag + 46Ag |
3.2 Simulation of the naphthalene spectrum at the CC2 level
At the second-order approximate coupled-cluster (CC2) level, the order of the 1B2u and 1B3u states is the same as observed in experiment.61,67,68 The vertical excitation energy of the 1B3u state calculated at the CC2 level is 4.49 eV with a very weak oscillator strength, whereas the 1B2u state lies higher in energy with a vertical excitation energy of 4.89 eV. The excitation energies calculated at the CC2 level are in good agreement with previously calculated values35 and with experimental data obtained in high-resolution spectroscopy measurements.67,68 The absorption spectrum calculated at the CC2 level shown in Fig. 3 is very reminiscent of the experimental one. The calculated vibrational bands are though slightly blue shifted as compared to the experimental spectrum. The first and second vibrational peaks of the calculated spectrum are slightly stronger than the experimental ones at the PBE0 and CC2 levels. The calculated spectrum has a few small peaks above 5.1 eV, which are not present in the older experimental spectrum,61,69 whereas a shoulder can be seen in the more recently reported experimental spectrum by Grosch et al.71,72 The vibrational bands in the absorption spectrum are assigned in Table 4.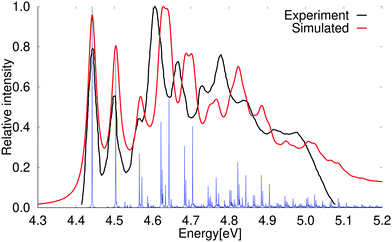 | ||
| Fig. 3 Comparison of the experimental and the simulated spectra of the 1B2u state of naphthalene at CC2 level of theory. The 0–0 transition energy of the simulated spectrum has been shifted by 0.12 eV. The experimental spectrum is taken from ref. 69. The red spectrum has been computed with lifetime (τ) of 72.6 fs; in the blue spectrum τ was set to 2420 fs. | ||
| Energy (in eV) | Shift (in cm−1) | Rel. intensity | Assignment |
|---|---|---|---|
| 4.442 | 0 | 1.000 | 0–0 |
| 4.504 | 497 | 0.746 | 15Ag |
| 4.565 | 992 | 0.269 | 15Ag + 15Ag |
| 4.572 | 1048 | 0.154 | 30Ag |
| 4.587 | 1168 | 0.132 | 33Ag |
| 4.622 | 1450 | 0.426 | 40Ag |
| 4.626 | 1478 | 0.189 | 41Ag |
| 4.643 | 1620 | 0.544 | 45Ag |
| 4.684 | 1948 | 0.305 | 15Ag + 40Ag |
| 4.705 | 2117 | 0.404 | 15Ag + 45Ag |
| 4.823 | 3070 | 0.228 | 40Ag + 45Ag |
| 4.844 | 3240 | 0.161 | 45Ag + 45Ag |
| 4.885 | 3568 | 0.161 | 15Ag + 40Ag + 45Ag |
3.3 Simulation of the anthracene spectrum at the PBE0 level
The vertical excitation energy of the first excited state of anthracene is 3.30 eV (3.54 eV) at the PBE0 (BHLYP) level. It has an oscillator strength of 0.056 (0.078) and belongs to the B2u irreducible representation of the D2h point group. The second excited state is a B3u state with a vertical excitation energy of 3.96 eV (4.15 eV). It is a very weak absorption band with an oscillator strength of 2.47 × 10−4 (3.64 × 10−4). At the CC2 level, the first transition is also to the B2u state having an excitation energy of 3.70 eV and an oscillator strength of 0.077. The 1B3u state lies higher in energy with a vertical excitation energy of 3.92 eV and a small oscillator strength of 2.69 × 10−4. In contrast to naphthalene, the lowest B2u and B3u states are obtained in the same order at the PBE0 and CC2 levels.The absorption spectrum including vibrational contributions calculated at the PBE0 level for the lowest 1B2u state of anthracene is compared to the experimental one in Fig. 4. A simulated absorption spectrum of anthracene obtained with a scaling factor of 0.85 is reported in the ESI.† The 0–0 transition energy of the simulated spectrum for the 1B2u state is 3.92 eV, which is 0.49 eV larger than the experimental 0–0 transition energy. The simulated spectrum in Fig. 4 has been shifted in order to fit the experimental one.69,73–75 Calculations without accounting for the Duschinsky mixing showed that it has a very small influence on the absorption spectrum of anthracene, which is generally expected for rigid polycyclic aromatic hydrocarbons. A comparison of the absorption spectra of anthracene calculated with and without Duschinsky rotation is given in the ESI.†
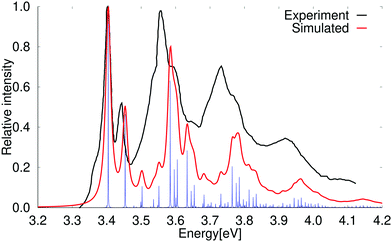 | ||
| Fig. 4 Comparison of the experimental and simulated spectra of the 1B2u state of anthracene at the PBE0 level. The 0–0 transition energy of the simulated spectrum has been shifted by 0.49 eV. The experimental spectrum is taken from ref. 69. The red spectrum has been computed with lifetime (τ) of 72.6 fs; in the blue spectrum τ was set to 2420 fs. | ||
The vibrational bands have been assigned in Table 5 by comparing the energy shifts with the vibrational energies of the vibrational states that belong to the total symmetric irreducible representation (Ag) of the D2h point group. Comparison of the calculated and recorded spectra shows that the high-energy peaks of the calculated spectrum are blue shifted as compared to experiment probably due to the use of the harmonic approximation. The blue shift is larger at the high-energy part of the spectrum, because several slightly overestimated vibrational frequencies contribute to the shift. A similar DFT study has recent been performed at the generalized gradient approximation (GGA) level,76 where they obtained a large red shift of the vertical excitation energy as compared to the experimental spectrum. All vibrational bands of the shifted spectrum were in good agreement with the experimental spectrum.76 In a similar DFT study, Dierksen and Grimme obtained an absorption spectrum that also agreed well with the experimental one.36 The high-energy vibrational bands were slightly red shifted relative to the experimental ones even though they employed the harmonic approximation that usually overestimates vibrational energies. The absorption spectrum calculated using a temperature of 423 K has a hot band below the 0–0 transition peak, which is seen as a shoulder on the low-energy side of the 0–0 band of the experimental spectrum.15 The hot band is missing in our simulated spectra, because in our calculations we assume a temperature of 0 K where only the lowest vibrational state of the electronic ground state is occupied.
| Energy (in eV) | Shift (in cm−1) | Rel. intensity | Assignment |
|---|---|---|---|
| 3.402 | 0 | 1.000 | 0–0 |
| 3.451 | 396 | 0.463 | 14Ag |
| 3.500 | 763 | 0.106 | 27Ag |
| 3.549 | 1187 | 0.102 | 44Ag |
| 3.582 | 1452 | 0.631 | 53Ag |
| 3.593 | 1547 | 0.191 | 58Ag |
| 3.602 | 1618 | 0.239 | 61Ag |
| 3.631 | 1848 | 0.285 | 14Ag + 53Ag |
| 3.643 | 1943 | 0.079 | 14Ag + 58Ag |
| 3.651 | 2015 | 0.111 | 14Ag + 61Ag |
| 3.680 | 2245 | 0.063 | 27Ag + 53Ag |
| 3.729 | 2639 | 0.067 | 14Ag + 27Ag + 53Ag |
| 3.762 | 2904 | 0.205 | 53Ag + 53Ag |
| 3.773 | 2999 | 0.121 | 53Ag + 58Ag |
| 3.782 | 3070 | 0.158 | 53Ag + 61Ag |
| 3.810 | 3300 | 0.087 | 14Ag + 53Ag + 53Ag |
| 3.831 | 3467 | 0.066 | 14Ag + 53Ag + 61Ag |
| 3.962 | 4522 | 0.050 | 53Ag + 53Ag + 61Ag |
Vibrational modes belonging to the Ag, B1g and B3g irreducible representations may contribute to the absorption spectrum of the 1B2u state of anthracene. Only the Ag modes are active at the Franck–Condon level, whereas the B1g modes may contribute at the Renner–Herzberg–Teller level via intensity borrowing from the strong ground-state transition of the 2B3u state. Vibrational modes of the B3g irreducible representation are expected to be less important, because the 1B1u state is very high in energy.77 Calculated and experimental values for the vibrational energies of the 1B2u state are compared in Table 6. The calculated values for the low-energy Ag and B1g modes agree well with the experimental ones, whereas the calculated values for high-energy modes differ significantly from the experimental ones.77 Fewer vibrational modes are deduced from the experimental data rendering the comparison difficult. Since the high-energy vibrational peaks of the calculated absorption spectrum are generally blue shifted as compared to the experimental one, the vibrational mode corresponding to the calculated mode with an energy of 1282 cm−1 is most likely missing in the experimental spectrum. The Renner–Herzberg–Teller effect does not play an important role for anthracene, since the main features of the calculated and measured absorption spectra agree. The lower-energy shoulder of the experimental spectrum is a hot band originating from the absorption of higher vibrational levels of the ground state.
| Mode | E(Calc.) | E(Exp.) | Mode | E(Calc.) | E(Exp.) |
|---|---|---|---|---|---|
| 14Ag | 396 | 385 | 13B1g | 238 | 232 |
| 21Ag | 601 | 583 | 20B1g | 453 | 473 |
| 27Ag | 763 | 755 | 26B1g | 511 | |
| 40Ag | 1061 | 1019 | 33B1g | 728 | |
| 44Ag | 1187 | 1168 | 38B1g | 919 | 889 |
| 47Ag | 1282 | 41B1g | 1098 | ||
| 53Ag | 1452 | 1380 | 45B1g | 1214 | 1184 |
| 58Ag | 1547 | 1420 | 48B1g | 1299 | |
| 61Ag | 1618 | 1501 | 52B1g | 1418 | 1409 |
| 64Ag | 3175 | 57B1g | 1544 | 1514 | |
| 68Ag | 3189 | 59B1g | 1583 | 1635 | |
| 72Ag | 3219 |
3.4 Simulation of the pentacene spectrum at the PBE0 level
The vertical excitation energy of the first excited state of pentacene is 1.95 eV (2.18 eV) at the PBE0 (BHLYP) level and has an oscillator strength of 0.040 (0.064). It belongs to the B2u irreducible representation of the D2h point group. The second excited state belonging to the B3u irreducible representation has an oscillator strength of 0.004. The vertical excitation energy of the 1B3u state calculated at the PBE0 level is 3.30 eV (3.48 eV).At the second-order approximate coupled-cluster (CC2) level of theory, the calculated vertical excitation energy of the 1B2u state is 2.34 eV with an oscillator strength of 0.057. The second excited state (1B3u) has a vertical excitation energy of 3.29 eV and an oscillator strength of 0.003 at the CC2 level.
The absorption spectrum of pentacene has been recorded in rare gas matrices,78 where significant vibrational transitions were reported at 85 cm−1, 258 cm−1, 1181 cm−1, 1514 cm−1, 2733 cm−1, and 2991 cm−1. The transitions can be assigned by comparing the vibrational energies with calculated ones. The vibrational transition at 85 cm−1 most likely originates from the lowest B1u mode.79 The vibrational band at 258 cm−1 corresponds to the lowest vibrational Ag mode, whose energy is calculated to 265 cm−1. Since higher vibrational energies are blue shifted as compared to the experimental spectrum, an energy of 1226 cm−1 is calculated for the band at 1181 cm−1. The vibrational mode at 1184 cm−1 also contributes to the peak. Several vibrational modes form the peak at 1514 cm−1 in the experimental spectrum. The assignment of the high-energy part of the spectrum is difficult, because many combined vibrations contribute to the broad absorption band between 2.6 eV and 2.7 eV.
The absorption spectrum of the 1B2u state of pentacene simulated at the PBE0 level is compared to the experimental one in Fig. 5.78 A simulated absorption spectrum of pentacene obtained with a scaling factor of 0.95 is reported in the ESI.† The simulated spectrum shows that the first peaks in the experimental spectrum consist of one vibrational transition each, whereas the higher vibrational bands have significant contributions from several vibrational modes. The 0–0 transition energy of the simulated spectrum is 1.71 eV, which is 0.57 eV smaller than the experimental one. The assignment of the strongest vibrational contributions to the vibrational modes belonging to the total symmetric irreducible representation (Ag) of the D2h point group is shown in Table 7. Three of the stronger bands are not assigned, because they are not due to any simple vibrational coupling with Ag modes. Comparison of the calculated and measured absorption spectra show that there are more peaks in the experimental spectrum than in the calculated one. The peak at the high-energy side of the 0–0 transition is 74 cm−1 above the 0–0 transition, which can be compared to twice the vibrational energy of the first B1u mode, whose energy is 39 cm−1. Amirav, Even and Jortner79 suggested that the low-energy butterfly mode belonging the B1u irreducible representation leads to a fluorescence transition at about 77 cm−1 below above the 0–0 peak, which is a plausible interpretation of the second peak that appears 74 cm−1 above the 0–0 peak. Griffiths and Freedman had an alternative interpretation,80 which is most likely incorrect judged from the present calculations. A closer inspection of the experimental absorption spectrum of pentacene in the Ne matrix shows that there is a weak transitions at about 346 cm−1, which might also involve the lowest B1u mode, since it is 81 cm−1 above the vibrational transition corresponding to the first Ag mode.
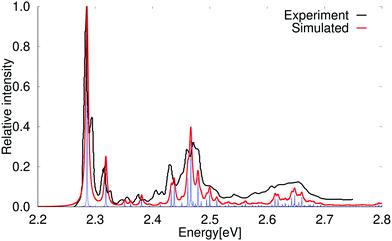 | ||
| Fig. 5 Comparison of the experimental and simulated spectra of the 1B2u state of pentacene calculated at the PBE0 level. The 0–0 transition energy of the simulated spectrum has been shifted by 0.57 eV. The experimental spectrum is taken from ref. 78. The red spectrum has been computed with lifetime (τ) of 72.6 fs; in the blue spectrum τ was set to 2420 fs. | ||
| Energy (in eV) | Shift (in cm−1) | Rel. intensity | Assignment |
|---|---|---|---|
| 2.286 | 0 | 1.000 | 0–0 |
| 2.319 | 265 | 0.245 | 15Ag |
| 2.381 | 767 | 0.052 | 39Ag |
| 2.433 | 1184 | 0.082 | 64Ag |
| 2.438 | 1226 | 0.117 | 68Ag |
| 2.462 | 1417 | 0.141 | 78Ag |
| 2.467 | 1460 | 0.331 | 81Ag |
| 2.479 | 1522 | 0.144 | 85Ag |
| 2.484 | 1560 | 0.028 | 87Ag |
| 2.494 | 1653 | 0.036 | |
| 2.500 | 1680 | 0.076 | 15Ag + 78Ag |
| 2.512 | 1787 | 0.034 | 15Ag + 85Ag |
| 2.614 | 2621 | 0.041 | 60Ag + 87Ag |
| 2.619 | 2662 | 0.039 | 60Ag + 90Ag |
| 2.643 | 2855 | 0.044 | 75Ag + 85Ag |
| 2.648 | 2896 | 0.056 | 75Ag + 87Ag |
| 2.660 | 2992 | 0.049 |
The absorption spectrum of pentacene calculated at the GGA level has recently been reported.76 They obtained a large red shift of the vertical excitation energy, whereas all vibrational bands of the shifted spectrum were in good agreement with the experimental spectrum, even though vibrational energies calculated in the harmonic approximation are generally overestimated.
3.5 Simulation of the pyrene spectrum at the PBE0 level
The vertical excitation energy of the first singlet excited state of pyrene is 3.78 eV (3.99 eV) at the PBE0 (BHLYP) level. The transition to the 1B2u state has a relatively large oscillator strength of 0.272 (0.314). The calculated excitation energy of the other low-lying excited singlet state is 3.85 eV (4.07 eV). It belongs to the B3u irreducible representation of the D2h point group and has a very small oscillator strength.At the CC2 level of theory, the two states appear in the reverse order, which is agreement with experiment. At the CC2 level, the vertical excitation energies of the 1B2u and 1B3u states are 4.07 eV and 3.78 eV, respectively. The B2u has a large oscillator strength of 0.368 at the CC2 level, whereas for the B3u state it is only 0.001. The experimental values for the excitation energy of the two states are 3.56 eV for the weak transition to the 1B3u state and 3.82 eV for the strong transition to the B2u state.81,82
The experimental spectrum and simulated absorption spectrum calculated at the PBE0 level for the strong transition to the 1B2u state are compared in Fig. 6. The two spectra agree well. A slightly better agreement is obtained when using a scaling factor of 0.90 as shown in the ESI.†
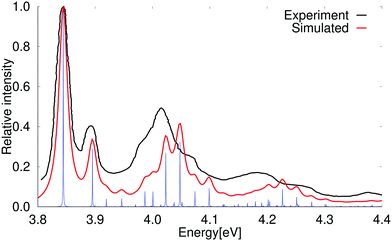 | ||
| Fig. 6 Comparison of the experimental and simulated spectra of the 1B2u state of pyrene. The 0–0 transition energy of the simulated spectrum has been shifted by 0.46 eV. The experimental spectrum is taken from ref. 69. The red spectrum has been computed with lifetime (τ) of 72.6 fs while in the blue spectrum τ was set to 2420 fs. | ||
The higher vibrational bands of the calculated spectrum are slightly blue shifted as compared to the experimental spectrum, because the harmonic approximation generally yields too large vibrational energies. The vibrational bands were assigned by comparing the energies of the vibrational modes belonging to the total symmetric irreducible representation (Ag) of the D2h point group. The assignment in Table 8 shows that the main contribution to the lowest vibrational bands originates mainly from one vibrational mode, whereas several modes contribute to the high-energy bands. Experimental and simulated absorption and emission spectra of pyrene have been previously reported by several research groups.36,64,69,74,76 Understanding the pyrene spectrum is of general interest, because the ratio between the intensities of the first and third vibrational band of the emission spectrum of pyrene is used for probing the dielectric constant of the environment of molecules in different contexts.83–85
| Energy (in eV) | Shift (in cm−1) | Rel. intensity | Assignment |
|---|---|---|---|
| 3.842 | 0 | 1.000 | 0–0 |
| 3.894 | 411 | 0.288 | 14Ag |
| 3.945 | 822 | 0.041 | 14Ag + 14Ag |
| 3.985 | 1149 | 0.076 | 47Ag |
| 3.999 | 1261 | 0.075 | 52Ag |
| 4.021 | 1441 | 0.268 | 59Ag |
| 4.046 | 1641 | 0.323 | 68Ag |
| 4.072 | 1854 | 0.077 | 14Ag + 59Ag |
| 4.097 | 2054 | 0.091 | 14Ag + 68Ag |
4 Summary and conclusions
The absorption spectra of naphthalene, anthracene, pentacene and pyrene in the UV-Vis range have been calculated at the PBE0 and CC2 levels of theory using an efficient real-time generating function method. The vibrational coupling has been considered at the Franck–Condon level using the full Duschinsky formalism. We have neglected the Renner–Herzberg–Teller effect, which is less important for the lowest Ag → B2u transition of these rigid molecules. The calculated absorption spectra agree well with available experimental data. We have considered only the electronic transition to the B2u state, which is the lowest excited singlet state of anthracene and pentacene, whereas the weakly absorbing B3u state is the lowest excited singlet state of naphthalene and pyrene. The electronic excitation energies are significantly underestimated at the PBE0 level, whereas the excitation energies calculated at the CC2 level are in better agreement with experimental data. The absorption spectra simulated at the PBE0 level agree well with the experimental ones when they are shifted by 0.48 eV, 0.49 eV, 0.57 eV and 0.46 eV for naphthalene, anthracene, pentacene and pyrene, respectively. At the CC2 level, the corresponding energy shift for naphthalene is 0.12 eV. Calculations employing simplified models such as the displaced harmonic oscillator approximation and the frequency-shifted displacement harmonic approximation models showed that they yield qualitatively the same spectra as obtained with the full Duschinsky treatment. Since the studied molecules are very rigid, the vibrational modes of the ground and excited states do not significantly differ. The individual vibrational peaks in the absorption spectra have been assigned by comparing the transition energies with vibrational energies of the Ag vibrational modes of the B2u state. The peaks in the low-energy part of the spectra originate from single vibrational modes, whereas many vibrational modes contribute to the high-energy part of the absorption spectra rendering an accurate assignment difficult. The PBE0 and CC2 models generally tend to overestimate the harmonic vibrational frequencies leading to a blue shift of the high-energy part of the absorption spectra. We obtained a better overall agreement with experimental absorption spectra by using scaling factors of 0.90, 0.85, 0.95, 0.90 for naphthalene, anthracene, pentacene, and pyrene, respectively. Even though we were not able to find any universal scaling factor for the vibrational frequencies, we found that scaling factors smaller than one improve the agreement with the experimental spectra.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research has been supported by the Academy of Finland through projects (275845, 287791 and 314821 and the MESIOS project 277579). CSC – the Finnish IT Center for Science and the Finnish Grid and Cloud Infrastructure (persistent identifier urn:nbn:fi:research-infras-2016072533) are acknowledged for computer time.Notes and references
- E. Stendardo, F. Avila Ferrer, F. Santoro and R. Improta, J. Chem. Theory Comput., 2012, 8, 4483–4493 CrossRef CAS PubMed.
- J. Bloino, A. Baiardi and M. Biczysko, Int. J. Quantum Chem., 2016, 116, 1543–1574 CrossRef CAS.
- F. Santoro and D. Jacquemin, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2016, 6, 460–486 CAS.
- E. Tapavicza, F. Furche and D. Sundholm, J. Chem. Theory Comput., 2016, 12, 5058–5066 CrossRef CAS PubMed.
- E. Brunk and U. Röthlisberger, Chem. Rev., 2015, 115, 6217–6263 CrossRef CAS PubMed.
- E. Tapavicza, G. D. Bellchambers, J. C. Vincent and F. Furche, Phys. Chem. Chem. Phys., 2013, 15, 18336–18348 RSC.
- I. Tavernelli, U. F. Röhrig and U. Rothlisberger, Mol. Phys., 2005, 103, 963–981 CrossRef CAS.
- C.-M. Suomivuori, A. P. Gamiz-Hernandez, D. Sundholm and V. R. I. Kaila, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 7043–7048 CrossRef CAS PubMed.
- C. Cisneros, T. Thompson, N. Baluyot, A. C. Smith and E. Tapavicza, Phys. Chem. Chem. Phys., 2017, 19, 5763–5777 RSC.
- T. Thompson and E. Tapavicza, J. Phys. Chem. Lett., 2018, 9, 4758–4764 CrossRef CAS PubMed.
- E. Tapavicza, T. Thompson, K. Redd and D. Kim, Phys. Chem. Chem. Phys., 2018, 20, 24807–24820 RSC.
- S. Mukamel, S. Abe and R. Islampour, J. Phys. Chem., 1985, 89, 201–204 CrossRef CAS.
- Y. J. Yan and S. Mukamel, J. Chem. Phys., 1986, 85, 5908–5923 CrossRef CAS.
- F. Santoro, A. Lami, R. Improta, J. Bloino and V. Barone, J. Chem. Phys., 2008, 128, 224311 CrossRef PubMed.
- Y. Niu, Q. Peng, C. Deng, X. Gao and Z. Shuai, J. Phys. Chem. A, 2010, 114, 7817–7831 CrossRef CAS PubMed.
- H. Ma, J. Liu and W. Liang, J. Chem. Theory Comput., 2012, 8, 4474–4482 CrossRef CAS PubMed.
- H.-C. Jankowiaka, J. L. Stuber and R. Berger, J. Chem. Phys., 2007, 127, 234101 CrossRef PubMed.
- J. Huh and R. Berger, J. Phys.: Conf. Ser., 2012, 380, 012019 CrossRef.
- M. Etinski, J. Tatchen and C. M. Marian, J. Chem. Phys., 2011, 134, 154105 CrossRef PubMed.
- M. Etinski, V. Rai-Constapel and C. M. Marian, J. Chem. Phys., 2014, 140, 114104 CrossRef PubMed.
- M. Etinski, M. Petković, M. M. Ristić and C. M. Marian, J. Phys. Chem. B, 2015, 119, 10156–10169 CrossRef CAS PubMed.
- M. P. Kabir, Y. Orozco-Gonzalez and S. Gozem, Phys. Chem. Chem. Phys., 2019, 21, 16526–16537 RSC.
- T. R. Faulkner and F. S. Richardson, J. Chem. Phys., 1979, 70, 1201–1213 CrossRef CAS.
- F. Duschinsky, Acta Physicochim. URSS, 1937, 7, 551–566 Search PubMed.
- A. M. Mebel, M. Hayashi, K. K. Liang and S. H. Lin, J. Phys. Chem. A, 1999, 103, 10674–10690 CrossRef CAS.
- F. Metz, M. Robey, E. Schlag and F. Dörr, Chem. Phys. Letters, 1977, 51, 8–12 CrossRef CAS.
- A. Baiardi, J. Bloino and V. Barone, J. Chem. Theory Comput., 2013, 9, 4097–4115 CrossRef CAS PubMed.
- R. Renner, Z. Phys., 1934, 92, 172–193 CrossRef CAS.
- G. Herzberg and E. Teller, Z. Phys. Chem., Abt. B, 1933, 21, 410–446 Search PubMed.
- G. Atkinson and C. Parmenter, J. Mol. Struct., 1978, 73, 52–95 CAS.
- A. Bacon, J. Hollas and T. Ridley, Can. J. Phys., 1984, 62, 1254–1263 CrossRef CAS.
- L. A. Bizimana, W. P. Carbery, T. A. Gellen and D. B. Turner, J. Chem. Phys., 2017, 146, 084311 CrossRef PubMed.
- G. Orlandi and W. Siebrand, J. Chem. Phys., 1973, 58, 4513–4523 CrossRef CAS.
- G. J. Small, J. Chem. Phys., 1971, 54, 3300–3306 CrossRef CAS.
- H. Fliegl and D. Sundholm, Phys. Chem. Chem. Phys., 2014, 16, 9859–9865 RSC.
- M. Dierksen and S. Grimme, J. Chem. Phys., 2004, 120, 3544–3554 CrossRef CAS PubMed.
- N. O. C. Winter, N. K. Graf, S. Leutwyler and C. Hättig, Phys. Chem. Chem. Phys., 2013, 15, 6623–6630 RSC.
- A. S. Coolidge, H. M. James and R. D. Present, J. Chem. Phys., 1936, 4, 193–211 CrossRef CAS.
- T. Sharp and H. Rosenstock, J. Chem. Phys., 1964, 41, 3453–3463 CrossRef CAS.
- W. Siebrand, J. Chem. Phys., 1967, 46, 440–447 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, J. Chem. Phys., 1996, 105, 9982–9985 CrossRef CAS.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- P. Deglmann and F. Furche, Chem. Phys. Letters, 2002, 362, 511–518 CrossRef CAS.
- R. Ahlrichs, M. Bär, M. Häser, H. Horn and C. Kölmel, Chem. Phys. Letters, 1989, 162, 165–169 CrossRef CAS.
- F. Furche, R. Ahlrichs, C. Hättig, W. Klopper, M. Sierka and F. Weigend, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 91–100 CAS.
- TURBOMOLE V7.3 2018, a development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989–2007, TURBOMOLE GmbH, since 2007; available from http://www.turbomole.com.
- C. Møller and M. S. Plesset, Phys. Rev., 1934, 46, 618–622 CrossRef.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS PubMed.
- R. Bauernschmitt and R. Ahlrichs, Chem. Phys. Letters, 1996, 256, 454–464 CrossRef CAS.
- F. Furche and R. Ahlrichs, J. Chem. Phys., 2002, 117, 7433–7447 CrossRef CAS.
- M. E. Casida and M. Huix-Rotllant, Annu. Rev. Phys. Chem., 2012, 63, 287–323 CrossRef CAS PubMed.
- M. E. Casida, in Recent Advances in Density Functional Methods, Part I, ed. D. P. Chong, World Scientific, Singapore, 1995, p. 155 Search PubMed.
- E. Runge and E. K. U. Gross, Phys. Rev. Lett., 1984, 52, 997–1000 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 1372–1377 CrossRef CAS.
- O. Christiansen, H. Koch and P. Jørgensen, Chem. Phys. Letters, 1995, 243, 409–418 CrossRef CAS.
- J. Schirmer, Phys. Rev. A: At., Mol., Opt. Phys., 1982, 26, 2395–2416 CrossRef CAS.
- C. Hättig and F. Weigend, J. Chem. Phys., 2000, 113, 5154–5161 CrossRef.
- A. Köhn and C. Hättig, J. Chem. Phys., 2003, 119, 5021–5036 CrossRef.
- C. Hättig, Adv. Quantum Chem., 2005, 50, 37–60 CrossRef.
- G. A. George and G. C. Morris, J. Mol. Spectrosc., 1968, 26, 67–71 CrossRef CAS.
- G. Herzberg, Electronic spectra and electronic structure of polyatomic molecules, Van Nostrad Reinhold, New York, 1966 Search PubMed.
- J. G. Angus and G. C. Morris, Mol. Cryst. Liq. Cryst., 1970, 11, 257–277 CrossRef CAS.
- A. Y. Freidzon, R. R. Valiev and A. A. Berezhony, RSC Adv., 2014, 4, 42054–42065 RSC.
- W. Domcke, D. Yarkony and H. Köppel, Conical intersections: electronic structure, dynamics & spectroscopy, World Scientific, 2004 Search PubMed.
- F. G. Mehler, J. Reine Angew. Math., 1866, 66, 161–176 Search PubMed.
- M. Krykunov, S. Grimme and T. Ziegler, J. Chem. Theory Comput., 2012, 8, 4434–4440 CrossRef CAS PubMed.
- A. Bree and T. Thirunamachandran, Mol. Phys., 1962, 5, 397–405 CrossRef CAS.
- J. Ferguson, L. W. Reeves and W. G. Schneider, Can. J. Chem., 1957, 35, 1117–1136 CrossRef CAS.
- J. P. Merrick, D. Moran and L. Radom, J. Phys. Chem. A, 2007, 111, 11683–11700 CrossRef CAS PubMed.
- M. Suto, X. Wang, J. Shan and L. C. Lee, J. Quant. Spectrosc. Radiat. Transfer., 1992, 48, 79–89 CrossRef CAS.
- H. Grosch, Z. Sárossy, H. Egsgaard and A. Fateev, J. Quant. Spectrosc. Radiat. Transfer, 2015, 156, 17–23 CrossRef CAS.
- L. E. Lyons and G. C. Morris, J. Chem. Soc., 1959, 1551–1558 RSC.
- A. Thöny and M. J. Rossi, J. Photochem. Photobiol., A, 1997, 104, 25–33 CrossRef.
- A. Bree and L. E. Lyons, J. Chem. Soc., 1956, 2662–2670 RSC.
- R. Rüger, T. Niehaus, E. van Lenthe, T. Heine and L. Visscher, J. Chem. Phys., 2016, 145, 184102 CrossRef PubMed.
- W. R. Lambert, P. M. Felker, J. A. Syage and A. H. Zewail, J. Chem. Phys., 1984, 81, 2195–2208 CrossRef CAS.
- T. M. Halasinski, D. M. Hudgins, F. Salama, L. J. Allamandola and T. Bally, J. Phys. Chem. A, 2000, 104, 7484–7491 CrossRef CAS.
- A. Amirav, U. Even and J. Jortner, Chem. Phys. Letters, 1980, 72, 21–24 CrossRef CAS.
- A. M. Griffiths and P. A. Freedman, J. Chem. Soc., Faraday Trans. 2, 1982, 78, 391–398 RSC.
- J. B. Briks, Photophysics of Aromatic Molecules, Wiley, New York, 1970 Search PubMed.
- Y. L. Wang and G. S. Wu, Int. J. Quantum Chem., 2008, 108, 430–439 CrossRef CAS.
- V. Glushko, M. Thaler and C. Karp, Arch. Biochem. Biophys., 1981, 210, 33–42 CrossRef CAS PubMed.
- M. D'Abramo, M. Aschi and A. Amadei, Chem. Phys. Lett., 2015, 639, 17–22 CrossRef.
- K. W. Street and W. E. Acree, Appl. Spectrosc., 1988, 42, 1315–1318 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: The Cartesian coordinates of the optimized molecular structures and the calculated harmonic frequencies of the studied molecules. The scaled absorption spectra. The absorption spectra for anthracene calculated with and without Duschinsky rotation are compared. See DOI: 10.1039/c9cp04178h |
| This journal is © the Owner Societies 2019 |
