Rate constants for the N(2D) + C2H2 reaction over the 50–296 K temperature range
Abstract
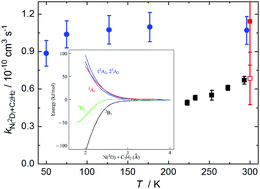
The reactions of metastable atomic nitrogen N(2D) are important processes in the gas-phase chemistry of several planetary atmospheres. Here we present a combined experimental and theoretical investigation of the N(2D) + acetylene reaction due to its potential significance for the photochemistry of Titan's atmosphere. Experimentally, a continuous supersonic flow reactor was used to study this reaction over the 50–296 K temperature range employing pulsed laser photolysis and vacuum ultraviolet laser induced fluorescence to produce and detect N(2D) atoms, respectively. The measured rate constants are substantially larger than those obtained in earlier work and remain constant as a function of temperature. Moreover, these results are supported by new electronic structure calculations, which indicate that this process is likely to be barrierless. The impact of the new rate constants on Titan's atmospheric chemistry is tested through simulations using a 1D coupled ion–neutral photochemical model.
- This article is part of the themed collection: 2019 PCCP HOT Articles


 Please wait while we load your content...
Please wait while we load your content...