Hydrophobic pattern of alkylated ureas markedly affects water rotation and hydrogen bond dynamics in aqueous solution

Abstract

Alkylated ureas are frequently used amphiphiles to mediate biomolecule water interactions, yet their hydrophobic substitution pattern critically affects their function. These differences can be traced back to their hydration, which is poorly understood. Here, we investigate subtle effects of the hydrophobic pattern of ureas on hydration dynamics using a combination of linear and non-linear infrared spectroscopies on the OD stretching vibration of HDO. Isomeric 1,3-dimethylurea (1,3-DMU), 1,1-dimethylurea (1,1-DMU) and 1-ethylurea (1-EU) exhibit very similar and rather weak modulation of the water hydrogen-bond strength distribution. Yet, only 1,3-DMU and 1,1-DMU enhance the hydrogen-bond heterogeneity and slow-down its fluctuation dynamics. In turn, rotational dynamics of water molecules, which is dominated by hydrogen bond switches, is significantly impeded in the presence of 1,3-DMU and only weakly by 1,1-DMU and 1-EU. These marked differences can be explained by both excluded volume effects in hydration and self-aggregation, which may be the key to their biotechnological function.

---

Introduction

The interaction of hydrophobic moieties is largely mediated by the solvent water¹ and is arguably the most abundant origin for assembly of molecules in both biology and technology. Amphiphilic molecules, like e.g. alkylated ureas (RUs), can efficiently alter such solute–water interactions and RUs are, as such, used as solubilizers^2–5 or denaturants.^6–12 Obviously, RUs amphiphilicity stems from the spatial variation of their interaction with water and the hydrophobic substitution pattern thus critically affects RUs function.⁶

As such, the effect of amphiphilic solutes on water structure and dynamics has been intensively studied: ultrafast infrared (IR),^13–20 optical Kerr effect,²¹ dielectric relaxation (DR),^15,22–25 NMR relaxometry^26,27 and diffusometry experiments²⁸ as well as classical^23,24,29,30 and ab initio molecular dynamics (MD) simulations^31–34 have evidenced a slowdown of the water dynamics near hydrophobic moieties. In particular, comparison between aqueous solutions of ‘hydrophilic’ urea (U) and amphiphilic tetramethylurea (TMU) reveals a marked retardation of water dynamics in the presence of methyl groups.^{16,18,21,22,27,29,31,35,36} Despite its (entropic) consequences for the hydration of hydrophobic groups, the temporal and spatial extent of this effect is still discussed controversially: while some experiments^{13,14,16,17,20,34,35,37} and simulations^31,34,38 find strongly retarded (≥4 fold compared to bulk) dynamics of a few water molecules, other theoretical^30,39,40 and experimental²⁶ studies suggest that water dynamics are only moderately slowed down. In essence, experiments suggest that the extent of the slow-down simply scales with the number of methyl(ene) groups.¹⁸ Conversely, according to the extended jump model for water reorientation,^39,41–43 the spatial extent is somewhat larger.³⁰ In this jump model rapid large-angle ‘jumps’ of water are temporally separated by long waiting intervals. Within this model, slowed-down water dynamics can stem from impeded frame rotation, solute–water hydrogen-bonds (H-bonds) stronger than water–water H-bonds, and/or volume exclusion of H-bonding partners. For solutions of TMU, the latter has been suggested to prevail.³⁰

Different alkylation patterns of U^22–24,27 can be used to disentangle these scenarios and therefore relate hydration to RUs biological function: depending on the position and the length of the alkyl groups, the number of methyl(ene) groups at U can be kept constant, while the excluded volume of the adjacent hydrophobic groups may be non-additive due to partial intramolecular overlap for spatially close hydrophobic groups. Recent DR experiments have pointed at the importance of the alkylation pattern: only for solutions of 1,3-dimethylurea (1,3-DMU) a marked slow-down of water dynamics has been observed, while 1,1-dimethylurea (1,1-DMU) has been found to hardly perturb water.^23,24 Force-field MD simulations have suggested that shorter residence times of the water molecules in the vicinity of the methyl groups of 1,1-DMU and their lower hydration number are responsible for the very limited retardation of water dynamics, as measured with DR spectroscopy.²³ As DR probes the collective rotational dynamics, correlations between the dynamics of the solutes and water can be significant: indeed, the dwell times of water in the hydration shell of DMUs have been reported to be rather long.^23,24 The resulting correlated motion together with potential aggregation of RUs,⁴⁰ most pronounced for longer alkyl substituents,²² makes it challenging to elucidate the inherent dynamics of water in the hydrophobic hydration shell.²²

Here, we isolated the inherent water dynamics using the OD stretching vibration of trace HDO molecules in water as a probe. Using ultrafast IR spectroscopies, we study the dynamics of water in aqueous solutions of three isomeric alkyl ureas (RUs). To reduce the aggregation tendency, we restrict the degree of substitution to two methyl(ene) groups (Fig. 1): 1,3-DMU, 1,1-DMU and 1-ethylurea (1-EU). We find that despite rather weak changes in the average H-bond strength of water as observed in the IR absorption spectra, RUs perturb H-bond inhomogeneity, spectral diffusion, and reorientation dynamics of water very differently with the alkylation pattern being decisive for the extent of the slow-down of the hydration dynamics.

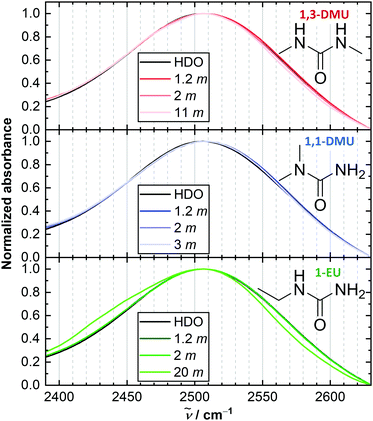Fig. 1 Intensity-normalized linear IR absorption spectra in the region of ν(OD) vibration of trace HDO in solutions of the studied RUs in 4% D₂O/H₂O at selected concentrations. Chemical structures of RUs are shown in insets. An additional low frequency shoulder is observed for 1-EU at very high solute concentrations. A similar shoulder has been attributed to N-D stretching vibrations of solute.^35,45

Results and discussion

Linear IR spectra

We use the OD stretching mode, ν(OD), of dilute HOD molecules in aqueous solutions of RUs, as a probe for the local environment and dynamics of water.^13–20 The ν(OD) band, which is centred at ∼2500 cm⁻¹ in the IR absorption spectra (Fig. 1), reveals two features common to solutions of all studied RUs: (i) no pronounced peak maximum shift with increasing solute molality, b, and (ii) a reduction of the absorption at the high frequency wing. (i) Implies a negligible solute-induced perturbation of the overall water hydrogen bond strength, similar to U.^14,19,36,44 In turn, (ii) resembles findings for TMU^14,16,44 and suggests that RUs slightly decrease the fraction of weakly H-bonded water. This is often ascribed to changes in the local water structure induced by the alkyl groups.⁴⁴ Yet, the distributions of hydrogen-bond strengths are similar between the studied RUs.

Polarization-resolved IR pump–probe experiments

To probe the picosecond dynamics of ν(OD), we perform polarization-resolved IR pump–probe experiments. In these experiments HOD molecules are ‘labelled’ via excitation of the ν(OD) mode into the first excited state. The isotropic pump–probe data, which provide the relaxation of the excitation to thermal equilibrium, reveal that the energy relaxation slows down with increasing RU concentration (see Fig. S2 and Discussion in the ESI†). Yet, this slow-down, which reflects a reduced number of and/or reduced coupling to lower frequency modes, merely scales with concentration and is not specific to the alkylation pattern.

The pump–probe experiments also label OD groups with a specific orientation. As such, the excitation is anisotropic, which is measured by the excitation anisotropy as function of waiting time, T_w. The decay of the excitation anisotropy in the pump–probe experiments is for dilute HOD in H₂O a measure for the rotational dynamics of the OD group of water.^46,47 Clearly, these rotation dynamics of water are sensitive to the concentration and to the nature of RUs (Fig. 2A, see the ESI† for details) as addition of RUs gradually slows down these water rotation: a more pronounced retardation is observed for 1,3-DMU, while 1-EU and 1,1-DMU slow down water rotation to a somewhat lesser extent.

Fig. 2 (A) Anisotropy dynamics of the ν(OD) mode of trace HDO in solutions of the studied RU in 4% D₂O/H₂O at selected concentrations. Solid lines show fits of the model described in the text to the data. The error bars (only shown for the 1,1-DMU for visual clarity) are standard deviations from four scans obtained by error propagation. They have similar magnitude for other systems with larger values at long delays due to higher uncertainties in the measured weak transient modulation. (B and C) Relative amount of water with non-bulk rotational dynamics as a function of RU molality, b, represented as its fraction f_s (B) and as apparent hydration number Z^app (C). Lines are mere guides to the eye. The error bars are standard deviations from the fits of eqn (S4) (ESI†) to the data. The inset in panel (B) shows an expanded view at low solute concentrations.

To compare these results quantitatively to similar experiments reported for U³⁵ and TMU,^14,18,25 we fit a two-state decay model to the anisotropy decays: we model the measured anisotropy as a mole-fraction-weighted average of contributions from bulk-like water and from non-bulk-like water whose dynamics are slowed down by the solute (see further details in the ESI†). We note that – despite MD simulations suggested a broad distribution of retardation factors within the hydration shell of similar amphiphilic small molecular solutes^30,32,33 – this model with two rotation time scales (eqn (S4) in the ESI†) suffices to describe the data with the least number of adjustable parameters. While the exact number of perturbed water molecules depends on the model (Fig. S3 in the ESI†), the trends across the studied RUs are also reproduced assuming different degrees of retardation.

The fraction of slowed-down water molecules, f_s, are shown in Fig. 2B together with the apparent hydration numbers Z^app (= f_s/(b × 10⁻³ × 18 g mol⁻¹)) in Fig. 2C, which correspond to the number of thus detected slowed-down water molecules per solute molecule. At low solute concentrations (see inset in Fig. 2B), f_s rises nearly linearly for all studied RUs, which suggests the non-bulk water fraction to originate from a perturbation of water molecules in the solutes’ hydration shell.^14,18,19 The perturbation at low solute concentrations is more pronounced for 1,3-DMU compared to 1,1-DMU and 1-EU. At higher solute concentrations (>5 m) the increase of f_s with concentration levels off, which is equivalent to a decrease of Z^app with increasing solute concentration (Fig. 2C). Such effect is commonly ascribed to solvation shell overlap and/or solute aggregation.^18,23,24,40 At very high concentrations, close to the solubility limit, the apparent hydration numbers seem to converge to similar values of ≈2–2.5 for 1,3-DMU and 1,1-DMU, whereas for 1-EU, Z^app further decreases to ≈1.5 at 24 m. Our estimations of the apparent hydration numbers of RUs fall in between the previously reported values for U (Z^app ≈ 1)³⁵ and TMU (Z^app ≈ 16)^14,18,25 across similar concentration ranges.

At low solute concentrations, where self-aggregation of RUs is less probable²² (see inset of Fig. 2B and discussion on aggregation below), the perturbation of water dynamics does not simply scale with the number of CH₂/CH₃ groups.^14,17,18,20 For rather dilute solutions a slow-down due to a retardation of the frame rotation within the extended jump model, is unlikely to cause the observed slow-down, because viscosities – a proxy for the frame dynamics – of aqueous RU solutions are rather similar.¹² The rather unperturbed linear spectra (Fig. 1) render also enthalpic effects due to solute acting as a strong H-bond donor/acceptor^32,39,41 unlikely. Thus, within the framework of the jump model, excluded volume effects appear to dominate the slow-down of water's rotational dynamics. Remarkably, despite the total solvent accessible volume is nearly identical for the three studied RUs (see ref. 48 and Table S1, ESI†), 1,3-DMU slows-down water rotation to a larger extent, than 1,1-DMU and 1-EU, in line with the DR studies.^23,24 These differences amongst the studied RUs may in part be explained by the different exposure of the hydrophobic groups to water, which can vary by a factor of ∼1.4 (Table S1, ESI†). Yet, the Z^app values at low concentrations differ by a factor of ∼4 at low concentrations (Fig. 2C). Hence, our results suggest that not only the excluded volume due to the hydrophobic methyl(ene) groups affects the magnitude of the retardation, but also their distribution within the solute. Apparently, rather distant methyl groups, like in 1,3-DMU disturb water's rotational dynamics more efficiently, than hydrophobic substituents located at a single N atom, like in 1,1-DMU and 1-EU. The strong retardation due to 1,3-DMU could be explained by enhanced restriction of the rotational mobility of water molecules forming H-bonds with urea's C=O and/or N–H groups due to combined steric shielding by the two methyl groups. Thus, for 1,3-DMU the potential approach of new H-bonding partners, which is required for a successful rotational jump, is more restricted by the two distant methyl groups of 1,3-DMU, as compared to 1,1-DMU and 1-EU.

At high solute concentrations, self-aggregation and hydration shell overlap obviously affect the observed retardation of water rotational dynamics, which is most pronounced for 1,3-DMU. Indeed, MD simulations^23,24 suggest that 1,3-DMU forms polar H-bonded head-to-tail aggregates and parallel stacks where both methyl and carbonyl groups are substantially solvent exposed. Conversely, 1,1-DMU has been reported²³ to have lower geometric hydration number for the methyl groups compared to 1,3-DMU and to prefer anti-parallel stacked dimers, which has been reported to result in a lower net-hydration number for the methyl groups of 1,1 DMU, compared to 1,3-DMU. Despite these differences and the general trend of enhanced aggregation with increasing alkyl chain length,^{11,23,24,28,49,50} the overall tendency to self-aggregate seems to be rather similar, as the diffusivities of 1,3-DMU and 1-EU show comparable deviations from ideal behaviour.⁴⁹ Noteworthy, we find Z^app ranging from 1–3 for 1-EU and 1,1-DMU at all concentrations and also for 1,3-DMU Z^app approaches this value at high solute concentrations where aggregation certainly plays a role. These limiting values are consistent with 1,1-DMU²³ and 1,3-DMU²⁴ slaving the dynamics of 2–3 water molecules primarily next to the carbonyl moiety at similarly high concentrations.

2D-IR

The rotational dynamics of water primarily report on the kinetics of successful H-bond switches, i.e. only those H-bond dynamics that also involve switching of the H-bond acceptor.^39,43,46 Yet, the overall H-bond fluctuations, including those that precede such switches, may differ. To study the effect of RUs on all H-bond fluctuations, we perform time-resolved two-dimensional infrared (2D-IR) spectroscopy experiments,^29,41,51 which provide information on the presence and the lifetime of inhomogeneity of H-bond strengths in solutions. This is achieved by mapping temporal correlations of excitation ([small nu, Greek, tilde]_pump) and detection ([small nu, Greek, tilde]_probe) frequencies in a 2D-IR experiment.⁵² For a sample with a distribution of microenvironments, like in aqueous solutions, the correlation is present (at T_w = 0) and molecules keep memory of the initial excitation frequency, i.e. inhomogeneous broadening.⁵² In a 2D-IR spectrum this broadening corresponds to an elongation of the signals along the diagonal line ([small nu, Greek, tilde]_pump = [small nu, Greek, tilde]_probe). Fluctuations of H-bond environments lead to a loss of the memory, resulting in a reduction of the elongation with increasing T_w.

The 2D-IR signals corresponding to |0〉–|1〉 transitions of ν(OD) of trace HDO in water and in 3 m 1,1-DMU solution exhibit a finite elongation along the diagonal (e.g. the left column in Fig. 3A). We quantify the elongation using the center line slope (CLS) method^52–55 by tracking the maximum signal corresponding to |0〉–|1〉 transitions along the probe axis at a given [small nu, Greek, tilde]_pump (see white symbols in the top left panel of Fig. 3A). The CLS is thus defined as d[small nu, Greek, tilde]_probe/d[small nu, Greek, tilde]_pump and obtained from a linear fit to these points around the peak maximum⁵⁴ (red lines in Fig. 3A).

Fig. 3 (A) 2D-IR spectra of the ν(OD) vibration of trace HOD measured at selected waiting times T_w in 4% D₂O/H₂O solvent (top row) and in the 3 m 1,1-DMU solution (bottom row). Each spectrum is normalized to its absolute maximum and the contour levels are symmetrically spaced around zero at 10% increments. Signal corresponding to negative |0〉–|1〉 signatures are shown in blue, the positive |1〉–|2〉 contributions are shown in red. White symbols in the top left panel are an example of the center line points. Red solid lines are linear fits through the center line points at [small nu, Greek, tilde]_pump = 2500 ± 50 cm⁻¹. (B) Center line slope (CLS) values at different waiting times T_w. Data before 0.2 ps were omitted to avoid pulse overlap artifacts. Error bars are standard errors of the linear fits. Lines are exponential fits with decay times 0.71 ± 0.05 ps (HDO), 1.12 ± 0.06 ps (1,3-DMU), 1.1 ± 0.1 ps (1,1-DMU) and 0.83 ± 0.15 ps (1-EU).

As already apparent from the 2D-IR spectra in Fig. 3A for a 3 m solution of 1,1-DMU and quantitatively compared for 3 m solutions of other RUs in Fig. 3B, addition of 1,1-DMU and 1,3-DMU leads to a significant increase of the initial CLS value (at T_w = 200 fs). This implies higher inhomogeneity of microenvironments experienced by the ν(OD) in the solution as compared to neat water, despite the negligible changes in the absorption spectra (Fig. 1). Similar enhancements of the inherent spectral inhomogeneity were reported for ν(OH) of trace HOD in D₂O for solutions of TMU.^16,20 Conversely, the initial CLS value of ν(OD) of trace HOD in 3 m solution of 1-EU is very close to that measured in neat water. This implies that 1-EU does not significantly perturb the distribution of the local microenvironments sampled by the ν(OD).

Similar to the initial heterogeneity, also the decay of the CLS is slowed down in the presence of 1,1-DMU and 1,3-DMU, as opposed to solutions of 1-EU, which are comparable to neat water (Fig. 3B). At higher solute concentrations of 1-EU (5 m) we detect also changes of the CLS dynamics as compared to water, yet the marked difference between 1-EU and 1,3-DMU persists (see Fig. S4, ESI†). The decay of the CLS (spectral diffusion) is due to the excited OD oscillators exploring all types of H-bonding environments with increasing T_w. Clearly, 1,1 DMU and 1,3-DMU effectively slow-down frequency–frequency decorrelation dynamics, which are characteristic to the elongation/shortening of the H-bonds.^52,55 For a 3 m solution of 1-EU these fluctuations are very similar to the fluctuations in neat water, where the H-bond weakening/strengthening dynamics that precede switching of an H-bonded partner can account for the full decay of the CLS.²⁹

The observed slow-down of the CLS dynamics for 1,1-DMU and 1,3-DMU provides evidence for a retardation of H-bond dynamics within the solvation shell,^31,38,45 which is typically due to less dynamic water–solute H-bond exchange.^29,39,41 The slow-down of the CLS decay is thus consistent with an increasing H-bond lifetime between the solutes and water, as has been reported for both 1,3-DMU²⁴ and 1,1-DMU.²³ Given the slow-down is dominated by less dynamic solute–water H-bonds,^29,39,41 our results suggest that the H-bond accepting and donating groups of 1,3-DMU and 1,1-DMU are similarly exposed to the solvent water. In turn, the absence of significant effect of 1-EU on the CLS points to less exposure to water, which can be related to a slightly higher tendency to self-aggregate.

Conclusions

Taken together, our results demonstrate that the substitution pattern of hydrophobic fragments in RUs is decisive for solute hydration. We observe in the IR absorption spectra only weak and non-specific solute-induced perturbation of the distribution of water H-bond strengths. Yet, the H-bond heterogeneity and fluctuation dynamics are affected by 1,1-DMU and 1,3-DMU and not by 1-EU. We attribute these differences to different exposure of H-bonding groups of urea to water as a result of differences in self-aggregation tendencies (most pronounced for 1-EU). This trend is almost certainly also true for hetero-aggregation with biomacromolecules^6–12 or poorly soluble compounds^2–5 where concentrated solutions of RUs (2–8 m) are used to denature or solubilize these solutes, respectively.

Conversely, rotational dynamics associated with water H-bond switching is slowed down most by 1,3-DMU due to excluded volume of two distant methyl groups. The marked slow-down of water rotation by 1,3-DMU can be explained by steric shielding of a subset of water molecules between the two rather distant methyl groups of 1,3-DMU, in line with the extended jump model. Conversely, restricting the volume exclusion to the vicinity of only one N atom of urea (1,1-DMU and 1-EU) results in a weaker perturbation of water's rotation. Our results thus demonstrate the relevance of the distribution of hydrophobic moieties to hydration, similar to recent findings for hydrophilic groups.⁵⁶ Together these findings may help developing a better understanding of the subtle interplay of these effects.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

BAM gratefully acknowledges funding from the Alexander von Humboldt Foundation. This project has received funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation program (grant agreement no. 714691) and support from the MaxWater project of the Max Planck Society is acknowledged. We thank Ellen H. G. Backus for valuable comments on the manuscript. We also acknowledge stimulating discussions with Vira Agieienko and Richard Buchner. Open Access funding provided by the Max Planck Society.

References

1. D. Ben-Amotz, Annu. Rev. Phys. Chem., 2016, 67, 617–638.
2. H. Suzuki and H. Sunada, Chem. Pharm. Bull., 1998, 46, 125–130.
3. K. Nidhi, S. Indrajeet, M. Khushboo, K. Gauri and D. J. Sen, Int. J. Drug Dev. Res., 2011, 3, 26–33.
4. S. Feldman and M. Gibaldi, J. Pharm. Sci., 1967, 56, 370–375.
5. H. Suzuki and H. Sunada, Chem. Pharm. Bull., 1997, 45, 1688–1693.
6. T. T. Herskovits and H. Jaillet, Science, 1969, 163, 282–285.
7. B. Ding, L. Yang, D. Mukherjee, J. Chen, Y. Gao and F. Gai, J. Phys. Chem. Lett., 2018, 9, 2933–2940.
8. Y. Gao, J. Yang, H. Fan, Y. Ding and X. Ye, J. Polym. Sci., Part B: Polym. Phys., 2016, 54, 1145–1151.
9. L. B. Sagle, Y. Zhang, V. A. Litosh, X. Chen, Y. Cho and P. S. Cremer, J. Am. Chem. Soc., 2009, 131, 9304–9310.
10. T. T. Herskovits, H. Jaillet and B. Gadegbeku, J. Biol. Chem., 1970, 245, 4544–4550.
11. F. Rodríguez-Ropero and N. F. A. van der Vegt, J. Phys. Chem. B, 2014, 118, 7327–7334.
12. Í. F. T. de Souza and E. P. G. Arêas, J. Colloid Interface Sci., 2017, 507, 190–199.
13. C. Petersen, A. A. Bakulin, V. G. Pavelyev, M. S. Pshenichnikov and H. J. Bakker, J. Chem. Phys., 2010, 133, 164514.
14. Y. L. A. Rezus and H. J. Bakker, J. Phys. Chem. A, 2008, 112, 2355–2361.
15. J. Hunger, K.-J. Tielrooij, R. Buchner, M. Bonn and H. J. Bakker, J. Phys. Chem. B, 2012, 116, 4783–4795.
16. A. A. Bakulin, C. Liang, T. la Cour Jansen, D. A. Wiersma, H. J. Bakker and M. S. Pshenichnikov, Acc. Chem. Res., 2009, 42, 1229–1238.
17. Y. L. A. Rezus and H. J. Bakker, Chem. Phys., 2008, 350, 87–93.
18. Y. L. A. Rezus and H. J. Bakker, Phys. Rev. Lett., 2007, 99, 148301.
19. Y. L. A. Rezus and H. J. Bakker, J. Phys. Chem. B, 2009, 113, 4038–4044.
20. A. A. Bakulin, M. S. Pshenichnikov, H. J. Bakker and C. Petersen, J. Phys. Chem. A, 2011, 115, 1821–1829.
21. K. Mazur, I. A. Heisler and S. R. Meech, J. Phys. Chem. B, 2011, 115, 2563–2573.
22. U. Kaatze, J. Chem. Phys., 2018, 148, 014504.
23. V. Agieienko, C. Hölzl, D. Horinek and R. Buchner, J. Phys. Chem. B, 2018, 122, 5972–5983.
24. V. Agieienko, D. Horinek and R. Buchner, Phys. Chem. Chem. Phys., 2017, 19, 219–230.
25. K.-J. Tielrooij, J. Hunger, R. Buchner, M. Bonn and H. J. Bakker, J. Am. Chem. Soc., 2010, 132, 15671–15678.
26. J. Qvist and B. Halle, J. Am. Chem. Soc., 2008, 130, 10345–10353.
27. A. Shimizu, K. Fumino, K. Yukiyasu and Y. Taniguchi, J. Mol. Liq., 2000, 85, 269–278.
28. L. Costantino, G. D’Errico, O. Ortona and V. Vitagliano, J. Mol. Liq., 2000, 84, 179–191.
29. G. Stirnemann, J. T. Hynes and D. Laage, J. Phys. Chem. B, 2010, 114, 3052–3059.
30. D. Laage, G. Stirnemann and J. T. Hynes, J. Phys. Chem. B, 2009, 113, 2428–2435.
31. J. T. Titantah and M. Karttunen, J. Am. Chem. Soc., 2012, 134, 9362–9368.
32. G. Stirnemann, E. Duboué-Dijon and D. Laage, J. Phys. Chem. B, 2017, 121, 11189–11197.
33. K. Usui, J. Hunger, M. Sulpizi, T. Ohto, M. Bonn and Y. Nagata, J. Phys. Chem. B, 2015, 119, 10597–10606.
34. W. Homsi Brandeburgo, S. T. van der Post, E. J. Meijer and B. Ensing, Phys. Chem. Chem. Phys., 2015, 17, 24968–24977.
35. Y. L. A. Rezus and H. J. Bakker, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 18417–18420.
36. J. K. Carr, L. E. Buchanan, J. R. Schmidt, M. T. Zanni and J. L. Skinner, J. Phys. Chem. B, 2013, 117, 13291–13300.
37. S. T. van der Post, S. Scheidelaar and H. J. Bakker, J. Phys. Chem. B, 2013, 117, 15101–15110.
38. J. T. Titantah and M. Karttunen, Sci. Rep., 2013, 3, 2991.
39. D. Laage, G. Stirnemann, F. Sterpone, R. Rey and J. T. Hynes, Annu. Rev. Phys. Chem., 2011, 62, 395–416.
40. G. Stirnemann, F. Sterpone and D. Laage, J. Phys. Chem. B, 2011, 115, 3254–3262.
41. D. Laage, G. Stirnemann and J. T. Hynes, J. Photochem. Photobiol., A, 2012, 234, 75–82.
42. D. Laage and J. T. Hynes, Science, 2006, 311, 832–835.
43. D. Laage and J. T. Hynes, J. Phys. Chem. B, 2008, 112, 14230–14242.
44. A. Panuszko, P. Bruździak, E. Kaczkowska and J. Stangret, J. Phys. Chem. B, 2016, 120, 11159–11169.
45. C. Yan, P. L. Kramer, R. Yuan and M. D. Fayer, J. Am. Chem. Soc., 2018, 140, 9466–9477.
46. L. Piatkowski, K. B. Eisenthal and H. J. Bakker, Phys. Chem. Chem. Phys., 2009, 11, 9033.
47. Y. L. A. Rezus and H. J. Bakker, J. Chem. Phys., 2005, 123, 114502.
48. S. Cabani, P. Gianni, V. Mollica and L. Lepori, J. Solution Chem., 1981, 10, 563–595.
49. R. Sartorio, P. Padulano, L. Costantino and V. Vitagliano, J. Solution Chem., 1981, 10, 111–119.
50. Y. Cui, J. Pharm., 2013, 2013, 1–15.
51. C. P. Lawrence and J. L. Skinner, J. Chem. Phys., 2003, 118, 264–272.
52. P. Hamm and M. T. Zanni, Concepts and Methods of 2D Infrared Spectroscopy, Cambridge University Press, Cambridge, 2011.
53. Q. Guo, P. Pagano, Y.-L. Li, A. Kohen and C. M. Cheatum, J. Chem. Phys., 2015, 142, 212427.
54. E. E. Fenn and M. D. Fayer, J. Chem. Phys., 2011, 135, 074502.
55. K. Kwak, S. Park, I. J. Finkelstein and M. D. Fayer, J. Chem. Phys., 2007, 127, 124503.
56. B. Ensing, A. Tiwari, M. Tros, J. Hunger, S. R. Domingos, C. Pérez, G. Smits, M. Bonn, D. Bonn and S. Woutersen, Nat. Commun., 2019, 10, 2893.

---

Footnote

† Electronic supplementary information (ESI) available: Experimental procedures, isotropic transient absorption data, details of the fitting model for the isotropic and anisotropic data, additional CLS results and estimation of accessible solvent area. See DOI: 10.1039/c9cp04108g

---