Shedding light on the atomic-scale structure of amorphous silica–alumina and its Brønsted acid sites

Abstract

In spite of the widespread applications of amorphous silica–aluminas (ASAs) in many important industrial chemical processes, their high-resolution structures have remained largely elusive. Specifically, the lack of long-range ordering in ASA precludes the use of diffraction methods while NMR spectroscopy has been limited by low sensitivity. Here, we use conventional as well as DNP-enhanced ²⁹Si–²⁹Si, ²⁷Al–²⁷Al, and ²⁹Si–²⁷Al solid-state NMR experiments to shed light on the ordering of atoms in ASAs prepared by flame-spray-pyrolysis. These experiments, in conjunction with a novel Monte Carlo-based approach to simulating RESPDOR dephasing curves, revealed that ASA materials obey Loewenstein's rule of aluminum avoidance. 3D ¹⁷O{¹H} and 2D ¹⁷O{¹H,²⁷Al} experiments were developed to measure site-specific O–H and HO–Al distances, and show that the Brønsted acid sites originate predominantly from the pseudo-bridging silanol groups.

---

Introduction

As one of the most popular solid acids, silica–alumina catalysts, including amorphous silica–alumina (ASA) and zeolites, are widely used in organic synthesis, bio-refining, and the petrochemical industry.^1,2 Their catalytic performance strongly depends on the local structure surrounding the catalytically-important Brønsted acid sites (BASs). It is well-known that the BASs in crystalline zeolites derive from the presence of protons required to balance the negatively charged oxygens resulting from the substitution of Si by tetracoordinated Al (Al^IV) species. These are known as bridging silanol groups (Si(OH)Al^IV). It has been hypothesized that the formation of BASs in ASAs is analogous to that in zeolites,^3–6 but this hypothesis is controversial, as many researchers believe that ASAs generally provide only moderate acidity, unlike the strong zeolitic Brønsted acidity.^7,8 Specifically, it has been proposed that the BASs in ASAs are formed by silanols interacting with nearby aluminum sites; these have been termed pseudo-bridging silanol groups.^7–10

Although it has been theorized that the amorphous structure of ASA weakens the Al–OH bonds (e.g. 2.94–4.43 Å for pseudo-bridging silanols),⁹ when compared to those in crystalline zeolites (1.88–2.0 Å for bridging silanols, SiO(H)Al^IV), this is difficult to prove experimentally.¹¹ The amorphous nature of ASAs prevents the study of their structure by the diffraction-based techniques that have been used extensively to characterize crystalline zeolites. Given that the assignment of vibrational frequencies can be debatable,^12,13 solid-state nuclear magnetic resonance (SSNMR) appears to be the best tool for investigating the local structure of BASs in ASA.^14–20 For example, SSNMR spectroscopy was used to determine that SiO₄ tetrahedra directly coordinate to tetracoordinated (Al^IV) and pentacoordinated (Al^V) Al sites (principally Al^IV).^21,22 Moreover, ¹H–²⁷Al through-space correlation experiments have revealed that Al^IV and Al^V sites in the vicinity of silanol groups can contribute to the formation of surface BASs in ASA.²³ Nevertheless, the amorphous structure of ASAs still makes it challenging to obtain detailed structural information, such as bond lengths, using SSNMR. Again, this is in direct contrast to zeolites, whose well-ordered structures can be determined by advanced SSNMR spectroscopic methods.^24–29

The recent development of efficient high-field dynamic nuclear polarization (DNP)^30–33 has provided new opportunities for the precise structural characterization of surface sites by SSNMR. DNP operates by partially saturating an allowed, or forbidden, electron paramagnetic resonance transition with high-power microwaves, and subsequently transferring the electrons’ high polarization to the nuclear spins. With DNP, the sensitivity of SSNMR experiments can be increased by a factor of several hundred, enabling experiments that were previously inaccessible. A particular application of DNP concerns the hyperpolarization of surfaces wherein the radical polarizing agent is introduced near the surfaces of the materials by incipient wetness impregnation.^31,32 The methods’ enhanced sensitivity has already enabled the acquisition of challenging ²⁹Si–²⁷Al correlation spectra that have provided new insights into the structures of ASAs.²¹ DNP has also been applied to identifying dilute SiO₄ sites that were deposited on alumina surfaces through atomic layer deposition as well as chemical liquid deposition.^34,35 Additionally, the technique has notably enabled the observation of the ¹⁷O SSNMR resonance of hydroxyl groups situated at the surfaces of silica–alumina and the quantification of their average acidity.³⁶ In this case, however, the resolution was insufficient to afford a clear distinction of Brønsted acid sites from non-acidic silanols and aluminols.

To date, the above mentioned SSNMR studies have only been able to comment on the very short-range structure of ASA. Also of importance, however, is the question of whether the silicon and aluminum atoms distribute homogeneously throughout the material or whether Loewenstein's rule³⁷ (Al^IV–O–Al^IV linkages are forbidden) is still operative. For example, the presence of significant aluminum clustering could lessen the acidity of the catalyst. Based on entropic arguments, some reports have suggested that a statistical, or near-statistical, distribution of silicon and aluminum is expected in ASAs,^38,39 while studies of MCM-41-type aluminosilicates suggest the contrary.⁴⁰ A recent theoretical study of zeolites also showed that Al–O–Al linkages may in fact be favored in the absence of bulky counter-cations.⁴¹ Lastly, in related aluminosilicate glasses, ¹⁷O multiple-quantum magic-angle-spinning (MQMAS) experiments have shown that Al–O–Si linkages are favored over Al–O–Al and Si–O–Si linkages.^42,43

Herein, we used DNP-enhanced SSNMR to determine the long-range ordering of atoms in ASAs prepared by flame-spray pyrolysis (FSP).⁴⁴ Using ²⁹Si and ²⁷Al homonuclear correlation experiments, the potential clustering, or lack thereof, of Si and Al sites could be addressed. ²⁹Si{²⁷Al} resonance-echo saturation-pulse double-resonance (RESPDOR)⁴⁵ experiments were then used to tackle questions regarding the overall ordering of these sites in the material. A novel simulation model was designed that could directly yield, from a single ²⁹Si{²⁷Al} RESPDOR curve, the fraction of Si atoms in the clustered (silica) phase and the local Al concentration surrounding Si atoms in the mixed silica–alumina phase, as well as provide conclusive evidence of the validity of Loewenstein's rule in ASAs.

Furthermore, we used DNP-enhanced SSNMR to acquire, for the first time, three-dimensional (3D) ¹⁷O{¹H} spectra in order to improve the resolution and enable distinction of the signals corresponding to Brønsted acid sites. The proximities of these sites to ²⁷Al were assessed using ¹⁷O{²⁷Al} transfer-of-population double-resonance (TRAPDOR)^46,47 experiments, which are expected to distinguish bridging and pseudo-bridging Brønsted acid sites. We note that in all ²⁷Al–²⁷Al, ²⁹Si–²⁹Si, ²⁹Si–²⁷Al, ¹⁷O–²⁷Al, and ¹⁷O–¹H recoupling measurements we have deliberately chosen to focus on the dipolar interactions since a significant portion of what makes ASAs great catalysts, such as the presence of pseudo-bridging silanols, would have been lost when looking through the lens of the J-coupling.

Results and discussion

Throughout this paper, for conciseness, we will be referring to all the FSP-derived ASA samples as ASA/x, where x is the Al concentration, here defined as the atomic percentage of Al atoms used in the precursor (with the rest being Si).

1D and 2D ²⁷Al NMR

²⁷Al MAS spectra of ASA materials are dominated by three resonances at 0, 30, and 60 ppm that can be assigned to hexa-, penta- and tetracoordinated (Al^VI, Al^V, and Al^IV) Al species, respectively (see Fig. 1a). We note that the samples were packed in air which may influence the relative proportions of the different Al coordination numbers. Due to the limited resolution, information about the second coordination sphere can only be obtained through multidimensional SSNMR methods.^21,22 As such we used ²⁷Al–²⁷Al double-quantum–single-quantum (DQ/SQ) spectroscopy to detect the formation of Al clusters, (Fig. 1). In contrast to the 1D MAS spectrum, the DQ/SQ spectrum of the ASA/30 is dominated by a resonance corresponding to the correlation between nearby Al^VI sites in addition to a second, minor, correlation between Al^VI and Al^V sites. It thus follows that the Al^V and Al^IV sites must be primarily coordinated to silicon sites in a silica-rich phase, in agreement with Loewenstein's rule and a previous DNP-based study,²¹ which used ASA materials prepared via a controlled grafting approach. As the Al concentration is increased to 70% (in ASA/70), we observe the appearance of a number of new cross-peaks between all three types of Al coordination, indicating that at high Al concentrations the Al^IV and Al^V sites can no longer avoid each other. This leads to the formation of Al–O–Al linkages that can have a detrimental impact on catalytic activity through a reduction in local electronegativity.¹ These results are corroborated by 1D and 2D ²⁹Si SSNMR (see ESI†).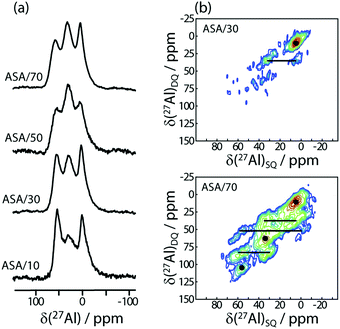

Fig. 1 ²⁷Al 1D MAS (a) and 2D DQ/SQ (b) spectra of ASA samples with different concentrations of aluminum, as indicated on the figure.

RESPDOR simulation model

To probe the arrangements of the silicon and aluminum sites in a quantitative way, we used the ²⁹Si{²⁷Al} dipolar recoupling experiments. Dipolar recoupling in spin systems containing many dipolar coupled spins is generally avoided since multispin effects often lead to complications in the analysis of the recoupling curves. This is not the case, however, for heteronuclear zero-quantum recoupling sequences such as rotational-echo double-resonance (REDOR)⁴⁸ and RESPDOR.^49,50 The misconception originates from the well-known dipolar truncation effect that plagues double-quantum homonuclear recoupling sequences and single-quantum heteronuclear recoupling sequences. Notably, sequences such as REDOR and RESPDOR are immune to dipolar truncation,⁵¹ meaning that each spin pair is recoupled simultaneously as though it were isolated. This assumes that the homonuclear dipolar coupling between the recoupled spins is removed by MAS. As a result, the total dipolar recoupling curve for a given crystallite within a powder average is simply the product of the dephasing generated by each individual spin pair (see ESI†) and can be calculated in seconds for arbitrary spin systems.

The principle challenge in applying heteronuclear dipolar recoupling to large spin systems is thus the need to design an accurate and representative model of the surroundings of the observed nucleus. In a previous study, we applied this simulation approach in order to quantify the proximities of various ¹³C sites from the support surface in Al₂O₃-supported Pd catalysts.⁵⁰ That model consisted of a slice along the 100 surface of γ-Al₂O₃. We did, however, notice that the exact structural model used was inconsequential and that the curves were instead most sensitive to the root sum squares dipolar coupling when a large number of spins were present.

A reasonable model in the case of silica–alumina consists of the first four silicon shells surrounding a silicon atom in quartz.⁵² This model incorporates all of the nearest silicon atoms and, given that the total local Si/Al density is expected to remain fairly constant in the vicinity of a silicon atom, it should be able to accurately reproduce experimental RESPDOR curves. Although the generation of RESPDOR curves for a discrete model built from quartz is relatively straightforward, simulating an amorphous material is somewhat more challenging. To simplify the following discussion, we tabulated the definitions of the various silicon and aluminum fractions that are used (Table 1).

Table 1 Definitions of the Si and Al fractions

Parameter	Definition
f Si	Overall fraction of Si atoms in the material; known from synthesis
f Al	Overall fraction of Al atoms in the material; known from synthesis
f Si,SiO2	Fraction of Si atoms that are in the segregated silica phase; obtained from RESPDOR and corresponding to 1 − fSi,mix
f Si,mix	Fraction of Si atoms that are in the mixed silica–alumina phase; obtained from RESPDOR and corresponding to 1 − fSi,SiO2
f mix,Al	Fraction of the atoms in the mixed phase that are Al; obtained from RESPDOR and corresponding to 1 − fmix,Si
f mix,Si	Fraction of the atoms in the mixed phase that are Si; obtained from RESPDOR and corresponding to 1 − fmix,Al
f mix,Al,pred.	Fraction of the atoms in the mixed phase that would be Al in the absence of a segregated alumina phase; predicted using eqn (2).

---

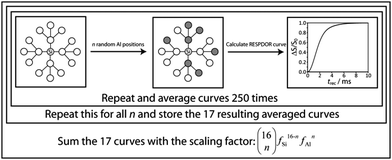
In order to represent an amorphous solid in which the silicon and aluminum sites are homogeneously distributed, we have opted for a Monte Carlo model. In this model, ‘n’ of the silicon neighbors (where 0 ≤ n ≤ 98) in the quartz model are substituted for aluminum (Fig. 2). The RESPDOR dephasing curve for this randomly generated model is then calculated using eqn (S6) (ESI†). This process is repeated 250 times for each value of n and these 99 averaged curves are stored. In order to then calculate the overall RESPDOR curve for a given Al concentration, a statistical average over the 99 RESPDOR curves needs to be taken. This is accomplished by summing all calculated RESPDOR curves with the following scaling factors:

Fig. 2 The simulation model used to calculate the RESPDOR curves for a homogeneous mixture of silica and alumina. Note that a simplified 2D model having only 2 shells (with 0 ≤ n ≤ 16) is depicted here to aid in the visualization of the simulation process while in practice a 3D model composed of 4 shells is used.

This generates a Bernoulli distribution of silicon environments which is representative of the requested aluminum concentration. This simulation process is depicted in Fig. 2 for a simpler model involving only 2 shells. A similar approach to the simulation of REDOR curves has been used in the case of multivariate metal–organic frameworks.⁵³

If we assume a perfect saturation of the ²⁷Al spins, the simulation model described above has only two variable parameters: the value of f in eqn (S6) (ESI†) represents f_Si,mix⁵⁴ and the best fit of the dephasing curve yields f_mix,Al. The other fractions can be obtained through some simple relationships (see Table 1).

This simulation model can additionally be modified to calculate the expected curves for a system that would favor compliance with Loewenstein's rule of Al avoidance. In this case Al positions are still added at random; however, each ensuing Al substitution is only allowed to take the position of a Si atom with the lowest number of Al neighbors. Since the model is truncated, the atoms in the outer shell only have a single neighbor. In order to remedy this, these atoms are assigned other outer shell atoms as neighbors in order to complete their coordination spheres. A consequence of this model is that the Al atoms become better distributed and have a higher chance of being found around the central ²⁹Si spin, particularly since the first shell atoms can only have 3 Al neighbors while those of the outer shell have 4. As such, aside from yielding information regarding the Al segregation and concentration, the Monte Carlo model is also sensitive to the overall arrangement of the atoms in the silica–alumina phase (i.e. homogeneous distribution vs. Al avoidance).

Although the RESPDOR measurement does not directly provide insights into the alumina phase, it is possible to calculate the expected Al concentration in the silica–alumina phase if all of the aluminum sites were situated in this phase; i.e., if there were no alumina phase.

If this number is in disagreement with the experimentally determined value of f_mix,Al it can be inferred that the remaining aluminum atoms must form an alumina phase, as observed by ²⁷Al–²⁷Al correlation in Fig. 1.

²⁹Si{²⁷Al} RESPDOR and the importance of Loewenstein's rule

The experimental ²⁹Si{²⁷Al} RESPDOR curves measured for all the ASA samples are shown in Fig. 3. DNP was used to enhance the sensitivity of the recoupling experiments as well as the precision of the measurements.⁵⁵ Note that the higher-frequency end of the spectrum does dephase faster than the lower-frequency portion, due to the correlation between ²⁹Si chemical shifts and the number of Al neighbors, in agreement with previous reports.⁵⁶ We did not have the necessary resolution, however, to extract neighbor information from the 1D ²⁹Si spectrum.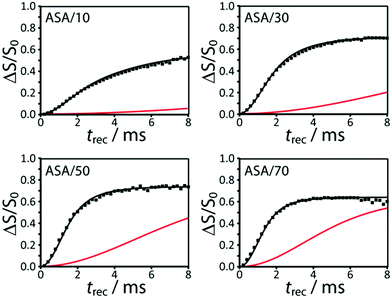

Fig. 3 DNP-enhanced ²⁹Si{²⁷Al} RESPDOR curves for the ASA samples discussed in the text. These are fit using a homogeneous model that favors Al avoidance (black). Fits calculated using a purely homogeneous model, with the same parameters, are shown in red. An enlarged version of this figure is shown in the ESI.†

We initially attempted to fit the ²⁹Si{²⁷Al} RESPDOR dephasing curves using a purely homogeneous distribution of Al, vide supra. We discovered, however, that this model yielded very poor quality fits (see red curves in Fig. 3), and required unreasonably high Al concentrations to generate a comparable dephasing as was seen experimentally. Contrary to this we managed to obtain very reasonable simulations with the model that favored Al avoidance (see black curves in Fig. 3). We can therefore conclude that the Al atoms within the silica–alumina phase must obey, to a considerable degree, Loewenstein's rule of aluminum avoidance. Note that this has also been observed in aluminosilicate glasses using ¹⁷O MQMAS.^42,43 The results from the fits are tabulated in Table 2.

Table 2 The structural parameters extracted from the ²⁹Si{²⁷Al} RESPDOR curves

Sample	f Si,mix (±0.02)	f mix,Al (±0.05)	f mix,Al,pred
ASA/10	0.58	0.21	0.16
ASA/30	0.71	0.42	0.37
ASA/50	0.73	0.58	0.58
ASA/70	0.64	0.72	0.78

---

Two additional important conclusions can be immediately inferred from the curves in Fig. 3. Firstly, the rate of dephasing increases with the aluminum loading, in agreement with an increase in the aluminum content in the silica–alumina phase. Secondly, we notice that the saturation levels of the dephasing curves are relatively high, from 0.58 and 0.73 (see f_Si,mix in Table 2), thus indicating that the majority of silicon atoms are intermixed with aluminum. At least a quarter of Si atoms in ASAs reside in a segregated silica phase (f_Si,SiO2 = 1 − f_Si,mix), with this number increasing in the samples that are closest to pure silica and alumina, as evidenced by the lower saturation level. Note that any degree of phase segregation is expected to have a negative impact on catalytic activity.

Also given in Table 2 are the values of f_mix,Al,pred, obtained from the RESPDOR data using eqn (2). As the Al concentration is increased, f_mix,Al,pred increases faster than f_mix,Al, an indication that there is the formation of a segregated alumina phase. Still, the close agreement between the two values suggests that the vast majority of the Al atoms are found in the mixed phase. This was, in fact, confirmed by ²⁷Al DQ/SQ spectroscopy (see Fig. 1).

To recapitulate, we were able to obtain two key structural insights through ²⁹Si{²⁷Al} RESPDOR.

1. The dephasing curves could only be fit by implementing a model that approximates Loewenstein's rule, strongly suggesting that aluminum avoidance remains a powerful structural ordering force in these amorphous materials.

2. Phase segregation of Al₂O₃ and SiO₂ is observed to be most prominent in the materials with the largest and smallest f_Al values.

We should finally note that energy-dispersive X-ray (EDX) measurements were carried do detect the distribution of Si and Al in all samples. Although the resulting images indicated regions with higher than average overall Si or Al concentrations (see ESI†), no extended SiO₂ or Al₂O₃ domains were detected, suggesting that the segregated phases must be highly-localized.

¹⁷O identification of acid sites

Although a great deal of information regarding the arrangements of silicon and aluminum sites in ASAs could be obtained by using ²⁹Si–²⁹Si, ²⁷Al–²⁷Al, and ²⁹Si–²⁷Al SSNMR techniques, these methods did not yield direct insight into the structures of the BASs. To gain structural understanding on these sites, it is necessary to detect the nuclei that make up the BAS, namely ¹H, and ¹⁷O. Indeed, ¹H SSNMR has been extensively used for the detection and characterization of such sites,^57,58 including the recent discovery that Al^V sites are important for the Brønsted acidity of ASAs.²³¹H SSNMR alone cannot, however, be used to characterize the environment of oxygen, namely whether it is a bridging or pseudo-bridging acid site. With DNP, however, it is possible to characterize catalytically-important surface ¹⁷O sites directly.^59–64,76

Recently, we have used ¹H{¹⁷O} dipolar recoupling experiments to characterize the Brønsted acidity of surfaces.^36,65 These experiments, however, were found to have insufficient resolution to separate the O–H distances of the sites responsible for the Brønsted acidity of silica–aluminas from those of the non-acidic silanols and aluminols. One promising approach to improving the resolution is to spread the resonances along a third dimension during which the ¹H chemical shifts are allowed to evolve. A similar approach was recently used to distinguish μ-1 and μ-2 OH sites at the surface of γ-Al₂O₃.⁶⁶ Given that typical BASs are expected to resonate near 5 ppm, while the silanols in our material resonate at 1.3 ppm,⁵⁷ it should be possible to separate the ¹⁷O–¹H dipolar couplings for the BAS from the other hydroxyls.

We have thus developed the 3D ¹⁷O{¹H} PDLF-PRESTO-HETCOR pulse sequence depicted in Fig. 4a (with PDLF being proton-detected local-field, PRESTO being phase-shifting effects a smooth transfer of polarization, and HETCOR standing for heteronuclear correlation). The experiment first starts with the excitation of ¹H spins followed by their evolution for a period of t₁ under frequency-switched Lee-Goldburg (FSLG) homonuclear decoupling. The ¹H magnetization is then z-filtered and ¹H{¹⁷O} dipolar recoupling, using a windowed symmetry-based R18₂⁵ sequence, is applied. The use of a windowed R sequence and a phase shift ensures that the recoupled curves are insensitive to rf field maladjustments and ¹H chemical shift anisotropy.⁸⁰ The ¹H longitudinal magnetization is subsequently transferred to ¹⁷O by a PRESTO-II polarization transfer using the R18₁⁷ recoupling sequence. The 3D Fourier transform of an experiment acquired using this pulse sequence then gives a 3D spectrum correlating ¹H chemical shift, ¹⁷O chemical shift, and ¹H–¹⁷O dipolar coupling. Note that these measurements were performed using a non-hydrogen bonding solvent (1,1,2,2-tetrachloroethane, TCE) such that the distance measurements reflect the correct structures of the material, as was previously demonstrated.³⁶ The solvent's inertness was additionally confirmed through the room temperature ¹H MAS experiments (see ESI†).

Fig. 4 (a) Pulse sequence diagram for the 3D ¹⁷O{¹H} PDLF-PRESTO-HETCOR experiment. (b) DNP-enhanced 2D ¹⁷O–¹H chemical shift projection of the ¹⁷O{¹H} PDLF-PRESTO-HETCOR spectrum of ASA/50. (c) Projections along the PDLF dimension for the two ¹H resonances that were detected. An enlarged view of the higher-frequency PDLF peak, with the lower-frequency one (right) set to 0 kHz, is also shown to highlight the differences in the splittings.

We applied this 3D experiment to the ¹⁷O-enriched ASA/50 material, using DNP to enable the measurement. The ¹⁷O enrichment level was estimated at ∼30% (see ESI† for details). This material was chosen since it has the highest density of Brønsted acid sites, as previously demonstrated.⁴⁴ A 2D ¹H–¹⁷O HETCOR projection is shown in Fig. 4b, where at least 2 types of hydroxyls can be clearly seen along the ¹H dimension at approximately 1.3 and 5 ppm. As previously observed,⁵⁹ these resonances’ chemical shifts are also correlated to the peak positions along the ¹⁷O dimension. The resonance at 1.3 ppm can be unambiguously assigned to non- or pseudo-bridging silanols while the peak at 5 ppm could potentially be assigned to aluminols, bridging silanol groups, or hydrogen-bonded hydroxyls.⁵⁷ Note that since the formal bonding interactions are unaffected by the nearby Al site, pseudo-bridging silanols cannot be distinguished from non-bridging silanols using chemical shifts. Therefore, the resonance at 1.3 ppm must be assigned to both isolated (i.e. non-hydrogen bonding) non-bridging silanols as well as isolated pseudo-bridging silanols. The one-dimensional, DNP-enhanced, ¹⁷O{¹H} PRESTO spectrum is shown in Fig. S11 (ESI†).

Slices taken along the dipolar dimension for each of these ¹H chemical shifts enable us to measure and compare the average O–H bond lengths of both sites. Note that while there is a distribution of O–H bond lengths, this method only allows us to determine the average value; albeit one that is well-correlated to the acidity of a hydroxyl.³⁶ The hydroxyls resonating at 1.3 ppm have an average O–H bond length of 0.992 Å with the other site having an average O–H bond length of 1.003 Å. The uncertainties in the dipolar couplings for the 1.3 ppm and 5 ppm peaks, determined as FWHM/(S/N),⁶⁷ are 300 Hz and 700 Hz, respectively, which roughly translates to distance uncertainties of 0.005 Å and 0.013 Å. Thus, while these two values are within the experimental error from one another, it is reasonable to rule out an assignment of the 5 ppm resonance to aluminols, as these would be expected to have a much shorter average O–H bond length than silanols.^36,68 To further corroborate this assignment, we attempted ²⁷Al{¹H} CP and PRESTO experiments, in combination with DNP. They were both unsuccessful, strongly suggesting that aluminols are quite sparse on this material. The ¹⁷O{¹H} PDLF-PRESTO-HETCOR experiment cannot, however, distinguish between a bridging silanol and a hydrogen-bonded silanol, due to the lack in resolution in the dipolar dimension. However, we can take advantage of the fact that the two types of silanols observed here are partially resolved in the ¹⁷O dimension of the HETCOR spectrum, and use an ¹⁷O–²⁷Al double-resonance experiment to assign the site resonating at ∼15 ppm.

Unfortunately, there are currently no reliable dipolar recoupling methods that are applicable to measure accurate distances between pairs of quadrupolar nuclei (such as ¹⁷O and ²⁷Al). In this case, however, since the O–Al distances in bridging silanols (1.88 to 2.0 Å) are expected to be far shorter than in pseudo-bridging silanols (2.94 to 4.43 Å),⁹ qualitative ¹⁷O–²⁷Al double-resonance experiments should be able to clarify the assignment. More specifically, if the hydroxyls resonating at ∼15 ppm for ¹⁷O correspond to bridging silanols, they should dephase significantly faster than those at ∼−60 ppm, which were assigned to non- or pseudo-bridging silanols. We have thus designed a ¹⁷O{¹H, ²⁷Al} PRESTO-TRAPDOR experiment (Fig. 5a) that can be used to measure TRAPDOR dephasing curves for hydroxyl oxygens. In this sequence we have simply lengthened the PRESTO echo delay in order to insert an optional ²⁷Al decoupling period to perform TRAPDOR.

Fig. 5 (a) Pulse sequence diagram for the 2D ¹⁷O{¹H, ²⁷Al} PRESTO-TRAPDOR experiment. Experimental, DNP-enhanced, ¹⁷O{²⁷Al} TRAPDOR curves for the two types of hydroxyls identified in Fig. 4 are shown in (b), as indicated on the figure. TRAPDOR curves simulated using the same experimental parameters are also shown in (b) for hydroxyls which correspond to bridging silanols (black line, O–Al distance of 2 Å) and pseudo-bridging silanols (gray shaded area, O–Al distance range of 3 to 4.4 Å).

The ¹⁷O{²⁷Al} TRAPDOR dephasing curves measured using this sequence for the same ¹⁷O-enriched ASA/50 sample are shown in Fig. 5b. The experimental data are overlaid with simulated curves calculated using SIMPSON for an HO–Al distance of 2 Å (bridging site) and an HO–Al distance range of 3 to 4.4 Å (pseudo-bridging site). Clearly, the ¹⁷O resonance at 15 ppm, which is correlated to ¹H spins at 5 ppm (Fig. 4), cannot be assigned to bridging silanol groups as it has the slower dephasing of the two sites. This resonance can thus be assigned to hydrogen-bonded non- or pseudo-bridging silanols as these would have a TRAPDOR dephasing rate that is comparable with that from the 1.3 ppm silanol resonance. Additionally, both silanol resonances have TRAPDOR dephasing rates that are congruent with that of pseudo-bridging BASs. It is thus likely that pseudo-bridging silanols are responsible for the majority of the Brønsted acidity in these amorphous silica–alumina materials, as was proposed earlier.²³ We do note here that, in an earlier study,⁶ minute (2–3 orders of magnitude lower) quantities of bridging silanols have been implicated in the bulk of ASA's catalytic activity. While our study found no discernable NMR signature that can be assigned to such sites, we cannot conclusively assert that bridging silanols are entirely absent.

Experimental

All ASA samples were prepared using literature procedures⁴⁴ and were characterized using N₂ adsorption, X-ray diffraction (XRD), and EDX (see ESI†). Prior to performing the XRD, EDX, and NMR measurements, the samples were activated by dehydration at 723 K under vacuum (below 10⁻² bar) for 12 hours.

²⁷Al 1D and 2D DQ/SQ spectra were acquired using a 600 MHz Varian NMR system equipped with a 3.2 mm MAS probe. Samples were packed into 3.2 mm zirconia rotors and spun to 16 kHz. 1D spectra were acquired using a simple Bloch decay experiment with a 31.25 μs central transition-selective excitation pulse, corresponding to a radiofrequency (rf) power of 2.7 kHz. Between 128 and 2048 scans were accumulated with a recycle delay set to 0.5 s. For the 2D DQ/SQ experiments, three cycles of the BR2₂¹ recoupling sequence⁶⁹ were used to excite and reconvert 2-spin DQ coherences. A central transition-selective 180° pulse was applied during the rotor-synchronized t₁ evolution in order to filter out single-spin DQ coherences, as well as scale the chemical shifts by 52% to avoid aliasing and allow for all resonances to appear within a 16 kHz window.⁷⁰ Phase-sensitive detection was performed using the states-TPPI method. ²⁷Al MAS NMR spectra of the as-synthesized and ¹⁷O-enriched ASA/50 samples were also acquired on a Bruker AVANCE III 400 MHz solid-state NMR spectrometer, equipped with a 4 mm MAS probe, to gauge the sample integrity (see ESI†). The MAS rate was set to 8 kHz and a total of 7200 scans were accumulated with a 1 μs excitation pulse (corresponding to a flip angle of π/6) and a 0.5 s relaxation delay.

DNP-enhanced SSNMR experiments were performed on a 400 MHz Bruker DNP system equipped with an AVANCE III console, a 9.7 T gyrotron, and a 3.2 mm low-temperature MAS probe. All samples were impregnated with 16 mM solutions of the TEKPol biradical⁷¹ in TCE, packed into 3.2 mm sapphire rotors, pre-spun at room temperature outside the magnet and then at 110 K in the NMR probe.

²⁹Si{²⁷Al} RESPDOR experiments were acquired under 10 kHz MAS. CP from ¹H was achieved using a 2.5 μs ¹H excitation pulse and a 4 ms contact time and the recycle delay was set to 1.3T₁, as measured using a saturation recovery experiment. The ²⁹Si refocusing pulse lasted 10.2 μs and the ²⁷Al saturation pulse had an rf power of 100 kHz. The first-order simultaneous frequency and amplitude modulation (SFAM-1) recoupling sequence^72,73 was used with both the maximum rf and the offset modulation amplitudes set to 30 kHz. A total of 50 recoupling time increments of 2 SFAM-1 pulses were used, with 16 to 256 scans being acquired for each increment.

¹⁷O SSNMR experiments were performed on an ¹⁷O-enriched ASA/50 sample at a spinning frequency of 12.5 kHz. The PRESTO-II sequence^74–76 was used for polarization transfer using the R18₁⁷ recoupling sequence.⁷⁷ The ¹⁷O central transition-selective 90° and 180° pulses lasted 5 and 10 μs, respectively, and used an rf power of 16.7 kHz. For the ¹H–¹⁷O HETCOR experiment, the ¹H rf power for both the excitation and z-filter pulses, as well as the FSLG⁷⁸ homonuclear decoupling, was set to 100 kHz. For the PDLF^79,80 experiment, the wR18₂⁵ sequence was used during the dipolar evolution with a 50% window.⁸¹ The 3D PDLF-PRESTO-HETCOR spectrum was acquired using 32 t₁ increments of 130.7 μs for the ¹H chemical shift evolution and 24 increments of 40 μs for the dipolar evolution, each increment being composed of 32 scans with a 2.5 s recycle delay. The states-TPPI method was used for phase-sensitive detection in the ¹H chemical shift dimension, while the dipolar dimension was not phase-sensitive. Lastly, in the case of the PRESTO-TRAPDOR experiment, the power for the ²⁷Al saturation pulse was set to 100 kHz and its duration was incremented in steps of 320 μs. A total of 31 increments were used, each requiring 512 scans.

Simulations of the ¹⁷O{²⁷Al} TRAPDOR curves were performed using the SIMPSON program (ver. 4.1.1).^82,83 The quadrupolar coupling constants of the ¹⁷O and ²⁷Al nuclei were set to the expected values of 6 and 5 MHz,⁷⁶ respectively, and the asymmetry parameters were set to 0.5. The irradiation was applied on resonance for both nuclei. The parameters used replicated those from the experiment, namely a 12.5 kHz MAS frequency and a 100 kHz ²⁷Al TRAPDOR irradiation field. Powder averaging was accomplished using 232 ZCW orientations and 4 γ angles. Simulations are shown in the ESI† while varying the ²⁷Al quadrupolar coupling constant (Fig. S12, ESI†).

Conclusions

Numerous homo- and heteronuclear correlation and recoupling experiments were performed to gain detailed structural insights regarding the atom ordering in amorphous silica–alumina materials prepared using an FSP approach. The results are summarized in Fig. 6.

Fig. 6 The structural arrangements of ASA obtained through SSNMR. The existence of acid sites based on Al^V is taken from previous work.²³ PBS refers to pseudo bridging silanols.

First, using ²⁷Al DQ/SQ spectroscopy, we observed the formation of a distinct alumina-rich phase that is mostly composed of Al^VI sites (Fig. 1). As the alumina content is increased, this phase is connected to a far larger silica–alumina phase, in part through Al^V sites as evidenced by the Al^VI–Al^V correlation. For low Al concentrations the silica–alumina phase mostly contains isolated Al^IV and Al^V sites, although increased connections between all three types of Al sites were observed in the samples with the highest loadings.

²⁹Si{²⁷Al} RESPDOR experiments were then used to study the mixing of silica and alumina. For this purpose, a Monte Carlo simulation model was developed to analyze the ²⁹Si{²⁷Al} RESPDOR data and probe the spatial distribution (segregation and Al avoidance) of Si and Al. The results demonstrated the presence of a silica phase whose size is generally larger in materials with either a very high, or low Al concentration. In agreement with the ²⁷Al DQ/SQ results, the RESPDOR data could only be fitted with a model that prioritizes Loewenstein's rule of aluminum avoidance within the silica–alumina phase, providing strong evidence that it is still operative in amorphous materials such as these.

The structure of the dominant Brønsted acid sites on ASA materials was characterized using DNP-enhanced ¹⁷O SSNMR experiments. A 3D ¹H-¹⁷O-dipolar correlation experiment was performed to resolve two different types of hydroxyls possessing different O–H bond lengths. An ¹⁷O{¹H, ²⁷Al} PRESTO-TRAPDOR experiment was then applied to probe the proximity of these sites to Al and as such determine the type of BAS found in ASA. The HO–Al proximities for both sites were found to be comparable to those of pseudo-bridging silanols, and thus neither site could be assigned to bridging silanol BAS such as those reported for zeolites. These results suggest that the Brønsted acidity of the FSP-derived ASA materials originates predominantly from pseudo bridging silanols; however, we cannot exclude the existence of additional catalytically important, bridging silanols present in these materials that are below our limits of detection.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This research was supported by the U.S. Department of Energy (DOE), Office of Science, Basic Energy Sciences, Division of Chemical Sciences, Geosciences, and Biosciences. Dr Tao Ma and Yaroslav Mudryk of Ames Laboratory are thanked for help in performing the electron microscopy and XRD measurements, respectively. Ames Laboratory is operated for the DOE by Iowa State University under Contract No. DE-AC02-07CH11358. J. H. (materials synthesis) acknowledges the Australian Research Council Discovery Projects (DP150103842 and DP180104010), the SOAR Fellowship, the Faculty's MCR Scheme, Energy and Materials Clusters and the Early Career Research Scheme and the Major Equipment Scheme from the University of Sydney for the support of this project.

References

1. A. Corma, Chem. Rev., 1995, 95, 559–614.
2. G. Busca, Chem. Rev., 2007, 107, 5366–5410.
3. K. Góra-Marek and J. Datka, Appl. Catal., A, 2006, 302, 104–109.
4. B. Xu, C. Sievers, J. A. Lercher, J. A. R. van Veen, P. Giltay, R. Prins and J. A. van Bokhoven, J. Phys. Chem. C, 2007, 111, 12075–12079.
5. D. G. Poduval, J. A. R. van Veen, M. S. Rigutto and E. J. M. Hensen, Chem. Commun., 2010, 46, 3466–3468.
6. E. J. M. Hensen, D. G. Poduval, V. Degirmenci, D. A. J. M. Ligthart, W. Chen, F. Maugé, M. S. Rigutto and J. A. R. van Veen, J. Phys. Chem. C, 2012, 116, 21416–21429.
7. M. Trombetta, G. Busca, S. Rossini, V. Piccol, U. Cornaro, A. Guercio, R. Catani and R. J. Willey, J. Catal., 1998, 179, 581–596.
8. G. Crépeau, V. Montouillout, A. Vimont, L. Marieu, T. Cseri and F. Maugé, J. Phys. Chem. B, 2006, 110, 15172–15185.
9. C. Chizallet and P. Raybaud, Angew. Chem., Int. Ed., 2009, 48, 2891–2893.
10. C. Chizallet and P. Raybaud, ChemPhysChem, 2010, 11, 105–108.
11. U. Eichler, M. Brandle and J. Sauer, J. Phys. Chem. B, 1997, 101, 10035–10050.
12. F. Leydier, C. Chizallet, A. Chaumonnot, M. Digne, E. Soyer, A.-A. Quoineaud, D. Costa and P. Raybaud, J. Catal., 2011, 284, 215–229.
13. F. Leydier, C. Chizallet, D. Costa and P. Raybaud, Chem. Commun., 2012, 48, 4076–4078.
14. J. Trébosc, J. W. Wiench, S. Huh, V. S.-Y. Lin and M. Pruski, J. Am. Chem. Soc., 2005, 127, 3057–3068.
15. M. Haouas, S. Walspurger, F. Taulelle and J. Sommer, J. Am. Chem. Soc., 2004, 126, 599–606.
16. S. Li, A. Zheng, Y. Su, H. Zhang, L. Chen, J. Yang, C. Ye and F. Deng, J. Am. Chem. Soc., 2007, 129, 11161–11171.
17. J. Kanellopoulos, C. Gottert, D. Schneider, B. Knorr, D. Prager, H. Ernst and D. Freude, J. Catal., 2008, 255, 68–78.
18. L. Peng and C. P. Grey, Microporous Mesoporous Mater., 2008, 116, 277–283.
19. A. G. Stepanov, S. S. Arzumanov, M. V. Luzgin, H. Ernst, D. Freude and V. N. Parmon, J. Catal., 2005, 235, 221–228.
20. L. Peng, Y. Liu, N. Kim, J. E. Readman and C. P. Grey, Nat. Mater., 2005, 4, 216–219.
21. M. Valla, A. J. Rossini, M. Caillot, C. Chizallet, P. Raybaud, M. Digne, A. Chaumonnot, A. Lesage, L. Emsley, J. A. van Bokhoven and C. Copéret, J. Am. Chem. Soc., 2015, 137, 10710–10719.
22. A. G. M. Rankin, P. B. Webb, D. M. Dawson, J. Viger-Gravel, B. J. Walder, L. Emsley and S. E. Ashbrook, J. Phys. Chem. C, 2017, 121, 22977–22984.
23. Z. Wang, Y. Jiang, O. Lafon, J. Trébosc, K. D. Kim, C. Stampfl, A. Baiker, J.-P. Amoureux and J. Huang, Nat. Commun., 2016, 7, 13820.
24. D. H. Brouwer, R. J. Darton, R. E. Morris and M. H. Levitt, J. Am. Chem. Soc., 2005, 127, 10365–10370.
25. D. H. Brouwer, P. E. Kristiansen, C. A. Fyfe and M. H. Levitt, J. Am. Chem. Soc., 2005, 127, 542–543.
26. D. H. Brouwer, J. Am. Chem. Soc., 2008, 130, 6306–6307.
27. D. H. Brouwer, S. Cadars, J. Eckert, Z. Liu, O. Terasaki and B. F. Chmelka, J. Am. Chem. Soc., 2013, 135, 5641–5655.
28. D. H. Brouwer and K. P. Langendoen, CrystEngComm, 2013, 15, 8748–8762.
29. D. H. Brouwer and J. Van Huizen, Magn. Reson. Chem., 2019, 57, 167–175.
30. T. Maly, G. T. Debelouchina, V. S. Bajaj, K.-N. Hu, C.-G. Joo, M. L. Mak-Jurkauskas, J. R. Sirigiri, P. C. A. van der Wel, J. Herzfeld, R. J. Temkin and R. G. Griffin, J. Chem. Phys., 2008, 128, 052211.
31. A. Lesage, M. Lelli, D. Gajan, M. A. Caporini, V. Vitzthum, P. Miéville, J. Alauzun, A. Roussey, C. Thieuleux, A. Mehdi, G. Bodenhausen, C. Copéret and L. Emsley, J. Am. Chem. Soc., 2010, 132, 15459–15461.
32. A. J. Rossini, A. Zagdoun, M. Lelli, A. Lesage, C. Copéret and L. Emsley, Acc. Chem. Res., 2013, 46, 1942–1951.
33. T. Kobayashi, F. A. Perras, I. I. Slowing, A. D. Sadow and M. Pruski, ACS Catal., 2015, 5, 7055–7062.
34. A. R. Mouat, C. George, T. Kobayashi, M. Pruski, R. P. van Duyne, T. J. Marks and P. C. Stair, Angew. Chem., Int. Ed., 2015, 54, 13346–13351.
35. A. R. Mouat, T. Kobayashi, M. Pruski, T. J. Marks and P. C. Stair, J. Phys. Chem. C, 2017, 121, 6060–6064.
36. F. A. Perras, Z. Wang, P. Naik, I. I. Slowing and M. Pruski, Angew. Chem., Int. Ed., 2017, 56, 9165–9169.
37. W. Loewenstein, Am. Mineral., 1954, 39, 92–96.
38. G. N. Greaves, F. Meneau, A. Sapelkin, L. M. Colyer, I. ap Gwynn, S. Wade and G. Sankar, Nat. Mater., 2003, 2, 622–629.
39. M. J. Toplis, D. B. Dingwell, K.-U. Hess and T. Lenci, Am. Mineral., 1997, 82, 979–990.
40. M. T. Janicke, C. C. Landry, S. C. Christiansen, S. Birtalan, G. D. Stucky and B. F. Chmelka, Chem. Mater., 1999, 11, 1342–1351.
41. R. E. Fletcher, S. Ling and B. Slater, Chem. Sci., 2017, 8, 7483–7491.
42. S. K. Lee and J. F. Stebbins, J. Non-Cryst. Solids, 2000, 270, 260–264.
43. E. Yildirim and R. Dupree, Bull. Mater. Sci., 2004, 27, 269–272.
44. J. Huang, N. van Vegten, Y. Jiang, M. Hunger and A. Baiker, Angew. Chem., Int. Ed., 2010, 49, 7776–7781.
45. Z. Gan, Chem. Commun., 2006, 4712–4714.
46. E. R. H. Van Eck, R. Janssen, W. E. J. R. Maas and W. S. Veeman, Chem. Phys. Lett., 1990, 174, 428–432.
47. C. P. Grey and W. S. Veeman, Chem. Phys. Lett., 1992, 192, 379–385.
48. T. Gullion and J. Schaefer, J. Magn. Reson., 1989, 81, 196–200.
49. J. M. Goetz and J. Schaefer, J. Magn. Reson., 1997, 127, 147–154.
50. F. A. Perras, J. D. Padmos, R. L. Johnson, L.-L. Wang, T. J. Schwartz, T. Kobayashi, J. H. Horton, J. A. Dumesic, B. H. Shanks, D. D. Johnson and M. Pruski, J. Am. Chem. Soc., 2017, 139, 2702–2709.
51. L. Chen, Q. Wang, B. Hu, O. Lafon, J. Trébosc, F. Deng and J.-P. Amoureux, Phys. Chem. Chem. Phys., 2010, 12, 9395–9405.
52. M. G. Tucker, D. A. Keen and M. T. Dove, Mineral. Mag., 2001, 65, 489–507.
53. X. Kong, H. Deng, F. Yan, J. Kin, J. A. Swisher, B. Smit and O. M. Yaghi, Science, 2013, 341, 882–885.
54. X. Lu, O. Lafon, J. Trébosc and J.-P. Amoureux, J. Magn. Reson., 2012, 215, 34–49.
55. F. Pourpoint, A. S. L. Thankamony, C. Volkringer, T. Loiseau, J. Trébosc, F. Aussenac, D. Carnevale, G. Bodenhausen, H. Vezin, O. Lafon and J.-P. Amoureux, Chem. Commun., 2014, 50, 933–935.
56. J. Ren, L. Zhang and H. Eckert, J. Phys. Chem. C, 2014, 118, 4906–4917.
57. M. Hunger, Catal. Rev.: Sci. Eng., 1997, 39, 345–393.
58. Y. Jiang, J. Huang, W. Dai and M. Hunger, Solid State Nucl. Magn. Reson., 2011, 39, 116–141.
59. F. A. Perras, U. Chaudhary, I. I. Slowing and M. Pruski, J. Phys. Chem. C, 2016, 120, 11535–11544.
60. V. K. Michaelis, E. Markhasin, E. Daviso, J. Herzfeld and R. G. Griffin, J. Phys. Chem. Lett., 2012, 3, 2030–2034.
61. V. K. Michaelis, B. Corzilius, A. A. Smith and R. G. Griffin, J. Phys. Chem. B, 2013, 117, 14894–14906.
62. F. Blanc, L. Sperrin, D. A. Jefferson, S. Pawsey, M. Rosay and C. P. Grey, J. Am. Chem. Soc., 2013, 135, 2975.
63. N. J. Brownbill, D. Gajan, A. Lesage, L. Emsley and F. Blanc, Chem. Commun., 2017, 53, 2563–2566.
64. F. A. Perras, K. C. Boteju, I. I. Slowing, A. D. Sadow and M. Pruski, Chem. Commun., 2018, 54, 3472–3475.
65. J. Camacho-Bunquin, M. Ferrandon, H. Sohn, D. Yang, C. Liu, P. Anne, P. A. Ignacio-deLeon, F. A. Perras, M. Pruski, P. C. Stair and M. Delferro, J. Am. Chem. Soc., 2018, 140, 3940–3951.
66. W. Li, Q. Wang, J. Xu, F. Aussenac, G. Qi, X. Zhao, P. Gao, C. Wang and F. Deng, Phys. Chem. Chem. Phys., 2018, 20, 17218–17225.
67. G. Kontaxis, G. M. Clore and A. Bax, J. Magn. Reson., 2000, 143, 184–196.
68. M.-P. Gaigeot, M. Sprik and M. Sulpizi, J. Phys.: Condens. Matter, 2012, 24, 124106.
69. Q. Wang, B. Hu, O. Lafon, J. Trébosc, F. Deng and J. P. Amoureux, J. Magn. Reson., 2009, 200, 251–260.
70. G. Mali, G. Fink and F. Taulelle, J. Chem. Phys., 2004, 120, 2835–2845.
71. A. Zagdoun, G. Casano, O. Ouari, M. Schwarzwälder, A. J. Rossini, F. Aussenac, M. Yulikov, G. Jeschke, C. Copéret and A. Lesage, J. Am. Chem. Soc., 2013, 135, 12790–12797.
72. R. Fu, S. A. Smith and G. Bodenhausen, Chem. Phys. Lett., 1997, 272, 361–369.
73. X. Lu, O. Lafon, J. Trébosc, G. Tricot, L. Delevoye, F. Méar, L. Montagne and J. P. Amoureux, J. Chem. Phys., 2012, 137, 144201.
74. X. Zhao, W. Hoffbauer, J. S. auf der Günne and M. H. Levitt, Solid State Nucl. Magn. Reson., 2004, 26, 57–64.
75. J. D. Van Beek, R. Dupree and M. H. Levitt, J. Magn. Reson., 2006, 179, 38–48.
76. F. A. Perras, T. Kobayashi and M. Pruski, J. Am. Chem. Soc., 2015, 137, 8336–8339.
77. W. Zhao, J. L. Sudmeier, W. W. Bachovchin and M. H. Levitt, J. Am. Chem. Soc., 2001, 123, 11097–11098.
78. A. Bielecki, A. C. Kolbert and M. H. Levitt, Chem. Phys. Lett., 1989, 155, 341–346.
79. S. V. Dvinskikh, H. Zimmermann, A. Maliniak and D. Sandström, J. Magn. Reson., 2004, 168, 194–201.
80. A. Gansmüller, J.-P. Simorre and S. Hediger, J. Magn. Reson., 2013, 234, 154–164.
81. M. Edén, Chem. Phys. Lett., 2003, 378, 55–64.
82. M. Bak, J. T. Rasmussen and N. C. Nielsen, J. Magn. Reson., 2000, 147, 296–330.
83. Z. Tošner, A. Rasmussen, B. Stevensson, M. Edén, N. C. Nielsen and T. Vosegaard, J. Magn. Reson., 2014, 246, 79–93.

---

Footnote

† Electronic supplementary information (ESI) available: One-dimensional ¹H, ²⁹Si and ²⁷Al, and two-dimensional ²⁹Si–²⁹Si SSNMR spectra; N₂ physisorption; EDX and XRD characterization; additional details regarding the RESPDOR simulation model, and simulated ¹⁷O{²⁷Al} TRAPDOR curves. See DOI: 10.1039/c9cp04099d

---