Dynamic water bridging and proton transfer at a surface carboxylate cluster of photosystem II

Abstract

Proton-transfer proteins are often exposed to the bulk clusters of carboxylate groups that might bind protons transiently. This raises important questions as to how the carboxylate groups of a protonated cluster interact with each other and with water, and how charged protein groups and hydrogen-bonded waters could have an impact on proton transfers at the cluster. We address these questions by combining classical mechanical and quantum mechanical computations with the analysis of cyanobacterial photosystem II crystal structures from Thermosynechococcus elongatus. The model system we use consists of an interface between PsbO and PsbU, which are two extrinsic proteins of photosystem II. We find that a protonated carboxylate pair of PsbO is part of a dynamic network of protein–water hydrogen bonds which extends across the protein interface. Hydrogen-bonded waters and a conserved lysine sidechain largely shape the energetics of proton transfer at the carboxylate cluster.

---

Introduction

Proton transfer is ubiquitous in biology. Prominent examples of bio-systems that rely on proton transfers for their functioning include proton transporters which move protons across cell membranes,¹ ATP synthase which couples proton transfers with the synthesis of adenosine triphosphate,² and photosystem (PS) II which uses light energy to oxidatively cleave water molecules generating molecular oxygen, electrons and protons.³ A feature that is often observed in proton-transfer proteins is that they are exposed to the bulk clusters of carboxylate groups, sometimes to histidine groups, which can bind protons, functioning as a proton-binding cluster, or proton antennas.^4–10 In a proton antenna, the surface carboxylate groups that are located close to each other might retain a proton for longer times than a single carboxylate component of the cluster.⁸ Such proton antennas have been discussed, for example, in the reaction center,⁸ cytochrome c oxidase,^4,8 bacteriorhodopsin,⁶ green fluorescent protein,¹⁰ and the PsbO subunit of PSII.^9,11,12 In order to understand the dynamics of water hydrogen bonding and proton transfer in a surface carboxylate cluster, we carried out computations with classical and quantum mechanics, dissected water dynamics, and analyzed the crystal-structure interactions at a protein interface where PsbO might bind a proton.

The high-resolution structure of dimeric Thermosynechococcus vulcanus PSII solved at 100 K to a resolution of 1.9 Å allowed the assignment of 19 protein subunits for each of the PSII monomers, cofactors and special lipid molecules, and of numerous water molecules.¹³ The protein subunits include the intrinsic membrane subunits CP43/CP47, D1/D2, and cytb-559, and twelve other small subunits (Fig. 1).

Fig. 1 Interface between PsbO and PsbU in the crystal structure. The protein subunits of PSII from ref. 13 are shown as green ribbons, except for PsbO and PsbU, which are colored brown and ice blue, respectively. The selected protein groups are shown as bonds with carbon atoms colored cyan, nitrogen-blue, and oxygen-red. The inset shows a close view of the interface between PsbO and PsbU.³¹ The small cyan spheres indicate water oxygen atoms observed in the crystal structure. We note that the groups of PsbO also interact closely with the membrane-intrinsic protein subunit D1 and CP43. Fig. 1, 5, 6 and 7 were prepared using PyMol version 2.20.⁹¹

Three extrinsic subunits – PsbO, PsbV and PsbU – which are also denoted as, respectively, the 33 kDa protein, cytochrome c-550 and 12 kDa, bind at the lumen side of PSII.¹⁴ PsbO stabilizes the inorganic Mn₄CaO₅ cluster,¹⁵ where the catalytic oxidation of two water molecules occurs. PsbU plays a role in heat protection of PSII,^16–18 optimal oxygen evolution,^19,20 energy transfer and electron transport.²¹ PsbO binds to PSII at the late stages of the assembly of the complex²² and it can bind independently of cyt c-550 and PsbU.^14,23 By contrast, the effective binding of PsbU to photosystem II requires other extrinsic proteins to be present.^14,23

The mechanism of water splitting at the Mn₄CaO₅ cluster is described using the Kok cycle as a four-photon induced, four electron/four proton reaction with the formation of five intermediate states, S₀ to S₄, at different time points.^24,25 The cycle starts in the dark-stable state S₁, in which the two manganese ions of the Mn₄CaO₅ complex are thought to be in the oxidation state (III), and the other two manganese ions are in the oxidation state (IV);²⁶ the same average manganese oxidation level might be compatible with different sequences of manganese oxidation states.²⁷

A fundamental question for PSII research is how protons that are generated during the water-splitting reaction will be released to the lumen. The potential pathways for proton transfer in the protein environment of PSII, and protein groups that might be directly involved in proton transfer, have been discussed based on experiments and computations (see, e.g., ref. 11 and 28–35). An intriguing aspect is that the surface of PsbO has numerous carboxylate groups,^11,12 some of which are thought to function as a proton antenna.^9,11,12 In the crystal structure of PSII¹³ and of a truncated PsbO model³⁶ the highly conserved¹² PsbO-E97 and D102 are within the direct H-bond distance (Fig. 1), which was interpreted to suggest that a proton binds at this site.^31,36

In PSII,¹³ E97 and D102 are located at the interface between PsbO and PsbU, where they are part of an extended polar cluster of protein groups and water molecules (Fig. 1 inset). This molecular picture from the static crystal structure raises the question as to whether the PsbO proton-binding site could bridge to PsbU via dynamic hydrogen-bonded water chains.

Atomistic molecular dynamics (MD) computations are a valuable tool to study dynamic protein–water interactions, as they allow us to, for example, characterize interactions between water molecules and specific protein groups, and to evaluate the energetics of proton transfer. Previous MD simulations indicated that the residence times of waters largely depend on the location of the hydration site: waters in the convex regions of myoglobin were found to have short residence times of ≤10 ps, whereas waters trapped inside the protein or in groove regions could have residence times as long as ∼457 ps;³⁷ a qualitatively similar observation was made in recent computations of the SecA protein motor.³⁸ The upper value of water residence times obtained from MD simulations is compatible with Nuclear Magnetic Resonance (NMR) studies indicating a subnanosecond range for the residence times of water molecules on a protein surface.³⁹

To dissect dynamic interactions at the interface between PsbO and PsbU we analyzed the crystal structures of PSII, performed classical mechanical MD simulations, implemented a protocol to compute the residence times of waters interacting with PsbO and PsbU, and pursued extensive analysis of dynamic carboxylate–water H-bond networks. To evaluate the energetics of proton transfer, we performed quantum mechanical (QM) computations of proton transfers for model clusters. We find that the interface between PsbO and PsbU has several sites with long water lifetimes, and that the proton-binding site is part of a dynamic H-bonded network that extends across the interface. The energetic cost for transferring a proton within the carboxylate cluster is relatively high.

Methods

Protein structure

The coordinates for the PsbO–PsbU complex were extracted from the crystal structure of PSII from T. vulcanus¹³ (PDB ID: 3WU2, monomer 1). The calcium ion associated with PsbO in the crystal structure and 302 water molecules associated with PsbO and PsbU were included with the complex. We used CHARMM-GUI^40,41 to place the PsbO–PsbU complex in a cubic box of TIP3P⁴² water molecules, with the addition of potassium ions for charge neutrality. C19 and C44 of PsbO are disulfide bridged.⁴³

Previous crystal structure analysis and computations suggested that PsbO-D102 was likely protonated.^31,36 We thus considered PsbO-D102 as protonated (neutral), and all other titratable groups of PsbO and PsbU in standard protonation states, with Asp and Glu sidechains – negatively charged, Arg and Lys sidechains positively charged, and His sidechains single protonated on the Nδ atom. The simulation system has in total 262 627 atoms.

Potential energy function and the MD simulation protocol

We used CHARMM36m^44–48 for the potential energy function and NAMD^49,50 to perform the computations. Short-range real-space interactions were switched off using a switch function between 10 and 12 Å, and long-range Coulomb interactions were described with the smooth-particle mesh Ewald summation.^51,52 The length of all covalent bonds to H atoms was constrained.^53,54

Starting from the same set of coordinates of the simulation system, we performed 3 independent simulations (Sim1, Sim2 and Sim3) as described below and summarized in Table 1. All 3 simulations use as starting coordinates the PsbO–PsbU complex embedded in a water box.

Table 1 Summary of the simulations performed

Simulation^a	Starting coordinate set	Constraints during production run^b	Length (ns)
a Simulations labeled with a–d are short NVE simulations started from the selected coordinate snapshots of the parent NPT simulation. b The 8 Cα atoms on which constraints were placed in Sim3 are shown in Fig. 2B.
Sim1	Crystal structure	None	185.0
Stop1a	Sim1 at 24 ns		1.0
Stop1b			1.0
Stop1c			1.0
Stop1d	Sim1 at 185 ns		1.0
Stop1e			1.0
Stop1f			1.0
Sim2	Crystal structure	None	185.0
Stop2a	Sim2 at 151 ns		1.0
Stop2b			1.0
Stop2c			1.0
Sim3	Crystal structure	8 Cα atoms	185.0
Stop3a	Sim3 at 151 ns		1.0
Stop3b			1.0
Stop3c			1.0

---

Simulation Sim1 started with a geometry optimization followed by 100 ps equilibration with velocity rescaling and harmonic constraints applied to the backbone and sidechain heavy atoms with force constants of 1 kcal mol⁻¹ Å⁻² and 0.1 kcal mol⁻¹ Å⁻², respectively. All constraints were switched off for the remaining of the production run. We used a Langevin dynamic scheme^55,56 with a Nosé–Hoover piston to perform the simulations in the NPT ensemble (constant number of atoms N, constant pressure P = 1 bar, and constant temperature T = 300 K); the damping coefficient was set to 5 ps⁻¹. During equilibration with velocity rescaling we used anisotropic coupling and an integration step of 1 fs. For the production run we used isotropic coupling and a multiple time integration scheme^57,58 with 1 fs for the bonded forces, 2 fs for short-range non-bonded, and 4 fs for long-range electrostatics.

Simulation Sim2 uses the same starting coordinates and the same MD protocol as Sim1, but it starts with an independent assignment of atom velocities. Sim2 is thus a repeat simulation of Sim1.

Simulation Sim3 was performed with weak harmonic constraints (1 kcal mol⁻¹ Å⁻²) on 8 Cα atoms from the interface between PsbO and PsbU (Fig. 1); the harmonic constraints on these 8 Cα atoms were maintained throughout the entire Sim3. Except for these constraints, the MD protocol used for Sim3 is the same as that for Sim1 and Sim2. We saved coordinates each 10 ps.

To sample fast water motions, we used coordinate sets from Sim1–Sim3 to perform 12 additional, independent NVE simulations (constant volume V and constant energy E). Each of the NVE simulations was prolonged to 1 ns using an integration step of 1 fs and saving coordinates each 10 fs. To distinguish these short trajectories from the parent simulation, we denote them as Stops (Table 1).

Calculations of the distance between PsbO and PsbU

To monitor fluctuations in the relative orientation of PsbO and PsbU, we first used VMD⁵⁹ to calculate the principal axis the PsbO–PsbU complex and to align this axis with the z axis of the coordinate system. We then divided PsbO and PsbU into 4 slices each, and for each of these slices we computed the center of mass using MDAnalysis.^60,61 We monitored 4 center-of-mass distances between PsbO and PsbU slices (colored pink, cyan, magenta, and blue in Fig. 2B), and used these distances to characterize the relative orientation of PsbO and PsbU.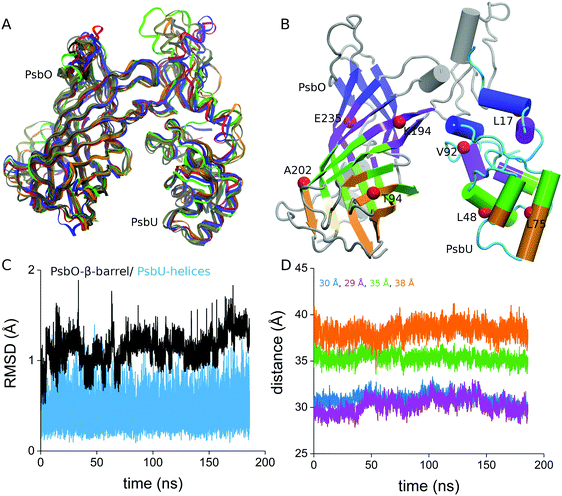

Fig. 2 Structural stability of the PsbO–PsbU complex in aqueous solution at room temperature. (A) Overlap of 5 coordinate snapshots from Sim3 with the starting coordinates from the crystal structure (colored red); the coordinate snapshots were taken from Sim3 at times 1 ns, 50 ns, 100 ns, 150 ns, and 185 ns. (B) Starting structure of the complex illustrating the 4 slices used for the center-of-mass distance calculation. The red spheres indicate the eight Cα atoms on which we placed weak harmonic constraints throughout Sim3: T94, K194, A202, and E235 of PsbO, and L17, L48, L75, and V92 of PsbU. (C) Cα RMSD values computed from Sim3; as a reference structure we used the starting crystal structure. (D) Time series of the center-of-mass distances computed for the 4 slices indicated in panel B. Numbers indicating the center-of-mass distances in the starting crystal structure¹³ are color coded according to the distance profiles. The details of the RMSD profiles for PsbO and PsbU, and a RMSD matrix for the PsbO–PsbU complex, are presented in Fig. S1 (ESI†). Additional analyses of the structural stability of PsbO and PsbU are presented in Fig. S2 (ESI†).

Algorithm to detect carboxylate–water H-bond bridges

We consider that two groups are H bonded when the distance between the heavy atom of the acceptor and the H atom of the donor group is ≤2.5 Å. The H-Bond bridges between carboxylate oxygen atoms are defined as two carboxylate groups bridged by a chain of up to 5 H-bonded water molecules.^11,35 The number of H-bonded waters in the bridge, L, gives the length of that bridge.

The maximum value allowed for L was chosen for computational simplicity, because it allows us to account for the H-bond paths that could be relevant to proton transfer: in acid–base proton transfer reactions studied in aqueous solution, the probability for proton transfer was higher when there were 2–3 intervening waters between the acid and the base, and essentially zero probability of proton transfer for 5 intervening waters.⁶²

To find water-mediated H-bond bridges between carboxylates we used an algorithm (Scheme 1) similar to that we implemented recently to analyze water–phosphate bridges at lipid membrane interfaces.⁶³ Briefly, we first determine water oxygen atoms within 11 Å of each carboxylate oxygen atom (Scheme 1A); this distance threshold suffices to capture water bridges with L = 5. For all carboxylate groups and water molecules included in the selection, we calculate all water–water and water–carboxylate H bonds, and use these H bonds to construct a graph whose nodes are oxygen atoms (carboxylate or water), and whose edges are H bonds (Scheme 1B). To reduce memory cost, we used adjacency lists to represent the graph. Each carboxylate oxygen atom is then used as a starting point for a modified depth first search⁶⁴ that starts from one carboxylate oxygen atom to search along vertices (edges of the H-bond graph) until another carboxylate group, or until a 6th water molecule is reached. The result of the search is a path or a set of paths from the starting carboxylate oxygen atom to another carboxylate oxygen atom via 1–5 H-bonded waters (Scheme 1C). We report all L ≤ 5 water bridges.

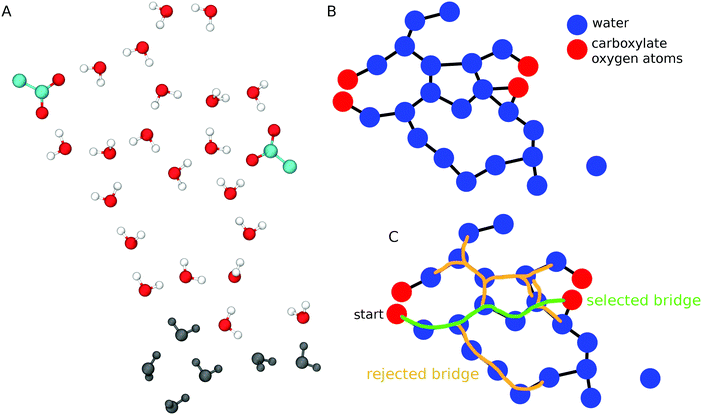Scheme 1 Algorithm to detect H-bonded water wires between carboxylate groups. (A) Schematic representation of two carboxylate groups and nearby waters. Water molecules within 11 Å of any of the carboxylate oxygen atoms are shown with oxygen atoms colored red, and H atoms colored white; waters that are further away from the carboxylates are shown in dark gray. (B) A H-bond network is constructed as a graph whose nodes are carboxylate (red) and water oxygen atoms (blue), and whose edges (black lines) are H bonds between these atoms. A water molecule on the right side of the graph has no H bond (no edge) to other groups. (C) Selection of carboxylate–water bridges. The bridge colored in green connects two carboxylate oxygen atoms via 5 H-bonded waters, and it is accepted as a valid bridge for further analysis. The water bridges colored in orange have L > 5, and are rejected. Unless specified otherwise, all molecular graphics were prepared using VMD 1.9.2.⁵⁹

Occupancy of H-bonded bridges

Two carboxylate groups are part of a H-bonded water bridge if they bridge via at least one H-bonded water chain (Scheme 1C). When this condition is met, we denote the bridge as being occupied. For Sim1–Sim3, we used the entire simulation trajectories to compute average occupancies.

Lifetime of water bridges

To estimate the lifetime of the H-bonded water bridges of a given H-bond path, we first calculate the correlation functionwhere N(t) is the number of time intervals, N_w is the number of water bridges, t₀ is the time origin, and the function p_j(t₀,t₀ + t) = 1 if the water bridge is present (connecting a specific pair of carboxylate oxygen atoms) at time interval t without interruption, and it is equal to 0 otherwise.^63,65 The calculation is performed separately for each value L of the water bridge length. The normalized correlation functionis then fitted using a stretched exponential (the Kohlrausch–Williams–Watts, KWW, function),and the lifetime of the water bridge, τ_B, is given by⁶⁶where Γ is the gamma function. To evaluate the quality of the fit we compute the Residual Sum of Squares, RSS,⁶⁷ according to the equationwhere C_N(t) is the original value, and Ĉ_N(t) is the value obtained from the fit. A value RSS = 0 is obtained when the fit reproduces the data points. We discarded the residence times obtained from fits with RSS ≥ 0.1 (as such values indicate that the fit is a poor representation of the data), the residence times of bridges sampled fewer than 20 times, and the residence times of bridges that are sampled in only one of the Stop trajectories generated from each Sim (Table 1).

For each bridge we calculated the average lifetime separately for each value of L, and for sets of Stop trajectories generated from the same coordinate set. We report the average lifetimes computed from Stop1–Stop1c, Stop1d–Stop1f, Stop2a–Stop2b, and Stop3a–Stop3c (Table 1).

Residence times of water in the first hydration shells of PsbO and PsbU

For each amino acid residue of PsbO and PsbU we calculated the water residence times from Stop3a. We used the correlation function C(t) from eqn (1) by considering p_j(t₀,t₀ + t) = 1 if the distance between the oxygen atom of water molecule j and any heavy atom of a specific amino acid residue is <4 Å. To estimate errors in C(t) we used block averaging.⁶⁸

The KWW stretched exponential from eqn (3) had been used to calculate the water residence times of water molecules interacting with proteins^38,65,69 and lipid bilayers.⁶³ Our initial test computations indicated that, for a relatively large number of sites of the PsbO–PsbU complex, the KWW exponential gives relatively poor fits of C(t); this result is compatible with previous observations.³⁷

To circumvent difficulties with the fitting when using the KWW stretched exponential, we implemented an algorithm whereby we estimated the water residence time independently by using three additional different expressions for functions used to fit C(t),

A sum of exponentials as given by eqn (6) was used in ref. 37 to calculate the residence times of waters at the hydration sites of myoglobin. The weighting parameter a gives the fraction of water molecules that enter a site and remain there for average time τ₁, relative to fast waters that enter and depart quickly with residence time τ₂, such that the terms weighted by a and (1 − a) describe the slow and fast waters, respectively.³⁷

A sum of an exponential function and a stretched exponential function, as we used in eqn (7), was introduced in ref. 70 to describe water dynamics at the interface between hydrophobic solutes. The exponential function was proposed for dynamic waters that exchange rapidly with bulk waters, and the stretched exponential – with stretch exponent λ − was proposed for trapped waters that exchange more slowly with the bulk.⁷⁰ The pre-exponent a in eqn (7) describes the fraction of water molecules whose dynamics are described by the stretched exponential and takes values a ∈ [0,1]. We note that in ref. 70 the exponential function was weighted by another parameter b. Our tests suggested that, in the particular system studied here, using (1 − a) as the weight of the exponential function provides a good model of the correlation function for small values of time t ≤ 20 ps.

A simpler exponential from eqn (8) was used in ref. 71 to describe relatively slow waters at a micelle surface.

For the stretched exponential terms – eqn (3) and the first term in eqn (7) – we report the mean residence time as calculated with eqn (4). The resulting average values are denoted as τ₃ if eqn (7) was used, and as τ₆ if eqn (3) was used to fit C(t).

For each site on the surface of PsbO and PsbU, we estimated the water residence time independently using eqn (3) and (6)–(8) for the fits. To find out which of the four individual fits approximates best the correlation function from eqn (2), and select a unique value of the water residence times, we used the Bayesian Information Criterion, BIC, as defined in ref. 72 and 73 as

BIC = p ln(n) − 2 ln (K), (9)

where p provides the number of parameters used in the individual fits (here, λ, τ₁, τ₂, τ₃*, τ₄, τ₅, a, and τ in eqn (3) and (6)–(8)); n is the size of the sample – here, n is the number of time origins t₀ from eqn (1) for which C_N(t) is nonzero; K is the maximum likelihood of the estimated model and gives the likelihood of the fitting parameters used to describe the correlation function. The lower the BIC value, the better the fit. For values a ∉ [0,1], i.e., unphysical fitting parameters, we used the next best fit according to the BIC criterion. Fits with large errors were removed and replaced with fits for which visual inspection indicated good fits of the correlation function.

Cross-correlation and orientational dynamics analysis for carboxylates of H-bonded bridges

To find out whether carboxylates of H-bond bridges have correlated motions, we used Carma 1.7⁷⁴ to analyze the correlations between motions of two atoms i and j according to the equation⁷⁵with

Δr_i = r_i(t) − 〈r_i(t)〉 (11)

where r_i(t) and r_j(t) are the position vectors for the two atoms. The correlation function C_ij has values between −1 (atoms move in opposite directions) and 1 (atoms move in the same direction); C_ij = 0 indicates lack of correlation, i.e., the atoms move independently from each other.

As our analyses are focused on H-bond networks, we computed C_ij only for pairs of heavy atoms within 22 Å during at least 50% of the MD simulation.

To probe the relative orientation of carboxyl groups involved in H-bond bridges at the interface between PsbO and PsbU, we monitored, for pairs of carboxyl groups, (i) the distance d_cc between the carbon atoms of carboxyl group pairs; (ii) the distance d_MM between the midpoints of carboxyl oxygen atoms (Scheme 2). We used the difference Δd = d_cc − d_MM to characterize the relative orientation of the pairs of carboxyl groups: positive Δd values indicate that the carboxyl groups of the pairs are oriented with the oxygen atoms towards each other, whereas negative Δd values indicate the opposite.

Scheme 2 Distances used to probe the orientational dynamics of carboxylate groups at the PsbO–PsbU interface. (A) Δd > 0 indicates that the two carboxylate groups orient towards each other. (B) Δd < 0 indicates that the two carboxylate groups orient away from each other.

Cluster models for QM proton transfer calculations

We performed QM computations to test the energetics of proton transfer at the interface between PsbO and PsbU. For computational efficiency we used four clusters of protein groups and water molecules taken from the snapshots of the equilibrated NPT simulations (Scheme 3).

Scheme 3 Clusters used for QM proton transfer calculations. The energetics of paths 1–8 is summarized in Table 3.

A first set of coordinate sets for the QM calculations was taken from Sim3, as the interface between PsbO and PsbU is best preserved due to the weak harmonic constraints used (Table 1). For an additional set of coordinate sets we inspected the relative orientation of the protonated PsbO-D102 relative to that of PsbO-E97 in Sim1 and Sim2. The two simulations indicate similar orientations of PsbO-E97 relative to the protonated PsbO-D102, with an average distance between E97-Cδ and D102-Cγ of 6.3 ± 0.7 Å in Sim1 and 5.8 ± 0.3 Å in Sim2. As in Sim2 the distance between PsbO and PsbU is somewhat shorter than that in Sim1 – which could result in shorter water bridges and reduced computational costs, and we used Sim2 to select coordinates for QM computations.

The clusters used for QM calculations (Scheme 3) contain 2–4 Asp/Glu groups, 1–2 Lys groups, 1 Asn group, and 39–47 water molecules (Scheme 3). The water molecules included in QM were selected based on the visual inspection of the trajectories in VMD. We started with the protein groups to be included in the computations, and selected all water molecules within 7 Å of these protein amino acid residues; this initial selection of the water molecules was manually filtered to include those water molecules located between any protein groups of the cluster, and waters of the hydration shell of these protein-bound waters.

To further reduce computational costs, backbone groups were not included and instead each protein group was capped by a methyl group at Cβ. To preserve the starting relative positioning of the protein groups, all Cβ atoms were fixed throughout the QM computations. The number of atoms in the QM clusters ranges from 171 in cluster A1 to 216 atoms in cluster B.

QM description of carboxylate–water clusters

QM computations were performed with 3rd-order SCC-DFTB (Self-Consistent Charge Density Functional Tight Binding^76,77) in CHARMM^44,78 using the 3ob parameters with modified parameters for the sp³-hybridized nitrogen atom.⁷⁹ Using the standard CHARMM settings for SCC-DFTB, the starting configurations of the four clusters in the reactant state were energy minimized to an energy gradient of 10⁻⁴ kcal mol⁻¹ Å⁻¹.

Proton-transfer calculations

The starting geometries of the clusters used for QM computations (Scheme 3) have protonated PsbO-D102, as set in the parent NPT simulation. We denote PsbO-D102 as the proton donor group, and cluster configurations with protonated PsbO-D102 as the reactant states of the proton transfer paths. The proton acceptor group is either PsbO-E97 or PsbO-D99, and we denote as product states cluster configurations in which PsbO-D102 is negatively charged and PsbO-E97 or PsbO-D99 is protonated.

We optimized with QM the structures of the parent A–C clusters whose coordinates originated from Sim2 or Sim3 (Scheme 3). Smaller clusters A1, B1 and B2 were generated by removing from the original coordinate set of the parent cluster selected protein groups and water molecules (Scheme 3), and re-optimizing the geometry with QM.

The QM-optimized structures of the six clusters (A, B, C, A1, B1, and B2) in their reactant states were independent of proton-transfer computations. In the first step, we used coordinate driving^80,81 with the distance d = d_D − d_A as the reaction coordinate; here, d_D is the distance between the proton and the donor oxygen atom, and d_A is the distance between the proton and the acceptor oxygen atom.⁸¹

The coordinate sets from the coordinate driving paths were then used as the input for computations of proton-transfer paths with Conjugate Peak Refinement, CPR,⁸² and with default convergence criteria from the TReK module of CHARMM. CPR has been used successfully to calculate minimum energy paths (MEPs) for proton transfer,^81,83–85 hydrolysis of ATP,⁸⁶ and isomerization reactions.^87–90 CPR starts with an initial guess of the path that consists of energy-optimized reactants and product states, with or without intermediate configurations, and finds a MEP that connects the reactant and the product by identifying the first-order saddle point(s) along the path. The selected local minima along the MEPs were further geometry optimized using the same convergence criterion as for the reactant and product states. The highest-energy first-order saddle point along the reaction path provides the rate-limiting step of that pathway.

Conserved water binding sites in the crystal structures of PsbO and PSII

To identify the conserved binding sites for water on the surface of PsbO and PsbU we used a data set of 8 recent crystal structures of PSII solved at resolutions of 2.5 Å or higher (Table 2). The crystal structures chosen for data analysis were collected for the S₁ state of dimeric PSII at 100 K, and at room temperature using femtosecond X-ray Free Laser (fs-XFEL) crystallography.

Table 2 Crystal structures of PSII in the S1 state used for analysis of water binding sites

PDB ID	Resolution (Å)	Temperature (K)	Method	Ref.
a X-ray diffraction. b Serial femtosecond X-ray crystallography.
3WU2	1.9	100	XRD^a	13
4UB6	1.95	100		97
4UB8	1.95	100		97
6DHE	2.05	298	XFEL^b	98
5WS5	2.35	293	XFEL	99
5GTH	2.5	293	XFEL	99
5B66	1.85	100	XRD	100
5B5E	1.87	100	XRD	100

---

We used PyMol⁹¹ to calculate the number of water oxygen atoms within the 3.5 Å distance of the nitrogen or oxygen atoms of all amino acid residues of the PsbO and PsbU, and to inspect amino acid residues and water molecules that could bridge PsbO and PsbU via H bonds. The average values for inter-atomic distances were computed using the 8 crystal structures listed in Table 2.

To further assess the H-bond network at the interface between PsbO and PsbU in crystal structures, we used the crystal-structure coordinates of PsbO and PsbU from ref. 13 together with the associated calcium ion and the 302 water oxygen atoms, and we added H atoms as described above for the MD system preparation, fixed all heavy atoms to their crystal-structure coordinates, and then used CHARMM to geometry optimize the coordinates of the H atoms.

Results and discussion

The 3 independent simulations of PsbO–PsbU indicate that the structures of PsbO and PsbU are stable, with relatively small values of the root-mean-square distances (RMSD) for the β-barrel region of PsbO and for the helical regions of PsbU (Fig. 2C and Fig. S1, ESI†), and with overall good preservation of the secondary structure (Fig. S2, ESI†). In Sim1 and Sim2, which were performed without any constraints, the changes in the center-of-mass distances computed for the interface between PsbO and PsbU suggest reorientation with an overall smaller opening of the cavity between PsbO and PsbU (Fig. S3, ESI†). In Sim3, in which we used weak harmonic constraints on eight Cα atoms from the PsbO–PsbU interface, the center-of-mass distances indicate that the relative orientation between PsbO and PsbU is well preserved (Fig. 2D). In what follows we will use Sim3 as a reference for the discussion.

Water dynamics on the protein surface

Most of the water molecules visit the surface of PsbO and PsbU for short times: for numerous sites, the water residence times are ∼5–10 ps, and ∼90% of the waters from the first hydration shells of PsbO and PsbU have residence times of ≤25 ps (Fig. 3 and Fig. S4, ESI†). The minority of waters with longer residence times of ∼100–500 ps are found in cavities on the surface of the protein – cavities that can be as small as to bind a single water molecule (Fig. 4 and Fig. S5, ESI†).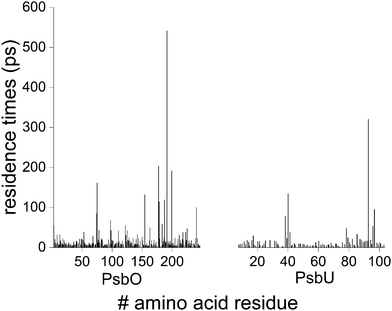

Fig. 3 Water residence times at the surface of PsbO and PsbU. Converged water residence times obtained by fitting with eqn (3), (6), (7) or (8) are shown as a function of the amino acid residue for PsbO and PsbU. For ∼87% of the total number of sites, convergence of the water residence times was obtained when using eqn (3) and (8), suggesting that most of the sites have short water residence times. The water residence times from each fit are presented in Fig. S4 (ESI†).

Fig. 4 Water binding at the interface between PsbO and PsbU. (A) PsbO and PsbU colored according to the water residence time, ranging from blue (short residence time) to red (long residence time). Green indicates water residence times ≥500 ps, and yellow indicates sites for which convergence of the water residence time computations could not be obtained (e.g., due to the small number of waters visiting these sites). For protein groups for which water residence times were computed according to eqn (5) or (7), we use the longer residence time value. The amino acid residues with water residence times ≥30 ps are shown as bonds. (B and C) Cavities at the interface between PsbO and PsbU where water molecules have long residence times. Additional molecular graphics illustrating PsbO groups with long average water residence times are presented in Fig. S5 (ESI†).

Some of the longest water residence times are observed for groups at the interface between PsbO and PsbU: waters close to PsbO-S191 and PsbU-E93 have residence times of 541.3 ± 0.9 ps and 320.6 ± 0.6 ps, respectively (Fig. 4A). At the interface, several charge and polar groups have water residence times longer than the average: PsbO-E97 (67.9 ± 0.1 ps), PsbO-E98 (42.9 ± 0.1 ps), PsbO-N154 (134 ± 0.1 ps), PsbU-D96 (53.3 ± 0.2 ps), and PsbU-R97 (95.1 ± 0.1 ps). Taken together, the computations of the water residence times indicate that the interface between PsbO and PsbU has several sites with relatively long-lived waters.

To test the robustness of the water residence time calculations, we excluded from the calculations a long-lived water molecule, and recomputed the residence times. The water molecule we excluded in this test is within 4 Å of PsbU-E93 for 99.986% steps of the MD trajectory.

We find that eqn (6) gives the best fit of C(t) for both computations, with and without the water molecule. When we exclude the stable water molecule from the water residence time computation, the residence times for waters close to PsbU-E93 are slightly reduced from τ₁ = 320.6 ± 0.6 ps to τ₁ = 312.2 ± 0.5 ps, and from τ₂ = 15.04 ± 0.02 to τ₂ = 13.96 ± 0.02 ps. Pursuant to these considerations, we suggest that the computations of water residence times are robust.

Protein–water H bonds at the PsbO–PsbU interface in crystal structures of PSII

The 8 crystal structures of PSII we analyzed (Table 2 and Fig. S6, ESI†) indicate common features of interactions at the PsbO–PsbU interface. PsbO-E97 and PsbO-D102 H bond in all structures (Fig. 5), such that the average distance between their carboxylate groups is 2.6 ± 0.1 Å; a nearby water molecule is within the H-bond distance of D102 (Fig. 5).

Fig. 5 Interactions at the PsbO proton binding site in crystal structures. The molecular graphics in Fig. 5–7 are based on PDB ID:3WU2.¹³ The carbon atoms of PsbO and PsbU groups are colored brown and gray, respectively; for both protein chains, the oxygen atoms are colored red, and nitrogen in blue. The water oxygen atoms are colored teal; the electron density represented at 1.5σ, 1σ and 0.75σ is colored light red, light green and light blue, respectively. The electron densities shown at contour levels 0.5σ, 1.0σ and 1.5σ indicate that the carboxylate groups of E97 and D102 are within the H-bond distance. The water molecule could donate a H bond to D102.

There are 4–5 waters within the H-bond distance from PsbU-D96 (Fig. 6A). 6 of the crystal structures have 4 conserved water sites within ≤3.1 Å from PsbU-E93 (Fig. 6B); the 2 remaining crystal structures (PDB IDs 5WS5 and 6DHE in Table 2) have only 2 waters close to PsbU-E93, which could be due to waters being mobile at room temperature. Some of the waters could mediate H-bond bridges between PsbO and PsbU, e.g., between PsbU-E93 and PsbO-N124 (Fig. 7A), and between PsbU-D96 and PsbO-N155 (Fig. 7C, D and Fig. S7, ESI†).

Fig. 6 Water H bonding at the surface of PsbU. (A) Close view of water H bonding to PsbU-D96. There are 5 water oxygen atoms within the H-bond distance of D96; 2 of these waters could bridge D96 to the backbone carbonyl of A90. (B) There are 4 water oxygen atoms within the H-bond distance from PsbU-E93, and one of these waters bridges the carboxylate group to the backbone amide group of G94.

Fig. 7 Water-mediated H bonding between PsbO and PsbU in the crystal structure. (A) There are 2 water molecules within the H-bond distance from PsbO-N124 and PsbU-E93. One of these waters, for which the H-bond angle is 133.6°, could H bond simultaneously to PsbU-E93 and PsbU-N124; the second water, for which the H-bond angle is 172.4°, is more likely to only H bond only to PsbU-E93. (B) A water oxygen atom bridges PsbO-D169 and PsbU-D14. (C and D) Water H bonding between PsbU-D96 and PsbO-N155. In panel C, two water molecules could bridge simultaneously to PsbO-N155 and PsbU-D96. In panel D, a 3rd water molecule can bridge PsbU-D96 with PsbO-T153.

The observation here that PsbO-E97, PsbO-N154, PsbU-E93, and PsbU-D96 interact closely with water oxygen atoms in crystal structures (Fig. 5, 6, 7A–D and Fig. S7, ESI†) is compatible with the relatively long water residence times that MD simulations indicate for these protein groups (Fig. 4). For two other carboxylate groups, PsbO-D169 and PsbU-D14, which in the crystal structure bridge via one water molecule (Fig. 7B), the water residence times are relatively short, ∼9–13 ps, suggesting the rapid exchange of waters at this site.

Dynamic carboxylate–water bridges at the proton-binding site

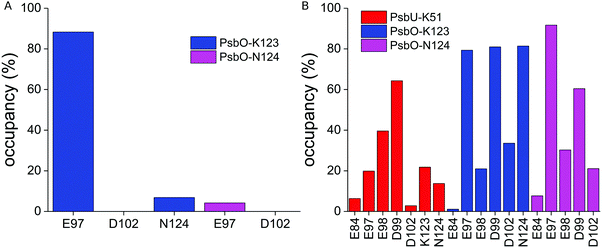
The MD simulations indicate that PsbO-E97, PsbO-D102, and PsbU-E93 are part of an extended network of protein–water H bonds at the interface between PsbO and PsbU (Fig. 8, 9 and Fig. S8, ESI†).

Fig. 8 Carboxylate–water bridges at the interface between PsbO and PsbU. The protein sidechains are shown as bonds, and water molecules as van der Waals spheres. The image is based on a coordinate snapshot from Sim3. We inspected the results of the water bridge analysis and chose a coordinate snapshot at which the carboxylate groups depicted explicitly are bridged by H-bonding waters.

Fig. 9 Direct and water-mediated H bonds between the sidechains at the interface between PsbO and PsbU. (A) Histogram of the occupancy of the selected H bonds at the proton-binding site. The blue bars show the occupancy of the H bonds between the selected sidechains and PsbO-K123; the magenta bar indicates H bonding between PsbO-E97 and PsbO-N124. (B) Histogram of water-mediated H bonds between the selected sidechains at the interface between PsbO and PsbU. The red, blue and magenta bars indicate occupancies of H bonds with PsbU-K51, PsbO-K123 and PsbO-N124, respectively. Note that PsbU-K51 samples high-occupancy H bonding with PsbO-D99; PsbO-K123 samples high-occupancy H bonding with PsbO-E97 and D99, and lower-occupancy H bonding with PsbO-D102.

PsbO-E97 samples frequent H bonds with PsbO-K123, and infrequent H bonds with PsbO-N124 (Fig. 9A). PsbO-K123 further samples water-mediated H bonds with several other carboxylate groups, including PsbO-D102 (Fig. 9B); likewise, PsbU-K51 samples transient H bonds with several PsbO carboxylate groups, including E97 and D99 (Fig. 9B). PsbO-E97 and D102, which bridge each other via a high-occupancy water bridge (Fig. 10A and C), can also bridge transiently to PsbU-E93, which bridges to PsbU-D96 (Fig. 10A, C and Fig. S8, ESI†). The somewhat higher occupancy of the water mediated bridge between PsbO-D99 and PsbU-E93 in Sim2 (∼90%) than in Sim3 (∼60%, Fig. 10C) likely arises from PsbO-D99 being closer to PsbU-E93 in Sim2 than in Sim3. Overall, we find that the shorter the bridge, the higher its occupancy (Fig. 10B).

Fig. 10 Dynamic carboxylate–water bridges connect PsbO with PsbU. (A) Close view of the PsbO–PsbU interface based on a coordinate snapshot from Sim3. The lines connecting carboxylate groups indicate H-bonded water bridges between the carboxylates. For clarity, we used carbon atoms of the carboxylate groups (Cγ for Asp, Cδ for Glu) as end points for the lines. We consider all bridges that have occupancies of at least 1% throughout the entire Sim3. The analyses performed for Sim1 are presented in Fig. S6 (ESI†). (B) Occupancy of the carboxylate–water bridges as a function of the distance between the carboxylate groups, computed from Sim1–Sim3. To measure these distances, we used the center of coordinates of the carboxylate oxygen atoms of each carboxylate group. When the carboxylate oxygen atoms are far away from each other, close to the ∼22 Å maximum separation allowed here, the occupancy of the water bridges is zero. (C) Occupancy of carboxylate–water bridges at the interface between PsbO and PsbU.

The observation of water-mediated interactions between PsbO-E97 and D102 (Fig. 10C) might appear at odds with the direct H bonding in crystal structures (Fig. 5). There is, however, a water molecule within the H-bond distance from PsbO-D102 in the crystal structure (Fig. 5), and a preference for water-mediated bridging in aqueous solution at room temperature might arise from protein and water dynamics. Alternatively, the preference for water-mediated interactions between PsbO-E97 and D102 in simulations could arise from limitations of the force field.

Carboxylate–water bridges have short lifetimes

The occupancy of a carboxylate–water bridge indicates the percentage of time during which two carboxylate groups are bridged by a H-bonded water chain, regardless of the length L of the water chain. That is, the occupancy of a bridge does not inform on the time during which the same water molecules bridge the carboxylates.

To find out for how long a pair of carboxylates can bridge via the same waters, we calculated the lifetime τ_B of the water bridges of L = 1–5 (Fig. 11). We found that τ_B is small, in the picosecond–subpicosecond range, and that it decays exponentially with the bridge length L (Fig. 11A). At the interface between PsbO and PsbU, where most water bridges have L = 3–5, τ_B is within 0.5 ps (Fig. 11B).

Fig. 11 Lifetime of carboxylate–water bridges. (A) Lifetime of water bridges as a function of the water bridge length L. For each Stop, we calculated the bridge lifetimes for each length L and for each carboxylate pair of the PsbO–PsbU complex. The average bridge lifetime of each carboxylate pair was computed separately for Stop1a–c, Stop1d–f, Stop2a–c, and Stop3a–c. The total number of carboxylate pairs used to compute the averages is ∼100 at each Stop. (B) Lifetimes of water bridges at the interface between PsbO and PsbU as calculated from Stop3. The error bars indicate the standard error. (C) Cross-correlation analysis of the carboxyl-group carbon atoms. (D) Average orientation of the carboxyl groups at the interface between PsbO and PsbU. Additional analyses are presented in Fig. S9 (ESI†).

Correlated motions and orientational dynamics of carboxylate groups

We mapped onto the structure of PsbO–PsbU inter-atomic correlations between groups sufficiently close to each other to engage in direct or water-mediated H bridging (Fig. 11C). We observe several sites of PsbO and PsbU where pairs of protein groups have correlated motions, particularly at loops and turns (Fig. 11C and Fig. S9, ESI†).

At the interface between PsbO and PsbU there are weak, if any, correlations – for example, weak correlations involve PsbO-E84, E97, E98, D99 and PsbU-E93 (C_ij takes values between 0.1 and 0.34 (Fig. 11C)); this is compatible with the short lifetimes of water-mediated bridges between PsbO and PsbU (Fig. 11B).

Although motions of PsbO-E97 and PsbU-E93 are not correlated (C_ij = −0.07), their carboxylate groups are oriented towards each other most of the time (Δd = 0.98 Å, Fig. 11D), which is compatible with the relatively high occupancy (62%) of their water-mediated bridging (Fig. 10C). But high-occupancy water bridging for a particular carboxylate pair need not necessarily associate with small orientational dynamics – for example, the occupancy of the water bridge between PsbO-D99 and PsbU-E93 is 59%, even though these two groups orient almost perpendicular to each other (Δd = 0.28 Å, Fig. 11D and Fig. S9B, ESI†)

Proton transfers at the interface between PsbO and PsbU

To characterize the energetics of proton transfer at the PsbO-D102 site, we computed 8 different paths (paths 1–8 in Table 3) starting from the QM-optimized geometries of 6 different protein–water clusters – the 3 parent clusters A–C, and the sub-clusters A1, B1 and B2, derived from parent clusters by removing selected protein groups and water molecules (Scheme 3). Parent clusters A and C use 2 different coordinate snapshots of Sim3, and cluster B uses coordinates from Sim2 (Scheme 3). The results and analysis of the QM proton-transfer computations are summarized in Table 3, Fig. 12–14 and Fig. S10–S14 (ESI†).

Table 3 Summary of the proton-transfer computations. The energy profiles of the proton-transfer pathways are presented in Fig. 8

Path	Proton acceptor	Lys included^a	Proton-transfer path	L of proton-transfer wire	ΔE^# (kcal mol^−1)	ΔE (kcal mol^−1)
a We included in the QM clusters PsbO-K123 or PsbU-K51, or both of these Lys groups. b The lower energy of the product state obtained for path 6 as compared to path 3 is due to the rearrangements of several water molecules from the vicinity of PsbO-N124 after proton transfer has already been completed. At reaction coordinate ζ = 0.7 of path 6, when proton transfer is completed, the energy of the intermediate path point is 4 kcal mol^−1 higher than that of the reactant state.
Path 1	PsbO-E97	K123	Via water	1	5.0/2.2	−3.3
Path 2		K51, K123	Via water	1	7.3	3.7
Path 3			Via water	1	10.8	4.9
Path 4		K51	Via water	1	9.0	−0.6
Path 5	PsbO-D99	K51, K123	Via water	3	21.1	14.2
Path 6	PsbO-E97	K51, K123	Direct	0	9.8	−10.8^b
Path 7		K51	Direct	0	8.4	3.9
Path 8		K123	Direct	0	9.7	5.4

---

Fig. 12 Proton-transfer paths computed with QM. (A) Molecular graphics of the initial coordinates (snapshot from Sim2 at 151 ns) of cluster B. (B) Energy profiles computed for path 1–4 (panel B), path 5 (panel C), and path 6–8 (panel D). The energy taken relative to the reactant state is represented as a function of the normalized reaction coordinate ζ, such that ζ = 0 and ζ = 1 indicate the reactant and product states, respectively. We present molecular graphics of the QM-optimized geometries in Fig. S7 and S8, and the structural rearrangements along selected paths in Fig. S9–S11 (ESI†).

Fig. 13 Water interactions at the proton-transfer site. We report the average number of water molecules within 3 Å of the functional groups of PsbO-E97 (panel A), D102 (panel B), and K123 (panel C). The average and standard deviation were calculated numerically in the integral form using the trapezoidal rule to account for the uneven spacing of the path points.

Fig. 14 Distances between the selected protein groups as monitored along paths 1–8. Panels A–D present the distance between, respectively, PsbO-E97 and K123, PsbO-D102 and K123, PsbO-N124 and K123, and the distance between the proton donor and acceptor groups. All distances are measured between the closest oxygen and nitrogen atoms of the functional groups.

Cluster A includes the proton-binding site PsbO-D102, its immediate PsbO environment E97, K123 and K124, 2 PsbU groups from the interface – K51 and E93, and 47 water molecules (Fig. 8 and 12B). In the QM-optimized structure of the reactant state, protonated PsbO-D102 H bonds to E97 via water (Fig. S10A, ESI†). Proton transfer from PsbO-D102 to PsbO-E97 via the intervening water (path 2, Table 3) involves an increase by ∼1 Å of the distance between PsbO-E97 and K123 (Fig. 14A), and shortening by ∼1 Å of the donor–acceptor distance (Fig. 14D and Fig. S9B, ESI†); the energy barrier of the path is 7.3 kcal mol⁻¹ (Table 3).

Given the relatively short distance between PsbO-E97 and PsbU-K51 (Fig. 12A), we sought to test how the absence of PsbO-K51 might have an impact on proton-transfer energetics. We thus removed PsbU-K51 and nearby waters, re-optimized the geometry with QM (cluster A1 in Table 1 and Fig. S10A, ESI†), and calculated water-mediated proton transfer from PsbO-D102 to PsbO-E97 (path 1 in Table 3). The initial segment of the MEP (from the reactant state at ζ = 0 to the local minimum at ζ = 0.52 in Fig. 12B) includes relocation of a water molecule away from PsbO-D102, with an associated energy barrier of 5 kcal mol⁻¹ (Table 3 and Fig. S12A, ESI†). At the local minimum at ζ = 0.52 (Fig. 12B), PsbO-D102 and E97 H bond via only one intervening water molecule; proton transfer from PsbO-D102 to E97 via this intervening water costs 2.2 kcal mol⁻¹ (Fig. 12A, 13, 14A and Table 3).

Cluster B was prepared from a different coordinate snapshot from that used for cluster A (Scheme 3). While in the coordinate snapshot used for cluster A the shortest distance between PsbO-D102 and D99 is 9.0 Å, in cluster B this distance is 5.2 Å; likewise, the shortest distance between PsbO-D102 and E98 is 4.4 Å shorter in cluster B as compared to cluster A. Pursuant to these considerations, the carboxylates close to the proton donor/acceptor pair in cluster B are PsbO-E98 and D99 (Scheme 2 and Fig. S10C, ESI†).

When starting from the QM-optimized geometry of cluster B (Fig. S7C, ESI†), the transfer of a proton from PsbO-D102 to E97 via a water molecule (path 3) costs 10.8 kcal mol⁻¹, which is 3.5 kcal mol⁻¹ higher than that obtained for path 2 (Table 3). We note that, compared to path 2, in path 3 there is less change in interactions between PsbO-E97 and K123 (Fig. 14A), as PsbO-K123 maintains a stable H bond with N124 (Fig. 14C and Fig. S10C, ESI†); we suggest that the reduced flexibility of PsbO-K123 could contribute to path 3 having a somewhat higher energy barrier than path 2.

Starting from the same QM-optimized structure of cluster B (Fig. S11A, ESI†) we obtained for the direct transfer of a proton from PsbO-D102 to E97 (path 6) a MEP with two transition states (the pink profile in Fig. 12D). The path starts with two water molecules moving away from PsbO-D102 and E97 (Fig. S13B and C, ESI†), such that at the transition state at ζ = 0.3 (Fig. 12D) the distance between the donor and oxygen atoms has shortened to 2.7 Å (Fig. 14D); this structural rearrangement is associated with an energy barrier of ∼5 kcal mol⁻¹ (Fig. 12D); proton transfer (ζ = 0.5 in Fig. 12D) requires 9.8 kcal mol⁻¹ relative to the lowest-energy local minimum at ζ = 0.1 (Fig. 12D and Table 3). Thus, cluster B gives largely similar proton-transfer barriers for both the direct and water-mediated paths.

To further verify the impact that selected interactions might have on the energetics of proton transfer, we used cluster B to generate clusters B1 and B2, in which we removed PsbO-K123 and PsbU-K51, respectively (Scheme 3).

When PsbO-K123 is removed (cluster B1), the transfer of a proton from PsbO-D102 to E97 is associated with an energy barrier of 9.0 kcal mol⁻¹ when transfer occurs via a water molecule (path 4), and 9.8 kcal mol⁻¹ when transfer is direct (path 7). These energy barriers for proton transfers are close to those of paths 3 and 6 computed with K123 present (Table 3). A possible explanation for paths computed with vs. without K123 having similar energy barriers is that, when PsbO-K123 is absent, the waters near the proton donor and acceptor groups relocate, such that there are more waters close to PsbO-E97 in path 4 than in path 3 (Fig. 13A and B).

In the absence of PsbU-K51 (path 8, cluster B2), direct proton transfer from PsbO-D102 to E97 requires reorientation of PsbO-E97 (Fig. S14C and D, ESI†), and it has an energy barrier of 9.7 kcal mol⁻¹ – which is almost the same as for the direct path 6 computed with PsbU-K51 (Table 3). As observed for cluster B1 above, when PsbO-K51 is removed (cluster B2), during QM geometry optimization water molecules relocate (Fig. 13), potentially influencing structural rearrangements and energetics along the path. For example, the distance between PsbO-K123 and N124 increases by 3.4 Å along path 6, but it remains a direct H-bond distance along path 8 (Fig. 14C).

In cluster C we started from a different coordinate snapshot of Sim3 and used the same composition of protein groups as in cluster B. Because in the QM-optimized cluster C PsbO-D99 H bonds to D102 via a chain of 3 water molecules (Fig. S7E and S10A, ESI†), we calculated proton transfer from PsbO-D102 to D99 via water (path 5 in Table 3); the high-energy barrier of this proton transfer (21.1 kcal mol⁻¹, Table 3 and Fig. 12C) suggests that the proton transfer is highly unlikely.

Taken together, the QM path computations suggest that proton transfer from PsbO-D102 to a nearby carboxylate group tends to be energetically unfavorable; this observation is compatible with the observation of direct H bonding between PsbO-D102 and E97 in crystal structures (Fig. 5), and with the hypothesis that a proton is bound at this site.^31,36

Conclusions

We studied the crystal structure and pursued extensive computations of PsbO and PsbU to characterize structural and energetic elements that could have an impact on water H bonding and proton transfer at the interface between these two proteins.

In the crystal structure of the dimeric PSII complex at 100 K,¹³ PsbO-E97 and D102 are part of a network of water molecules and charged protein groups which connects PsbO with PsbU (Fig. 1 inset). On the timescale of the 3 simulations performed on the PsbO–PsbU complex in aqueous solution, the two proteins remained bound to each other (Fig. 2 and Fig. S1, ESI†) – though the interface between PsbO and PsbU was best preserved when we placed weak harmonic constraints on 8 atoms (Sim3 in Table 1). We thus used as a reference simulation Sim3, in which these weak constraints were used (Table 1).

To characterize water dynamics on the surface of PsbO–PsbU we implemented a protocol whereby we compute and choose between 4 different functions to fit the correlation function. This protocol improved the overall convergence of the water residence time computations. For water-mediated bridges we implemented an algorithm that relies on a modified depth first search and a description of the carboxylate groups and water oxygen atoms as nodes of a graph.

We found that most water molecules that visit the surfaces of PsbO and PsbU do so only transiently – about 90% of these waters have residence times <25 ps (Fig. 3 and Fig. S4, ESI†). Some of the longest water residence times are observed at the interface between PsbO and PsbU, including for PsbO-E97 and PsbU-E93, which are close to the putative proton-binding site PsbO-D102 (Fig. 3, 4 and Fig. S4, S5, ESI†). That waters close to PsbU-E93 have long residence times in MD simulations (Fig. 3 and 4) is consistent with the presence of at least 2 waters within the H-bond from PsbO-E93 in all crystal structures we analyzed (Fig. 6B and 7A).

A network of dynamic carboxylate–water H-bond bridges connects the protonated PsbO-D102 to carboxylates of both PsbO and PsbU (Fig. 8 and 10A). A few of the water-mediated bridges across the interface, e.g., between PsbO-E97 and PsbU-E93, and between PsbO-D99 and PsbU-E93, can have relatively high occupancy (Fig. 10A and C), i.e., there is a significant probability that these groups bridge via H-bonding water. That is, the proton-binding site on the surface of PsbO connects, via water-mediated bridges, to the charged groups on the surface of PsbU.

Water-mediated bridges at the interface between PsbO and PsbU are quite dynamic, as water molecules of the bridge exchange rapidly with nearby waters. The longer the bridge, the shorter is the time during which the same waters constitute the bridge (lifetime, Fig. 11A), and most water-mediated bridges at the interface between PsbO and PsbU have short lifetimes, on the order of picoseconds or sub-picoseconds. Such short lifetimes of the water bridges are compatible with the picosecond–subpicosecond timescale for bulk water H bonding,^92–95 and with the ∼4 ps timescale for water bridges between lipid phosphate groups.⁶³

The energetics of putative proton binding and proton transfer at the surface of PsbO is poorly described. Our QM computations suggest that the energy barrier for proton transfer from PsbO-D102 to E97 tends to be relatively high. For the largest protein–water cluster used in the QM computations, cluster B, proton transfer is associated with energy barriers of ∼10–11 kcal mol⁻¹, i.e., facile proton transfer at the PsbO-D102 site appears unlikely – a proton bound to D102 could be stored, at least in the conformation used for our computations. Charged groups of PsbU participate in H-bond bridges and could have an impact on the energetics of proton transfer at the PsbO-D102 proton binding site (see PsbU-K51 in path 5), suggesting that the dynamic water-mediated bridges between PsbO and PsbU need to be accounted for in consideration of the proton antenna functionality of PsbO.

A potential caveat of our QM computations is that we derived MEPs for proton transfer, and the energy barrier might be lower at room temperature: for example, in computations of proton transfer for the bacteriorhodopsin proton pump, the energy barrier for the primary proton transfer step from the Schiff base to a nearby carboxylate was ∼3 kcal mol⁻¹ lower at room temperature than when computed with MEPs.⁸⁵ We attempted to circumvent this caveat by using clusters of protein groups and water molecules selected from three different coordinate snapshots, and with different compositions of the clusters.

Further computational studies would be needed to dissect the energetics of putative proton transfers on the surface of PsbO along the Kok cycle of PSII, including at other carboxylate groups of PsbO and other subunits of PSII. Of particular interest is, for example, PsbO-D224, which in the PSII complex is part of a H-bond network leading to the reaction center,¹¹ PsbU-D96, which might participate in the release of protons from the manganese cluster,³⁴ and the heme-propionic groups of cyt-550, for which pH-dependent protonation was discussed.⁹⁶ The analysis protocol implemented here for the analysis of dynamic water-mediated bridges could be extended to study the complete PSII complex, and other proteins are thought to be used as proton antennas.

Conflicts of interest

There are no conflicts of interest do declare.

Acknowledgements

Financial support was provided in part by the Collaborative Research Center ‘Protonation Dynamics in Protein Function’ SFB 1078 funded by the German Research Foundation (DFG), Projects A5 (to MI, AZ and HD) and C4 (to A-NB), and by the Excellence Initiative of the German Research Foundation provided via the Freie Universität Berlin (to A-NB). Computing resources were provided by the HLRN, the North-German Supercomputing Alliance (to A-NB) and by the Department of Physics of the Freie Universität Berlin. We thank Christian Tuma and Jens Dreger for excellent technical support.

References

1. M. J. Buch-Pedersen, B. P. Pedersen, B. Veierskov, P. Nissen and M. G. Palmgren, Pflugers Arch., 2009, 457, 573–579.
2. M. Yoshida, E. Muneyuki and T. Hisabori, Nat. Rev. Mol. Cell Biol., 2001, 2, 669–677.
3. J. Barber, Curr. Opin. Struct. Biol., 2002, 12, 523–530.
4. Y. Marantz, E. Nachliel, A. Aagaard, P. Brzezinski and M. Gutman, Proc. Natl. Acad. Sci. U. S. A., 1998, 95, 8590–8595.
5. V. Sacks, Y. Marantz, A. Aagaard, S. Checover, E. Nachliel and M. Gutman, Biochim. Biophys. Acta, 1998, 1365, 232–240.
6. S. Checover, Y. Marantz, E. Nachliel and M. Gutman, Biochemistry, 2001, 40, 4281–4292.
7. M. Gutman, E. Nachliel and R. Friedman, Biochim. Biophys. Acta, 2006, 1757, 931–941.
8. P. Ädelroth and P. Brzezinski, Biochim. Biophys. Acta, 2004, 1655, 102–115.
9. T. Shutova, V. V. Klimov, B. Andersson and G. Samuelsson, Biochim. Biophys. Acta, 2007, 1767, 434–440.
10. A. Shinobu, G. J. Palm, A. J. Schierbeek and N. Agmon, J. Am. Chem. Soc., 2010, 132, 11093–11102.
11. S. Lorch, S. Capponi, F. Pieront and A.-N. Bondar, J. Phys. Chem. B, 2015, 119, 12172–12181.
12. C. del Val and A.-N. Bondar, Biochim. Biophys. Acta, 2017, 1858, 432–441.
13. Y. Umena, K. Kawakami, J.-R. Shen and N. Kamiya, Nature, 2011, 473, 55–60.
14. J.-R. Shen and Y. Inoue, Biochemistry, 1993, 32, 1825–1832.
15. M. Miyao and N. Murata, FEBS Lett., 1984, 170, 350–354.
16. Y. Nishiyama, D. A. Los, H. Hayashi and N. Murata, Plant Physiol., 1997, 115, 1473–1480.
17. Y. Nishiyama, D. A. Los and N. Murata, Plant Physiol., 1999, 120, 301–308.
18. A. Kimura, J. J. Eaton-Rye, E. H. Morita, Y. Nishiyama and H. Hayashi, Plant Cell Physiol., 2002, 43, 932–938.
19. J.-R. Shen, M. Ikeuchi and Y. Inoue, J. Biol. Chem., 1997, 272, 17821–17826.
20. N. Inoue-Kashino, Y. Kashino, K. Satoh, I. Terashima and H. B. Pakrasi, Biochemistry, 2005, 44, 12214–12228.
21. J. Veerman, F. K. Bentley, J. J. Eaton-Rye, C. W. Mullineaux, S. Vasil'ev and D. Bruce, Biochemistry, 2005, 44, 16939–16948.
22. A. Rokka, M. Suorsa, A. Saleem, N. Battchikova and E.-M. Aro, Biochem. J., 2005, 388, 159–168.
23. R. Nagao, A. Moriguchi, T. Tomo, A. Niikura, A. Nakajima, T. Suzuki, A. Okumura, M. Iwai, J.-R. Shen, M. Ikeuchi and I. Enami, J. Biol. Chem., 2010, 38, 29121–29199.
24. B. Kok, B. Forbush and M. McGloin, Photochem. Photobiol., 1970, 11, 457–475.
25. J. Shen, Annu. Rev. Plant Biol., 2015, 66, 23–48.
26. N. Cox and J. Messinger, Biochim. Biophys. Acta, 2013, 1827, 1020–1030.
27. P. Gatt, S. Petrie, R. Stranger and R. J. Pace, Angew. Chem., Int. Ed., 2012, 51, 12025–12028.
28. K. N. Ferreira, T. M. Iverson, K. Maghlaoui, J. Barber and S. Iwata, Science, 2004, 303, 1831–1838.
29. H. Ishikita, W. Saenger, B. Loll, J. Biesiadka and E.-W. Knapp, Biochemistry, 2006, 45, 2063–2071.
30. A. Gabdulkhakov, A. Guskov, M. Broser, J. Kern, F. Müh, W. Saenger and A. Zouni, Structure, 2009, 17, 1223–1234.
31. A.-N. Bondar and H. Dau, Biochim. Biophys. Acta, 2012, 1817, 1177–1190.
32. S. Nakamura, R. Nagao, R. Takahashi and T. Noguchi, Biochemistry, 2014, 53, 3131–3144.
33. M. Amin, L. Vogt, W. Szejgis, S. Vassiliev, G. W. Brudvig, D. Bruce and M. R. Gunner, J. Phys. Chem. B, 2015, 119, 7366–7377.
34. K. Saito, A. W. Rutherford and H. Ishikita, Nat. Commun., 2015, 6, 8448.
35. F. Guerra, M. Siemers, C. Mielack and A.-N. Bondar, J. Phys. Chem. B, 2018, 122, 4625–4641.
36. M. Bommer, A.-N. Bondar, A. Zouni, H. Dobbek and H. Dau, Biochemistry, 2016, 55, 4626–4635.
37. V. A. Makarov, B. K. Andrews, P. E. Smith and B. M. Pettitt, Biophys. J., 2000, 79, 2966–2977.
38. K. Karathanou and A.-N. Bondar, J. Chem. Inf. Model., 2019, 59, 1882–1896.
39. G. Otting, E. Liepinsh and K. Wüthrich, Science, 1991, 254, 974–980.
40. S. Jo, T. Kim, V. G. Iyer and W. Im, J. Comput. Chem., 2008, 29, 1859–1865.
41. J. Lee, X. Chheng, J. M. Swails, M. S. Yeom, P. K. Eatsman, J. A. Lemkul, S. Wei, J. Buckner, J. C. Jeong, Y. Qi, S. Jo, V. S. Pande, D. A. Case, C. L. Brooks, A. D. MacKerell Jr, J. B. Klauda and W. Im, J. Chem. Theory Comput., 2016, 12, 405–413.
42. W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935.
43. J. Nikitina, T. Shutova, B. Melnik, S. Chernyshov, V. Marchenkov, G. Semisotnov, V. Klimov and G. Samuelsson, Photosynth. Res., 2008, 98, 391–403.
44. B. R. Brooks, R. E. Bruccoleri, B. D. Olafson, D. J. States, S. Swaminathan and M. Karplus, J. Comput. Chem., 1983, 4, 187–217.
45. D. Beglov and B. Roux, J. Chem. Phys., 1994, 100, 9050–9063.
46. A. D. MacKerell Jr., D. Bashford, M. Bellot, R. L. Dunbrack, J. D. Evanseck, M. J. Field, S. Fischer, J. Gao, H. Guo, S. Ha, D. Joseph-McCarthy, L. Kuchnir, K. Kuczera, F. T. K. Lau, C. Mattos, S. Michnick, T. Ngo, D. T. Nguyen, B. Prodhom, W. E. I. Reiher, B. Roux, M. Schlenkrich, J. C. Smith, R. Stote, J. Straub, M. Watanabe, J. Wiorkiewicz-Kuczera, D. Yin and M. Karplus, J. Phys. Chem. B, 1998, 102, 3586–3616.
47. A. D. MacKerell Jr., M. Feig and C. L. I. Brooks, J. Comput. Chem., 2004, 25, 1400–1415.
48. J. Huang, S. Rauscher, G. Nawrocki, T. Ran, M. Feig, B. L. de Groot, H. Grubmüller and A. D. MacKerell Jr., Nat. Methods, 2016, 40, 71–73.
49. L. Kalé, R. Skeel, M. Bhandarkar, R. Brunner, A. Gursoy, N. Krawetz, J. Phillips, A. Shinozaki, K. Varadarajan and K. Schulten, J. Comput. Phys., 1999, 151, 283–312.
50. J. C. Phillips, B. Braun, W. Wang, J. Gumbart, E. Takjkhorshid, E. Villa, C. Chipot, R. D. Skeel, L. Kale and K. Schulten, J. Comput. Chem., 2005, 26, 1781–1802.
51. T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089–10092.
52. U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, J. Chem. Phys., 1995, 103, 8577–8593.
53. J.-P. Ryckaert, G. Ciccotti and H. J. C. Berendsen, J. Comput. Phys., 1977, 23, 327–341.
54. S. Miyamoto and P. A. Kollman, J. Comput. Chem., 1992, 13, 952–962.
55. G. J. Martyna, D. J. Tobias and M. L. Klein, J. Chem. Phys., 1994, 101, 4177–4189.
56. S. E. Feller, Y. Zhang, R. W. Pastor and B. Brooks, J. Chem. Phys., 1995, 103, 4613–4621.
57. H. Grubmüller, H. Heller, A. Windemuth and K. Schulten, Mol. Simul., 1991, 6, 121–142.
58. M. Tuckermann, B. J. Berne and G. J. Martyna, J. Chem. Phys., 1992, 97, 1990–2001.
59. W. Humphrey, W. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38.
60. N. Michaud-Agrawal, E. J. Denning and T. B. Woolf, J. Comput. Chem., 2011, 32, 2319–2327.
61. R. J. Gowers, M. Linke, J. Barnoud, T. J. E. Reddy, M. N. Melo, S. L. Seyler, D. L. Dotson, J. Domanski, S. Buchoux, I. M. Kenney and O. Beckstein, in Proceedings of the 15th Phyton in Science Conference, ed. S. Benthall and S. Rostrup, Austin, TX, 2016 SciPy, 2016, pp. 102–109.
62. B. J. Siwick, M. J. Cox and H. J. Bakker, J. Phys. Chem. B, 2008, 112, 378–389.
63. K. Karathanou and A.-N. Bondar, J. Membr. Biol., 2018, 251, 461–473.
64. R. Sedgewick, Algorithms in C, Part 5: Graph Algorithms, Addison-Wesley Professional, 2001.
65. N. Sengupta, S. Jaud and D. J. Tobias, Biophys. J., 2008, 95, 5257–5267.
66. C. P. Lindsey and G. D. Patterson, J. Chem. Phys., 1980, 73, 3348–3357.
67. N. R. Draper and H. Smith, Applied regression analysis, John Wiley, 1998.
68. H. Flyvbjerg, J. Chem. Phys., 1989, 91, 461–466.
69. E. Jardon-Valadez, A.-N. Bondar and D. J. Tobias, Biophys. J., 2010, 99, 2200–2207.
70. N. Choudhury and M. B. Pettitt, J. Phys. Chem. B, 2005, 109, 6422–6429.
71. S. Balasubramaniam, S. Pal and B. Bagchi, Phys. Rev. Lett., 2002, 89, 11505.
72. A.-N. Spiess and N. Neumayer, BMC Pharmacol., 2010, 10, 6.
73. G. Schwartz, Ann. Stat., 1978, 6, 461–464.
74. N. M. Glykos, J. Comput. Chem., 2006, 27, 1765–1768.
75. T. Ichiye and M. Karplus, Proteins: Struct., Funct., Genet., 1991, 11, 205–217.
76. M. Elstner, D. Porezag, G. Jungnickel, J. Elner, M. Haugk, T. Frauenheim, S. Suhai and G. Seifert, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 7260–7268.
77. M. Gaus, Q. Cui and M. Elstner, J. Chem. Theory Comput., 2011, 7, 931–948.
78. Q. Cui, M. Elstner, E. Kaxiras, T. Frauenheim and M. Karplus, J. Phys. Chem. B, 2001, 105, 569–585.
79. M. Gaus, A. Goez and M. Elstner, J. Chem. Theory Comput., 2013, 9, 338–354.
80. K. P. Eurenius, D. C. Chatfield, B. R. Brooks and M. Hodoscek, Int. J. Quantum Chem., 1996, 60, 1189–1200.
81. A.-N. Bondar, S. Suhai, S. Fischer, J. C. Smith and M. Elstner, J. Struct. Biol., 2007, 157, 454–469.
82. S. Fischer and M. Karplus, Chem. Phys. Lett., 1992, 194, 252–261.
83. A.-N. Bondar, S. Fischer, J. C. Smith, M. Elstner and S. Suhai, J. Am. Chem. Soc., 2004, 126, 14668–14677.
84. R. Friedman, S. Fischer, E. Nachliel, S. Scheiner and M. Gutman, J. Phys. Chem. B, 2007, 111, 6059–6070.
85. A.-N. Bondar, J. Baudry, S. Suhai, S. Fischer and J. C. Smith, J. Phys. Chem. B, 2008, 112, 14729–14741.
86. F. A. Kiani and S. Fischer, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 2947–2956.
87. A. N. Bondar, S. Fischer, S. Suhai and J. C. Smith, J. Phys. Chem. B, 2005, 109, 14786–14788.
88. A. D. Gruia, A.-N. Bondar, J. C. Smith and S. Fischer, Structure, 2005, 13, 617–627.
89. Q. Sun, Z. Li, Z. Lan, C. Pfisterer, M. Doerr, S. Fischer, S. C. Smith and W. Thiel, Phys. Chem. Chem. Phys., 2012, 14, 11413–11424.
90. T. Wolter, M. Elstner, S. Fischer, J. C. Smith and A.-N. Bondar, J. Phys. Chem. B, 2015, 119, 2229–2240.
91. L. Schrödinger, The PyMOL Molecular Graphics System, Version 1.8, 2015.
92. M. Gutman and E. Nachliel, Biochim. Biophys. Acta, 1990, 1015, 391–414.
93. A. Luzar and D. Chandler, Nature, 1996, 379, 55–57.
94. B. Bagchi, Chem. Rev., 2005, 105, 3197–3219.
95. S. K. Sinha and S. Bandyopadhyay, Phys. Chem. Chem. Phys., 2012, 14, 899–913.
96. H. Ishikita and E.-W. Knapp, FEBS Lett., 2005, 579, 3190–3194.
97. M. Suga, F. Akita, K. Hirata, G. Ueno, H. Murakami, Y. Nakajima, T. Shimizu, K. Yamashita, M. Yamamoto, H. Ago and J.-R. Shen, Nature, 2015, 517, 99–103.
98. J. Kern, R. Chatterjee, I. D. Young, F. D. Fuller, L. Lasalle, M. Ibrahim, S. Gul, T. Fransoon, A. S. Brewster, R. Alonso-Moti, R. Hussein, M. Zhang, L. Douthit, C. de Lichtenberg, M. Hon Cheah, D. Shevela, J. Wersig, I. Seuffert, D. Sokaras, E. Pastor, C. Weninger, T. Kroll, R. G. Sierra, P. Aller, A. Butryn, A. M. Orville, M. Liang, A. Batyuk, J. E. Koglin, S. Carbajo, S. Boutet, N. W. Moriarty, J. M. Holton, H. Dobbeck, P. D. Adams, U. Bergmann, N. K. Sauter, A. Zouni, J. Mesinger, J. Yano and V. K. Yachandra, Nature, 2018, 563, 421–425.
99. M. Suga, F. Akita, M. Sugahara, M. Kubo, Y. Nakajima, T. Nakane, K. Yamashita, Y. Umena, M. Nakabayashi, T. Yamane, T. Nakano, M. Suzuki, T. Masuda, S. Inoue, T. Kimura, T. Nomura, S. Yonekura, L.-J. Yu, T. Sakamoto, T. Motomura, J.-H. Chen, Y. Kato, T. Noguchi, K. Tono, Y. Joti, T. Kameshima, T. Hatsui, E. Nango, R. Tanaka, H. Naitow, Y. Matsuura, A. Yamashita, M. Yamamoto, O. Nureki, M. Yabashi, T. Ishikawa, S. Iwata and J.-R. Shen, Nature, 2017, 543, 131–135.
100. A. Tanaka, Y. Fukushima and N. Kamiya, J. Am. Chem. Soc., 2017, 139, 1718–1721.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c9cp03926k

---