Experimental and numerical analysis to identify the performance limiting mechanisms in solid-state lithium cells under pulse operating conditions†
Abstract
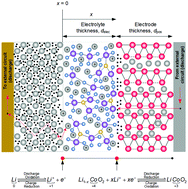
Solid-state lithium batteries could reduce the safety concern due to thermal runaway while improving the gravimetric and volumetric energy density beyond the existing practical limits of lithium-ion batteries. The successful commercialisation of solid-state lithium batteries depends on understanding and addressing the bottlenecks limiting the cell performance under realistic operational conditions such as dynamic current profiles of different pulse amplitudes. This study focuses on experimental analysis and continuum modelling of cell behaviour under pulse operating conditions, with most model parameters estimated from experimental measurements. By using a combined impedance and distribution of relaxation times analysis, we show that charge transfer at both interfaces occurs between the microseconds and milliseconds timescale. We also demonstrate that a simplified set of governing equations, rather than the conventional Poisson–Nernst–Planck equations, are sufficient to reproduce the experimentally observed behaviour during pulse discharge, pulse charging and dynamic pulse. Our simulation results suggest that solid diffusion in bulk LiCoO2 is the performance limiting mechanism under pulse operating conditions, with increasing voltage loss for lower states of charge. If bulk electrode forms the positive electrode, improvement in the ionic conductivity of the solid electrolyte beyond 10−4 S cm−1 yields marginal overall performance gains due to this solid diffusion limitation. Instead of further increasing the electrode thickness or improving the ionic conductivity on their own, we propose a holistic model-based approach to cell design, in order to achieve optimum performance for known operating conditions.
- This article is part of the themed collection: 2019 PCCP HOT Articles


 Please wait while we load your content...
Please wait while we load your content...