Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Dendrite nucleation in lithium-conductive ceramics
Guanchen
Li
 ab and
Charles W.
Monroe
ab and
Charles W.
Monroe
 *ab
*ab
aDepartment of Engineering Science, University of Oxford, Parks Road, Oxford, OX1 3PJ, UK. E-mail: charles.monroe@eng.ox.ac.uk; Fax: +44 (0)1865 273010; Tel: +44 (0)1865 273188
bThe Faraday Institution, Harwell Campus, Didcot, OX11 0RA, UK
First published on 9th September 2019
Abstract
Solid-state lithium batteries cannot achieve reasonable power densities because of dendrites, whose formation mechanisms remain uncertain. This paper applies principles of chemomechanics to investigate the critical current above which dendrites form in lithium-conductive ceramics. Applied voltage induces stress in solid electrolytes; dendrites appear to nucleate in the exemplary garnet-oxide material Li7La3Zr2O12 (LLZO) when the interfacial pressure exceeds a particular value. The critical pressure of polycrystalline LLZO correlates well with the surface-energy changes incurred by lithium plating in its grain boundaries. A derived formula, validated by experiments, predicts quantitatively how critical current varies with properties including interfacial impedance, bulk permittivity, and grain size. As well as suggesting novel strategies to create more resilient ion-conductive ceramics, the proposed mechanism rationalizes experimental observations of bulk lithium plating and explains how LLZO exhibits an electrically activated transition from stable low-current cyclability to high-current dendrite nucleation.
1 Introduction
Ceramic electrolytes hold promise because many have shear moduli that suppress dendrite nucleation from morphological instability,1,2 which could enable metallic Li batteries. Ion conductors based on solid Li7La3Zr2O12 (LLZO) garnet have wide voltage stability windows3 and viable room-temperature conductivities.3–6 LLZO also has near-unit cation transference;7 ion diffusion should not limit the current as it does in liquids. Despite its advantages, LLZO still exhibits a ‘critical current’, above which dendrites form.8–10 Porz et al. hypothesize that dendrites propagate from pre-existing surface cracks,10 carrying forward an earlier theory of Feldman and de Jonghe.11 These models describe dendrites without reference to morphological instability or mass-transfer limitations, but predict critical currents far below experimental values. It seems that propagating dendrites will eventually cause failure whenever present. Thus we shift the focus here to nucleation mechanisms.Experimentalists have refined garnet performance by many routes, some of which affect critical currents. Planar Li|LLZO|Li cells heated near Li's melting point (180 °C) attain lower interfacial impedances and higher critical currents – effects that remain after cooling.8 In traditionally sintered polycrystalline LLZO, finer grains reduce interfacial impedance and raise the critical current.12 Yamamoto et al. probed electric fields near electrode/garnet boundaries,13 finding space-charge penetration deep into the ceramic. Theories of space charge in solid ion conductors based on Fermi distributed carriers have existed for decades.14 Latz et al. illuminated some mechanical aspects of this Poisson-Fermi screening in solid electrolytes, coupling charge screening with stress.15 Conductivity, interfacial impedance, and failure mechanics remain to be analyzed.
This paper proposes a theory describing electrochemical/mechanical coupling in space-charge layers to elucidate solid–electrolyte failure. We find that the critical current density correlates with critical pressure, a material property that expresses information about an electrolyte's mechanical properties, grain structure, bulk cohesion, and Li-wetting energetics. A model combining electrochemical and mechanical dynamics shows how the relative pressure at the LLZO surface scales with interfacial impedance and bulk permittivity. Critical-current data from the literature reveal that similarly prepared LLZO samples held at different temperatures all fail at the same critical pressure, which is much lower than the fracture stress. A rough analysis of Li plating energetics in grain boundaries allows this critical pressure to be estimated. Data gathered from atomistic calculations predict critical currents that match experiments on polycrystalline LLZO.
2 Model and parameters
Critical currents for solid electrolytes are sufficiently low that an isothermal steady state can be assumed, in which case current density![[i with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0069_20d1.gif) is divergence-free. In a domain with permittivity ε, the mean electric field
is divergence-free. In a domain with permittivity ε, the mean electric field ![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) induces local excess charge density ρe through Poisson's equation
induces local excess charge density ρe through Poisson's equation | (1) |
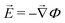 .
.
Analysis of the local energy dissipation reveals that charge motion follows an extended form of Ohm's law, the MacInnes equation
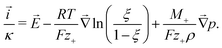 | (2) |
Together with the constraint that 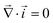 , eqn (1) and (2) extend the classical Poisson-Fermi equilibrium model to electrolytes under steady applied currents. This dynamical model is readily solved for the case of a one-dimensional slab with thickness L in the x direction, sandwiched between metal electrodes. In this case i is uniform throughout the slab and global conservation of charge requires that E|0 = E|L = Σ/ε, where Σ is the surface-charge density on the electrode at x = 0, which we take to be ground. The potential distribution within the electrolyte, Φ(x), is obtained through
, eqn (1) and (2) extend the classical Poisson-Fermi equilibrium model to electrolytes under steady applied currents. This dynamical model is readily solved for the case of a one-dimensional slab with thickness L in the x direction, sandwiched between metal electrodes. In this case i is uniform throughout the slab and global conservation of charge requires that E|0 = E|L = Σ/ε, where Σ is the surface-charge density on the electrode at x = 0, which we take to be ground. The potential distribution within the electrolyte, Φ(x), is obtained through 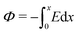 , and the voltage bias is ΔΦ = Φ(0) − Φ(L). To find the distribution of lattice occupancy, ξ(x), one can integrate eqn (2).
, and the voltage bias is ΔΦ = Φ(0) − Φ(L). To find the distribution of lattice occupancy, ξ(x), one can integrate eqn (2).
The Lorentz force ρe![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) and mechanical stress
and mechanical stress 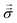 drive momentum accumulation through
drive momentum accumulation through
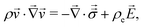 | (3) |
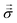 , and consequently σxx = 3p − 2pθ.§ Within a planar electrolyte slab, the pressure distribution,
, and consequently σxx = 3p − 2pθ.§ Within a planar electrolyte slab, the pressure distribution, 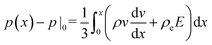 , can be acquired by integrating eqn (3).
, can be acquired by integrating eqn (3).
All the relevant phenomenological properties for polycrystalline LLZO can be found in the literature. Cations are univalent, z+ = 1. In unbiased equilibrium at 300 K and 1 atm, the density of LLZO is ρeq = 5.4 g cm−3.17 According to the calculations of Meier et al., there are 15 available sites for lithium per La3Zr2O12 formula unit, 7 of which are occupied at equilibrium,18 yielding occupancy ξeq = 0.467 and cation concentration ceq+ = 45 mol L−1. If occupancy deviates from equilibrium at a given pressure, the mass density varies as ρ(ξ)/ρeq = 1 − 0.0534(1 − ξ/ξeq). The electroneutral ionic conductivity is κeq = 0.4 mS cm−1 at 300 K, with an Arrhenius dependence involving energy Ea = 28 kJ mol−1,3,8 and an occupancy dependence κ = κeq(T)ξ/ξeq. Impedance spectroscopy shows the dielectric constant to be 50.19,20
3 Results and discussion
Ceramic electrolytes exhibit substantial electrical polarizability, as well as being conductive. The range of possible electrical responses can be explored by comparing the portion of the voltage drop across the electrolyte owing to electrode surface charge (capacitive behavior) to that arising from faradaic current (resistive). Garnets cannot presently be fabricated with thicknesses much below 5 μm,21 but an artificially thin electrolyte with L = 2 nm – about 50 Debye lengths – is modelled first to make features near the boundaries visible when plotted. Very thick (1 cm) LLZO samples have been studied experimentally by Sharafi et al.,8 and are modelled later.Fig. 1 shows potential, pressure, and site-occupancy profiles as functions of voltage bias in the capacitive and resistive extremes. To probe the ideally capacitive end of the spectrum, i was set to zero, making the voltage bias control Σ alone. One can achieve this experimentally by using electrodes like Pt or Ni that block Li redox.21,22 (If one neglects the pressure diffusion term in eqn (2), the ideal capacitive case produces a model identical to that of Braun et al.15) Surface charge builds up on blocking electrodes, producing a field that causes layers of countercharge to form near the electrolyte's boundaries, as seen in Fig. 1a and c. Screening of the fields emanating from the exterior surface charges on the electrodes produces steep potential gradients near the electrolyte's edges, which act on the compensating space-charge layers there to produce large compressive forces at the boundary relative to the bulk. Fig. 1b shows just 0.3 V of bias producing a surface pressure 200 MPa above the bulk. Site-occupancy profiles in Fig. 1c show how the Fermi distribution that underpins cation chemical potential causes dilation of the space-charge layers with rising bias, contrasting the Debye-length contraction typical of liquid diffuse layers. An inflection in the site-occupancy profile appears near the outer boundary as Li saturates available sites. The inflection is mirrored near the inner boundary due to global charge conservation, which forces Li depletion in a layer about ten Debye lengths thick.
Ideally resistive responses were investigated by setting Σ to zero, forcing voltage to drive faradaic current alone. (For ξ sufficiently below unity, this produces results similar to Nernst–Planck–Poisson models of liquid electrolytes23 under Dickinson and Compton's zero-field approximation.24) Resistive character leads to potential profiles like those depicted in Fig. 1d, which are linear across the bulk and flat at the boundaries, because Ohmic dissipation produces a field in the electrolyte's interior that is screened before it penetrates the outer edges. Fig. 1f shows how diffusion limitations embedded in the MacInnes equation (eqn (2)) cause cations to accumulate near the electrode where they are produced, and be depleted where they are consumed. Since the anode resides at a higher voltage, it supports a positive space charge, inducing compressive stress in the bulk relative to the boundary as seen in Fig. 1e. This pressure is 6 MPa at 0.3 V, small in magnitude compared to the ideally capacitive case. The cathode is starved of Li, as it would be for typical liquid diffusion. Thus, although there is unit cation transference, diffusion in the cathodic space-charge layer still brings about an apparent limiting current.
Practically, voltage bias produces both surface charge and current; no intrinsic bulk-electrolyte property sets their relative proportion. Instead, charge-transfer reaction kinetics, surface chemistry, and polarizability across the electrode/electrolyte interface together determine the functional dependence Σ(i,ΔΦ). Kinetic (faradaic) processes are electrically resistive; other interfacial phenomena are mostly capacitive.
All surface phenomena occur in parallel across the electrode/electrolyte boundary, so the associated voltage drops match in a steady state. Thus the relative resistive and capacitive characters of a given interface can be described by an interfacial characteristic frequency fint = i/(2πΣ), which is directly measurable by impedance spectroscopy. Qualitatively, fint is the frequency where the negative imaginary part of the interfacial impedance reaches a maximum on a Nyquist plot. The model here treats fint as a constant, which determines the surface charge associated with a given current.
The simplest interfacial model is a parallel RC circuit, for which Kirchhoff's laws imply fint = 1/(2πRintCint). Data that so establish fint are available from literature.8 We therefore accept the phenomenological nature of this property, leaving a detailed mechanistic analysis of interfacial electrodynamics for future research.¶
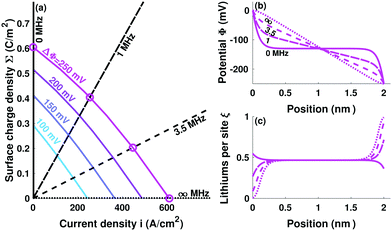
Fig. 2 shows how electrolytes respond as their interfacial characteristic frequencies vary across the capacitive/resistive spectrum. Again, an artificially thin 2 nm slab polarized by ΔΦ = 250 mV is depicted to make charge-screening effects visible. Fig. 1 and 2 show that the occupancy and electric field are both constant outside the space-charge layers, an observation confirmed by operando neutron depth profiling (NDP).26 Larger electrolyte thickness L merely extends the domains of constant ξ and E, without changing the space-charge layers' structures. The potential distributions in Fig. 2b transition from showing double layers at low fint to being linear when fint is large. Fig. 2c shows how tuning fint causes cations to accumulate or disperse at a given boundary.
Space charging produces Maxwell stresses at Li|LLZO interfaces. Whether the character of a given system is predominantly capacitive or resistive tunes this mechanical response. Regardless of the constitutive law for mixing free energy, characteristic screening length, or electrolyte thickness,|| the pressure drop from the electrolyte's interior to its edge, Δp = pbulk − p|0, can always be acquired by integrating eqn (3) across the space-charge layer directly with the help of Poisson's equation (eqn (1)). Under the assumption that L is much larger than the Debye length, neither length scale affects the pressure drop: the bulk field satisfies Ohm's law, Ebulk = i/κ; the field at the boundary relates to the interfacial frequency through E|0 = i/(2πfintε). Neglecting inertia, then, integration of eqn (3) shows that
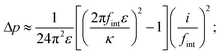 | (4) |
The experimental data in Table 1 suggest that state-of-the-art Li|LLZO interfaces are essentially capacitive: even at temperatures near the melting point of Li, fint is well below 100 kHz. In fact, literature suggests that fint ≪ f0 for most interfaces with ion-conductive ceramics.27 Voltage bias therefore causes the bulk electrolyte to experience tensile stress relative to the edge. Importantly, this relative pressure Δp is insensitive to LLZO's conductivity, being controlled by permittivity and interfacial impedance.
| T [K] | 303 | 343 | 373 | 403 | 433 |
|---|---|---|---|---|---|
| i c (model) [A m−2] | 0.32 | 2.04 | 10.87 | 46.57 | 181.09 |
| i c (experiment) [A m−2] | 0.5 | 2 | 8 | 35 | 200 |
| κ [mS cm−1] | 0.4 | 1.2 | 2.4 | 4.3 | 7.0 |
| R int [Ω cm2] | 514 | 80 | 15 | 3.5 | 0.9 |
| f int [kHz] | 0.03 | 0.20 | 1.06 | 4.55 | 17.68 |
Fig. 4 incorporates properties from LLZO samples with L = 1 cm sandwiched between Li electrodes at different temperatures (Table 1) – a system studied by Sharafi et al.8 – to show how Δp varies with current at different temperatures. Putting experimental data for critical current density8 on the same plot suggests that dendrites nucleate whenever current induces a particular critical pressure, Δpc. Through the capacitive limit of eqn (4), the law
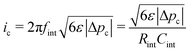 | (5) |
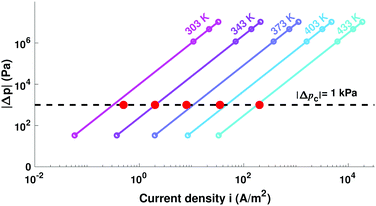 | ||
| Fig. 4 Variation of relative pressure with applied current density for LLZO at different temperatures, based on data from Table 1. Red dots indicate experimental critical currents, reached when the applied voltage drives the interface to critical pressure Δpc = −1 kPa. | ||
We propose that polycrystalline LLZO fails by an electrochemically activated mechanism. Interfaces between conductive ceramics and Li are capacitive, and therefore sustain space-charge layers under pressure. Dendrites form when the compressive energy at the Li/LLZO boundary makes the free-energy cost of interfacial deposition high enough that it becomes more favorable to deposit Li in grain boundaries. This ‘grain-coating’ process involves formation of a new phase between grains, a chemical mechanism that would not require brittle fracture. Experiments probing finer-grain LLZO samples after failure support this notion, confirming the presence of an intergranular phase made up of metallic Li filaments.29
If phase segregation does not induce large strain, then the excess energy needed to plate Li in a grain boundary is the change in energy when the boundary (surface energy γLLZO|LLZO) is replaced with two fresh Li-metal/electrolyte interfaces (γLi|LLZO). Dendrite nucleation is spontaneous when Δp + aVΔγ < 0, where aV is the grain area per electrolyte volume and Δγ is the net surface energy associated with forming the new Li-metal intergranular phase. Adopting the typical definition of grain size d = 6/aV based on spherical closed packing, the critical pressure scales as
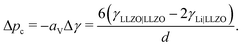 | (6) |
Like other mechanical properties, the critical pressure Δpc can be influenced by grain characteristics in quite a convoluted way: grain shape determines aV, whereas misorientation angle decides the grain-boundary energy difference.31Eqn (6) helps to justify the counterintuitive observation by Cheng et al. that critical current rises as interfacial grain size falls in traditionally sintered LLZO;12 in those experiments, no notable changes in grain orientation or misorientation occurred among samples with different grain sizes. A contradicting trend—that critical current rises with grain size—has been reported for hot-pressed LLZO samples.32 Sharafi et al. provided an extensive discussion about the contradictory results delivered by different synthetic approaches.32 Specifically, hot-pressed samples show significant variation in misorientation and grain shape between small- and large-grain samples. Misorientation would impact the Δγ value in eqn (6); changes in grain shape would require a more detailed consideration of the parameter aV, and would invalidate the grain-packing assumptions that underpin the expression for Δpc involving d.
It is difficult to isolate the effects of grain size, shape, and orientation, because critical currents are very sensitive to interfacial impedance. All of the different grain structures Sharafi et al. produced by varying hot-pressing conditions yielded LLZO samples with very small interfacial resistances. It is notable that the range of these resistances – between 2 and 5 Ω cm2 – corresponds well with the observed variation in critical current, which was of the same order – 0.3 to 0.6 mA cm−2 at room temperature.32 This observation is precisely in line with the expectation set by eqn (5).
The present model suggests several quantitative procedures by which to probe or modify critical currents. Since they have similar grain structure, similarly prepared samples in principle share the same critical pressure, Δpc. From a practical standpoint, if one has several electrolyte samples synthesized by the same process, one can measure the interfacial impedance and critical current of a single sample, then use eqn (5) to calculate |Δpc| for the whole batch. The effects of differences in interfacial contact, surface chemistry, or ambient conditions are wholly embedded in the interfacial impedance (quantified by Rint and Cint), which can be measured non-destructively from an impedance spectrum once an electrolyte has been loaded into a cell. On a more theoretical front, if surface energetics have been calculated and grain microstructure is known, Δpc can be estimated using eqn (6), as discussed above.
It is worth emphasizing that the grain-coating dendrite-nucleation mechanism proposed here is based on chemical deposition energetics, rather than mechanics, and therefore differs fundamentally from mechanisms that assume flow or creep of metallic lithium at the electrode surface or rely on the surface energetics of crack propagation.10,11 In particular, within the present model, the coating of grain boundaries by lithium is not constrained to occur immediately adjacent to the electrode surface. This admits the possibility of sporadic bulk plating, the presence of which has recently been confirmed in LLZO and various other solid electrolytes by Han et al.26Eqn (6) indicates that above the critical current, plating in grain boundaries will be energetically favored anywhere outside the space-charge layer, because the pressure there is lower than at the interface. Of course, for such plating to occur, electrons must be available to reduce lithium cations out of the LLZO. Han et al. show that LLZO exhibits electronic, as well as ionic conductivity, so mobile electrons are available in the bulk; they further observe that higher electronic conductivity correlates with more bulk plating.26 If free electrons are present, lithium plating will be particularly favored at high-energy grain boundaries, which lead to a less negative critical pressure.
4 Conclusions
A theory predicting the critical current above which polycrystalline ceramic lithium-ion conductors succumb to dendrites was developed by considering the mechanical consequences of charge flow in the bulk electrolyte and space charging near its boundaries alongside the energetics of electrolyte cohesion and lithium/electrolyte adhesion. Charge screening and faradaic processes respectively induce tensile and compressive stresses in the bulk relative to a solid electrolyte's outer edges; the balance of these stresses is struck by interfacial impedance. For the exemplary material Li7La3Zr2O12 (LLZO), critical current correlates with a particular interfacial pressure, which remains fairly constant over a wide range of temperatures. Dendrites appear to nucleate in polycrystalline LLZO when the stress induced by the voltage makes it more favorable to plate lithium in grain boundaries.The grain-coating mechanism we propose rationalizes recent reports of bulk lithium plating. Many new design opportunities are also brought to light by the model: in a dense, defect-free polycrystalline electrolyte, critical current can be raised by increasing the permittivity, decreasing the grain size, raising the surface energy of lithium/electrolyte interfaces, lowering the interfacial kinetic resistance, or lowering the interfacial capacitance. We next aim to model interfacial chemistry, whose impedance signature appears to control solid–electrolyte mechanical failure.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Faraday Institution SOLBAT challenge, grant no. FIRG007, and the Engineering and Physical Sciences Research Council (EPSRC), grant no. EP/P003532/1.Notes and references
- C. Monroe and J. Newman, J. Electrochem. Soc., 2004, 151, A880–A886 CrossRef CAS.
- C. Monroe and J. Newman, J. Electrochem. Soc., 2005, 152, A396–A404 CrossRef CAS.
- R. Murugan, V. Thangadurai and W. Weppner, Angew. Chem., Int. Ed., 2007, 46, 7778–7781 CrossRef CAS PubMed.
- J. Janek and W. G. Zeier, Nat. Energy, 2016, 1, 16141 CrossRef.
- H. Buschmann, J. Dolle, S. Berendts, A. Kuhn, P. Bottke, M. Wilkening, P. Heitjans, A. Senyshyn, H. Ehrenberg, A. Lotnyk, V. Duppel, L. Kienle and J. Janek, Phys. Chem. Chem. Phys., 2011, 13, 19378–19392 RSC.
- H. Buschmann, S. Berendts, B. Mogwitz and J. Janek, J. Power Sources, 2012, 206, 236–244 CrossRef CAS.
- T. Thompson, S. Yu, L. Williams, R. D. Schmidt, R. Garcia-Mendez, J. Wolfenstine, J. L. Allen, E. Kioupakis, D. J. Siegel and J. Sakamoto, ACS Energy Lett., 2017, 2, 462–468 CrossRef CAS.
- A. Sharafi, H. M. Meyer, J. Nanda, J. Wolfenstine and J. Sakamoto, J. Power Sources, 2016, 302, 135–139 CrossRef CAS.
- R. D. Schmidt and J. Sakamoto, J. Power Sources, 2016, 324, 126–133 CrossRef CAS.
- L. Porz, T. Swamy, B. W. Sheldon, D. Rettenwander, T. Frömling, H. L. Thaman, S. Berendts, R. Uecker, W. C. Carter and Y.-M. Chiang, Adv. Energy Mater., 2017, 1701003 CrossRef.
- L. A. Feldman and L. C. De Jonghe, J. Mater. Sci., 1982, 17, 517–524 CrossRef CAS.
- L. Cheng, W. Chen, M. Kunz, K. Persson, N. Tamura, G. Chen and M. Doeff, ACS Appl. Mater. Interfaces, 2015, 7, 2073–2081 CrossRef CAS PubMed.
- K. Yamamoto, Y. Iriyama, T. Asaka, T. Hirayama, H. Fujita, C. Fisher, K. Nonaka, Y. Sugita and Z. Ogumi, Angew. Chem., Int. Ed., 2010, 49, 4414–4417 CrossRef CAS PubMed.
- A. Kornyshev and M. Vorotyntsev, Electrochim. Acta, 1981, 26, 303–323 CrossRef CAS.
- S. Braun, C. Yada and A. Latz, J. Phys. Chem. C, 2015, 119, 22281–22288 CrossRef CAS.
- P. Goyal and C. W. Monroe, J. Electrochem. Soc., 2017, 164, E3647–E3660 CrossRef CAS.
- S. Yu, R. D. Schmidt, R. Garcia-Mendez, E. Herbert, N. J. Dudney, J. B. Wolfenstine, J. Sakamoto and D. J. Siegel, Chem. Mater., 2016, 28, 197–206 CrossRef CAS.
- K. Meier, T. Laino and A. Curioni, J. Phys. Chem. C, 2014, 118, 6668–6679 CrossRef CAS.
- D. Rettenwander, A. Welzl, L. Cheng, J. Fleig, M. Musso, E. Suard, M. M. Doeff, G. J. Redhammer and G. Amthauer, Inorg. Chem., 2015, 54, 10440–10449 CrossRef CAS PubMed.
- C. Loho, R. Djenadic, M. Bruns, O. Clemens and H. Hahn, J. Electrochem. Soc., 2017, 164, A6131–A6139 CrossRef CAS.
- E. Kazyak, K.-H. Chen, K. N. Wood, A. L. Davis, T. Thompson, A. R. Bielinski, A. J. Sanchez, X. Wang, C. Wang, J. Sakamoto and N. P. Dasgupta, Chem. Mater., 2017, 29, 3785–3792 CrossRef CAS.
- S. Afyon, F. Krumeich and J. L. M. Rupp, J. Mater. Chem. A, 2015, 3, 18636–18648 RSC.
- R. P. Buck, J. Electroanal. Chem. Interfacial Electrochem., 1973, 46, 1–23 CrossRef CAS.
- E. J. Dickinson and R. G. Compton, Chem. Phys. Lett., 2010, 497, 178–183 CrossRef CAS.
- J. Song and M. Z. Bazant, Phys. Rev. Lett., 2018, 120, 116001 CrossRef CAS PubMed.
- F. Han, A. S. Westover, J. Yue, X. Fan, F. Wang, M. Chi, D. N. Leonard, N. J. Dudney, H. Wang and C. Wang, Nat. Energy, 2019, 4, 187–196 CrossRef CAS.
- J. T. S. Irvine, D. C. Sinclair and A. R. West, Adv. Mater., 1990, 2, 132–138 CrossRef CAS.
- A. Foster, Mechanical Property Changes in the Ceramic Electrolyte Due to Porosity, Microcracking and Lithium Incorporation, Master's thesis, Michigan State University, USA, 2016.
- E. J. Cheng, A. Sharafi and J. Sakamoto, Electrochim. Acta, 2017, 223, 85–91 CrossRef CAS.
- A. Sharafi, E. Kazyak, A. L. Davis, S. Yu, T. Thompson, D. J. Siegel, N. P. Dasgupta and J. Sakamoto, Chem. Mater., 2017, 29, 7961–7968 CrossRef CAS.
- S. Yu and D. J. Siegel, Chem. Mater., 2017, 29, 9639–9647 CrossRef CAS.
- A. Sharafi, C. G. Haslam, R. D. Kerns, J. Wolfenstine and J. Sakamoto, J. Mater. Chem. A, 2017, 5, 21491–21504 RSC.
Footnotes |
| † A term involving cation volume was neglected in the pressure-diffusion contribution to eqn (2), since lattice dimensions are relatively insensitive to ξ. |
| ‡ The diffusion stress discussed by Goyal and Monroe16 has been neglected. |
§ This follows because the deformation stress 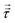 is, by definition, traceless; since σyy = σzz = pθ, τyy = τzz = pθ − p; thus τxx = 2(p − pθ) and σzz = p + τxx = 3p − 2pθ. is, by definition, traceless; since σyy = σzz = pθ, τyy = τzz = pθ − p; thus τxx = 2(p − pθ) and σzz = p + τxx = 3p − 2pθ. |
| ¶ Often frequency dispersion is observed and a constant-phase element is needed to model the interfacial impedance. Including such factors can affect the process by which fint is identified, and may make fint depend on bias. A powerful strategy to approach such issues has been put forward by Song and Bazant.25 |
| || Space-charge domains might extend as much as 1 μm according to Yamamoto et al.,13 an observation that could be rationalized by a different constitutive law for conformational free energy, a lower ceq+, or by additional, unknown interfacial chemistry. The result in eqn (4) is independent of these alterations. |
| This journal is © the Owner Societies 2019 |