Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
On short-ranged pair-potentials for long-range electrostatics†‡
Björn
Stenqvist
 *a and
Mikael
Lund
*a and
Mikael
Lund
 bc
bc
aDivision of Physical Chemistry, Lund University, POB 124, SE-22100 Lund, Sweden. E-mail: bjorn.stenqvist@teokem.lu.se
bDivision of Theoretical Chemistry, Lund University, POB 124, SE-22100 Lund, Sweden
cLINXS – Lund Institute of Advanced Neutron and X-ray Science, Scheelevägen 19, SE-22370 Lund, Sweden
First published on 24th October 2019
Abstract
In computer simulations, long-range electrostatic interactions are surprisingly well approximated by truncated, short-ranged pair potentials. Examples are reaction field methods; the Wolf method; and a number of schemes based on cancellation of electric multipole moments inside a cut-off region. These methods are based on the assumption that the polarization of the neglected surroundings can be inferred from a local charge distribution. Multipole moments themselves are only approximations to the true charge distribution, approximations which many times are needed to simplify calculations in complex systems. In this work we investigate a new, generalized pair-potential based on the idea of moment cancellation that covers interactions between electrostatic moments of any type. We find that moment cancellation in itself is insufficient to generate accurate results and a more restricted formalism is needed, in our case to cancel the virtual charges of the imposed moments. Thus, it is unfeasible to cancel higher-order moments with explicit higher-order moments such as dipoles and instead image charges are needed. The proposed pair-potential is general and straight forwardly implementable for any electrostatic moment – monopole, dipole, quadrupole, etc. – with a computational complexity scaling with the number of particles in the system.
Introduction
Accounting for long-ranged electrostatic interactions in computer simulations is an exquisite task1–4 and although formally exact theories exist for repetitive structures subjected to periodic boundary conditions (PBC),5,6 these are computationally expensive and may impose artificial symmetry from periodicity. Finite-ranged or truncated pair-potentials are fast alternatives to such lattice-sum models and can be more relevant (and often only valid) for isotropic systems.7,8 Research of truncated pair-potentials covers many different approaches and we here highlight the concept of electric multipolar moment cancellation. That is, the effect of long ranged electrostatic interactions is approximated by cancelling one, two, or more electric multipolar moments in the cut-off sphere,1,3 mimicking polarization of the surroundings. The newly developed q-potential9 for ion–ion interactions is a generalization of this concept, and allows for cancellation of an arbitrary number of moments while being free from empirical damping parameters. In this work we expand the q-potential model to include any type of higher-order interactions, i.e. ion–dipole, dipole–dipole, etc. The methodology applied on dipole–dipole interactions is validated via fluid phase simulations and two distinct strategies for cancelling moments are critically investigated and compared with results from Ewald summation. Our discussion entails connections to existing methodologies and, hence, the next section is a brief overview of the field.Overview
Developing and deriving approximate pair-potentials for long range electrostatic interactions is an active and long-studied research topic. Instead of rigorously obeying the Poisson equation for the system of interest, an approximate solution is used. For example, for ion–ion interactions, the Coulomb potential is simply scaled with a short-ranged function![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) (q), see eqn (1).
(q), see eqn (1).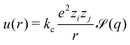 | (1) |
![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) = 0. The choice of the short-ranged function is however delicate. Many variants have been developed and Table 1 gives a non-exhaustive list of such
= 0. The choice of the short-ranged function is however delicate. Many variants have been developed and Table 1 gives a non-exhaustive list of such ![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) (q). In this table we have selected three main groups of pair-potentials: reaction field methods; damping based methods; and damping free methods. The reaction field methods are based on a cavity occupied by explicit particles which in turn is surrounded by a dielectric continuum. The particles induce electrostatic moments in the implicit medium which in turn induce a field which interacts with the particles. The damping based methods are mainly evolved from the Ewald summation method, neglecting reciprocal space. To avoid a discontinuity at the cut-off distance, the potential and/or its derivative is shifted to zero. The damping free methods are somewhat differently derived: some are empirically fitted; some are derived as approximations to the Poisson equation; and some implicitly incorporate the damping parameter into a polynomial form. Like the damping based methods they usually also shift the potential and its higher order derivatives at the cut-off.
(q). In this table we have selected three main groups of pair-potentials: reaction field methods; damping based methods; and damping free methods. The reaction field methods are based on a cavity occupied by explicit particles which in turn is surrounded by a dielectric continuum. The particles induce electrostatic moments in the implicit medium which in turn induce a field which interacts with the particles. The damping based methods are mainly evolved from the Ewald summation method, neglecting reciprocal space. To avoid a discontinuity at the cut-off distance, the potential and/or its derivative is shifted to zero. The damping free methods are somewhat differently derived: some are empirically fitted; some are derived as approximations to the Poisson equation; and some implicitly incorporate the damping parameter into a polynomial form. Like the damping based methods they usually also shift the potential and its higher order derivatives at the cut-off.
![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) (q), for various electrostatic schemes for ion–ion interactions where q = r/Rc with r being the distance between the charges and Rc the cut-off. η = αRc, where α is the commonly used damping-parameter. For the top three reaction field type methods εRF is the relative permittivity of the surrounding medium, and for the bottom scheme P is the number of cancelled moments. Note that
(q), for various electrostatic schemes for ion–ion interactions where q = r/Rc with r being the distance between the charges and Rc the cut-off. η = αRc, where α is the commonly used damping-parameter. For the top three reaction field type methods εRF is the relative permittivity of the surrounding medium, and for the bottom scheme P is the number of cancelled moments. Note that ![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) (q) = 0 for q > 1, i.e. for r > Rc
(q) = 0 for q > 1, i.e. for r > Rc
Short-range function, ![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) (q) (q) |
Ref. |
|---|---|
| Reaction field methods | |
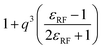
|
Reaction field10 |

|
7 |
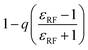
|
11 |
| Damping based methods | |
| erfc(qη) | Real-space Ewald5 |
| [η = 0 → 1] | |
erfc(qη) − q![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) erfc(η) erfc(η) |
Wolf1 |
| [η = 0 → 1 − q] | |
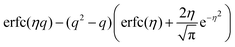
|
12 |
| [η = 0 → 1 + q − q2] | |
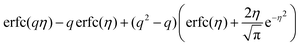
|
13 |
| [η = 0 → (1 − q)2] | 14 |
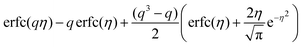
|
3 |
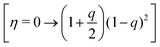
|
|
| Damping free methods | |
| (1 − q)3 | 15 |
| (1 − q)4 | 16 |
| (1 + q)(1 − q)3 | 17 |
| (1 + 2q + 2q2)(1 − q)4 | 4 |
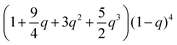
|
18 |
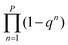
|
q-Potential9 |
In addition to Table 1 there are many other schemes: effective potentials,19 image methods,2,20 lattice-methods,5,6,21–23 and the fast-multipole-method24,25 among others. However, many times the charge distribution of a system is anisotropic and it is convenient to approximate it by electric point multipole moments instead of point charges. These moments each account for a portion of the charge distribution and do therefore inherently contain the (now implicit) charges. Several of the mentioned ion–ion approaches have also been expanded to, or do cover, multipole moment (i.e. higher-order) interactions.6,10,26–28 Each scheme has (dis)advantages and the choice of the summation method is sensitive to the specific system. Often short-range pair-potentials for electrostatics are derived based on the assumption of a homogeneous and isotropic distribution beyond the cut-off region. Therefore such approaches should be used with care in systems where this might not be true, for example at interfaces.29 In the following we expand the theory of the q-potential to higher order interactions and connect the formalism to existing schemes presented in Table 1.
Theory
Multipolar energy in a periodic system
For a cuboidal unit cell with periodic boundaries, the total interaction energy between N particles with electric point moments of type v and w is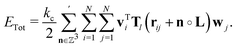 | (2) |
![[Doublestruck N]](https://www.rsc.org/images/entities/char_e171.gif) 0, is introduced as
0, is introduced as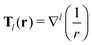 | (3) |
Derivation of the multipolar q-potential
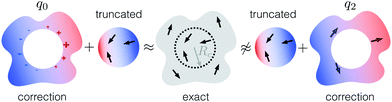
Consider a local region of an isotropic system – a spherical cut-off sphere, for example – where the contained charge distribution is self-consistently polarized by its surroundings. We now describe both the local charge distribution and the surroundings as two multipoles. These will be oppositely polarized and, given that the local region is sufficiently large, perfectly cancel each other. This physical relation is the main idea behind the q-potential,9 where image charges (or moments) of the local region are used to generate the opposing multipole of the surroundings (see Fig. 1). Perfect cancellation of the local and surrounding multipole moments is achieved by requiring that their sum results in zero-tensors, leading to an effectively short-ranged potential. Therefore, for a reasonably large cut-off region, the presented approach is valid for both PBC and non-PBC systems. A similar observation has been made in lattice systems6,30 where the effective Coulomb interaction rapidly decays as r−5.By enforcing total moments described by zero-tensors,1,3,9i.e. achieving a short-ranged potential, eqn (2) is simplified to a single cell n = 0, or for non-PBC systems, a local region. This has previously been done for ion–ion interactions (see especially eqn (9) in ref. 9) and generalizing this procedure, we obtain the modified interaction tensor for any type of electrostatic interactions,
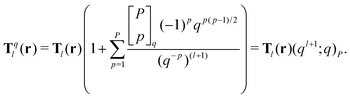 | (4) |
![[Doublestruck N]](https://www.rsc.org/images/entities/char_e171.gif) index the number of cancelled moments,
index the number of cancelled moments, 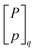 is the q-analogue of the binomial coefficient, and (a;q)P is the q-Pochhammer symbol.9 Since the multiplicative factor to the original interaction-tensor is a q-analogue, we index the modified interaction-tensor with a superscript q and from here on include the derived potential in the q-potential notation. Like for the Coulomb q-potential, we deduce the number of cancelled higher-order moments P − 1 to equal the number of derivatives of Tql(r) with respect to r to be zero at the cut-off. From now on, when we mention the derivative of Tql(r), it is with respect to r.
is the q-analogue of the binomial coefficient, and (a;q)P is the q-Pochhammer symbol.9 Since the multiplicative factor to the original interaction-tensor is a q-analogue, we index the modified interaction-tensor with a superscript q and from here on include the derived potential in the q-potential notation. Like for the Coulomb q-potential, we deduce the number of cancelled higher-order moments P − 1 to equal the number of derivatives of Tql(r) with respect to r to be zero at the cut-off. From now on, when we mention the derivative of Tql(r), it is with respect to r.
Moment cancellation schemes
We now detail two moment cancellation schemes – see Fig. 1 – differing in how they cancel moments. The first approach, which has previously been validated for ion–ion interactions,9 uses image charges (l = 0) while the second approach uses image-like dipoles (l = 2) to cancel higher-order moments. We later revisit the meaning of image-like dipoles.The image charge approach is derived using the ion–ion interaction-tensor from the Coulomb q-potential, where higher-order interactions are described by applying the gradient(s) to the same, that is ∇kTq0(r) where k ∈ ![[Doublestruck N]](https://www.rsc.org/images/entities/char_e171.gif) 0. This approach thus cancels the (implicit) charges of the moments and their higher-order moments by using image charges. Note that there is an arbitrariness in image charge positioning while still achieving moment cancellation, yet the q-potential is based on a physically inspired scheme.9,20,31 For each use of the gradient-operator on Tq0(r), one loses the highest order derivative of the interaction-tensor to be zero at the cut-off. This is expressed in eqn (5), for any l, where the gradient-operator is applied k times, leaving p ≤ P − 1 − k higher-order derivatives zero at the cut-off.
0. This approach thus cancels the (implicit) charges of the moments and their higher-order moments by using image charges. Note that there is an arbitrariness in image charge positioning while still achieving moment cancellation, yet the q-potential is based on a physically inspired scheme.9,20,31 For each use of the gradient-operator on Tq0(r), one loses the highest order derivative of the interaction-tensor to be zero at the cut-off. This is expressed in eqn (5), for any l, where the gradient-operator is applied k times, leaving p ≤ P − 1 − k higher-order derivatives zero at the cut-off.
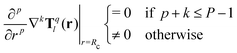 | (5) |
The second approach simply makes use of the dipole–dipole interaction-tensor Tq2 directly, and thus 0 + 0 ≤ P − 1 → P ≥ 1 is enough for the interaction-energy to be zero at the cut-off distance. Here the explicit dipole moment is cancelled but not the implicit charges, nor necessarily the quadrupole moment.
We define ql(P) to be the q-potential, where the cancellation is based either on image charges (l = 0) or on image-like dipoles (l = 2), which cancel P − 1 higher-order moments where P is counted from what type of base moment is used in the cancellation procedure. When not using the index (P), like in ql, we refer to the general group of pair-potentials using l but for any P.
The presented q-potential approaches can be viewed as a generalization of global electroneutrality. Since long-range electrostatic interactions solely come in the form of ion–ion, ion–dipole, dipole–dipole, and ion–quadrupole interactions, we recognize that to accurately compensate for the neglected contributions outside of the cut-off region we generally need to cancel at least up to the quadrupole-moment. Higher order interactions are short-ranged and thus given a large enough cut-off region, these interactions will be explicitly accounted for. However, the cut-off region will also need to be large enough as to capture the local anisotropy of the system8 with an upper limit of Rc ≤ min(L)/4. Thus, the long-range interactions determine P and the short-range ones together with the length-scale of the local anisotropy determine Rc.
Now we address the use of image-like dipoles. For a charge at position r relative to the origin, its image charge in a conductive sphere with radius Rc centered in the origin has a charge scaled by −Rc/r as compared to the charge at r. Since potentials due to charges are isotropic, the charge and image charge have the same angular (in)dependence with regard to the origin. For dipoles however this is not true. Given a dipole moment μ not perpendicular to r, there is an angular alteration to its image-dipole μ′; see eqn (6) where the hats indicate normalized vectors.
μ′ ∝ μ − 3(![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) ·μ) ·μ)![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) | (6) |
Summarizing the above, the final interaction tensor for dipole–dipole interactions using the q-potential is given by
| Tq(r) = T2(r)a(q) + I|r|−3b(q) | (7) |
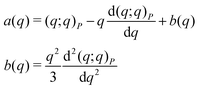 | (8) |
In the original study9 ion–ion interactions (i.e. the q0-potential) were investigated, and indeed the potential was found to be isotropic enough for water-systems. From a theoretical point-of-view the q0 approach is more isotropic than that of q2, due to the isotropy of the image charges and anisotropy of the image-like dipoles. However, this does not exclude the q2-potential from being isotropic itself. Similarly it does not prove that the q0 approach is isotropic enough for being an efficient pair-potential using dipole–dipole interactions. That is why we in the next section investigated the presented potentials using numerical simulations.
Metropolis Monte Carlo simulations
Metropolis Monte Carlo simulations of dipolar Stockmayer fluids32 in the canonical ensemble were performed using the Faunus software,33 with N = 3000, density ρ* = 0.924, temperature T* = 1.333, and squared dipole moment μ*2 = 3.470, where stars indicate reduced units. The equilibration used N × 105 steps each consisting of a combined translational and rotational Monte Carlo attempt. Production runs were ten times longer. The Ewald summation method was used as a reference, and comparisons will always be with regard to this scheme if not stated otherwise. The used cutoff was Rc* = 4 for the pair-potentials while Ewald summations used a real-space cut-off of half the box-length, a reciprocal-space spherical integer cut-off of 9, a damping-parameter equal to π/Rc, and a conducting surrounding dielectric medium. The q0-potential was tested from P = 3 and higher values, and the q2-potential from P = 1. These values were chosen since their respective interaction tensors are zero at the cut-off distance for such P, with no higher-order derivatives cancelled. Thus P = 3 for q0 and P = 1 for q2 are directly comparable in this regard.Results
Radial distribution functions
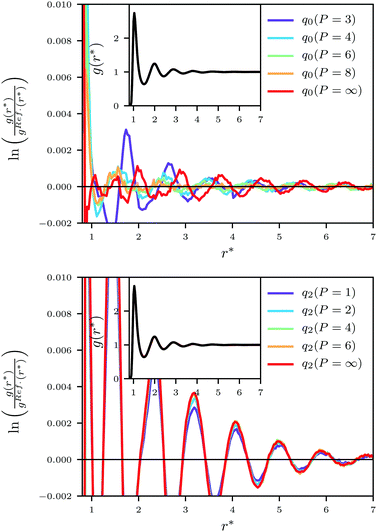
To validate the developed pair-potentials, we first compare radial distribution functions, g(r), with reference Ewald summation results. Fig. 2 shows the logarithm of the ratio between ql-potential and Ewald radial distribution functions. It is clear that q0 is closer to the reference than q2, and that the largest discrepancy is between the smallest P-values for both q0 and q2. However, while for q0 going from P = 3 to P = 4 gives more accurate results, for q2 going from P = 1 to P = 2 gives (slightly) less accurate results. Yet, no q2-potential rivals the results from any q0-potential.Dipole–dipole correlations
Fig. 3 shows dipole–dipole correlation differences to Ewald results, and it is clear that q2 is incapable of capturing the system properties, even being negative at small distances. We also see that q0(P = 4), i.e. up until the first derivative of the interaction-tensor is zero at the cut-off, is closest to the reference akin to q0(P = 5) (see ESI‡), and that increasing P beyond these values gives worse agreement.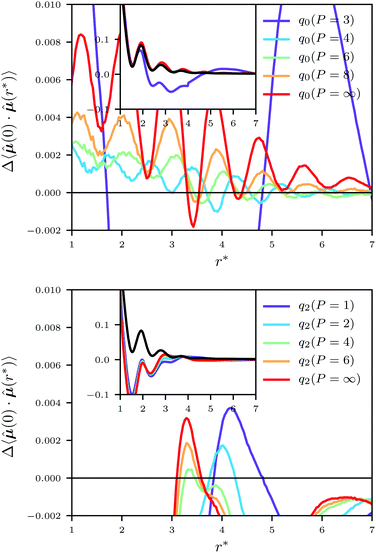 | ||
Fig. 3 Dipole–dipole correlation differences to the reference result using q0 (top) and q2 (bottom). The insets show the dipole–dipole correlation 〈![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b3.gif) (0)· (0)·![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b3.gif) (r*)〉. The black lines are Ewald results. (r*)〉. The black lines are Ewald results. | ||
In the ESI,‡ we have included more results from the simulations (energies, mean squared dipole moments), and presented results for different cut-offs. Those data qualitatively show the same behaviour of q0 and q2 as shown so far and thus further verify the outcome of the analysis in the next section.
Discussion
The q2-potentials cancel moments by using image-like dipoles, yet the simulation results are far from the Ewald summation reference. By expanding the ion–ion interaction-tensor to dipolar systems, i.e. by using the q0-potentials which cancel moments by means of image charges, we get more reasonable outcomes. Though both approaches make use of moment cancellation there is a salient difference in how they do so, which is reflected in the simulation results. We conclude that moment cancellation in itself is insufficient whereas neutralizing the (implicit) charges of the moments and cancelling their higher-order moments provide accurate results. This contrasts other works which like the q2-potential uses explicit dipole-cancellation, but needs to introduce an arbitrary damping parameter to remedy poor results.27,28 A single higher-order cancellation is sufficient in many regards to accurately retrieve valid results when using the q0-potential. This is convenient from a computational point-of-view since molecular dynamics equivalently requires zero force at the cutoff. A modest increase in the cancellation-order improves the results slightly.There are two main theoretical differences between the q0- and q2-approaches beyond the ones mentioned in the previous paragraph. First, the q0 image particles can be interpreted as having a non-localized charge-distribution on the shell of a sphere, whereas the q2 image particles are true point-particles (see Fig. 1). Thus the nature of the q0-potential is more isotropic than that of the q2-potential, a feature which seemingly affects the results. Second, the q0 image particles are exact image particles, whereas the q2 image particles are image-like as discussed earlier. Since we have found that q0 provides more accurate results than q2, which might be a consequence of the just mentioned facts, there may be a corresponding version of the q2-potentials which utilizing explicit dipole cancellation and generates accurate results using non-localized image dipole distributions, or exact image particles. For example, by using a non-localized dipole moment at the cut-off sphere (P = 1) instead of image-like dipoles, we regain the reaction-field method10 using εRF = ∞. By comparing our results to those in a previous study using the described reaction-field method on an identical system as simulated here,28 we note that such an approach is more accurate than q2 yet less so than q0.
Furthermore, we note that the currently proposed formalism is only one of formally infinitely many using the concept of electrostatic cancellation of moments. This since the position of the image moments can be altered while keeping the feature of moment-cancellation intact (see eqn (7) in the derivation of the q-potential9). The positions chosen in this work, and for the Coulomb q-potential, are however physically based and in line with previous works on image moments.9,20,31
We have found that q0 using P = 4–5 gives most accurate results for the simulated bulk Stockmayer-system, like for the ionic q-potential for water-systems.9 From theory we might however expect P = ∞ to give most accurate results since all moments then are cancelled and no explicit interactions with the surrounding are sustained. Nonetheless, most systems exhibit some form of local fluctuations and a too large value of P will therefore suppress this inherent quality. Higher order interactions than dipole–dipole or ion–quadrupole are short-range and thus can be captured with a large enough cut-off region. Hence, infinite cancellation is not necessarily needed. Assuming that the fluctuations of the cut-off region will decay while increasing its size, a large P in combination with a large enough Rc will still give accurate results. Thus, the order of the fluctuations in the system seems to determine the upper limit of P while the order of long-range interactions determines the lower limit, P = 3.
Finally, the presented formalism based on the Tql(r)-tensors is applicable, though not tested, for other electrostatic interactions. For example, the ion–quadrupole interaction makes use of the same interaction-tensor as in the dipole–dipole interaction. We therefore surmise our presented results to be generalizable to this case, i.e. q0 will render more accurate results than q2. Though there is little need to use summation methods for even higher-order electrostatic interactions, the procedure is valid for similar cases outside the electrostatic framework in which arbitrary higher-order moments need cancellation.
Conclusion
We have expanded a formalism accounting for long-ranged Coulomb (ion–ion) interactions by means of moment cancellation to include higher-order electrostatic interactions. The expansion was done in two fundamentally different ways: cancellation of the implicit charges inherent to any higher-order electrostatic moment and their higher-order moments by means of image charges; and cancellation of the explicit moments and their higher-order moments by means of images of said moments. The results unambiguously show moment cancellation to be insufficient to generate accurate results, rather we find that cancellation of the (implicit) charges inherent to the used moments gives comparable results to the standard Ewald summation.The expanded validated formalism is general and straight forwardly implementable for higher-order electrostatic interactions with a computational cost proportional to the number of particles in the system. The method utilizes a cut-off region large enough to represent the sample, and a cancelling parameter directly connected to the relevant higher-order moments in this region, and it therefore avoids any arbitrary damping-parameter.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Swedish Research Foundation (grant number 2017-04372) for financial support and LUNARC in Lund for computational resources.Notes and references
- D. Wolf, P. Keblinski, S. R. Phillpot and J. Eggebrecht, J. Chem. Phys., 1999, 110, 8254–8282 CrossRef CAS.
- X. Wu and B. R. Brooks, J. Chem. Phys., 2005, 122, 044107 CrossRef PubMed.
- I. Fukuda, Y. Yonezawa and H. Nakamura, J. Chem. Phys., 2011, 134, 164107 CrossRef PubMed.
- B. Stenqvist, New J. Phys., 2019, 21, 063008 CrossRef.
- P. P. Ewald, Ann. Phys., 1921, 369, 253–287 CrossRef.
- A. Ladd, Mol. Phys., 1977, 33, 1039–1050 CrossRef CAS.
- I. G. Tironi, R. Sperb, P. E. Smith and W. F. van Gunsteren, J. Chem. Phys., 1995, 102, 5451–5459 CrossRef CAS.
- B. Stenqvist and M. Lund, EPL, 2018, 123, 10003 CrossRef.
- B. Stenqvist, V. Aspelin and M. Lund, Generalized Moment Cancellation for Long-Range Electrostatics, 2019, arXiv:1904.10335 Search PubMed.
- J. Barker and R. Watts, Mol. Phys., 1973, 26, 789–792 CrossRef CAS.
- B. Stenqvist, Electric interactions: a study of cellulose, Department of Theoretical Chemistry, Lund University, Lund, 2016 Search PubMed.
- D. Zahn, B. Schilling and S. M. Kast, J. Phys. Chem. B, 2002, 106, 10725–10732 CrossRef CAS.
- C. J. Fennell and J. D. Gezelter, J. Chem. Phys., 2006, 124, 234104 CrossRef PubMed.
- M. Levitt, M. Hirshberg, R. Sharon and V. Daggett, Comput. Phys. Commun., 1995, 91, 215–231 CrossRef CAS.
- S. Kale and J. Herzfeld, J. Chem. Theory Comput., 2011, 7, 3620–3624 CrossRef CAS PubMed.
- B. W. McCann and O. Acevedo, J. Chem. Theory Comput., 2013, 9, 944–950 CrossRef CAS PubMed.
- T. E. Markland and D. E. Manolopoulos, Chem. Phys. Lett., 2008, 464, 256–261 CrossRef CAS.
- G. S. Fanourgakis, T. E. Markland and D. E. Manolopoulos, J. Chem. Phys., 2009, 131, 094102 CrossRef PubMed.
- S. Izvekov and G. A. Voth, J. Phys. Chem. B, 2005, 109, 2469–2473 CrossRef CAS PubMed.
- H. L. Friedman, Mol. Phys., 1975, 29, 1533–1543 CrossRef CAS.
- J. Lekner, Phys. A, 1991, 176, 485–498 CrossRef.
- T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089–10092 CrossRef CAS.
- U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, J. Chem. Phys., 1995, 103, 8577–8593 CrossRef CAS.
- A. W. Appel, SIAM J. Sci. Stat. Comput., 1985, 6, 85–103 CrossRef.
- L. Greengard and V. Rokhlin, J. Comput. Phys., 1987, 73, 325–348 CrossRef.
- H. Kornfeld, Z. Phys. A: Hadrons Nucl., 1924, 22, 27–43 CrossRef.
- M. Lamichhane, K. E. Newman and J. D. Gezelter, J. Chem. Phys., 2014, 141, 134110 CrossRef PubMed.
- B. Stenqvist, M. Trulsson, A. I. Abrikosov and M. Lund, J. Chem. Phys., 2015, 143, 014109 CrossRef PubMed.
- F. N. Mendoza, J. López-Lemus, G. A. Chapela and J. Alejandre, J. Chem. Phys., 2008, 129, 024706 CrossRef PubMed.
- D. Wolf, Phys. Rev. Lett., 1992, 68, 3315–3318 CrossRef CAS PubMed.
- A. N. Tichonov and A. A. Samarskij, Equations of mathematical physics, Pergamon, New York, 1963 Search PubMed.
- W. H. Stockmayer, J. Chem. Phys., 1941, 9, 398–402 CrossRef CAS.
- B. Stenqvist, A. Thuresson, A. Kurut, R. Vácha and M. Lund, Mol. Simul., 2013, 39, 1233–1239 CrossRef CAS.
Footnotes |
| † A C++ implementation of the derived potential as well as other truncation based schemes are available at https://doi.org/10.5281/zenodo.3522058. |
| ‡ Electronic supplementary information (ESI) available: Detailing cutoff effects; derivation of self-energies and the dielectric constant. See DOI: 10.1039/c9cp03875b |
| This journal is © the Owner Societies 2019 |