Combined co-solvent and pressure effect on kinetics of a peptide hydrolysis: an activity-based approach†
Abstract
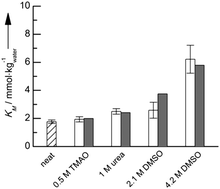
The application of co-solvents and high pressure has been reported to be an efficient means to tune the kinetics of enzyme-catalyzed reactions. Co-solvents and pressure can lead to increased reaction rates without sacrificing enzyme stability, while temperature and pH operation windows are generally very narrow. Quantitative prediction of co-solvent and pressure effects on enzymatic reactions has not been successfully addressed in the literature. Herein, we are introducing a thermodynamic approach that is based on molecular interactions in the form of activity coefficients of substrate and of enzyme in the multi-component solution. This allowed us to quantitatively predict the combined effect of co-solvent and pressure on the kinetic constants, i.e. the Michaelis constant KM and the catalytic constant kcat, of an α-CT-catalyzed peptide hydrolysis reaction. The reaction was studied in the presence of different types of co-solvents and at pressures up to 2 kbar, and quantitative predictions could be obtained for KM, kcat, and finally even primary Michaelis–Menten plots using activity coefficients provided by the thermodynamic model PC-SAFT.
- This article is part of the themed collection: 2019 PCCP HOT Articles


 Please wait while we load your content...
Please wait while we load your content...