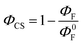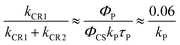Electron transfer reactions in sub-porphyrin–naphthyldiimide dyads†
Received
2nd July 2019
, Accepted 8th July 2019
First published on 8th July 2019
Abstract
A series of donor–acceptor compounds based on a sub-porphyrin (SubP) as an electron donor and naphthyldiimide (NDI) as an acceptor has been designed, synthesized and investigated by time-resolved emission and transient absorption measurements. The donor and acceptor are separated by a single phenyl spacer substituted by methyl groups in order to systematically vary the electronic coupling. The electron transfer reactions in toluene are found to be quite fast; charge separation is quantitative and occurs within 5–10 ps and charge recombination occurs in 1–10 ns, depending on the substitution pattern. As expected, when steric bulk is introduced on the adjoining phenyl group, electron transfer rates slow down because of smaller electronic coupling. Quantum mechanical modelling of the potential energy for twisting the dihedral angles combined with a simplified model of the electronic coupling semi-quantitatively explains the observed variation of the electron transfer rates. Investigating the temperature variation of the charge separation in 2-methyltetrahydrofuran (2-MTHF) and analyzing using the Marcus model allow experimental estimation of the electronic coupling and reorganization energies. At low temperature, relatively strong phosphorescence is observed from the donor–acceptor compounds with onset at 660 nm signaling that charge recombination occurs, at least partially, through the sub-porphyrin localized triplet excited state. Finally, it is noted that charge separation in all SubP–NDI dyads is efficient even at cryogenic temperatures (85 K) in 2-MTHF glass.
Introduction
Factors that govern electron transfer reactions are crucial to understand and optimize in many photochemical applications including molecular based solar cells,1 natural2 and artificial photosynthesis,3–5 and logical operations based on molecular switches6 to just mention a few. During the last few decades donor–acceptor model systems of increasing sophistication have been studied to unravel how the driving force, reorganization energy and electronic coupling influence the rates for charge separation and recombination.7–17 One important goal has been to achieve long-lived charge separated states to be able to drive subsequent chemical transformations using the stored photochemical energy.18 We and others have been particularly interested in understanding how molecular structures influence the somewhat elusive electronic coupling.19–22 In this vein, we have experimentally and theoretically studied how the electronic coupling for charge separation and recombination depends on the tunneling barrier,23–27 the donor–acceptor distance28 and the interplay between these two factors.29,30 The distance dependence of electron transfer reactions is normally exponential and the attenuation factor, β, describing how fast the electronic coupling decays with distance has been reported for many donor–bridge–acceptor systems. Typically, the attenuation factor is 1 Å−1 for saturated molecular bridges and varies widely between 0.1 and 0.8 Å−1 for π-conjugated bridges.31 Since the tunneling barrier height determines the size of the attenuation factor it must be realized that the relative energies of the relevant donor and bridge states determine the value of β. This means that β is not a property of a particular bridge but reflects the system as a whole. For saturated bridges with relatively large tunneling barriers this has minor importance but for the π-conjugated bridges this has been shown both experimentally and through quantum mechanical modeling to result in dramatic differences between systems with the same bridge but with different donors.
In the π-conjugated systems, conformation has a large influence on the electronic coupling. A few studies have been performed in which the dihedral angle between the components in donor–bridge–acceptor systems has been varied.30,32–34 As expected, the through bond electronic coupling in such systems varies approximately in the same way as the orbital overlap, i.e. as the cosine square of the angle between the molecular planes in the conjugated bridges or between the planes of the donor and the bridge. In addition to through bond coupling through the π-system there is also contributions from the σ-electrons, but this is generally believed to have a smaller impact. The simple rationale being that the tunneling barrier for π-electrons is substantially smaller. When designing donor–acceptor systems, in addition to selecting appropriate thermodynamic factors such as driving force and reorganization energies, it is also important to consider factors that influence the electronic coupling such as the stereoelectronic properties of the bridging structure.
In this study we have designed a set of novel donor–acceptor compounds comprised of a sub-porphyrin (SubP) donor and a naphthyldiimide (NDI) acceptor separated by a single phenyl group. The phenyl group is substituted with one or two methyl groups to systematically vary either of the two dihedral angles (Fig. 1) and thereby modulating the electronic coupling. The SubP donor is different from “normal” porphyrins in many ways but particularly it is non-planar and possesses a smaller degree of steric bulk allowing the bridging phenyl and donor to be strongly conjugated. This is expected to lead to larger electronic couplings and potentially higher effects of introducing steric bulk.
 |
| | Fig. 1 Molecular structure of the reference systems SubP and NDI along with SubP–XMe–NDI dyads where X indicates the position of the methyl substituent(s) on the phenyl spacer (XMe = none; 2Me; 3Me; 2,6DiMe; 3,6DiMe). Dihedral angles α and β describe the relative orientation of the three ring systems (90° – perpendicular, 0° – co-planar). | |
Materials and methods
Steady-state absorption spectra of the compounds were recorded on a Varian-Cary 50Bio UV-vis spectrophotometer and steady state emission measurements were performed on a Spex Fluorolog 3 spectrofluorimeter (JY Horiba). The low temperature emission measurements were performed in anhydrous 2-MTHF by using a temperature-controlled liquid nitrogen cryostat (Optistat-Oxford Instrument). The fluorescence lifetime of the SubP was determined on a time-correlated single photon counting (TCSPC) setup using a 483 nm laser diode (PicoQuant) and a MCP-PMT detector. The quenched fluorescence lifetimes of donor–acceptor compounds were measured by time resolved emission using a streak camera system; excitation pulses were generated using a Tsunami Ti:sapphire solid-state laser (Spectra-Physics) which was pumped using a Millennia Pro X laser (Spectra-Physics). The output wavelength of the Tsunami laser was set to 760 nm and by frequency doubling (GWU, Spectra Physics), 380 nm was obtained as an excitation wavelength. The emitted photons were analyzed using a spectrometer (Acton SP2300, Princeton Instruments) and detected using a streak camera (C5680, Hamamatsu) combined with a synchroscan sweep unit (M5675, Hamamatsu).
Transient absorption spectra and decays were recorded on a home-built ultrafast pump–probe spectroscopy setup. A Ti:sapphire oscillator (Tsunami, Spectra Physics) pumped using a Millennia Vs CW laser (Spectra-Physics) generated pulses about 100 fs broad (fwhm) and used to seed a Ti:sapphire regenerative amplifier (Spitfire, Spectra Physics) that was pumped using a frequency-doubled diode-pumped Nd:YLF laser (Evolution-X, Spectra Physics). The amplified pulse at 800 nm with approximately 200 fs duration (fwhm) and 1 kHz repetition rate was split into two beams to create pump and probe light. The pump beam wavelength was tuned using an OPA (TOPAS, Light Conversion Ltd) to 490 nm with 3 μJ pump energy to excite the samples and was delayed relative to the probe light using a motorized optical delay stage (0–10 ns). White light, generated in a rotating CaF2 crystal (380–780 nm), was used as a probe light. The probe light was focused on the entrance slit of a spectrograph and detected using a CCD camera (iXon-Andor) synchronized with a 1 kHz laser. Data were collected through a home written LabVIEW program.
Results and discussion
The results in this paper are organized in five sections. Firstly, the synthesis and ground state characterization of the novel dyads are described. Secondly, time-resolved emission and absorption measurements reveal that charge separation is very efficient and relevant kinetic parameters such as charge separation and recombination rate constants are determined. Thirdly, a quantum mechanical model semi-quantitatively explains the difference in electron transfer rates among the five dyads. Fourthly, the temperature dependence of charge separation is studied and used to estimate the electronic couplings. Finally, from the observation of relatively strong phosphorescence in 2-MTHF glass at 85 K we conclude that charge recombination occurs mainly through the lowest SubP triplet state at cryogenic temperature.
Synthesis and ground state characterization
The synthesis of the five dyads involved several steps. At first, the subporphyrin and NDI based precursors were synthesized according to the modified procedure which is shown in the ESI.† In the final step, the designed subporphyrin–NDI dyads were synthesized by Suzuki–Miyaura coupling with a 5-bromo-10,15-diphenyl-BIII-subporphyrin (13) and the respective NDI–Bpin derivatives (8–12) afforded SubP–XMe–NDI dyads in 50–60% yields (Scheme 1). Newly synthesized target molecules were characterized by the mass spectrometric analysis where it showed the parent molecular ion signals at m/z = 846.26, 860.28, 86.34, 874.31 and 874.44 with (M-axial OMe), respectively, indicating the exact compositions of the dyads (Fig. S11–S15, ESI†). Furthermore, the 1H NMR spectra of the dyads were measured in CDCl3 solution. Interesting observation in the 1H NMR analysis was that SubP–3Me–NDI and SubP–3,6DiMe–NDI dyads existed as a 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 exo/endo mixture in CDCl3. The other dyads such as SubP–NDI, SubP–2Me–NDI and SubP–2,6DiMe–NDI did not show such atropisomers in solution. Furthermore, the structure of SubP–3Me–NDI was successfully characterized by X-ray crystal analysis (Fig. 2). The meso-phenylene bridge is tilted from the subporphyrin plane with a dihedral angle of 84.89°(7), which is larger than those (50–60°) of usual meso-phenylene bridges in subporphyrins. The electronic properties were examined by both cyclic voltammetry and differential pulse voltammetry (DPV) in dichloromethane (DCM) solutions containing 0.1 M of tetrabutylammonium hexafluorophosphate (TBAPF6) as a supporting electrolyte (Fig. S48–S52, ESI†) and their redox potentials were tabulated (Table S3, ESI†).
1 exo/endo mixture in CDCl3. The other dyads such as SubP–NDI, SubP–2Me–NDI and SubP–2,6DiMe–NDI did not show such atropisomers in solution. Furthermore, the structure of SubP–3Me–NDI was successfully characterized by X-ray crystal analysis (Fig. 2). The meso-phenylene bridge is tilted from the subporphyrin plane with a dihedral angle of 84.89°(7), which is larger than those (50–60°) of usual meso-phenylene bridges in subporphyrins. The electronic properties were examined by both cyclic voltammetry and differential pulse voltammetry (DPV) in dichloromethane (DCM) solutions containing 0.1 M of tetrabutylammonium hexafluorophosphate (TBAPF6) as a supporting electrolyte (Fig. S48–S52, ESI†) and their redox potentials were tabulated (Table S3, ESI†).
 |
| | Scheme 1 Synthesis of SubP–XMe–NDI dyads where X indicates the position of the methyl substituent(s) on the phenyl spacer and values in parentheses represent the estimated yields (XMe = none (55%); 2Me (60%); 3Me (50%); 2,6DiMe (60%); and 3,6DiMe (50%)). | |
 |
| | Fig. 2 Single crystal X-ray structure of SubP–3Me–NDI. (a) Top view and (b) side view. The meso-aryl groups in (b) and hydrogen atoms in (a) and (b) are omitted for clarity. | |
Room temperature absorption and emission spectra
The dyads have absorption and emission spectra very similar to the sum of their components. The SubP donor dominates the absorption spectrum in the 350–550 nm region because it has much larger molar absorptivity than the NDI acceptor (Fig. 3). This is important and shows that the electronic coupling is weak enough to allow kinetically isolated donor and acceptor moieties. There is a minor change in the vibrionic envelope of the lowest absorption band (the Q-band) and slightly blue-shifted emission upon methyl substitution at the 3-position next to the SubP. The SubP fluorescence is strongly quenched in all the five dyads at room temperature. Although possible to do, we refrain from evaluating the degree of quenching from these intensity variations mainly because it is not unlikely that minor amounts of SubP impurities (<0.1%) could dominate the weak fluorescence at room temperature. Instead, we will use time-resolved measurements for evaluating the quantum yield and rate for the charge separation process.
 |
| | Fig. 3 Room temperature absorption and emission spectra of all compounds in toluene; excitation at 460 nm, concentrations ∼10−6 M. | |
Fluorescence decays
The SubP donor has a singlet excited state lifetime of 2.3 ns measured by time-correlated single photon counting (TCSPC, Fig. S55 in the ESI†).35–37 Upon conjugation with the NDI acceptor the lifetime becomes about 500 times shorter and thereby impossible to be measured by TCSPC. In Fig. 4, instead the fluorescence decays for the five dyads along with the SubP donor are measured with a streak camera with a time resolution of about 5 ps. The measurements are slightly under-resolved but it could be clearly seen that there is a systematic variation of the singlet excited state lifetime with the substitution pattern. In all cases there is a minor remaining component with long lifetime most likely reflecting small amounts of unquenched SubP impurities. The fluorescence lifetimes were estimated from deconvolution with a Gaussian shaped excitation pulse to be in the range of 5–15 ps corresponding to near quantitative charge separation since, as will be shown below, the singlet excited state decays through the charge separated state in the dyads.
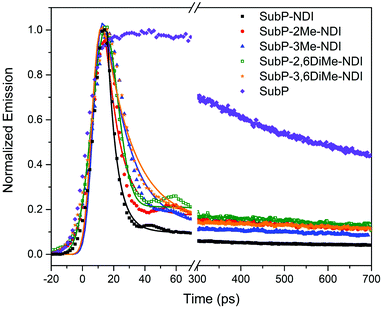 |
| | Fig. 4 Room temperature SubP fluorescence decays from streak camera measurements. The five dyads, as indicated in the legend, are compared to the decay of the SubP reference compound. | |
Transient absorption spectroscopy
In order to confirm the electron transfer reactions by identifying the products of charge separation, SubP and NDI radical cations and anions, respectively, and to get accurate value for the rates of the charge separation (CS) and charge recombination (CR) reactions, femtosecond transient absorption (TA) measurements were performed. In Fig. 5 the TA spectra of SubP–3Me–NDI are shown at a few selected time delays. All other transient absorption spectra of dyads and the SubP reference are found in the ESI† (Fig. S56–S60). At early times (t < 5 ps) the TA resembles the corresponding spectra of the SubP reference and is assigned to the first singlet excited state. At longer times, growing with a rate constant of about (10 ps)−1, we find bands in the TA spectra corresponding to the SubP radical cation (SubP˙+ at 540 and 700 nm) and the radical anion of the acceptor (NDI˙− at 475 nm) in agreement with earlier studies of these radical species.38–41Fig. 5 also shows the time dependence of the TA signal for the five dyads at 475 nm where the NDI˙− absorption dominates. At longer times (t > 5 ns) the bands due to the radical species decay into a spectrum that we assign to the triplet excited state of SubP (vide infra).
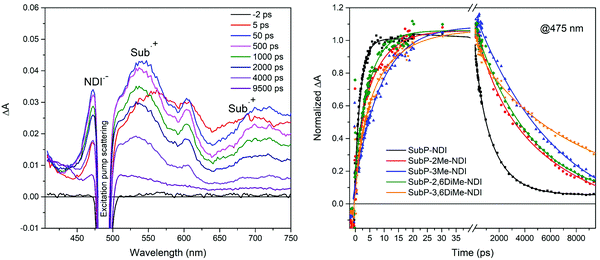 |
| | Fig. 5 Transient absorption spectra of SubP–3Me–NDI in toluene at various time delays as indicated in the legend. Transient absorption at 475 nm for all five dyads where absorption from NDI˙− dominates; a distinct rise on the 2–10 ps time scale followed by decay on the 1–10 ns time-scale clearly signals charge separation and recombination, respectively. Excitation at 490 nm. | |
The transient decays at 475 nm in Fig. 5 corresponding to the growth and decay of NDI˙− (transient decays at 540 nm corresponding to the growth and decay of SubP˙+ are found in the ESI,† Fig. S61) are fitted with biexponential functions in which the risetime is related to the rate constant for charge separation and the decay time to charge recombination. Table 1 comprises the rate constants for charge separation (CS) and charge recombination (CR) across the series of dyads. Again, charge separation is near quantitative and the charge separated state lives for a few nanoseconds. As can be seen in Table 1, both CS and CR times vary systematically when steric bulk is introduced, reflecting that the electronic coupling between the donor and acceptor becomes smaller as the dihedral angles between the donor/acceptor and the adjoining phenyl group are increased. A few things are important to note. Firstly, the effect of steric bulk seems to be larger for charge recombination than for charge separation leading to more long-lived charge separated states while maintaining quantitative charge separation. Secondly, the effect of introducing steric bulk next to the SubP donor (3-position) is more pronounced than the corresponding substitution next to the NDI acceptor (2- and 6-positions). This difference is not easily understood from simple steric arguments but will become clear when we model the potential energy surfaces with respect to the two dihedral angles (vide infra).
Table 1 Rate constants for charge separation (CS) and recombination (CR) from room temperature transient absorption measurements in toluene
|
|
CS |
CR |
|
Average of two lifetimes from the biexponential fit of the decay.
|
|
SubP–NDI
|
(4.6 ps)−1 |
(1200 ps)−1 |
|
SubP–2Me–NDI
|
(3.8 ps)−1 |
(4300 ps)−1 |
|
SubP–3Me–NDI
|
(10.4 ps)−1 |
(6300 ps)−1 |
|
SubP–2,6DiMe–NDI
|
(5.4 ps)−1 |
(4800 ps)−1 |
|
SubP–3,6DiMe–NDI
|
(13 ps)−1 |
(8500 ps)−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a |
As mentioned above, we have a residual TA for times longer than the lifetime of the charge separated state. In Fig. 6, this residual transient absorption is shown at 10 ns delay time for all five dyads compared to the corresponding spectrum of the SubP donor. All these spectra are also similar to the TA spectrum at 10 μs delay time measured on a nanosecond flash photolysis spectrometer (inset in Fig. 6). Since charge separation is much faster than the intrinsic intersystem crossing, a long-lived triplet transient absorption spectrum clearly shows that the charge separated state, at least partially, recombines to the SubP localized triplet state (3SubP*). As will be shown below, this assignment is also supported by low temperature measurements.
 |
| | Fig. 6 Remaining normalized transient absorption at 10 ns for all dyads compared to the SubP donor. These spectra are assigned to excited triplet absorption of the SubP moiety and signal that recombination occurs partially through the triplet state. The inset shows a comparison with the nanosecond transient absorption spectrum of SubP–3,6DiMe–NDI at 10 μs time delay. | |
From spectroscopic and electrochemical data, a state energy diagram could be constructed (Fig. 7). State energies in Fig. 7 were estimated from the steady state spectra and for the charge separated state (CSS) they were estimated from the Weller equation (eqn (1)), which is a fairly approximate treatment, but it is useful for qualitative considerations.27,42–45
| | 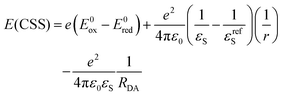 | (1) |
Here
Eox = 0.71 V and
Ered = −1.07 V are the oxidation and reduction potentials (
vs. Fc/Fc
+) for SubP and NDI in DCM,
37,46–49 respectively (Table S3, ESI
†). The second term compensates for the difference in solvent polarity between electrochemical and spectroscopic measurements where
εS = 2.38 (toluene) and
εrefS = 8.93 (DCM) are the relative dielectric constants and
r = 5 Å is the estimated average of the radii of the donor and acceptor. Finally, the last term gives the Coulomb stabilization of the charge separated state where
RDA = 12.2 Å is the donor–acceptor (center–center) distance estimated from the DFT optimized structure (Fig. S53, ESI
†). This gives
E(CSS) = 2.1 eV in toluene estimated to be above the SubP localized triplet at 1.8 eV (
vide infra). This rationalizes why we observe recombination to both the ground state and the SubP triplet state, although with a small driving force for the latter in toluene.
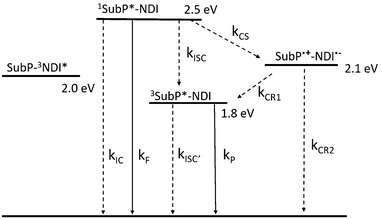 |
| | Fig. 7 State energy diagram for SubP–NDI in toluene. Energies estimated from spectroscopic and electrochemical measurements (Weller equation for the CSS). Radiative processes are shown with full lines and non-radiative with dashed. The rate constants are discussed in the text and in the ESI† (Section S12). | |
Quantum mechanical modelling of relative rates for the electron transfer reactions
The relative rates for electron transfer in the series of SubP–XMe–NDI systems were estimated from a simple model of how the electronic coupling varies with the dihedral angle combined with DFT calculations of the potential energy surfaces for changing the two dihedral angles α and β. From Fermi's Golden rule we know that the square of the electronic coupling is proportional to the electron transfer rate (k ∝ |V|2) in the diabatic limit when the electronic coupling is not too large. The electronic coupling has been calculated and experimentally studied for a few systems containing a flexible dihedral angle in otherwise rigid donor–acceptor systems. The general conclusion from these studies was that the π-electronic coupling varies approximately as the cosine square of the dihedral angle between the donor and acceptor planes.30,33,34 The dihedral angle between the phenyl group and the planar NDI acceptor is simply defined as the angle between the molecular planes whereas the dihedral angle between the phenyl group and the non-planar donor was defined as the angle between the phenyl plane and the plane defined by the three meso carbons of the SubP molecule. One could then simply write:| | V(θ) = Vπ + Vσ = Vπ0cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ + Vσ θ + Vσ | (2) |
where θ is either of the dihedral angles α or β, and Vπ and Vσ are the π- and σ-electron contributions to the electronic coupling, respectively. The σ-electron contributions are expected to be similar across the series whereas the π-electron contributions will depend strongly on the dihedral distributions. In order to estimate the relative electronic coupling for the differently substituted dyads we calculated the potential energy as a function of the dihedral angles (E(θ), B3LYP/6-31G**, relaxed scan, ESI†) and Boltzmann averaged the π-electron contribution according to:| |  | (3) |
In Fig. 8, the calculated potential energy surfaces are shown together with Boltzmann distributions for all five dyads. It is clearly seen that introducing steric bulk moves the population of conformers away from regions of high electronic coupling to regions of lower electronic coupling (closer to the perpendicular orientation, 90°). The effect is particularly strong for substitution of the linking phenyl group at the 3-position, next to the SubP donor. Of course, the potential energy surfaces are calculated for the ground-state which is strictly not correct for either charge separation (starting from the singlet excited state of the SubP) or charge recombination (starting from the charge separated state). However, we believe this to be of minor importance since considering the level of approximation used in the calculations we could only expect semi-quantitative agreement with experiments.
 |
| | Fig. 8 Calculated potential energy surfaces (lines + symbols), and Boltzmann populations at 298 K (shaded) as a function of the dihedral angles α and β (cf.Fig. 1). Addition of steric hindrance through methyl substitutions increases the barrier and moves the population of conformers away from regions of larger to smaller electronic coupling. | |
Table 2 shows the averaged π-electronic couplings relative to SubP–NDI compared to the experimental relative rates for charge separation and recombination. The predicted order of the relative electronic coupling for charge separation (and charge recombination) is: SubP–NDI > SubP–2Me–NDI > SubP–2,6DiMe–NDI > SubP–3Me–NDI > SubP–3,6DiMe–NDI in fair agreement with the rates experimentally observed. However, there is most likely a substantial σ-electron contribution in all the dyads as judged from the smaller relative changes in charge separation rates observed experimentally. Again, both experiments and theoretical estimations agree that a steric encumbrance in the 3- (or 5-) position next to the SubP donor has a much larger effect than that at the corresponding positions next to the NDI acceptor.
Table 2 Calculated relative π-electronic coupling and relative experimental rates for charge separation (CS) and charge recombination (CR) in the five dyads
|
|
(〈Vπ〉/Vπ0)rel |
(kCS)rel |
(kCR)rel |
|
SubP–NDI
|
1 |
1 |
1 |
|
SubP–2Me–NDI
|
0.65 |
1.2 |
0.27 |
|
SubP–3Me–NDI
|
0.19 |
0.44 |
0.19 |
|
SubP–2,6DiMe–NDI
|
0.27 |
0.85 |
0.25 |
|
SubP–3,6DiMe–NDI
|
0.13 |
0.35 |
0.14 |
Temperature dependence of charge separation
The SubP emission was studied in the glass forming solvent 2-methyltetrahydrofuran (2-MTHF) and it was found that the temperature dependence in any of the dyads was much stronger than for the donor alone (Fig. 9 and Fig. S62–S67, ESI†). This reflects the decrease in the charge separation rate upon lowering the temperature. Table S5 (ESI†) shows the fluorescence quantum yields of the five dyads and SubP for the selection of temperatures. The absolute fluorescence quantum yields at room temperature were estimated from the quantum yield of SubP (in toluene), ΦF = 0.16,36,37,49 and from the singlet excited state lifetimes of SubP and the five dyads (cf.Table 1). The relative changes in intensity, compensated for changes in solvent density and refractive index, were used to estimate the charge separation quantum yields (Table S6, ESI†) and rate constants for charge separation at other temperatures (Fig. 10).
 |
| | Fig. 9 (left) Emission spectra of all five dyads and the SubP reference at 85 K in 2-MTHF. (right) Emission spectra of SubP–3Me–NDI as a function of temperature. Excitation at 460 nm. | |
 |
| | Fig. 10 Temperature dependence of the rate for charge separation estimated from the change in the SubP fluorescence quantum yields. | |
As seen in Table S5 (ESI†) and Fig. 9, the SubP–XMe–NDI fluorescence increases between 15 and 40 times upon cooling from room temperature to 85 K. However, the decrease in fluorescence (intensity and lifetimes) when connecting the NDI electron acceptor to the SubP donor is much larger, about 500 times, signaling that the charge separation at 85 K in a rigid 2-MTHF glass is still quite efficient. The charge separation quantum yield is related to the relative fluorescence quantum yields of the dyads (ΦF) and the SubP reference (Φ0F) through eqn (4):
| | 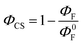 | (4) |
and data for the five dyads are collected in Table S6 (ESI
†).
The temperature dependence of the rate for electron transfer reactions is usually described by the semiclassical Marcus equation:
| |  | (5) |
where
λ, Δ
G° and
V are the reorganization energy, driving force and electronic coupling parameters, respectively. These parameters are typically regarded as temperature independent, at least compared to the much stronger inherent exponential temperature dependence. In this case we expect the electronic coupling to decrease upon lowering the temperature as a consequence of a narrower conformational distribution (
vide supra). The rate constant for charge separation is estimated from the fluorescence quantum yields through:
| |  | (6) |
and with the usual assumption of temperature independent
kf the temperature variation of
kCS is, thus, experimentally estimated from the temperature dependence of the fluorescence.
Fig. 10 shows the measured rates fitted to the linearized Marcus equation and plotted on a logarithmic scale. All dyads have similar slopes with minor variations. Since driving forces and reorganization energies must be the same (properties of the donor and acceptor) any difference in the slope is attributed to the difference in the temperature dependence of the electronic coupling. The fitting shown in
Fig. 10 with parameters compiled in
Table 3 gave reasonable values of the reorganization energy and a quite large electronic coupling using the experimentally determined driving force for charge separation, Δ
G° = −0.4 eV (
cf.Fig. 7).
Table 3 Reorganization energy (λ) and electronic coupling (V) for charge separation
|
|
λ (eV) |
V (cm−1) |
|
SubP–NDI
|
1.09 |
75 |
|
SubP–2Me–NDI
|
1.08 |
79 |
|
SubP–3Me–NDI
|
1.10 |
54 |
|
SubP–2,6DiMe–NDI
|
1.05 |
61 |
|
SubP–3,6DiMe–NDI
|
1.10 |
49 |
The values of the reorganization energies and electronic couplings are reasonable when compared to systems with similar donor–acceptor distances reported in the literature. A zinc-porphyrin–C60 dyad had an electronic coupling for a charge separation of 44 cm−1 and a reorganization energy of 0.85 eV (in toluene)28,50 while a zinc-porphyrin–gold-porphyrin dyad with a slightly larger donor–acceptor separation had corresponding values of 19 cm−1 and 1.1 eV (in dichloromethane).51 Obviously, the exact nature of the bridging structure and the stereoelectronic effects plays a fairly large role as should be evident from this study, preventing a quantitative comparison.
Phosphorescence and charge recombination at low temperature
As seen in Fig. 9 a longer wavelength emission is observed at 85 K for all dyads. This emission was also detected for the SubP alone but with much lower relative intensity. The lifetime was τP = 350 ms (Fig. S68, ESI†) and this observation together with a strong viscosity/temperature dependence clearly shows that this is phosphorescence from the lowest triplet state of SubP.
The relatively strong phosphorescence in the dyads supports the fact that CS is efficient also at low temperature and that the recombination occurs through the excited triplet state. As seen in Table S6 (ESI†) there is quite efficient charge separation also in the low-temperature 2-MTHF glass, ΦCS > 80% for all five dyads at 85 K. At room temperature we observed charge recombination both through the triplet state and directly to the ground state, with the latter dominating. At 85 K it seems that recombination is mainly through the triplet state as concluded from an estimate of its contribution to triplet formation. The argument goes as follows.
The phosphorescence quantum yields for the dyads (ΦP) are related to two different triplet formation channels; direct intersystem crossing with rate constant kisc, and charge recombination with rate constant kCR1 (cf. energy level diagram, Fig. 7). After some straight-forward algebra (ESI,† Section S12) we get eqn (7) to describe the phosphorescence quantum yields of the dyads.
| |  | (7) |
The first term of the right-hand side of
eqn (7) is the direct (intrinsic) intersystem contribution and the second term is the recombination path to the triplet state. Table S5 (ESI
†) lists the phosphorescence quantum yields for the five dyads and SubP reference and they are of the order of 1–3%. The first intrinsic intersystem crossing term of
eqn (7) is of the order of
Φ0P/11 and it therefore contributes less than 10% to the observed phosphorescence yield of the dyads. At the same time, we know the lifetime of the triplet state (350 ms) and that the quantum yield for charge separation is larger than 0.8 at 85 K (Table S6, ESI
†). Thus, everything in
eqn (7) is known, except the radiative rate constant for phosphorescence (
kP). Given these conditions, the branching ratio of the decay of the charge separated state into the triplet for
SubP–NDI is:
| | 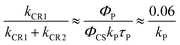 | (8) |
The values of the radiative rate constants for phosphorescence vary many orders of magnitude depending on the molecular system. However, in the absence of heavy atoms and carbonyl centered n → π* transitions, very small values in the range
kP = 0.02–0.06 s
−1 have been reported for many aromatic hydrocarbons
52 and, in particular, for free base porphyrins.
53 If similar radiative rate constants for phosphorescence are valid for the SubP chromophore,
eqn (8) predicts that nearly 100% of the charge separated state recombines through the triplet state at 85 K.
Concluding remarks
From studying the photophysics of the series of SubP–XMe–NDI dyads the following has been learned. (i) Sub-porphyrins are excellent electron donors to be used in applications that rely on photoinduced charge transfer reactions. (ii) By introducing steric bulk on the phenyl group connecting the SubP donor and NDI acceptor the electron transfer rates are modulated in a predictable way. A methyl substituent placed next to the SubP donor has a larger effect than that placed next to the NDI acceptor as explained by the modelling of the potential energy surfaces. (iii) SubP has the lowest triplet excited state at 1.8 eV that functions as a recombination channel for the SubP–XMe–NDI charge separated state. (iv) Charge separation is surprisingly efficient even at cryogenic temperatures. At low temperature, recombination through the SubP localized triplet state seems to dominate the deactivation of the charge separated state.
Conflicts of interest
There are no conflicts of interest to declare.
Acknowledgements
Dr Mélina Gilbert and Jens Nordmark are acknowledged for performing preliminary spectroscopic measurements on the SubP–NDI compound. The Swedish Energy Agency and the Swedish Research Council are acknowledged for generous financial support to B. Albinsson. This work was supported by JSPS KAKENHI Grant Numbers 25220802, 18H03910, and 18K19074. B. Adinarayana thanks the JSPS for a Postdoctoral Fellowship.
References
- A. Hagfeldt, G. Boschloo, L. C. Sun, L. Kloo and H. Pettersson, Chem. Rev., 2010, 110, 6595–6663 CrossRef CAS.
- G. D. Scholes, G. R. Fleming, A. Olaya-Castro and R. van Grondelle, Nat. Chem., 2011, 3, 763–774 CrossRef CAS.
- D. Gust, T. A. Moore and A. L. Moore, Faraday Discuss., 2012, 155, 9–26 RSC.
- M. R. Wasielewski, Acc. Chem. Res., 2009, 42, 1910–1921 CrossRef CAS.
- M. R. Wasielewski, J. Org. Chem., 2006, 71, 5051–5066 CrossRef CAS PubMed.
- J. Andreasson and U. Pischel, Chem. Soc. Rev., 2010, 39, 174–188 RSC.
- M. Gilbert and B. Albinsson, Chem. Soc. Rev., 2015, 44, 845–862 RSC.
- B. Albinsson and J. Mårtensson, J. Photochem. Photobiol., C, 2008, 9, 138–155 CrossRef CAS.
- O. S. Wenger, Chem. Soc. Rev., 2011, 40, 3538–3550 RSC.
- M. Natali, S. Campagna and F. Scandola, Chem. Soc. Rev., 2014, 43, 4005–4018 RSC.
- J. Vura-Weis, S. H. Abdelwahed, R. Shukla, R. Rathore, M. A. Ratner and M. R. Wasielewski, Science, 2010, 328, 1547–1550 CrossRef CAS PubMed.
- A. Harriman, L. J. Mallon, K. J. Elliot, A. Haefele, G. Ulrich and R. Ziessel, J. Am. Chem. Soc., 2009, 131, 13375–13386 CrossRef CAS.
- T. Aoki, H. Sakai, K. Ohkubo, T. Sakanoue, T. Takenobu, S. Fukuzumi and T. Hasobe, Chem. Sci., 2015, 6, 1498–1509 RSC.
- D. Villamaina, S. V. Bhosale, S. J. Langford and E. Vauthey, Phys. Chem. Chem. Phys., 2013, 15, 1177–1187 RSC.
- M. Wolf, C. Villegas, O. Trukhina, J. L. Delgado, T. Torres, N. Martin, T. Clark and D. M. Guldi, J. Am. Chem. Soc., 2017, 139, 17474–17483 CrossRef CAS.
- J. M. Hodgkiss, N. H. Damrauer, S. Presse, J. Rosenthal and D. G. Nocera, J. Phys. Chem. B, 2006, 110, 18853–18858 CrossRef CAS.
- A. Heckmann and C. Lambert, Angew. Chem., Int. Ed., 2012, 51, 326–392 CrossRef CAS.
- H. Imahori, Y. Sekiguchi, Y. Kashiwagi, T. Sato, Y. Araki, O. Ito, H. Yamada and S. Fukuzumi, Chem. – Eur. J., 2004, 10, 3184–3196 CrossRef CAS.
- J. F. Martinez, N. T. La Porte, S. Chaudhuri, A. Sinopoli, Y. J. Bae, M. Sohail, V. S. Batista and M. R. Wasielewski, J. Phys. Chem. C, 2019, 123, 10178–10190 CrossRef CAS.
- K. P. Chen, J. Z. Zhao, X. X. Li and G. G. Gurzadyan, J. Phys. Chem. A, 2019, 123, 2503–2516 CrossRef CAS.
- D. M. Guldi, Chem. Soc. Rev., 2002, 31, 22–36 RSC.
- B. Z. Wang, S. Bauroth, A. Saha, M. Q. Chen, T. Clark, X. Lu and D. M. Guldi, Nanoscale, 2019, 11, 10782–10790 RSC.
- D. Hanss, M. E. Walther and O. S. Wenger, Coord. Chem. Rev., 2010, 254, 2584–2592 CrossRef CAS.
- D. Hanss and O. S. Wenger, Inorg. Chem., 2008, 48, 671–680 CrossRef.
- D. Hanss and O. S. Wenger, Inorg. Chem., 2008, 47, 9081–9084 CrossRef CAS.
- K. Pettersson, J. Wiberg, T. Ljungdahl, J. Mårtensson and B. Albinsson, J. Phys. Chem. A, 2005, 110, 319–326 CrossRef PubMed.
- K. Kilså, J. Kajanus, A. N. Macpherson, J. Mårtensson and B. Albinsson, J. Am. Chem. Soc., 2001, 123, 3069–3080 CrossRef.
- M. U. Winters, E. Dahlstedt, H. E. Blades, C. J. Wilson, M. J. Frampton, H. L. Anderson and B. Albinsson, J. Am. Chem. Soc., 2007, 129, 4291–4297 CrossRef CAS.
- M. P. Eng and B. Albinsson, Angew. Chem., 2006, 118, 5754–5757 CrossRef.
- M. P. Eng and B. Albinsson, Chem. Phys., 2009, 357, 132–139 CrossRef CAS.
- B. Albinsson, M. P. Eng, K. Pettersson and M. U. Winters, Phys. Chem. Chem. Phys., 2007, 9, 5847–5864 RSC.
- A. C. Benniston, A. Harriman, P. Li, P. V. Patel and C. A. Sams, Phys. Chem. Chem. Phys., 2005, 7, 3677–3679 RSC.
- M. P. Eng, J. Mårtensson and B. Albinsson, Chem. – Eur. J., 2008, 14, 2819–2826 CrossRef CAS.
- A. C. Benniston, A. Harriman, P. Li, P. V. Patel and C. A. Sams, Chem. – Eur. J., 2008, 14, 1710–1717 CrossRef CAS.
- W. Y. Cha, J. Oh, M. Kitano, A. Osuka and D. Kim, J. Porphyrins Phthalocyanines, 2017, 21, 152–157 CrossRef CAS.
- J. Oh, J. Sung, M. Kitano, Y. Inokuma, A. Osuka and D. Kim, Chem. Commun., 2014, 50, 10424–10426 RSC.
- S. Hayashi, Y. Inokuma, S. Easwaramoorthi, K. S. Kim, D. Kim and A. Osuka, Angew. Chem., Int. Ed., 2010, 49, 321–324 CrossRef CAS.
- W. Y. Cha, J. M. Lim, K. H. Park, M. Kitano, A. Osuka and D. Kim, Chem. Commun., 2014, 50, 8491–8494 RSC.
- M. E. El-Khouly, J. H. Kim, J. H. Kim, K. Y. Kay and S. Fukuzumi, J. Phys. Chem. C, 2012, 116, 19709–19717 CrossRef CAS.
- S. Goswami, J. N. Nelson, T. Islamoglu, Y. L. Wu, O. K. Farha and M. R. Wasielewski, Chem. Mater., 2018, 30, 2488–2492 CrossRef CAS.
- J. F. Martinez, N. T. La Porte and M. R. Wasielewski, J. Phys. Chem. C, 2018, 122, 2608–2617 CrossRef CAS.
- R. A. Marcus, Can. J. Chem., 1959, 37, 155–163 CrossRef CAS.
- R. A. Marcus, J. Chem. Phys., 1965, 43, 679–701 CrossRef CAS.
- D. Rehm and A. Weller, Ber. Bunsen-Ges., 1969, 73, 834–839 CAS.
- A. Weller, Z. Phys. Chem., 1982, 133, 93–98 CrossRef CAS.
- Y. Inokuma, S. Easwaramoorthi, S. Y. Jang, K. S. Kim, D. Kim and A. Osuka, Angew. Chem., Int. Ed., 2008, 47, 4840–4843 CrossRef CAS.
- N. Zainalabdeen, B. Fitzpatrick, M. Kareem, V. Nandwana, G. Cooke and V. Rotello, Int. J. Mol. Sci., 2013, 14, 7468 CrossRef CAS.
- K. Yoshida and A. Osuka, Chem. – Asian J., 2015, 10, 1526–1534 CrossRef CAS.
- G. Copley, J. Oh, K. Yoshida, D. Shimizu, D. Kim and A. Osuka, Chem. Commun., 2016, 52, 1424–1427 RSC.
- A. Kahnt, J. Kärnbratt, L. J. Esdaile, M. Hutin, K. Sawada, H. L. Anderson and B. Albinsson, J. Am. Chem. Soc., 2011, 133, 9863–9871 CrossRef CAS.
- K. Pettersson, J. Wiberg, T. Ljungdahl, J. Mårtensson and B. Albinsson, J. Phys. Chem. A, 2006, 110, 319–326 CrossRef CAS.
-
J. B. Birks, Photophysics of Aromatic Molecules, John Wiley & Sons Ltd, 1970 Search PubMed.
- M. Gouterman and G. Khalil, J. Mol. Spectrosc., 1974, 53, 88–100 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9cp03725j |
| ‡ These authors contributed equally to this study. |
|
| This journal is © the Owner Societies 2019 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article a,
B.
Adinarayana‡
b,
Atsuhiro
Osuka
a,
B.
Adinarayana‡
b,
Atsuhiro
Osuka
 b and
Bo
Albinsson
b and
Bo
Albinsson
 *a
*a
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 exo/endo mixture in CDCl3. The other dyads such as SubP–NDI, SubP–2Me–NDI and SubP–2,6DiMe–NDI did not show such atropisomers in solution. Furthermore, the structure of SubP–3Me–NDI was successfully characterized by X-ray crystal analysis (Fig. 2). The meso-phenylene bridge is tilted from the subporphyrin plane with a dihedral angle of 84.89°(7), which is larger than those (50–60°) of usual meso-phenylene bridges in subporphyrins. The electronic properties were examined by both cyclic voltammetry and differential pulse voltammetry (DPV) in dichloromethane (DCM) solutions containing 0.1 M of tetrabutylammonium hexafluorophosphate (TBAPF6) as a supporting electrolyte (Fig. S48–S52, ESI†) and their redox potentials were tabulated (Table S3, ESI†).
1 exo/endo mixture in CDCl3. The other dyads such as SubP–NDI, SubP–2Me–NDI and SubP–2,6DiMe–NDI did not show such atropisomers in solution. Furthermore, the structure of SubP–3Me–NDI was successfully characterized by X-ray crystal analysis (Fig. 2). The meso-phenylene bridge is tilted from the subporphyrin plane with a dihedral angle of 84.89°(7), which is larger than those (50–60°) of usual meso-phenylene bridges in subporphyrins. The electronic properties were examined by both cyclic voltammetry and differential pulse voltammetry (DPV) in dichloromethane (DCM) solutions containing 0.1 M of tetrabutylammonium hexafluorophosphate (TBAPF6) as a supporting electrolyte (Fig. S48–S52, ESI†) and their redox potentials were tabulated (Table S3, ESI†).



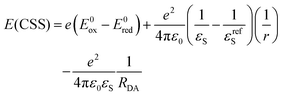

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ + Vσ
θ + Vσ