Core–valence-separated coupled-cluster-singles-and-doubles complex-polarization-propagator approach to X-ray spectroscopies
Abstract
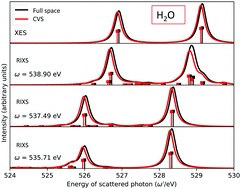
The iterative subspace algorithm to solve the complex linear response equation of damped coupled cluster response theory presented, up to CCSD level, by Kauczor et al., J. Chem. Phys., 2013, 139, 211102, and recently extended to the solution of the complex left response multipliers by Faber and Coriani, J. Chem. Theory Comput., 2019, 15, 520, has been modified to include a core–valence separation projection step in the iterative procedure. This allows one to overcome serious convergence issues that specifically manifest themselves at the CCSD level when addressing core-related spectroscopic effects using large basis sets. The spectra, obtained adopting the new scheme for X-ray absorption and circular dichroism, as well as resonant inelastic-X-ray scattering, are presented and discussed. Core–valence separated results for non-resonant X-ray emission are also reported.
- This article is part of the themed collections: XFELs: cutting edge X-ray light for chemical and material sciences and 2019 PCCP HOT Articles


 Please wait while we load your content...
Please wait while we load your content...