Open Access Article
Open Access ArticleResolving structures of transition metal complex reaction intermediates with femtosecond EXAFS†
Alexander
Britz
 *ab,
Baxter
Abraham
bc,
Elisa
Biasin
a,
Tim Brandt
van Driel
b,
Alessandro
Gallo
de,
Angel T.
Garcia-Esparza
*ab,
Baxter
Abraham
bc,
Elisa
Biasin
a,
Tim Brandt
van Driel
b,
Alessandro
Gallo
de,
Angel T.
Garcia-Esparza
 c,
James
Glownia
b,
Anton
Loukianov
b,
Silke
Nelson
b,
Marco
Reinhard
a,
Dimosthenis
Sokaras
*c and
Roberto
Alonso-Mori
*b
c,
James
Glownia
b,
Anton
Loukianov
b,
Silke
Nelson
b,
Marco
Reinhard
a,
Dimosthenis
Sokaras
*c and
Roberto
Alonso-Mori
*b
aStanford PULSE Institute, SLAC National Accelerator Laboratory, Menlo Park, CA 94025, USA. E-mail: abritz@slac.stanford.edu
bLinac Coherent Light Source, SLAC National Accelerator Laboratory, Menlo Park, CA 94025, USA. E-mail: robertoa@slac.stanford.edu
cStanford Synchrotron Radiation Lightsource, SLAC National Accelerator Laboratory, Menlo Park, CA 94025, USA. E-mail: dsokaras@slac.stanford.edu
dSUNCAT Center for Interface Science and Catalysis, Department of Chemical Engineering, Stanford University, Stanford, CA 94305, USA
eSUNCAT Center for Interface Science and Catalysis, SLAC National Accelerator Laboratory, Menlo Park, CA 94025, USA
First published on 23rd August 2019
Abstract
Femtosecond-resolved Extended X-ray Absorption Fine Structure (EXAFS) measurements of solvated transition metal complexes are successfully implemented at the X-ray Free Electron Laser LCLS. Benchmark experiments on [Fe(terpy)2]2+ in solution show a signal-to-noise ratio on the order of 500, comparable to typical 100 ps-resolution synchrotron measurements. In the few femtoseconds after photoexcitation, we observe the EXAFS fingerprints of a short-lived (∼100 fs) intermediate as well as those of a vibrationally hot long-lived (∼ns) excited state.
Introduction
Transition Metals are ubiquitous in biological systems, e.g. Fe in the Heme group in Myoglobin1 and the Mn cluster in Photosystem II.2 Furthermore, they play essential roles in catalytic applications; Transition Metal (TM) complexes are used as photosensitizers for hydrogen evolution,3 for conversion of solar to electric energy4 and TM oxide nanoparticles are exploited as photocatalysts.5,6 Hard X-ray absorption spectroscopy (XAS) is ideally suited to investigate such TM centers due to its element specificity and sensitivity to changes in the geometric and electronic structures. The X-ray Absorption Near Edge Structure (XANES), i.e. the region around the absorption edge typically up to a few tens of eV above the edge, is rich in electronic structure information (e.g. oxidation state or valence orbital occupation) through transitions of a core electron to unoccupied valence states.7,8 Furthermore, the shape of the absorption edge can be analyzed to obtain geometric structure information.9 Analyzing the Extended X-ray Absorption Fine Structure (EXAFS), a wide region from tens of eV to several hundreds of eV above the absorption edge, is very beneficial, as it is dominated by the local geometry in the close vicinity of the absorbing atom. EXAFS spectra can be very well understood and modeled in a single photo-electron picture, which is generated in the X-ray absorption process and scatters of the neighboring atoms. The modulations in the X-ray absorption probability are due to interferences of this photo-electron wave with itself and can be analyzed by Fourier transformation to produce pseudo-radial distribution functions of the local atomic surroundings.10–12X-ray Free Electron Lasers (XFELs) provide intense and ultrashort X-ray pulses,13 which ultimately enable the measurement of ultrafast XAS with a temporal resolution of <100 fs, limited among other things (e.g. laser pulse duration, sample thickness, timing jitter) by the pulse duration of the X-rays. Furthermore, the intense XFEL pulses can be used to obtain XANES measurements free of radiation damage (which is induced e.g. by radical diffusion),14 similar to diffract-before-destroy crystallography experiments.15 XFEL based XANES was first used at the Linac Coherent Light Source (LCLS) to study the ultrafast spin switching in the model systems [Fe(bpy)3]2+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 16 and [Fe(phen)2(NCS)2].17 Since then, femtosecond XANES has found numerous applications: the photoactivation and the subsequent ultrafast structural and electronic dynamics of the active sites of several biomolecules have been investigated, including carbonmonoxy myoglobin,18 vitamin B12,19,20 and in model Ni-porphyrins.21 Next to TM complex systems, fs time-resolved XAS has been applied to condensed matter charge carrier dynamics; at the SACLA XFEL, the charge-carrier dynamics of anatase TiO2 nanoparticles in an aqueous solution were investigated via Ti K-edge XANES, which revealed trapping of the conduction band electrons in ∼100 fs.6 The energy range of the XANES can be increased in order to enhance the structural sensitivity. For example, XAS scanned up to ∼110 eV above the Fe K-edge in cytochrome c has been exploited to capture the low energy portion of the EXAFS region, which facilitated tracking the Fe–S bond distance in the Fe–methionine dissociation and recombination.22 Despite the success of these experiments, analyzing and interpreting XANES spectra remains challenging due to the tangled electronic and geometric structure information contained in the spectra. Time-resolved X-ray diffuse scattering (XDS), a complementary technique to study the structural dynamics of solvated molecular systems, suffers from another disadvantage. Since the scattering signal consists, due to the lack of element specificity, of contributions from all atoms in the sample, disentangling the numerous inter- and intra-nuclear degrees of freedom involved in photoinduced structural dynamics can be troublesome.23–26
16 and [Fe(phen)2(NCS)2].17 Since then, femtosecond XANES has found numerous applications: the photoactivation and the subsequent ultrafast structural and electronic dynamics of the active sites of several biomolecules have been investigated, including carbonmonoxy myoglobin,18 vitamin B12,19,20 and in model Ni-porphyrins.21 Next to TM complex systems, fs time-resolved XAS has been applied to condensed matter charge carrier dynamics; at the SACLA XFEL, the charge-carrier dynamics of anatase TiO2 nanoparticles in an aqueous solution were investigated via Ti K-edge XANES, which revealed trapping of the conduction band electrons in ∼100 fs.6 The energy range of the XANES can be increased in order to enhance the structural sensitivity. For example, XAS scanned up to ∼110 eV above the Fe K-edge in cytochrome c has been exploited to capture the low energy portion of the EXAFS region, which facilitated tracking the Fe–S bond distance in the Fe–methionine dissociation and recombination.22 Despite the success of these experiments, analyzing and interpreting XANES spectra remains challenging due to the tangled electronic and geometric structure information contained in the spectra. Time-resolved X-ray diffuse scattering (XDS), a complementary technique to study the structural dynamics of solvated molecular systems, suffers from another disadvantage. Since the scattering signal consists, due to the lack of element specificity, of contributions from all atoms in the sample, disentangling the numerous inter- and intra-nuclear degrees of freedom involved in photoinduced structural dynamics can be troublesome.23–26
Time-resolved EXAFS with ∼70 ps resolution is to date measured routinely at synchrotrons with numerous applications to investigate a broad range of materials. While the aforementioned XANES measurements of photoexcited TiO2 revealed the timescale of the electron trapping, the extension to the EXAFS regime to study ZnO nanoparticles allowed the precise characterization of the hole trapping site as a singly charged oxygen vacancies.5 A further advantage of time-resolved EXAFS is the high accuracy – on the order of 1 picometer – in resolving the TM–ligand bond distances and the changes therein,27 as well as the sensitivity in resolving asymmetries in the first coordination shell around the TM.28–32 Extending EXAFS of weakly concentrated solvated samples to the femtosecond regime with beam slicing at synchrotrons33 or tabletop plasma source34 is not viable due to the low photon flux and/or limited photon energy tunability of these source. Measuring femtosecond resolved EXAFS at XFELs is challenging due several reasons: (i) the extremely large pulse-to-pulse fluctuations due to the Self-Amplified Spontaneous Emission (SASE) process require a systematic and rigorous normalization and (ii) scanning the incident X-ray energy over a broad range is technically challenging, as it either requires a very accurate scanning of the long (∼100 m) undulator gaps, or, in the case of LCLS with fixed gap undulators, a continuous modulation of the accelerator electron energy. Recently, a first steady-state EXAFS spectrum acquired at LCLS has been published.35
Here, we present the extension of EXAFS to the femtosecond regime. We show full range time resolved EXAFS spectra up to ∼500 eV above the absorption edge (k ≃ 12 Å−1) and demonstrate the possibility of extracting structural information of ∼100 fs lived intermediate states in the relaxation pathways of photoactivated TM complexes.
1. Experimental methodology to measure EXAFS at LCLS
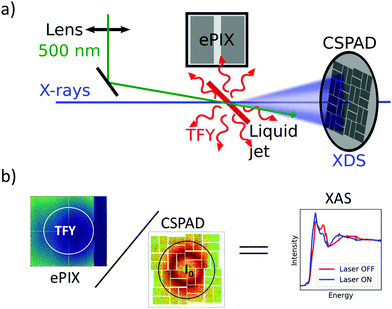
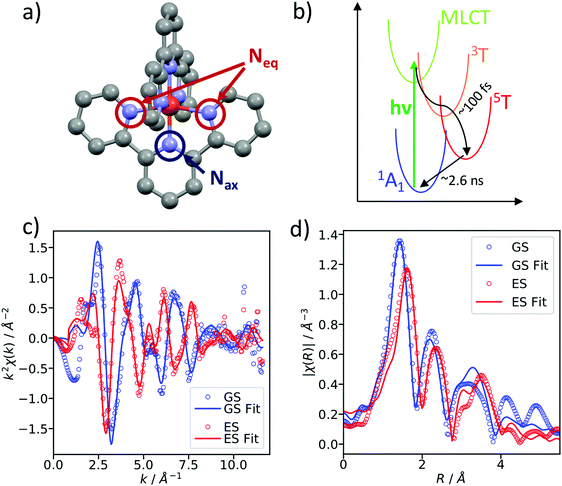
Ultrafast XAS of Fe complexes in solution was measured at the X-ray Pump Probe instrument (XPP)36 of the Linac Coherent Light Source (LCLS). The incident X-ray beam with a bandwidth of ∼30 eV and pulse energy of typically 2–3 mJ was monochromatized to ΔE/E ≃ 1.4 × 10−4 with a channel cut Si(111) monochromator,37 which effectively reduces the pulse energy by two orders of magnitude. The incident X-ray energy was scanned through a combination of accelerator electron beam variation and monochromator adjustment. The X-ray beam was focused to ∼25 μm at the sample using a set of Be compound refractive lenses. To compensate for the change of refractive index of Be while scanning the incident X-ray energy, and thus the change in focal position with respect to the lens, the lens stack position along the X-ray propagation direction was adjusted according to the X-ray energy. The sample, a 20 mM solution of [Fe(terpy)2]2+ (where terpy is 2,2′:6′,2′′-terpyridine, see Fig. 3a) in H2O, was contained in a free-flowing round liquid jet with 50 μm thickness. The X-ray absorption signal was measured in total fluorescence yield (TFY) mode with an ePix100 detector with 768 × 704 pixels of 50 × 50 μm2 size,38 mounted in the X-ray beam propagation plane and perpendicular to the beam direction in order to minimize the collection of elastic scattering. A circular region of interest (ROI) in the center of the ePix100 detector was selected and integrated for the TFY signal. The intensity of the incident X-ray beam (I0) was measured by collecting the diffuse scattering of the solvent (H2O) using a CSPAD 2.3M,38 with the advantage of a single-shot normalization to fluctuations in the jet thickness as well the incoming X-ray intensity. An ROI to select the water ring was integrated as I0. Dividing the TFY by I0 yields the normalization corrected XAS signal (Fig. 1). To measure time-resolved XAS, the sample was excited with visible laser pulses at a wavelength of 500 nm and a pulse energy of 12 μJ, which were focused to a 150 μm (fwhm) spot at the sample position. Arbitrary data acquisition patterns of laser-excited and ground state (no visible excitation laser) can be chosen, and 2 out of 9 X-ray pulses were used to measure the ground state, while 7 out 9 pulses were used for the laser-excited XAS measurement.2. Benchmark picosecond EXAFS measurements of transition metal complexes
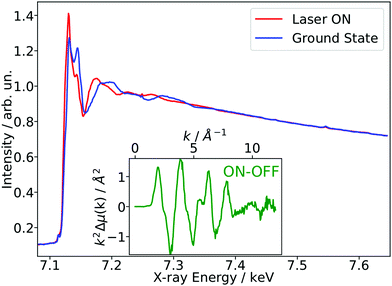
As a benchmark test, EXAFS spectra of a 20 mM solution [Fe(terpy)2]2+ in H2O were acquired 10 ps after 500 nm excitation in the metal-to-ligand charge transfer (MLCT) bands. The photophysical processes (see Fig. 3b) of [Fe(terpy)2]2+ are expected to be very similar to those of other low spin (LS) Fe(II) complexes such as [Fe(bpy)3]2+.30 Optical excitation to the MLCT states is followed by ultrafast relaxation to a longer-lived high-spin (HS) 5T2 state. The initial MLCT lifetime is on the order of ∼100 fs, and the relaxation cascade involves the crossing of a metal-centered (MC) intermediate spin (IS) 3T state with a similar lifetime of ∼100 fs, the ground state recovery time from the final HS state is comparably long (≫100 ps).39 In the LS ground state of (quasi) octahedral Fe(II) complexes, all six 3d electrons occupy the non-bonding t2g orbitals, leaving the anti-bonding eg* orbitals empty. In the IS and HS excited states, the eg* orbitals are singly and doubly occupied, respectively. In the case of [Fe(terpy)2]2+, the long-lived (∼2.6 ns in H2O) HS state has been extensively studied with hard X-ray spectroscopy, including EXAFS, and the Fe–N bond elongation was found to be ∼0.2 Å.28–30 This bond elongation of ∼0.2 Å is typical for Fe(II) complexes during the LS–HS transition and due to the double occupation of the eg* orbitals. A single change in the eg* configuration, as is the case for the triplet IS state in Fe(II) systems, is expected to result in a smaller average bond length change on the order of ∼0.1 Å. Similarly, an average metal–ligand bond elongation of ∼0.1 Å has been observed for the doublet–quartet transition in [Co(terpy)2]2+.23The XAS spectrum, with and without laser excitation (Fig. 2) was removed from artifacts (see ESI† for details on the deglitching procedure). The measured energy range allows the analysis of the EXAFS spectrum up to a photoelectron wavevector k of ∼11.9 Å−1 and optically induced transient differences are visible over the whole spectral range (see inset on Fig. 2). The total acquisition time of the data shown in Fig. 2 was ∼3.5 h, with ∼250 energy points equidistant in k-space. The laser excitation fraction is determined to be f = 76% by comparing the intensity of the transient difference (normalized to the K-edge amplitude) of [Fe(terpy)2]2+ to the published synchrotron measurements, in which complementary X-ray emission spectroscopy (XES) measurements were used to precisely determine the excited state fraction.30 The laser excited spectrum μLON contains contributions from both ground and excited state, as not all molecules are turned over to the HS state by the optical laser. As the excited state fraction f is known, the ES absorption spectrum μES is obtained by removing the contribution from the ground state absorption spectrum μGS (= μLOFF) via31
| μES = μLOFF + (1/f) × (μLON − μLOFF) | (1) |
3. Femtosecond EXAFS measurements
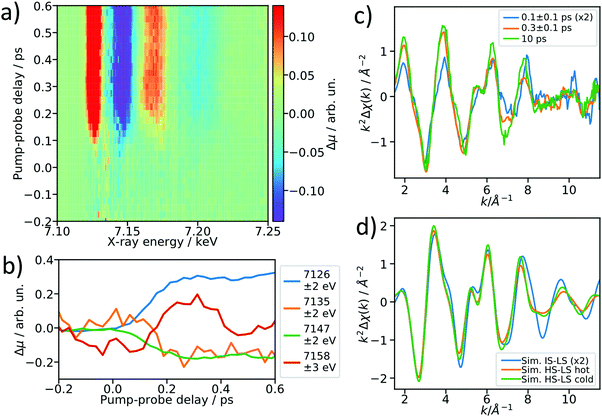
After establishing the feasibility of time-resolved EXAFS at LCLS, we performed femtosecond-resolved EXAFS measurements by continuously moving a delay stage in the optical pump arm over a range from −300 to 600 fs while acquiring the XAS signal. The arrival time jitter is corrected using the timing tool43 and the data are binned on an incident X-ray energy and a pump–probe delay axis, forming a 2D intensity map of the transient intensity as shown in Fig. 4a (see also Fig. S7 for binned femtosecond XAS data as a function of X-ray energy, ESI†). Cuts along the time axis of the 2D maps, e.g. at 7.156 keV, show coherent oscillations (Fig. 4b) analogous to a previous study on [Fe(bpy)3]2+.44 The detailed analysis of these oscillations is outside of scope of this paper, we merely show these as an indication of a temporal resolution <100 fs. The transient signals at 7135 eV and 7158 eV change their respective signs 200 fs after optical excitation, and in the case of [Fe(bpy)3]2+ these were found to be due to the crossing of a short-lived intermediate state.44 Using a kinetic model for the LS → IS → HS transition, in which we assume a Gaussian instrument response function of 70 fs (FWHM), a lifetime of 100 fs for the IS state, and neglecting the MLCT intermediate, we estimate that the average excited state population is >50% in the IS state for the 0–200 fs range (see ESI† for further details). Accordingly, we re-bin the transient differences in the delay axis to obtain difference spectra for the delay bins 0–200 fs and 200–400 fs and compare them to the 10 ps-difference spectrum from Fig. 2.To visualize the general trend below the noise of the transient EXAFS spectra, we used a Savitzky–Golay filter45 with 11 point window size and third order polynomial (Fig. 4c). The difference spectra for 300 ± 100 fs and 10 ps are qualitatively identical, except for a decrease in amplitude at higher k in the case of the 300 fs spectrum. This amplitude difference is due to an increase in the Debye–Waller factor at time delays earlier than internal vibrational relaxation and energy dissipation to the solvent, which occur with time constants on the ∼1 ps time scale for this class of materials.25 The resulting filtered spectra at 100 ± 100 fs and 300 ± 100 fs show a clear qualitative difference, which points towards the crossing of an intermediate state.
We simulated the EXAFS of the intermediate triplet and the long-lived quintet state in FEFF6 using the DFT structures from literature.41 To simulate the cold and thermally equilibrated IS state, the same EXAFS fit parameters obtained from the GS fit were used (Debye–Waller and amplitude reduction factors, energy shift, correction to the bond lengths). Additionally, to gain a better understanding of the observed amplitude reduction in the 300 fs-transient, we simulated a hot HS–LS difference (orange) by doubling the Debye–Waller factors compared to the cold HS–LS transient. The obtained simulated EXAFS transient for the cold HS–LS (green) difference is in good agreement with the 10 ps data and the simulation reproduces the amplitude reduction characteristic for the hot HS state. While all 6 Fe–N bonds expand isotropically by ∼0.2 Å in the HS state compared to the GS, in the IS state only the equatorial Fe–N bonds expand by ∼0.15 Å and the axial ones stay contracted, resulting in an asymmetric, axially-compressed structure of the IS state with a significantly distinct EXAFS pattern. Most interestingly, the simulation of the IS–LS transient qualitatively resembles the relative trend visible in the 100 fs-data, which further indicates a crossing of the triplet IS state. The differences between the spectra of the IS and HS states are most pronounced in the k region between 7–12 Å−1, which stresses again the need to measure full EXAFS spectra up to several hundred eV above the absorption edge.
4. Discussion and outlook
In conclusion, we have demonstrated the viability of time-resolved EXAFS with ∼100 fs resolution using fixed gap undulators at LCLS. The benchmark experiments on a 20 mM solution of [Fe(terpy)2]2+ in a 50 μm jet show a comparable S/N to synchrotron time-resolved measurements with ∼70 ps resolution. Furthermore, we have shown that femtosecond EXAFS can be used to track structural changes of a short-lived (∼100 fs) intermediate spin state in the optically induced low- to high-spin transition.In the future, we envisage combining these measurements with simultaneous ultrafast dispersive XES46 when the incident beam is at the high energy part of the EXAFS spectrum. In the aforementioned spin-transition example, the XES Kβ fingerprints can then be used to quantitatively disentangle the EXAFS of the intermediate spin state species. The EXAFS spectrum can then be thoroughly analyzed in R-space and the structure of the 100 fs-lived intermediate can be determined. Such capabilities will be especially compelling at XFELs with variable gap undulators, such as the upgraded LCLS-II47 and the high-repetition rate European XFEL.48 The variable gap undulator will ease the incident X-ray energy scanning and the high repetition rate will increase the average flux by 2–3 orders of magnitude. These light sources will enable EXAFS measurements of traditionally challenging samples with low concentration or weak transient changes, which are particularly interesting for chemistry, materials science, and biology.
Author contributions
AB, DS and RAM designed the research; all authors conducted the X-ray experiments at the LCLS; AB analyzed the data. The manuscript was written by AB, DS and RAM, with contributions from all authors.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Computational Materials Sciences Program funded by the U.S. Department of Energy, Office of Science, Basic Energy Sciences, under Award No. DE-SC0014607. Use of the Linac Coherent Light Source (LCLS), SLAC National Accelerator Laboratory, are supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences under Contract No. DE-AC02-76SF00515. AB thanks Amy Cordones-Hahn for her support in characterizing the synthesized [Fe(terpy)2]2+ and Clemens Weninger for his support with data processing.References
- J. C. Kendrew, R. E. Dickerson, B. E. Strandberg, R. G. Hart, D. R. Davies, D. C. Phillips and V. C. Shore, Nature, 1960, 185, 422–427 CrossRef CAS.
- K. N. Ferreira, T. M. Iverson, K. Maghlaoui, J. Barber and S. Iwata, Science, 2004, 303, 1831 CrossRef CAS PubMed.
- J. I. Goldsmith, W. R. Hudson, M. S. Lowry, T. H. Anderson and S. Bernhard, J. Am. Chem. Soc., 2005, 127, 7502–7510 CrossRef CAS PubMed.
- M. Grätzel, Inorg. Chem., 2005, 44, 6841–6851 CrossRef PubMed.
- T. J. Penfold, J. Szlachetko, F. G. Santomauro, A. Britz, W. Gawelda, G. Doumy, A. M. March, S. H. Southworth, J. Rittmann, R. Abela, M. Chergui and C. J. Milne, Nat. Commun., 2018, 9, 1–9 CrossRef CAS PubMed.
- Y. Obara, H. Ito, T. Ito, N. Kurahashi, S. Thürmer, H. Tanaka, T. Katayama, T. Togashi, S. Owada, Y. I. Yamamoto, S. Karashima, J. Nishitani, M. Yabashi, T. Suzuki and K. Misawa, Struct. Dyn., 2017, 4, 044033 CrossRef PubMed.
- J. Wong, F. W. Lytle, R. P. Messmer and D. H. Maylotte, Phys. Rev. B: Condens. Matter Mater. Phys., 1984, 30, 5596–5610 CrossRef CAS.
- T. E. Westre, P. Kennepohl, J. G. Dewitt, B. Hedman, K. O. Hodgson and E. I. Solomon, J. Am. Chem. Soc., 1997, 119, 6297–6314 CrossRef CAS.
- M. Benfatto, S. D. Longa and C. R. Natoli, J. Synchrotron Radiat., 2003, 10, 51–57 CrossRef CAS PubMed.
- D. E. Sayers, E. A. Stern and F. Lytle, J. Phys. Chem. Lett., 1971, 27, 1204 CAS.
- D. C. Koningsberger, B. L. Mojet, G. E. van Dorssen and D. E. Ramaker, Top. Catal., 2000, 10, 143–155 CrossRef CAS.
- J. J. Rehr and R. C. Albers, Rev. Mod. Phys., 2000, 72, 621–654 CrossRef CAS.
- P. Emma, R. Akre, J. Arthur, R. Bionta, C. Bostedt, J. Bozek, A. Brachmann, P. Bucksbaum, R. Coffee, F.-J. Decker, Y. Ding, D. Dowell, S. Edstrom, A. Fisher, J. Frisch, S. Gilevich, J. Hastings, G. Hays, P. Hering, Z. Huang, R. Iverson, H. Loos, M. Messerschmidt, A. Miahnahri, S. Moeller, H.-D. Nuhn, G. Pile, D. Ratner, J. Rzepiela, D. Schultz, T. Smith, P. Stefan, H. Tompkins, J. Turner, J. Welch, W. White, J. Wu, G. Yocky and J. Galayda, Nat. Photonics, 2010, 4, 641–647 CrossRef CAS.
- M. Kubin, J. Kern, S. Gul, T. Kroll, R. Chatterjee, H. Löchel, F. D. Fuller, R. G. Sierra, W. Quevedo, C. Weniger, J. Rehanek, A. Firsov, H. Laksmono, C. Weninger, R. Alonso-mori, D. L. Nordlund, B. Lassalle-kaiser, J. M. Glownia, J. Krzywinski, S. Moeller, J. J. Turner, M. P. Minitti, G. L. Dakovski, S. Koroidov, A. Kawde, J. S. Kanady, E. Y. Tsui, S. Suseno, Z. Han, E. Hill, T. Taguchi, S. Andrew, T. Agapie, J. Messinger, A. Erko, A. Föhlisch, U. Bergmann, R. Mitzner, V. K. Yachandra, J. Yano, P. Wernet, M. Kubin, J. Kern, S. Gul, T. Kroll, F. D. Fuller, R. G. Sierra, W. Quevedo, C. Weniger, J. Rehanek, A. Firsov, H. Laksmono, C. Weninger, R. Alonso-mori, D. L. Nordlund, B. Lassalle-kaiser, J. M. Glownia, J. Krzywinski, S. Moeller, J. J. Turner, M. P. Minitti, G. L. Dakovski, S. Koroidov, A. Kawde and J. S. Kanady, Struct. Dyn., 2017, 4, 054307 CrossRef.
- R. Neutze, R. Wouts, D. Van Der Spoel and E. Weckert, Nature, 2000, 406, 752–757 CrossRef CAS.
- H. T. Lemke, C. Bressler, L. X. Chen, D. M. Fritz, K. J. Gaffney, A. Galler, W. Gawelda, K. Haldrup, R. W. Hartsock, H. Ihee, J. Kim, K. H. Kim, J. H. Lee, M. M. Nielsen, A. B. Stickrath, W. Zhang, D. Zhu and M. Cammarata, J. Phys. Chem. A, 2013, 117, 735–740 CrossRef CAS.
- M. Cammarata, R. Bertoni, M. Lorenc, H. Cailleau, S. Di Matteo, C. Mauriac, S. F. Matar, H. Lemke, M. Chollet, S. Ravy, C. Laulhé, J. F. Létard and E. Collet, Phys. Rev. Lett., 2014, 113, 227402 CrossRef.
- M. Levantino, H. T. Lemke, G. Schirò, M. Glownia, A. Cupane and M. Cammarata, Struct. Dyn., 2015, 2, 041713 CrossRef CAS.
- N. A. Miller, A. Deb, R. Alonso-Mori, B. D. Garabato, J. M. Glownia, L. M. Kiefer, J. Koralek, M. Sikorski, K. G. Spears, T. E. Wiley, D. Zhu, P. M. Kozlowski, K. J. Kubarych, J. E. Penner-Hahn and R. J. Sension, J. Am. Chem. Soc., 2017, 139, 1894–1899 CrossRef CAS.
- N. A. Miller, A. Deb, R. Alonso-Mori, J. M. Glownia, L. M. Kiefer, A. Konar, L. B. Michocki, M. Sikorski, D. L. Sofferman, S. Song, M. J. Toda, T. E. Wiley, D. Zhu, P. M. Kozlowski, K. J. Kubarych, J. E. Penner-Hahn and R. J. Sension, J. Phys. Chem. A, 2018, 122, 4963–4971 CrossRef CAS.
- M. L. Shelby, P. J. Lestrange, N. E. Jackson, K. Haldrup, M. W. Mara, A. B. Stickrath, D. Zhu, H. T. Lemke, M. Chollet, B. M. Hoffman, X. Li and L. X. Chen, J. Am. Chem. Soc., 2016, 138, 8752–8764 CrossRef CAS.
- M. W. Mara, R. G. Hadt, M. E. Reinhard, T. Kroll, H. Lim, R. W. Hartsock, R. Alonso-Mori, M. Chollet, J. M. Glownia, S. Nelson, D. Sokaras, K. Kunnus, K. O. Hodgson, B. Hedman, U. Bergmann, K. J. Gaffney and E. I. Solomon, Science, 2017, 356, 1276–1280 CrossRef CAS.
- E. Biasin, T. B. Van Driel, K. S. Kjær, A. O. Dohn, M. Christensen, T. Harlang, P. Chabera, Y. Liu, J. Uhlig, M. Pápai, Z. Németh, R. Hartsock, W. Liang, J. Zhang, R. Alonso-mori, M. Chollet, J. M. Glownia, S. Nelson, D. Sokaras, T. A. Assefa, A. Britz, A. Galler, W. Gawelda, C. Bressler, K. J. Gaffney, H. T. Lemke, K. B. Møller, M. M. Nielsen, V. Sundström, G. Vankó, K. Wärnmark, S. Canton and K. Haldrup, Phys. Rev. Lett., 2016, 117, 013002 CrossRef.
- E. Biasin, T. B. van Driel, G. Levi, M. G. Laursen, A. O. Dohn, A. Moltke, P. Vester, F. B. K. Hansen, K. S. Kjaer, T. Harlang, R. Hartsock, M. Christensen, K. J. Gaffney, N. E. Henriksen, K. B. Møller, K. Haldrupa and M. M. Nielsen, J. Synchrotron Radiat., 2018, 25, 306–315 CrossRef CAS PubMed.
- K. Haldrup, W. Gawelda, R. Abela, R. Alonso-Mori, U. Bergmann, A. Bordage, M. Cammarata, S. E. Canton, A. O. Dohn, T. B. van Driel, D. M. Fritz, A. Galler, P. Glatzel, T. Harlang, K. S. Kjær, H. T. Lemke, K. B. Møller, Z. Németh, M. Pápai, N. Sas, J. Uhlig, D. Zhu, G. Vankó, V. Sundström, M. M. Nielsen and C. Bressler, J. Phys. Chem. B, 2016, 120, 1158–1168 CrossRef CAS.
- D. Rimmerman, D. Leshchev, D. J. Hsu, J. Hong, B. Abraham, R. Henning, I. Kosheleva and L. X. Chen, J. Phys. Chem. B, 2018, 122, 5218–5224 CrossRef CAS.
- X. Zhang, S. E. Canton, G. Smolentsev, C. Wallentin, Y. Liu, Q. Kong, K. Attenkofer, A. B. Stickrath, M. W. Mara, L. X. Chen, K. Wärnmark and V. Sundström, J. Am. Chem. Soc., 2014, 136, 8804–8809 CrossRef CAS.
- S. E. Canton, X. Zhang, M. L. Lawson Daku, A. L. Smeigh, J. Zhang, Y. Liu, C. Wallentin, K. Attenkofer, G. Jennings, C. A. Kurtz, D. Gosztola, A. Hauser and V. Sundström, J. Phys. Chem. C, 2014, 118, 4536 CrossRef CAS.
- X. Zhang, M. L. Lawson Daku, J. Zhang, K. Suarez-Alcantara, G. Jennings, C. A. Kurtz and S. E. Canton, J. Phys. Chem. C, 2015, 119, 3312–3321 CrossRef CAS.
- G. Vankó, A. Bordage, M. Pápai, K. Haldrup, P. Glatzel, A. M. March, G. Doumy, A. Britz, A. Galler, T. A. Assefa, D. Cabaret, T. B. Van Driel, K. S. Kjær, A. O. Dohn, K. B. Moller, H. T. Lemke, M. Rovezzi, Z. Németh, E. Rozsályi, T. Rozgonyi, J. Uhlig, V. Sundstrom, M. M. Nielsen, L. Young, S. H. Southworth, C. Bressler and W. Gawelda, J. Phys. Chem. C, 2015, 119, 5888–5902 CrossRef.
- A. Britz, W. Gawelda, T. A. Assefa, L. L. Jamula, J. T. Yarranton, A. Galler, D. Khakhulin, M. Diez, M. Harder, G. Doumy, A. M. March, É. Bajnóczi, Z. Németh, M. Pápai, E. Rozsályi, D. S. Szemes, H. Cho, S. Mukherjee, C. Liu, T. K. Kim, R. W. Schoenlein, S. H. Southworth, L. Young, E. Jakubikova, N. Huse, G. Vankó, C. Bressler and J. K. McCusker, Inorg. Chem. DOI:10.1021/acs.inorgchem.9b01063.
- J. Zhang, X. Zhang, K. Suarez-alcantara, G. Jennings, C. A. Kurtz, L. Daku and S. E. Canton, ACS Omega, 2019, 4, 6375–6381 CrossRef CAS.
- C. Bressler, C. J. Milne, V.-T. Pham, A. ElNahhas, R. M. van der Veen, W. Gawelda, S. L. Johnson, P. Beaud, D. Grolimund, M. Kaiser, C. N. Borca, G. Ingold, R. Abela and M. Chergui, Science, 2009, 323, 489–492 CrossRef CAS.
- J. Weisshaupt, V. Juvé, M. Holtz, S. Ku, M. Woerner, T. Elsaesser, S. Ališauskas, A. Pugžlys and A. Baltuška, Nat. Photonics, 2014, 8, 927–930 CrossRef CAS.
- R. Chatterjee, C. Weninger, A. Loukianov, S. Gul, F. D. Fuller, M. H. Cheah, T. Fransson, S. Nelson, S. Song, A. Britz, J. Messinger, U. Bergmann, R. Alonso-Mori, V. K. Yachandra, J. Kern and J. Yano, J. Synchrotron Radiat. DOI:10.1107/S1600577519007550.
- M. Chollet, R. Alonso-Mori, M. Cammarata, D. Damiani, J. Defever, J. T. Delor, Y. Feng, J. M. Glownia, J. B. Langton, S. Nelson, K. Ramsey, A. Robert, M. Sikorski, S. Song, D. Stefanescu, V. Srinivasan, D. Zhu, H. T. Lemke and D. M. Fritz, J. Synchrotron Radiat., 2015, 22, 503–507 CrossRef CAS.
- S. Narayanan, A. Sandy, D. Shu, M. Sprung, C. Preissner and J. Sullivan, J. Synchrotron Radiat., 2008, 15, 12–18 CrossRef PubMed.
- G. Blaj, P. Caragiulo, G. Carini, S. Carron, A. Dragone, D. Freytag, G. Haller, P. Hart, J. Hasi, R. Herbst, S. Herrmann, C. Kenney, B. Markovic, K. Nishimura, S. Osier, J. Pines, B. Reese, J. Segal, A. Tomada and M. Weaver, J. Synchrotron Radiat., 2015, 22, 577–583 CrossRef CAS.
- W. Zhang, R. Alonso-Mori, U. Bergmann, C. Bressler, M. Chollet, A. Galler, W. Gawelda, R. G. Hadt, R. W. Hartsock, T. Kroll, K. S. Kjær, K. Kubiček, H. T. Lemke, H. W. Liang, D. A. Meyer, M. M. Nielsen, C. Purser, J. S. Robinson, E. I. Solomon, Z. Sun, D. Sokaras, T. B. van Driel, G. Vankó, T.-C. Weng, D. Zhu and K. J. Gaffney, Nature, 2014, 509, 345–348 CrossRef CAS.
- B. Ravel and M. Newville, J. Synchrotron Radiat., 2005, 12, 537–541 CrossRef CAS.
- D. N. Bowman, A. Bondarev, S. Mukherjee and E. Jakubikova, Inorg. Chem., 2015, 54, 8786–8793 CrossRef CAS.
- A. Britz, T. A. Assefa, A. Galler, W. Gawelda, M. Diez, P. Zalden, D. Khakhulin, B. Fernandes, P. Gessler, H. S. Namina, A. Beckmann, M. Harder, H. Yavaş and C. Bressler, J. Synchrotron Radiat., 2016, 23, 1–15 CrossRef.
- M. Harmand, R. Coffee, M. R. Bionta, M. Chollet, D. French, D. Zhu, D. M. Fritz, H. T. Lemke, N. Medvedev, B. Ziaja, S. Toleikis and M. Cammarata, Nat. Photonics, 2013, 7, 215–218 CrossRef CAS.
- H. T. Lemke, K. S. Kjær, R. Hartsock, T. B. van Driel, M. Chollet, J. M. Glownia, S. Song, D. Zhu, E. Pace, S. F. Matar, M. M. Nielsen, M. Benfatto, K. J. Gaffney, E. Collet and M. Cammarata, Nat. Commun., 2017, 8, 15342 CrossRef CAS.
- A. Savitzky and M. J. E. Golay, Anal. Chem., 1964, 36, 1627–1639 CrossRef CAS.
- R. Alonso-Mori, J. Kern, D. Sokaras, T. C. Weng, D. Nordlund, R. Tran, P. Montanez, J. Delor, V. K. Yachandra, J. Yano and U. Bergmann, Rev. Sci. Instrum., 2012, 83, 073114 CrossRef.
- https://lcls.slac.stanford.edu/lcls-ii (accessed June 13, 2019).
- T. Tschentscher, C. Bressler, J. Grünert, A. Madsen, A. P. Mancuso, M. Meyer, A. Scherz, H. Sinn and U. Zastrau, Appl. Sci., 2017, 7, 1–35 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9cp03483h |
| This journal is © the Owner Societies 2020 |