Open Access Article
Open Access ArticleSulfur adsorption on coinage metal(100) surfaces: propensity for metal–sulfur complex formation relative to (111) surfaces
Da-Jiang
Liu
 *a,
Peter M.
Spurgeon
*a,
Peter M.
Spurgeon
 b,
Jiyoung
Lee
ab,
Theresa L.
Windus
ab,
Patricia A.
Thiel
b,
Jiyoung
Lee
ab,
Theresa L.
Windus
ab,
Patricia A.
Thiel
 abc and
James W.
Evans
abc and
James W.
Evans
 ad
ad
aAmes Laboratory – USDOE, Iowa State University, Ames, Iowa 50011, USA. E-mail: dajiang@ameslab.gov
bDepartment of Chemistry, Iowa State University, Ames, Iowa 50011, USA
cDepartment of Materials Science & Engineering, Iowa State University, Ames, Iowa 50011, USA
dDepartment of Physics and Astronomy, Iowa State University, Ames, Iowa 50011, USA
First published on 18th November 2019
Abstract
Experimental data from low-temperature Scanning Tunneling Microscopy (LTSTM) studies on coinage metal surfaces with very low coverages of S is providing new insights into metal–S interactions. A previous LTSTM study for Cu(100), and a new analysis reported here for Ag(100), both indicate no metal–sulfur complex formation, but an Au4S5 complex was observed previously on Au(100). In marked contrast, various complexes have been proposed and/or observed on Ag(111) and Cu(111), but not on Au(111). Also, exposure to trace amounts of S appears to enhance mass transport far more dramatically on (111) than on (100) surfaces for Cu and Ag, a feature tied to the propensity for complex formation. Motivated by these observations, we present a comprehensive assessment at the level of DFT to assess the existence and stability of complexes on (100) surfaces, and compare results with previous analyses for (111) surfaces. Consistent with experiment, our DFT analysis finds no stable complexes on Ag(100) and Cu(100), but several exist for Au(100). In addition, we systematically relate stability for adsorbed and gas-phase species within the framework of Hess's law. We thereby provide key insight into the various energetic contributions to stability which in turn elucidates the difference in behavior between (100) and (111) surfaces.
1 Introduction
There has been sustained interest in additive-enhanced surface mass transport on metal (M) surfaces exposed to chalcogens, especially sulfur (S) and oxygen (O).1–3 This relates to the broader emerging theme that metal surfaces can be dynamic or fluxional in nature (rather than static or frozen) under operating conditions during catalysis.4,5 With regard to additive-enhanced transport on coinage metals, previous studies revealed a contrasting dramatic enhancement for Ag(111)6versus limited enhancement for Ag(100)7 upon exposure to S. A similar dramatic enhancement was also observed for Cu(111).2 While no experiments are currently available for Cu(100), we expect limited enhancement as for Ag(100).There has long been speculation that metal mass transport across surfaces can be facilitated by the presence of readily-formed metal-additive complexes.1,8,9 An early example was the suggestion that the reported degradation of supported Pt catalyst nanoparticles was due at least in part to formation of PtO2 which can efficiently transport Pt either across the surface or through the gas phase.1,10,11 Historically, this idea was only speculative as such complexes were not directly observed. However, low-temperature Scanning Tunneling Microscopy (LTSTM) with liquid He cooling offers the possibility to freeze the diffusive motion of any such complexes and thereby directly image them confirming (or disproving) their existence. When applied to Cu surfaces exposed to minuscule amounts of S, LTSTM reveals Cu2S3 “hearts” on Cu(111) and concatenations of these especially near steps,12,13 but no complexes and only isolated S adatoms on Cu(100).14 LTSTM applied to Ag surfaces exposed to minuscule amounts of S reveals larger complexes on Ag(111) including Ag16S13,15 and in this paper we present new data demonstrating the lack of complexes on Ag(100). In contrast to Cu and Ag, for Au surfaces exposed to S, no complexes were observed by LTSTM on Au(111),16 but an Au4S5 complex and fragments of this complex were found on Au(100).17
Motivated by dramatic enhancement of mass transport for Cu(111) and Ag(111) exposed to trace amounts of S,2,6 previously Density Functional Theory (DFT) analyses was undertaken to assess stability of various M–S complexes on M(111) surfaces for M = Cu and Ag. The first such DFT study considered Cu3S3 on Cu(111) which was proposed to facilitate accelerated transport across the Cu(111) surface.8 However, it was soon recognized that other complexes such as MS2 and M2S3 could also be relevant for M = Cu or Ag.6 A recent more comprehensive DFT study considered nine distinct M–S complexes on M(111) for coinage metals M = Cu, Ag, and Au, as is appropriate for development of a comprehensive and reliable kinetic model for enhanced mass transport.18 The above observations motivate the comprehensive DFT study presented in this paper of M–S complexes on M(100) surfaces for M = Cu, Ag, and Au at very low coverages of S. In this regime, behavior is not impacted by ordered adsorbate structures or reconstructions which can occur for higher S coverages. Of particular interest is comparison of behavior to that on M(111) surfaces.
The content of the paper is as follows. In Section 2, we describe methodology both for DFT analysis and the LTSTM experiments. In Section 3, we briefly review experimental studies of S on Ag(100) and Ag(111) surfaces where information is more complete than for other coinage metals. Next, in Section 4, we present our DFT results for the energetics of nine different M–S complexes adsorbed on M(100) surfaces. A systematic comparison of energetics for gas-phase versus adsorbed complexes, within the framework of Hess's law, is presented in Section 5. The discussion in Section 6 elucidates the difference in behavior for M = Cu and Ag versus M = Au, and also the difference in behavior for adsorbed complexes on M(100) and M(111) surfaces. Conclusions are provided in Section 7.
2 Methodology
For DFT analysis of extended periodic bulk and surface systems, it is most natural to use a plane-wave (PW) basis set. For such analyses, we use the VASP package (v5.4),19,20 the standard PAW potentials,21,22 and an energy cut-off of 280 eV. The surface is represented by a periodic array of slabs, separated by 1.2 nm of vacuum. Testing with a 400 eV energy cutoff and a 2.1 nm vacuum thickness shows that resulting adsorbate formation energies (defined later) have converged with 0.01 eV for the choices listed above. Lattice constants for the fcc metal substrates are taken as theoretical values. S and M–S complexes are adsorbed on top of each slab (rather than on both sides). The total energy of the system is then minimized allowing both the adsorbate and metal substrate or slab atoms to relax, except for the bottom layer of the slab. We find that surface energetics converges slightly more quickly to behavior for thick slabs fixing a single layer versus, say, two layers at the bottom of the slab (but either choice is reasonable producing essentially identical result for sufficiently thick slabs). A related observation is that the deviation of the metal atoms at the center of the slab from their ideal bulk positions decreases rapidly as the thickness of the slab increases. We have tested that with adsorption of a Cu4S5 complex, the root mean square of deviation of the bond lengths from the (theoretical) bulk lattice constant for such atoms decreases from 0.54% to 0.05% as the slab thickness L increases from 4 to 7. The convergence criterion requires that all forces are below 0.02 eV Å−1. The PBE23 functional is used for these slab calculations.For our comparative analysis of the energetics of gas phase versus adsorbed complexes, we will utilize the results of DFT calculations for gas phase complexes carried out previously using both PW and atomic or Gaussian-type orbitals (GTO) as basis sets. Analysis for the latter was performed with NWChem software and with a variety of different sized basis sets. See ref. 18 for more details. We found excellent consistency for the PBE functional between the PW and GTO basis set analyses when using large quadruple zeta basis sets for the latter. This provides additional support for the reliability of these results.
For the LTSTM studies, the experimental instrumentation and procedures were similar to those used previously in analysis of S adsorption on Cu(111),12 Cu(100),14 Ag(111),6 Au(111),16 and Au(100).17 In the current work, the single crystal Ag(100) sample was cleaned via several Ar+ sputtering (10–15 mA, 2 kV, 10 min) and annealing (700 K, 10 min) cycles. Imaging by STM was performed at 5 K in UHV, at pressure < 6.0 × 10−11 Torr. Sulfur was deposited in situ via an electrochemical Ag|AgI|Ag2S|Pt source. The sample was held at 300 K during S deposition, and then cooled to 5 K for measurement. Tunneling conditions during imaging were in the range −3.00 V to +3.00 V sample bias (VS), and 0.7 to 1.5 nA tunneling current (I). The STM piezoelectric calibration was checked by comparing measured and theoretical dimensions for well-defined features. The measured separation of S adatoms in a p(2 × 2) adlayer along the close packed direction of 0.570 ± 0.012 nm corresponds closely to the theoretical value of 2a, where a = 2.89 nm is the surface lattice constant for Ag(100). The heights of monoatomic steps on the Ag(100) surface were measured at 0.192 ± 0.012 nm fairly consistent with the theoretical value of 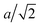 . The sulfur coverage (θS) in monolayers was obtained by counting protrusions in STM images (associating each small protrusion with a single S adatom), and dividing by the areal density of atoms in a bulk Ag(100) plane. We present results for coverages of around 0.01 and 0.03 in units of absolute monolayers (ML).
. The sulfur coverage (θS) in monolayers was obtained by counting protrusions in STM images (associating each small protrusion with a single S adatom), and dividing by the areal density of atoms in a bulk Ag(100) plane. We present results for coverages of around 0.01 and 0.03 in units of absolute monolayers (ML).
3 Illustrative case study: S on Ag surfaces at low coverages
First, we review Scanning Tunneling Microscopy studies assessing S-enhanced mass transport and nanostructure decay on low-index Ag surfaces. In these studies, a submonolayer amount of Ag was first deposited on the low-index Ag surface, which had a terrace-step morphology with a moderate to low density of preexisting extended steps. Ag deposition creates a distribution of monolayer Ag islands. This surface was then exposed to controlled amounts of S resulting in low surface coverages of S. The focus was on coarsening of Ag islands, and specifically on the decay of islands close to extended step edges by transfer of Ag from the island to the step edges. In experiments for Ag on Ag(111) at 300 K,6 a critical S coverage θcS ≈ 0.008 ML was identified (specific to the sample used) which we associate with complete saturation by S of preexisting steps on the surface. For θS < θcS, S has no effect on coarsening as S is completely accommodated at step edges, but for θS > θcS there is a dramatic enhancement associated with the presence of “excess” S on terraces which facilitates the formation of complexes. For θS ≈ 0.011 ML at 300 K, a 2000 nm2 island decays in about 5 min by transfer of Ag to nearby extended step edges versus about 550 min for decay of an island of this size when θS < θcS. Thus, the rate of decay increases by a factor of about 100. For higher coverages, island decay was so fast (occurring in less than the acquisition time for a single STM image) that it could not be quantified by STM imaging. In experiments for Ag on Ag(100) at 300 K,7 the decay of 10 nm2 islands roughly 5 nm away from an extended step was monitored as a function of θS. The decay time decreases from 70 min at θS ≈ 0.035 ML to 30 min at θS ≈ 0.13 ML, corresponding to only a modest increase in decay rate by a factor of 2.3.Next, we describe LTSTM studies undertaken with the goal of directly imaging and identifying Ag–S complexes on Ag(111) and Ag(100) surfaces which could be responsible for facilitating mass transport. LTSTM studies of Ag(111) exposed to S at 5 K15 were undertaken, noting that previous theory6 suggested the possible role of complexes such as AgS2 as well as Ag3S3. As indicated in Section 1, these studies actually revealed the presence of Ag16S13 and even larger Ag13n+3S9n+4 complexes with n > 1. The presence of such large complexes versus the smaller complexes suggested to facilitate mass transport in studies at 300 K can be understood as follows. At the very low temperature of 5 K used for LTSTM imaging, all S should be incorporated into the complex with the lowest chemical potential at 0 K, with the caveat that kinetic limitations could impede formation of very large complexes. Indeed, our recent analysis of M–S complexes on M(111) indicates a trend of decreasing chemical potential at 0 K for increasing Ag–S complex size consistent with the observation of large complexes.18 To assess behavior for T > 0, Russell et al.15 used a kinetic ‘polymerization’ model to argue that the equilibrium population, Pn, of linear aggregates of n “monomer units” with neighboring attractive bond strength ϕ > 0 satisfies Pn ≈ ρ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[+ϕ/(kBT)]Pn−1 where the monomer density ρ ≪ 1 increases with θS. This result supports the picture that upon increasing T, there is a switch from dominance of large complexes to small complexes.
exp[+ϕ/(kBT)]Pn−1 where the monomer density ρ ≪ 1 increases with θS. This result supports the picture that upon increasing T, there is a switch from dominance of large complexes to small complexes.
To provide a more complete experimental assessment of behavior on Ag surfaces, we briefly present results of a new LTSTM analysis of Ag(100) exposed to S at 5 K. The key observation is that these studies reveal a lack of Ag–S complex formation, and instead just isolated S adatoms are observed on the Ag(100) surface. Detailed confirmation that the dots surrounded by a darker ring are single S adatoms have been presented elsewhere.24 However, exactly the same features were observed in imaging of isolated S adatoms on Cu(100).14
Fig. 1 shows LTSTM images comparing behavior on Ag(100) and Ag(111) surfaces. Fig. 1(a and b) reveal isolated S adatoms on Ag(100) for S coverages of 0.01 ML and 0.03 ML. Fig. 1(c) shows a distribution of Ag13n+3S9n+4 complexes for n > 1 on Ag(111) for 0.01 ML S, and Fig. 1(d) provides an close-up image of a single Ag16S13 complex and a schematic of its structure.
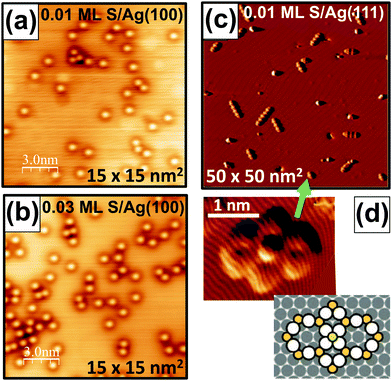 | ||
| Fig. 1 LTSTM images of S on low-index Ag surfaces. (a and b) S adatoms on Ag(100) at: (a) 0.01 ML S; and (b) 0.03 ML S. (c) Ag13n+3S9n+4 complexes on Ag(111) at 0.01 ML S.15 (d) Expanded image and a schematic of an Ag16S13 complex.15 Copyright American Institute of Physics 2013 for (c and d). | ||
4 Energetics of adsorbed M–S complexes on M(100)
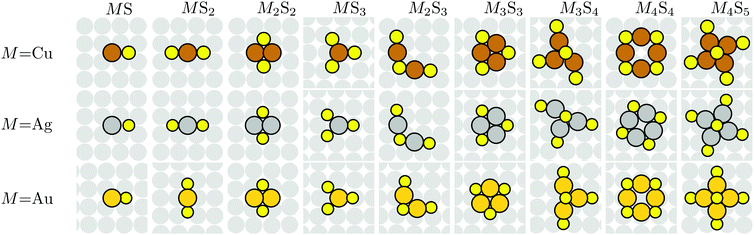
DFT analysis is applied to characterize the energetics of various MmSn complexes adsorbed on M(100) surfaces. Most calculations use a (4 × 4) lateral supercell which is generally sufficiently large that there are no direct interconnections between complexes. For M = Au, this analysis does not incorporate the hex reconstruction of extended Au(100) surfaces. This is not a significant shortcoming since exposure of clean Au(100) to S, with possible subsequent formation of an ordered S adlayer and/or of M–S complexes, lifts this reconstruction. In general, there can be multiple metastable configurations for adsorbed complexes, so determination of the most stable adsorbed structure is non-trivial, especially for larger m and n. However, we have reasonable confidence that the lowest energy configurations have been identified. Fig. 2 shows top views of the proposed most stable configuration of various adsorbed M–S complexes based upon DFT-PBE.Surface atomization energy for complexes
We consider the energy required to completely fragment adsorbed (ads) complexes MmSn into isolated M adatoms and isolated chemisorbed S atoms remaining on the surface,| Ea(MmSn)(ads) = mE[M(ads)] + nE[S(ads)] − E[MmSn(ads)], | (1) |
| S2 | MS | MS2 | M2S2 | MS3 | M2S3 | M3S3 | M3S4 | M4S4 | M4S5 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Cu(100) | −1.82 | −0.15 | 0.02 | −1.15 | −1.84 | 0.11 | 0.00 | 0.50 | 0.38 | 2.11 |
| Ag(100) | −0.96 | −0.17 | 0.00 | −0.98 | −1.54 | 0.10 | 0.27 | 0.43 | 0.55 | 1.58 |
| Au(100) | −0.16 | −0.37 | 0.37 | −1.85 | −1.72 | 0.57 | 0.04 | 1.22 | 1.00 | 2.36 |
We emphasize below that a different and more demanding criterion for stability of adsorbed complexes than that described above is typically more appropriate in an experimental context. However, based upon the above prescription, the general trend revealed by Table 1 is that smaller complexes tend to be unstable in that they have negative surface atomization energies, but larger ones become stable. In addition to stability (or otherwise) against complete fragmentation into atomic components, one should also assess stability for complexes with Ea(MmSn)(ads) > 0 with against decomposition into, say, two fragments (each with Ea(MmSn)(ads) ≥ 0) which remain on the terrace on the surface. Possible fragmentation processes within this class include M4S5 → M4S4 + S, M4S5 → M3S3 + MS2, and M3S4 → M3S3 + S. However, none of these processes is energetically favorable as the sum of Ea(MmSn)(ads) for the fragmentation products is less than Ea(MmSn)(ads) for the larger complex (where we use that Ea(S)(ads) = 0).
Formation energy of complexes assembled from S adatoms and bulk M
Rather than the surface atomization energy described above, generally the most appropriate measure of the stability of adsorbed complexes is their formation energy from S adatoms on terraces, and from M atoms extracted from the substrate (e.g., via detachment of M atoms at kink sites along step edges).6,8,13,18,25 Schematically, this reaction is represented as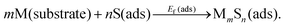 | (2) |
Although our primary interest is in behavior at very low T = 5 K, it is convenient to first define the formation energy, Ef(MmSn)(ads), for the complex MmSn for general finite T via
| Ef(MmSn)(ads) = F(MmSn+ slab) − F(slab) − mμM − nμS, | (3) |
Given the presence of primarily repulsive interactions within this S adlayer, μS increases somewhat with θS. Thus, one natural strategy to simplify the interpretation of behavior is to select a specific S coverage which is sufficiently low that these interactions are not significant (but not so low that configurational entropy of the adlayer provides a significant contribution to the chemical potential). There is a broad range of coverage for which these conditions are satisfied. See the ESI for ref. 17. However, such analysis is computationally costly as it requires very large unit cells for complexes with many S atoms.
Thus, instead to achieve a major reduction in computational cost, we first we present results using a fixed (4 × 4) supercell, so that the corresponding complex coverage is fixed at 1/16 ML, but the sulfur coverage of n/16 ML varies for different n. Formation energies for the adsorbed complexes in Fig. 2 (as well as the formation energy for M) are summarized in Table 2. We claim that these should correspond to Ef with a low fixed S coverage. To confirm this claim, we have performed additional analysis of formation energies for a subset of complexes on Cu(100) for various fixed S coverages (the lowest coverage requiring largest unit cell). Results are shown in Table 4 in the Appendix A. One generally finds excellent agreement with the results in Table 2 for fixed supercell size. The one exception is for M4S5 complexes, where 5/16 ML S coverage for the (4 × 4) supercell is too high to avoid significant lateral interactions. However, using a larger 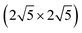 supercell, one finds the result agrees with that for fixed low S coverage in Appendix A. For convenient comparison with the results Table 2 for M(100) surfaces, formation energies for analogous complexes on M(111) surfaces are listed in the Appendix B.
supercell, one finds the result agrees with that for fixed low S coverage in Appendix A. For convenient comparison with the results Table 2 for M(100) surfaces, formation energies for analogous complexes on M(111) surfaces are listed in the Appendix B.
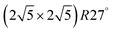 are also reported as the second number in the column
are also reported as the second number in the column
| M | MS | MS2 | M2S2 | MS3 | M2S3 | M3S3 | M3S4 | M4S4 | M4S5 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Cu(100) | 0.57 | 0.72 | 0.56 | 2.32 | 2.42 | 1.05 | 1.80 | 1.30 | 2.03 | 0.30, 1.25 |
| Ag(100) | 0.42 | 0.58 | 0.42 | 1.82 | 1.96 | 0.73 | 1.01 | 0.85 | 1.18 | 0.15, 0.88 |
| Au(100) | 0.19 | 0.57 | −0.17 | 2.20 | 1.92 | −0.20 | 0.71 | −0.47 | 0.07 | –1.31, –0.57 |
A negative formation energy means that the complex is stable against fragmentation where the M atoms are incorporated into the bulk, and where the S atoms remain as adatoms on terraces. A positive formation energy means that it is unstable. Note that for positive formation energies, the (low) population of such complexes on the surface is given by the corresponding Boltzmann factor. For negative formation energies, essentially all S adsorbed on terraces should be incorporated into such complexes. The results in Table 2 show that all formation energies are positive for M = Ag and Cu, entirely consistent with experimental results indicating an absence of M–S complexes on M(100) surfaces for those metals. However, the formation energy for M4S5 is quite low, so those complexes should have a non-negligible population at say 300 K, although likely significant mobility would preclude imaging at that temperature. Furthermore, the Cu4S5 motif has been identified as a component of the 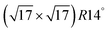 reconstruction on Cu(100) at high S coverages.14,27
reconstruction on Cu(100) at high S coverages.14,27
In marked contrast, formation energies are negative for multiple complexes on Au(100). To determine the relative stability of such complexes, we define a final state chemical potential of the S atom in a complex through μS(MnSn) = [F(MmSn + slab) − F(slab) − mμM]/n. Note that from eqn (3), the difference between the final and initial state chemical potentials of S in a metal–sulfur complex MmSn and in a S adlayer, respectively, can be simply obtained from the formation energy through ΔμS(MmSn) = μS(MmSn) − μS = Ef(MmSn)(ads)/n. Thus, the formation energy, after dividing by n, provides direct information on the relative stability of various complexes. The complex with the lowest ΔμS(MnSn) would be thermodynamically preferred. Applying this criterion, the most stable complex on Au(100) is Au4S5, which is believed to correspond to the feature observed in LTSTM studies which existed within or at the edges of p(2 × 2) S islands.17 In addition, AuS2, Au3S4 and Au2S3 complexes, which can be viewed as incomplete Au4S5 complexes, were also observed. As all of these complexes have negative formation energies, the predictions of our DFT analysis are in excellent agreement with experiments. DFT energetics of stable Au–S complexes were reported previously in ref. 17 and are consistent with the results reported here. Again, we note that although clean Au(100) has a hex reconstruction, this is lifted by S adsorption and complex formation aiding the veracity of our analysis.
5 Relating gas phase and surface energetics: Hess's law
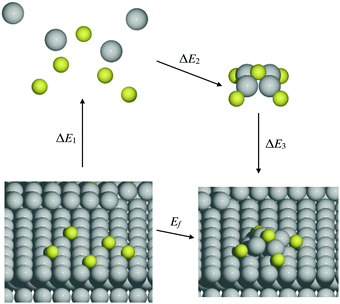
It is natural to compare at least trends in stability for M–S complexes adsorbed on surfaces with those in the gas phase. A systematic approach to relate these energies comes from considering an indirect pathway for formation of adsorbed complexes which involves three steps: (1) desorption of atomic constituents from the surface; (2) formation of the complex in the gas phase; and (3) adsorption of the complex onto the surface. Schematically, this process is described by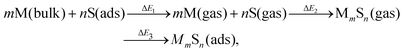 | (4) |
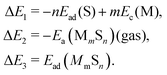 | (5) |
We note that there is no unique choice for the pathway for complex formation, or for the individual steps in the pathway. The current choice is motivated by the following appealing features: (i) ΔE1 is readily determined by quantities, Ead(S) and Ec(M), which are independent of the complex; (ii) ΔE2 is simply the atomization energy of the gas-phase complex, which is a familiar concept in gas-phase chemistry and has been obtained previously in ref. 18; and (iii) ΔE3 is the adsorption energy for the complex, a central concept in surface chemistry.
In Table 3, we tabulate the ΔEj in each individual step of eqn (4) (or Fig. 3). Step 1 is destabilizing while steps 2 and 3 are stabilizing in the formation of adsorbed complexes. PBE values of ΔE1 are calculated from the theoretical bulk cohesive energies, EMc = 3.47, 2.52, and 3.04 eV for Cu, Ag, and Au, respectively, and from theoretical S adsorption energies, Ead(S) = −4.97, −4.04, and −3.78 eV for Cu(100), Ag(100), and Au(100), respectively. The negative of the gas phase atomization energy, ΔE2, is reported in the second column where these values were obtained from our previous study of gas phase energetics in ref. 18. Note that the gas phase atomization energies are far larger in magnitude than the corresponding surface atomization energies. Adsorption energies, ΔE3 = Ead(MmSn), for complexes are listed in the third column. In general, there is not a strong correlation between the gas phase atomization energy and the surface atomization and formation energies. This is not surprising particularly for the latter which are relatively small quantities determined by differences between much larger quantities. Also, a stronger M–S interaction increases the magnitude of both the desorption energies in step 1 and the adsorption energies in step 3, precluding a clear trend in the formation energies.
| Complex | ΔE1 | ΔE2 | ΔE3 | E f(ads) |
|---|---|---|---|---|
| CuS | 8.43 | −3.23 | −4.48 | 0.71 |
| CuS2 | 13.34 | −5.82 | −6.96 | 0.55 |
| Cu2S2 | 16.81 | −10.02 | −4.48 | 2.31 |
| CuS3 | 18.23 | −7.75 | −8.07 | 2.41 |
| Cu2S3 | 21.70 | −11.87 | −8.79 | 1.04 |
| Cu3S3 | 25.17 | −16.63 | −6.76 | 1.78 |
| Cu3S4 | 30.07 | −17.34 | −11.44 | 1.28 |
| Cu4S4 | 33.54 | −23.06 | −8.46 | 2.01 |
| Cu4S5 | 37.36 | −22.41 | −14.67 | 0.28 |
| AgS | 6.58 | −2.46 | −3.54 | 0.58 |
| AgS2 | 10.60 | −4.52 | −5.66 | 0.42 |
| Ag2S2 | 13.12 | −7.44 | −3.86 | 1.81 |
| AgS3 | 14.61 | −5.78 | −6.87 | 1.96 |
| Ag2S3 | 17.13 | −9.06 | −7.33 | 0.73 |
| Ag3S3 | 19.65 | −12.69 | −5.95 | 1.00 |
| Ag3S4 | 23.66 | −13.32 | −9.50 | 0.84 |
| Ag4S4 | 26.19 | −17.49 | −7.53 | 1.16 |
| Ag4S5 | 29.42 | −17.34 | −11.95 | 0.13 |
| AuS | 6.83 | −2.94 | −3.34 | 0.56 |
| AuS2 | 10.59 | −5.92 | −4.85 | −0.18 |
| Au2S2 | 13.63 | −8.49 | −2.92 | 2.22 |
| AuS3 | 14.35 | −7.51 | −4.93 | 1.91 |
| Au2S3 | 17.39 | −11.51 | −6.07 | −0.20 |
| Au3S3 | 20.43 | −14.92 | −4.81 | 0.69 |
| Au3S4 | 24.19 | −16.41 | −8.26 | −0.49 |
| Au4S4 | 27.22 | −21.60 | −5.54 | 0.09 |
| Au4S5 | 30.12 | −20.87 | −10.53 | −1.27 |
Finally, we provide some specific examples comparing gas phase and surface behavior. As noted above, in general, trends in gas phase stability do not correlate with those for adsorbed complexes. Consider first the sequence of complexes Au4S5, Au4S4, Au3S4, Au3S3, Au2S3, and AuS3. For adsorbed species, there is a alternating pattern of negative (stable) and positive (unstable) Ef(MmSn)(ads). This pattern is also reflected in the surface atomization energies which alternate from higher to lower values. The most stable adsorbed complex in this set is Au4S5 which has the lowest (relative) chemical potential ΔμS(M4S5) = −0.32 eV. In contrast, for these complexes in the gas phase, Au4S5 is unstable against detachment of an S (as its atomization energy, −ΔE2, is lower than that for Au4S4). Similarly, there is a relatively low cost of 1.49 eV to detach an S from Au3S4 in the gas phase, despite the feature that this complex is quite stable when adsorbed. Another general feature is that Ag–S complexes are less stable than Cu–S complexes in the gas phase, but they have lower (more negative) formation energies than Cu–S complexes on the surface. Overall, Ag–S complexes have weaker adsorption energies, a feature which does not enhance their stability when adsorbed relative to Cu–S complexes. However, the energy cost to extract Cu from the substrate is much higher than for Ag, and the adsorption of S on Cu(100) is stronger than on Ag(100). These latter factors dominate the relative values of formation energies.
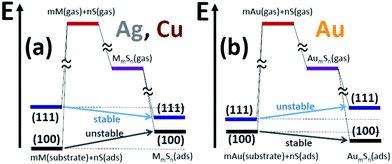
6 Discussion: comparison of behavior on M(100) and M(111) surfaces
In this section, we return to one of our key goals of comparing the stability of M–S complexes on M(111) and M(100) surfaces. For this purpose, the decomposition of energies in Section 5 using Hess's law is particularly instructive since the second step involving gas phase formation and the associated energy, ΔE2, is independent of the type of surface. As discussed below, a key factor controlling the differing behavior for the M(100) and M(111) surfaces is the difference in adsorption energies for (isolated) S adatoms. For Cu and Ag, there is a strong preference for adsorption on (100) over (111) surfaces: Ead(S) = −4.97 eV versus −4.40 eV for Cu(100) versus Cu(111); and Ead(S) = −4.04 eV versus −3.64 eV for Ag(100) versus Ag(111). In contrast, values of Ead(S) = −3.78 eV versus −3.69 eV for Au(100) versus Au(111), are much closer.The stronger adsorption of S on the four-fold hollow (4fh) sites on Cu(100) versus the three-fold hollow (3fh) sites on Cu(111) has been analyzed in detail not just for extended surfaces, but also for nanoclusters (where quantum size effects somewhat disrupt this feature for smaller nanocluster sizes).28 The difference in adsorption was attributed to weaker antibonding interactions at the 4fh site relative the 3fh site, where we note that bonding interactions with the substrate at 4fh and 3fh sites are similar. A recent DFT study of S adsorption on low-index surfaces considered not just coinage metals, but also Ni, Pd, Pt, Rh, and Ir.29 In all cases, adsorption on the (100) surface is stronger than on the (111) surfaces, although the difference is much smaller for Au than all other metals (consistent with the results reported above). Ref. 29 also reports S diffusion barriers which are far higher on (100) surfaces. The high diffusion barrier on Ag(100) was previously suggested to impact the limited additive-enhanced mass transport observed on this surface.7
Now we take up the challenge of elucidating the difference in behavior on Ag(111) and Ag(100) surfaces. For Ag2S3, there is little difference between the adsorption energy, ΔE3, of the complex on the (100) and (111) surfaces of Ag. Thus, the source of the difference between the positive formation energy of Ag(100) and the negative formation energy on Ag(111) comes almost exclusively from the difference in ΔE1. This difference is in turn exclusively tied to the difference in adsorption energies of S on the Ag(100) and Ag(111) surfaces. Specifically, the feature that S adsorbs much more strongly on Ag(100) as isolated adatoms inhibits the formation of complexes on that surface relative to the Ag(111) surface. This same interpretation applies to describe the lack of stability of Ag3S3, Ag3S4, and Ag4S4 on Ag(100) contrasting their stability on Ag(111). For Ag4S5, adsorption on the Ag(111) surface is significantly stronger than on Ag(100), which has the effect of making this complex only weakly unstable on Ag(100) versus being stable on Ag(111). (However, since larger complexes such as Ag16S13 have even lower chemical potentials than the above smaller complexes on Ag(111), our LTSTM studies find only the latter and not, e.g., Ag4S5 on Ag(111).)
Similarly for Cu2S3, there is little difference between the adsorption energy, ΔE3, on Cu(100) and Cu(111). Thus, the source of the difference between the lack of stability on Cu(100) and the stability on Cu(111) comes from the difference in ΔE1, which in turn comes from the difference in Ead(S) on Cu(100) and Cu(111) surfaces. Specifically, stronger S adsorption on Cu(100) inhibits complex formation relative to Cu(111).
The picture is quite different for Au. For AuS2, Au2S3, Au3S4, and Au4S5, the difference in ΔE1 for Au(100) and Au(111) surfaces is relatively small (compared to Cu and Ag) due to the relatively small difference in adsorption energies for S on these two surfaces. However, the stability of these complexes on Au(100), but not Au(111), derives from their stronger adsorption on the Au(100) surface.
The contrasting behavior for Ag and Cu surfaces with that for Au surfaces is summarized schematically in Fig. 4. This figure also illustrates the difference in behavior between (100) and (111) surfaces.
7 Conclusions
Our DFT-based analysis of the stability (or otherwise) of M–S complexes on coinage metal M = Cu, Ag, and Au surfaces is entirely consistent with experiment. Stability of complexes is lacking on (100) surfaces of Cu and Ag, in contrast to the (111) surfaces. Stable complexes are found on Au(100), but not on Au(111). The contrasting behavior for (100) versus (111) surfaces, and for Ag and Cu versus Au, is effectively elucidated within the framework of Hess's law and shown schematically in Fig. 4. This approach allows an unambiguous decomposition of the various energetic contributions to the stability of complexes. This decomposition demonstrates that a key factor in the lack of stability on (100) surfaces of Cu and Ag, in contrast to (111) surfaces, is the significantly stronger adsorption of S adatoms on the (100) surfaces. However, for Au, there is a relatively small difference in adsorption energy for S on (100) versus (111) surfaces. This feature together with stronger adsorption of complexes on the Au(100) surface produces different behavior than for Cu and Ag, i.e., complexes are stable on Au(100) and not on Au(111).The lack of stable complexes on M(100) surfaces for M = Ag and Cu is consistent with observation of only moderately enhanced mass transport of Ag(100) in the presence of S. We expect that the same will be true for Cu(100) exposed to S. Again, this contrasts the dramatic enhancement of mass transport on Ag(111) and Cu(111) exposed to S. To explain this behavior, we note that for the mass transport pathway associated with a specific mass carrier, the effective activation barrier is given by the sum of the diffusion barrier and the formation energy for the mass carrier (or just the diffusion barrier if the complex formation energy is negative).3,6,8 This applies irrespective of whether the carrier is a metal adatom or a complex (although there could be an additional attachment barrier which must be included for the latter). Since the formation energies of metal adatoms are high as indicated in Table 2, even complexes with small positive formation energies (rather than just negative formation energies) can dominate mass transport provided that their diffusion barriers are not too high compared to metal adatoms.
This study also motivates further experimental analysis of mass transport on Au surfaces exposed to S. In particular, such work should assess if significant enhancement occurs on Au(100) due to stable Au4S5 and other complexes. In addition, it is of interest to check if exposure of Au(111) to just trace amounts of S produces limited enhancement of mass transport, at least compared to the dramatic enhancement seen on Ag(111) and Cu(111). It should, however, be noted that strong S-induced surface dynamics has already been observed on Au(111) for higher surface coverages.30,31
Conflicts of interest
There are no conflicts to declare.Appendix A: formation energies calculated with alternative methods
In Table 4, we provide results for formation energies for various Cu–S complexes on Cu(100) obtained at a fixed S coverage. Analysis for lowest S coverage requires the largest supercells, and thus is particularly computationally demanding. Complexes including more S atoms also require larger unit cells. In experiment, conversion between S adatoms and various M–S complexes most naturally occurs at a fixed S coverage, corresponding to the analysis presented here. However, as noted in the text, results obtained with fixed supercell size (corresponding to fixed complex coverage) at far lower computational cost are in excellent agreement with the results presented here.| Coverage | CuS | CuS2 | Cu2S2 | Cu2S3 | Cu3S3 | Cu3S4 | Cu4S4 | Cu4S5 |
|---|---|---|---|---|---|---|---|---|
| 0.250 | 0.76 | 0.57 | 2.26 | 1.34 | 1.82 | 1.30 | 2.03 | 1.29 |
| 0.200 | 0.81 | 0.62 | 2.24 | 1.06 | 1.81 | 1.26 | 2.08 | 1.27 |
| 0.125 | 0.72 | 0.56 | 2.32 | 1.07 | 1.85 | 1.19 | 2.03 | 1.32 |
| Various | 0.69 | 0.56 | 2.32 | 1.09 | 1.84 | 1.38 | 2.11 | 1.49 |
We should also mention that an alternative method which uses the same supercell [e.g., (4 × 4)] that is sufficiently large to minimize interactions between complexes, and uses the result of S adsorption at low coverage [e.g., at 1/16 ML using the same (4 × 4) supercell], can also lead to very reliable estimate of the formation energy. Results using such an approach are included in Table 4. They are mostly the same as the fixed coverage results at θS = 1/8 ML, except for Cu3S4 and Cu4S5. This is because these two complexes are less compact than the others, thus a (4 × 4) supercell is too small to completely ignore interactions between these complexes.
Appendix B: energetics of M–S complexes on M(111) surfaces
We summarize energetics for M–S complexes on M(111) surfaces to facilitate comparison with behavior on M(100) surfaces. Results for the formation energy, Ef(MmSn)(ads), of adsorbed complexes are decomposed within the framework of Hess's law into energies associated with three steps: (1) desorption of atoms from the surface; (2) formation of the complex in the gas phase; and (3) adsorption of the complex onto the surface. Results are presented in Table 5 in a format entirely analogous to the presentation for M(100) surfaces in Table 3. These data were published previously in ref. 18.| Complex | ΔE1 | ΔE2 | ΔE3 | E f(ads) |
|---|---|---|---|---|
| CuS | 7.88 | −3.23 | −3.98 | 0.66 |
| CuS2 | 12.23 | −5.82 | −6.31 | 0.10 |
| Cu2S2 | 15.70 | −10.02 | −4.74 | 0.94 |
| CuS3 | 16.57 | −7.75 | −8.70 | 0.11 |
| Cu2S3 | 20.04 | −11.87 | −8.23 | −0.06 |
| Cu3S3 | 23.51 | −16.63 | −6.77 | 0.11 |
| Cu3S4 | 27.81 | −17.34 | −10.47 | 0.00 |
| Cu4S4 | 31.28 | −23.06 | −7.98 | 0.23 |
| Cu4S5 | 35.32 | −22.41 | −12.82 | 0.08 |
| AgS | 6.19 | −2.46 | −3.14 | 0.59 |
| AgS2 | 9.79 | −4.52 | −5.26 | 0.01 |
| Ag2S2 | 12.32 | −7.44 | −4.01 | 0.86 |
| AgS3 | 13.38 | −5.78 | −7.47 | 0.13 |
| Ag2S3 | 15.90 | −9.06 | −7.03 | −0.19 |
| Ag3S3 | 18.43 | −12.69 | −5.85 | −0.12 |
| Ag3S4 | 21.98 | −13.32 | −8.96 | −0.31 |
| Ag4S4 | 24.50 | −17.49 | −7.33 | −0.32 |
| Ag4S5 | 27.81 | −17.34 | −10.94 | −0.47 |
| AuS | 6.77 | −2.94 | −2.98 | 0.85 |
| AuS2 | 10.30 | −5.92 | −3.92 | 0.46 |
| Au2S2 | 13.34 | −8.49 | ||
| AuS3 | 13.79 | −7.51 | ||
| Au2S3 | 16.82 | −11.51 | −4.81 | 0.50 |
| Au3S3 | 19.86 | −14.92 | −4.65 | 0.29 |
| Au3S4 | 23.29 | −16.41 | −6.74 | 0.14 |
| Au4S4 | 26.33 | −21.60 | −4.97 | −0.23 |
| Au4S5 | 29.57 | −20.87 | −8.26 | 0.44 |
Acknowledgements
D.-J. L., J. L., T. L. W., and J. W. E. performed the theoretical analysis and computations in this work, and were supported by the U.S. Department of Energy (USDOE), Office of Basic Energy Sciences, Division of Chemical Sciences, Geosciences, and Biosciences through the Ames Laboratory Chemical Physics program. We acknowledge use of resources of the National Energy Research Scientific Computing Center, a DOE Office of Science User Facility supported by the Office of Science of the U.S. DOE under Contract No. DE-AC02-05CH11231. P. M. S. performed the S/Ag(100) LTSTM experiment under the supervision P. A. T. who also contributed to the formulation of this project, and they were supported for this work by NSF Grant No. CHE-1507223. The work was performed at Ames Laboratory which is operated for the USDOE by Iowa State University under Contract No. DE-AC02-07CH11358.Notes and references
- P. J. F. Harris, Int. Mater. Rev., 1995, 40, 97–115 CrossRef CAS.
- W. L. Ling, N. C. Bartelt, K. Pohl, J. de la Figuera, R. Q. Hwang and K. F. McCarty, Phys. Rev. Lett., 2004, 93, 166101 CrossRef CAS PubMed.
- P. A. Thiel, M. Shen, D.-J. Liu and J. W. Evans, J. Vac. Sci. Technol., A, 2010, 28, 1285 CrossRef CAS.
- K. F. Kalz, R. Kraehnert, M. Dvoyashkin, R. Dittmeyer, R. Gläser, U. Krewer, K. Reuter and J.-D. Grunwaldt, ChemCatChem, 2017, 9, 17–29 CrossRef CAS PubMed.
- https://science.energy.gov//media/bes/pdf/reports/2017/BRNCatalysisScience_rpt.pdf, Basic Research Needs for Catalysis Science to Transform Energy Technologies, USDOE BES Workshop, Gaithersburg, Maryland.
- M. Shen, D.-J. Liu, C. J. Jenks, P. A. Thiel and J. W. Evans, J. Chem. Phys., 2009, 130, 094701 CrossRef PubMed.
- M. Shen, S. M. Russell, D.-J. Liu and P. A. Thiel, J. Chem. Phys., 2011, 135, 154701 CrossRef PubMed.
- P. J. Feibelman, Phys. Rev. Lett., 2000, 85, 606 CrossRef CAS PubMed.
- A. R. Layson, J. W. Evans and P. A. Thiel, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 193409 CrossRef.
- P. Wynblatt and N. A. Gjostein, Acta Metall., 1976, 24, 1165 CrossRef CAS.
- N. Philipp and F. Abild-Pedersen, ACS Catal., 2016, 6, 7098–7108 CrossRef.
- H. Walen, D.-J. Liu, J. Oh, H. Lim, J. W. Evans, C. M. Aikens, Y. Kim and P. A. Thiel, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 045426 CrossRef.
- H. Walen, D.-J. Liu, J. Oh, H. Lim, J. W. Evans, Y. Kim and P. A. Thiel, J. Chem. Phys., 2015, 142, 194711 CrossRef PubMed.
- H. Walen, D.-J. Liu, J. Oh, H. J. Yang, P. M. Spurgeon, Y. Kim and P. A. Thiel, J. Phys. Chem. B, 2018, 122, 963–971 CrossRef PubMed.
- S. M. Russell, Y. Kim, D.-J. Liu, J. W. Evans and P. A. Thiel, J. Chem. Phys., 2013, 138, 071101 CrossRef PubMed.
- H. Walen, D.-J. Liu, J. Oh, H. Lim, J. W. Evans, Y. Kim and P. A. Thiel, J. Chem. Phys., 2015, 143, 014704 CrossRef PubMed.
- H. Walen, D.-J. Liu, J. Oh, H. J. Yang, Y. Kim and P. A. Thiel, Phys. Chem. Chem. Phys., 2016, 18, 4891 RSC.
- J. Lee, T. L. Windus, P. A. Thiel, J. W. Evans and D.-J. Liu, J. Phys. Chem. C, 2019, 123, 12954 CAS.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, R558–R561 CrossRef PubMed.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251 CrossRef CAS PubMed.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- P. M. Spurgeon, D.-J. Liu, H. Walen, J. Oh, H. J. Yang, Y. Kim and P. A. Thiel, Phys. Chem. Chem. Phys., 2019, 21, 10540–10551 RSC.
- D.-J. Liu, J. Lee, T. L. Windus, P. A. Thiel and J. W. Evans, Surf. Sci., 2018, 676, 2–8 CrossRef CAS.
- D.-J. Liu, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 035415 CrossRef.
- M. K. Bradley, D. P. Woodruff and J. Robinson, Surf. Sci., 2013, 613, 21–27 CrossRef CAS.
- J. S. Boschen, J. Lee, T. L. Windus, J. W. Evans, P. A. Thiel and D.-J. Liu., J. Chem. Phys., 2016, 145, 164312 CrossRef PubMed.
- C. R. Bernard Rodríguez and J. A. Santana, J. Chem. Phys., 2018, 149, 204701 CrossRef PubMed.
- M. M. Biener, J. Biener and C. M. Friend, Langmuir, 2005, 21, 1668 CrossRef CAS PubMed.
- M. M. Biener, J. Biener and C. M. Friend, Surf. Sci., 2007, 601, 1659–1667 CrossRef CAS.
| This journal is © the Owner Societies 2019 |