Low energy (1–19 eV) electron scattering from condensed thymidine (dT) II: comparison of vibrational excitation cross sections with those of tetrahydrofuran and the recalibrated values of thymine†
Abstract
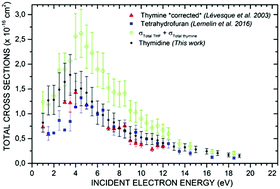
Recent measurements of absolute vibrational cross sections (CSs) for low-energy electron (LEE) scattering from condensed thymidine (dT) allows comparison with CSs of its constituents; thymine and tetrahydrofuran (THF). To facilitate this comparison, the vibrational CSs of condensed thymine were remeasured at six electron incident energies and a correction was applied to the earlier thymine CS values measured by Lévesque et al. [Nucl. Instrum. Methods Phys. Res., Sect. B, 2003, 208, 225]. The incident energy dependence of the CS of each vibrational mode of dT is compared with the corresponding modes in thymine and/or THF. It is found that the magnitude of the CSs of the thymine breathing mode and the C–C stretch mode of THF are greatly attenuated in dT. Finally, the magnitudes of the total vibrational CSs of each molecule are compared. Below 4 eV, the total vibrational CSs of dT is greater than each of its two constituents. Interestingly, at higher energy (>6 eV), the magnitude of the total vibrational CS of dT is roughly equal to that of THF and is greater than thymine by only 15% at 10 eV, showing that the CSs of dT cannot be approximated by the addition of the CSs of its constituents over the entire energy range. These comparisons are discussed in terms of the basic principles involved in the formation and decay of shape resonances, which are known to be responsible for major enhancements of LEE-induced vibrational excitation at low electron energies.
- This article is part of the themed collection: 2019 PCCP HOT Articles


 Please wait while we load your content...
Please wait while we load your content...