Low energy (1–19 eV) electron scattering from condensed thymidine (dT) I: absolute vibrational excitation cross sections

Abstract

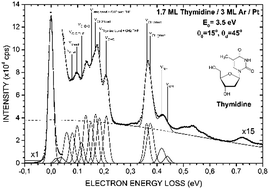
Absolute cross sections (CSs) for vibrational excitation by electrons of energy between 1–19 eV scattering from condensed thymidine (dT) were measured by means of high-resolution electron energy loss spectroscopy (HREELS). The CSs were extracted from electron energy loss spectra of dT condensed on multilayers film of Ar held at about 20 K under ultra-high vacuum (∼1 × 10⁻¹¹ Torr). dT is one of the most complex molecules to be studied in condensed phase by HREELS. The magnitudes of the vibrational CSs lie within the 10⁻¹⁷ cm² range. Structures observed in the energy dependence of the vibrational CSs under 3 eV and around 4 eV were compared with previous results of gas- and solid-phase studies on dT and related molecules (e.g., thymine and tetrahydrofuran). These structures were attributed to the formation of shape resonances.