Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Directional and regioselective hole injection of spiropyran photoswitches intercalated into A/T-duplex DNA†
Davide
Avagliano
 ,
Pedro A.
Sánchez-Murcia
,
Pedro A.
Sánchez-Murcia
 * and
Leticia
González
* and
Leticia
González
 *
*
Institute of Theoretical Chemistry, Faculty of Chemistry, University of Vienna, Währinger Str. 17, A-1090 Vienna, Austria. E-mail: pedro.murcia@univie.ac.at; leticia.gonzalez@univie.ac.at
First published on 25th July 2019
Abstract
The electron-hole injection from a family of spiropyran photoswitches into A/T-duplex DNA has been investigated at the molecular level for the first time. Multiscale computations coupled with automatized quantitative wavefunction analysis reveal a pronounced directionality and regioselectivity towards the template strand of the duplex DNA. Our findings suggest that this directional and regioselective photoinduced electron-hole transfer could thus be exploited to tailor the charge transport processes in DNA in specific applications.
Light-driven charge transport processes through DNA play a central role in photodamage1 and are the key to design DNA-based molecular wires.2–4 Upon illumination, one electron is excited from a donor unit to an acceptor species, generating a hole – a positive charge – in DNA.5 This electron-hole can efficiently migrate long molecular distances through the DNA helix.2,6 Given its importance for a wide range of applications, understanding the dynamics of electron transport in DNA has been a subject of study for decades.7–9 For instance, it is known that the migration of the electron-hole strongly depends on stacking10 and on the energies of the involved nucleobases.11 However, despite several experimental12 and theoretical13 setups that have been used to investigate the electron-hole injection and migration in DNA, the characterization of the initial electronic excited states is in most cases unknown.
The donor and acceptor units can be covalently bound14–16 or intercalated in DNA,17–21 such as the spiropyran (SP) photoswitches. After light irradiation, SPs undergo heterocyclic cleavage to yield the open merocyanine (MC) form.22,23 Actually, the SP form (1 in Scheme 1) does not bind DNA but the protonated open MCH form (2) does.24,25 While the photocleavage of SP in solution has been widely investigated,26–31 and it is known that the protonated open MCH form is able to oxidize DNA nucleobases in cell culture,32 the excited states of these photoswitches intercalated in DNA have never been investigated. This is the subject of this work. We address here the central question of how electron-hole injection operates from merocyanine derivatives to a duplex A/T DNA strand. We use atomistic multiscale calculations coupled with quantitative wavefunction analysis to model explicitly the hole injection from two MCH derivatives (2a and 2b) into 12-mer (poly-dAT)2, for which these compounds show selectivity.24
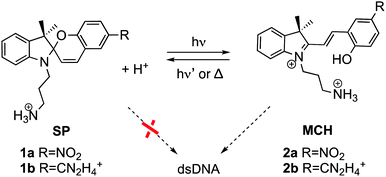 | ||
| Scheme 1 Spiropyran (SP) and protonated merocyanine (MCH) derivatives studied in this work bearing a nitro (2a)24 or an amidinium (2b)33 group. Only MCH species, and not SP, bind to dsDNA. | ||
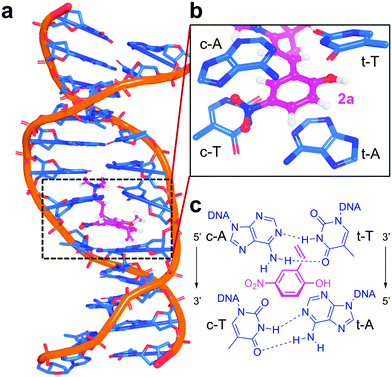
The intercalation mechanism of the nitro (2a) and amidinium (2b) derivatives into a 12-mer (poly-dAT)2 is described elsewhere.25 An ensemble of geometries of 2a:DNA and 2b:DNA obtained by unrestrained classical and Born Oppenheimer molecular dynamics simulations in an explicit solvent is used to ensure an efficient sampling of the environment and of the vibrational space of the chromophore.34,35 A total of 4000 excited states per complex were calculated within a quantum mechanics/molecular mechanics (QM/MM) framework, where the chromophore and the first four surrounding nucleobases (121 atoms for 2a:DNA and 125 atoms for 2b:DNA, see Fig. 1a and b) are considered quantum mechanically. Further computational details can be found in the Computational details section.
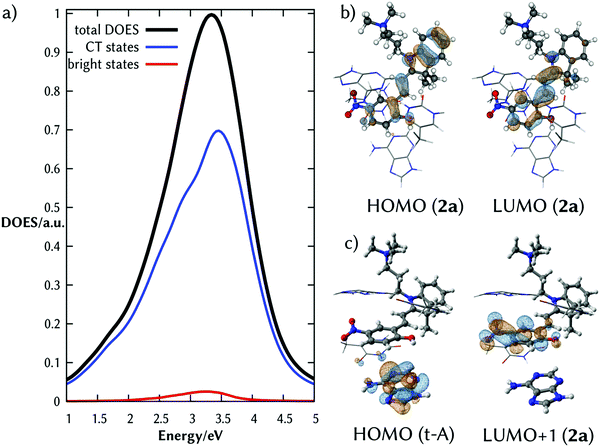
Our theoretical protocol is validated by the good agreement of the computed absorption spectra (Fig. S1, ESI†) of 2a in water and 2b intercalated in DNA with available experimental data.33,36 The spectra consist of two absorption bands. The lower-energy band corresponds to the intramolecular excitation from a π orbital (HOMO) to a π* molecular orbital (LUMO), with absorption maxima at 382 and 398 nm, respectively. The peaks are slightly blue-shifted (<30 nm) with respect to the experimental ones, as usual at this level of theory.34 The bright states of 2a and 2b are the same in solution as bound to the DNA. However, upon DNA intercalation, the brightest state is surrounded by dark states with strong charge transfer (CT) character involving nucleobases, see Table 1 for the excited states of 2a:DNA and Table S1 (ESI†) for 2b:DNA.
| State | Energy | f | CT number | Electron hole population | Excited electron population |
|---|---|---|---|---|---|
| S1 | 2.40 | 0.004 | 0.996 | 0.969 (t-A) | 0.953 (2a) |
| S2 | 2.51 | 0.004 | 0.997 | 0.985 (t-T) | 0.958 (2a) |
| S3 | 2.72 | 0.001 | 0.996 | 0.977 (t-A) | 0.956 (2a) |
| S4 | 2.99 | 0.001 | 0.996 | 0.905 (t-A) | 0.925 (2a) |
| S5 | 3.07 | 0.000 | 0.998 | 0.990 (t-T) | 0.964 (2a) |
| S6 | 3.31 | 0.004 | 0.997 | 0.900 (t-A) | 0.927 (2a) |
| S7 | 3.53 | 0.696 | 0.087 | 0.846 (2a) | 0.874 (2a) |
| S8 | 3.89 | 0.006 | 0.987 | 0.958 (t-T) | 0.950 (2a) |
| S9 | 3.94 | 0.009 | 0.928 | 0.709 (c-A) | 0.887 (2a) |
| S10 | 3.97 | 0.009 | 0.774 | 0.503 (c-T) | 0.885 (2a) |
The CT character, defined by the CT number37 from 0 to 1, measures the intermolecular light-driven electron transfer between the donor and the acceptor. To define CT numbers, the system is split into five fragments, the chromophore (e.g.2a) and the four interacting nucleobases: adenine (c-A) and thymine (c-T) of the coding strand (5′ → 3′) and the corresponding ones of the template strand (t-A and t-T, 3′ → 5′), see Fig. 1c.
The total density of excited states (DOES) of the lowest absorption band of the complex 2a:DNA (black line of Fig. 2a) calculated from the ensemble of the structures and classified according to their CT character clearly shows that there are a few absorbing states (red line) embedded by many dark states with strong CT character (blue line). Fig. 2b and c illustrate the natural transition orbitals for the brightest state and one representative CT state, respectively. The brightest state corresponds to an intramolecular excitation; the CT state is an intermolecular excitation from the probe to t-A.
The fact that the brightest state of 2a in solution and in the duplex DNA is the same, indicates that upon intercalation an electron of 2a is excited creating a hole on the HOMO. This orbital is surrounded by the electron-rich HOMOs of the nucleobases. Therefore, one electron from the orbitals of the nucleobase can relax to the half-occupied HOMO of 2a, transferring the hole from 2a to one of the stacked nucleobases of the dsDNA. The hypothesis that 2a acts as a photooxidant probe of the surrounding nucleobases is supported by its substantial reduction potential E0(2a) (calculated value 3.94 V, see Computational details) and that the related merocyanine 540 derivative is able to oxidize the DNA nucleobases in cell culture.32
Finding this high density of CT states for the minimum geometry of the 2a:DNA complex urged us to investigate the excited electron and electron-hole populations of these CT states within the first ten excited states of the ensemble of geometries (1000 excited states per complex, see Computational details). We found that upon light absorption, 97% of the population of the excited electron is localized on 2a. Complementarily, 70% of the hole population is found in only one nucleobase and 24% is delocalized in two different fragments. In principle, the electron hole could have been transferred from the probe to any of the four nucleobases since 2a intercalates in the middle of the site with similar distance to all the nucleobases (Table S2, ESI†). However, the four nucleobases are not chemically equivalent, as they are located in different strands and they are affected by the asymmetrical binding of 2a, recall Fig. 1b and c. As a consequence, the majority of the electron hole is localized on the template strand (3′ → 5′), with 38% and 33% on t-T and t-A, respectively, and 29% on the coding strand (Fig. 3, pink bars). The strand selectivity is ascribed to the presence of the NO2 group, a strong electron-withdrawing group (EWG), oriented to the coding strand and a hydroxyl group (OH), an electron-donating group (EDG), projected to the template strand. Due to its electronic character, the NO2 group prevents the hole injection in the nucleobases around it. Moreover, since the differences between the electron-hole populations between t-A and t-T are small, 2a promotes the electron-hole injection into the template strand, in a static picture, in both directions (5′ ↔ 3′).
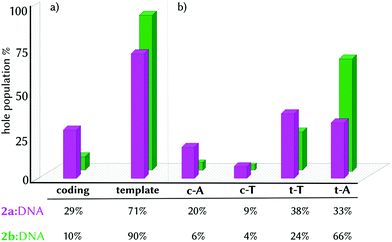 | ||
| Fig. 3 Histogram representation of electron-hole localization percentage in the CT states group by strand (a) and by single nucleobases (b) in the complexes 2a:DNA (pink) and 2b:DNA (green). | ||
The strand selectivity increases in 2b:DNA, as the template/coding ratio is 90/10 (Fig. 3a, green bars), compared to 2a (71/29). Of greater importance is the fact that in the complex 2b:DNA, the electron-hole injection goes preferentially into t-A (66%) instead of t-T (24%). This observation suggests that the electron-hole injection into the template strand propagates unidirectionally (3′ → 5′) in the presence of 2b.
A possible explanation for such discrimination between t-T and t-A could be found in geometrical differences between the two complexes, which would promote the electron-hole injection unidirectionally in the case of 2b. In our previous work25 and in Fig. S3 (ESI†), we showed that the two complexes shared the same intercalative binding site and the same average distance differences between the two nucleobases of the template strand and the probe for both complexes (Table S2, ESI†). These observations led us to exclude geometrical reasons as a discriminant for the regioselectivity and to investigate other possible reasons. The origin of the structural and electronic differences that regulate the electron-hole injection directionality into DNA can be traced back to the interactions between the π-systems of the chromophore and those of the neighbouring nucleobases. These interactions can be assessed in the minimum energy geometries with two descriptors. One is the non-covalent interaction energy between the probe and the nucleobases of each of the strands or π–π stacking interactions (Table 2), calculated via the Grimme's dispersion energy correction (D3).38,39 The other descriptor is the energy difference between the HOMO of the probe and the HOMO of each of the nucleobases forming the binding site (Table 3 and Fig. S2, ESI†).11
| Complex | D3 dispersion energy (kcal mol−1) | ||
|---|---|---|---|
| Coding strand (3′ → 5′) | Template strand (5′ → 3′) | ΔD3 | |
| 2a:DNA | −75.49 | −63.04 | −12.44 |
| 2b:DNA | −79.59 | −72.28 | −6.81 |
| Nucleobase | ΔεHOMO (eV) | |
|---|---|---|
| 2a:DNA | 2b:DNA | |
| t-A | +1.82 | +0.96 |
| t-T | +1.72 | +0.24 |
| c-A | −0.10 | −1.24 |
| c-T | −0.37 | −2.16 |
The presence of the strong nitro EWG (2a) or amidinium (2b) EWGs exerts a strong interaction with the nucleobases of the coding strand (−75.49 kcal mol−1 for 2a and −79.59 kcal mol−1 for 2b, Table 2). As a consequence, the probe induced an energy split of the HOMOs of the nucleobases. In particular, the nucleobases of the coding strand are lower in energy than the HOMO of the probes (Table 3). In contrast, the interaction with the template strand is weaker (−63.04 kcal mol−1 for 2a and −72.28 kcal mol−1 for 2b), and thus, the HOMOs of t-A and t-T are lying higher in energy than the HOMOs of the probes (Table 3). This explains why most of the electron-hole population is found on the template strand. Upon light absorption by the photoprobe, one electron from the HOMO of the template strand relaxes in energy and occupies the HOMO of the probe, injecting the hole into the template strand. Remarkably, the derivative 2a shows a stronger interaction with the coding strand than with the template one (ΔE = −12.44 kcal mol−1, Table 2), while in 2b, this difference is half (ΔE = −6.81 kcal mol−1). This means that the HOMOs of t-A and t-T, although higher in energy, are more stabilized by 2b due to favourable π–π stacking interactions. In addition, whereas in 2a the HOMOs of t-A and t-T are close in energy (ΔεHOMO = +1.82 and +1.72, respectively), in 2b t-T is much more stabilized than t-A. This is why most of the total electron-hole population (66%) is found on t-A (Fig. 3b, green bar)—the nucleobase with the higher HOMO level.
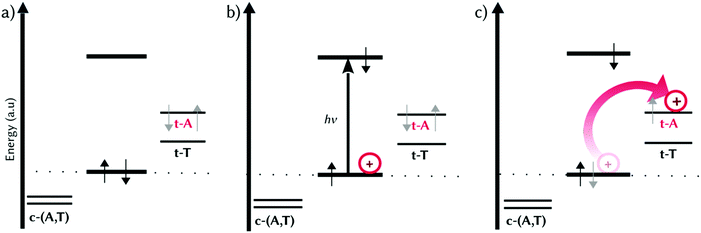
We are now in the position to propose a mechanistic model for the electron-hole injection in dsDNA by MCH derivatives containing EWGs, such as 2a and 2b (Fig. 4). It is the combination of π–π stacking interactions and the presence of an EWG that stabilizes the HOMOs of the nucleobases differently at the binding site (Fig. 4a). Upon irradiation by UV light, the brightest excited state is populated, which can decay to one of the lower-lying dark CT states. That is, one electron from the π-system of the probe (HOMO) is promoted to an excited state with π* character fully localized on the probe, creating a hole within the intercalated photoprobe (circle, Fig. 4b). The proximity in the energy of the HOMOs of t-A and t-T allows the migration of one electron of the nucleobases to MCH. The probe oxidizes thus the neighbouring nucleobases, injecting the hole into the DNA (arrow, Fig. 4c) and triggering hole migration through the double strand. This process is directional because the probe oxidizes the DNA, injecting an electron hole; is asymmetric because the binding mode of the open merocyanin species projecting the EWG to the coding strand promotes the hole injection into the template strand; and is regioselective because the nature of this EWG affects the energy levels of the HOMOs of the nucleobases of the template strand. As an example, in 2b the hole injection happens mainly into t-A, allowing a 5′ → 3′ electron-hole propagation.
In conclusion, we have portrayed how chemical modification of spiropyrans can modulate the directionality of the hole transport in DNA, arguably offering many application prospects. The quantitative direct observation of the CT states between a photooxidant and nucleobases, where the ligand is intercalated, has no precedent in the study of spiropyran photoswitches and evidences the importance of characterizing their excited states in order to prevent or enhance the photoinduced process involving DNA. Our findings open new questions on how the temporal evolution of these excited states is influenced by this selectivity and its biological implications. To answer these questions, further theoretical and experimental studies on the photodynamics of the injected electron hole are necessary.
Computational details
MD simulations
The initial structures of both probes 2a and 2b intercalated into a 12-mer dsDNA (poly-dAT)2 were obtained from umbrella sampling MD simulation studies, as described elsewhere.25 In all cases, each complex was immersed in a cubic box of 30 Å from the solute to the border of the box filled with TIP3P water molecules40 20 (2a) and 19 (2b) Na+ to ensure electroneutrality. To reproduce the experimental conditions reported by Andersson et al.,24 a final NaCl concentration of 1 × 10−5 M was achieved by the addition of Na+ and Cl− atoms. Each of the systems was simulated for 100 ns without any restraint following the protocol described in ref. 25QM/MM MD simulations
A total of 100 equidistant snapshots from the former MD simulations were selected to carry out QM/MM MD simulations using the sander program implemented in the AMBER17 suite.41 The system was partitioned in two regions: the QM and the MM region. Each of the probes (2a or 2b) and the four nucleobases around them (after cutting the glycosidic bond) were included in the QM region (121 and 125 atoms, respectively). The rest of the atoms were treated classically using the ff14SB42 force field and the TIP3P40 model for the water molecules. The QM region was treated with density-functional tight-binding (version 3, DFTB3),43 the semiempirical method of DFT, which is internally provided within the AMBER17 suite. The interaction term between the QM and the MM regions was calculated using the electrostatic embedding scheme.44 In the MM part, periodic boundary conditions were used and the electrostatic interactions were computed using the Ewald method45 with a grid spacing of 1 Å. The cutoff distance for the non-bonded interactions was 10 Å and the SHAKE algorithm46 was applied to all bonds involving hydrogen atoms. An integration step of 2.0 fs was defined. In the QM region, the PME and SHAKE algorithms were deactivated and a cutoff of 10 Å was defined for the interaction between the two regions. Each of the 100 QM/MM MD trajectories was propagated for 1 ps, with a time step of 0.1 fs at 300 K and 1 atm. In this way, the QM/MM MD sampling included the quantum mechanical effects in the phase space sampling, obtaining more accurate initial conditions for the excited state calculations.Static TD-DFT vertical excitations
The final geometries from the QM/MM MD simulations were used to compute the first 40 singlet states using time-dependent density functional theory (TD-DFT). As above, the QM region included the probe and the four surrounding nucleobases (c-T, c-A, t-A and t-T), in this case treated with the long-range corrected functional CAM-B3LYP47 and the def2-svp48 basis set. Grimme's dispersion correction D3 was considered.38,39 The rest of the system was printed as MM point charges and they were included in the Hamiltonian by means of electrostatic embedding. These calculations were performed with the TeraChem code49,50 on GeForce Nvidia GTX 1080Ti GPUs.Wavefunction analysis
The quantitative wavefunction analysis was performed in a second step after calculating the vertical excitations and the corresponding orbitals in TeraChem. Such an analysis was possible using the TheoDORE software.37,51 Detailed information can be found on the documentation of TheoDORE;51 here we only summarize the features employed.Vis/UV spectra
The Vis/UV spectra were convoluted as a sum of Gaussian functions (eqn (1)):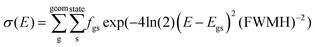 | (1) |
Transition density matrix, charge transfer numbers and natural transition orbitals
TheoDORE relies on the transition density matrix (DOI) analysis,52 computed as shown in eqn (2). Briefly, considering the states I and J and the orbitals α and β, one element of the one-particle transition density matrix is given by: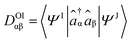 | (2) |
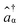 and âβ are the creation and annihilation operators, respectively.
and âβ are the creation and annihilation operators, respectively.
For the charge transfer (CT) analysis, the system was divided into five fragments: the probe and each of the four nucleobases. The CT numbers were computed using the Mulliken-like population analysis:
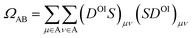 | (3) |
Natural transition orbitals (NTOs)53
NTO is built through a singular value decomposition of the DOI given by:| DOn = UXV† | (4) |
Redox potential calculation
The standard redox potential of the probe in a DNA environment is calculated using the Born–Haber cycle54 and the Nernst equation, based on the Gibbs free energy difference in gas and solvated environments for both the reduced and oxidized species. The oxidized (closed-shell, singlet, net charge = +2) and the reduced (open shell, doublet, net charge = +1) species were optimized at the CAM-B3LYP/def2-SVP level of theory. With this, we obtained the value of Ggas. Then, the geometries of both species were solvated with an acetonitrile shell (ε = 35.688), which is known to reproduce a more similar DNA-like environment than water,55 and the free energies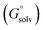 were calculated with the polarizable continuum model (PCM).56 The standard redox potential E° was then calculated from the Gibbs free energy change
were calculated with the polarizable continuum model (PCM).56 The standard redox potential E° was then calculated from the Gibbs free energy change 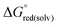 as shown in eqn (5) and (6):
as shown in eqn (5) and (6):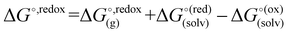 | (5) |
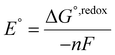 | (6) |
These calculations are performed with Gaussian 09, version D.01.57
Conflicts of interest
There are no conflicts to declare.Acknowledgements
D. A. acknowledges funding from the European Union's Horizon 2020 research and innovation programme under the Marie Sklodowska-Curie grant agreement no. 765266 (LightDyNAmics). P. A. S.-M. would like to thank the Austrian FWF, Project M 2260. The authors thank the Vienna Scientific Cluster (VSC) for the allocation of computational resources.References
- D. B. Hall, R. E. Holmlin and J. K. Barton, Nature, 1996, 382, 731–735 CrossRef CAS PubMed.
- J. D. Slinker, N. B. Muren, S. E. Renfrew and J. K. Barton, Nat. Chem., 2011, 3, 228 CrossRef CAS PubMed.
- C. H. Wohlgamuth, M. A. McWilliams and J. D. Slinker, Anal. Chem., 2013, 85, 8634–8640 CrossRef CAS PubMed.
- A. R. Chandrasekaran, ChemBioChem, 2017, 18, 1886–1887 CrossRef CAS PubMed.
- H. Wagenknecht, Charge Transfer in DNA: From Mechanism to Application, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, 2005 Search PubMed.
- B. Giese, Acc. Chem. Res., 2000, 33, 631–636 CrossRef CAS PubMed.
- K. Kawai and T. Majima, Acc. Chem. Res., 2013, 46, 2616–2625 CrossRef CAS PubMed.
- F. D. Lewis, R. M. Young and M. R. Wasielewski, Acc. Chem. Res., 2018, 51, 1746–1754 CrossRef CAS PubMed.
- J. C. Genereux and J. K. Barton, Chem. Rev., 2010, 110, 1642–1662 CrossRef CAS PubMed.
- A. J. A. Aquino, D. Nachtigallova, P. Hobza, D. G. Truhlar, C. Hättig and H. Lischka, J. Comput. Chem., 2011, 32, 1217–1227 CrossRef CAS PubMed.
- K. Kawai, M. Hayashi and T. Majima, J. Am. Chem. Soc., 2012, 134, 4806–4811 CrossRef CAS PubMed.
- I. Kratochvílová, T. Todorciuc, K. Král, H. Němec, M. Bunček, J. Šebera, S. Záliš, Z. Vokáčová, V. Sychrovský, L. Bednárová, P. Mojzeš and B. Schneider, J. Phys. Chem. B, 2010, 114, 5196–5205 CrossRef PubMed.
- D. Rawtani, B. Kuntmal and Y. Agrawal, Front. Life Sci., 2016, 9, 214–225 CrossRef CAS.
- N. Renaud, M. A. Harris, A. P. N. Singh, Y. A. Berlin, M. A. Ratner, M. R. Wasielewski, F. D. Lewis and F. C. Grozema, Nat. Chem., 2016, 8, 1015 CrossRef CAS PubMed.
- F. D. Lewis, X. Liu, Y. Wu and R. L. Letsinger, J. Am. Chem. Soc., 1999, 121, 9905–9906 CrossRef CAS.
- K. E. Brown, A. P. N. Singh, Y.-L. Wu, A. K. Mishra, J. Zhou, F. D. Lewis, R. M. Young and M. R. Wasielewski, J. Am. Chem. Soc., 2017, 139, 12084–12092 CrossRef CAS PubMed.
- A. Jacques, A. Kirsch-De Mesmaeker and B. Elias, Inorg. Chem., 2014, 53, 1507–1512 CrossRef CAS PubMed.
- C. Murphy, M. Arkin, Y. Jenkins, N. Ghatlia, S. Bossmann, N. Turro and J. Barton, Science, 1993, 262, 1025–1029 CrossRef CAS PubMed.
- G. B. Schuster, Acc. Chem. Res., 2000, 33, 253–260 CrossRef CAS PubMed.
- F. Shao, K. Augustyn and J. K. Barton, J. Am. Chem. Soc., 2005, 127, 17445–17452 CrossRef CAS PubMed.
- F. Shao and J. K. Barton, J. Am. Chem. Soc., 2007, 129, 14733–14738 CrossRef CAS PubMed.
- C. L. Fleming, S. Li, M. Grøtli and J. Andréasson, J. Am. Chem. Soc., 2018, 140, 14069–14072 CrossRef CAS PubMed.
- J. Kohl-Landgraf, M. Braun, C. Özçoban, D. P. N. Gonçalves, A. Heckel and J. Wachtveitl, J. Am. Chem. Soc., 2012, 134, 14070–14077 CrossRef CAS PubMed.
- J. Andersson, S. Li, P. Lincoln and J. Andréasson, J. Am. Chem. Soc., 2008, 130, 11836–11837 CrossRef CAS PubMed.
- D. Avagliano, P. A. Sánchez-Murcia and L. González, Phys. Chem. Chem. Phys., 2019, 21, 8601–8966 RSC.
- I. Gómez, M. Reguero and M. A. Robb, J. Phys. Chem. A, 2006, 110, 3986–3991 CrossRef PubMed.
- A. Eilmes, J. Phys. Chem. A, 2013, 117, 2629–2635 CrossRef CAS PubMed.
- Y. Kalisky, T. E. Orlowski and D. J. Williams, J. Phys. Chem., 1983, 87, 5333–5338 CrossRef CAS.
- C. J. Wohl and D. Kuciauskas, J. Phys. Chem. B, 2005, 109, 22186–22191 CrossRef CAS PubMed.
- N. A. Murugan, S. Chakrabarti and H. Ågren, J. Phys. Chem. B, 2011, 115, 4025–4032 CrossRef CAS PubMed.
- R. A. Rogers, A. R. Rodier, J. A. Stanley, N. A. Douglas, X. Li and W. J. Brittain, Chem. Commun., 2014, 50, 3424–3426 RSC.
- M. Dušinská, A. Mateášik, D. J. Chorvát, I. Lajdová, V. Spustová and A. Chorvátová, Neoplasma, 1999, 46, 69–70 Search PubMed.
- M. Hammarson, J. R. Nilsson, S. Li, P. Lincoln and J. Andréasson, Chem. – Eur. J., 2014, 20, 15855–15862 CrossRef CAS PubMed.
- J. J. Nogueira, F. Plasser and L. González, Chem. Sci., 2017, 8, 5682–5691 RSC.
- J. J. Nogueira and L. González, Annu. Rev. Phys. Chem., 2018, 69, 473–497 CrossRef CAS PubMed.
- M. Hammarson, J. R. Nilsson, S. Li, T. Beke-Somfai and J. Andréasson, J. Phys. Chem. B, 2013, 117, 13561–13571 CrossRef CAS PubMed.
- F. Plasser and H. Lischka, J. Chem. Theory Comput., 2012, 8, 2777–2789 CrossRef CAS PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935 CrossRef CAS.
- I. Y. B.-S. D. A. Case, S. R. Brozell, D. S. Cerutti, T. E. Cheatham, III, V. W. D. Cruzeiro, T. A. Darden, R. E. Duke, D. Ghoreishi, M. K. Gilson, H. Gohlke, A. W. Goetz, D. Greene, R. Harris, N. Homeyer, S. Izadi, A. Kovalenko, T. Kurtzman, T. S. Lee, S. LeGrand, P. Li, C. Lin, J. Liu, T. Luchko, R. Luo, D. J. Mermelstein, K. M. Merz, Y. Miao, G. Monard, C. Nguyen, H. Nguyen, I. Omelyan, A. Onufriev, F. Pan, R. Qi, D. R. Roe, A. Roitberg, C. Sagui, S. Schott-Verdugo, J. Shen, C. L. Simmerling, J. Smith, R. Salomon-Ferrer, J. Swails, R. C. Walker, J. Wang, H. Wei, R. M. Wolf, X. Wu, L. Xiao, D. M. York and P. A. Kollman, AMBER, University of California, 2018 Search PubMed.
- J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, J. Comput. Chem., 2004, 25, 1157–1174 CrossRef CAS PubMed.
- M. Gaus, Q. Cui and M. Elstner, J. Chem. Theory Comput., 2011, 7, 931–948 CrossRef CAS PubMed.
- A. W. Götz, M. A. Clark and R. C. Walker, J. Comput. Chem., 2014, 35, 95–108 CrossRef PubMed.
- U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, J. Chem. Phys., 1995, 103, 8577–8593 CrossRef CAS.
- J.-P. Ryckaert, G. Ciccotti and H. J. C. Berendsen, J. Comput. Phys., 1977, 23, 327–341 CrossRef CAS.
- T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57 CrossRef CAS.
- A. Schäfer, H. Horn and R. Ahlrichs, J. Chem. Phys., 1992, 97, 2571–2577 CrossRef.
- I. S. Ufimtsev and T. J. Martinez, J. Chem. Theory Comput., 2009, 5, 2619–2628 CrossRef CAS PubMed.
- TeraChem, v. 1.9, PetaChem LLC, 2015 Search PubMed.
- F. Plasser, TheoDORE, A package for Theoretical Density, Orbital Relaxation and Exciton analysis, 2019 Search PubMed.
- F. Plasser, M. Wormit and A. Dreuw, J. Chem. Phys., 2014, 141, 024106 CrossRef PubMed.
- F. Plasser, J. Chem. Phys., 2016, 144, 194107 CrossRef PubMed.
- D. F. C. Morris and E. L. Short, Nature, 1969, 224, 950–952 CrossRef CAS.
- C. A. M. Seidel, A. Schulz and M. H. M. Sauer, J. Phys. Chem., 1996, 100, 5541–5553 CrossRef CAS.
- J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3094 CrossRef CAS PubMed.
- G. W. T. M. J. Frisch, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9cp03398j |
| This journal is © the Owner Societies 2019 |