Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A dithiocarbamate anchoring group as a flexible platform for interface engineering†
Eric
Sauter‡
a,
Giulia
Nascimbeni‡
b,
Daniel
Trefz
c,
Sabine
Ludwigs
 c,
Egbert
Zojer
*b,
Florian
von Wrochem
c,
Egbert
Zojer
*b,
Florian
von Wrochem
 *d and
Michael
Zharnikov
*d and
Michael
Zharnikov
 *a
*a
aApplied Physical Chemistry, Heidelberg University, Im Neuenheimer Feld 253, 69120 Heidelberg, Germany. E-mail: Michael.Zharnikov@urz.uni-heidelberg.de
bInstitute of Solid State Physics, NAWI Graz, Graz University of Technology, Petersgasse 16, 8010 Graz, Austria. E-mail: egbert.zojer@tugraz.at
cChair for Structure and Properties of Polymeric Materials, Institute of Polymer Chemistry (IPOC), University of Stuttgart, Pfaffenwaldring 55, 70569 Stuttgart, Germany
dInstitute of Materials Science, University of Stuttgart, Heisenbergstr. 3, 70569 Stuttgart, Germany. E-mail: vonwrochem@gmx.de
First published on 4th October 2019
Abstract
The molecular organization and electronic properties of dithiocarbamate (DTC) anchored self-assembled monolayers (SAMs) linked to Au(111) substrates are studied by a combination of X-ray photoelectron spectroscopy (XPS), near-edge X-ray absorption fine structure (NEXAFS) spectroscopy, and state-of-the-art density functional theory calculations. For that, several piperidine/piperazine precursors with different architecture and substitution patterns are selected. The presented data show that the DTC anchor provides a useful building block for monomolecular self-assembly on coinage metals with both sulfur atoms bonded to the substrate in a way similar to what is usually observed for the more commonly applied thiolate docking group. The combination of the DTC group with the quite flexible piperidine/piperazine cyclic linkers results in a dense molecular packing with an upright orientation of the terminal moieties. The latter comprise phenyl rings bearing various substituents, which enables tuning the interfacial dipole over a wide range. Simulations on two prototypical DTC-docked SAMs help to better understand the experimental observations and provide insight into the local origin of the SAM-induced shifts in the electrostatic energy. In particular, a comparison of measured and simulated XP spectra reveals the significant contribution of the DTC group to the interfacial dipole.
1. Introduction
Energy level alignment and injection control at the interfaces between electrodes, organic semiconductors, and buffer layers are highly important issues in the context of modern organic electronics and photovoltaics. A popular approach in this regard is the use of self-assembled monolayers (SAMs),1–16 which are densely packed molecular assemblies of typically rod-shaped molecules adsorbed on a substrate in a well-defined upright geometry. Generally, such molecules consist of three major building blocks, viz. a docking group that provides anchoring to the substrate, a tail group comprising the “outer” SAM-ambient interface, and a spacer that separates the docking and tail groups and drives the self-assembly.17,18 While all these building blocks can contribute to the joint dipole moment of the molecules constituting the film, it is mostly a dipolar tail group2,3,5,10,19 or a polar mid-chain moiety20–24 which is selected to specifically adjust the interfacial dipole. In contrast, the docking group is predominantly chosen based on its affinity to a particular substrate serving as the electrode or, in the context of organic photovoltaics, also as the buffer layer. Examples for docking groups comprise phosphonic acids for zinc oxide surfaces10,25 (a popular interfacial layer material in organic electronics devices), phosphonic acids and triethoxy- or trichlorsilanes for indium tin oxide9,25,26 (standard transparent electrode material for organic solar cells), and thiolates for coinage metal substrates,7,18,19 such as gold and silver (frequently used electrode materials).Recently, as an alternative to thiolates, the dithiocarbamate (DTC) anchoring group27–32 has been suggested as a basis for the functionalization of gold nanoparticles, for molecular electronics, and for the fabrication of dipolar SAMs to be applied in organic electronics.33,34 In combination with piperazine and piperidine as an intermediate linker, this group provides a versatile and robust platform for the attachment of different spacer moieties and tail groups. In particular, the piperidine/piperazine linker, forming a bridge between the DTC group and the aromatic substituents, ensures rod-like symmetry of the molecular backbone.33,35 This allows a perpendicular orientation of the molecular axis relative to the substrate (a feature not available in earlier aromatic DTC derivatives),27,30,36 which is favorable in the context of work function engineering. Consequently, a family of monolayers was realized, which delivered work functions of SAM-covered Au electrodes between 4.8 eV and 3.2 eV.33 Although the performance of DTC-docked systems in polymer junctions has been demonstrated and a first spectroscopic characterization of the films along with molecule-based calculations has been provided,33 the precise structure and molecular orientation of DTC-based SAMs is still largely unexplored. In addition, a deeper understanding of the electronic properties of such SAMs is of fundamental interest in view of the largely unexplored potential of the used unconventional docking group. Of particular relevance in this context is the question which of the contained functional blocks is actually responsible for the shift in the energy landscape that gives rise to the comparably large work function changes.
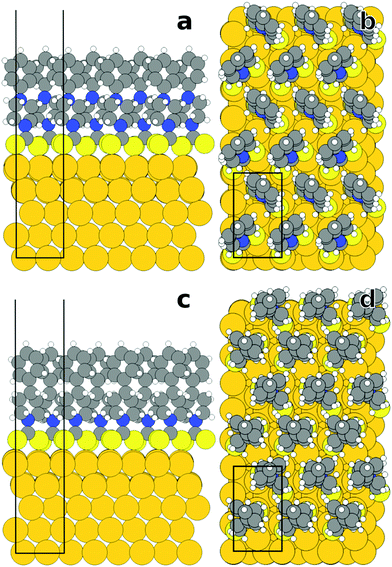
In the present work, to gain this understanding, we applied advanced spectroscopic tools in combination with state-of-the-art quantum mechanical simulations of SAM/Au interfaces. This combination of simulations and experiments, on the one hand, provides insight into the molecular orientation and order of these films, which need to be understood to correlate the molecular properties with the electrostatic potential drop across the metal−organic interface. On the other hand, it affords an in-depth and reliable insight into the atomistic origins of potential shifts and charge rearrangements. Consequently, the primary emphasis of the following discussion is put on the two very basic systems, viz. phenyl-piperidine-DTC (PPd) and phenyl-piperazine-DTC (PPz) SAMs on Au(111) (Fig. 1). These monolayers represent highly suitable model systems, which were specifically designed for the present experiments and selected for the simulations to address the distinct properties of the piperidine-DTC and piperazine-DTC docking platforms. The terminal phenyl ring of both molecules is a non-polar and well-defined structural unit supporting the formation of ordered SAMs. Convenient in the present context, it also provides a marker for the spectroscopic experiments (see below). The other DTC derivatives investigated in this study are derived from these two basic systems (parent compounds) by a substitution of the phenyl ring in the para position or by its fluorination. The structures of the respective SAMs and the used abbreviations are shown in Fig. 1.
 | ||
| Fig. 1 Schematic structures of the DTC-based SAMs (represented by the single constituents) used in this study along with their respective abbreviations. Note that the C12N-PPd, OMe-PPz, and FP-Pz monolayers have been studied before, but in a somewhat different context compared to the present work.33 | ||
2. Experimental and theoretical methods
2.1. SAM preparation
The synthesis of the DTC-based SAM constituents (Fig. 1) was done within an “in situ” process involving coupling the precursor amines to CS2. The amine precursor of C12N-PPd (Fig. 1) was custom-synthesized as reported in the literature.33 All other amine precursors for the synthesis of the OMe-PPz, FP-Pz, PPd and PPz DTC derivatives (Fig. 1), i.e. the 1-(4-methoxphenyl)piperazine, 1-(pentafluorophenyl)-piperazine hydrochloride, 4-phenylpiperidine, and 1-phenylpiperazine were obtained in highest purity from ABCR, Sigma Aldrich, Enamine, and Sigma Aldrich, respectively, and used as received. CS2 (p.a.), ethanol (p.a.), and triethylamine were obtained from Sigma Aldrich and Fluka, respectively. The coupling of the precursor amines to CS2 was performed according to the following protocol, established in previous studies.33 Initially, concentrated stock solutions of CS2 (100 mM), the amine-terminated precursors (5 mM), and triethylamine (100 mM) were prepared in ethanol. Subsequently, the CS2 and triethylamine solutions, along with some ethanol, were added (in this sequence) to the amine precursor solution to form an equimolar 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 precursor
1 precursor![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CS2
CS2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) triethylamine mixture (with a concentration of 1 mM each). The mixture causes a spontaneous reaction of CS2 with the respective amine precursor yielding the desired dithiocarbamate species (1 mM), which spontaneously and irreversibly reacts with the Au(111) substrate when the latter is added to the mixture.27,29 All steps were carried out in a glove box under nitrogen atmosphere to avoid oxidation reactions. The above DTC solutions were directly used for SAM preparation on gold substrates. As a side note, great care has to be taken in order to avoid any contamination in the glove box, because of the significant risk that thiolate species in the vapor phase might compete with the (rather slow) chemisorption process of dithiocarbamates on Au (thus compromising SAM purity and uniformity). As substrates, atomically flat template stripped gold (TSG) was employed and prepared according to the reported procedures.37,38 The Au films exhibited a root mean square (RMS) roughness of 0.3 nm, exposing preferably (111) oriented surfaces. The organic monolayers were prepared under nitrogen by immersing the freshly stripped TSG substrates into DTC solutions for ∼20 h at room temperature. After immersion, the films were copiously rinsed with ethanol, immediately blown dry with N2 and placed in glass containers, predominantly filled with nitrogen, for transport from the individual laboratories to the synchrotron radiation facilities (see below). No specific degradation was observed on the scale of several days (up to a week) but some minor sample to sample variations were recorded in some of the experiments. All vials and tweezers were cleaned with piranha acid and isopropyl alcohol before usage. In addition, reference SAMs of dodecanethiolate (DDT) and hexadecanethiolate (HDT) were prepared on analogous gold substrates using a standard procedure.39
triethylamine mixture (with a concentration of 1 mM each). The mixture causes a spontaneous reaction of CS2 with the respective amine precursor yielding the desired dithiocarbamate species (1 mM), which spontaneously and irreversibly reacts with the Au(111) substrate when the latter is added to the mixture.27,29 All steps were carried out in a glove box under nitrogen atmosphere to avoid oxidation reactions. The above DTC solutions were directly used for SAM preparation on gold substrates. As a side note, great care has to be taken in order to avoid any contamination in the glove box, because of the significant risk that thiolate species in the vapor phase might compete with the (rather slow) chemisorption process of dithiocarbamates on Au (thus compromising SAM purity and uniformity). As substrates, atomically flat template stripped gold (TSG) was employed and prepared according to the reported procedures.37,38 The Au films exhibited a root mean square (RMS) roughness of 0.3 nm, exposing preferably (111) oriented surfaces. The organic monolayers were prepared under nitrogen by immersing the freshly stripped TSG substrates into DTC solutions for ∼20 h at room temperature. After immersion, the films were copiously rinsed with ethanol, immediately blown dry with N2 and placed in glass containers, predominantly filled with nitrogen, for transport from the individual laboratories to the synchrotron radiation facilities (see below). No specific degradation was observed on the scale of several days (up to a week) but some minor sample to sample variations were recorded in some of the experiments. All vials and tweezers were cleaned with piranha acid and isopropyl alcohol before usage. In addition, reference SAMs of dodecanethiolate (DDT) and hexadecanethiolate (HDT) were prepared on analogous gold substrates using a standard procedure.39
2.2. SAM characterization
The fabricated SAMs were characterized by synchrotron-based X-ray photoelectron spectroscopy (XPS) and angle-resolved near-edge X-ray absorption fine structure (NEXAFS) spectroscopy. XPS serves as an efficient local probe for the potential distribution within a SAM, at the same time representing a reliable benchmark for theoretical simulations.20,21,40 NEXAFS spectroscopy represents a complementary technique, which not only shows high chemical sensitivity but also has the capability of providing information on molecular orientation in adsorbate assemblies and molecular films.41 Significantly, such information can be obtained not only for highly ordered systems, but also for samples, in which short- or medium-range order prevails. The latter is frequently the case for SAMs due to structural defects, polymorphism, and a limited size of crystalline domains. These are associated with possible imperfections of the self-assembly process and misfits between the optimal molecular lattice and the structural template provided by the substrate, as well as by the nucleation-type growth of SAMs (leading to domain boundaries).18The measurements were carried out at room temperature under UHV conditions (a base pressure of ∼1.5 × 10−9 mbar). The data acquisition time at a particular sample spot was kept short to minimize possible X-ray induced damage occurring during the measurements.42 Experiments were performed at the HE-SGM beamline of the synchrotron storage ring BESSY II (Helmholtz Zentrum Berlin, Germany) and at the D1011 beamline of the MAX IV synchrotron radiation facility (Lund, Sweden). Both are bending magnet beamlines, providing a moderate X-ray intensity, which is a prerequisite for avoiding X-ray induced damage of the comparably sensitive organic films.
XP spectra were acquired using either a Scienta R3000 electron energy analyzer (BESSY II) or a SCIENTA SES200 spectrometer (Max IV) having established performance and reliability.23,24,40,42 Spectra acquisition was carried out in normal emission geometry with an energy resolution of either ∼0.1 eV (Max IV) or ∼0.3 eV, ∼0.6 eV, and 0.7 eV (BESSY II) at excitation energies of 350 eV, 580 eV, and 720 eV, respectively. The binding energy (BE) scale of the XP spectra was referenced to the Au 4f7/2 peak of the underlying substrate at a BE of 84.0 eV, at each particular excitation energy.43 The obtained spectra were decomposed into individual component peaks and doublets using symmetric Voigt functions and a linear or Shirley-type background. The full width at half-maximum (fwhm) was kept the same for all individual components within each individual spectrum. To fit the S 2p3/2,1/2 doublets we used two peaks with the same fwhm, employing the standard43 spin-orbit splitting of ∼1.18 eV (verified by the fit), and a branching ratio of 2 (S 2p3/2/S 2p1/2). The accuracy of the resulting BE and fwhm values is 0.02–0.03 eV.
Based on the XPS data, the effective thickness and the packing density of the SAMs were calculated. The evaluation was performed using standard procedures,44,45 based on the C 1s/Au 4f and S 2p/Au 4f intensity ratios. A standard expression for the attenuation of the photoemission signal was assumed (see ESI† and ref. 46) and literature values for the attenuation lengths in densely packed organic films were used, including 11.3 Å for a kinetic energy (KE) of 290 eV (C 1s at a PE of 580 eV), 15.7 Å for a KE of 490 eV (Au 4f at a PE of 580 eV), 8.5 Å for a KE of 185 eV (S 2p at a PE of 350 eV), and 10.5 Å for a KE of 260 eV (Au 4f at a PE of 350 eV).47 The spectrometer-specific coefficients were determined using reference monolayers (dodecanethiolate and hexadecanethiolate SAMs on Au) of known thickness (14.9 Å and 18.9 Å, respectively) and packing density (4.63 × 1014 molecules per cm2 or 21.6 Å2 per molecule).39,48
The acquisition of the NEXAFS spectra was carried out at the carbon K-edge in the partial electron yield (PEY) mode with a retarding voltage of −150 V. Linearly polarized synchrotron light with a polarization factor of either ∼89% (Bessy II) or ∼95% (Max IV) was used as the primary X-ray source; the incidence angle was varied to monitor linear dichroism effects.41,49 The photon energy (PE) scale was referenced to the pronounced π* resonance of highly oriented pyrolytic graphite at 285.38 eV.50 Raw NEXAFS spectra were normalized to the incident photon flux determined from the spectrum of a clean, freshly sputtered gold sample. Afterwards, they were reduced to the standard form by subtracting a linear pre-edge background and by normalizing to the unity edge jump.
In addition to the spectroscopic characterization, the work function of the DTC-based SAMs was measured. The measurements were performed using a UHV Kelvin Probe 2001 system (KP technology Ltd, UK). The pressure in the vacuum chamber was ∼10−9 mbar. As a reference, we used a HDT SAM with the work function value set to 4.3 eV according to the literature.22 The latter value was additionally verified by its referencing to the work function of freshly sputtered gold set to 5.2 eV.33
Note that the work functions measured for the PPz and PPd SAMs displayed some sample to sample variation. Analysis of these data resulted in the values given in Section 3.3; they are considered to be representative of the PPz and PPd monolayers.
2.3. DFT simulations
Theoretical simulations were performed for the two most fundamental DTC structures, namely PPd and PPz, as these represent the basic motifs of the investigated class of compounds. A complication in this context is that neither the structure the molecules adopt on the surface, nor the surface unit cell (for the case of commensurate growth) are known. Considering, however, that for PPz essentially the same surface coverage is observed as for the reference SAMs (DDT and HDT; see below), it is reasonable to assume a structure with two molecules in a (√3 × 3)rect unit cell. For the sake of consistency, we chose the same surface unit cell also for the PPd SAM, although there the surface coverage is by ca. 10% lower. The latter could, however, also be caused by a coexistence of differently ordered regions as will be discussed below. The unit cells for the systems with more bulky substituents and even lower surface coverage (C12N-PPd, OMe-PPz, and FP-Pz) are virtually impossible to estimate in the absence of LEED and STM data and we, thus, refrain from modelling those SAMs. With the surface unit cell fixed, the next complication arises with regard to the choice of the relative arrangement of the two molecules within the unit cell, the positions of the S atoms, and the molecular conformations (planar vs. twisted). To tackle this issue, in an attempt to sample the most important regions of the extended potential energy surface, we calculated a significant number of different structures, as described in detail in the ESI.† The properties of the most relevant conformations are discussed below.For performing the simulations, we used the FHI-aims code,51 version 150706, employing the PBE functional52 in combination with the Tkatchenko–Scheffler dispersion correction53 in its parametrization for interfaces.54 van der Waals interactions between the substrate Au atoms were turned off. The systems were simulated using periodic boundary conditions and the repeated slab approach, inserting a vacuum region of at least 20 Å in the z direction and including a self-consistently calculated dipole correction55 between the slabs. The dimensions of the (√3 × 3)rect unit cell in the x and y directions were defined according to the calculated Au lattice constant (see ESI†). The substrate surface was described using five layers of Au; the three bottom layers were held fixed in all calculations. A converged Γ-centered 9 × 5 × 1 k-point grid was applied. Otherwise, the default “tight” settings of FHI-aims were used, which corresponds to the following settings for the basis functions: The C and N atoms were described using a “Tier 2” basis consisting of the minimal basis plus one set of basis functions up to an angular momentum of 3 (d-functions) and one set of basis functions up to an angular momentum of 5 (g-functions). The ‘Tier 2’ basis for H consists of two sets of basis functions up to p and d functions, respectively. The S atoms were described using the minimal basis plus the full “Tier 1”, consisting of one set of basis functions up to an angular momentum of 4 (f-functions), and the d- and g-functions from the “Tier 2” set. The Au atoms were described using a “Tier 1” basis, consisting of the minimal basis plus one set of basis functions up to an angular momentum of 6 (h-functions). The cutoff potential of all basis functions was set to 4 Å. Further details of the employed basis functions can be found in the ESI.†
The total energy convergence criterion for the self-consistency cycle was set to 10−6 eV and the optimizations were performed until the maximum residual force component per atom was below 0.01 eV Å−1.
To understand the impact of chemical vs. electrostatic shifts in the XP spectra, reduced coverage systems with nominal coverages of 1/16 and 1/36 were also considered. This dilutes dipoles to a degree that collective electrostatic effects essentially disappear.21 Reduced coverage systems were modeled by replicating the optimized full coverage unit cell. In the obtained supercell only one molecule was kept. The geometries of the reduced coverage systems were not separately optimized to prevent the molecule from lying flat on the surface, which would result in a completely changed electronic structure dominated by Pauli pushback effects.56 This would not serve the purpose of solely eliminating electrostatic shifts. To limit the computational cost, for the largest unit cells the metal substrate was modeled with only three Au layers, a reduced basis set, and less tight numerical settings. This was done after convergence tests to ensure that it had only a negligible impact on the obtained results (see ESI†).
The core-level binding energies were simulated within the initial state approach to avoid artefacts arising from a combination of periodic boundary conditions and explicit excitations in each unit cell.21 The latter would, for example, occur when performing calculations based on final state approaches57–64 in conjunction with upright standing SAMs, in which the excited electron is put into a state at the Fermi level (i.e., into the metal). Due to collective electrostatic effects,65 the resulting dipole in every unit cell would lead to a significant artificial shift of core level energies. The magnitude of that shift would scale with the distance of the considered atom in the SAM from the metal substrate. For obtaining the XP spectra, we followed the procedure described by Taucher et al.21 In short, the 1s core level energies for every C atom were taken from the atom projected density of states output files. The screening of the core hole by the metal substrate was included using an electrostatic image charge model66,67
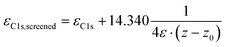 | (1) |
3. Results and discussion
3.1. Experiments: XPS
The S 2p, C 1s, and N 1s XP spectra of the DTC-based SAMs are presented in Fig. 2. The S 2p spectra of all films exhibit a single S 2p3/2,1/2 doublet at a BE position of 161.82–161.85 eV (S 2p3/2), as previously shown for dithiocarbamates in general27 and for the C12N-PPd, OMe-PPz, and FP-Pz monolayers in particular.33 Significantly, the BE of this doublet is lower by ∼0.15 eV than the characteristic value for thiolate species bound to noble metal surfaces (162.0 ± 0.05 eV),42 in agreement with earlier observations.27 This suggests a higher negative partial charge on the S atoms compared to the thiolate sulfur, indeed validated by basic considerations based on DTC resonance hybrid structures (a stronger donating character of the amine group coordinated to the CS2 unit). In this sense, the lower BE of the S 2p doublet as compared to thiolate does not necessarily mean that each of the sulfur atoms in the DTC moiety is bound stronger to the substrate than in the thiolate. This is, however, the case for the entire DTC moiety, as demonstrated by thermal stability experiments in which the desorption peak of n-butanethiol assembled on Au(111) was observed at a noticeably lower temperature (380 ± 10 K) than that of a test DTC compound (470 ± 10 K).27 Also, the occurrence of just a single doublet at a BE of ∼161.85 eV is significant, as it serves as direct evidence for the formation of SAMs with chemically homogeneous bonding to the substrate. This contrasts positively the situation encountered usually for thiol- and thioether-based ligands with multiple attachment points, where the formation of a variety of different chemical species such as thiolates, atomic sulfur, unbound sulfur, etc. is commonly observed (identified through core level shifts in their S 2p3/2 signal).71–74 The bonding of the DTC-based SAMs to the substrate in a “thiolate-like fashion” also provides a good chemical link. This is an advantage for efficient charge transport, which is important in the context of organic and molecular electronics applications.The spacing between both S atoms in the DTC group amounts to ∼3.06 Å (calculated employing the methodology described in Section 2.3 both for the isolated, H-saturated molecules and for the densely-packed SAMs). As this value does not fit the periodicity of the Au(111) template, multiple adsorption sites can be expected. This is indeed implied by the rather high value for the fwhm of the S 2p3/2,1/2 components for the DTC-based SAMs, viz. 0.73–0.93 eV compared to the dodecanthiolate monolayers measured under analogous conditions, viz. 0.54–0.59 eV.42 Consistently, also in the simulations assuming a very high degree of order with two molecules in the unit cell, inequivalent docking positions of the S atoms were found (see ESI†).
Interestingly, the fwhm value for the PPz SAMs (0.73 eV) is somewhat smaller than that for their derivatives, OMe-PPz, and FP-Pz (0.84 and 0.80 eV, respectively). This suggests an even larger heterogeneity of the adsorption sites (configurations) in the latter cases. The same applies to the PPd and C12N-PPd monolayers, although here the difference (0.89 eV vs. 0.93 eV) is somewhat smaller.
The C 1s spectra of the DTC-based SAMs in Fig. 2b and c can be decomposed into several component peaks denoted by numbers in the plot. The assignment of these peaks to specific functional groups and specific C atoms is based on electronegativity considerations,33 the comparison to spectra of systems containing similar building blocks, and the analysis of the spectra acquired at different photon energies. The latter is particularly useful considering the stronger contribution of the buried species at a higher excitation energy (580 eV vs. 350 eV). For the PPz and PPd SAMs these tentative peak assignments will be refined in Section 3.4 building on the atomistic insights provided by the DFT calculations.
The C 1s spectrum of the PPd SAM exhibits only one, nearly symmetric peak at ∼284.9 eV (1) originating from a superposition of core-level excitations of the terminal phenyl ring and the piperidine moiety. A signal associated with the DTC carbon, expected at a significantly higher BE (see Section 3.4), is not perceptible because of its strong attenuation. Similarly, the signal of the two C atoms in the bottom ring bonded to N, which should also appear at a higher BE, is not clearly resolved and is presumably hidden in the high BE tail of the main peak. The joint contribution of the phenyl ring and piperidine can also be identified upon decomposition of the asymmetric peak in the C 1s spectra of the C12N-PPd SAM into two component peaks. The low BE component peak at ∼284.7 eV (1) is then assigned to the same C atoms as the sole peak in PPd, while the high BE component at 285.4 eV (2) is ascribed to the terminal aliphatic chains. Such a comparably high value for the aliphatic chains is presumably related to electrostatic effects, since similar and even higher values were observed for the alkanethiolate SAMs with embedded dipolar groups.22 The intensity of this peak is comparably high since the signal from the phenyl ring and piperidine is more strongly attenuated. This is also the case for the signal stemming from the C atoms bound to the uppermost N atom.
The spectra of the PPz SAM exhibit two peaks at 285.5 eV (2) and 284.5 eV (1), according to the fits. They are assigned to the C atoms bonded to N atoms (all atoms in the piperazine ring and the lowest atom in the phenyl ring) (2) and to all other C atoms in the terminal phenyl ring (1), respectively. The origin of the splitting of the peaks in this system will become clear from the discussion in Section 3.4. The above two components can also be identified in the spectra of the OMe-PPz film, where they are accompanied by an additional peak at 286.5 eV (3), which originates from the carbon atom in the terminal OCH3 group. Finally, the piperazine component peak (2) is clearly resolved also in the spectra of the FP-Pz monolayer. The dominant component in these spectra is, however, the peak at 287.5 eV (4), which is related to the fluorine-bonded carbon atoms in the terminal ring. In addition, a low intensity component peak at 286.3 eV (5) can be identified upon spectral decomposition. This peak can be tentatively associated with the carbon atom of the upper ring, which is directly bonded to the piperazine, but is also somewhat affected by the F atoms in the vicinity. Finally, there is a low BE shoulder at 284.3 eV (6), which cannot be assigned to any functional group of FP-Pz and, most likely, stems from a contamination. This contamination stems most likely from a non-complete self-cleaning upon SAM formation, as can be expected for such a bulky molecule as FP-Pz.
The N 1s spectra of all DTC-based SAMs in Fig. 2d exhibit a single peak at ∼399.5 eV assigned to the nitrogen atoms in the piperazine and piperidine rings as well as to the nitrogen atom in the terminal dihexylamine group of the C12N-PPD film. The relative intensities of the N 1s peaks correlate coarsely with the amount of the nitrogen atoms and their locations within the molecular backbone (affecting the attenuation of the respective signal). The F 1s spectrum of the FP-Pz monolayer (not shown) acquired at a photon energy of 720 eV exhibits a single peak at ∼687.9 eV, assigned to the fluorine atoms in the terminal ring.
The quantitative evaluation of the XP spectra (see Section 2) yields the values for the effective thicknesses and packing densities of the DTC-based SAMs shown in Table 1. The effective thicknesses of the monolayers are close to the sum of the respective molecular lengths and the length of the S–Au bond, suggesting an upright molecular orientation. The packing densities of the parent PPd and PPz films are very close to the value characteristic of the densely packed (2√3 × √3)R30° structure typical of non-substituted alkanethiolate SAMs on Au(111), viz. 4.63 × 1014 mol cm−2.39,48 In view of the almost double density of the sulfur atoms in the DTC case, the similarity of the packing densities is a direct indication that the packing is mostly determined by the interaction between the molecular backbones rather than by the docking groups. This also implies that the docking groups in conventional thiolate SAMs, with only one S atom per molecular chain, are comparably loosely packed. An important implication of this finding is that the presence of atomic sulfur, which is frequently observed in thiolate SAMs as a minor contamination,42 does not necessarily indicate a poor or limited quality of the monolayers, since on the surface there is, apparently, enough space for the coexistence of thiolate anchors packed in the standard fashion and additional sulfur atoms, without resulting in serious interference.
| Monolayer | PPd | C12N-PPd | PPz | OMe-PPz | FP-Pz |
|---|---|---|---|---|---|
| Thickness (Å) | 9.9 | 13.3 | 10.8 | 11.9 | 13.1 |
| Packing density (molecules per cm2) | 4.25 × 1014 | 3.5 × 1014 | 4.65 × 1014 | 3.4 × 1014 | 2.75 × 1014 |
| Relative density | 0.92 | 0.76 | 1.0 | 0.74 | 0.59 |
The packing densities of the C12N-PPd and OMe-PPz SAMs are somewhat lower than those of the parent PPd and PPz monolayers (Table 1). For the FP-Pz monolayer a further reduction in the packing density is observed, which can be associated with the much larger van-der-Waals radii of the fluorine atoms compared to hydrogens and the resulting larger van-der-Waals dimension of the fluorinated phenyl.45,75 For the C12N-PPd and OMe-PPz SAMs, the lower packing densities are associated with the substituents, which, especially for C12N-PPd (two aliphatic chains per molecule), are comparably bulky. Moreover, the larger monolayer unit cells resulting from the more extended molecular backbones are presumably also no longer commensurate with the positions of the docking sites on the Au surface. This, together with the flexibility of some of the substituents, is expected to cause an increase of the disorder in the films. An additional factor for OMe-PPz SAMs could be interactions between the polar tail groups, disturbing the molecular packing and leading to a reduction of the packing density.76 A further fingerprint of the comparably lower quality of the C12N-PPd and OMe-PPz SAMs is the presence of an additional doublet in the S 2p spectra of these monolayers (Fig. 2a), appearing as a weak shoulder at the low BE side of the main feature. This doublet, at ∼161.0 eV (S 2p3/2), can be either ascribed to atomic sulfur or to a distinctly different (compared to the standard ones) bonding configuration of the S atom (see discussion in ref. 42 and 77). The atomic sulfur scenario is more realistic in our opinion.
3.2. Experiments: NEXAFS spectroscopy
The C K-edge NEXAFS spectra of the DTC-based SAMs acquired at an X-ray incident angle of 55° (magic angle) are presented in Fig. 3a; the differences between the spectra collected under normal (90°) and grazing (20°) incidence are shown in Fig. 3b. The 55° spectra are not affected by molecular orientation effects and are, thus, directly representative of the electronic structure of the studied films.41 In contrast, the difference spectra provide insight into the dependence of the magnitude of the absorption resonances on the incidence angle of the primary X-ray beam, termed as linear dichroism. This provides information on preferential molecular orientation.41The 55° spectra of the basic PPd and PPz SAMs are dominated by the characteristic absorption resonances of the terminal phenyl ring,41,78–80viz. the most intense π1* resonance at ∼285.1 eV (1), the respective π2* peak at 288.8–288.9 eV (3), a further π* resonance at 290.2 eV (4), and several σ* resonances (5–6) at higher excitation energies. In addition, there are the R*/C–S* resonances41,80 at ∼287.3 eV (2) and the comparably strong π* resonance at ∼286.5 eV (7) in the case of the PPz SAM, which stems presumably from the splitting of the π1* feature of the phenyl ring (1) due to the effect of the adjacent piperazine moiety.41 Such a splitting also affects the π2* resonance (3) in this spectrum,41 resulting in a stronger intensity of the 290.2 eV feature (4) compared to the PPd case. The absorption structure associated with the piperidine (in PPd) and piperazine (in PPz) moieties cannot be unequivocally identified, since the spectra of these species do not exhibit intense, discrete features in the pre-edge and at-edge regions (see ref. 81 and 82) and the related σ* resonances overlap with those of the phenyl ring.
The 55° spectra of the C12N-PPd and OMe-PPz SAMs exhibit a significant relative weakening of the π1* resonance (1), which is associated with the substitution. This effect is especially pronounced for the C12N-PPd film, the spectrum of which also shows an additional resonance at ∼287.7 eV (8) associated with the alkyl chains (most likely excitations into Rydberg states,83 but there are also alternative assignments). Additionally, there is a pattern of σ* resonances at higher photon energies. The latter resonances stem predominantly from the alkyl chains and are presumably the reason for the comparably low intensity of the π1* resonance, since the spectrum is normalized to the height of the absorption edge proportional to the entire number of the carbon atoms. Moreover, we expect a stronger contribution from the alkyl chains due to the more pronounced attenuation of the signal originating from the PPd moiety. The spectrum of the OMe-PPz SAM exhibits a π* resonance at 287.3 eV (9) stemming from the splitting of the π1* feature of the phenyl ring (1) due to its substitution,41 and an additional π* resonance at ∼288.6 eV (10), which most likely has π2* (3) character.
The 55° spectrum of the FP-Pz SAM is dominated by the absorption resonances of the fluorinated phenyl ring, with the most prominent characteristic features at ∼286.65 eV (11) and ∼287.8 eV (12) assigned to the C1s → π* transitions at the carbon atoms which are not bonded and directly bonded to fluorine atoms, respectively.78,84 Interestingly, the position of the former feature is distinctly higher than that for pentafluorobenzene (∼285.5 eV)78 and pentafluorobenzene terminated SAMs (285.7 eV).45 This is presumably related to the bonding of the respective carbon atom to the adjacent piperazine ring. There are also several additional less intense π*- and σ*-like resonances, for which the positions and assignments can be found in the literature.78,84
In addition to the magic angle spectra analyzed above, the linear dichroism effects in the DTC-based SAMs were monitored. The 90°–20° curves for all monolayers in Fig. 3b exhibit intense difference peaks at the positions of the absorption resonances. They reflect a pronounced linear dichroism suggesting high orientational order in the monolayers. In addition, the signs of the observed difference peaks, viz. positive signs for resonances with π*-character and negative signs for those with σ*-character indicate (in view of the orientation of the respective orbitals) an upright molecular orientation in all studied SAMs.
Along with these qualitative considerations, a quantitative analysis of the entire set of the NEXAFS data acquired at different X-ray incidence angles was performed to get information about molecular orientation in the DTC SAMs. The analysis was carried out within a standard theoretical framework,41 comparing the angular dependence of the intensities of selected absorption resonances, I, with the appropriate theoretical expression. The average angle describing the orientation of the respective molecular orbital in terms of its transition dipole moment (TDM) is used as a fitting parameter.45,80 For this analysis we chose either the most prominent resonance associated with the phenyl ring (1) or the most prominent π* resonance of the fluorinated phenyl ring (C1sC–F → π*; 12), using these moieties as markers for orientation determination. The average tilt angle, α, of the corresponding orbitals (with their “direction” defined perpendicular to the plane of the ring) relative to the surface normal can be derived from a standard expression for a vector-type orbital41
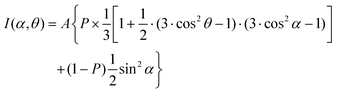 | (2) |
| cos(α) = sin(β)cos(γ) | (3) |
| Monolayer | PPd | C12N-PPd | PPz | OMe-PPz | FP-Pz |
|---|---|---|---|---|---|
| Tilt angle of the π* orbitals, α | 72.5° | 70° | 81.5° | 72° | 79° |
| Minimum molecular tilt angle, β′ | 17.5° | 20.0° | 8.5° | 18.0° | 11.0° |
Larger values of the twist angle will result in larger values of the molecular tilt angles for a given α. Regretfully, the twist angle cannot be determined experimentally, which is a general constraint of NEXAFS experiments on aromatic SAMs. Therefore, for the most basic PPd and PPz SAMs, we rely on theoretical simulations (Section 3.4), deriving β and γ from the optimized molecular structures, calculating the respective α, and comparing them with the experimental values (such an approach was recently implemented in ref. 24).
Interestingly, the inclination of the π-system expressed by α in PPz/Au is smaller than that in PPd/Au, in full agreement with the packing density values (Table 1). The substitution of the terminal phenyl rings in C12-PPd/Au and OMe-PPz/Au results in an increase of the inclination, which is a common behavior observed in different types of SAMs. Finally, the fluorination of the terminal phenyl ring in FP-Pz/Au does not result in a noticeable disturbance of the molecular inclination, which again appears to be a general trend for SAMs containing perfluorinated aromatic moieties.45,86
3.3. Experiments: work function
The work function values of Au surfaces modified with the PPz and PPd SAMs were determined to be 3.9 eV and 3.7 eV (±0.05), respectively; accordingly, compared to a work function of a reference Au substrate of 5.2 eV, the shifts amount to −1.3 eV and −1.5 eV. The work function values of the C12N-PPd, OMe-PPz, and FP-Pz SAMs are 3.2 eV, 3.5 eV, and 4.3 eV according to the literature.33 They show the expected trends when compared to the work function values of the parent PPz and PPd derivatives, viz. a decrease in the work function upon substitution with electron-donating groups (C12N and OMe) and an increase in the work function upon partial or complete substitution of the terminal moiety with electronegative fluorine atoms (FP-Pz).7,10,19,223.4. Quantum-mechanical simulations
| Arrangement | ΔEtot (eV) | α/° | BEC1s/eV | ΔΦ (eV) | |
|---|---|---|---|---|---|
| PPz | Herringbone, coplanar | 0 | 81.2 | 284.45 | −1.71 |
| Herringbone, twisted | 0.135** | 83.6 | 285.34 | −2.60 | |
| Cofacial, coplanar | 0.211 | 82.0 | 284.29 | −1.57 | |
| Cofacial, twisted | 0.340 | 89.1 | 285.12 | −2.38 | |
| PPd | Herringbone, coplanar | 0.083 | 81.2 | 285.26 | −2.54 |
| Herringbone, twisted | 0 | 81.5 | 285.30 | −2.58 | |
| Cofacial, coplanar | 0.275 | 73.0 | 285.03 | −2.29 | |
| Cofacial, twisted | 0.214 | 85.5 | 284.98 | −2.29 | |
The data in Table 3 reveal that in the SAMs there are different polymorphs that are reasonably close in energy. Interestingly, the lowest energy structures of the two molecules in the SAMs are fundamentally different, with a coplanar structure being most stable for PPz, while for PPd a twisted conformation represents the energetic minimum. This difference is attributed to the kink in the molecular backbone induced by the sp3 hybridized top C atom in the piperidine ring. This interpretation is supported by the finding that the relative energetic order of twisted/coplanar conformations obtained for the periodic SAMs on the surface is recovered also when calculating isolated molecules. Generally, in all cases two molecules per unit cell arranged in a herringbone pattern are more stable than a cofacial arrangement, consistent with what is known for oligophenylenethiol SAMs.87,88 Especially for SAMs containing aromatic entities this packing can be traced back to multipole interactions between the negative charge in the π-system and the partially positive hydrogen atoms, as explained in detail for biphenylthiolates in ref 89.
The average angle of the π* orbitals of the terminal rings relative to the substrate surface (the values of α from Section 3.2) has been obtained via cos2(α) = 0.5·(cos2(α1) + cos2(α2)) from the angles of the individual molecules, α1 and α2. This takes into consideration that the intensities associated with the absorption resonances are proportional to cos2(α) (see eqn (2); the sin2(α) component in that equation is comparably small). For the PPz SAM, we see a near perfect agreement between simulations (81.2°) and experiments (81.5°) when considering the lowest-energy structure. For the PPd system, the calculated value (81.5°) is larger than the experimental one (72.5°). This deviation is attributed to a non-negligible amount of disorder in the experimentally studied PPd film, which is consistent with the reduced coverage measured for the PPd SAM compared to the PPz monolayer (Table 1). Considering the twisted molecular backbone of PPd in the lowest-energy structure, a reduced film quality for that system appears indeed plausible.
An advantage of the simulations is that they provide direct access to the tilt and twist angles of the individual molecules, which are shown, for the lowest-energy conformations, in Table 4. These data suggest nearly upright-standing molecules in full agreement with the XPS data (see Section 3.1). Notably, the tilt angles calculated for PPd are smaller than the minimum tilt angles derived from the measurements (see Table 2), which can again be attributed to some disorder in the experimentally investigated PPd films.
| Tilt | Twist | |||
|---|---|---|---|---|
| β 1 | β 2 | γ 1 | γ 2 | |
| PPz | 7.4 | 13.7 | 37.6 | 36.1 |
| PPd | 14.2 | 12.6 | 58.0 | 41.1 |
As far as the shapes of the XP spectra are concerned, they agree very well between the simulations and experiments. This can be seen in Fig. 5, where it should be noted that the energy scale in the simulations has been shifted to higher BEs by 18.95 eV. This value has been chosen to make the calculated and experimental spectra of PPz/Au lie on top of each other and, for the sake of consistency, was then also chosen in the PPd case. Such a shift is necessary considering that within the initial state approach one approximates the ionization energies by the (Kohn–Sham) orbital energies of the core levels. In this way, one only obtains core-level shifts, which eventually need to be aligned relative to a reference system.90–93
 | ||
| Fig. 5 Comparison between experimental and suitably aligned (see below) simulated C 1s XP spectra. (a) Experimental (black) and simulated (red) C 1s spectra of PPz/Au(111); (b) calculated core level energies for each carbon atom in the PPz molecule in the respective SAM including screening by the metal; (c) experimental (black) and simulated (red) C 1s XP spectra of PPd/Au(111); and (d) calculated core level energies for each carbon atom in the PPd molecule in the respective SAM including screening by the metal. Please note that in panels b and d the energy values are given for only one of the two molecules in the full coverage unit cell. Since these two molecules are differently tilted, they are not symmetry equivalent and the calculated energy values vary slightly between them. Such differences are, however, very small, as shown in the ESI.† To ease the comparison between simulations and experiments, the energy scale for the simulated data has been shifted to higher BEs by 18.95 eV (aligning the measured and calculated spectra for PPz). | ||
For PPz/Au, the simulations fully reproduce the occurrence of a pronounced shoulder at higher binding energies (the feature denoted as “1” in the XP spectrum of PPz/Au in Fig. 2b). Conversely, for PPd/Au only a single dominant peak is observed in full agreement with the experiments. The atomically resolved core-level binding energies in Fig. 5b and d support the original peak assignment from Section 3.1; i.e. the low BE feature in PPz/Au is associated with the carbon atoms in positions 2–6 of the topmost phenyl ring, while the weaker, high BE feature originates from the carbon atoms directly bonded to the nitrogen atoms in the piperazine moiety. Conversely, for PPd/Au the core-level BEs of all C atoms in the rings are between 285.3 and 285.7 eV; as a consequence of this comparably small energetic spread and due to the absence of two energetically distinct groups of carbon atoms, we obtain only a somewhat broadened single peak that dominates the spectrum.
Beyond confirming and refining the peak assignment, the simulations provide additional insight that is not apparent in the experiments due to the finite energy resolution: (i) they reveal that in PPz/Au the core level energy of the topmost carbon in the phenyl ring is shifted by 0.2 eV compared to the neighboring carbons, an effect that is not observed in PPd/Au. (ii) The aliphatic carbons in PPd/Au have essentially the same BEs as the aromatic ones in the topmost ring. (iii) Finally, the BE associated with the carbon atom bonded to the two sulfurs is shifted to higher BEs by ∼1.0 eV (1.3 eV) in PPz/Au and by ∼0.7 eV (1.0 eV) in PPd/Au compared to the C atoms in the lower ring, disregarding (including) screening effects. Due to the finite escape depth of the photoelectrons, this is at best manifested as a high BE tail in the experimental spectra.
To understand the above-described peculiarities of the XP spectra, it is useful to keep in mind that core-level energies are determined by two factors: the local chemical environment of an atom and the local electrostatic energy.20,21,40,60,94 The latter can, for example, be changed through collective electrostatic effects via a periodic arrangement of polar groups common in SAMs21 or by the Madelung energy in ionic crystals.95,96 Conceptually, chemically and electrostatically induced shifts can be separated by reducing the density of the polar moieties in the adsorbate layer.21 This is straightforward, at least as long as reducing the dipole density does not modify atomic charges, e.g., by changing the charge transfer between the substrate and adsorbate. For atoms in a SAM that are at a sufficient distance from the docking groups, this means that core-level energies will depend on the coverage only, if there are dipole layers between them and the metal substrate.21 To analyze this, one needs to compare the core levels of densely packed films to those obtained from a calculation carried out at significantly reduced molecular coverage. In the latter case, the remaining molecules need to be fixed in the geometries they adopted in the dense SAM in order to avoid a superposition of effects arising from molecular rearrangements (see Section 2.3).
When applying this approach to the PPd and PPz SAMs, the spectra shown in Fig. 6 are obtained for full, 1/16 and 1/36 coverage. Their comparison reveals three crucial aspects: (i) the low-coverage spectra are significantly shifted with respect to the full coverage ones with the shifts of the 1/36 spectra slightly exceeding those of the 1/16 spectra; (ii) the shape of the spectra remains essentially unchanged; i.e., there is a rigid shift; and (iii) the shift for the PPd SAM (1.90 eV between full and 1/36 coverage, as measured from the positions of the maxima) clearly exceeds that for the PPz SAM (1.32 eV). As can be inferred from the description in the preceding paragraph, the first aspect suggests that significant dipoles are present in the system; the second indicates that the most significant dipoles are in the region of the immediate metal/SAM interface, i.e., closer to the metal than the carbon atoms most strongly contributing to the C 1s spectra; finally, the third aspect implies that this dipole is larger for PPd than for PPz. In addition, the comparably small shift between the 1/16 and 1/36 spectra for both PPd and PPz SAMs suggests a convergence of the calculations in terms of approaching the isolated-molecule limit. We note that the pronounced difference in the core level shifts observed for PPz and PPd in Fig. 6 cannot result from a different tilt angle of the DTC anchoring group. According to our calculations, the plane spanned by the S–S–N atoms (with N being the nitrogen atom that belongs to the DTC group) forms an angle of 6° and 5.8° relative to the surface normal for PPz and PPd, respectively, which is a very small difference and, thus, cannot significantly affect the interface dipole.
 | ||
| Fig. 6 Comparison between the simulated XP spectra of PPz (a) and PPd (b) on Au(111) obtained for full, 1/16 and 1/36 coverage. The legend is given in the panels. | ||
To consider the above trends in more detail, we analyze the atomistically resolved core-level energies shown in Fig. 7 for the PPd and PPz SAMs at full and 1/36 coverage. In this context we report the as calculated core-level energies; i.e., no rigid shift of the spectra is applied and no screening of the core hole by the metal substrate is considered. Otherwise, “artificial” shifts due to different dielectric constants of the adsorbate layer at different coverages (cf., eqn (1)) would obscure the more fundamental trends.
We start with a discussion of the PPz case (Fig. 7a): the horizontal arrows associated with the C atoms most strongly contributing to the XP spectrum have very similar lengths (average ΔEBE ≈ 1.15 eV, for numerical details see ESI†). This supports the conclusion drawn already from the rigid shift of the spectra that significant dipoles exist that are mostly found in the vicinity of the docking region.
Interestingly, ΔEBE is essentially the same also for the topmost C atom, which suggests a chemical origin for the different binding energy of that atom compared to the other phenyl carbons. As this difference is not observed in the PPd case (Fig. 7b), its origin must be the N atom bonded to the C in the 1-position of the phenyl ring in PPz. Its impact can be more straightforwardly investigated using aniline as a model system. Considering the possible resonance structures of aniline indeed allows rationalizing the chemical origin of the shift, as described in detail in the ESI.†
For the carbon atoms in positions 3 and 5 and in positions 2 and 6 of the piperazine ring, the shift is on average reduced to ∼1.05 eV and ∼0.72 eV, respectively, and it almost disappears (ΔEBE = 0.12 eV) for the carbon atom bonded to the two sulfurs (see Fig. 7a). The shift of the 1s energies of the lower nitrogen between full (378.80 eV) and 1/36 coverage (378.39 eV) amounts to 0.41 eV, which is intermediate between that for the two adjacent C atoms. This, together with the vanishingly small coverage-dependent shift of the S 2p core levels energies (calculated to be 0.045 eV on average), suggests that the dipoles causing the electrostatic shifts reside in the region around those atoms.
Here, it, however, has to be noted that an analysis of the coverage-dependence of the core-level shifts of atoms close to the substrate and in the immediate vicinity of the dipole is not straightforward. The reasons for that are two-fold: on the one hand, coverage dependent interfacial charge rearrangements resulting from the formation of the metal to SAM bond97 lead to coverage-dependent chemical shifts, which can easily mask the electrostatic ones. This aspect is discussed in detail in the ESI.† On the other hand, for reduced dipole densities the change in electrostatic energy close to the dipoles can no longer be approximated by a simple step.65 Consequently, at low coverages and close to the dipoles the magnitudes of electrostatic core-level shifts subtly depend on the exact positions of the respective atoms.
In passing we note that in an attempt to pinpoint the exact location of the dipole, we also tested various charge partitioning schemes, but (not really unexpectedly) observed significant variations between different SAM conformations and methodological approaches rendering these attempts inconclusive.
With regards to the coverage-dependent core-level energies of PPd/Au, qualitatively similar trends as in PPz/Au are observed (see Fig. 7b and ESI†), the main difference being that the overall coverage-dependent shift is larger even for the bottom ring, indicative of a larger dipole in the region of the docking group.
As a matter of curiosity, it should be mentioned that in the PPz SAMs changing the molecular conformation by rotating the phenyl ring such that it is nearly perpendicular to the piperazine unit (twisted configuration) massively increases the work function change. This can be traced back to a significant increase of the dipole moment of the molecule (for an isolated molecule it increases from 2.8 Debye for the planar configuration to 3.9 Debye for the twisted one). Even though in the experiments there is no indication of the occurrence of the twisted structure, this result shows that inducing a twist (e.g., by chemical substitutions) could be a viable strategy for boosting the molecular dipole moment of PPz derivatives and to maximize the achievable work-function modification. Note that for the PPd SAM, a change from the twisted to the planar configuration has a much weaker impact on the molecular dipoles and on the work function changes (see Table 3 and ESI†), which we attribute to the absence of heteroatoms in the vicinity of the rotated bond.
When comparing the calculated SAM-induced work function decrease of PPz and PPd, PPd yields a work function that is larger by 0.87 eV. This coincides with the shifts in the simulated core-level binding energies for C 1s states in the phenyl ring (see the last two columns of Table 3), a correlation that is expected based on the equivalent electrostatic origins of core-level shifts and work function changes (see above and ref. 21). In the experiments, however, a distinctly smaller difference in the work functions of PPz and PPd samples is observed, which is on the order of only 0.2 eV. This is even smaller than the measured 0.42 eV shift in the binding energy of the main features in the XP spectra related to the phenyl C 1s signal. The origin of this deviation between theory and experiment is not fully understood, and appears too large to be solely attributed to the lower coverage of the PPd SAMs as reported in Table 1. Here, we cannot fully exclude a certain parameter variation for the different samples employed for the different measurements within the project. Also, we cannot rule out an overestimation of the particularly large calculated dipole associated with the bonded DTC group for the PPd system.
4. Summary
In the present work we combined synchrotron-based XPS, NEXAFS spectroscopy, work function measurements and state-of-the-art DFT calculations to study the molecular organization and electrostatic properties of SAMs on Au(111) formed by dithiocarbamates with rod-like symmetry, taking several representative monolayers as test systems. As the piperazine/piperidine unit constitutes a common platform of these derivatives, particular emphasis is given to the investigation of the two parent compounds, PPd and PPz. They can be substituted with different functional terminal groups, thus allowing a wide range of molecular dipoles and offering a promising avenue for work function engineering at metal−organic interfaces. From our study, it emerges that the DTC anchoring group represents a useful building block for monomolecular self-assembly on coinage metal substrates. Its combination with the piperidine or piperazine moiety allows for a sufficient flexibility, enabling the self-assembly of more rigid terminal groups (such as the phenyl rings in the case of PPd, PPz, and FP-Pz). It also allows the substitution with additional groups such as secondary amines, alkoxy groups, cyano groups, and many more (e.g. for C12N-PPd and OMe-PPz). Importantly, both sulfur atoms in the DTC anchoring group bind to the substrate in a bidentate fashion, a very advantageous feature distinguishing the DTC moiety from other thiol-based dipodal and tripodal docking groups, which frequently show a heterogeneous chemistry for each individual sulfur atom (with coexisting thiolate, atomic sulfur, unbound sulfur, and disulfide configurations). Notwithstanding its bulkier bonding configuration, the DTC anchor, in combination with the piperidine or piperazine linkers, allows a dense molecular packing (see Table 1), with almost the same density as for monodentate docking groups such as thiolates in alkanethiolate and arylthiolate SAMs on Au(111). Such a dense molecular packing is characterized by small molecular inclinations, as evidenced both by NEXAFS experiments and theoretical simulations (see Tables 2 and 3). This inclination is only slightly altered upon substitution of the PPd and PPz backbones with dipolar tail groups, or by partial fluorination of these moieties, a very favorable property in view of interface-dipole engineering, e.g. for the efficient alignment of transport levels in organic semiconductors.As an overall trend, we find excellent agreement between the results from spectroscopic experiments and theoretical simulations in terms of molecular organization of PPd and PPz films. This not only refers to the molecular orientation but, for example, also to the heterogeneity of sulfur absorption sites in DTC anchoring groups. In addition, the XP spectra of the films could be reproduced by theory, in spite of a certain deviation between calculated and measured work function values. The most important conclusion with regards to the electrostatic properties of PPd and PPz SAMs concerns the location of the electrostatic dipole layer within these films, found to be in a region immediately adjacent to the metal/SAM interface. Interestingly, there is no significant potential step in the region of the additional nitrogen atom in PPz, at least as long as in PPz a coplanar molecular geometry prevails. The additional nitrogen atoms, however, induce a minor chemical shift affecting the carbon atoms in the terminal phenyl ring in the PPz SAM.
The most relevant difference found between the PPd and PPz platforms is a more upright orientation of the molecular backbone associated with a higher coverage for PPz, making especially this platform promising in view of further substitution of the terminal phenyl ring by polar groups, thereby providing access to a broad variety of interface dipoles.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank the Max IV facility and the Helmholtz-Zentrum Berlin (BESSY II) for the allocation of the beamtime, A. Nefedov and Ch. Wöll for technical cooperation at BESSY II, A. Preobrajenski for valuable technical assistance at Max IV, and BESSY II and Max IV staff for the technical support. We also thank Oliver T. Hofmann and Thomas C. Taucher for fruitful discussions regarding the computational part of this study. This work has been supported financially by the German Research Foundation (DFG; grant ZH 63/22-1) and by the Austrian Science Fund (FWF): I2081-N20. The computational results presented have been achieved using the Vienna Scientific Cluster (VSC).References
- I. H. Campbell, S. Rubin, T. A. Zawodzinski, J. D. Kress, R. L. Martin, D. L. Smith, N. N. Barashkov and J. P. Ferraris, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 14321–14324 CrossRef PubMed.
- B. de Boer, A. Hadipour, M. M. Mandoc, T. van Woudenbergh and P. W. M. Blom, Adv. Mater., 2005, 17, 621–625 CrossRef CAS.
- G. Heimel, L. Romaner, J. L. Brédas and E. Zojer, Phys. Rev. Lett., 2006, 96, 196806 CrossRef PubMed.
- B. H. Hamadani, D. A. Corley, J. W. Ciszek, J. M. Tour and D. Natelson, Nano Lett., 2006, 6, 1303–1306 CrossRef CAS PubMed.
- X. Cheng, Y.-Y. Noh, J. Wang, M. Tello, J. Frisch, R.-P. Blum, A. Vollmer, J. P. Rabe, N. Koch and H. Sirringhaus, Adv. Funct. Mater., 2009, 19, 2407–2415 CrossRef CAS.
- S. A. DiBenedetto, A. Facchetti, M. A. Ratner and T. J. Marks, Adv. Mater., 2009, 21, 1407–1433 CrossRef CAS.
- D. Boudinet, M. Benwadih, Y. Qi, S. Altazin, J.-M. Verilhac, M. Kroger, C. Serbutoviez, R. Gwoziecki, R. Coppard, G. Le Blevennec, A. Kahn and G. Horowitz, Org. Electron., 2010, 11, 227–237 CrossRef CAS.
- M. Halik and A. Hirsch, Adv. Mater., 2011, 23, 2689–2695 CrossRef CAS.
- J. M. Chiu and Y. Tai, ACS Appl. Mater. Interfaces, 2013, 5, 6946–6950 CrossRef CAS PubMed.
- I. Lange, S. Reiter, M. Pätzel, A. Zykov, A. Nefedov, J. Hildebrandt, S. Hecht, S. Kowarik, C. Wöll, G. Heimel and D. Neher, Adv. Funct. Mater., 2014, 24, 7014–7024 CrossRef CAS.
- C. K. Song, K. A. Luck, N. Zhou, L. Zeng, H. M. Heitzer, E. F. Manley, S. Goldman, L. X. Chen, M. A. Ratner, M. J. Bedzyk, R. P. H. Chang, M. C. Hersam and T. J. Marks, J. Am. Chem. Soc., 2014, 136, 17762–17773 CrossRef CAS PubMed.
- J. Kim, Y. S. Rim, Y. Liu, A. C. Serino, J. C. Thomas, H. Chen, Y. Yang and P. S. Weiss, Nano Lett., 2014, 14, 2946–2951 CrossRef CAS.
- F. Piersimoni, R. Schlesinger, J. Benduhn, D. Spoltore, S. Reiter, I. Lange, N. Koch, K. Vandewal and D. Neher, J. Phys. Chem. Lett., 2015, 6, 500–504 CrossRef CAS PubMed.
- H. Ju Lee, A. C. Jamison and T. R. Lee, Acc. Chem. Res., 2015, 48, 3007–3015 CrossRef PubMed.
- S. Casalini, C. A. Bortolotti, F. Leonardi and F. Biscarini, Chem. Soc. Rev., 2017, 46, 40–71 RSC.
- A. Petritz, M. Krammer, E. Sauter, M. Gärtner, G. Nascimbeni, B. Schrode, A. Fian, H. Gold, A. Cojocaru, E. Karner-Petritz, R. Resel, A. Terfort, E. Zojer, M. Zharnikov, K. Zojer and B. Stadlober, Adv. Funct. Mater., 2018, 28, 1804462 CrossRef.
- A. Ulman, Chem. Rev., 1996, 96, 1533–1554 CrossRef CAS PubMed.
- J. C. Love, L. A. Estroff, J. K. Kriebel, R. G. Nuzzo and G. M. Whitesides, Chem. Rev., 2005, 105, 1103–1169 CrossRef CAS.
- C. Schmidt, A. Witt and G. Witte, J. Phys. Chem. A, 2011, 115, 7234–7241 CrossRef CAS PubMed.
- T. Abu-Husein, S. Schuster, D. A. Egger, M. Kind, T. Santowski, A. Wiesner, R. Chiechi, E. Zojer, A. Terfort and M. Zharnikov, Adv. Funct. Mater., 2015, 25, 3943–3957 CrossRef CAS.
- T. C. Taucher, I. Hehn, O. T. Hofmann, M. Zharnikov and E. Zojer, J. Phys. Chem. C, 2016, 120, 3428–3437 CrossRef CAS.
- O. M. Cabarcos, S. Schuster, I. Hehn, P. P. Zhang, M. M. Maitani, N. Sullivan, J.-B. Giguère, J.-F. Morin, P. S. Weiss, E. Zojer, E. Zojer, M. Zharnikov and D. L. Allara, J. Phys. Chem. C, 2017, 121, 15815–15830 CrossRef CAS.
- E. Sauter, C.-O. Gilbert, J. Boismenu-Lavoie, J.-F. Morin and M. Zharnikov, J. Phys. Chem. C, 2017, 121, 23017–23024 CrossRef CAS.
- M. Gärtner, E. Sauter, G. Nascimbeni, A. Petritz, A. Wiesner, M. Kind, T. Abu-Husein, M. Bolte, B. Stadlober, E. Zojer, A. Terfort and M. Zharnikov, J. Phys. Chem. C, 2018, 122, 28757–28774 CrossRef.
- S. A. Paniagua, A. J. Giordano, O. N. L. Smith, S. Barlow, H. Li, N. R. Armstrong, J. E. Pemberton, J.-L. Brédas, D. Ginger and S. R. Marder, Chem. Rev., 2016, 116, 7117–7158 CrossRef CAS PubMed.
- K. M. Knesting, P. J. Hotchkiss, B. A. MacLeod, S. R. Marder and D. S. Ginger, Adv. Mater., 2012, 24, 642–646 CrossRef CAS PubMed.
- F. von Wrochem, D. Gao, F. Scholz, H. G. Nothofer, G. Nelles and J. M. Wessels, Nat. Nanotechnol., 2010, 5, 618–624 CrossRef CAS PubMed.
- J. M. Wessels, H. G. Nothofer, W. E. Ford, F. von Wrochem, F. Scholz, T. Vossmeyer, A. Schroedter, H. Weller and A. Yasuda, J. Am. Chem. Soc., 2004, 126, 3349–3356 CrossRef CAS PubMed.
- Y. Zhao, W. Pérez-Segarra, Q. Shi and A. Wei, J. Am. Chem. Soc., 2005, 127, 7328–7329 CrossRef CAS.
- D. Gao, F. Scholz, H.-G. Nothofer, W. E. Ford, U. Scherf, J. M. Wessels, A. Yasuda and F. von Wrochem, J. Am. Chem. Soc., 2011, 133, 5921–5930 CrossRef CAS.
- N. E. A. Reeler, K. A. Lerstrup, W. Somerville, J. Speder, S. V. Petersen, Bo W. Laursen, M. Arenz, X. Qiu, T. Vosch and K. Nørgaard, Sci. Rep., 2015, 5, 15273 CrossRef CAS PubMed.
- J. B. Simonsen, N. E. A. Reeler, A. Fossum, K. A. Lerstrup, Bo W. Laursen and K. Nørgaard, Nano Res., 2016, 9, 3093–3098 CrossRef CAS.
- W. E. Ford, D. Gao, N. Knorr, R. Wirtz, F. Scholz, Z. Karipidou, K. Ogasawara, S. Rosselli, V. Rodin, G. Nelles and F. von Wrochem, ACS Nano, 2014, 8, 9173–9180 CrossRef CAS PubMed.
- D. Meyer, T. Schäfer, P. Schulz, S. Jung, J. Rittich, D. Mokros, I. Segger, F. Maercks, C. Effertz, R. Mazzarello and M. Wuttig, Langmuir, 2016, 32, 8812–8817 CrossRef CAS PubMed.
- Y. Zhao, J. N. Newton, J. Liu and A. Wei, Langmuir, 2009, 25, 13833–13839 CrossRef CAS PubMed.
- W. E. Ford, D. Gao, F. Scholz, G. Nelles and F. von Wrochem, ACS Nano, 2013, 7, 1943–1951 CrossRef CAS PubMed.
- R. Naumann, S. M. Schiller, F. Giess, B. Grohe, K. B. Hartman, I. Karcher, I. Koper, J. Lubben, K. Vasilev and W. Knoll, Langmuir, 2003, 19, 5435–5443 CrossRef CAS.
- S. Nakamaru, F. Scholz, W. E. Ford, Y. Goto and F. von Wrochem, Adv. Mater., 2017, 29, 1605924 CrossRef PubMed.
- F. Chesneau, J. Zhao, C. Shen, M. Buck and M. Zharnikov, J. Phys. Chem. C, 2010, 114, 7112–7119 CrossRef CAS.
- I. Hehn, S. Schuster, T. Wächter, T. Abu-Husein, A. Terfort, M. Zharnikov and E. Zojer, J. Phys. Chem. Lett., 2016, 7, 2994–3000 CrossRef CAS PubMed.
- J. Stöhr, NEXAFS spectroscopy, Springer-Verlag, Berlin, 1992 Search PubMed.
- M. Zharnikov, J. Electron Spectr. Relat. Phenom., 2010, 178-179, 380–393 CrossRef CAS.
- J. F. Moulder, W. E. Stickle, P. E. Sobol and K. D. Bomben, Handbook of X-ray Photoelectron Spectroscopy, ed. J. Chastian, PerkinElmer Corp., Eden Prairie, MN, 1992 Search PubMed.
- J. Thome, M. Himmelhaus, M. Zharnikov and M. Grunze, Langmuir, 1998, 14, 7435–7449 CrossRef CAS.
- F. Chesneau, B. Schüpbach, K. Szelągowska-Kunstman, N. Ballav, P. Cyganik, A. Terfort and M. Zharnikov, Phys. Chem. Chem. Phys., 2010, 12, 12123–12127 RSC.
- M. Ratner and D. Castner, in Surface Analysis – The principal techniques, ed. J. Vickerman, Wiley, Chichester, 1997 Search PubMed.
- C. L. A. Lamont and J. Wilkes, Langmuir, 1999, 15, 2037–2042 CrossRef CAS.
- F. Schreiber, Prog. Surf. Sci., 2000, 65, 151–256 CrossRef CAS.
- M. Zharnikov and M. Grunze, J. Phys.: Condens. Matter., 2001, 13, 11333–11365 CrossRef CAS.
- P. E. Batson, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 2608–2610 CrossRef CAS PubMed.
- V. Blum, R. Gehrke, F. Hanke, P. Havu, V. Havu, X. Ren, K. Reuter and M. Scheffler, Comput. Phys. Commun., 2009, 180, 2175–2196 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed ; Erratum: Phys. Rev. Lett., 1997, 78, 1396.
- A. Tkatchenko and M. Scheffler, Phys. Rev. Lett., 2009, 102, 073005 CrossRef PubMed.
- V. G. Ruiz, W. Liu, E. Zojer, M. Scheffler and A. Tkatchenko, Phys. Rev. Lett., 2012, 108, 146103 CrossRef PubMed.
- C. Freysoldt, P. Eggert, P. Rinke, A. Schindlmayr and M. Scheffler, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 214517 CrossRef.
- E. Verwüster, O. T. Hofmann, D. A. Egger and E. Zojer, J. Phys. Chem. C, 2015, 119, 7817–7825 CrossRef.
- E. Pehlke and M. Scheffler, Phys. Rev. Lett., 1993, 71, 2338–2341 CrossRef CAS PubMed.
- S. Lizzit, S. Baraldi, A. Groso, K. Reuter, M. V. Ganduglia-Pirovano, C. Stampfl, M. Scheffler, M. Stichler, C. Keller, W. Wurth and D. Menzel, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 205419 CrossRef.
- W. Olovsson, C. Göransson, T. Marten and I. A. Abrokosov, Phys. Status Solidi B, 2006, 243, 2447–2464 CrossRef CAS.
- J. L. Cabellos, D. J. Mowbray, E. Goiri, A. El-Sayed, L. Floreano, D. G. de Oteyza, C. Rogero, J. E. Ortega and A. Rubio, J. Phys. Chem. C, 2012, 116, 17991–18001 CrossRef CAS.
- S. García-Gil, A. García and P. Ordejón, Eur. Phys. J. B, 2012, 85, 239 CrossRef.
- E. J. Baerends, O. V. Gritsenko and R. van Meer, Phys. Chem. Chem. Phys., 2013, 16, 16408–16425 RSC.
- N. Pueyo Bellafont, F. Illas and P. S. Bagus, Phys. Chem. Chem. Phys., 2015, 17, 4015–4019 RSC.
- N. Pueyo Bellafont, P. S. Bagus and F. Illas, J. Chem. Phys., 2015, 142, 214102 CrossRef PubMed.
- G. Heimel, F. Rissner and E. Zojer, Adv. Mater., 2010, 22, 2494–2513 CrossRef CAS PubMed.
- J. D. Jackson, Classical electrodynamics, Wiley, New York, 3rd edn, 1999 Search PubMed.
- J. Neaton, M. Hybertsen and S. Louie, Phys. Rev. Lett., 2006, 97, 216405 CrossRef CAS PubMed.
- Y. Li, D. Lu and G. Galli, J. Chem. Theory Comput., 2009, 5, 881–886 CrossRef CAS PubMed.
- D. A. Egger, Z.-F. Liu, J. B. Neaton and L. Kronik, Nano Lett., 2015, 15, 2448–2455 CrossRef CAS PubMed.
- O. M. Cabarcos, A. Shaporenko, T. Weidner, S. Uppili, L. S. Dake, M. Zharnikov and D. L. Allara, J. Phys. Chem. C, 2008, 112, 10842–10854 CrossRef CAS.
- J.-S. Park, A. N. Vo, D. Barriet, Y. S. Shon and T. R. Lee, Langmuir, 2005, 21, 2902–2911 CrossRef CAS PubMed.
- T. Weidner, N. Ballav, U. Siemeling, D. Troegel, T. Walter, R. Tacke, D. G. Castner and M. Zharnikov, J. Phys. Chem. C, 2009, 113, 19609–19617 CrossRef CAS.
- F. Sander, T. Peterle, N. Ballav, F. von Wrochem, M. Zharnikov and M. Mayor, J. Phys. Chem. C, 2010, 114, 4118–4125 CrossRef CAS.
- M. Lindner, M. Valášek, J. Homberg, K. Edelmann, L. Gerhard, W. Wulfhekel, O. Fuhr, T. Wächter, M. Zharnikov, V. Kolivoška, L. Pospisil, G. Meszaros, M. Hromadova and M. Mayor, Chem. – Eur. J., 2016, 22, 13218–13235 CrossRef CAS PubMed.
- W. E. Ford, F. Abraham, F. Scholz, G. Nelles, G. Sandford and F. von Wrochem, J. Phys. Chem. C, 2017, 121, 1690–1703 CrossRef CAS.
- S. Frey, A. Shaporenko, M. Zharnikov, P. Harder and D. L. Allara, J. Phys. Chem. B, 2003, 107, 7716–7725 CrossRef CAS.
- A. Shaporenko, A. Terfort, M. Grunze and M. Zharnikov, J. Electron Spectrosc. Relat. Phenom., 2006, 151, 45–51 CrossRef CAS.
- A. P. Hitchcock, P. Fisher, A. Gedanken and M. B. Robin, J. Phys. Chem., 1987, 91, 531–540 CrossRef CAS.
- T. Yokoyama, K. Seki, I. Morisada, K. Edamatsu and T. Ohta, Phys. Scr., 1990, 41, 189–192 CrossRef CAS.
- S. Frey, V. Stadler, K. Heister, W. Eck, M. Zharnikov, M. Grunze, B. Zeysing and A. Terfort, Langmuir, 2001, 17, 2408–2415 CrossRef CAS.
- O. Plashkevych, A. Snis, L. Yang, H. Ågren and S. F. Matar, Phys. Scr., 2001, 63, 70–86 CrossRef CAS.
- Y. Zubavichus, M. Zharnikov, A. Shaporenko and M. Grunze, J. Electron Spectrosc. Relat. Phenom., 2004, 134, 25–33 CrossRef CAS.
- P. S. Bagus, K. Weiss, A. Schertel, Ch. Wöll, W. Braun, H. Hellwig and C. Jung, Chem. Phys. Lett., 1996, 248, 129 CrossRef CAS.
- O. Plashkevych, L. Yang, O. Vahtras, H. Agren and L. G. M. Pettersson, Chem. Phys., 1997, 222, 125–137 CrossRef CAS.
- N. Ballav, B. Schüpbach, O. Dethloff, P. Feulner, A. Terfort and M. Zharnikov, J. Am. Chem. Soc., 2007, 129, 15416–15417 CrossRef CAS PubMed.
- Z. Zhang, T. Wächter, M. Kind, S. Schuster, J. W. Bats, A. Nefedov, M. Zharnikov and A. Terfort, ACS Appl. Mater. Interfaces, 2016, 8, 7308–7319 CrossRef CAS PubMed.
- W. Azzam, C. Fuxen, A. Birkner, H.-T. Rong, M. Buck and C. Wöll, Langmuir, 2003, 19, 4958–4968 CrossRef CAS.
- A. Bashir, E. Sauter, M. Rohwerder, M. Zharnikov and W. Azzam, ChemPhysChem, 2017, 18, 702–714 CrossRef CAS PubMed.
- E. Verwüster, E. Wruss, E. Zojer and O. T. Hofmann, J. Chem. Phys., 2017, 147, 024706 CrossRef PubMed.
- J. Vackář, M. Hyt’ha and A. Šimůnek, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 12712–12720 CrossRef.
- Y. Morikawa, T. Hayashi, C. C. Liew and H. Nozoye, Surf. Sci., 2002, 507, 46–50 CrossRef.
- G. Heimel, L. Romaner, J.-L. Brédas and E. Zojer, Surf. Sci., 2006, 600, 4548–4562 CrossRef CAS.
- M. Giesbers, A. T. M. Marcelis and H. Zuilhof, Langmuir, 2013, 29, 4782–4788 CrossRef CAS PubMed.
- A. El-Sayed, P. Borghetti, E. Goiri, C. Rogero, L. Floreano, G. Lovat, D. J. Mowbray, J. L. Cabellos, Y. Wakayama, A. Rubio, J. E. Ortega and D. G. de Oteyza, ACS Nano, 2013, 7, 6914–6920 CrossRef CAS PubMed.
- P. S. Bagus, G. Pacchioni, C. Sousa, T. Minerva and F. Parmigiani, Chem. Phys. Lett., 1992, 196, 641–646 CrossRef CAS.
- P. S. Bagus, E. S. Ilton and C. J. Nelin, Surf. Sci. Rep., 2013, 68, 273–304 CrossRef CAS.
- G. Heimel, L. Romaner, J.-L. Brédas and E. Zojer, Surf. Sci., 2006, 600, 4548–4562 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9cp03306h |
| ‡ E. S. and G. N. contributed equally to the present paper. |
| This journal is © the Owner Societies 2019 |