Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Mapping a single-molecule folding process onto a topological space†
Maziar
Heidari
ab,
Vahid
Satarifard
ac and
Alireza
Mashaghi
 *a
*a
aLeiden Academic Centre for Drug Research, Faculty of Mathematics and Natural Sciences, Leiden University, Leiden, The Netherlands. E-mail: a.mashaghi.tabari@lacdr.leidenuniv.nl
bMax Planck Institute for Polymer Research, Mainz, Germany
cMax Planck Institute of Colloids and Interfaces, Potsdam, Germany
First published on 22nd August 2019
Abstract
Physics of protein folding has been dominated by conceptual frameworks including the nucleation–propagation mechanism and the diffusion–collision model, and none address the topological properties of a chain during a folding process. Single-molecule interrogation of folded biomolecules has enabled real-time monitoring of folding processes at an unprecedented resolution. Despite these advances, the topology landscape has not been fully mapped for any chain. Using a novel circuit topology approach, we map the topology landscape of a model polymeric chain. Inspired by single-molecule mechanical interrogation studies, we restrained the ends of a chain and followed fold nucleation dynamics. We find that, before the nucleation, transient local entropic loops dominate. Although the nucleation length of globules is dependent on the cohesive interaction, the ultimate topological states of the collapsed polymer are largely independent of the interaction but depend on the speed of the folding process. After the nucleation, transient topological rearrangements are observed that converge to a steady-state, where the fold grows in a self-similar manner.
I. Introduction
The topology of a folded polymer chain is one of its key, yet less understood properties. For example, the physics of protein folding has been dominated by several theoretical frameworks including the nucleation–propagation mechanism and the diffusion–collision model, and none address the topological properties of a chain during a folding process.1–5 Even a solid definition of the topology of a folded linear chain was lacking until recently, and most studies have been focused on knot formation.6 Circuit topology has been recently proposed that formalizes the arrangement of intra-chain molecular contacts and allows for topology characterization of unknot folded chains, such as the majority of identified proteins (>97% do not form knots).7–15 How the molecules explore the topology landscape during folding and how the trajectory to the final topology is affected by external constraints are intriguing open questions. There are ubiquitous examples in nature and technology that macromolecules undergo drastic conformational changes under constraints,16 including the translocation process of (bio)polymers through nanopores,17–21 folding–unfolding transitions of globular proteins in shear flow22–24 and constraining the chain ends by molecular chaperones and ribosomes.25–27 In such processes, depending on the speed of the folding process, which can be considered as a measure of deviation from the equilibrium or quasi-equilibrium state, and geometrical constraints, the molecule undergoes different intermediate states before folding into its final state.There have been a number of numerical and analytical studies on stretching globular homopolymers under a controlled constant force or a constant unwinding velocity.28–33 However, they all lack information on how the internal organization and structure of the polymer changes during folding to the final compact globular state. Here, we provide the first circuit topological mapping of a folding process and search for the determinants of fold topology during the folding process and of the final “native” structure. We ask whether and how constraints on the end of the molecules and cohesive interactions affect the fold topology. While the latter is important for understanding biomolecular folding, the former is also technically important as single-molecule pulling tools are emerging as key technologies for resolving folding processes (formation and disruption of contacts).34–36 These techniques work by applying constraints on the polymer ends which raises a critical question whether the constraint itself affects the folding process.
II. Model
We used molecular dynamics (MD) to simulate a restrained linear polymer chain. The chain has N = 1000 monomers whose interactions are modeled by a coarse-grained potential (U). The potential consists of non-bonded and bonded interactions and a constraining potential: U = ULJ + UFENE + UC. The pairwise potentials between the monomers are described by the Lennard-Jones (LJ) potential,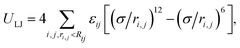 | (1) |
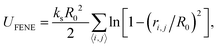 | (2) |
 . The simulations are carried out by the LAMMPS program in the canonical ensemble (NVT) using a Langevin thermostat.39,40 In all simulations, we set the parameters εrep = kBT, ks = 30kBT and R0 = 1.5σ. The strength of the cohesive interaction varies within the range ε = 1.0–2.0kBT over which the quality of the solvent is poor, and the chain is in the collapsed state (see Fig. S1 in the ESI†). The time step and the damping parameter for the Langevin thermostat are chosen, respectively to be Δt = 0.01τ and λ = 10τ−1. Both ends of the chain are constrained in each direction independently by harmonic potentials with spring constant kc = 100kBT/σ2:
. The simulations are carried out by the LAMMPS program in the canonical ensemble (NVT) using a Langevin thermostat.39,40 In all simulations, we set the parameters εrep = kBT, ks = 30kBT and R0 = 1.5σ. The strength of the cohesive interaction varies within the range ε = 1.0–2.0kBT over which the quality of the solvent is poor, and the chain is in the collapsed state (see Fig. S1 in the ESI†). The time step and the damping parameter for the Langevin thermostat are chosen, respectively to be Δt = 0.01τ and λ = 10τ−1. Both ends of the chain are constrained in each direction independently by harmonic potentials with spring constant kc = 100kBT/σ2: | (3) |
The equilibrium positions of the first and last monomer are given by x10 = [−0.5L, 0, 0]T and xN0 = [xN0(t), 0, 0]T, respectively. The chain is initially equilibrated in the fully stretched (or coil) configuration for 104τ with xN0(t) = 0.496L. This corresponds to the initial distance between the two ends as xN0 − x10 = 0.996L (see Fig. 1 right panel or Fig. S2 in the ESI†). Then the position of the last monomer decreases by folding velocity vf, i.e. xN0(t) = 0.496L − vft. The folding process continues until the end-to-end distance reaches lee = 0.025L. At this point, it is ensured that the size of the formed globule is smaller than the end-to-end distance (see Fig. 1 right panel). Since the chain does not have bending elasticity, the persistence length is one monomer size, i.e. lp = σ. For all cases, the averages and the error bars are calculated over 10 independent simulation runs. The initial equilibration process with different random seeds ensures that the initial conditions of the folding processes of all trajectories are independent.
 | ||
| Fig. 1 (left panel) Folding process of a chain whose initial condition is in coil configuration (FCC) is shown with three successive snapshots generated by VMD.37 (middle panel) The folding pathway of the FCC and RC in a topological space (SPX) is shown. (right panel) Nucleation and folding sequence of a restrained chain (RC) is illustrated at different end-to-end lengths (lee) when the folding speed is vf = 1 × 10−3σ/τ. The chains start to nucleate at lee = 0.726L and the region in proximity to the nucleating globule is marked by a dashed circle. The cohesive strength between the monomers is ε = 2.0kBT in both the FCC and RC. | ||
We define contact between two non-bonded monomers if their relative distance is <1.5σ. We analyzed the topology of the chains during the folding processes by categorizing the intra-chain contact arrangements as defined previously. In this so-called circuit topology approach, the pair-wise arrangement of contacts from a partially or fully folded polymer chain is categorized into different arrangement types namely, series (S), parallel (P) and crossing (X). As it is shown in Fig. 2, such an arrangement is analogous to the arrangement of elements in an electrical circuit. The topological fraction of each category is calculated by the number of loop pairs in that category divided by the total number of loop pairs.
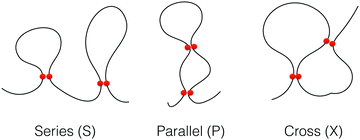 | ||
| Fig. 2 Illustration of loops in three different topological states, series (S), parallel (P) and cross (X). The contacts are displayed by two red circles. | ||
III. Results
We first examine the chains with no restraints. Depending on the initial conditions, the free chain is either fully stretched (FSC) or coiled (FCC). The former is simply a linear alignment of monomers spaced at the equilibrium bond length while the initial configuration of the latter is sampled from the thermalized (kBT) conformations of the chain in a good solvent (i.e. the cohesive strength and the cut-off radius of the LJ potential between non-neighboring monomers are ε = 1.0kBT and Rij = 21/6σ, respectively). The folding velocity of the FSC is approximated by the linear velocity at which the two ends of a fully stretched chain approach each other and depending on ε; it lies within the range of vf = 0.3 − 0.7σ/τ (see Fig. S3 in the ESI†). During the folding sequence of the FSC, since the local mobility and deformation of the free chain's ends are more pronounced for the excited vibrational modes, two globules are formed at both ends of the chain, and they grow until they meet to form a massive globule (see Fig. S2 in the ESI†). However for the FCC, several nuclei form along the free chain, consequently, leading to a hierarchy of globules and ultimately formation of a massive globule (see Fig. 1 left panel or Fig. S2 in the ESI†). Since each globule forms a domain with high local density of contacts, the final globule exhibits a self-similar structure also known as the fractal globule.41,42 However, when the restrained chain (RC) is folded with velocity vf = 10−3σ/τ, the slowest velocity under examination which is two orders of magnitude slower than the collapsing velocity of the FSC, a single globule is nucleated and while two ends are closing, the nucleus grows into a larger globule. Thus, due to the locality of the loops in the domains of the FCC or FSC, it is more probable to find two well-separated loops, each in different domains, having a serial topology compared with the internal structure of the RC (Fig. 3). This explanation is also valid for the other topological fractions, P and X, which are more likely for the RC structure as the loops are more intertwined. By increasing ε, more intermediate and local globules are nucleated along the FCC and the FSC, leading to enhancement of the collapsing velocity and subsequently, the rise in the fraction of the S-loop pairs. While in the case of RC, since the globule grows more slowly, the nucleation and growth processes continue slowly and hence, a much weaker increasing trend in the topological fraction of S-loop pairs is observed.It is worth mentioning that when the folding process occurs rapidly the monomers do not have enough time to relax and they form local separate compartments within the globule (Fig. 1 left panel) whereas such compartments disappear in a slow folding process as the monomers can diffuse within the globule and relax the structure (Fig. 1 right panel).
The effect of the out-of-equilibrium collapsing process on the internal structures is investigated by comparing the circuit topology of the resulting folded chains at different collapsing speeds. As shown in Fig. 4 for two cohesive strengths ε = 1.0, 2.0kBT, when the collapsing speed increases to vf = 10−2σ/τ, the topological fractions of the RC internal loops approach those of the FSC (solid and dashed lines). As displayed in Fig. 4d, the number of contacts within the globules having a larger cohesive strength, ε = 2.0kBT, is higher than when ε = 1.0kBT. This is expected since in the collapsed globule with ε = 2.0kBT, the attractive forces are larger, and it is more probable to find two monomers within the contact region (1.5σ). Furthermore, the number of contacts of the RC is approximately equal to that of the FSC and does not change by varying the folding velocities. This implies the necessity of the topological arrangement as a piece of extra information to distinguish between different globular structures having the same number of contacts.
 | ||
| Fig. 4 Topology fractions of series (a), parallel (b) and cross (c) loops of the restrained globules against folding speeds vf. In each panel, the circles and squares correspond to cohesive strength ε = 1.0kBT and 2.0kBT, respectively and the solid and dashed black lines represent the topological fractions obtained from freely collapsed chains (see Fig. 2). The number of contacts in the globules is shown in panel (d). | ||
The evolution of the internal structures of the globules against the end-to-end distance lee is shown in Fig. 5 for slow (panel a) and high (panel b) folding speeds. In both folding speeds when the chain is in the elongated regime (lee/L > 0.8), transient (entropic) loops appear along the chain, thus occupying the serial topology. Due to the chain elongation, the transient loops do not collide leading to zero fractions of parallel and cross topology. At the nucleation length (lnuc), the chain starts to nucleate and form its primary collapsed structure. The topological states of the loops within the nuclei are different from the transient loops leading to sudden drops in the serial topological fraction and rises in the fractions of the parallel and cross topology. This event confirms that within the nucleus, the dominant topological classes of the loops are parallel and cross; this is similar to the the topological changes associated with the formation of secondary structures (i.e., alpha helices and beta-sheet) during protein folding processes. Then the nucleus grows into a larger globule as the chain's moving end approaches the other end. During the growth process, while the monomers are added into the globule with the rate of the folding velocity vf, the topological states of the globule are preserved. Additionally, as it is shown in Fig. 3 for the slow folding speed, within the statistical error bars, the topological fractions of the final structures of the collapsed chains converge to the same values. This is interesting because although for the chain having a larger cohesive strength, the onset of the nucleation is earlier, this does not affect the final topological states of the globules. The self-similar circuit of the loops and the corresponding sizes after the nucleation events are also shown in Fig. S5 of the ESI.†
 | ||
| Fig. 5 Topology fractions of the loops against end-to-end distance lee for different cohesive strengths (ε) and when the folding velocity is vf = 0.001σ/τ (a) and vf = 0.01σ/τ (b). | ||
To analyze the statistics of the loop size, we computed the probability of contacts Pc(s) as a function of monomer distance s (loop length) along the contour length of the chain (Fig. 6). A universal decay with scaling Pc ∼ s−1 is observed within the intermediate distance interval (approximately 10–100σ) for all globules, resembling the fractal-like structure.41 The contact probability distribution of the FCC and the FSC also follows the same decay (see Fig. 6 in the ESI†). It has been proven that for a network of interconnected chain, the configurational weight of the loops obeys power-law decay ∼s−α whose exponent α is universal and it is dependent on the topology of the loops, i.e. the number of emerging strands from the loop.43 Such a universal property has been used to study analytically the RNA translocation through nanopores44 and thermodynamics of RNA molecules close to folding transition.45
The size of the loops formed in each topological state can be quantified by calculating the contact orders. The contact order of two loops with topology of i is calculated by  , where Ni is the number of double loops, which are categorized in the topological state i, and ΔL1i and ΔL2i are the monomer separation of each loop and L is the chain contour length. The contact orders of each topological sets in the course of folding are shown in Fig. 7 when the cohesive strength is ε = 2kBT and folding speed is vf = 0.001, 0.01σ/τ. As has also been found for the compact structure of the chain under spherical confinement,13 there is a universal trend i.e., COs < COp < COx. The reason is that the loop pairs in S topology are locally formed along the chain and the contour distance between the loop pairs is not important in the contact order. However the loop pairs in P and X are the result of nonlocal contacts of the chain segment that subsequently leads to the formation of large loops. The non-equilibrium effect of folding speed is also reflected by the decrease in the size of loops of all topological states. This is the consequence of the compartmentization of monomers in the globule structure and the emergence of large local domains in which the loops are mainly formed by the contacts between the monomers having a small distance along the contour length (see Fig. 1).
, where Ni is the number of double loops, which are categorized in the topological state i, and ΔL1i and ΔL2i are the monomer separation of each loop and L is the chain contour length. The contact orders of each topological sets in the course of folding are shown in Fig. 7 when the cohesive strength is ε = 2kBT and folding speed is vf = 0.001, 0.01σ/τ. As has also been found for the compact structure of the chain under spherical confinement,13 there is a universal trend i.e., COs < COp < COx. The reason is that the loop pairs in S topology are locally formed along the chain and the contour distance between the loop pairs is not important in the contact order. However the loop pairs in P and X are the result of nonlocal contacts of the chain segment that subsequently leads to the formation of large loops. The non-equilibrium effect of folding speed is also reflected by the decrease in the size of loops of all topological states. This is the consequence of the compartmentization of monomers in the globule structure and the emergence of large local domains in which the loops are mainly formed by the contacts between the monomers having a small distance along the contour length (see Fig. 1).
To specify the nucleation length at which a stable globule is formed and then grows, we computed the number of contacts during the folding process for all trajectories. The average 〈nc〉 and variance 〈nc2〉 − 〈nc〉2 of ten trajectories are plotted in Fig. 8. For all cohesive strengths, in the extended regime (lee/L > 0.8) the transient entropic loops are formed along the chain, and since the looping probability is proportional to the length L − lee, there is an increasing trend as the ends of the chain are closing (Fig. 8a). Such an increasing trend is observed in all trajectories and thus the variance becomes negligible (Fig. 8b). When lee approaches the vicinity of the nucleation length lnuc, the chain starts to nucleate and subsequently, there is an abrupt rise in the number of contacts. The uncertainty of the nucleation length in each trajectory is captured by the large change in the contact number variance. After the nucleation lee > lnuc, as the nucleus starts to grow to a larger globule, the number of internal contacts increases linearly with 1 − lee/L while the variance of the contacts among the trajectories becomes negligible.
To determine the nucleation length, the contact variations are fitted with Gaussian curves (solid curves in Fig. 8b). The means and standard deviations which are considered as the error bars of the Gaussian fits are plotted in Fig. 9.
As is described in the following, we build a thermodynamic model involving the internal energy and entropy of the chain during the folding and then we try to investigate the nucleation events and explain the observed trend in Fig. 9. It is supposed that we have a freely rotating LJ chain of length L whose cohesive inter-monomer interaction is ε. The chain is initially stretched along the x-direction, and the two ends of the chain are fixed. Then, one of the chain's ends approaches the other end along the x-axis by a constant velocity vf. If the distance between both ends reaches lnuc, the chain starts to nucleate. For a very slow speed, the process can be considered as quasi-static and close to equilibrium and then we can write the equilibrium free energy difference  between the nucleated and nonnucleated states as follows:
between the nucleated and nonnucleated states as follows:
 | (4) |
| ΔE = −ε(γVNG + γSNG2/3). | (5) |
![[small gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c4.gif) V = 12.5 and
V = 12.5 and ![[small gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c4.gif) S = −27.0, for the rest of the study (see the rescaled internal energy ULJ/ε in the inset of Fig. 5).
S = −27.0, for the rest of the study (see the rescaled internal energy ULJ/ε in the inset of Fig. 5).
To calculate the entropy difference in the nucleation event (ΔS in eqn (4)), it is required to formulate the configuration entropy of the chain. In this respect, we neglect the chain cohesive interaction and assume it as a self-avoiding chain (SAC) instead, i.e. non-bonded monomers only interact through the repulsive part of the LJ potential (i.e. ε = kBT, the cut-off radius is set at Rij = 21/6σ and the potential is shifted by ε). Then we use Jarzynski's equality46,47 to relate the free energy difference between the chain's fully stretched state and the state at which the chain's end-to-end distance is lee to the work required to transit the chain between the two states. We use the same constraining harmonic potential as in eqn (3). The work required to contract the chain with a constant velocity vf is calculated by48
 | (6) |
| e−ΔF/kBT = 〈e−W/kBT〉. | (7) |
 | (8) |
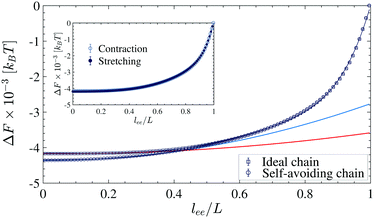
In the slow contraction speed, i.e., the quasi-static process, the chain remains close to the equilibrium state during the contraction process. In this case, one can neglect second and higher cumulants. Therefore, the equilibrium free energy is equal to the thermal average of work. Since in the SAC, the interaction of the monomers is short-ranged and repulsive, only the chain's configurational entropy contributes to the free energy, ΔF = −TΔS. The entropy of the fully stretched chain is zero because, in this state, the chain has only one configuration and we set it as the reference, i.e., F(lee) = −TS(lee). The free energy profile (FEP) of the SAC when vf = 10−3σ/τ is shown inFig. 11. Additionally, we calculate the FEP when the chain is being stretched. As shown in the inset, the FEPs in both directions of the contraction and stretching are approximately equal (there is maximum 20kBT deviation for the interval lee/L < 0.1 which is not under examination). This implies that under the velocity vf = 10−3σ/τ, the contracting/stretching process is quasi-static and reversible for lee/L > 0.1. It is worth mentioning that the contraction time scale τc = 1000τ is also comparable with the slowest relaxation time obtained from the Rouse model, τp = ζN2σ2/3π2kBT.49–51 In the Rouse model, the chain is assumed to be ideal and given the length of N = 1000 and the friction coefficient of the surrounding solvent ζ = 10−1 (this coefficient is obtained from the ratio of the monomer mass to the damping coefficient used in the Langevin thermostat, i.e. m/λ39), the slowest relaxation time becomes τp ≈ 3370τ. In addition to the SAC, we calculated the free energy of an ideal chain (IC). I.e. ULJ = 0 for non-bonded pairs. In the extended regime lee/L > 0.5, the excluded volume interaction is negligible. Thus FEPs of the IC and SAC follow similar trends. However, when the chain's ends approach closer lee/L ≲ 0.4, the self-avoiding interaction becomes more apparent, and FEPs deviate. We approximate the FEPs by the following polynomial functions:
 | (9) |
In the nucleation event, the entropy of the chain is given by  . After the nucleation event, we assume that the tails of the chain are stretched, i.e. NG = L − lee, and there is only the contribution of nucleus translational entropy along the chain
. After the nucleation event, we assume that the tails of the chain are stretched, i.e. NG = L − lee, and there is only the contribution of nucleus translational entropy along the chain  . Thus, we can rewrite the free energy difference (eqn (4)) as
. Thus, we can rewrite the free energy difference (eqn (4)) as
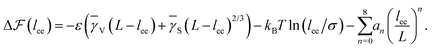 | (10) |
Fig. 12 shows the free energy change of the chain in the nucleation events against lee for different strengths of cohesive interaction. As it is expected from the classical nucleation theory, there is a free energy barrier in the extended regime due to the interplay between the internal energy of nuclei and the chain's configurational entropy change upon nucleation. The nucleation lengths are obtained by letting 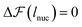 and plotted in Fig. 9. Similar to the simulation results, there is a monotonic increase in the nucleation length as ε increases. However, quantitatively, there is a mismatch which originated from the simplification and assumption we used to obtain the chain entropy and nucleation energy.
and plotted in Fig. 9. Similar to the simulation results, there is a monotonic increase in the nucleation length as ε increases. However, quantitatively, there is a mismatch which originated from the simplification and assumption we used to obtain the chain entropy and nucleation energy.
IV. Conclusion
Despite the simplicity of the approach, the topology analysis conducted here provides insights that might be relevant generically to folded linear (bio)polymers. We looked for the determinants of native state topology as well as the determinants of the fold topology during folding pathways. We find that the initial end-to-end distance of an unfolded chain has negligible effects on the native state topology. The final state topology is however affected by folding speed if the chain ends approach in a controlled manner as the chain folds. This is particularly noticeable when a chain with tight native contacts folds under low folding speeds. By fast reduction of the end-to-end distance, a native state topology, similar to that of a freely folding chain will be obtained. This is important as in single-molecule pulling experiments, and the independence of final topology on the folding pathway is often assumed.In our analysis, the strength of the interaction energies appears as the main determinant of the folding pathway in the space of fold topologies. Importantly, we find that the interaction strength determines the onset of nucleation events. Our observation has also been justified using a thermodynamic model which is built on the chain internal energy and entropy. The interaction energy affects the native state topology as well. We noticed that by increasing the interaction energies, the total number of contacts increases and the series arrangement is slightly promoted in the final folded state.
We note that our model ignores the complexity of linear chains found in nature including biological molecules (e.g., proteins and nucleic acids). We however believe that despite its simplicity, the model enables us to reveal a generic topological picture of a chain folding process. The coarse-grained polymer model we used in this work can represent a mean-field picture of a protein in which the monomers of the chain represent a group of residues with uniform interaction. The protein folding problem can be seen at different levels of coarse-graining; at each level, the onset of folding often refers to the emergence of a nucleus which is composed of either large unstructured loops or partially formed secondary structures.52 In the future, our study can readily be extended to include more complex models. Furthermore, our topological analysis was limited primarily to the frequency changes in basic topological arrangements i.e., X, P and S. Circuit topology matrices however include additional information which could be relevant.6 Finally, our predictions however are theoretical and thus call for experimental validation. The experimental validations of our findings will be considered in our future studies.
Conflicts of interest
There are no conflicts to declare.References
- S. Lifson and A. Roig, J. Chem. Phys., 1961, 34, 1963 CrossRef CAS.
- B. H. Zimm and J. Bragg, J. Chem. Phys., 1959, 31, 526 CrossRef CAS.
- R. Zwanzig, Proc. Natl. Acad. Sci. U. S. A., 1995, 92, 9801 CrossRef CAS PubMed.
- M. Karplus and D. L. Weaver, Nature, 1976, 260, 404 CrossRef CAS PubMed.
- M. Karplus and D. L. Weaver, Protein Sci., 1994, 3, 650 CrossRef CAS PubMed.
- A. Mashaghi, R. J. van Wijk and S. J. Tans, Structure, 2014, 22, 1227 CrossRef CAS PubMed.
- A. Mugler, S. J. Tans and A. Mashaghi, Phys. Chem. Chem. Phys., 2014, 16, 22537 RSC.
- A. Mashaghi and A. Ramezanpour, RSC Adv., 2015, 5, 51682 RSC.
- A. Mashaghi and A. Ramezanpour, Soft Matter, 2015, 11, 6576 RSC.
- S. K. Verovšek and A. Mashaghi, Frontiers in Applied Mathematics and Statistics, 2016, vol. 2, p. 6 Search PubMed.
- N. Nikoofard and A. Mashaghi, Nanoscale, 2016, 8, 4643 RSC.
- M. Heidari, V. Satarifard, S. J. Tans, M. R. Ejtehadi, S. Mashaghi and A. Mashaghi, Phys. Chem. Chem. Phys., 2017, 19, 18389 RSC.
- V. Satarifard, M. Heidari, S. Mashaghi, S. J. Tans, M. R. Ejtehadi and A. Mashaghi, Nanoscale, 2017, 9, 12170 RSC.
- M. Ghafari and A. Mashaghi, Phys. Chem. Chem. Phys., 2017, 19, 25168 RSC.
- N. Nikoofard and A. Mashaghi, J. Phys. Chem. B, 2018, 122, 9703 CrossRef CAS PubMed.
- B.-Y. Ha and Y. Jung, Soft Matter, 2015, 11, 2333 RSC.
- J. Chuang, Y. Kantor and M. Kardar, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2001, 65, 011802 CrossRef PubMed.
- R. Bundschuh and U. Gerland, Phys. Rev. Lett., 2005, 95, 208104 CrossRef PubMed.
- K. Luo, T. Ala-Nissila, S.-C. Ying and R. Metzler, EPL, 2010, 88, 68006 CrossRef.
- A. Mair, C. Tung, A. Cacciuto and I. Coluzza, J. Mol. Liq., 2018, 265, 603 CrossRef CAS.
- I. Coluzza, S. M. van der Vies and D. Frenkel, Biophys. J., 2006, 90, 3375 CrossRef CAS PubMed.
- A. Alexander-Katz, M. Schneider, S. Schneider, A. Wixforth and R. Netz, Phys. Rev. Lett., 2006, 97, 138101 CrossRef CAS PubMed.
- M. Heidari, M. Mehrbod, M. R. Ejtehadi and M. R. K. Mofrad, J. R. Soc., Interface, 2015, 12, 20150334 CrossRef PubMed.
- S. Schneider, S. Nuschele, A. Wixforth, C. Gorzelanny, A. Alexander-Katz, R. Netz and M. F. Schneider, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 7899 CrossRef CAS PubMed.
- S. Haldar, R. Tapia-Rojo, E. C. Eckels, J. Valle-Orero and J. M. Fernandez, Nat. Commun., 2017, 8, 668 CrossRef PubMed.
- A. Hoffmann, A. Becker, B. Zachmann-Brand, E. Deuerling, B. Bukau and G. Kramer, Mol. Cell, 2012, 48, 63 CrossRef CAS PubMed.
- F. Wruck, A. Katranidis, K. H. Nierhaus, G. Büldt and M. Hegner, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, E4399 CrossRef CAS PubMed.
- T. Frisch and A. Verga, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 65, 041801 CrossRef PubMed.
- F. Celestini, T. Frisch and X. Oyharcabal, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 70, 012801 CrossRef PubMed.
- A. Craig and E. Terentjev, J. Chem. Phys., 2005, 122, 194902 CrossRef CAS PubMed.
- S. Bell and E. M. Terentjev, J. Chem. Phys., 2015, 143, 184902 CrossRef PubMed.
- A. Alexander-Katz, H. Wada and R. R. Netz, Phys. Rev. Lett., 2009, 103, 028102 CrossRef PubMed.
- T. R. Einert, C. E. Sing, A. Alexander-Katz and R. R. Netz, Eur. Phys. J. E: Soft Matter Biol. Phys., 2011, 34, 130 CrossRef PubMed.
- A. Mashaghi, G. Kramer, P. Bechtluft, B. Zachmann-Brand, A. J. M. Driessen, B. Bukau and S. J. Tans, Nature, 2013, 500, 98 CrossRef CAS PubMed.
- A. Mashaghi, G. Kramer, D. C. Lamb, M. P. Mayer and S. J. Tans, Chem. Rev., 2014, 114, 660 CrossRef CAS PubMed , pMID: 24001118.
- A. Mashaghi, S. Bezrukavnikov, D. P. Minde, A. S. Wentink, R. Kityk, B. Zachmann-Brand, M. P. Mayer, G. Kramer, B. Bukau and S. J. Tans, Nature, 2016, 539, 448 CrossRef CAS PubMed.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33 CrossRef CAS PubMed.
- K. Kremer and G. S. Grest, J. Chem. Phys., 1990, 92, 5057 CrossRef CAS.
- B. Dünweg and W. Paul, Int. J. Mod. Phys. C, 1991, 02, 817 CrossRef.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1 CrossRef CAS.
- L. A. Mirny, Chromosome Res., 2011, 19, 37 CrossRef CAS PubMed.
- A. Y. Grosberg, S. K. Nechaev and E. I. Shakhnovich, J. Phys., 1988, 49, 2095 CrossRef CAS.
- B. Duplantier, Phys. Rev. Lett., 1986, 57, 941 CrossRef CAS PubMed.
- R. Bundschuh and U. Gerland, Phys. Rev. Lett., 2005, 95, 208104 CrossRef PubMed.
- T. R. Einert, P. Näger, H. Orland and R. R. Netz, Phys. Rev. Lett., 2008, 101, 048103 CrossRef PubMed.
- C. Jarzynski, Phys. Rev. Lett., 1997, 78, 2690 CrossRef CAS.
- C. Jarzynski, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1997, 56, 5018 CrossRef CAS.
- S. Park, K. Fatemeh, E. Tajkhorshid and K. Schulten, J. Chem. Phys., 2003, 119, 3559 CrossRef CAS.
- P. E. Rouse, J. Chem. Phys., 1953, 21, 1272, DOI:10.1063/1.1699180.
- M. Doi, Introduction to polymer physics, Oxford University Press, 1996 Search PubMed.
- P.-G. D. Gennes, Scaling concepts in polymer physics, Cornell University Press, 1979 Search PubMed.
- L. Mirny and E. Shakhnovich, Annu. Rev. Biophys. Biomol. Struct., 2001, 30, 361 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9cp03175h |
| This journal is © the Owner Societies 2019 |