Ab initio spectroscopy of water under electric fields†
Abstract
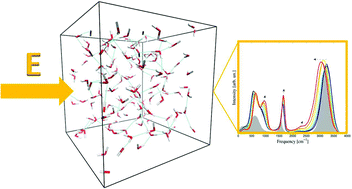
Whereas a broad range of literature exists on the spectroscopy of water in disparate conditions, infrared (IR) and Raman spectra of water subjected to electric fields have never extensively been investigated so far. Based on ab initio molecular dynamics simulations, here we present IR and Raman spectra of bulk liquid water under the effect of static electric fields. A contraction of the entire frequency range is recorded upon increasing the field intensity both in the IR and in the Raman spectra. Whilst the OH stretching band is progressively shifted toward lower frequencies – indicating a field-induced strengthening of the H-bond network – all the other bands are up-shifted by the field. Furthermore, an evident modification of the librational mode band appears in all the spectra. Finally, the order-maker action of the field emerges also from the increase of the water orientational tetrahedral order. Upon field exposure, the water structure becomes more “ice like”.
- This article is part of the themed collection: 2019 PCCP HOT Articles


 Please wait while we load your content...
Please wait while we load your content...